Michela Massimi and John Peacock
Cosmology has established itself as a successful scientific discipline in its own right, as we saw in the previous chapter. But contemporary cosmological research faces new pressing philosophical challenges. The current cosmological model, the so-called 'concordance model' or ACDM - which builds on Einstein's general-relativity (GR) and the so-called Friedmann-Lemaitre-Robertson-Walker (FLRW) models - maintains that we live in an infinite universe, with approximately 5 per cent ordinary matter (baryons), 25 per cent cold dark matter, and 70 per cent dark energy. According to this picture, the vast majority of our universe is populated by two exotic entities, called dark matter (DM) and dark energy (DE). While the search for experimental evidence for DM and DE is at the forefront of contemporary research in cosmology, from a philosophical point of view we should ask how scientists came to believe in the existence of these two new kinds of entities, and their reasons and justification for this view. What are DE and DM? How justified are we in believing in them?
The philosophical debate behind these central questions concerns the rationality of theory choice. What reasons do scientists have for choosing one scientific theory over a rival one? How do we go about making rational choices when there is more than one candidate that seems compatible with the same experimental evidence? The history of physics offers an embarrassment of riches in this respect (see Lahav and Massimi 2014). Consider, for example, the discovery of the planet Neptune back in 1846. The anomalous perihelion of the planet Uranus was known for some time, and two astronomers Urbain Le Verrier and John Couch Adams, independently of each other, tried to reconcile this observed conflict with Newtonian theory by postulating the existence of a new planet,1 called Neptune, whose orbit and mass interfered with and explained the anomalous orbit of Uranus. The new planet was indeed observed on 23 September 1846, the actual position having been independently predicted with a good degree of accuracy by both Adams and Le Verrier. A very similar phenomenon was also observed for the planet Mercury. Also in this case Le Verrier postulated the existence of a new planet, Vulcan, to explain the observed anomaly. But this time the predicted planet was not found, and a final explanation of the phenomenon came only with the advent of GR.
Or, to take another example, consider the negative evidence for ether drag in the Michelson-Morley experiment of 1887. The experiment used an interferometer, which was designed to record the velocity of two orthogonal beams of light at different angles to the direction of the Earth's motion through the presumed ether (via slight changes in their interference patterns). But no such changes in the interference patterns were ever observed. Rather than abandoning altogether the hypothesis of the ether, however, scientists tried to reconcile this piece of negative evidence with Newtonian mechanics (and the hypothesis of the ether) by assuming a contraction of length to occur in the interferometer arm (the so-called Lorentz-Fitzgerald contraction hypothesis). A final conclusive explanation of this piece of negative evidence came only in 1905 when the young Albert Einstein introduced the special theory of relativity, which overthrew the Newtonian assumption that the velocity of light is dependent on the frame of reference employed (the assumption that underpinned the very search for ether drag in the Michelson-Morley experiment).
These two historical examples illustrate a phenomenon that we have already encountered in Chapter 1, namely underdetermination of theory by evidence: in the presence of more than one possible scientific theory or hypothesis, the available experimental evidence may underdetermine the choice among them. In other words, experimental evidence per se may not be sufficient to determine the choice for one scientific theory or hypothesis over a rival one (e.g. that there is a new planet, as opposed to Newtonian mechanics being false). To understand underdetermination of theory by evidence, we need to bear in mind what we discussed in Chapter 1 about Pierre Duhem's observation (1906/1991) that a scientific hypothesis is never tested in isolation, but always with a collection of other main theoretical and auxiliary hypotheses. For example, to use again the case of Uranus, the anomalous perihelion was evidence that something was wrong with the set of hypotheses including both main theoretical assumptions about Newtonian mechanics and auxiliary hypotheses about the number of planets, their masses, sizes, and orbits. But the anomaly per se does not tell us which of these (main or auxiliary) hypotheses is the culprit for the anomaly. Thus, if an anomaly is found, the question naturally arises of whether we should reject or modify one of the main theoretical hypotheses (i.e. Newtonian mechanics and its laws), or tweak and add one auxiliary hypothesis (i.e. change the number of planets in the solar system). And, as the similar case of the anomalous perihelion of Mercury shows, finding the right answer to this kind of question may well be far from obvious. Duhem concluded that scientists typically follow their 'good sense' in making decisions in such situations.
Even if 'good sense might be the most fairly distributed thing among human beings (as Descartes used to say), Duhenr's answer to the problem of the rationality of theory choice is not satisfactory. For one thing, it is not clear what 'good sense' is, nor why scientists X's good sense should lead them to agree with scientists Y's good sense. Worse, it delegates the rationality of theory choice to whatever a scientific community might deem the 'most sensible' choice to make, even if that choice may well be the wrong one. Not surprisingly perhaps, Duhem's problem of underdetermination of theory by evidence was expanded upon, fifty years or so later, by the American philosopher W. V. O. Quine (1951), who showed the far-reaching implications of the view and concluded by appealing to what he called 'entrenchment'. In Quine's view, as we discussed in Chapter 1, our hypotheses form a web of beliefs that impinges on experience along the edges and where every single belief, including the most stable ones of logic and mathematics, are subject to the 'tribunal of experience', and can be revised at any point. What confers stability to some beliefs more than others, more peripheral ones in the web, is simply their 'entrenchment' within the web. One may wonder at this point why these observations about the nature of scientific theories, and how scientists go about choosing and revising them, should pose a problem for the rationality of theory choice. This is where the argument from underdetermination is typically employed to draw anti-realist conclusions about science. Let us then see the argument in more detail, and why it poses a problem.
The argument from underdetermmation to the threat to the rationality of theory choice proceeds from three premises (see Kukla 1996):
Therefore premise 1 must be false.
To appreciate the strength of the argument here, let us go back to our example about the observed anomalous perihelion of Mercury in the nineteenth century. Astronomers had sufficient data and measurements to be sure of the existence of this anomalous phenomenon. They also had very good reasons for (1) believing that Newtonian mechanics (T1) was the true or correct theory about planetary motions: after all, Newton's theory was the best available theory back then; it had proved very successful over the past century, and had also been further confirmed by the recent discovery of the planet Neptune. Astronomers also (2) took what Newtonian mechanics (T1) said about planetary motions at face value. For example, if the theory said that given the mass of Mercury and its orbit around the sun, we should expect to observe the perihelion of Mercury (the closest point to the sun during its orbit) to be subject to a slight rotation or precession, and this precession to be of the order of 5,557 seconds of arc per century, then given premise 2 astronomers took the 5,557 seconds of arc per century to be the case. Hence, the observed discrepancy of 43 seconds of arc per century from the predicted figure of 5,557 became the anomalous phenomenon in need of explanation.
But, to complicate things, suppose that in addition to Newtonian mechanics (T1) a new theory comes to the fore, Einstein's GR (T2), and these two theories prove empirically equivalent as far as the anomalous perihelion of Mercury (let us call it APM) is concerned. Being empirically equivalent here means that both T1 and T2 imply or entail the same empirical consequence, e.g. APM. In other words, we can deduce APM from either Newtonian mechanics (plus the auxiliary hypothesis of a new planet, Vulcan, having a certain mass and orbit which interferes with Mercury's) or from GR (i.e. the anomalous 43 seconds of Mercury follows from Einstein's field equations). Thus, it follows that if we take Newtonian mechanics and its predictions of 5,557 seconds for the precession of Mercury at face value, and there is another theory (GR) that can equally account for the same anomaly about Mercury's perihelion, we have no more overwhelming reasons for retaining Newtonian mechanics as the true theory than we have for taking GR as the true theory instead. This is the threat that the underdetermination argument poses to the rationality of theory choice.
We can now say 'Of course, that was the sign that Newtonian mechanics was false, after alF. But back in the nineteenth century when the anomaly was first discovered, and before scientific consensus gathered around Einstein's relativity theory in the early twentieth century, one might reasonably conclude that the rationality of theory choice was in fact underdetermined by evidence. Why should it have been 'rational' for astronomers at the beginning of the century to abandon Newtonian mechanics in favour of GR? Were not the reasons on both sides equally good, back then?
We can then appreciate the anti-realist conclusions that seem to follow from the underdetermination argument. Scientific realism is the view that science aims to give us with its theories a literally true story of what the world is like (van Fraassen 1980). If the underdetermination argument above is correct, then scientific realism is in trouble: given any two empirically equivalent theories, we seem to have no more reason for taking one of them to be more likely to be the case than the other. Indeed, neither may be true. Newtonian mechanics is not the way the world really functions - but it is often convenient to think about matters as though Newtonian mechanics were true, because we know it is an accurate approximation within well-understood regimes of validity. Thus, the underdetermination argument challenges the claim that in theory choice there are objectively good reasons for choosing one (more likely to be true) theory over a (less likely to be true) rival. Not surprisingly, as we saw in Chapter 1, these anti-realist considerations resonate in the work of the influential historian and philosopher of science Thomas Kuhn (1962/1996). Kuhn dismantled the scientific realist picture of science as triumphantly marching towards the truth by accumulating a sequences of theories that build on their predecessors and are more and more likely to be true the closer we come to contemporary science. Kuhn's profound commitment to the history of science led him to debunk this irenic picture of how scientific inquiry grows and unfolds, and to replace it with a new cyclic picture, whereby science goes through periods of normal science, crises and scientific revolutions.
Although Kuhn never formulated the underdetermmation argument as above, he clearly subscribed to some version of this argument. For example, he claimed that theory choice, far from being a rational and objective exercise, is indeed affected by external, contextual considerations including the beliefs and system of values of a given community at a given historical time (captured by Kuhn's notion of scientific paradigm). In his 1977 work, Kuhn pointed out that theory choice seems indeed governed by five objective criteria: accuracy (i.e. the theory is in agreement with experimental evidence); consistency (i.e. the theory is consistent with other accepted scientific theories); broad scope (i.e. the theory has to go beyond the original phenomena it was designed to explain); simplicity (i.e. the theory should give a simple account of the phenomena); and fruitfulness (i.e. the theory should be able to predict novel phenomena). Yet, Kuhn continued, these criteria are either imprecise (e.g. how to define 'simplicity'?) or they conflict with one another (e.g. while Copernicanism seems preferable to Ptolemaic astronomy on the basis of accuracy, consistency would pick out Ptolemaic astronomy given its consistency with the Aristotelean-Archimedean tradition at the time). Kuhn thus reaches the anti-realist conclusion that these five joint criteria are not sufficient to determine theory choice at any given time, and instead external, sociological factors seem to play a decisive role in theory choice (e.g. Kepler's adherence to Neoplatonism seems to have been a factor in leading him to endorse Copernicanism). It is no surprise that, rightly or wrongly, Kuhn s reflections on theory choice opened the door to Feverabend's (1975) methodological anarchism and to what became later known as the sociology of scientific knowledge.
This is not the place for us to enter into a discussion of the sociological ramifications of Kuhn's view. Instead, going back to our topic in this chapter, we should ask what the evidence is for the current standard cosmological model, and whether in this case there might also be empirically equivalent rivals. We are at a key juncture in the history of cosmology: the search for DE and DM is still ongoing, with several large spectroscopic and photometric galaxy surveys either under way. In a few years down the line, we will be able to know whether the anomalous phenomena of an accelerating expansion of the universe, and flat galaxy rotation curves, are indeed the signs for the existence of DE and DM - or whether we should actually abandon the framework of relativity theory (the FLRW models). In the next section, we review the scientific evidence for DE and DM, as well as some of their proposed rivals to date. In the final section, we return to the underdetermination problem and the rationality of theory choice and we assess the prospects and promises of the current standard cosmological model.
Modern observations tell us much about the universe globally (its expansion history) and locally (development of structure). But making a consistent picture from all this information is only possible with the introduction of two new ingredients: DM and DE. To understand what these are, we must look at the Friedmann equation. This governs the time dependence of the scale factor of the universe, R(t). Separations between all galaxies increase in proportion to R(t), and its absolute value is the length scale over which we must take into account spacetime curvature. The equation is astonishingly simple, and resembles classical conservation of energy: [dR(t)/dt]2 - (8πG/3) ρ(t) R(t)2 = -K, where G is the gravitational constant, p is the total mass density, and AT is a constant. One deep result from Einstein's relativistic theory of gravity is that K is related to the curvature of spacetime, i.e. whether the universe is open (infinite: negative K) or closed (finite: positive K). This says that the universe expands faster if you increase the density, or if you make the curvature more negative. Because the universe is inevitably denser at early times, curvature is unimportant early on. This means that, if we can measure the rate of expansion today and in the past, then we can infer both the density of the universe and its curvature.
In practice, we can match observations using Friedmann's equation only if K = 0, and if the density, p, is larger than expected based on ordinary visible matter. There must be DM, with a density about five times that of normal matter, and dark energy (a poor name), which is distinguished by being uniformly distributed (unlike other matter, which clumps). The universe appears to be dominated by DE, which contributes about 70 per cent of the total density.
This standard cosmological picture is called the ΛCDM model, standing for A (the cosmological constant) plus cold dark matter ('cold' here implies that the dark matter has negligible random motion, as if it were a gas at low temperature). The claim that the universe is dominated by two unusual components is certainly cause for some scepticism, so it is worth a brief summary of why this is widely believed to be a correct description. The main point to stress is that the ΛCDM model can be arrived at by using a number of lines of evidence and different classes of argument. Removing any single piece of evidence reduces the accuracy with which the cosmological parameters are known, but does not change the basic form of the conclusion: this has been the standard cosmological framework since the 1990s, and it has witnessed a great improvement in the quality and quantity of data without coming under serious challenge. If the model is wrong, this would require an implausible conspiracy between a number of completely independent observations. It is impossible in a short space to list all the methods that have contributed, but the two main types of approach are as follows.
The easiest to understand is based on standard candles, or standard rulers. If we populate the universe with identical objects, their relative distances can be inferred. Suppose we have two copies of the same object, A and B, where B is twice as far from us as A. Object B will subtend half the angle that A does, and we will receive energy from it at a rate that is four times smaller (the inverse-square law). Finding identical objects is hard: the angular sizes of the sun and moon are very similar, but the moon is a small nearby object, whereas the sun is much larger and more distant. But suppose that standard objects can be found, and that we can also measure their redshifts: these relate to the distance via Hubble's law, but because we are looking into the past, we need the rate of expansion as it was in the past, and this depends on the contents of the universe. A universe containing only matter will have a much higher density in the past compared with one dominated by DE, where the density appears not to change with time. In the latter case, then, the expansion rate will be lower at early times for a given distance; alternatively, for a given redshift (which is all we observe directly) the distance will be larger at early times (and hence objects will appear fainter), if DE dominates. This is exactly what was seen around 1998 with the use of Type la supernovae. These exploding stars are not quite identical objects (their masses vary), but the more luminous events shine for longer, so they can be corrected into standard objects that yield relative distances to about 5 per cent precision. By now, hundreds of these events have been accurately studied, so that the overall distance-redshift relation is very precisely measured, and the evidence for DE seems very strong. This work was honoured with the 2011 Nobel Prize.
But although supernova cosmology is a very direct method, the first strong evidence for DE was in place at the start of the 1990s, on the basis of the information contained in the large-scale structure of the universe (see Figure 3.1).
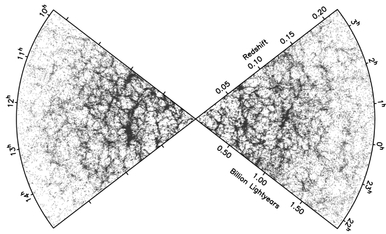
Figure 3.1 The large-scale structure ol the umverse, as revealed m the distribution of the galaxies by the 2-degree Field Galaxy Redshift Survey. The chains of galaxies stretching over hundreds of millions of light years represent the action of gravity concentrating small initial density irregularities that were created in the earliest stages of the expanding universe. (Copyright photo: John Peacock)
The fluctuations in density that we see in the CMB (cosmic microwave background) and in large-scale galaxy clustering contain a standard length, which is set by the time when the universe passed through the era of 'matter-radiation equality'. What this means is that the density of the universe was dominated at early times by relativistic particles such as photons, but as the universe expands and cools, non-relativistic matter (DM plus normal matter) becomes more important (see Figure 3.2).
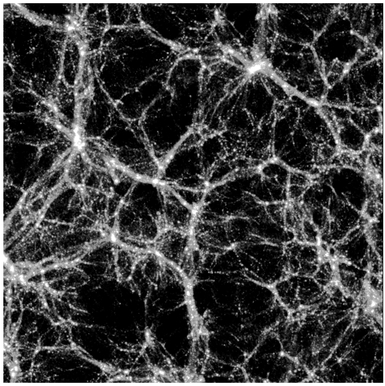
Figure 3.2 A slice through a computer simulation of structure formation in a standard-model universe, dominated by dark matter and dark energy. The scale of the image is approximately 650 million light years on a side. The dark matter clumps under gravity, generating a network of filaments and voids that bears a striking resemblance to the structure seen in the real galaxy distribution, as illustrated in Figure 3.1. (Copyright photo: John Peacock)
This is useful in two ways: the transition scale depends on the matter density, so it is a useful means of 'weighing' the universe, and determining the matter density. But the scale can also be seen at high redshift in the CMB, and so again we are sensitive to the change in the expansion rate at high redshift. Combining galaxy clustering with the CMB in this way already strongly pointed to the need for DE as early as 1990. There is an interesting sociological point here, namely that the 1990 evidence did not meet with immediate acceptance. This is not so much because the arguments were weak, but because many researchers (including one of the current authors) were reluctant to believe that the density of the vacuum really could be non-zero (the physical problems with this are discussed below). But the 1998 supernova results were accepted almost immediately, and ΛCDM became the standard model. Those who were reluctant to accept a non-zero Λ now had to search for reasons why two such different arguments should conspire to yield the same conclusion; most workers found this implausible, and so the consensus shifted.
The explanation tor DM need not be particularly radical. It is plausibly an exotic massive particle left as a relic of early times (in the same way as the photons of the CMB, or the nuclei resulting from primordial nucleosynthesis). Such a particle would be collisionless (i.e. it would not support sound waves in the same way as ordinary gas), and there is good evidence that DM has this character. There are a number of ways in which this conjecture could be tested, most directly by seeing the relic DM particles interacting in the laboratory. Although these WIMPs (weakly interacting massive particles) are by definition hard to detect other than via gravity, they will suffer occasional rare collisions with normal particles. The challenge is to distinguish such events from the background of less exotic processes, and consequently the direct-detection experiments operate many kilometres underground, using the Earth itself to shield out potential contaminants such as cosmic rays. If relic WIMPs can be detected, we may also hope to make new particles of the same properties in accelerators (pre-eminently the LHC 'Large Hadron Collider" at CERN). So far, neither route has yielded sight of a new particle, but it remains plausible that detection could happen within the next few years.
A third indirect route exploits the fact that WIMPs will also interact weakly with themselves: relic WIMPs and anti-WIMPs should exist in equal numbers, and the relics are those particles that failed to annihilate at an earlier stage of the universe. In regions of high density, such as the centres of galaxies, annihilations could continue at a sufficient rate to generate detectable radiation in the form of gamma rays. Indeed, there have been tantalizing signals reported in the past few years by NASA's Fermi gamma-ray observatory, which could be exactly this signal. But other sources of gamma-ray emission are possible, so this route does not yet prove the WIMP hypothesis for DM.
In contrast, DE seems hardly a form of matter at all: it behaves as if it were simply an energy density of a vacuum - a property of 'empty' space that remains unchanged as the universe expands. Although this sounds contradictory, it is easy to show from the uncertainty principle that an exactly zero vacuum density would not be expected. This argument goes back to the early days of quantum mechanics and the attempt to understand the form of black-body radiation. Planck's solution was to envisage the space inside an empty box as being filled with electromagnetic wave modes, each of which can be excited in steps of energy E = hv, where h is Planck s constant and v is the frequency of the mode, each step corresponding to the creation of one photon. The black-body spectrum cuts off at high frequencies because eventually hv becomes larger than a typical thermal energy, and therefore not even one photon can typically be created. But Einstein and Stern realized in 1913 that Planck's original expression for the energy of an oscillator was wrong: instead of E = n hv for « photons, it should be E = (n + 1/2) hv, adding a constant zero-point energy that is present even in the vacuum (n = 0). It is impressive that this is more than a decade before Heisenberg showed that the zero-point energy was predicted by the new uncertainty principle in quantum mechanics. This states that the uncertainty in position (x) and in the momentum of a particle (p, which stands for mass x velocity) is in the form of a product: δx δp = constant. Thus it is impossible for a particle to be completely at rest, as both its position and momentum would be perfectly known. Similarly, a perfectly still electromagnetic field is impossible. By 1916, Nernst had realized that the energy density of the vacuum therefore diverged, unless a maximum frequency for electromagnetic radiation was imposed. Cutting off at an X-ray frequency of 1020 Hz gave Nernst a vacuum density of 100 times that of water, which seemed puzzlingly high even then. This problem is still with us today.
The gravitational effects of this vacuum density are identical to those of a leading feature of cosmology: the cosmological constant introduced by Einstein in 1917. In effect, the cosmological constant and the density of zero-point energy add together into one effective density of DE (to which there can be further contributions, as we will see). As mentioned in Chapter 2, Einstein added the cosmological constant to his gravitational field equations in order to achieve a static universe. This is possible because DE in effect displays antigravity, i.e. its gravitational force is repulsive when the density is positive. This unexpected property can be deduced from the fact that DE does not dilute with expansion. For normal matter, doubling the size of the universe increases the volume by a factor of 8, so the density declines to 1/8th its initial size; but no such effect is seen with DE. This fact means that the mass inside a sphere of vacuum increases as the sphere expands, rather than remaining constant - so that it becomes more gravitationally bound, requiring an increase in kinetic energy to balance.
Conversely, for normal matter the gravitational effects decline in importance as the expansion progresses, leading to a decelerating expansion. In the past, the density of normal matter was higher, and so the universe is expected to have started out in a decelerating expansion. But today we live in a universe where the density of DE outbalances that of DM plus visible matter by a ratio of roughly 70:30, which means that the gravitational repulsion of DE dominates, yielding an accelerating universe. By the time the universe is twice its current age, it will have settled almost exactly into a vacuum-dominated exponentially expanding state - the very same one discovered by de Sitter in 1917.
Clearly it is impressive that we can account quantitatively for so many different astronomical observations using a standard model with relatively few ingredients. It can also be seen as a tribute to the science of astronomy that it was able to reveal such a fundamental ingredient of the universe as DE. But in a sense these achievements of modern cosmology have been obtained illegally. The basic laws of physics have been obtained entirely from experiments carried out on Earth - on characteristic length scales ranging from perhaps 1,000 km to subnuclear scales (~10-15 m). Although observational support for these laws thus covers over 20 powers of 10, the largest observable cosmological scales are 20 powers of 10 again larger than the Earth, so it is a considerable extrapolation to assume that no new physics exists that only manifests itself on very large scales. Nevertheless, this is how cosmologists choose to play the game: otherwise, it is impossible to make any predictions for cosmological observations. If this approach fails, we are clearly in trouble: ad hoc new pieces of cosmological physics can be invented to account for any observation whatsoever. Nevertheless, a significant number of scientists do indeed take the view that the need for DM and DE in effect says that standard physics does not work on astronomical scales, and that we should consider more radical alternatives.
One option is MOND: modified Newtonian dynamics. By changing the Newtonian equation of motion in the limit of ultra-low accelerations, one can remove the need for DM in matching internal dynamics of galaxies. Although the most precise evidence for DM is now to be found in large-scale clustering, the first clear evidence did emerge from galaxy dynamics, particularly the observation of 'flat rotation curves': the speed at which gas orbits at different distances from the centres of galaxies can be measured, and is generally found to stay nearly constant at large radii. This is puzzling if we consider only visible matter: for orbits beyond the edge of the starlight, the enclosed mass should be constant and the rotation speed should fall. The fact that this is not seen appears to show that the enclosed mass continues to grow, implying that galaxies are surrounded by halos of invisible matter. Within the standard ACDM model, this is certainly not a surprise: computer simulation of gravitational collapse from generic random initial conditions reveals that DM automatically arranges itself in nearly spherical blobs, and the gas from which stars are made is inevitably attracted to the centres of these objects.
Nevertheless, it is empirically disturbing that DM only seems to show itself in galaxies when we are far from the centres, so that the accelerations are lower than the regime in which Newton's F = m a has ever been tested. If this law changes at low accelerations in a universal way, it is possible to achieve impressive success in matching the data on galaxy rotation without invoking DM; and MOND proponents claim that their fits are better than those predicted in models with DM. Indeed, there is a long-standing problem with explaining dwarf galaxies, which are apparently dominated by DM everywhere, and so should be able to be compared directly to DM simulations. The inferred density profiles lack the sharp central cusp that is predicted from gravitational collapse - so these models are apparently ruled out at a basic level. But most cosmologists have yet to reject the DM hypothesis, for reasons that can be understood via Bayes' theorem in statistics.
The probability of a theory is a product of the prior degree of belief in the theory and the probability of the theory accounting for a given set of data: when the prior belief for DM is strong (as it is here, given the success in accounting for the CMB, for example), there must be extremely strong reasons for rejecting the hypothesis of DM. Also, we need to bear in mind that it is easy to reject a theory spuriously by making excessive simplifications in the modelling used to compare with data. In the case of dwarf galaxies, normal (baryonic) matter is almost entirely absent, even though on average it makes up 20 per cent of the cosmic matter content. Therefore, some violent event early in the evolution of the dwarfs must have removed the gas, and could therefore plausibly have disturbed the DM. Until such effects are modelled with realistic sophistication, cosmologists are rightly reluctant to reject a theory on the basis of possibly simplistic modelling.
The problem with MONO, on the other hand, is that it seemed ad hoc and non-relativistic - so that it was impossible to say what the consequences for the cosmological expansion would be. Bekenstein removed this objection in 2004, when he introduced a relativistic version of MOND. His model was part of a broader class of efforts to construct theories of modified gravity. Such theories gain part of their motivation from DE, which manifests itself as the need to introduce a constant density into the Friedmann equation in order to yield accelerating expansion. But perhaps the Friedmann equation may itself be wrong. It derives from Einstein's relativistic gravitational theory, and a different theory would modify Friedmann"s equation. On this view, DE could be an illusion caused by the wrong theory for gravity. Flow can we tell the difference?
The answer is that gravity not only affects the overall expansion of the universe, but also the formation of structure (voids and superclusters) within it. Therefore, much current research effort goes into trying to measure the rate of growth of such density perturbations, and asking if they are consistent with standard gravity plus the existence of DE as a real physical substance. Currently, at the 10 per cent level of precision, this test is passed. This consistency check is pleasing and important: previous generations of cosmologists took without question the assumption that Einstein's approach to gravity was the correct one; but such fundamental assumptions should be capable of being challenged and probed empirically.
Going back then to the underdetermmation problem and the rationality of theory choice, we may ask to what extent the current concordance model λCDM is well supported by the available evidence. The story told in the second section ("Dark Matter and Dark Energy') shows already how the hypothesis of DE met with a certain resistance in the scientific community in the early 1990s, when the first mam evidence for it came from large-scale galaxy clustering. Only in 1998, when supernova la data became available as further evidence, did the scientific community come to endorse the idea of an energy density of the vacuum that manifests itself as a form of antigravity or repulsion. (Kant, who, as we saw in Chapter 2, believed in a counterbalance between attraction and repulsion as the mechanism at work in the constitution of the universe, would be delighted to hear that his intuitions seem vindicated by the idea of a repulsive antigravity outbalancing DM and baryonic matter.) The reluctance of the scientific community to embrace the hypothesis of DE back in the 1990s might be explained by the exotic nature of the entity (that 'empty' space can have a non-zero energy density still feels wrong to many physicists, even though they know how to derive the result). Here we find replicated Duliem's story about how a piece of negative or anomalous evidence does not unequivocally speak against a main theoretical assumption, but may instead argue in favour of an additional auxiliary hypothesis. Underdetermination looms again on the horizon, as Table 3.1 shows (adapted from Lahav and Massimi 2014).
If the underdetermmation argument is correct, the choice between the ACDM model vs its rivals would not seem to be on rational grounds. Indeed, one might be tempted to bring in sociological explanations behind scientists gathering their consensus around the standard cosmological model rather than its rivals. For example, one might argue that it is easier to hold onto an accepted and well-established theory such as GR (plus DE) than trying to modify it (nor do we currently possess a well-established alternative to GR). And even in those cases where we do have a well-worked out alternative (such as MOND), one might be tempted to hold onto the accepted theory (plus DM), on grounds of the ad hoc nature of the modification of Newton's second law involved in MOND. Are scientists following again their 'good sense' in making these decisions? And what counts as 'good sense' here? After all, MOND supporters would argue that their theory is very successful in explaining not only galaxy rotation curves (without resorting to DM) but also other cosmological phenomena. From their point of view, 'good sense' would recommend taking relativistic MOND seriously.
To give an answer to these pressing questions at the forefront of contemporary research in cosmology, we should then examine first the premise of empirical equivalence in the underdetermination argument. After all, as we
| Anomaly | Reject a main theoretical assumption? | Add a new auxiliary hypothesis? |
|---|---|---|
| Galaxy flat rotation curves | Modify Newtonian dynamics (MOND)? | Halos of dark matter? |
| Accelerating universe | Modify GR? Retain GR, modify FLRW? |
Dark energy? |
saw in the introductory section, this premise is the culprit of the argument itself. In the next section, we review both the physical data behind the prima facie empirical equivalence between the standard cosmological model and its rivals, and draw some philosophical considerations about this debate and the challenge to the rationality of theory choice.
Let us then look a bit more closely to some of the rivals to the current ACDM model, starting with DE. Critics of DE typically complain on two main grounds: first, the lack of direct empirical evidence for DE as of today; and second, lack of understanding of why the vacuum would have a non-zero energy density. The first problem is admittedly real, as we have only inferred the existence of DE via the fact of the accelerating expansion of the universe. Future experiments, e.g. the Dark Energy Survey, will have mapped 200 million galaxies by 2018, using four different probes, with the aim of measuring the signature of DE precisely, but they will only at best show that the acceleration is measured consistently: we do not expect to touch DE. The second worry is also difficult to dismiss, and is of a more philosophical nature. Critics complain about what seems to be the ad hoc introduction of DE into the current cosmological model, as the latest incarnation of Einstein's infamous cosmological constant (i.e. tweak a parameter, give a non-zero value to it, and accommodate in this way the theory to the evidence). Dark energy, critics say (Sarkar 2008, p. 269), 'may well be an artifact of an oversimplified cosmological model, rather than having physical reality". Can DE really be an artefact of an oversimplified model? And do we have any better, DE-free model?
One rival DE-free model would be an inhomogeneous Lemaître-Tolman Bondi (LTB) model (rather than the standard FLRW model, which assumes, with the cosmological principle, that the universe is roughly homogeneous and isotropic). If we deny homogeneity (but retain isotropy ), we could assume that there are spatial variations in the distribution of matter in the universe, and that we might be occupying an underdense or 'void' region of the universe (a 'Hubble bubble'), which is expanding at a faster rate than the average. Thus, the argument goes, our inference about DE may well be flawed because based on a flawed model, i.e. by assuming a homogeneous FLRW model. A rival LTB model, it is argued (Sarkar 2008), can fit data about the fluctuations in the CMB responsible for large-scale structure (see Chapter 2), and can also account for the main source of evidence for DE, namely the use of supernova la data as standard candles, with an important caveat though.
Supernova la data, which typically are the mam evidence for an accelerating expansion of the universe (which is in turn explained by appealing to DE), are now interpreted without assuming acceleration. For example, DE critics argue, light travelling through an inhomogeneous universe does not 'see' the Hubble expansion, and we make inferences about an accelerating expansion using effectively redshifts and light intensity, neither of which can track the matter density or eventual inhomogeneities of the universe through which light travels: 'could the acceleration of the universe be just a trick of light, a misinterpretation that arises due to the oversimplification of the real, inhomogeneous universe inherent in the FRW [FLRW] model?' (Enqvist 2008, p. 453). However, it should be noted that most cosmologists find LTB models unappealing, because of the need to place ourselves very close to the centre of an atypical spherical anomaly: having us occupy a 'special' position (a 'Hubble bubble') in the universe violates the Copernican principle.
Whatever the intrinsic merit of an alternative, inhomogeneous LTB model of the universe might be, one may legitimately retort against DE critics that the charge of being ad hoc seems to affect, after all, the interpretation of supernova la data here (as implying no acceleration), no less than it affects postulating a non-zero vacuum energy density to explain the same data as those for an accelerating expansion of the universe.
What if, instead of modifying FLRW models, we try to modify GR itself to avoid DE? So far, we do not have convincing alternatives to GR. Some physicists appeal to string theory to speculate that there might be many vacua with very many different values of vacuum energy, and again we might just happen to occupy one with a tiny positive energy density. Along similar lines, 'dark gravity' is also invoked to explain the accelerated expansion of the universe without DE, but in terms of a modified GR with implications for gravity. But it is fair to say that 'at the theoretical level, there is as yet no serious challenger to ΛCDM" (Durrer and Maartens 2008, p. 328).
Shifting to rivals to DM, as mentioned above, the prominent alternative candidate is MOND (modified Newtonian dynamics), first proposed by Milgrom (1983), and in its relativistic form by Bekenstein (2010). As mentioned above, MOND was introduced to explain the flat rotation curves of galaxies without the need to resort to halos of DM, but by tweaking instead Newton's second law. MOND-supporters appeal to arguments from simplicity and mathematical elegance to assert that 'for disk galaxies MOND is more economical, and more falsifiable, than the DM paradigm' (Bekenstein 2010, p. 5). Moreover, Bekenstein's work has made it possible to extend the applicability of MOND to other phenomena that were previously regarded as only explicable within the ΛCDM model, i.e. the spatial distribution of galaxies and fluctuations in the CMB. It is interesting here that appeal should be made again to Popper's fal-sifiability and even to the simplicity of MOND as an argument for preferring MOND over DM, which brings us back to our philosophical topic for this chapter. Is theory choice really underdetermined in current cosmology? Was Kuhn right in claiming that neither simplicity, nor accuracy or any of the other criteria involved in theory choice, will ever be sufficient to determine the rationality of theory choice?
Two considerations are worth noting in this context. First, the empirical equivalence premise in the underdetermination argument relies on the idea that two theories may have the same empirical consequences. So given an anomalous phenomenon (say, galaxy flat rotation curves) DM and MOND can be said to be empirically equivalent because they can both entail this phenomenon. Or, given the accelerating expansion as a phenomenon, both DE and inhomogeneous LTB models can be said to be empirically equivalent, because the accelerating expansion of the universe follows from either. But obviously there is much more to the choice between two theories than just considerations of their ability to imply the same piece of empirical evidence. Philosophers of science have sometimes appealed to the notion of empirical support as a more promising way of thinking about theory choice (Laudan and Leplin 1991). A model, say ACDM, is empirically supported not just when there is direct experimental evidence for some of its main theoretical assumptions (DE and DM), but when the model is integrated/embedded into a broader theoretical framework (i.e. GR). In this way, the model in question (e.g. ACDM) can receive indirect empirical support from any other piece of evidence which, although not a direct consequence of the model itself, is nonetheless a consequence of the broader theoretical framework in which the theory is embedded. The rationale for switching to this way of thinking about empirical support is twofold. First, as Laudan and Leplin (1993) wittily point out, having direct empirical evidence for a hypothesis or theory may not per se be sufficient to establish the hypothesis or theory as true: a televangelist that recommends reading scriptures as evidence for inducing puberty in young males and cites as evidence a sample of the male population in his town would not be regarded as having established the validity of his hypothesis.
Second, and most importantly, scientists reluctance to modify Newtonian dynamics or to amend GR (by rejecting FLRW models for example) reflects more than just good sense, or 'entrenchment'. There are very good reasons for holding onto such theories given the extensive range of empirical evidence for them. Thus, one might argue that although MOND is indeed an elegant and simple mathematical alternative to DM, there are reasons for resisting modifications of Newtonian dynamics in general, given the success of Newtonian dynamics over centuries in accounting for a variety of phenomena (from celestial to terrestrial mechanics). Although none of the phenomena from terrestrial mechanics (e.g. harmonic oscillator, pendulum) are of course directly relevant to galaxy flat rotation curves, one might legitimately appeal to the success of Newtonian dynamics across this wide-ranging spectrum of phenomena as an argument for Newtonian dynamics being well supported by evidence and not being in need of ad hoc modifications to account for recalcitrant pieces of evidence in cosmology.
Not surprisingly, the philosophers" notion of empirical support chimes with and complements the physicists' multiprobe methodology in the search for DE in large galaxy surveys. Integrating multiple probes presents of course important challenges, especially when it comes to calibration, cross-checks, and the perspectival nature of the data set coming from different methods. But it also shows how methodologically important and heuristically fruitful the multiprobe procedure may be to dissipating the threat of empirical equivalence, which - as we have seen - looms in current debates about DE and DM. But this is a story for some other time.
1 In the 1820s, the astronomer Friedrich Wilhelm Bessel hypothesized a possible departure from Newton's inverse-square law of gravity to account for the anomalous perihelion of Uranus, due to specific gravity varying from one body to another. But the hypothesis was experimentally falsified and abandoned by the 1840s.
Duhem, P. (1906/1991) The Aim and Structure of Physical Theory, Princeton: Princeton University Press. (This is the classic book where the problem of underdetermination was expounded for the first time.)
Feyerabend, P. (1975) Against Method: Outline of an Anarchist Theory of Knowledge, London: New Left Books. (Another must read for anyone with an interest in scientific methodology, or better lack thereof!)
Kuhn, T. S. (1962/1996) The Structure of Scientific Revolutions, 3rd edn, Chicago: University of Chicago Press. (A cult book that has shaped and changed the course of philosophy of science in the past half century. )
Kuhn, T. S. (1977) 'Objectivity, value judgment, and theory choice', in T. S. Kuhn, The Essential Tension, Chicago: University of Chicago Press. (Excellent collection of essays by Kuhn. This chapter in particular discusses the five aforementioned criteria for theory choice.)
Kukla, A. (1996) 'Does every theory have empirically equivalent rivals?', Erkenntnis 44: 137-66. (This article presents the argument from empirical equivalence to underdetermnation and assesses its credentials.)
Lahav, O. and Massimi, M. (2014) 'Dark energy, paradigm shifts, and the role of evidence', Astronomy & Geophysics 55: 3.13-3.15. (Very short introduction to the underdetermination problem in the context of contemporary research on dark energy.)
Laudan, L. and Leplin, J. (1991) "Empirical equivalence and underdetermination', Journal of Philosophy 88: 449-72. (This is the article that put forward the notion of empirical support as a way of breaking the empirical equivalence premise. )
van Fraassen, B. (1980) The Scientific Image, Oxford: Clarendon Press. (This book is a landmark in contemporary philosophy of science. It is a manifesto of a prominent anti-realist view, called constructive empiricism.)
Bekenstem, J. D. (2010) 'Alternatives to dark matter: modified gravity as an alternative to dark matter', ArXiv e-prints 1001.3876.
Durrer, R. and Maartens, R. (2008) 'Dark energy and dark gravity: theory overview', General Relativity and Gravitation 40: 301-28.
Enqvist, K. (2008) 'Lemaitre-Tolman-Bondi model and accelerating expansion', General Relativity and Gravitation 40: 1-16.
Jain, B. and Khoury, J. (2010) 'Cosmological tests of gravity', ArXiv e-prints 1004.3294
Milgrom, M. (1983) 'A modification of the Newtonian dynamics: implications for galaxy systems', Astrophysical Journal 270: 384—9.
Quine, W. V. O. (1951) 'Two dogmas of empiricism', Philosophical Review 60: 20-43. (An all-time classic on the problem of underdetermination. It builds on Duhem's pioneering work and further develops the thesis. Very advanced reading.)
Sarkar, S. (2008) 'Is the evidence for dark energy secure?', General Relativity and Gravitation 40: 269-84.
Dark Energy Survey (n.d.) [website], www.darkenergysurvey.org (accessed 2 June 2014). (This is the official site of one of the current largest dark energy survey by mapping 200 million galaxies by 2018 by integrating four different probes.)