INTRODUCTION
The Spanish conquest of Mexico in 1521 crushed the Aztec State and also signalled an end to four millennia of autocthonous development of Mesoamerican civilization. The century after the Conquest was demographically unsuccessful for native populations, so that knowledge of many aspects of Indian culture quickly disappeared. Much was already lost by the time the earliest chronicles describing native civilization were written. Piecing together the fragmentary record of Mesoamerican achievements has been a slow process. For example, it was not discovered until the late 19th century that the Maya had a mathematics based upon positional notation and the use of the zero.
Aztec civilization crowns a long line of cultural development in the Valley of Mexico. Large-scale engineering projects in and around their capital city of Tenochtitlan, in themselves, suggest that Aztec engineers utilized mathematics. The surviving written records of Aztec tribute reflect a complex system of counting expressed in numerous hieroglyphic symbols. Their State, built upon conquest and sustained by tribute payment from conquered provinces, extended to the southeast, well into the zone of Maya peoples and culture. Therefore, it is plausible that the Aztecs possessed a mathematical sophistication similar to that of the Maya, but the problem has been to uncover the direct evidence. The significance of our decipherment of two early post-Conquest census-cadastral documents from the Valley of Mexico is that it provides, for the first time, direct empirical evidence that Texcocan Aztecs used a positional notation system and also developed a special symbol for zero.
The system of numerical notation most frequently associated with the Aztecs is described in the preceding paper by Payne and Closs. However, there is an additional system, employed by the Texcocan-Aztecs, which may be labeled as 'positional-line-and-dot'. This system was more efficient to write, since it employed only four symbols which were easy to draw: a vertical line, a bundle of five lines linked at the top, a dot, a corn glyph (cintli), and position to indicate the value of the symbols. At present we have noted its use in land documents, but it would seem more widely applicable and, moreover, well suited in general for arithmetical calculations.
DOCUMENTARY EVIDENCE
Positional-line-and-dot notation is known from several early post-conquest native Texcocan pictorial manuscripts. The two most important are in library collections. One, the Códice de Santa María Asunción, is in the Biblioteca Nacional of Mexico. The other, the Codex Vergara, is in the Biblio-thèque Nationale of Paris. We were especially interested in these two native manuscripts because of their large corpus of quantitative data and fine state of preservation. Also intriguing were the large sections which had never been deciphered and the fact that the places mentioned in the codices had never been specifically located. Thus, the challenge was not only to decipher and analyze the contents of the codices, but also to locate the place names. Beginning first with the Códice de Santa María Asunción, we set out from Texcoco visiting all nearby towns and barrios whose patron is Santa María Asunción. Our search was finally rewarded in the village of Tepetlaoztoc, which has a barrio called Asunción. The native name of that barrio proved to be Cuauhtepoztla, the first and most prominent town listed in the codex of Asunción. Moreover, when we explained the purpose of our questions, residents of that barrio led us to their church and showed us a 19th century document, which they now call their "títulos". It was a copy of an early 17th century manuscript which described the codex of Santa María Asunción. We knew then that the origin of that codex was resolved. Subsequent field work led to the conclusion that the communities in the Codex Vergara have disappeared. However, our colleague Manuel Arredondo found for us a late 16th century map in Mexico's National Archive which aided us in locating several communities listed in the Codex Vergara. These were in another barrio of Tepetlaoztoc. Thus, both codices pertain to this village.
Each codex is bound as a book, the Asunción codex with 80 folios and the Vergara with 56. Each contains a census by household and records household landholdings for a total of 16 named localities. The writing is in native style hieroglyphics characteristic of the Acolhua (Texcocan) kingdom of the early 16th century. Both contain notations in script that were added subsequent to the original drafting, including some late 16th century dates. The documents were signed by Pedro Vásquez de Vergara, known to have been ordered by colonial authorities to go to Tepetlaoztoc in 1543 to adjust taxes. He appears again in litigation records of the 1550's between the Indians and their encomendero, Gonzalo de Salazar (Gibson 1964, pp.77-80). The fact that so many individuals included on the census were deceased, as indicated by the shading of their faces, together with several dated events on the documents, suggests that they were prepared before the onset of the great pestilence of 1545 to 1548, or circa 1545. Their appeal, in other words, is that they were drawn only one generation after the conquest.
Both codices are examples of cadastral records kept by Indian communities in preconquest and early colonial times. Alonso de Zorita, (1963, p.110) an astute mid-16th century observer of native life, stated that:
"This principal is responsible for guarding and defending the calpulli lands. He has pictures on which are shown all the parcels, and the boundaries, and where and with whose fields the lots meet, and who cultivates what field, and what each one has … The Indians continually alter these pictures according to the changes worked by time, and they understand perfectly what these pictures show...".
We know that the Indians of Tepetlaoztoc specifically kept such records because in 1551 the judge assigned to the litigation between the Indians and their encomendero ordered the Indians to exhibit their paintings and explain their meaning to him (AGI, Justicia, leg.151). Certainly their contents were not any more self-evident then than they are today to one unacquainted with the Indian conventions of writing and notation. It is quite possible that both codices (or copies thereof) were among the documents presented by the Indians, since the documents had shortly before been officially certified by Pedro Vásquez de Vergara.
Each of the two codices is divided into three parts by locality. The first section (tlacatlacuiloli, tlacanyotl) contains a census by household, usually five households to a page. The name for each head of household is written in glyphic form beside the conventional symbol for household head (fig. 9.1a). The second section (milcocoli) consists of a record of land parcels associated with each household. The term milcocoli may be a Náhuatl metaphor meaning field pattern. In modern Texcoco, certain small, rhombus-like cakes are called cocoles, and if many of these were arranged on a surface, they would create a lattice-like structure similar to field patterns. In the milcocoli section, the scribe drew the approximate shape of each field. The measurement of each side was recorded using lines and dots, a line equal to one linear unit, a dot equal to 20 (fig. 9.1b) (Cline 1966; 1968). The early 17th century native Texcocan historian, Fernando de Alva Ixtlilxóchitl (1977, II, p.93), tells us that in the Texcocan area the standard unit of linear measure, the quahuitl, was equal to 3 Spanish varas, or 2.5 meters. Units less than one quahuitl were indicated by glyphic symbols such as a hand, an arrow, and a heart. The modern equivalents of these glyphs can only be estimated at present (Williams 1984, p.107; Castillo 1972, p.217). In addition to recording linear measurements around the field perimeters, each field also contains a glyph in the center which indicates the type of soil (Williams 1980a; 1980b). The significance of the milcocoli section for our purposes is that it allows us to compute the area of each field and estimate the amount of land held by taxpaying commoner families (macehualtin) in the early post-conquest period. Since the two documents combined depict more than 1,000 land parcels, they provide a record of landholdings unparalleled in the area of Mesoamerica for such an early time period.
The third section of each locality contains another land register labeled tlahuelmantli, which follows the same household sequence. There is little question that the tlahuelmantli section is a second register of the same lands. However, the two land registers differ in several important aspects.
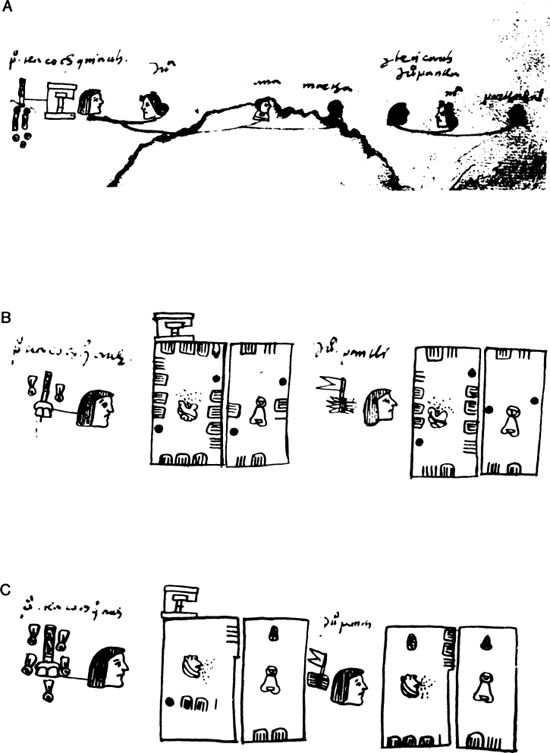
Fig. 9.1. Portions of the Códice de Santa María Asunción relating to the household of Pedro Tlacochquiauh. (a) The household census, tlacatlacuiloli, shows the head Pedro, his wife Juana, their two young daughters Ana and Martha, and the head’s younger brother (teicauh), Juan Pantli, his wife María, and their son Balthasar (Parthasal). The shaded heads indicate that the individual depicted was deceased. (b) The milcocoli section records the approximate shape, perimeter measurements, and soil type of four fields belonging to the household, two to the household head and two to the head’s brother. In the numerical notation employed in the milcocoli, lines equal 1 quahuitl and dots equal 20. The hand glyph shown in the first field indicates a fraction of a quahuitl. (c) The tlahuelmantli section shows the same fields as the milcocoli, but they are depicted as abstract rectangles, and a different numerical notation is used. In this positional-line-and-dot system, numbers occur in three registers. Lines in the upper right protuberance record units of 20. Lines on the bottom line of the rectangle (second register) or in the center (third register) are multiplied by 20. Dots, which occur only in the third register, equal 202 or 400. The corn glyph (cintli) at the top margin of the rectangle indicates zero in the third register. The numbers record the area of each field in square quahuitl. (Photographs from folios 2r, 10r, and 19v of the Códice de Santa María Asunción.)
The lands in the tlahuelmantli are shown in stylized form as rectangles of the same size. Perhaps not coincidently, the Nahuatl term tlahuelmantli literally means 'smoothed, leveled, or equalized', according to Simeon (1977, p.691). Also, the majority of these tlahuelmantli fields have a protuberance in the upper right hand corner (fig. 9.1c). In addition to the standardized field shapes, the placement of numbers in the tlahuelmantli is different than in the milcocoli. The numerical quantities using lines and dots are entered either in the center or on the bottom line of the rectangle and in the protuberance. When numbers (which never exceed 19) are entered on the bottom line, a cintli glyph occurs near the top border of the rectangle.1 In addition, most fields contain a number ranging from 1 to 19 in the upper right hand corner protuberance. We have determined that these numbers report the area of the field in square quahuitl by use of positional notation. With this knowledge we may interpret the standard tlahuelmantli field form as a glyph meaning "area".
POSITIONAL NOTATION
Both the Códice de Santa María Asunción and the Codex Vergara have formed part of the known native pictorial record for over 150 years, and the latter was studied by such noted Mexicanist scholars as J.M.A. Aubin (1891) and Eduard Seler (1904). However, the codices have been little used because large sections remained undeciphered, notably the tlahuelmantli, which comprises one-third of each manuscript.
Our decipherment of the tlahuelmantli code came about by comparing areas calculated by us from the milcocoli dimensions with the Indian notations in the tlahuelmantli. We calculated milcocoli areas by two methods. Since fields are not drawn to scale on the manuscripts, angles cannot be directly ascertained. Thus, for quadrilaterals, given the length of sides a, b, c, and d, we assumed a right angle between sides a and b, which allowed calculation of the area of the two resultant triangles. For non-quadrilaterals (roughly 40 percent of the cases), field sides were drawn to scale on graph paper and side angles were chosen so as to a) produce field shapes consistent with shapes observable today, b) maximize area, and c) preserve the relative shapes recorded in the drawings. Area was then derived by counting squares. Neither method accounted for side lengths in fractions of the standard quahuitl, which, where these occur, would result in an understatement of the actual area.
Pursuing the hypothesis that the tlahuelmantli section records a different set of data for the same fields illustrated in the milcocoli, we assumed that tlahuelmantli information might be related to field size, such as the amount of seed sown or harvested, or the tax to be paid on each parcel. We noted that in reading the tlahuelmantli numbers at face value (i.e., dots for 20 and lines for 1), the numbers fell consistently below those of the milcocoli areas in a ratio of approximately 20 to 1. We found in hundreds of cases that by multiplying the main tlahuelmantli number by 20, our area figures derived from milcocoli calculations were closely matched. In the process of testing this relationship further, it was discovered that in many cases our milcocoli area figure would exactly match the tlahuelmantli number if the lines in the upper right protuberance were treated as units rather than as multiples of 20. Thus, it became apparent that position of the numbers in the tlahuelmantli rectangles had arithmetical significance.
The Texcocan positional-line-and-dot notation system functions in the following manner. The tlahuelmantli rectangle records numbers in three positions, which we label "registers". The first register, located in the upper right protuberance, records the units of 20, indicated by 1 to 19 lines. Groups of 5 are bundled together by a connecting line. The value of this register ranges from 0 to 19, and when the number is zero, the protuberance is either not drawn or is left blank. The bottom line of the rectangle constitutes the second register, and it expresses 1 to 19 units of 20 (i.e., vigesimal multiples from 20 to 380). To derive the total value, the number in the second register is multiplied by 20 and then added to the number in the first register. The sum of the two registers never exceeds 399. The central portion of the rectangle constitutes the third register, and expresses quantities of 400 or greater in multiples of 20. Again, to derive the total, the number in the third register is multiplied by 20 and added to the quantity entered into the first register. The Texcocan symbol for 20 (the dot) only occurs in the third register, and according to its positional value means not 20 but 202 or 400. The second and third registers are never used concurrently. When there is no entry in the third register, the cintli glyph is drawn toward the top of the rectangle and signifies zero in the third register. Thus, for the first field illustrated in figure 9.1c the entries are one dot and 11 lines in the third register [202 + (11 x 20)] = 620 plus 4 lines in the first register, which totals 624 square quahuitl. The third field has an area of 333 square quahuitl as recorded by 16 lines in the second register (16 x 20 = 320) plus 13 lines in the first register, and a cintli glyph at the top of the rectangle indicating zero in the third register.
AREA COMPUTATION
The milcocoli register depicting linear dimensions of individual field boundaries confirms evidence from other native documents and early Spanish descriptions that native Mexicans maintained detailed cadastral records. However, decipherment of the tlahuelmantli adds to this knowledge the hitherto unknown practice of expressing landholdings in terms of area. Thus, it also provides an insight into the practical application of native arithmetic apart from its esoteric use in calendrics and astronomy.
Just how area was determined remains to be resolved. The milcocoli register does not provide enough information to calculate exact area of fields, particularly the highly complicated forms, since it does not record the true shape by means of angles or auxiliary measures. In other words, the milcocoli could not have been used as a "worksheet" for the tlahuelmantli section. Therefore, there must have been intermediate steps in area calculation between the milcocoli and tlahuelmantli records. One method could have employed a grid system in the field at the time of survey; another could have combined a grid system with computation; a third could have recorded in some fashion the required information for later computation of area. The key to discovering the most likely method rests potentially in the documents themselves.
To explore how area was determined and the degree of accuracy achieved, we examined quadrilaterals from the locality called Cuauhtepoztla. A preliminary analysis indicates that 55 percent of the tlahuelmantli areas fall within 5 percent of our areas calculated from milcocoli data; and 71 percent of the tlahuelmantli areas fall within 10 percent of our figures. Therefore, there is considerable concordance between our figures and theirs. More specifically, 8 percent of our area calculations based on milcocoli data and Texcocan calculations as expressed in the corresponding tlahuelmantli statements correspond exactly. Most of these cases involve quadrilaterals whose opposite sides are equal. We assumed these to be squares and rectangles for which the length times width algorithm applies. Since the Texcocan figures correspond to ours, this suggests that they also used the same algorithm. In 26 percent of the cases, the tlahuelmantli areas fall below our estimates, but the Texcocan figures may be more accurate than ours because, if our right angle assumption did not approximate the actual field form, then our method over-estimated the area. On the other hand, for 66 percent of the cases the tlahuelmantli areas are greater than our figures. This is puzzling because our right angle assumption approximates the maximum area possible given the side lengths reported in the milcocoli (Harvey and Williams 1980, pp.500-501).
Some of the discrepancies are explained by two additional algorithms. The tlahuelmantli area of many quadrilaterals which are nearly parallelograms can be obtained exactly by taking the area to be the sum of two right triangles whose legs are the sides of the fields. For more irregularly shaped quadrilaterals, we can frequently derive the tlahuelmantli estimate by summing the area of the largest possible rectangle within the field and the area of the remaining triangles. Thus, the data strongly suggest that Aztec surveyors used some sort of arithmetic calculation to derive area of fields surveyed.
Not all of the differences between our area calculations and the tlahuelmantli figures can be accounted for by different methods of computation. Internal evidence in the two codices suggests that the milcocoli and the tlahuelmantli registers were recorded at different times and perhaps by different surveyors. For example, the sequence of fields possessed by each household is not invariably the same in the two registers. Also, some individual households have added or lost parcels between the two registers. Therefore, it appears that the two registers were either based on separate surveys or one is an updated version of the other. Insofar as they may represent partially or entirely separate surveys, some discrepancies may be expected in the linear dimensions of the fields due to survey inconsistency. A time lapse between surveys might also have resulted in a real change in field size, such as the result of subdivisions or consolidation due to inheritance or property exchange. The larger discrepancies probably relate to such realignments.
It is noteworthy that when all (approximately 1100) individual field areas are aggregated at the household and locality level, the discrepancies between our estimates and the tlahuelmantli figures tend to even out. At the household level, in some cases large milcocoli fields are replaced by small fields in the tlahuelmantli and vice versa with the result that household aggregate landholdings remain fairly constant. At the locality level, the loss by one household is another's gain, so that aggregate locality totals show slight to negligible variation (Harvey and Williams 1980, p.503). Overall this implies not only reasonably accurate measuring and careful record keeping, but also methods to derive area that yielded reasonably accurate results.
APPLICATION
The functional significance of calculating land area is most apparent in relation to the system of taxation in ancient Mexico. Landholding commoners paid property taxes (tribute) based on the size and quality of their lands. Hernán Cortés (1538, p.542) reported that "... he who has them can pay tribute because for each measure [our emphasis] so much tribute is charged them according to where the lands are located." His son, Martín Cortés (1563, p.443) noted that "... he who has a piece of land paid a tribute; and the one with two, two; and the one with three, three; and he who had a piece of irrigated land, paid double that of one who had dry land." Central Mexico's topography is such that much of the taxed land had to have been located in hilly or mountainous terrain, and square or rectangular fields the exception rather than the rule. A tax system based on standard "measures" would have required a mechanism for equating oddly shaped fields with regular ones. This was the task of the surveyor, and as can be seen from the two Tepetlaoztoc codices, even very eccentrically shaped land parcels could be expressed accurately in terms of their square unit content. The importance of survey in Aztec society is reflected in 16th century Nahua vocabulary, which included numerous terms related to surveying, and interestingly, several referring to incompetent surveyors (Lameiras 1974).
There is increasing evidence that the basic areal "measure" of land (analogous to hectare) was 400 square units (20 x 20 linear units). In the case of Tepetlaoztoc, the 400 square measure was equivalent to .25 hectares
[(20 quahuitl x 2.5 meters)2] = 2500 square meters. Air photos of Tepetlaoztoc show small relic fields identifiable by soil discoloration in an area where fields recently have been enlarged for mechanized agriculture. These were square fields that measure 400 square quahuitl. In other areas of the Valley of Mexico the length of the linear unit varied, but the concept of a standard measure 20 by 20 square appears to have prevailed. Many extant pictorial documents from Central Mexico depict land parcels as rectangles and with dimensions or quantities expressed as multiples of 20. The Tepetlaoztoc codices suggest that some of the fields depicted in other documents might not be actual parcels, but tlahuelmantli-type abstractions. Precise shape or form of a field was less relevant for tax purposes than the size.
The Codex Mariano Jimenez (1967; also Leander 1967) offers a case in point. Folios 6 and 7 of that document depict a list of 11 rectangular fields, each 20 brazas in width, but increasing in length in regular increments from 100 to 800 brazas (fig. 9.2). They are ordered on the pages according to length, and tribute to be paid is noted beside each field. Of the three types of tribute assessed, two (firewood and turkeys) are fixed quantities regardless of field size; the third, cacao beans or coins, varies in direct proportion to the size of the field. For example, the tribute for a 400 square braza field is 20 cacao beans, indicating a tax rate of one cacao bean per 20 square brazas. These fields have been interpreted in the past as actual field dimensions of commoner landholdings in Otlazpan. An alternative interpretation is warranted because perfectly rectangular fields seem hardly possible, given the terrain of the Otlazpan area (modern Tepeji del Río), and especially considering that roads, ditches, trees, fences, and constructions make regular shaped fields unlikely even on lacustrine plains. Furthermore, the largest area shown on the Otlazpan document is 16,000 square brazas, which would have been extraordinarily large for a 16th century field possessed by a commoner. In Tepetlaoztoc the largest fields rarely exceeded 1000 square units, although in the aggregate many families possessed over 5000 square units. In our view, the Otlazpan field list appears to represent standardized abstractions of aggregate field areas with their associated tax levy. As such, the list functioned as a "tax table" from which a person could determine the tax on his holdings. If the Otlazpan tax rate of one cacao bean per 20 square units were applied to Tepetlaoztoc, then taxes on each parcel could also be read directly from the tlahuelmantli second and third registers by reading the numbers at face value rather than as multiples of 20. Thus, a tlahuelmantli field with two dots in the third register would be read as 800 square quahuitl in area, and the tax would have been 40 cacao beans.


Fig. 9.2. The Codex Mariano Jimenez (1967) shows eleven rectangular fields, each 20 brazas in width, but with lengths varying in regular increments from 100 to 800 brazas. In our view, the drawings are not of actual fields with these dimensions. Rather, the numbers indicate area in square brazas. Instead of indicating area measures directly, as in the Vergara and Asunción codices, the Otlazpan scribe assumed a constant multiplier (20 brazas) and a variable multiplicand, whose product would equal the area measure. For example, landholdings equal to 8000 square brazas were indicated by depicting a rectangle 20 brazas wide by 400 brazas long. To the right of the list of land areas is the tribute levy, so that a landholder could determine the tribute on his holdings.
CONCLUSIONS
As a result of the decipherment and preliminary analysis of two early post-conquest pictorial manuscripts from Tepetlaoztoc, three new features emerge concerning the native arithmetical system of the Texcocan Aztecs: 1) positional-line-and-dot notation; 2) a symbol to represent some functions of zero; 3) a probable set of algorithms to compute land area. However, since both documents were drafted in the 1540's we must ask whether the system was prehispanic in use and development or whether it might have been introduced by the Spaniards.
There are a number of features associated with Spanish mathematics which strongly contrast with the Texcocan-Aztec system. Spanish mathematics of the early 16th century used base 10, although some weights and measures were expressed in other bases such as 8 and 12, which derived from earlier conventions in the Mediterranean area. The Arabic system of notation had been adopted in Spain prior to the 16th century, but earlier Roman notation continued to be used extensively until the end of the 17th century. In both Arabic and Roman notation, horizontal but not vertical place value is of fundamental significance. In contrast, in Texcocan notation, horizontal position could be ignored so that, for example, the number 23 could be written either as ///• or •///, but vertical position was fundamental to reading the proper value of the number. The zero was highly developed in Arabic arithmetic but only weakly in Texcocan-Aztec. Finally, the Texcocan system was internally consistent throughout and reflected the idiosyncracies of the spoken language. The weight of evidence strongly supports an indigenous development of Texcocan-Aztec arithmetic rather than a post-conquest adaptation to new ideas. The absence of description of the native arithmetical system in the early chronicles suggests that Spanish observers of native culture, so astute in their description of some things, were either ignorant of native arithmetical practice or unimpressed (Morley 1915).
It is, perhaps, in the practical application of an arithmetical system to derive area that Spanish and native practices most sharply contrast. The Spanish could but usually did not express land units in square measures. The size of agricultural plots was frequently designated in terms of yield, such as so many fanegas of wheat. Also, Spanish land units such as the caballería were notoriously variable. Traditionally, the Spanish had been content with imprecise descriptions of land parcels, whereas the native Mexicans had not. This contrast suggests the continuation of prehispanic practices, rather than an adaptation to a Spanish system. As Anderson, Berdan and Lockhart (1976, p.5) observed "...from the mid-sixteenth century, as far back as our selections go, central Mexican Indians were measuring their lands very exactly, down to the yard in both dimensions, using quite sophisticated and individual terminology. At that time Spaniards in Mexico were still transferring land by the league, with no other description than the names of nearby owners or outstanding geographical features."
Three basic concepts of the Texcocan positional-line-and-dot system are shared with the Maya: base 20, vertical position, and the use of zero. As in Maya arithmetic (Lizardi Ramos 1962; Fulton 1948), the zero concept in Texcoco appears to have undergone only a limited development compared to functions and significance of the zero in Arabic mathematics. Since Aztec peoples were relative late-comers to the Valley of Mexico and the zone of high civilization, and since their area of political and economic control eventually extended to the borders of Maya-speaking peoples, the arithmetical system used in the Texcocan area may reflect a direct borrowing from the Maya. However, Texcocan-Aztec arithmetic was more likely a regional expression of a basic set of conventions and principles known throughout the Mesoamerican area for two millennia or more.
Ciphers expressed by picture symbols were geographically widespread in Mesoamerica, but 16th century pictorial documents from Central Mexico show that a number of other more abstract symbols were also used. In the Otlazpan manuscript, both a flag and a bar were employed as alternative symbols for 20. In Tenochtitlan, bars and dots, reminiscent of the Maya, were symbols used in calendrics. The Codex Kingsborough, also from Tepetlaoztoc, extensively employed picture symbols, in many cases combined with lines and dots (Paso y Troncoso 1912). While the choice of symbol to record numbers may have been the scribe's, it seems more likely that the determinant was the object to be counted and that the numerical classifier system of the spoken language was reflected in writing. This could explain why picture symbols appear in one context and abstract symbols in another.
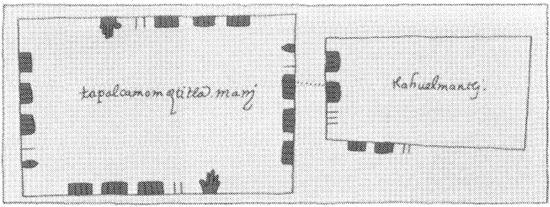
Fig. 9.3. The "tlahuelmantli convention", which indicates areal extent of a field by positional-line-and-dot notation, was utilized in Texcocan land documents other than the Vergara and Asunción codices. Shown above are drawings of a field called Tapalcamomoztitla from a document in the Papeles de la Embajada Americana Collection of the Archivo Histórico of the Museo Nacional de Antropología in Mexico City. The field on the left records data drawn in the milcocoli convention and the other linked to it by a dotted line is labeled tlahuelmantli. The area of the field shown in the milcocoli convention may be roughly calculated (omitting fractions of a quahuitl) by multiplying length (17 quahuitl) by width (16 quahuitl). The area is thus 272 square quahuitl. The number depicted in the tlahuelmantli convention is also 272. Thirteen lines on the inside left margin are multiplied by 20 (=260) and the 12 lines on the outside bottom line are multiplied by 1 (=12) totaling 272. (Archivo Histórico del INAH, leg.7, exp.2-24.)
The conventions and principles embodied in the Vergara and Asunción codices are not unique to those documents. The "milcocoli convention" of indicating measurements around the perimeter of fields by lines and dots with values of 1 and 20 is found on the Oztoticpac Lands Map in the U.S. Library of Congress (Cline 1966) and other Texcocan manuscripts. Similarly, the "tlahuelmantli convention" showing abstract fields with area indicated by positional-line-and-dot notation has been found on a late 16th century document from another Texcocan locality (fig. 9.3) (Papeles de la Embajada Americana n.d.). Further, the cintli glyph appears in a context other than tlahuelmantli to clarify place value. Since the direct evidence we have for the positional-line-and-dot notational system is thus far restricted to the Texcocan province of Acolhuacan, and largely to land documents within this area, it may well have been a special system devised for the purpose of land description. On the other hand, it is a system in which arithmetical computations could be accomplished with clarity and facility in contrast to the more elaborate picture symbols commonly used in tribute records. Until the Tepetlaoztoc documents were deciphered, use of positional notation, the zero symbol, and derivation of land area by Aztec peoples were unsuspected. The significance of the Tepetlaoztoc decipherment is that many documents with hitherto undeciphered numerical notations may now be re-examined and our understanding of prehispanic arithmetical practices possibly greatly expanded.
NOTE
ACKNOWLEDGEMENTS
This research was supported by NSF grant BNS 7725659 (to B.J.W.) and NSF grant BNS 8111804 (to H.R.H.). We thank the Centro Internacional de Mejoramiento de Maíz y Trigo for providing facilities in the field zone and La Recherche for permission to publish this modified version, in English, of the article "L'arithmétique azteque" (Harvey and Williams 1981).




