3.1 Introduction to Second-Order Linear Equations
3.2 Fundamental Solutions of the Homogeneous Equation
3.4 Homogeneous Equations with Constant Coefficients: Real Roots
3.5 Homogeneous Equations with Constant Coefficients: Complex Roots
3.7 Solving Nonhomogeneous Equations: Method of Undetermined Coefficients
3.8 Solving Nonhomogeneous Equations: Method of Variation of Parameters
3.9 Mechanical Systems and Simple Harmonic Motion
3.10 Unforced Damped Vibrations
3.12 Introduction to Higher-Order Equations (Optional)
To introduce some of the basic concepts and ideas related to the second-order linear differential equation
We introduce
• the corresponding homogeneous equation,
• the principle of superposition,
• the initial-value problem,
• the existence and uniqueness of solutions.
In Chapter 2 we saw how first-order differential equations were useful in the description of physical systems relating to heat flow, mixing problems, and a wide variety of other phenomena often relating to chemistry, physics, and biology. We now focus our attention on second-order differential equations. It could be argued that second-order differential equations are even more important than first-order equations.* Certainly, one can say that without an appreciation of second-order differential equations, one cannot obtain a deep understanding of many of the laws of physics. In this chapter we will solve various kinds of second-order equations and see how they are used to model various kinds of motion. Our main focus will be on the second-order linear differential equation
where a0(x) ≠ 0, a1(x), a2(x), and g(x) are continuous functions on some interval of interest I. When the functions a0(x), a1(x), and a2(x) are constants, the differential equation is said to have constant coefficients; otherwise, it is said to have variable coefficients. Inasmuch as we are interested in those differential equations for which a0(x) ≠ 0 for all x 
I, we rewrite Eq. (1) in standard form as
where p(x) = a1(x)/a0(x), q(x) = a2(x)/a0(x), and f(x) = g(x)/a0(x). Often Eq. (2) is written in the compact form
Associated with the nonhomogeneous Eq. (3) is the homogeneous equation
which is obtained from Eq. (3) by simply replacing/(x) by zero. We call Eq. (4) the corresponding homogeneous equation to Eq. (3).
The reader may wonder whether we are going to solve the second-order equation (3) in a manner similar to the way we solved the first-order equation by multiplying by an integrating factor, thereby turning the equation into a simple integration. If this idea occurred to you, then you are in good company, since the idea also occurred to the eminent mathematician Joseph Louis Lagrange (1736–1813), who proved the existence of such an integrating factor over 200 years ago. Although Lagrange showed that under certain conditions such a factor existed, he couldn't actually find it; he proved that it satisfied another differential equation that was just as difficult to solve as the original equation. Basically, Lagrange tried to find a function μ(x) that multiplication of the equation
by μ(x) would yield an equation of the form
where the function g(x) could be determined* from the coefficients p(x) and q(x). If such a function μ(X) could be found, then it would be possible to integrate Eq. (6) directly, arriving at the first-order equation.
This first-order equation (7) could then be solved by using the “first-order” integrating factor method studied in Chapter 2. The only flaw in this method is that to find μ(x), one must solve
which, called the adjoint equation, is every bit as hard to solve as the original equation. In other words, Lagrange essentially replaced solving one differential equation by another one of equal difficulty. If you think about it, the only reason Lagrange's integrating factor method is successful in solving the first-order equation
is because the adjoint equation is
which can be solved by separation of variables, which gives
The failure of the integrating factor method in solving the second-order equation means that we must start, so to speak, from square one. We begin our search for the general solution of the second-order equation by introducing some important properties of solutions of second-order equations. We start with one of the most important properties of linear homogeneous differential equations.
Two of the most important properties of the homogeneous linear equation are that the sum of any two solutions is again a solution and that any constant multiple of a solution is a solution. This principle is called the principle of superposition for homogeneous equations.
THEOREM 3.1: Principle of Superposition for Homogeneous Equations
If y1(x) and y2(x) are any two solutions of the linear homogeneous equation
on some interval I, then any linear combination
where c1 and c2 are arbitrary constants, is also a solution on the interval. I.
PROOF: The conclusion follows from elementary properties of the derivative. That is, if
then
Substituting Eq. (13) into the differential equation (12), we get
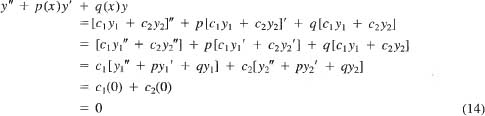
This verifies that Eq. (13) is a solution of Eq. (12).
Example 1
Superposition Example for Homogeneous Equations it is a simple matter to verify that both y1(x) = sin x and y2(x) = cos x are solutions of y″ + y = 0. Find five other solutions.
The principle of superposition for linear homogeneous equations says that any linear combination of y1(x) and y2(x) is a solution. Hence we arbitrarily select the five of the linear combinations y = c1 cos x + c2 sin x:
(a) 
(b) 
(c) 
(d) 
(e) 
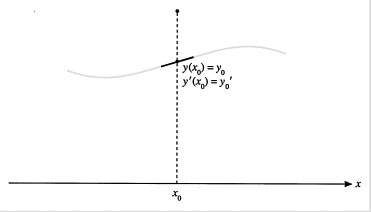
We have seen that the general solution of the first-order differential equation contains one arbitrary constant. Although we have not yet solved the general second-order equation, we know from calculus that the general solution of the trivial second-order equation y" = 1 is the two-parameter family of solutions, y(x) = c1 + c2x. This leads us to suspect that two side conditions are required to uniquely solve a second-order equation. We summarize these ideas by stating the initial-value problem for second- order differential equations.
DEFINITION: Initial-Value Problem for Second-Order Equations By an initial-value problem for a second-order differential equation
we mean the problem of finding the solution of the differential equation on an interval that also satisfies the initial conditions
where y0 and y1 are given constants.
Before we solve the second-order linear equation, it is useful to know if and when a solution actually exists and, if a solution does exist, on what interval it will exist. Also, how many solutions are there: zero, one, two, three, …? One of the interesting properties of a linear equation, whether it is a linear differential equation, a linear difference equation, a linear algebraic equation, or even a system of linear equations, is that the number of solutions is always zero, one, or infinity. There will never be two, three, four, …, solutions. The following existence and uniqueness theorem gives conditions sufficient for the second-order initial-value problem to have exactly one solution.
THEOREM 3.2 : Existence and Uniqueness Theorem
Let p(x), q(x), and f(x) be continuous functions on an open interval (a, b) containing a point x0. For any two numbers y0 and y1 there is one and only one function satisfying
on the entire interval (a, b) that also satisfies the initial conditions
Example 2
Verifying the Existence Theorem Determine the largest interval that contains x = 0 on which a unique solution of
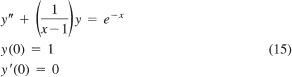
is certain to exist.
Solution
We identify the functions p(x) = 0, q(x) = l/(x - 1), and f(x) = e-x. The only value of x for which these functions are not all continuous is x = 1, where q(x) is undefined. Since the initial conditions are defined at the initial point x0 = 0, Theorem 3.2 guarantees that a unique solution exists on the interval (–∞, 1). We may not know the solution, but we know that one exists. We also know that a solution does not exist on any interval that contains x = 1.
Example 3
Finding the Arbitrary Constant Find the solution of the initial-value problem
Solution
It is easy to verify that both sin x and cos x satisfy the differential equation. Using the principle of superposition, we know that any linear combination
also satisfies the equation. To find c1 and c2, we substitute y(x) into the initial conditions, getting
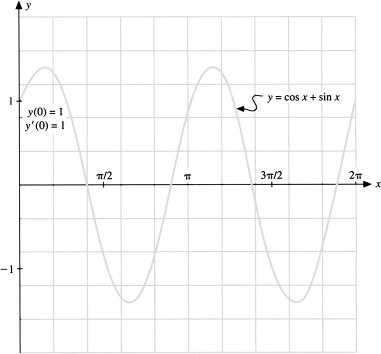
Hence we have c1 = c2 = 1, and so the unique solution of the initial-value theorem is
See Figure 3.1
Figure 3.1 The unique solution of the initial-value problem y″ + y = 0, y(0) = 1, y′(0) = 1
PROBLEMS: Section 3.1
For Problems 1–10, determine whether the given equation is linear or nonlinear. If it is linear, classify it as homogeneous or nonhomogeneous and with constant or variable coefficients.
11. Solutions of Second-Order Equations Verify that e- x and e2x and any linear combination c1 e-x + c2 e2x are all solutions of the differential equation
12. The Principle of Superposition Verify that ex and e-x and any linear combination c1ex + c2e2x are solutions of the differential equation
Show that the hyperbolic sine and cosine functions, sinh x and cosh x, are also solutions.
13. Interesting Comparison Show that the circular sine and cosine functions, sin x and cos x, are solutions of the equation y″ + y = 0, whereas the hyperbolic sine and cosine functions, sinh x and cosh x, are solutions of y" - y = 0.
For Problems 14–18, find the specific function among the given two-parameter family of functions that satisfies the specified initial conditions.
| Two-parameter family | Initial conditions |
14.  |
|
15.  |
|
16.  |
|
17.  |
|
18.  |
|
19. Boundary-Value Problems When the solution of a differential equation is specified at two different points, these conditions are called boundary conditions. This is in contrast to conditions that are specified at a single point, which are called initial conditions. Given that every solution of
has the form
where c1 and c2 are arbitrary constants, verify the following.
(a) Show that there is a unique solution to Eq. (19) that satisfies the boundary conditions
(b) Show that there is no solution to Eq. (19) that satisfies the boundary conditions
(c) Show that there are an infinite number of solutions to Eq. (19) that satisfy the boundary conditions
The solution of a second-order equation y" = F(x, y, y′) generally involves two arbitrary constants. Conversely, if a two-parameter family of functions y(x) = G(x, c1, c2) with parameters c1 and c2 is differentiated two times and the parameters are eliminated from the three resulting equations, one will obtain a second-order differential equation that will be satisfied by all the functions in the family. For Problems 20–24, find the differential equation satisfied by each of the given families.
It is possible to solve a second-order differential equation of the form y" = F(x, y′) by letting v = y′, v′ = y″ and arriving at a first-order equation of the form v′ = F(x, v). If this new equation in v can be solved, it is then possible to find y by integrating dy/dx = v(x). Note that a constant will be obtained in solving the first-order equation in v, and another constant will be obtained in integrating dy/dx. For Problems 25–30, solve the given differential equations with missing y.
31. The Hanging Cable A cable hanging with its ends fastened can be shown to satisfy the equation
where y = y(x) describes the shape of the cable, called a catenary. The constant k > 0 is related to the size of the cable. If the ends of the cable are fastened at the two points (a, f(a)) and (b, f(b)), find the shape of the cable.
If a second-order equation has the form y" = F(y, y′), where the independent variable x does not appear explicitly in the equation, then it is possible to make the substitution y = v′ and obtain a first-order equation dv/dx = F(y, v). Since the new right-hand side depends on v and y, the trick is to think of y as the new independent variable and use the chain rule to rewrite the derivative as
For Problems 32–37, solve the given differential equations with missing x. When initial conditions are given, find the solution satisfying the stated conditions.
38. Constants of Motion Given the second-order equation
a function F(x, y, y′) is called a constant of motion* (or integral) of Eq. (21) if
on a given domain.
(a) Show that if y = Φ(x) is a solution of Eq. (21) and F is a constant of motion of Eq. (21), then the expression F(x, Φ(x), Φ′(x)) is a constant.
(b) Show that
is a constant of motion of my″ + ky = 0.
(c) Constants of motion are generally difficult to find and are relatively rare. One use of constants of motion is that they can sometimes be used to reduce the order of the equation by one. To illustrate this idea, solve the equation F(y, y′) = c for y in part (b), and substitute this into the differential equation my″ + ky = 0, getting a first-order equation.
For Problems 39–45, use the existence and uniqueness theorem (Theorem 3.2) to determine intervals for which a unique solution to the differential equation with initial conditions y(x0) = y0, y′(x0) = y′ is certain to exist.
46. Lagrange's Adjoint Equation Prove that if the function μ(x) satisfies
for some function g(x), then μ(x) must satisfy the adjoint equation
Hint: By equating coefficients in Eq. (22) and eliminating g(x), one arrives at Eq. (23).
47. Computer Problem Use a graphing calculator or computer to sketch the graph of the solution of part (a) of Problem 19. Is the graph consistent with the differential equation and boundary conditions?
48. Computer Problem Use a graphing calculator or computer to sketch the shape of a cable as found in Problem 31. Use different values of the parameter k. Is the shape of the cable consistent with your intuition?
49. Journal Entry Summarize the results of this section.
PURPOSE
To show that all solutions of the second-order linear homogeneous equation
can be written as a linear combination
of two linearly independent solutions y1 and y2.
This section provides much of the theory for the remainder of the chapter. Before actually solving a second-order equation, it is important to know what one is looking for—the nature of the beast, so to speak. We begin with the important concept of linear independence (and linear dependence). This concept is important not only in the study of linear differential equations, but in the study of other areas of applied mathematics as well.*
DEFINITION: Linear Independence and Dependence
Two functions f and g are said to be linearly dependent on an interval I if there exist two constants k1 and k2, not both zero, that satisfy
for all x in the interval I. Two functions f and g are said to be linearly independent on an interval I if they are not linearly dependent on I. That is, Eq. (1) holds for all x in I only for k1 = k2 = 0.
Note: The above definitions of linear independence and dependence can be extended to more than two functions. In the special case of two functions, linear dependence on an interval I simply means that one function is a constant multiple of the other function, and linear independence means that neither function is a constant multiple of the other. (See Problem 21 at the end of this section.)
Example 1
Linearly Dependent Functions Determine whether the following pairs of functions are linearly independent or dependent on (− ∞, ∞).
(a) 
(b) 
(a) By observing the graphs y = f(x) and y = g(x) we can see that neither function is a constant multiple of the other. Indeed, if a constant k did exist that satisfied
for all −∞ < x < ∞, then simply by letting x = 0 and x = 1 we would get the contradiction
Hence ex and x + 1 are linearly independent on (−∞, ∞). In fact, they are linearly independent on any interval.
(b) Since f(x) = sin 2x = 2 sin x cos x, we have f(x) = 2g(x) for all x. Hence they are linearly dependent on (−∞, ∞). In fact, they are linearly dependent on any interval.
Example 2
Linearly Independent Functions The following functions are linearly independent on any interval:
(a) 
(b) 
(c) 
(d) 
(e) 
(f) 
(g) 
Example 3
Linearly Dependent Fuinctions The following functions are linearly dependent on any interval:
(a) 
(b) 
(c) 
Although it is generally a simple matter to determine whether two functions are linearly dependent, there is a useful tool for determining linear independence or dependence of two functions.
DEFINITION: The Wronskian
Given two differentiable functions y, and V2, the function
is called the Wronskian of y1 and y2.
Since the Wronskian is a function of x, we often denote it by W[y1, y2](x), or simply by W(x) when no confusion exists.
Example 4
Sample Wronskian
(a) The Wronskian of y1(x) = sin x and y2(x) = cos x is
(b) The Wronskian of y1(x) = ex and y2(x) = e-x is
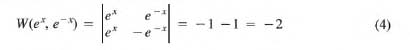
The importance of the Wronskian in the study of differential equations lies in the following theorem, which we state without proof.
THEOREM 3.3: Wronskian Test for Linear Independence
Assume that the coefficients p(x) and q(x) in the homogeneous equation
are continuous on (a, b) and that y1 and y2 are two given solutions. If any one of the following statements is true, then all of the others are also true.
• y1 and y2 are linearly independent solutions on (a, b).
• W[y1, y2](x) ≠ 0 for all x in (a, b).
• W[y1, y2](x0) ≠ 0 for at least one x0 in (a, b).
Note: Although we will not prove this theorem, note the interesting fact that if the Wronskian of two solutions is different from zero at a single point on an interval, then it will be different from zero at each point of the interval. (The reader can prove this in Problem 25 at the end of this section.) In other words, two solutions y1 and y2 of Eq. (5) are linearly independent on an interval I if and only if the Wronskian of y1 and y2 is not identically zero on I.
HISTORICAL NOTE
The Wronskian is named after the Polish mathematician |ozef Maria Hoene-Wronski (1778–1853). The Wronskian determinant was his sole contribution to mathematics. More a philosopher than a mathematician, he insisted that absolute truth could be attained only through mathematical reasoning. A gifted but troubled soul, his life was marked by heated disputes with individuals and institutions. He eventually went insane.
Wronskian Test for Linear Independence Show that the two functions y1(x) = sin x and y2(x) = cos x are linearly independent solutions of
on (−∞, ∞)
Solution By direct verification, y1 and y2 both satisfy Eq. (6). The Wronskian of y1 and y2 is
Since the Wronskian is never zero on (–∞, ∞), Theorem 3.3 guarantees that yx and y2 are linearly independent on (−∞, ∞).
We have seen that if two functions y1 and y2 are solutions of the second-order linear homogeneous equation, then every linear combination c1y1 + c1y2 of these functions is a solution. We now ask whether this collection of linear combinations includes all solutions of the equation. The answer to this important question is given in the following theorem.
THEOREM 3.4: Finding All Solutions of the Homogeneous Equation
If y1 and y2 are two linearly independent solutions of the linear homogeneous equation
on an interval (a, b) then any solution Y of the differential equation on the interval (a, b) can be expressed uniquely as a linear combination
for some constants c1 and c2.
PROOF: We must show that if y1 and y2 are linearly independent solutions of Eq. (8), then for any solution Y(x) of Eq. (8) it is possible to find two constants c1 and c2 such that Y(x) = c1y1(x) + c2y2(x). The idea behind the proof is to show there exist constants c1 and c2 so that both Y(x) and c1y1(x) + c2y2(x) satisfy the same initial conditions, and hence by uniqueness they must be the same function. To find such constants c1 and c2, we select an arbitrary point x0 in (a, b) and find c1 and c2 that satisfy
These two equations uniquely determine the constants c1 and c2, since by hypothesis, y1 and y2 are linearly independent on (a, b) and thus
Now, since both Y(x) and c1y1(x) + c2y2(x) satisfy the same differential equation (8) and have the same initial conditions (9), Theorem 3.2 from Section 3.1 says that we must have Y(x) = c1y1(x) + c2y2(x) for all x in (a, b). This proves the theorem.
Theorem 3.4 leads us to the following definition.
DEFINITION: Fundamental Set of Solutions
Any two linearly independent solutions y1 and y2 of
is called a fundamental set of solutions, and the collection of all linear combinations c1y1 + c2y2 that constitute the collection of all solutions of Eq. (11) is called the general solution.
Example 6
Fundamental Set of Solutions Show that the two functions y1(x) = ex and y2(x) = e-2x constitute a fundamental set of solutions of
and find the general solution.
Solution
First, we verify that both functions satisfy Eq. (12). Evaluating the Wronskian, we find
Since the Wronskian is nonzero at some point (in fact it's never zero), we conclude that ex and e-2x are linearly independent on (−∞, ∞). Hence ex and e-2x constitute a fundamental set of solutions of Eq. (12). Hence the general solution (all solutions) of Eq. (11) is
where c1 and c2 are arbitrary constants.
PROBLEMS: Section 3.2
For Problems 1–10, determine whether the functions f and g are linearly independent on (− 1, 1). Compute the Wronskian W(f, g).
For Problems 11–20, carry out the following steps.
(a) Verify that the functions y1 and y2are solutions of the specified differential equation.
(b) Verify that y1 and y2 are linearly independent.
(c) Find the general solution of the differential equation.
(d) Find the solution of the indicated initial-value problem.
21. Linear Dependence and Independence of Two Functions
(a) Show that if two functions/and g are linearly dependent on an interval, then one is a constant multiple of the other.
(b) Show that if neither of two functions is a multiple of the other on an interval, then the two functions are linearly independent on the interval.
22. More Than One Fundamental Set Consider the differential equation
(a) Show that both collections of functions {ex, e-x and {sinh x, cosh x} are fundamental sets of solutions.
(b) Are there any other fundamental sets of solutions?
23. Complex Fundamental Set of Solutions Consider the differential equation
Show that both collections of functions {eix, e-ix} and {sin x, cos x} are fundamental sets of solutions, where i is the complex constant i =
. Use Euler′s formulas:
24. Finding New Solutions from Old Ones Show that if y1(x) and y2(x) are linearly independent solutions of
then y3(x) = y1(x) + y2(x) and y4(x) = y1(x) – y2(x) are also linearly independent solutions.
25. Wronskian Identically Zero or Never Zero* A useful property of the Wronskian of two solutions y1(x) and y2(x) of
is that it is either identically zero for all x or never zero. Solve the following problems to verify this important property.
(a) First note that since y1(x) and y2(x) are solutions of Eq. (18), we have
Multiply the first equation in Eq. (19) by – y2 and the second by y1 and add. Now, noting that the derivative of the Wronskian can be written
show that the Wronskian W(x) satisfies the first-order equation
(b) Solve Eq. (20), getting the formula†
Hence, depending on whether the constant c is zero or nonzero, the Wronskian is either always zero or never zero.
26. Converting to Normal Form Show that the substitution y(x) = u(x)P(x), where
will transform the standard second-order linear homogeneous equation
into the second-order linear homogeneous equation in so-called normal form:
27. Exact Equations The differential equation
is called an exact equation if it can be written in the form
where g(x) is determined from p(x) and q(x). An exact equation can be integrated directly, getting a first-order linear equation. The first-order equation can then be integrated by using the integrating factor method from Chapter 2. For Problems 28–30, solve the following exact equations.
The concept of linear independence can be extended to more than two functions. We say that n functions y1 y2, …, yn are linearly dependent on an interval if there exist constants k1, k2, …, kn, not all zero, such that
for every x in the interval. Otherwise, they are called linearly independent.
For Problems 31–37, determine whether the following sets of functions are linearly independent or dependent.
38. Sturm's Claim In the 1800's the French mathematician Jacques Charles Sturm (1803–1855) studied the number of zeros (roots) of solutions of differential equations. Using nothing more than your intuition, can you say why Sturm claimed that any solution of the differential equation
would have an infinite number of roots?
39. Computer Problem Use a graphing calculator or computer to give you some idea whether the functions sin 2x and 3 sin x cos x are linearly independent or linearly dependent on the interval [0, 2π].
40. Journal Entry Summarize to yourself the concepts of linear independence and dependence. Can you relate these ideas to the study of vectors in the plane that you studied in calculus?
PURPOSE
To show how knowledge of one solution of the homogeneous linear equation
allows us to obtain a first-order equation in which one can (sometimes) find a second linearly independent solution.
In elementary algebra, knowledge that x = 1 is one root of the equation
allows one to find the other two roots by factoring out x – 1, getting
One can then solve the resulting quadratic equation, obtaining the second and third roots, x = –3, 2. Often in mathematics, knowledge of one solution of an equation provides means for finding other solutions.
In differential equations, reduction of order is a method whereby knowledge of one solution of a differential equation can be used to transform the equation to an equation of lower order from which the remaining solution(s) can (hopefully) be found. For instance, if we know one (nonzero) solution to a second-order linear homogeneous equation, the reduction of order method provides a systematic way to transform the second-order equation to a first-order equation. From this first-order equation it is possible to find a second linearly independent solution to the original equation.
We know that if y1 is a solution of
then so is cy1 where c is any constant. However, if we wish to find a second solution that is linearly independent of y1 we must pick a solution that is not of the form cy1. This suggests that we might replace the constant c by a. function and seek solutions of the form
where v is a differentiable function to be determined. We begin by computing y′, and y" which gives
HISTORICAL NOTE
The reduction of order method is due to the French mathematician, jean d′Alembert (1717–1783), who was a contemporary of Euler and Daniel Bernoulli. In 1 743 he published his Traité de dynamique, based on the now-famous principle of kinetics that bears his name. In 1 747 he studied vibrating strings, which led to the solution of the wave equation in partial differential equations. Any student who studies partial differential equations knows of the contributions of d′Alembert.
Substituting y, y′ and y" into Eq. (1) and collecting terms, we arrive at
Now since y1(x) is a solution of Eq. (1), the expression in the first set of parentheses in Eq. (2) is zero. Hence on any interval over which y1(x) does not vanish we can divide by y1(x), getting
Although Eq. (3) is a second-order equation in v, it is in fact a first-order equation in the derivative v′ Letting w = v′, we rewrite Eq. (3) as the first-order equation
But Eq. (4) is a first-order separable equation that can be solved by using either the integrating factor method or separation of variables. Using separation of variables, we arrive at
or
Finally, replacing w by v′ in Eq. (6) and integrating, we arrive at
This completes the method. We summarize the above discussion in the following theorem.
THEOREM 3.5: D′Alembert′s Reduction of Order Method
If a nonzero solution y1(x) of
is known, then a second linearly independent solution y2(x) can be found by substituting y2 = v(x)y1(x) into Eq. (8) and solving the resulting first-order separable equation in v′. Integrating v′ then gives v(x) from which the solution y2 = v(x)y1(x) can be found. Carrying out these steps, one arrives at
Normally, it is easier to carry out the steps described in Theorem 3.5 to find the second linearly independent solution y2(x) than to use the formula (9).
Reduction of Order Given that y1(x) = e3x is a solution of
find a second linearly independent solution. From the two linearly independent solutions, find the general solution.
Solution
One can easily verify that y1(x) = e3x is a solution of Eq. (10). To find a second linearly independent solution, let y = v(x)e3x. Differentiating, we get
Substituting y, y′, and y" into Eq. (10) gives
which simplifies to v" = 0. Solving this trivial differential equation for v(x) gives the expression v(x) = c1x + c2. And since we are interested in finding only one linearly independent solution, we simply pick c1 = 1, c2 = 0, which gives v(x) = x. Hence a second linearly independent solution is
which gives the general solution of Eq. (10) as
Example 2
Reduction of Order Given that y1 = ex is a solution of
on any interval not containing the origin, find a second solution. What is the general solution of this equation?
Solution
Letting
we compute
Substituting y, y′, and y″ into Eq. (12), we find
or
By letting w = v′, Eq. (13) can be written
Integrating, we obtain w = cx. Thus v′ = cx, and hence
Again, since we are interested only in finding one solution, we pick c = 2 and d = 0 for convenience, getting
Hence the general solution of Eq. (12) is
PROBLEMS: Section 3.3
For Problems 1–10, a differential equation and one solution are given. Use d’Alembert's reduction of order method to find a second linearly independent solution. What is the general solution of the differential equation?
| Differential equation | Solution |
1.  |
|
2.  |
|
3.  |
|
4.  |
|
5.  |
|
6.  |
|
7.  |
|
8.  |
|
9.  |
|
10.  |
|
11. Reducing the General Equation One solution of the equation
is y1(x) = ebx. Find a second linearly independent solution. What is the general solution?
It is possible to use the reduction of order method to find a single solution of the nonhomogeneous equation
knowing a nonzero solution y1(x) of the corresponding homogeneous equation
We use the same technique and substitute y(x) = v(x)y1(x) into Eq. (16), finding the unknown function v(x). For Problems 12–17, use this technique to find a solution of the given nonhomogeneous equation given the single solution y1(x) of the corresponding homogeneous equation.
| Nonhomogeneous equation | Homogeneous equation |
12.  |
|
13.  |
|
14.  |
|
15.  |
|
16.  |
|
17.  |
|
The equations in Problems 18–21 are some of the most famous differential equations in physics. Use the given solution y1(x) to find a second linearly independent solution of these equations.
18. Hermite's Equation of Order 2
19. Chebychev's Equation of Order 1
20. Laguerre's Equation of Order 1
21. Bessel's Equation of Order ½
For Problems 22–23, use the method of reduction to reduce the given third-order differential equation to a homogeneous linear equation of degree one less than the given degree. If possible, solve the lower-degree differential equation to find as many linearly independent solutions as the degree of the differential equation.
24. Interesting Equation A fascinating differential equation is
where n is a nonnegative integer.
(a) Verify that y1(x) = ex is a solution.
(b) Use the method of reduction to find a second solution of the form
(c) Calculate y2(x) for n = 1 and 2. Convince yourself (when c = − 1/n!) that y2(x) is the polynomial
This equation is interesting in that one solution is exwhile the second solution is the first n + 1 terms of the Maclaurin series for ex. (One wonders whether there are other differential equations that have one transcendental solution (In x, sin x, …) and a second solution that is a Taylor series polynomial approximation to the first solution.)
25. Another Way to Find a Second Solution Suppose y1(x) is a nonzero solution of
and y2(x) is a second linearly independent solution of the differential equation.
(a) Verify the identity
where W(y1 y2) is the Wronskian of y1(x) and y2(x).
(b) Use the formula in part (a) and Abel's formula
to find a second solution y2(x).
(c) Use the method discussed in parts (a) and (b) to find a second solution of
given that one solution is y1(x) = ex.
26. Solving Higher-Order Equations with Reduction of Order Let y1(x) be a solution of the ftth-order equation
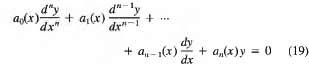
Substituting y(x) = y1(x)v(x) into Eq. (19) reduces the equation to a linear homogeneous equation of order n – 1 in v′(x). One can then solve this lower-order equation for v′(x) and then integrate to find v(x).
(a) Verify that Ji(x) = x is a solution of the third-order equation.
and show that by substituting y = y1v into Eq. (20), one arrives at the second-order equation in v′:
(b) Solve Eq. (21) for v′(x) and integrate to find two linearly independent solutions.
(c) Use the results from parts (a) and (b) to find the general solution to Eq. (20).
27. Computer Problem Use a graphing calculator or computer to sketch the graphs of the solutions y1(x) and y2(x) on 0 < x ≤ 1 of the differential equation in Problem 24 for n = 1, 2, 3, and 4.
28. Journal Entry Discuss how differential equations are used in your major area of interest. Are differential equations essential for an understanding of your major area of interest? Remember, your journal entry is for your own benefit.
PURPOSE
To find the general solution of the second-order linear homogeneous equation with constant coefficients
when the roots of the characteristic polynomial
are real and unequal and when they are real and equal.
We have seen that the general solution of the second-order linear homogeneous equation is a linear combination of two linearly independent solutions. In this and the next section we will actually find the general solution for second-order linear equations with constant coefficients. The corresponding problem with variable coefficients is more difficult, and in Chapter 4 we will study the special case in which the coefficient functions are analytic.
Consider solving the second-order linear homogeneous equation
where a, b, and c are constants with a ≠ 0. That is, we seek a function y(x) whose second derivative times a, plus its first derivative times b, plus itself times c is identically zero. Stated in this way, it seems natural to seek a function whose derivatives are constant multiples of itself. That is, we look for solutions* of the form
We have that y(x) = emx is a solution of Eq. (1) if and only if
or, equivalently,
But since emx is never zero, we conclude that y(x) = emx is a solution of Eq. (1) if and only if m satisfies the characteristic equation
Solving the characteristic equation, we get
We must consider three cases: when the roots are real and distinct, when the roots are real and equal, and when the roots are complex. The reader will recall that the nature of the roots depends on whether the discriminant, D ≡ b2 − 4ac, is positive, zero, or negative. In this section we consider the cases in which the roots are real and unequal (D > 0) and real and equal (D = 0).
We first consider the case in which the roots of the characteristic polynomial are real and unequal.
CASE 1: Real and Unequal Roots (b2 − 4ac > 0)
If the characteristic equation of
has real and distinct roots r1 and r2, er1x and er2x are linearly independent solutions of Eq. (5), and the general solution is
where c1 and c2 are arbitrary constants.
Example 1
Real and Unequal Roots Find the general solution of
Solution
The characteristic equation of Eq. (6) is
which has two real roots r1 = −6, r2 = 1. Hence two linearly independent solutions are
and the general solution is
Initial-Value Problem Solve the initial-value problem
Solution
The characteristic equation is m2 − 1 = 0, which has roots r1 = −1 and r2 = 1. Hence the general solution is
To obtain c1 and c2, we first differentiate y(x), getting
Substituting y(x) and y′(x) into the initial conditions, we obtain
Solving this linear system gives cx = c2 = ½. Hence the solution is
We now consider the equation
in which the roots of the characteristic equation are real and equal. This happens when D = b2 − 4ac = 0, which results in the single root r = − b/2a, which we call a repeated root. From this root we obtain one nonzero solution, y = e-(b/2a)x To find a second linearly independent solution, it is possible to use the reduction of order method and seek a second solution of the form
Differentiating Eq. (12), we obtain
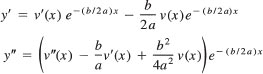
Substituting y, y′, and y" into
Collecting terms, we find
However, since b2 − 4ac = 0, this equation reduces to
Hence
where c1 and c2 are arbitrary constants. Since we are interested only in finding one solution, we pick c1 = 1 and c2 = 0, which gives v(x) = x. Hence we obtain a second solution
Thus the general solution of Eq. (13) is
These ideas are summarized below.
CASE II: Repeated Roots (b2-4ac = 0)
If the characteristic equation of
has repeated roots r = − b/2a, then Eq. (17) has two linearly independent solutions:
The general solution is
where c1 and c2 are arbitrary constants.
Example 3
Repeated Roots Find the general solution of
The characteristic equation
has repeated roots r1 = r2 = −2. Hence two linearly independent solutions are
and the general solution is
PROBLEMS: Section 3.4
For Problems 1–19, find the general solution of the given differential equation. When initial conditions are given, find the solution that satisfies the stated conditions.
20. Alternative Way of Writing the General Solution Show that the general solution of
can be written as
One of the most famous differential equations is Euler's equation:
where a ≠ 0, b, and c are constants. Show that Euler's equation has solutions of the form xr, which can be found by substituting xr into Eq. (20) and obtaining the characteristic equation
Hence if Eq. (21) has two distinct roots r1 and r2, then the general solution has the form
where c1 and C2 are arbitrary constants. Problems 21–23 involve Euler′s equation.
21. Finding Euler′s Characteristic Equation Substitute xr into Euler′s equation and show that r satisfies the characteristic equation (21).
22. Solving Euler′s Equation Solve the following Euler equations.
(a) 
(b) 
(c) 
23. Transforming Euler′s Equation
(a) Show that by making a change in the independent variable, Euler′s equation (20) can be transformed into the constant coefficient equation
by the substitution x = er. Hint: Show x dy/dx = dy/dt and x2 d2y/dt2 = d2y/dt2 − dy/dt.
(b) Use the result from part (a) to solve the Euler equation
24. Just a Final Test of Your Intuition We have two curves. The first curve starts at y(0) = 1, and its rate of increase is equal to its height, that is, it satisfies the first-order equation y′ = y. The second curve starts at the same point y(0) = 1 with y′(O) = 0, and its upward curvature is equal to its height, that is, it satisfies the second-order equation y" = y. Which curve lies above the other? Make a guess before resolving the question mathematically.
25. Journal Entry Without looking at the text, summarize this section to yourself in your own language.
PURPOSE
To find the general solution of the equation
when the roots of the characteristic equation are complex. If the roots are given by r1 = p + iq and r2 = p − iq, then we shall show that the general solution is
where c1 and c2 are arbitrary constants.
Until now, solutions of the differential equation
have consisted mostly of growth and decay type curves, such as e2x, e–x, or xe–3x. Now things are going to change, and we will obtain solutions that one often associates with second-order phenomena such as oscillating circuits, vibrating springs, and periodic motion of a pendulum.
Consider the case in which the discriminant, D = b2 − 4ac, of the characteristic equation
is negative. In this case the two roots are the complex conjugate numbers*
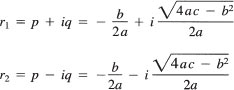
where i is the complex constant i = 
. Hence the general solution of Eq. (1) is
where c1 and c2 are arbitrary constants. We should point out that this function is a complex-valued function of the real variable x, whereas up to this point, all functions considered have been real-valued. Again, we advise readers who feel uncomfortable with complex numbers and functions to spend a brief time reading the Appendix at the back of the book.
Assuming now more familiarity with complex functions, we will show how it is possible to rewrite the complex-valued function in Eq. (3) in a more convenient form using (arguably) the most famous equation in mathematics, Euler's formula:
Using Euler's formula, we rewrite Eq. (3), getting
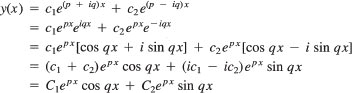
where C1 = c1 + c2 and C2 = ic1 − ic2. Since c1 and c2 are arbitrary constants, the new constants C1 and C2 are also arbitrary. We summarize these ideas.
CASE III: Characteristic Equation with Complex Roots
If the characteristic equation of the differential equation
has complex roots p ± iq, then Eq. (5) has two linearly independent solutions
The general solution of Eq. (5) is
where c1 and c2 are arbitrary constants.*
Because of the importance of Euler′s formula in mathematics, we present its proof.
THEOREM 3.6: Euler′s Formula
If x is any real number, then
PROOF: It is possible to expand the complex function eix by using the Taylor series expansion from calculus to get
This completes the proof. We can also replace x by - x to obtain a second formula*
Example 1
Complex Roots Find a general solution to
Solution
The roots of the characteristic equation
are
Since p = - 1 and q = 
, the general solution is
HISTORICAL NOTE
Leonhard Euler (1707–1783) was born in Basel, Switzerland, and studied under Johann Bernoulli. Euler, one of the greatest mathematicians of all time, was responsible for relating the three most famous constants of mathematics in a single equation: e2πi = 1. Today, students of mathematics often wear T-shirts bearing the slogan "Mathematicians-We′re Number e2πi.”
Complex Roots Find the solution to the initial-value problem
Solution
The roots of the characteristic equation m2 + 1 = 0 are r = ± 2i. Hence we identify p = 0 and q = 2, getting the general solution
where c1 and c2 are arbitrary constants. Substituting Eq. (11) into the initial conditions, we get
or
Hence the solution to the initial-value problem is
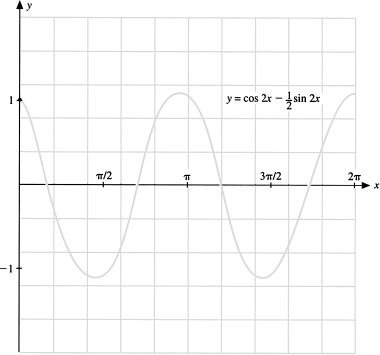
The graph of this function is shown in Figure 3.2.
Figure 3.2 Solution of the initial-value problem
Finally, Table 3.1 summarizes the general solution of the second-order linear differential equation with constant coefficients.
Table 3.1 General Solution of the Equation ay” + by' + cy = 0
PROBLEMS: Section 3.5
For Problems 1–15, determine the general solution of the given differential equation. If initial conditions are given, find the solution satisfying the stated conditions.
1. y″ + 9y = 0
2. y″ + y' + y = 0
3. y″ - 4y' + 5y = 0
4. y″ + 2y' + 8y = 0
5. y″ + 2y' + 4y = 0
6. y″ - 4y' + 7y = 0
7. y″ - 10y' + 26y = 0
8. 3y″ + 4y' + 9y = 0
9. y″ - y' + y = 0
10. y″ + y' + 2y = 0
11. y″ + 4y = 0 y(0) = 1 y'(0) = –1
12. y″ - 4y + 13y = 0 y(0) = 1 y'(0) = 0
13. y″ + 2y' + 2y = 0 y(0) = 1 y'(0) = 0
14. y″ - y' + y = 0 y(0) = 1 y'(0) = 0
15. y″ - 4y' + ly = 0 y(0) = – 1 y'(0) = 0
16. Change of Variables Method Solve
by letting v = dy/dx and rewriting
Show that the general solution can be written in the form
where A and α are arbitrary constants.
17. An Interesting Equation* Solve
Hint: Differentiate Eq. (15) with respect to x and then substitute Eq. (15) into the differentiated equation to find an equation you can solve.
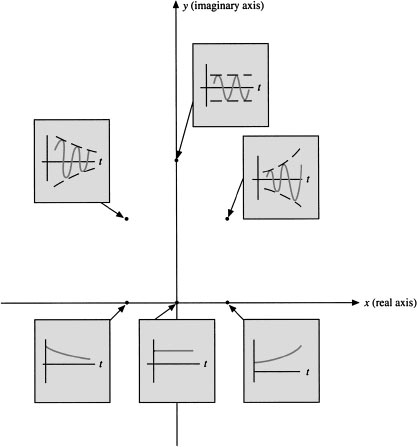
18. Nature of Solutions Figure 3.3 shows the qualitative nature of the solutions of
as a function of the roots r1 and r2 of the characteristic equation.
The solutions can be categorized as belonging to one of eight different cases:
(i) r1 < 0, r2 < 0
(ii) r1 < 0, r2 = 0
(iii) r1 = 0, r2 = 0
(iv) r1 = 0, r2 > 0
(v) r1 > 0, r2 > 0
(vi) r1, r2 = p ± iq (p < 0)
(vii) r1, r2 = p ± iq (p = 0)
(viii) r1, r2 = p ± iq (p > 0)
(a) Which cases approach zero as t → ∞?
(b) Which cases approach ∞ at t –> ∞?
(c) Which cases have damped oscillations?
(d) Which cases have oscillations that get larger?
Figure 3.3 Qualitative nature of the solution as a function of the roots of the characteristic equation
19. Riccati Equation
(a) Show that the substitution
transforms the equation
into the Riccati equation
Hence if one can solve the Riccati equation for v, then one solution of Eq. (17) can be found by simply evaluating y in Eq. (16).
(b) Transform
to a Riccati equation and solve the Riccati equation by inspection.
(c) Find one solution of Eq. (19).
(d) Find a second solution of Eq. (19).
20. Lesson in Complex Numbers Use Euler's formula to show that any complex number x + iy can be written in exponential form reiθ, where r≥0 and −π < θ≤π. Use this result to write the following complex numbers in exponential form.
(a) i
(b) – i
(c) –3
(d) 1 + i
(e) 1 – i
(f) – 1 + i
When the solution of a differential equation is specified at more than one point, these conditions are called boundary conditions, and the problem of finding the solution of the differential equation that also satisfies the boundary conditions is called a boundary-value problem.
21. The Easiest Boundary-Value Problem Anyone can solve this boundary-value problem. Plot the two points (0, 0) and (1, 1) in the xy-plane and connect them with a straight line. Congratulations! You have just solved the boundary-value problem
Can you find the formula for your solution?
22. Typical Boundary-Value Problem Given that the general solution of differential equation
is
where cl and c2 are constants, verify the following.
(a) There is exactly one solution of Eq. (20) that satisfies the boundary conditions y (0) = 1 andy(π/2) = 0.
(b) There are infinitely many solutions of Eq. (20) that satisfy the two boundary conditions y(0) = 1 and y(π) = –1.
(c) There are no solutions of Eq. (20) that satisfy the boundary conditions y(0) = 1 and y(π) = 0.
23. Journal Entry Summarize what you know about the solution of ay″ + by' + cy = 0.
PURPOSE
To show that the general solution of the second-order linear nonhomogeneous equation
has the form
where y1 and y2 are linearly independent solutions of the corresponding homogeneous equation
and yp(x) is any single solution of the nonhomogeneous equation.
In applied mathematics the differential equation
is often thought of as an input-output system in which the nonhomogeneous term f(x) represents the input to the system and the solution y(x) represents the output of the system resulting from f(x). See Figure 3.4.
Figure 3.4 A nonhomogeneous linear differential equation can be interpreted as a linear inputoutput system in which the nonhomogeneous term is the input and the solution of the equation is the output of the system
We have seen that linear homogeneous differential equations obey the principle of superposition. We now introduce a version of this principle that is satisfied for non-homogeneous linear equations. In terms of linear input-output systems the principle of superposition says the following.
DEFINITION: Superposition Principle for Input-Output Systems
1. Scalar Property of Superposition. If an input f gives rise to an output y, then the input ky gives rise to the output ky, where k is any constant.
2. Additive Property of Superposition. If the input f1 gives rise to an output y1 and f2 gives rise to the output y2, then f1 + f2 will give rise to the output of y1 + y2.
Roughly stated, the scalar property says that if you double (triple, etc.) the input, you wiJl double (triple, etc.) the output, and the additive property says that the sum of two inputs gives rise to the sum of the outputs. Stated in terms of differential equations, we have the following.
THEOREM 3.7: Superposition Principle for Nonhomogeneous Linear Equations
Scalar Property: If y is a solution of
then ky is a solution of
for any constant k.
Additive Property: If yt(x) is a solution of
and y2(x) is a solution of
then y1(x) + y2(x) is a solution of
PROOF: Both properties can be verified by using properties of the derivative. See Problem 11 at the end of this section.
Note: The scalar and additive properties of the principle of superposition can be combined by stating that if y1 and y2 are both solutions of the equation 
respectively, then 
where c1 and c2 are arbitrary constants.
Example 1
Principle of Superposition If
has a solution y1(x) = ½x – 1 and
has a solution 
, find a solution of
Solution
Note that the right-hand side, 5x + 3ex, of Eq. (4) can be written as 5f1(x) + 3f2(x), wher tfi(x) and/2(x) are the right-hand sides of Eqs. (2) and (3), respectively. Hence by the principle of superposition we have
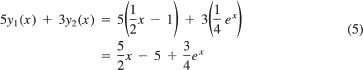
is a solution of Eq. (4).
Thus far we have studied mainly the homogeneous linear equations. We now pursue a comprehensive understanding of the nonhomogeneous linear equation
Since the form of the general solution of Eq. (6) often causes some bewilderment to beginning students, we start with a brief discussion of the general solution of a linear system of two algebraic equations.
General Solution of Nonhomogeneous Linear Systems
Consider for a moment the two simultaneous equations
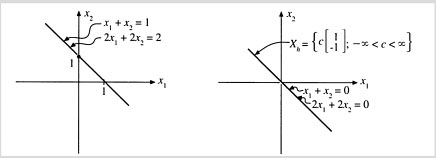
At first glance you may think that something is wrong, since the equations are in fact the same. This is intentional, however, and in fact the system is mathematically equivalent to the single equation x1 + x2 = 1. Hence the general solution (all solutions) of this trivial system (7) consists of the points on the line x1 + x2 = 1. See Figure 3.5(a).
Figure 3.5 The general solution of a linear system is the sum of all the homogeneous solutions plus any nonhomogeneous solution
(a) To find all the solutions of a nonhomogeneous linear system of equations …
(b) First find all the solutions of the corresponding homogeneous system. Call these solutions Xh.
Now suppose we solve the corresponding homogeneous system to Eqs.
(7). In other words,
The general solution (all solutions) of this homogeneous system (8) consists of all points on the line x1 + x2 = 0, which we can write in vector form as
where c is an arbitrary constant. See Figure 3.5(b). Now, let us find just one solution of the original nonhomogeneous system (7). We don't care which one—select any one. Picking one particular solution from an infinite number of solutions, we have
Figure 3.5 (continued)
See Figure 3.5(c). If we now add all the solutions Xh of the homogeneous linear system (8) to the single particular solution Xp of the original system
(7), we get the general solution (all solutions) X = Xh + Xp of the original system (7), which is
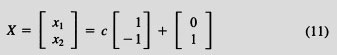
Of course, this equation is simply the straight line x1 + x2 = 1, which is drawn in Figure 3.5(d). What we have seen is that the general solution of the nonhomogeneous linear system (7) can be written as the general solution of the corresponding homogeneous system, plus any particular solution of the original nonhomogeneous system. The important observation in this example is that solutions of all linear systems, whether they be linear algebraic equations or linear differential equations, have the same general form.
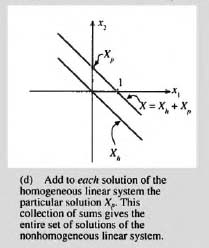
The above discussion now leads to the general solution of the nonhomogeneous differential equation.
THEOREM 3.8: Solution of the Nonhomogeneous Equation
If yp(x) is a particular solution (any single solution) of the nonhomogeneous equation
on an interval (a, b) and if y1,(x) and y2(x) are linearly independent solutions of the corresponding homogeneous equation
then any solution Y(x) of the nonhomogeneous equation (12) can be written in the form
where c1 and c2 are arbitrary constants. The collection of all solutions of the nonhomogeneous equation is called the general solution of the equation. Since the general solution of the corresponding homogeneous equation can be written as
one can also write the general solution of the nonhomogeneous equation in the form
PROOF: Since both Y(x) and yp(x) satisfy Eq. (12), we have
Subtracting (17b) from (17a), and after using a few simple properties of the derivative, we get
Hence we have proven that the difference between any two solutions of the nonhomogeneous equation (12) is a solution of the corresponding homogeneous equation (13). This is very important, since we know from Theorem 3.4 in Section 3.2 that any solution of the homogeneous equation (13) can be expressed uniquely as a linear combination of y1(x) and y2(x). Hence we can write
or
Using Theorem 3.8 as a guide, we now list the steps required to find the general solution of the nonhomogeneous equation.
Method for Solving Nonhomogeneous Equations
To solve the nonhomogeneous linear equation
carry out the following steps.
Step 1. Find the general solution
of the corresponding homogeneous equation
Step 2. Find any solution yp(x) of Eq. (20).
Step 3. Add the results from Steps 1 and 2, getting
Example 2
General Solution of a Nonhomogeneous Equation From inspection we see that yp(x) = 1 is a (particular) solution of
Find the general solution.
Solution
The corresponding homogeneous linear equation.
has the general solution
Hence the general solution of the nonhomogeneous solution is
PROBLEMS: Section 3.6
For Problems 1–10, find the general solution (all solutions) of the given nonhomogeneous equation. A single solution is given for each equation.
11. Proving the Superposition Principle Prove that if y1(x) is a solution of
and y2(x) is a solution of
then y(x) = c1y1(x) + c2y2(x) is a solution of
12. Applying the Superposition Principle Given that
find solutions of the following equations:
(a) 
(b) 
(c) 
13. Reduction of Order for Nonhomogeneous Equations
This problem shows how the reduction of order method can also be applied to the nonhomogeneous equation
(a) Make the substitution y = vy1 where y1 is a solution of the corresponding homogeneous equation, and reduce Eq. (24) to a first-order linear homogeneous equation in v.
(b) Given that y1(x) = x is a solution of
use the method of substitution described in part (a) to find the general solution of
We have seen that the general solution of a nonhomogeneous linear equation can be written as the sum of the solution of the corresponding homogeneous equation, plus any particular solution of the nonhomogeneous equation. For Problems 14&19, find the general solution of the given nonhomogeneous equation by adding the general solution of the corresponding homogeneous equation and any particular solution of the nonhomogeneous equation.
14. y′ = 1
15. y" = 1
16. y′ + y = 1
20. Journal Entry Summarize in your own words the theory of nonhomogeneous linear systems.
PURPOSE
To present a simple procedure for finding a particular solution yp(x) of the linear nonhomogeneous equation
when the nonhomogeneous term f(x) is either xn, eax, sin β x, cos β x, or products of these functions.
In the previous section we saw that the general solution of the nonhomogeneous equation is the sum of the solution of the corresponding homogeneous equation plus any particular solution of the nonhomogeneous equation. In this section we will learn how to find a particular solution to a nonhomogeneous equation with constant coefficients when the nonhomogeneous term f(x) is itself a solution of some linear differential equation with constant coefficients; that is, it is either a polynomial, an exponential, a sine or cosine, or some product of these functions. The method studied is called the method of undetermined coefficients.*
Example 1
Finding a Solution by inspection Find a particular solution of the differential equation
Solution
It is sometimes (but not often) possible to find a single solution by simple inspection. For this equation it is obvious that the constant function yp(x) = 2/3 is a solution. If we suspect that the equation has a constant solution but do not know what constant, we can try substituting a trial solution, yp(x) – A, into Eq. (1). If the constant A, called an undetermined coefficient, is to satisfy the equation, it must have the value 0 + 3A = 2, or A = 2/3.
Example 2
An Exponential Nonhorrsogeneoys Term Find a single solution of
Solution
Since the derivatives of the nonhomogeneous term 2e3x are multiples of the term (i.e., 6e3x, 18e3x,…), we suspect the equation should have a solution of the form
To find the value of A that makes Ae3x a solution, we substitute it into Eq. (2) and find
Eliminating the common factor e3x, we find A = 1/10. Hence one solution to Eq. (2)
is
Example 3
A Polynomial Nonhomogeneous Term Find a single solution of
Solution
Since the first and second derivatives of the nonhomogeneous term 2x2 are polynomials of degree one and zero, we seek a solution of the form
Substituting yp, yp′, and yp" into Eq. (5) gives
Rewriting this equation in terms of 1, x, and x2 gives
Setting the coefficients of 1, JC, and x2 equal to one another,* we have
Solving for A, B, and C from Eq. (8) gives A = 1, B = 4, and C = 7. Hence one solution is
The method of undetermined coefficients can also be used when the nonhomogeneous term involves a sine or cosine function.
Example 4
Sine or Cosine Nonhomogeneous Term Find a particular solution of
Solution
Since the derivatives of sin 2x are constant multiples of sin 2x and cos 2x, we seek a solution of the form
Differentiating gives
Substituting yp, y'p, and y″p into the differential equation gives
Rewriting this, we obtain
Setting the coefficients of the linearly independent functions sin 2x and cos 2x equal to each other gives
Solving for A and B, we get A = - 14/17, B = 12/17. Hence we have a solution
Example 5
Combination Nonhomogeneous Term Find a particular solution of
Solution
Using our experience from the previous examples, we seek a solution of the form
where we keep not only the term Axelx but the term Belx as well. Differentiating yp, we find
Substituting yp, yp′, and y” into the differential equation (14), we find
Rewriting in terms of e2x and xe2x, we find
Setting the coefficients of the linearly independent functions e and xe2x equal to each other gives
Solving for A and B gives A = 1/2 and B = - 1/4. Hence we have found a solution
The following example is not quite so easy.
Example 6
Nonhomogeneous Term Agrees with a Homogeneous Solution Find a solution of the differential equation
Solution We try
Differentiating, we get
Substituting yp, y'p, and y″p into Eq. (16) gives
or
or simply
0 = 1
Hence the equation has no solution of the form yp = Ae–x. The difficulty comes about from the fact that the nonhomogeneous term e ′ is also a solution of the corresponding homogeneous equation y″ – 3y' – Ay = 0, which has the solution yh = cxe–x + c2e4x. One might suspect that a trial solution of the form Ae–x would fail in this case, since it does not contribute anything “new” to the homogeneous solution yh. After trial and error, however, we discover that the equation does have a solution of the general form
Differentiating, we get
Substituting into the differential equation (16), we find
or
Setting coefficients of e-x and xe-xequal, we find
0 = 0
– 5A = 1
from which we conclude that A = – 1/5. Hence Eq. (16) has a solution
Table 3.2 summarizes the general rules we have alluded to in this section.
Table 3.2 Form of a Particular Solution yp of the Differential Equation ay″ + by' + cy = f(x)
Example 7
Using the Table Find the general solution of
Solution
Finding the solution of the corresponding homogeneous equation, we get
To find a single solution of the nonhomogeneous equation (19), it is clear that neither function of the form Aex or Axex is a solution, since both ex and xex are solutions of the homogeneous equation. However, when we look at Type 3 in Table 3.2, we are instructed to try a solution of the form
Substituting yp(x) into Eq. (19) results (after some computation) in A = 1/2. Hence a particular solution is
Correct Form for a Particular Solution Determine the form of a solution yp(x) of the equation
where f(x) is given as
(a) x2 + x – 3
(b) e– x
(c) xe– x
(d)2x sin 3x + cos 3x
(e)xe–2x sin x
Solution
First, it is necessary to find the solution of the homogeneous equation
which is
(a) 
Referring to Table 3.2, we recognize that f(x) is of Type 2. Since no terms in f(x) agree with any terms in yh(x), it is not necessary to multiply by x or x2. In other words, s = 0. Hence yp(x) has the form yp(x) = A0x2 + A1x + A2.
(b) 
The function f(x) is of Type 3 with a = 1 and α = – 1. And since e–x does not occur in the homogeneous solution (25), it is not necessary to multiply by x or x2. In other words, s = 0. Hence a solution can be found having the form
yp(x) = Ae–x
(c) 
The function f(x) is of Type 5. However, since the second term of (A0x + A1)ex also occurs in the homogeneous solution (25), we must multiply by x(s = 1), getting yp(x) = (A0x2 + A1x) ex.
(d) 
The terms of f(x) are of Types 6 and 7; both of these terms give rise to the same particular solution. Hence we choose (s = 0)
(e) 
The terms of f(x) are of Type 8, and so we choose (s = 0)
We summarize the method of undetermined coefficients.
Method of Undetermined Coefficients
The following are steps for finding a particular solution of the second-order linear equation with constant coefficients
where the nonhomogeneous term f(x) is a polynomial, exponential, sine, or cosine function or some product of these functions.
Step 1. Solve the corresponding homogeneous equation.
Step 2. Pick the form for a particular solution yp(x) depending on the nonhomogeneous term f(x). Remember that no term in the particular solution may also be a solution of the homogeneous equation. If agreement occurs, multiply yp(x) by x.
Step 3. Substitute yp(x) and its derivatives into the differential equation and set the coefficients of the algebraic expressions on each side of the equation equal to each other, getting a system of equations for which one can solve for the undetermined coefficients.
Step 4. Solve the system of equations for the undetermined coefficients.
It is possible, using the principle of superposition, to use the method of undetermined coefficients when the nonhomogeneous term contains sums of the forms described in the previous rules. The following example illustrates this idea.
Example 9
Using the Principle of Superposition Find a particular solution to the equation
Solution
Observe that the solution of the corresponding homogeneous equation is
To construct a particular solution of the nonhomogeneous equation (26), we use the principle of superposition and find particular solutions yPl(x) and yP2(x) of the two equations
Particular solutions of Eqs. (28) and (29) are
respectively. Hence a particular solution yp(x) of Eq. (26) is
PROBLEMS: Section 3.7
For each differential equation in Problems 1–21, find the general solution by finding the homogeneous solution and a particular solution.
For Problems 22–28, find the solution to the initial-value problem.
For Problems 29–38, determine the form of the particular solution yp(x). Do not actually determine the values of the coefficients.
There is a nice way to solve linear nonhomogeneous equations with constant coefficients whose right-hand sides consist of sine and cosine functions.
The idea is to solve a modified equation in which we replace the sine or cosine term on the right-hand side of the original equation by the complex exponential function Reiqx:
Equation (32) is then solved in the usual manner: A particular solution to the nonhomogeneous equation is sought of the form yP(x) = Aeiqx, where the complex constant 
is treated the same as any real constant. The important fact here is that the real part of the solution to Eq. (32) is the solution to Eq. (31) with the cosine term on the right-hand side and the complex part of the solution to Eq. (32) is the solution to Eq. (31) with the sine term on the right-hand side. For Problems 39–41, use this idea to find the solutions to the given equation.
42. Importance of Complex Exponents Solve the differential equation
and verify the real and complex parts of the solution are the solutions obtained when the right-hand side is replaced by 3 cos 2x and 3 sin 2x, respectively.
43. In Honor of Charles Proteus Steinmetz* In electrical engineering it is known that if a periodic electromotive force E = E0 cos wt, acts on a simple circuit containing a resistor with resistance R, an inductor with inductance L, and a capacitor with capacitance C, then the charge q on the capacitor is governed by the second-order equation
Show that a particular solution of this equation is
where
by finding a particular solution of the related equation
and then taking the real part.
44. Useful Property of Linear Independence Show that if the functions {f1(x), f2(x), f3(x), …, fn(x)} are linearly independent on an interval I, then
implies ai = bi for i = 1, 2, …, n. This is why it is valid to set the coefficients of terms equal to each other in finding the undetermined coefficients.
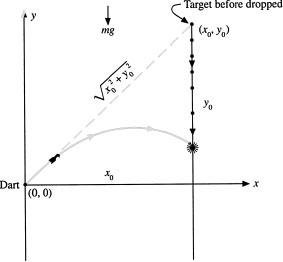
45. The Surefire Strategy Neglecting air friction, the planar motion (x(t), y(t)) of an object in a gravitational field is governed by the two second-order differential equations
where the “double dot” notation denotes the second derivative with respect to time and g is acceleration due to gravity. See Figure 3.6. Suppose you fire a dart gun, located at the origin, directly at a target located at (x0, y0). Suppose the dart has a velocity v and at the exact instant the dart is fired, the target starts falling.
(a) Find the heights of the dart and the target.
(b) Show that the dart will always hit the target (assuming that negative values of y are valid).
(c) At what height will the projectile hit the target?
46. Journal Entry Summarize the method of undetermined coefficients. Do you think it would be possible to write a computer program to evaluate the undetermined coefficients so that one could simply enter into a computer a certain differential equation and the computer would print out the solution?
Figure 3.6 The correct way to fire a projectile at an object that begins to fall at the instant of firing is to aim directly at the object
PURPOSE
To present a powerful technique, known as the method of variation of parameters, for finding a particular solution of the form
to the nonhomogeneous differential equation
where y1(x)and y2(x) are linearly independent solutions of the corresponding homogeneous equation and v1(x) and v2(x) are functions to be determined.
VARIATION OF PARAMETERS
In the previous section we discussed a simple method for finding a particular solution to a linear nonhomogeneous equation with constant coefficients, provided that the nonhomogeneous term had a special form. In this section we consider a method for finding a particular solution to the more general equation.
where p(x), q(x), and f(x) are continous functions. In addition to allowing variable coefficients p(x) and q(x), the nonhomogeneous term f(x) is not restricted as it is in the method of undetermined coefficients.
As did the method of undetermined coefficients, the method of variation of parameters requires knowledge of two linearly independent solutions and y2(x) of the corresponding homogeneous equation
from which one can find the general solution*
where c1 and c2 are arbitrary constants. The method of variation of parameters seeks to find a solution of the nonhomogeneous equation (1) by replacing the constants c1 and c2 in Eq. (3) by unknown functions v1(x) and v2 (x), thus obtaining an expression of the form
The unknown functions V1(x) and v2(x) are often called parameters, since they were initially intended by Lagrange to be “constants that vary.” Lagrange's strategy was to
substitute Eq. (4) into the nonhomogeneous equation (1) and solve for v1(x) and v2(x). It turns out that and v2(x) can be found quite easily.
HISTORICAL NOTE
The method of variation of parameters (or variation of constants) was formulated by the great Italian-French mathematician, Joseph Louis Lagrange (1 7361813). The two great mathematicians of the seventeenth century were Lagrange and the Swiss mathematician Leonhard Euler (1 707–1 783). Although Euler discovered the general solution to the homogeneous differential equation ay″ + by' + cy = 0, it was Lagrange who found a particular solution to the nonhomogeneous equation.
Carrying out Lagrange's strategy we differentiate Eq. (4), getting
We now choose v1 and v2 so that they satisfy
thus making the second derivative y″p more manageable.* With this condition imposed on v1 and v2, the second derivative becomes
As a result of condition (6), only the first derivatives or V1 and v2 appear in the expression for y″p. Substituting y'p and y″p into Eq. (1) leads to the second condition on v1, and v2:
Rewriting Eqs. (6) and (8), we arrive at the system of equations
in which we have interchanged the order of the factors to denote that the two derivatives v1′ and v2′ are the unknown functions. Note that all the other quantities are known. Solving this system of equations gives
where W(y1, y2) = y1y'2 – y'1y2 is the Wronskian of y1 and y2. Note that since y1 and y2 are linearly independent solutions of the homogeneous equation, we know that W(y1, y2) will not vanish on the interval of interest. Finally, integrating Eq. (10) and substituting V1 and v2 into Eq. (4), we find a particular solution to Eq. (1). We summarize this discussion in the following theorem.
THEOREM 3.9: Method of Variation of Parameters
If p(x), q(x), and f(x) are continuous functions and if y1(x) and y2(x) are linearly independent solutions of the homogeneous equation corresponding to the nonhomogeneous equation
then a particular solution of Eq. (11) is
The following examples illustrate the method of variation of parameters.
Example 1
Variation of Parameters Find the general solution of
Solution
The two linearly independent solutions y1 and y2 of the corresponding homogeneous equation y″ + y = 0 are y1(x) = cos x and y2(x) = sin x. Note that we cannot use the method of undetermined coefficients, since the right-hand side is not of the proper form. Using the method of variation of parameters, we write
For Eq. (14) to satisfy Eq. (13) we must have that v1 and v2 satisfy
Solving for v′1 and v2′, we obtain
Integrating this gives
Finally, substituting these values into yp, we have the particular solution
Example 2
Variation of Parameters Find the general solution of the nonhomogeneous Euler equation
given that y1(x) = x and y2(x) = x2 are linearly independent solutions of the corre sponding homogeneous Euler equation.
Solution
Substituting
into Eq. (19) gives the two equations
Solving these equations for v′1 and v′2 gives
or
Hence we find the particular solution
Adding this to the homogeneous solution, we obtain the general solution
We have now come to the end of the line in our search for the general solution to the differential equation
To use the method of variation of parameters, we assume without loss of generality* that a = 1. Table 3.3 summarizes the steps we have used in this chapter.
Table 3.3 Steps for Finding the General Solution to the Differential Equation y″ + by' + cy = f(x)
PROBLEMS: Section 3.8
For Problems 1–12, use the method of variation of parameters to find a particular solution of the given nonhomogeneous equation. Then find the general solution of the equation.
For Problems 13–17, find a particular solution of the nonhomogeneous equation, given that the functions y1(x) and y2(x) are linearly independent solutions of the corresponding homogeneous equation. Note: The coefficient of y″ must always be 1, and hence a preliminary division may be required.
The perceptive reader might have asked why we didn ’t add the solution of the homogeneous equation to a particular solution when we solved the first-order equation y' + p(x)y = f(x) back in Chapter 2. We could have; however, the integrating factor method found both of these components at the same time. Nevertheless, for Problems 18–23, solve the given first-order linear equation both by the integrating factor method and by adding the solution to the corresponding homogeneous equation to a particular solution of the nonhomo geneous equation.
24. Green's Function Representation of the Solution Show that a particular solution of
can be written in the integral form
Hint: Combine the two integrals that appear in the general variation of parameters formula given in the text. Denoting the dummy variable of integration by s and using a trigonometric identity, one obtains the desired integral form. The function sin (x – s) that appears inside the integral is called the Green's function for the differential equation. All linear equations have a Green's function, and once Green's function can be found, the solution can be written in integral form.
25. Higher-Order Equation Solve the third-order equation
using the method of variation of parameters.
26. Journal Entry We have come to the end of the line in solving the second-order linear equation with constant coefficients. (The remainder of this chapter deals with applications.) Give your own impressions of the subject of differential equations thus far.
PURPOSE
To show how second-order differential equations are useful in the description of dynamical systems. We study one of the simplest dynamical systems, the unforced undamped vibrating spring, described by
and study its motion, known as simple harmonic motion. We will study various properties of simple harmonic motion, such as frequency, period, and amplitude.
Many objects, when moved from their place of rest, exhibit a vibratory motion, oscillating back and forth about a fixed point. We could mention the vibrations of a tuning fork, the swinging of a pendulum, the motion of electric current moving back and forth through a circuit, or the vibrations of an electron in an electric field. An idealization of all these systems is the small vibrations of a mass attached to a spring.
We start with an unstretched spring of length L hanging from the ceiling. See Figure 3.7(a). To this spring we attach a mass m, which stretches the spring an additional amount AL to an equilibrium position. See Figure 3.7(b). We now let u measure the vertical displacement of the mass from this equilibrium position with the positive direction taken downward. See Figure 3.7(c).
To study the motion of the mass, we isolate the forces acting on the mass. When this is done, we can then resort to Newton's Second Law of motion, F = ma, to find an equation that describes the motion of the mass. There are basically four forces acting on the mass that one must consider.
Figure 3.7 Simple mass-spring system
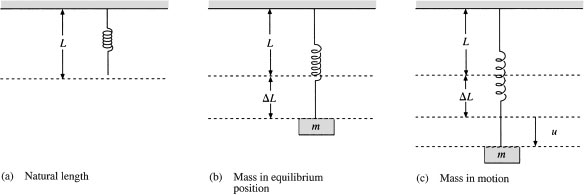
1. Fg = mg (force due to gravity). The force due to gravity Fg always acts downward with magnitude mg. This force is called the weight of the object. See Figure 3.8.
2. Fs = –k(
L + u) (restoring force of the spring). We assume that the restoring force Fscaused by the spring is directly proportional to the elongation L + u and always acts to restore the mass to its equilibrium position.* Calling k > 0 the constant of proportionality of this force, we have the relationship Fs= – k(L + u).
3. Fd = - d(du/dt) (damping force). We assume that the friction or resistance that the medium exerts on the mass, called the damping force, is proportional to the velocity of the mass and always acts in a direction opposite to the velocity of the mass. † Hence we have Fd = - d(du/dt), where d > 0 is called the constant of proportionality. Note that this equation says that the damping force Fd always acts in a direction opposite to the velocity, du/dt, of the mass. We have followed the common convention and have denoted the damping force by the usual dashpot mechanism.
4. Fe = F(t) (external forces). Often an external force, Fe = F(t), directed either upward or downward, is applied. The force might be applied directly to the mass or to the mount to which the spring is attached.
Figure 3.8 Mass-spring system with damping
We now apply Newton's Second Law, which states that the product of the mass times acceleration is equal to the sum of the external forces. If we use the common convention of denoting the first and second time derivatives of u by 
and , respectively, in honor of Sir Isaac Newton, who originated the notation, Newton's Second Law can be written as
or
But when the mass is in equilibrium position, the restoring force (kL) of the spring is equal to the force of gravity (mg). Hence we have the relationship kL = mg. These two terms in Eq. (lb) cancel, giving
This second-order differential equation with constant coefficients describes the motion of the vibrating spring. When F(t) = 0 for all t, the equation is called unforced; otherwise, it is called forced. When d = 0, the equation is called undamped; when the constant d > 0, it is called damped.
We will express the units of length (L), weight (w), and time (t) in this chapter mostly in the English or engineering system, which measures length in feet, weight or force in pounds, and time in seconds. The unit mass (m) is the slug, and it is defined to be that mass for which a force of 1 lb will give an acceleration of 1 ft/sec2. The conversion factor between the mass m of an object and its weight w (in pounds) is w = mg, where g is the acceleration due to gravity, which we take to be 32 ft/sec2. Other systems of units used in this book are shown in Table 3.4.
Table 3.4 Units of Measure in Different Systems
Example 1
Finding the Differential Equation A 16-lb weight is attached to a spring, which in turn is attached to the ceiling. The weight stretches the spring 4 inches and comes to rest in its equilibrium position. It is also known that friction in the spring gives rise to a damping force of 0.05 lb for a velocity of 3 in./sec. Find the differential equation that describes the motion of this vibrating mass.
We compute the three basic parameters m, d, and k that define the mass-spring-dashpot system. It is important that all units are commensurate.
Hence we have
If the mass was initially pulled down 6 inches from the equilibrium position and released without imparting an initial velocity, the initial conditions would be given by u(0) = 1/2 and u(0) = 0.
Many objects have a natural vibratory motion in which they oscillate back and forth about a fixed point of equilibrium. If the particle is attracted toward the equilibrium position with a force proportional to the displacement, the particle is said to undergo simple harmonic motion. Possibly, the best known occurrence of simple harmonic motion is the undamped movement of a mass attached to a spring that satisfies the differential equation
To find this motion, we first divide by m, arriving at
where w0 =√ k/mThe characteristic equation for this equation* is
which has the complex conjugate roots 
Hence the general solution of Eq. (4), and the simple harmonic motion that describes the mass-spring system, is
If we now multiply and divide the right-hand side of Eq. (7) by 
, we can rewrite this simple harmonic motion as
If we now define 8, called the phase angle, by the two equations
Equation (8) becomes
The quantity R is called the amplitude of the simple harmonic motion and can be determined from the formula 
The quantity 
is called the (circular) frequency of the simple harmonic motion, and it represents the number of oscillations the spring makes every 2π units of time.* More useful than the circular frequency is the natural frequency (or just frequency), defined as f= w0/2π, which represents the number of oscillations the spring makes every unit of time. Finally, the reciprocal of the frequency, 
, is the period of the motion and is the time required for the motion to undergo one complete oscillation. These ideas are illustrated in Figure 3.9.
In other words, the vibratory motion of an undamped spring is a simple sinusoidal curve.†
Figure 3.9 Simple harmonic motion
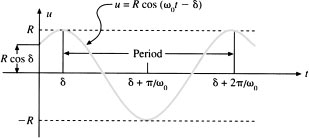
Example 2
Simple Harmonic Motion An 8-lb weight is attached to a spring, which in turn is suspended from the ceiling. The weight comes to rest in equilibrium position, stretching the spring 6 inches in the process. The weight is then pulled down an additional 1 ft and released with an upward velocity of 8 ft/sec. Assume that the resistance of the medium is negligible.
(a) Find the initial-value problem that describes the motion of the weight.
(b) Find the motion of the weight.
(c) Find the amplitude, phase angle, frequency, and period of the weight.
Solution
(a) We have
Hence the equation of motion is
or
where u is measured in feet and t in seconds. The initial conditions are u(0) = 1 (0) = –8,
(b) The solution of Eq. (11) is
Substituting Eq. (12) into the initial conditions gives
or C1 = 1, c2 = – 1. Hence the simple harmonic motion is described by
However, it is possible and is more illustrative to rewrite Eq. (13) in terms of a single sine or cosine curve. Using Figure 3.10 as a guide, we set
Since C1 is positive and c2 is negative, we see from Figure 3.10 that the phase angle δ lies in the second quadrant. Hence the phase angle is δ = 3π/4. Hence the polar form of the simple harmonic motion is
Figure 3.10 Geometric illustration of the transformation from Cartesian to polar coordinates
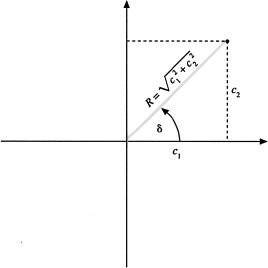
The graph of Eq. (14) is shown in Figure 3.11.
(c) From Eq. (14) we see that the amplitude is √2 feet, the phase angle is 
radians, the natural frequency is 
oscillations per second, and the period is 
seconds.
Figure 3.11 Simple harmonic motion
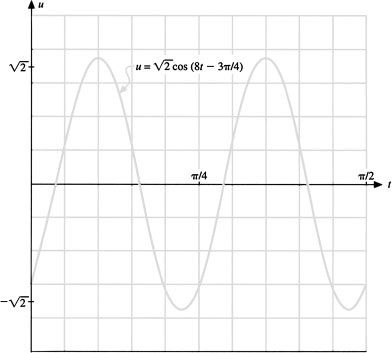
PROBLEMS: Section 3.9
For Problems 1–5, find the simple harmonic motion described by the given initial-value problem. Determine the amplitude, phase angle, frequency, and period of the motion.
6. Finding the Differential Equation An 8-lb weight is attached to a frictionless spring, which in turn is suspended from the ceiling. The weight stretches the spring 6 inches and comes to rest in its equilibrium position. The weight is then pulled down an additional 3 inches and released with a downward velocity of 1 ft/sec.
(a) Find the initial-value problem that describes the motion of the weight.
(b) Find the motion of the weight.
(c) Find the amplitude, phase angle, frequency, and period of the motion.
7. Finding the Initial-Value Problem A 16-lb weight is attached to a frictionless spring, which in turn is suspended from the ceiling. The weight stretches the spring 6 inches and comes to rest in its equilibrium position. Find the initial-value problem that describes the motion of the weight under the following conditions.
(a) The weight is pulled down 4 inches below its equilibrium position and released with an upward initial velocity of 4 ft/sec.
(b) The weight is pushed up 2 inches and released with a downward velocity of 1 ft/sec.
8. Finding Simple Harmonic Motion A 12-lb weight is attached to a frictionless spring, which in turn is suspended from the ceiling. The weight stretches the spring 1.5 inches and comes to rest in its equilibrium position. The weight is then pulled down an additional 2 inches and released.
(a) Find the resulting motion of the weight as a function of time.
(b) Find the amplitude, period, and frequency of the resulting motion.
(c) At what time does the weight first pass through the equilibrium position, and what is its velocity at that time?
(d) If you have access to a computer with graphing facilities, sketch the graph of the motion of the weight.
9. Finding Simple Harmonic Motion A 12-lb weight is attached to a frictionless spring, which in turn is attached to the ceiling. The weight stretches the spring 6 inches before coming to equilibrium. Find the equation of motion of the weight if it is initially pushed upward to a position 4 inches above equilibrium and given an upward velocity of 2 ft per sec…
10. Simple Harmonic Motion in Polar Form Rewrite the following simple harmonic motions in the new polar form R cos (ω0t – δ).
(a) cos t + sin t
(b) cos t – sin t
(c) – cos t + sin t
(d) – cos t - sin t
11. Simple Harmonic Motion as a Sine Function It was shown in the text that simple harmonic motion could be written as a pure cosine function by means of the formula
where R and δ were determined in terms of c1 and c2. Show that simple harmonic motion can also be written as a pure sine function
Find R and Φ in this formula in terms of c1 and c2.
12. An Alternative Equation for the Period Show that the period of motion for an undamped vibrating mass attached to a spring is 
where Δ L is the elongation of the spring due to the weight.
13. Simple Harmonic Motion from Conservation of Energy The conservation of energy says that if no energy is lost through friction, then in any mechanical system the sum of the kinetic and potential energies remains constant over time. Use the fact that the kinetic energy of a vibrating spring is KE = 1/2mü2 and the potential energy is given by PE = l/2ku2 to derive the differential equation
Hint: Differentiate the equation KE + PE = constant with respect to time.
14. Factoring Out the Friction We have seen that a mass-spring system in which friction is present is described by the differential equation
An old trick is to “factor out” the friction component of the solution by introducing the new variable 
.
(a) Show that U(t) satisfies the “frictionless” differential equation
(b) Assuming that 
, solve Eq. (17) for U(t) and then show that the solution of the damped Eq. (16) is
where 
15. An Interesting Property of Simple Harmonic Motion A mass attached to r spring is pulled down a given distance and released. The m e mass is then pulled down twice as far and released. What is the relationship between the periods of the two simple harmonic motions? Will the period of the second simple harmonic be twice as large as that of the first?
16. A Pendulum Experiment A rod of length L is suspended from the ceiling so that it can swing freely. A weight (the bob) is attached to the lower end of the rod, where the weight of the rod is assumed to be negligible compared to the weight of the bob. Let θ (radians) be the angular displacement from the vertical (plumb line), as shown in Figure 3.12. It can be shown that the differential equation that describes the motion of the pendulum is the pendulum equation
Determine the natural puiod for a pendulum of length L for small oscillations by approximating sin 
.
Figure 3.12 A simple pendulum
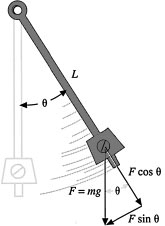
17. Simple Humonic Motion A particle moves around the circle x2 + y2 = r2 with a constant angular velocity of ω0 radians per unit time. Show that the projection of′the particle on the x-axis satisfies the equation 
.
18. Other Mass-Spring Sgstems It can be shown that the diffaential equation that describes the vibrations of the mass-spring-pulley system shown in Figure 3.13 is given by
Figure 3.13 Mass-spring-pulley system
where u is the displacemat from equilibrium of a weight of mass m; the valw R and I are the radius and moment of inertia, respectively, of the pulley; and k is the spring constant* Use the values of these quantities given in Eq. (20) to find the frequoncy of the mass.
19. Attractive Versus Repulsive Forces Simple harmonic motion of an object is the result of an attractive force that is proportional to the displacement of the object from quilibrium, that is. mü = − ku. On the other hand, if the force is repulsive, the equation of motion is mü = kx. Show that in the case of an attractive fonx, the displacement is described by the (circular) sine or cosine functions, whereas if the force is repulsive, the displacement is describad by the hyperbolic sine a d cosine functions.
20. Simple Harmonic Motion of a Buoy† A cylindrical buoy with a diameter of 18 inches floats in water with its axis vertical. See Figure 3.14. When it is depressed slightly and relad, its period of vibration is found to be 2.7 sec. Find the weight of the cylinder, Archimedes’ Rinciple says that an object submerged in wata is buoyed (ford) up by a force equal to the weight = volume × density of the water displaced. The density of water is taken to be 62.5 1b/ft3.
Figure 3.14 Simple harmonic motion of a buoy
21. Simple Harmonic Motion from Los Angeles to Tokyo It can be shown that the force on a particle inside a homogeneous spherical mass is directed toward the center of the sphere with a mangnitude proportional to the first power of the distance from the center of the sphere. By using this principle, a train starting at rest and traveling through a straight line tunnel from Los Angeles to Tokyo can be shown to satisfy the initial-value problem
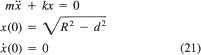
whtn x is the distance of the train from the center of the tunnel, R is the radius of the earth (4000 miles), and k is the constant of proportionality in the equation giving the force moving the train, F = kr. See Figure 3.15.
(a) Find the distance of the train from the center of the tunnel at any time t.
(b) If a train starts from my city on earth, find the time it takes to go to any other city on the earth through a tunnel of this type.
Figure 3.15 Tunnel from Los Angeles to Tokyo
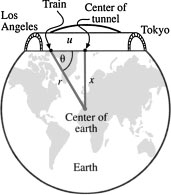
22 Computer Problem Use a graphing calculator or computer to sketch the graphs of simple harmonic motion as given by Eq. (7) for different values of c1, c2, and ω0.
23. Journal Entry Make a list of some of the concepts that we have studied thus far that you do not understand.
PURPOSE
To study phenomena described by the unforced damped equation
and to illustrate these phenomena by studying the damped vibrating spring. We study three cases: underdamped, critically damped, and overdamped, which depend on the numerical value of the discriminant d2 – 4mk.
In the previous section we studied undamped vibrating systems. Since in reality practically all vibrations have retarding forces acting on the moving mass, we now consider the vibration of a particle subject to a resistance or damping force. For simplicity we consider only damping forces that are proportional to the first power of the velocity. Although frictional forces are often proportional to higher powers of the velocity, these types of friction lead to nonlinear differential equations and require more advanced analyses.
We have seen that the motion of a mass attached to a damped vibrating spring is
and that the roots of the corresponding characteristic equation
are
Hence the motion of an unforced damped system depends on the nature of these roots. We consider separately the cases in which the discriminant, d2 – 4mk, or quantity under the square root, is negative, zero, and positive.
Here we are considering the case in which the resistance d is relatively weak in comparison with the spring constant k, and so we expect an oscillatory motion. If the quantity d2 – 4mk < 0, then the roots of the characteristic equation are complex conjugate numbers, and the general solution of Eq. (1) gives rise to damped oscillatory motion:
We can also express Eq. (4) in the more useful polar form
where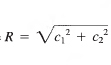 
and tan δ = c2/c1. The graph of Eq. (5) is shown in Figure 3.16.
Figure 3.16 Damped oscillatory motion
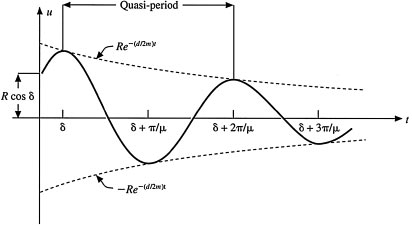
Since the cosine factor in Eq. (5) oscillates between + 1 and – 1 with the period 2π/μ, the function u(t) oscillates between 
While the motion of u(t) is not truly periodic, we define the quasi-frequency or damped (circular) frequency as ω d = μ and the damped (natural) frequency as f = μ/2π. Related to the frequency is the quasi-period or damped period, defined by
This damped period is the time elapsed between successive maxima or minima in the position of the mass. The factor 
is called the damped amplitude of the oscillation. Finally, the time constant τ of the oscillation is defined as τ = 2m/d and is the time required for the damped amplitude, to decay from its starting value of R to R/e—in other words, about two-thirds of the way from its starting value of R to its limiting value of zero.
When d2 – 4mk = 0, the characteristic equation (2) has the repeated root – d/2m. Hence the general solution to Eq. (1) gives rise to what is called critically damped motion:
To understand this type of motion, we use L’Hôpital's rule to find its behavior as t → ∞. We find
It can easily be shown that u(t) has at most one local maximum or minimum value for t > 0. Hence u(t) does not oscillate, and this leaves, qualitatively, only two possibilities for the motion of u(t), which are shown in Figure 3.17.
Figure 3.17 Critically clamped or overdamped motion crosses the equilibrium point either once or never, depending on the initial conditions
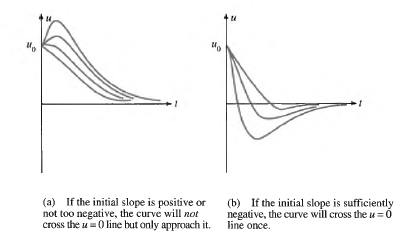
Here we are considering the case in which the friction d is relatively large in comparison with the spring constant k, and so we expect no oscillations in the motion of the spring. Mathematically, when d2 − 4mk > 0, the characteristic equation (2) has two distinct real roots:
Here the general solution to Eq. (1) gives rise to overdamped motion:
To understand better the behavior of overdamped motion, first realize the obvious fact that r2 < 0. With a little more thought, it is also not difficult to understand that r1 is also negative. Hence as t → ∞, we have u(t) → 0. Also, since
it follows that u′ (t) = 0 only when c1r1 + c2r2e(r2− r1)t = 0, and hence a nontrivial solution u(t) can have at most one maximum and minimum value for t > 0. Thus we conclude that, qualitatively, the possible motions of the spring are the same as for the critically damped case, as are drawn in Figure 3.17.
Note: For critically damped and overdamped motions the displacement u(t) “creeps” back to the equilibrium position. Depending on the initial conditions, this movement will cross the equilibrium point either exactly once or not at all. In other words, it will never cross the equilibrium point more than once. (See Problem 16 at the end of this section.) One should realize too that from a practical or engineering point of view the critically damped case has little meaning, serving only to separate the two major cases of underdamping and overdamping systems.
The reader has no doubt observed overdamped motion in the suspension of a car. Above each wheel are a large spring and a damper (shock absorber). When the suspension system is working properly, any disturbance will quickly die out. In a car with old shock absorbers, the damping may be underdamped, and the car may rock for some time after hitting a bump.
Example 1
Effect of Damping A mass-spring system with damping satisfies the initial-value problem
Compare the solution for the damping constants of d = 1, 2, and 4.
Solution
The characteristic equation for Eq. (12) is
whose roots are
When d = 1, the roots of Eq. (14) are 
. Hence the underdamped motion is given by
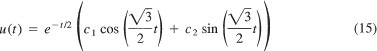
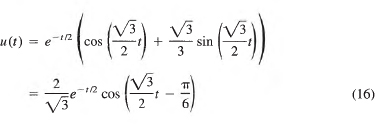
See Figure 3.18.
Figure 3.18 Comparison of underdamped, critically damped, and overdamped motion
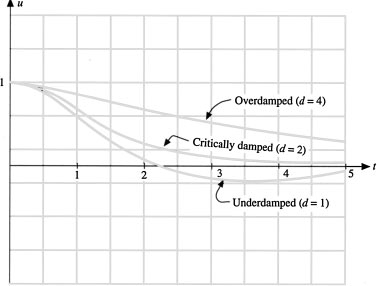
When d = 2, the characteristic equation (14) has a double root of − 1. Hence the damped motion is described by
Using the initial conditions u(0) = 1 and 
, we find c1 = c2 = 1. Hence
See Figure 3.18.
When d = 4, the roots of the characteristic equation (14) are −2 ± √3. Hence the overdamped motion is described by
Using the initial conditions u(0) = 1 and to find c1, and c2, we find
See Figure 3.18.
Note: Figure 3.19 shows how the roots of the characteristic equation change as the damping constant d increases from 0 to ∞. Note that for d = 0 there is no damping. However, with increasing d, the oscillations of u(t) damp to zero faster and faster until d reaches 2, when motion becomes critically damped. When d is larger than 2, the overdamped motion is described essentially by the exponential term containing the larger real root (the one that is less negative). Hence as d becomes larger than 2, the solution damps to zero more slowly. This phenomenon of maximum damping when the system is critically damped can be seen in the above example, when
d = 1 
u(t) tends to zero like e−0.5t
d = 2 u(t) tends to zero like e−1 (decays fastest)
d = 4 u(t) tends to zero like 
(decays the slowest)
Figure 3.19 The phenomena of maximum damping at critical damping can be seen by examining the dependence of the characteristic roots on the damping constant. When damping is d = 0, the roots are ±i and there is no damping. When 0 < d < 2, the roots are complex conjugate moving along the circle in the complex plane. When d = 2, there is a double root at −1. When 2 < d < ∞, both roots are real and negative, the more negative root approaching −∞ and the larger root approaching 0.
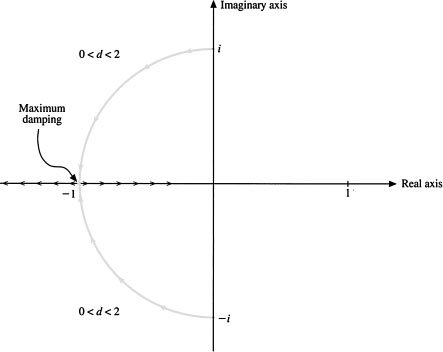
PROBLEMS: Section 3.10
Properties of Damped Oscillations
For Problems 1–4, determine the damped amplitude, the damped natural frequency, the damped period, and the time constant. Sketch the graphs of the functions.
Underdamped, Critically Damped, or Overdamped?
For Problems 5–11, determine whether the motion described by the given differential equation is underdamped, critically damped, or overdamped.
12. Unforced Damped Vibrations A 32-lb weight is attached to the lower end of a coil spring, which in turn is suspended from the ceiling. The weight stretches the spring 2 ft in the process. The weight is then pulled down 6 inches below its equilibrium position and released. The resistance of the medium is given as 4 lb/(ft/sec).
(a) Determine the motion of the weight.
(b) Determine the damped amplitude, damped frequency, damped period, and time constant of the subsequent motion.
(c) Sketch the graph of the motion.
13. Unforced Damped Vibrations A 10-lb weight is attached to a spring suspended from the ceiling. When the weight comes to rest, the spring is stretched by 1.5 inches. The damping constant for the system is 5√2 lbs/(ft/sec). The weight is pulled down 3 inches from the equilibrium position and released.
(a) Determine the motion of the weight.
(b) Determine the damped amplitude, damped natural frequency, and damped period of the subsequent motion.
(c) Sketch the graph of the motion.
14. Maximum Displacement An 8-lb weight stretches a spring 6 ft, thereby reaching its equilibrium position. Assuming a damping constant for the system of 4 lb/(ft/sec), the weight is pulled down 3 inches below its equilibrium position and given a downward velocity of 2 ft/sec. When will the mass attain its maximum displacement below equilibrium? What is the maximum displacement? Sketch the graph of the motion.
15. Finding the Differential Equation for Observations John starts in motion a vibrating mass attached to a spring. He observes that after 10 seconds the damping amplitude has decreased by 75% and that the damped period is 2 seconds. How does John determine the differential equation of motion from these two observations?
16. Interesting Phenomena Show that if the motion of a mass that is described by
is critically damped or overdamped, then the mass can pass through the equilibrium position at most once, regardless of the initial conditions.
17. Decrease in the Velocity For an underdamped mass-spring system, show that if v is the velocity of the mass at any time, then the velocity one (damping) period later is ve−(d/2m)Td
18. System Identification of the Damping Constant d It is generally almost impossible to measure the damping constant d directly. One of the important uses of differential equations is to find system parameters such as this indirectly. Starting with the equation for underdamped motion
verify the following mathematical steps that will allow one to estimate d for underdamped motion.
(a) Show that the ratio of two successive maximum displacements at time t and t + Td is e(d/2m)Td. Thus successive maximum displacements form a geometric sequence with ratio e−(d/2m)Td.
(b) Show that the natural logarithm of this ratio, called the logarithmic decrement, is given by
(c) How would you use the logarithmic decrement to find the damping constant d?
19. Need New Shocks? The vibrations of an automobile weighing 1600 lb (50 slugs) are controlled by a springshock system in which the shock absorbers provide the damping. Suppose the spring constant is k = 4800 lb/ft and the dashpot mechanism provides a damping constant of c = 200 lb-slug/ft. Find the speed (in miles per hour) at which resonance vibrations will occur if the car is driven on a washboard road surface with an amplitude of 2 inches and a wavelength of L = 30 ft. See Figure 3.20.
Figure 3.20 Shock-spring system
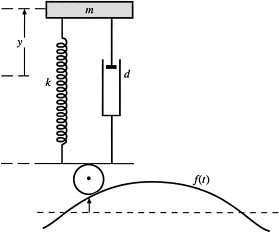
20. RLC Circuit Problem The charge q on the capacitor in an RLC series electrical circuit is described by the differential equation
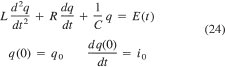
where L is the inductance of the inductor (henrys), R is the resistance of the resistor (ohms), C is the capacitance of the capacitor (farads), and E(t) is the electromotive force (volts). The initial conditions q0 and i0 are the initial charge across the capacitor and the initial current flowing through the circuit (amperes). See Figure 3.21. The current i(t) in the circuit is given by the derivative dq/dt. Find the charge q(t) on the capacitor for the LRC circuit described by the system when L = 0.25 henrys, R = 10 ohms, and C = 0.001 farads, E(t) = 0, g(0) = q0 coulombs, i(0) = 
(0) = 0.
Figure 3.21 RLC series electrical circuit
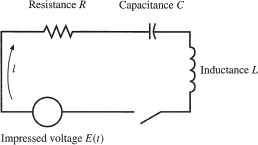
Assuming that there exists a differentiable function y = y(x) defined on an interval [x1 x2] that minimizes the integral
where F is a given function, Leonhard Euler showed in 1744 that y must satisfy the ordinary differential equation
called Euler's equation. The class of problems associated with finding the minimum of a function of a function such as Eq. (25) is called the calculus of variations.* Often a function y also satisfies an additional set of boundary conditions such as y(x1) = y1 and y(x2) = y2 For Problems 21–22, find the Euler equation associated with the given functional, and verify that the given function y = y(x) satisfies the Euler equation. Can you interpret the physical meaning of each minimizing curve y = y(x)?
21. Length of Curve Functional
Minimizing curve: y(x) = x
22. Surface of Revolution Functional
Minimizing curve: y = cosh x
23. Hamilton's Principle One of the basic principles of mechanics, Hamilton's principle, states that if a system of particles is governed by their mutual gravitational attractions, then their paths of motion will minimize the integral over time of the difference between the kinetic and potential energies of the system. For the undamped vibrating spring problem this integral is
where the kinetic and potential energies are given by T = ½ mx2 and V = ½ kx2, respectively. Find Euler's equation for the functional J(y), and find its general solution.
24. Varying Damping Constant Solve the initial—value problem
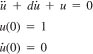
in terms of d, and sketch the graphs of u(t) for d = 0, 2, 4, and 6.
25. Varying Mass Solve the initial—value problem
in terms of the mass m, and sketch the graphs of u(t) for m = 0.1, 0.25, and 1.
26. Varying Spring Constant Solve the initial—value problem
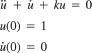
in terms of k, and sketch the graphs of u(t) for k = 0.1, 0. 25, and 0.50.
27. Running Time Backward In addition to using differential equations to determine the future of physical systems, we can use differential equations to determine the past of physical systems. If we introduce a backward time τ that runs in the opposite direction from the usual time t, in other words τ = − t, then for any “forward running” differential equation with independent variable t, we can find the corresponding “backward running” differential equation by simply letting τ = − t. For Problems (a)–(c), find the “backward running” differential equation in t corresponding to the given differential equation in t and observe that the solution of the “backward running” equation is the “backward” solution of the “forward running” equation.
(a) 
(b) 
(c) 
28. Computer Problem Use a graphing calculator or computer to sketch the graphs of the damped vibrations of a linear spring given by Eq. (5) for different values of the parameters d, m, and k.
29. Journal Entry Do you think that critically damped motions can occur in the real world, since they occur only when the discriminant is exactly zero?
PURPOSE
To show how forced vibrations of the undamped equation
give rise to beats when ω ≠ ω0) = √ k/m and to resonance when ω = ω0. We then show how forced vibrations to the damped equation
give rise to a steady state solution that has the same frequency, but is out of phase, and has a different amplitude as the driving force.
Consider the vibrations of a damped mass—spring system that acts under the influence of an external periodic force. Mathematically speaking, we will study vibrating systems governed by the differential equation
where m, d, and k have already been defined and F0 and co are nonnegative constants describing the amplitude and frequency of the periodic input. First, however, we will study the important subcase in which there is no damping, or when Eq. (1) reduces to
In the case of no damping, we consider two further subcases: the subcase in which the frequency of the forcing function is different from the natural frequency of the system (ω ≠ ω0), which gives rise to the phenomenon of beats, and the case in which the frequency of the forcing function is equal to the natural frequency (ω = ω0), which gives rise to the phenomenon of resonance.
When ω ≠ ω0 = √ k/m, the general solution of Eq. (2) is
where the constants c1 and c2 are determined from the initial conditions. In other words, the resultant motion described by Eq. (3) is the sum of two periodic motions with different frequencies. The first two terms in Eq. (3), which is the solution of the homogeneous equation corresponding to Eq. (2), is called the transient solution by engineers and applied scientists. Although for undamped systems the transient solution will not approach zero, it is that part of the solution that depends on the initial conditions. The last term in Eq. (3), which is a particular solution of Eq. (2), is called the steady state solution and is that part of the solution that depends on the external forcing term.
If we now assume the mass to be initially at rest, that is, u(0) = , the solution u(t) becomes
Note that this expression is the sum of two different oscillations with the same amplitude but different frequencies. Using the trigonometric identities
we can rewrite Eq. (4) as
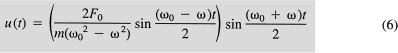
Note in this equation that when 
, the factor 
oscillates at a much faster rate than does 
. Consequently, Eq. (6) describes a rapidly oscillating function with (circular) frequency (ω0 + ω)/2, oscillating inside a slower sinusoidal function
This equation can be interpreted as a sinusoidal amplitude of the more rapidly oscillating function. This type of motion, which characterizes systems in which the driving frequency approximately equals the natural frequency of the system, exhibits the phenomenon of beats. See Figure 3.22.
The phenomenon of beats occurs in acoustics when two tuning forks vibrate with approximately the same frequency. One can often hear a definite rising and falling in the noise level. Also, each note of a musical instrument has a definite frequency associated with it. When a standard frequency and its corresponding musical note are played at the same time, beats will result if their frequencies are not in tune. The idea in tuning the instrument is to make the beats disappear. The musical note of the instrument then has the same frequency as the standard note.
Figure 3.22 Phenomenon of beats. We say that the faster oscilllating wave is amplitude modulated by the slower varying wave.
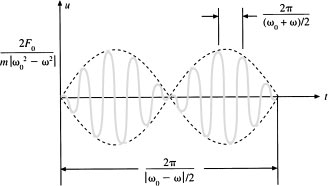
When the external frequency ω of the forcing function is the same as the natural vibrating frequency (ω0 of a vibrating spring, the system gives rise to the phenomenon of resonance. To understand this phenomenon, we study the equation
with ω = ω0. The important fact here is that the forcing term also appears in the solution of the corresponding homogeneous equation. We solved this equation earlier, using the method of undetermined coefficients. In this case the general solution of Eq. (8) is
Note that in Eq. (9), regardless of the values of c1 and c2, the particular solution (last term) contains the factor of t and hence oscillates with increasing amplitude as t → ∞. This type of motion, illustrated in Figure 3.23, represents the phenomenon of resonance.
The phenomenon of resonance is common in everyday life. Soldiers crossing a bridge are asked to break step so as not to create resonance for fear that their cadence is the same as, or near, the natural vibrating frequency of the bridge. The walls of Jericho, some assert, came tumbling down because the sound of the trumpets caused a wave motion equal to the natural frequency of the walls of the city. A diver jumping on a diving board can make the board vibrate with larger and larger amplitude by jumping with the same frequency as the natural frequency of the board. A ship will roll and pitch more wildly in a storm if the natural rolling frequency of the ship matches the frequency of the waves. And, annoyingly, the reader no doubt has heard rattles in his or her automobile caused by resonance.
Resonance is generally not a desired phenomenon for engineers. The engineers who designed the Tacoma Narrows Bridge in the state of Washington learned this the hard way when, on November 7, 1940, external periodic forces were generated by the periodic shearing of von Karman vortices. The bridge started shaking, and the roadway began to pitch and roll. A few minutes later the bridge was resting on the bottom of Puget Sound.
Figure 3.23 Phenomenon of resonance
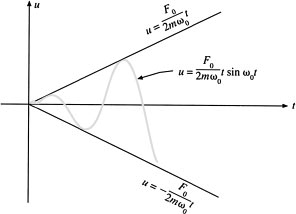
Example 1
Ten Miles of Bad Road Sally is rushing to her differential equations exam and must travel on a bumpy road. Her car weighs w = 2400 lb (75 slugs), and the springs on her car have a collective constant of k = 7200 lb/ft. Unfortunately, her shock absorbers are worn out, and so her springs have no damping. Suppose the road has a sinusoidal washboard surface with an amplitude of A = 1 ft and a given wavelength of L = 25 ft. See Figure 3.24. At what speed will resonance occur?
Solution
We think of the car as a mass—spring system as drawn in Figure 3.24, in which u measures the displacement of the mass from its equilibrium position. If Sally drives at v ft/sec, then the car bouncing over the road surface will give rise to the forcing term
Hence the differential equation that describes the vertical motion of the car is
or
For this equation to have resonance, it is necessary that ω = ω0 or
Solving for v gives 
(27 mph). Hence if Sally drives faster than this speed, she will avoid resonance and even arrive for her differential equations exam on time.
We now consider vibrations of a damped mass—spring system driven by a periodic force. That is, we study the system
Figure 3.24 Sinusoidal washboard surface
where d2 – 4mk < 0 (underdamped case). The general solution of Eq. (12) can be found by using the method of undetermined coefficients to obtain a particular solution. After several computations we obtain
where r1 and r2 are the roots of the characteristic equation and δ is determined by 
. Again, as in the undamped case, the solution depends on two terms. The first term, uτ (homogeneous solution), is called the transient solution. It depends on the initial condition, and it is important to note that it approaches zero as t → ∞ Hence after a period of time (sometimes almost instantaneously) the oscillations (13) will approach the steady state solution
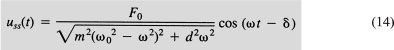
This second term, uss (a particular solution), is called the steady state solution. It is the consequence of the forcing term, F0 cos ω t, and like the forcing term has the same frequency ω. However, it is out of phase with the forcing term, and its amplitude is changed by the amplification factor*
When M(ω) is graphed as a function of input frequency ω, it is called the frequency response curve for the system, and it represents the gain in amplitude of the steady state response as a function of the frequency of the forcing term. For natural frequency 
, various frequency response curves are drawn in Figure 3.25.
Figure 3.25 Frequency response curves
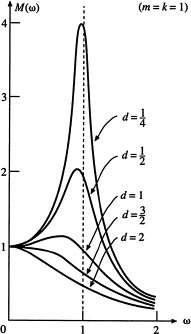
PROBLEMS: Section 3.11
1. Express cos 3t − cos t in the form A sin αt sin β t.
2. Express sin 3t − sin t in the form A sin αt cos β t.
For Problems 3–5, find the steady state solution having the form uss = A cos (W – 8).
6. Resonance A mass of one slug is hanging at rest on a spring whose constant is 12 lb/ft. At time t = 0 an external force of f(t) = 16 cos ω t lb is applied to the system.
(a) What is the frequency of the forcing function that is in resonance with the system?
(b) Find the equation of motion of the mass with resonance.
7. Good and Bad Resonance Sometimes resonance in a physical system is desirable, and sometimes it is undesirable. Discuss whether the resulting resonance would be helpful or destructive in the following systems.
(a) Soldiers marching on a bridge with the same frequency as the natural frequency of the bridge.
(b) A person rocking a car stuck in the snow with the same frequency as the natural frequency of the stuck car.
(c) A child pumping a swing.
(d) Vibrations caused by air passing over an airplane wing having the same frequency as the natural flutter of the wing.
(e) Acoustic vibrations having the same frequency as the natural vibrations of a wine glass (the “Memorex experiment”).
8. Ed's Buoy* Ed is sitting on the dock and observes a cylindrical buoy bobbing vertically in calm water. He observes that the period of oscillation is 5 sec and that 4 ft of the buoy are above water when it reaches its maximum height and 2 ft above water when it is at its minimum height. An old seaman tells Ed that the buoy weighs 2000 lb.
(a) How will this buoy behave in rough waters with the waves 6 ft from crest to trough and with a period of 7 sec?
(b) Will the buoy ever be submerged?
9. Forced Damped Motion Find the steady state motion of a mass that vibrates according to the law
10. Forced Damped Motion A 32–lb weight is attached to a spring suspended from the ceiling, stretching the spring by 1.6 ft before coming to rest. At time t = 0 an external force of f(t) = 20 cos 2t is applied to the system. Assume that the mass is acted upon by a damping force of 4 du/dt, where du/dt is the instantaneous velocity in feet per second. Find the displacement of the weight.
11. General Forced Damped Oscillations Show that the general solution of the forced damped system
is
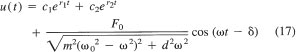
where r1 and r2 are the roots of the characteristic equation, c1 and c2 are arbitrary constants, and
12. How to Pump Up a Swing A child is sitting in a swing trying to pump it up by kicking his legs. Could you explain to this child, in terms of the amplitude amplification factor M(ω), how often to kick?
If you have access to a computer with graphing capabilities, draw the graphs of the vibratory motions given in Problems 13–14.
13. Beats The following functions are typical vibratory motions for an undamped system when the forcing frequency is close to the natural frequency of the system.
(a) u(t) = sin t sin 3t
(b) u(t) = 5 sin t sin 10t
(c) u(t) = 2 sin (0.050 sin 10t
(d) u(t) = 10 sin (0.0250 sin 20t
(e) u(t) = 10 sin (0.0005t) sin 20t
14. Resonance The following functions are typical vibratory motions for an undamped system when the forcing frequency is equal to the natural frequency of the system.
(a) u (t) = t sin 2πt
(b) u (t) = 2t sin t
(c) u (t) = 0.25t sin 4t
(d) u (t) = 0.50t sin 10t
(e) u (t) = 0.25t sin 20t
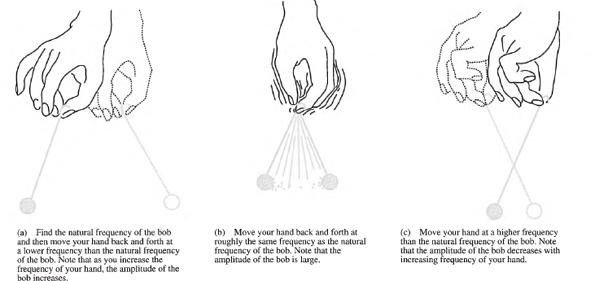
15. Graphing the Amplification Factor The function
represents the ratio of the output to input amplitude in the damped forced system
where ω02 = k/m. Sketch the graph of the amplification factor for m = ω0 = 1 and d = 0, 1, 2, 3, 4, and 5. In each, M(ω) should reach its maximum value at the value ω = ω0.
16. Amplitude Modulation When the function sin co t is multiplied by an “amplitude” function A(t), producing the function A(t) sin co t, the wave sin co tis said to be amplitude modulated. In acoustics the fluctuations in amplitude are called beats, with the sound being loud for large amplitude. Sketch the graphs of the following amplitude—modulated functions.
(a) 
(b) 
(c) 
17. The Game of Bob* The game of bob requires only a small weight tied to a string. The game illustrates how the frequency and amplitude of the output of a damped linear system depend on (“track”) the frequency and amplitude of the input to the system. (Although we have studied only the vibrating spring, the pendulum obeys the same second– order linear differential equation for small amplitudes.)
Part 1 (finding ω0): Begin your experiment by giving your hand a small jerk and then holding it still. See Figure 3.26(a). The bob will swing with a frequency of the unforced (damped) pendulum. Measure this frequency.
Part 2 (ω < ω0): Now that you know the natural frequency of the bob, move your hand back and forth with a frequency (ω) that is slower than the natural frequency (ω0). Note that the pendulum “follows” your hand, which means that the oscillations of the bob and your hand are close to being “in phase.” Note that as you increase the frequency of your hand movement, the amplitude of the bob also increases. See Figure 3.26(a). This is in agreement with the graph of the amplitude factor M(ω) shown in Figure 3.25.
Part 3 
: When you increase the frequency of your hand movement so that it is close to the natural frequency of the bob, the amplitude of the bob becomes large. See Figure 3.26(b).
Part 4 (ω > ω0): Finally, move your hand back and forth faster than the natural frequency of the bob. Note that the bob swings opposite to the motion of your hand. This means that the bob is way out of phase from the movement of your hand. Also, note that the amplitude of the bob decreases with increasing frequency of your hand movement. See Figure 3.26(c). This, of course, is a physical verification of the fact that the amplitude factor M(ω) approaches zero as ω → ∞.
18. Journal Entry Describe the phenomenon of resonance that results when you drive your car over a bumpy road. Do you ever try to hit the bumps faster than the resonance speed?
PURPOSE
To present a brief introduction of higher—order differential equations and show how the deflection of a beam can be described by a certain fourth—order equation.
This final section of Chapter 3 is a continuation from second—order differential equations to higher—order differential equations. Although we could have included an entire chapter on higher—order equations, the theory and methodology for solving higher—order linear equations closely parallel those of second—order equations, and so we have included only a brief introduction to the subject.
The following theorem, which gives the higher—order version of the existence and uniqueness result, should come as no surprise.
THEOREM 3.10 : Existence and Uniqueness Theorem
If a0(x), a1 (x), …, an(x) and f(x) are continuous on an interval I, and if x0 is a point in I, then the initial—value problem
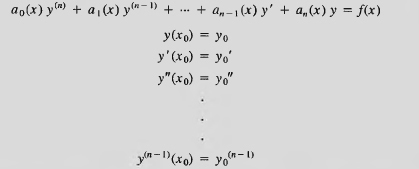
has exactly one solution on I.
The following theorem is a straightforward extension of a theorem that we saw in Chapter 2.
THEOREM 3.11: General Solution of the Homogeneous Equation
If y1(x), y2(x), yn(x) are solutions of the wth—order linear homogeneous equation
on an interval I, then so is
where c1, c2, …, cn are arbitrary constants. What's more, the functions y1(x), y2(x), …, yn(x) are linearly independent on I if and only if there is some x0 in I where W(y1, y2, yn) ≠ 0, where W is the n–dimensional Wronskian defined by
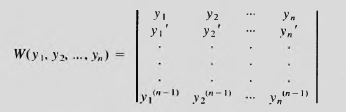
Such a set of solutions is called a fundamental set of solutions.
Example 1
A Fundamental Set of Solutions Show that cos x, sin x, and ex constitute a fundamental set of solutions of
on (− ∞, ∞).
Solution
By inspection it is easy to see that the three functions satisfy the differential equation. Computing the Wronskian, we find
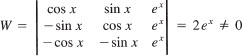
Hence the functions are linearly independent solutions of the equation, and the general solution is
We now solve the nth—order homogeneous equation with constant coefficients
by trying a function of the form emx. Doing this, we arrive at the characteristic equation
as we did for second—order equations. As it was in the case of second—order equations, the solution depends on the nature of the roots of the characteristic equation. Although we know from the theory of equations that (2) has exactly n roots (possibly repeated), the problem of actually finding the roots may require the use of approximate methods and a computer. The following examples illustrate these ideas.
Example 2
Real Unequal Roots Find the general solution of
Solution
The characteristic equation
has the roots r1 = − 1, r2 = 1, r3 = 2, and hence e−x, ex, and e2x are solutions. It is an easy matter to show that these functions are linearly independent, either from the definition of linear independence or by showing that the Wronskian is nonzero (at any point). Hence the general solution is
Example 3
Real Repeated Roots Solve
Solution
The roots of the characteristic equation
are − 1, − 1, and − 1. Hence the general solution is
Example 4
Complex Roots Solve
Solution
The roots of the characteristic equation
are − 1, +1, ± i. Hence the general solution is
The following theorem summarizes the theory for the higher—order nonhomogeneous linear equation.
THEOREM 3.12: Nonhomogeneous Solution
If yp(x) is any solution of the nonhomogeneous equation
and if y1, y2, …, yn are linearly independent solutions of the corresponding homogeneous equation
then the general solution of Eq. (3) is
As we did for second—order equations, we use the method of undetermined coefficients and variation of parameters to find a particular solution of the nonhomogeneous equation.
Example 5
Undetermined Coefficients Find the general solution of
Solution
We saw in Example 2 that the homogeneous solution is
To find a particular solution, the rules are essentially the same as for second—order equations, so we try yp(x) = Ax + B, from which we find A = 1, B = 0. Hence
Example 6
Undetermined Coefficients Find the general solution of
Solution
The characteristic equation
has roots r = –2, 3, 2 ±i. Hence the homogeneous equation has the four solutions
One can show that the Wronskian of this function is nonzero (at any x) and so the homogeneous solution is
To find a particular solution, we would normally try Ae−2x except that this function appears in the homogeneous solution, and so we try yp(x) = Axe−2x. Substituting this function into the nonhomogeneous equation, we eventually find A = – 1/95. Hence the general solution is
The method of variation of parameters can also be extended to higher—order equations. To find a particular solution of the rcth—order equation
where y1, y2, …, yn are n linearly independent solutions of the homogeneous equation are known, one seeks a solution of the form
Substituting this expression into Eq. (6), one arrives at the system of equations
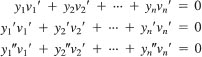
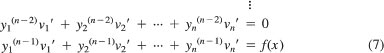
from which one can solve for v1′, v2′ …, vn′. After these values have been found, then by integration one can (hopefully) find v1 v2, vn and hence yp.
Example 7
Variation of Parameters Find a particular solution of
Solution
The homogeneous solution has three linearly independent solutions 1, cos x, and sin x. Hence we try a particular solution of the form
Substituting this expression into Eq. (8) yields the three equations
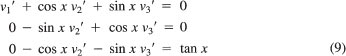
Solving these equations gives
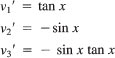
Integration of these expressions gives
Hence we have a particular solution
We summarize the method for solving a higher—order equation in Figure 3.27.
Figure 3.27 Summary of methods for solving a higher—order equation
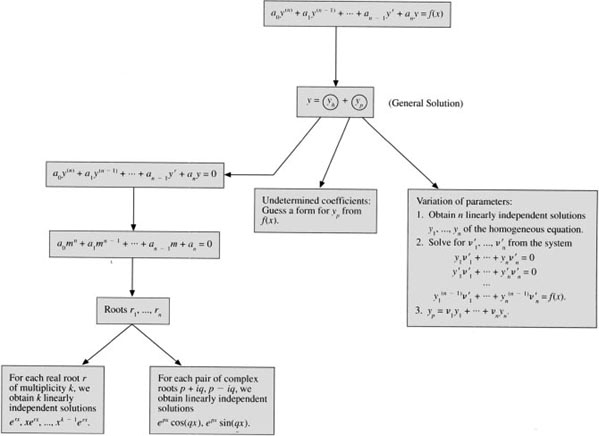
One of the useful applications of higher—order differential equations lies in the study of beams that have a uniform cross section (such as an I beam). Without going into the derivation,* one can show that the static deflection y(x) of a beam of length L carrying a load w(x) per unit length is governed by the fourth—order equation
where E is Young's modulus of elasticity, I is a moment of inertia of a cross section of the beam, and y is the downward deflection of the beam. See Figure 3.28.
Figure 3.28 One of the applications of fourth—order differential equations lies in the study of static and vibrating beams
Although all beams with uniform cross section satisfy the same differential equation (11), the boundary conditions that the beam satisfies at the two ends x = 0 and x = L depend on how the beam is attached at the ends. A few common types of attachments are the following.
Three Common Beams
Clamped Beam
If both ends of the beam are clamped, the boundary conditions are
Cantilever Beam
If the left end is clamped and the right end is free, then the boundary conditions are
Hinged Beam
If both ends are hinged, then the boundary conditions are
Clamped Beam Find the static deflection of a beam that is clamped at both ends when a constant load w0 is distributed uniformly along its length 0 ≤ x ≤ 1.
Solution
The boundary—value problem that governs this problem is
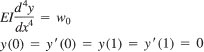
We first find the homogeneous solution by observing that the characteristic equation is m4 = 0, which has a root at 0 with multiplicity four. Hence the homogeneous solution is
To find a particular solution, we try yp(x) = Ax4, getting 
Hence the general solution of the nonhomogeneous equation is
We find the constants c1 c2, c3, and c4 by substituting y into the four boundary conditions, getting
Solving these equations gives
Substituting these values into Eq. (12) and simplifying give
PROBLEMS: Section 3.12
For Problems 1–4, find the Wronskian of the given functions.
For Problems 5–21, find the general solution of the given equation. Compute the Wronskian to determine that the solutions are linearly independent.
For Problems 22–27, find a particular solution of the given equation using the method of undetermined coefficients.
For Problems 28–29, find a particular solution of the given equation using the method of variation of parameters.
30. Cauchy–Euler Equation Find a particular solution of the nonhomogeneous Cauchy–Euler equation
given that {x, x2, x3} is a fundamental set for the corresponding homogeneous equation.
A procedure for finding the proper form of a particular solution to be used in the method of undetermined coefficients is based on the fact that the polynomial, exponential, and sinusoidal functions (and sums of products of such terms) are solutions of linear homogeneous differential equations with constant coefficients. If we let D denote d/dx, then for example the equation (D – 1) y = 0 has the solution ex, and we say that the differential operator D – 1 annihilates or is an annihilator of ex. Also, we would say that D2 + 1 annihilates sin x and cos x, that the operator (D + l)2 = D2 + 2D + 1 annihilates e−x and xe−x, and so on. Problems 31–33 show how annihi– lators can be used to find particular solutions.
31. Using Annihilators Suppose we wish to find a particular solution yp of
(a) Show that (D – 1)2 and D – 2 annihilate the first and second terms, respectively, on the right—hand side and that the combined operator (D – l)2 (D – 2) annihilates the entire right—hand side.
(b) Apply (D – 1)2 (D – 2) to Eq. (14) to obtain
Hence yp has the form
Since the homogeneous solution is
this means that yp should be chosen to be
32. Annihilator Method Use the annihilator method to find the form of a particular solution for
33. Annihilator Method Use the annihilator method to find the form of a particular solution for
34. Integral Formulas Find a formula involving integrals for the solution of
Hint: The functions cos x, sin x, cosh x, and sinh x constitute a fundamental set of solutions of the homogeneous equation.
35. Cantilever Beam A cantilever beam (of length L = 1) is clamped at its left end (x = 0) and is free at its right end (x = 1). Along with the fourth—order differential equation EIy(4) = w(x), it satisfies the given boundary conditions y(0) = y″ (0) = y(1) = y″(1) = 0. If the load w(x) = w0 is distributed uniformly, find the displacement y(x). How much does the free end sag below the clamped end?
36. Hinged Beam A beam of length L = 1 is hinged at both ends x = 0 and x = 1. Along with the differential equation EIy(4) = w(x), it satisfies the given boundary conditions y(0) = y″(0) = y(l) = y″( 1) = 0. If the load is given by w(x) = w0 is distributed uniformly, find the displacement y(x). How much does the center sag below the ends?
37. Hmmmmm Solve the differential equations y′ = y, y″ = y, y′″ = y, y(iv) = y, and so on.
38. Computer Problem Use a graphing calculator or computer to sketch the graph of the clamped beam as found in Example 8 for different values of the parameters E, I, and w0.
39. Journal Entry Summarize the similarities and differences between first–, second–, and higher—order linear differential equations.
* We probably should be careful, since later we will see that any second—order differential equation can be rewritten as a system of two first—order equations.
* We won't bother you with the formula for g(x). The important point is that it can be determined from p(x) and q(x).
* In practice, constants of motion are difficult to find and have limited use. One use lies in the reduction of order of a differential equation. In many physical systems, constants of motion represent the total energy of the system.
* Linear independence is intimately related to the concept of the dimension of a vector space and hence is essential to the study of many areas of mathematics.
* This problem was originally stated and proved by the Norwegian mathematician Niels Henrik Abel (1802–1829) and is often called AbeVs theorem.
† This formula is called Abel's formula.
* Looking for exponential solutions of this equation was the original idea of Leonhard Euler (1707–1783). Euler and Joseph Louis Lagrange (1736–1813) are considered to be the two greatest mathematicians of the eighteenth century.
* Readers who are uncomfortable with complex numbers and complex—valued functions can read the Appendix to obtain a brief overview.
* In fact the constants c1 and c2 can be complex constants. However, if we are interested in real solutions, then we should pick c1 and c2 to be real constants.
* In previous discussions in this section we glossed over many details concerning complex numbers and complex—valued functions. For example, in the proof of Euler′s formula (Theorem 3.6) we used the fact that it is possible to rearrange the terms of a power series with complex coefficients. For a quick overview of some of the ideas of complex numbers and functions, see the Appendix at the back of the book. For a more thorough discussion of complex numbers, see Complex Variables for Scientists and Engineers, Second Edition, by John D. Paliouras and Douglas S. Meadows (Macmillan, 1990).
* This problem was taken from Math. Magazine, vol. 47, no. 5 (1974).
* We could also call the method of undetermined coefficients “the method of judicious guessing.”
* We can set the coefficients of 1, x, and x2 equal to each other, since the functions are linearly independent. Although we have discussed linear independence only for two functions, linear independence has meaning for any number of functions. Problem 43 at the end of this section will allow the reader to gain more experience with this important concept.
* The person who pioneered the use of complex numbers in differential equations was the brilliant electrical engineer Charles Steinmetz (1865–1923). Steinmetz came to the United States from his home in Germany in 1889 and became the brains of the newly founded General Electric Company. It was Steinmetz who, with power of his own mind, determined ways to mass—produce electric motors and generators. Physically, he was a dwarf who was crippled by a congenital deformity, but mentally, he had no peer as an electrical engineer and scientist.
* Be aware that there is no general method for finding the general solution for equations with variable coefficients. However, it is often possible to find solutions by inspection, transformations, reduction of order methods, series methods, and on and on. We will study series methods in Chapter 4.
* Inasmuch as we seek two functions V1(x) and V2(x), we can specify two conditions. The main condition, of course, is that we require that yp(x) satisfies the differential equation. The second condition can be imposed arbitrarily, and Lagrange imposed the condition v1′y1 + v2′y2 = 0 so that the second derivative yp will be simplified.
* In using the method of variation of parameters we first divide the differential equation by the coefficient of the highest derivative. Hence for second—order differential equations we assume that the equation has the form y″ + by′ + cy = f(x).
* A spring is called linear if the restoring force is proportional to the elongation. In other words, it takes twice the force to stretch a spring twice the amount. Most springs, however, are hard springs, which means that it takes more than twice the force to stretch a spring twice the distance.
† For small velocities the damping force is often nearly proportional to the velocity. For larger velocities it may be closer to the square of the velocity or some other function of the velocity.
* We have called the variable in the characteristic equation r since we have used m for the mass.
* Although mathematically, 
represents the frequency of a vibrating spring, no person would be gullible enough to think a mass of 1050 lb attached to a spring constant with constant 1 lb/in. would vibrate with a frequency of 10–25 oscillations every 2π seconds or that a mass of 10–50 lb would vibrate with a frequency of 1025 oscillations every 2π seconds. One must be sure of the assumptions made in setting up a differential equation to know whether or not to have confidence in the equation and its solution.
† If we had interchanged the roles of c1and c2, we would have written Eq. (9) as R sin (w0t + ø), where tan (ø) = c2/c1 In other words, the only difference between a sine curve and a cosine curve is a phase angle.
* The derivation of this differential equation can be found in Differential Equations by C. Ray Wylie (McGraw–Hill, 1979), p. 137.
† This interesting problem is taken from the classic text Differential Equations by Lyman M. Kells. (McGraw–Hill, 1937).
* The function of a function J(y) is called a functional and is a mapping from a class of functions or vectors to a field of scalars. Although functions y that minimize J (y) were studied by Newton and the Bernoullis in the late seventeenth century, the subject of calculus of variations was launched in 1744 by Leonhard Euler with his discovery of the differential equation that now bears his name.
* Although we mention M(ω) only for underdamped vibrations, the function M(ω) is also well defined for overdamped and critically damped vibrations.
* This problem is based on a problem taken from Engineering Mathematics by Robert E. Gaskell (Dryden Press, 1958).
* This game was extracted from the delightful little book Dynamics: The Geometry o f Behavior, Part One: Periodic Behavior by Ralph Abraham and Christopher Shaw (The Visual Mathematics Library, Aerial Press, 1982).
* A derivation of the beam equation can be found in the excellent book Advanced Engineering Mathematics by Peter O’Neil (Wadsworth, New York, 1983).
