Chapter 3
THE DOCTRINE OF CHANCES
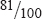
The third Illustrations article proved too large and had to be divided into two (W3:528). “The Doctrine of Chances” forms the first part; “The Probability of Induction” forms the second part.* Starting from the observation that “a science first begins to be exact when it is quantitatively treated,” Peirce began his discussion of the logic of science with a discussion of quantitative logic, postponing a discussion of deduction (which was typically considered the essence of logic) till the sixth article. Later, when working on a new edition of the Illustrations for the Open Court, Peirce spent considerable time and effort further developing his view, especially by contrasting it with the views expressed by Laplace in his Théorie analytique des probabilités and John Stuart Mill in his System of Logic, both of which he rejected (see chapters 7 and 9 below).
“The Doctrine of Chances” first appeared in Popular Science Monthly 12 (March 1878): 604–15. The text that follows is as it appeared in Popular Science Monthly. It is only minimally edited and italic brackets surround any text added by the editor. “The Doctrine of Chances” is listed as chapter 10 of Search for a Method, and was included under the title “Clearness of Apprehension” as chapter 18 of the 1894 logic book How to Reason, hereafter referred to as HTR. However, in the surviving typescript (R 424) Peirce made only a few minor changes. The Collected Papers editors include four notes they date 1893 that are not found in the annotated typescript for How to Reason (R 424). This suggests that they had access to a different version of the text, possibly intended for A Search for a Method. They did not include alterations made by Peirce in the R 424 typescript. Manuscripts R 703 and R 705, which were written between 10 and 15 August 1910, contain notes for the third Popular Science Monthly article. Most of this is reproduced, in part as footnotes and in part as an appendix to the current chapter. A more extensive discussion of the history of the article is found in the introduction.
I.
It is a common observation that a science first begins to be exact when it is quantitatively treated.* What are called the exact sciences are no others than the mathematical ones. Chemists reasoned vaguely until Lavoisier showed them how to apply the balance to the verification of their theories, when chemistry leaped suddenly into the position of the most perfect of the classificatory sciences.1 It has thus become so precise and certain that we usually think of it along with optics, thermotics, and electrics. But these are studies of general laws, while chemistry considers merely the relations and classification of certain objects; and belongs, in reality, in the same category as systematic botany and zoölogy. Compare it with these last, however, and the advantage that it derives from its quantitative treatment is very evident.*2
The rudest numerical scales, such as that by which the mineralogists distinguish the different degrees of hardness, are found useful. The mere counting of pistils and stamens sufficed to bring botany out of total chaos into some kind of form. It is not, however, so much from counting as from measuring, not so much from the conception of number as from that of continuous quantity, that the advantage of mathematical treatment comes. Number, after all, only serves to pin us down to a precision in our thoughts which, however beneficial, can seldom lead to lofty conceptions, and frequently descends to pettiness. Of those two faculties of which Bacon speaks, that which marks differences and that which notes resemblances,3 the employment of number can only aid the lesser one; and the excessive use of it must tend to narrow the powers of the mind. But the conception of continuous quantity has a great office to fulfill, independently of any attempt at precision. Far from tending to the exaggeration of differences, it is the direct instrument of the finest generalizations.4 When a naturalist wishes to study a species, he collects a considerable number of specimens more or less similar. In contemplating them, he observes certain ones which are more or less alike in some particular respect. They all have, for instance, a certain S-shaped marking. He observes that they are not precisely alike, in this respect; the S has not precisely the same shape, but the differences are such as to lead him to believe that forms could be found intermediate between any two of those he possesses. He, now, finds other forms apparently quite dissimilar—say a marking in the form of a C—and the question is, whether he can find intermediate ones which will connect these latter with the others. This he often succeeds in doing in cases where it would at first be thought impossible; whereas, he sometimes finds those which differ, at first glance, much less, to be separated in Nature by the non-occurrence of intermediaries. In this way, he builds up from the study of Nature a new general conception of the character in question. He obtains, for example, an idea of a leaf which includes every part of the flower, and an idea of a vertebra which includes the skull. I surely need not say much to show what a logical engine there is here. It is the essence of the method of the naturalist. How he applies it first to one character, and then to another, and finally obtains a notion of a species of animals, the differences between whose members, however great, are confined within limits, is a matter which does not here concern us. The whole method of classification must be considered later;*5 but, at present, I only desire to point out† that it is by taking advantage of the idea of continuity, or the passage from one form to another by insensible degrees,‡ that the naturalist builds his conceptions. Now, the naturalists are the great builders of conceptions; there is no other branch of science where so much of this work is done as in theirs; and we must, in great measure, take them for our teachers in this important part of logic. And it will be found everywhere that the idea of continuity§ is a powerful aid to the formation of true and fruitful conceptions. By means of it, the greatest differences are broken down and resolved into differences of degree, and the incessant application of it is the greatest value in broadening our conceptions. I propose to make a great use of this idea* in the present series of papers; and the particular series of important fallacies, which, arising from a neglect of it,† have desolated philosophy, must further on be closely studied. At present, I simply call the reader’s attention to the utility of this conception.
In studies of numbers, the idea of continuity is so indispensable, that it is perpetually introduced even where there is no continuity in fact, as where we say that there are in the United States 10.7 inhabitants per square mile, or that in New York 14.72 persons live in the average house.‡ Another example is that law of the distribution of errors which Quetelet, Galton, and others, have applied with so much success to the study of biological and social matters.6 This application of continuity to cases where it does not really exist illustrates, also, another point which will hereafter demand a separate study, namely, the great utility which fictions sometimes have in science.
II.
The theory of probabilities is simply the science of logic quantitatively treated. There are two conceivable certainties with reference to any hypothesis, the certainty of its truth and the certainty of its falsity. The numbers one and zero are appropriated, in this calculus, to marking these extremes of knowledge; while fractions having values intermediate between them indicate, as we may vaguely say, the degrees in which the evidence leans toward one or the other. The general problem of probabilities is, from a given state of facts, to determine the numerical probability of a possible fact. This is the same as to inquire how much the given facts are worth, considered as evidence to prove the possible fact. Thus the problem of probabilities is simply the general problem of logic.
Probability is a continuous quantity, so that great advantages may be expected from this mode of studying logic. Some writers have gone so far as to maintain that, by means of the calculus of chances, every solid inference may be represented by legitimate arithmetical operations upon the numbers given in the premises. If this be, indeed, true, the great problem of logic, how it is that the observation of one fact can give us knowledge of another independent fact, is reduced to a mere question of arithmetic. It seems proper to examine this pretension before undertaking any more recondite solution of the paradox.
But, unfortunately, writers on probabilities are not agreed in regard to this result. This branch of mathematics is the only one, I believe, in which good writers frequently get results entirely erroneous. In elementary geometry the reasoning is frequently fallacious, but erroneous conclusions are avoided; but it may be doubted if there is a single extensive treatise on probabilities in existence which does not contain solutions absolutely indefensible. This is partly owing to the want of any regular method of procedure; for the subject involves too many subtilties to make it easy to put its problems into equations without such an aid. But, beyond this, the fundamental principles of its calculus are more or less in dispute. In regard to that class of questions to which it is chiefly applied for practical purposes, there is comparatively little doubt; but in regard to others to which it has been sought to extend it, opinion is somewhat unsettled.
This last class of difficulties can only be entirely overcome by making the idea of probability perfectly clear in our minds in the way set forth in our last paper.7
III.
To get a clear idea of what we mean by probability,8 we have to consider what real and sensible difference there is between one degree of probability and another.
The character of probability belongs primarily, without doubt, to certain inferences. Locke explains it as follows: After remarking that the mathematician positively knows that the sum of the three angles of a triangle is equal to two right angles because he apprehends the geometrical proof, he thus continues: “But another man who never took the pains to observe the demonstration, hearing a mathematician, a man of credit, affirm the three angles of a triangle to be equal to two right ones, assents to it; i.e., receives it for true. In which case the foundation of his assent is the probability of the thing, the proof being such as, for the most part, carries truth with it; the man on whose testimony he receives it not being wont to affirm anything contrary to, or besides his knowledge, especially in matters of this kind.”9 The celebrated Essay concerning Humane Understanding contains many passages which, like this one, make the first steps in profound analyses which are not further developed. It was shown in the first of these papers that the validity of an inference does not depend on any tendency of the mind to accept it, however strong such tendency may be; but consists in the real fact that, when premises like those of the argument in question are true, conclusions related to them like that of this argument are also true. It was remarked that in a logical mind an argument is always conceived as a member of a genus of arguments all constructed in the same way, and such that, when their premises are real facts, their conclusions are so also. If the argument is demonstrative, then this is always so; if it is only probable, then it is for the most part so. As Locke says, the probable argument is “such as for the most part carries truth with it.”10
According to this, that real and sensible difference between one degree of probability and another, in which the meaning of the distinction lies, is that in the frequent employment of two different modes of inference, one will carry truth with it oftener than the other. It is evident that this is the only difference there is in the existing fact. Having certain premises, a man draws a certain conclusion, and as far as this inference alone is concerned the only possible practical question is whether that conclusion is true or not, and between existence and non-existence there is no middle term. “Being only is and nothing is altogether not,” said Parmenides; and this is in strict accordance with the analysis of the conception of reality given in the last paper.11 For we found that the distinction of reality and fiction depends on the supposition that sufficient investigation would cause one opinion to be universally received and all others to be rejected. That presupposition involved in the very conceptions of reality and figment involves a complete sundering of the two. It is the heaven-and-hell idea in the domain of thought. But, in the long run, there is a real fact which corresponds to the idea of probability, and it is that a given mode of inference sometimes proves successful and sometimes not, and that in a ratio ultimately fixed. As we go on drawing inference after inference of the given kind, during the first ten or hundred cases the ratio of successes may be expected to show considerable fluctuations; but when we come into the thousands and millions, these fluctuations become less and less; and if we continue long enough, the ratio will approximate toward a fixed limit. We may therefore define the probability of a mode of argument as the proportion of cases in which it carries truth with it.
The inference from the premise, A, to the conclusion, B, depends, as we have seen, on the guiding principle, that if a fact of the class A is true, a fact of the class B is true. The probability consists of the fraction whose numerator is the number of times in which both A and B are true, and whose denominator is the total number times in which A is true, whether B is so or not. Instead of speaking of this as the probability of the inference, there is not the slightest objection to calling it the probability that, if A happens, B happens. But to speak of the probability of the event B, without naming the condition, really has no meaning at all. It is true that when it is perfectly obvious what condition is meant, the ellipsis may be permitted. But we should avoid contracting the habit of using language in this way (universal as the habit is), because it gives rise to a vague way of thinking, as if the action of causation might either determine an event to happen or determine it not to happen, or leave it more or less free to happen or not, so as to give rise to an inherent chance in regard to its occurrence. It is quite clear to me that some of the worst and most persistent errors in the use of the doctrine of chances have arisen from this vicious mode of expression.*12
IV.
But there remains an important point to be cleared up. According to what has been said, the idea of probability essentially belongs to a kind of inference which is repeated indefinitely. An individual inference must be either true or false, and can show no effect of probability; and, therefore, in reference to a single case considered in itself, probability can have no meaning.13 Yet if a man had to choose between drawing a card from a pack containing twenty-five red cards and a black one, or from a pack containing twenty-five black cards and a red one, and if the drawing of a red card were destined to transport him to eternal felicity, and that of a black one to consign him to everlasting woe, it would be folly to deny that he ought to prefer the pack containing the larger proportion of red cards, although, from the nature of the risk, it could not be repeated. It is not easy to reconcile this with our analysis of the conception of chance. But suppose he should choose the red pack, and should draw the wrong card, what consolation would he have? He might say that he had acted in accordance with reason, but that would only show that his reason was absolutely worthless. And if he should choose the right card, how could he regard it as anything but a happy accident? He could not say that if he had drawn from the other pack, he might have drawn the wrong one, because an hypothetical proposition such as, “if A, then B,” means nothing with reference to a single case. Truth consists in the existence of a real fact corresponding to the true proposition. Corresponding to the proposition, “if A, then B,” there may be the fact that whenever such an event as A happens such an event as B happens. But in the case supposed, which has no parallel as far as this man is concerned, there would be no real fact whose existence could give any truth to the statement that, if he had drawn from the other pack, he might have drawn a black card. Indeed, since the validity of an inference consists in the truth of the hypothetical proposition that if the premises be true the conclusion will also be true, and since the only real fact which can correspond to such a proposition is that whenever the antecedent is true the consequent is so also, it follows that there can be no sense in reasoning in an isolated case, at all.
These considerations appear, at first sight, to dispose of the difficulty mentioned. Yet the case of the other side is not yet exhausted. Although probability will probably manifest its effect in, say, a thousand risks, by a certain proportion between the numbers of successes and failures, yet this, as we have seen, is only to say that it certainly will, at length, do so. Now the number of risks, the number of probable inferences, which a man draws in his whole life, is a finite one, and he cannot be absolutely certain that the mean result will accord with the probabilities at all. Taking all his risks collectively, then, it cannot be certain that they will not fail, and his case does not differ, except in degree, from the one last supposed. It is an indubitable result of the theory of probabilities that every gambler, if he continues long enough, must ultimately be ruined. Suppose he tries the martingale, which some believe infallible, and which is, as I am informed, disallowed in the gambling-houses.14 In this method of playing, he first bets say $1; if he loses it he bets $2; if he loses that he bets $4; if he loses that he bets $8; if he then gains he has lost 1 + 2 + 4 = 7, and he has gained $1 more; and no matter how many bets he loses, the first one he gains will make him $1 richer than he was in the beginning. In that way, he will probably gain at first; but, at last, the time will come when the run of luck is so against him that he will not have money enough to double, and must therefore let his bet go. This will probably happen before he has won as much as he had in the first place, so that this run against him will leave him poorer than he began; some time or other it will be sure to happen. It is true that there is always a possibility of his winning any sum the bank can pay, and we thus come upon a celebrated paradox that, though he is certain to be ruined, the value of his expectation calculated according to the usual rules (which omit this consideration) is large. But, whether a gambler plays in this way or any other, the same thing is true, namely, that he if he plays long enough he will be sure some time to have such a run against him as to exhaust his entire fortune. The same thing is true of an insurance company. Let the directors take the utmost pains to be independent of great conflagrations and pestilences, their actuaries can tell them that, according to the doctrine of chances, the time must come, at last, when their losses will bring them to a stop. They may tide over such a crisis by extraordinary means, but then they will start again in a weakened state, and the same thing will happen again all the sooner. An actuary might be inclined to deny this, because he knows that the expectation of his company is large, or perhaps (neglecting the interest upon money) is infinite. But calculations of expectations leave out of account the circumstance now under consideration, which reverses the whole thing. However, I must not be understood as saying that insurance is on this account unsound, more than other kinds of business. All human affairs rest upon probabilities, and the same thing is true everywhere. If man were immortal he could be perfectly sure of seeing the day when everything in which he had trusted should betray his trust, and, in short, of coming eventually to hopeless misery. He would break down, at last, as every great fortune, as every dynasty, as every civilization does. In place of this we have death.
But what, without death, would happen to every man, with death must happen to some man. At the same time, death makes the number of our risks, of our inferences, finite, and so makes their mean result uncertain. The very idea of probability and of reasoning rests on the assumption that this number is indefinitely great. We are thus landed in the same difficulty as before, and I can see but one solution of it. It seems to me that we are driven to this, that logicality inexorably requires that our interests shall not be limited. They must not stop at our own fate, but must embrace the whole community. This community, again, must not be limited, but must extend to all races of beings with whom we can come into immediate or mediate intellectual relation. It must reach, however vaguely, beyond this geological epoch, beyond all bounds. He who would not sacrifice his own soul to save the whole world, is, as it seems to me, illogical in all his inferences, collectively. Logic is rooted in the social principle.15
To be logical men should not be selfish; and, in point of fact, they are not so selfish as they are thought.16 The willful prosecution of one’s desires is a different thing from selfishness. The miser is not selfish; his money does him no good, and he cares for what shall become of it after his death. We are constantly speaking of our possessions on the Pacific, and of our destiny as a republic, where no personal interests are involved, in a way which shows that we have wider ones. We discuss with anxiety the possible exhaustion of coal in some hundreds of years, or the cooling-off of the sun in some millions, and show in the most popular of all religious tenets that we can conceive the possibility of a man’s descending into hell for the salvation of his fellows.
Now, it is not necessary for logicality that a man should himself be capable of the heroism of self-sacrifice. It is sufficient that he should recognize the possibility of it, should perceive that only that man’s inferences who has it are really logical, and should consequently regard his own as being only so far valid as they would be accepted by the hero. So far as he thus refers his inferences to that standard, he becomes identified with such a mind.
This makes logicality attainable enough. Sometimes we can personally attain to heroism. The soldier who runs to scale a wall knows that he will probably be shot, but that is not all he cares for. He also knows that if all the regiment, with whom in feeling he identifies himself, rush forward at once, the fort will be taken. In other cases we can only imitate the virtue. The man whom we have supposed as having to draw from the two packs, who if he is not a logician will draw from the red pack from mere habit, will see, if he is logician enough, that he cannot be logical so long as he is concerned only with his own fate, but that that man who should care equally for what was to happen in all possible cases of the sort could act logically, and would draw from the pack with the most red cards, and thus, though incapable himself of such sublimity, our logician would imitate the effect of that man’s courage in order to share his logicality.
But all this requires a conceived identification of one’s interests with those of an unlimited community. Now, there exist no reasons, and a later discussion will show that there can be no reasons, for thinking that the human race, or any intellectual race, will exist forever. On the other hand, there can be no reason against it;* and, fortunately, as the whole requirement is that we should have certain sentiments, there is nothing in the facts to forbid our having a hope, or calm and cheerful wish, that the community may last beyond any assignable date.
It may seem strange that I should put forward three sentiments, namely, interest in an indefinite community, recognition of the possibility of this interest being made supreme, and hope in the unlimited continuance of intellectual activity, as indispensable requirements of logic. Yet, when we consider that logic depends on a mere struggle to escape doubt, which, as it terminates in action, must begin in emotion, and that, furthermore, the only cause of our planting ourselves on reason is that other methods of escaping doubt fail on account of the social impulse, why should we wonder to find social sentiment presupposed in reasoning? As for the other two sentiments which I find necessary, they are so only as supports and accessories of that. It interests me to notice that these three sentiments seem to be pretty much the same as that famous trio of Charity, Faith, and Hope, which, in the estimation of St. Paul, are the finest and greatest of spiritual gifts.17 Neither Old nor New Testament is a text-book of the logic of science, but the latter is certainly the highest existing authority in regard to the dispositions of heart which a man ought to have.
V.
Such average statistical numbers as the number of inhabitants per square mile, the average number of deaths per week, the number of convictions per indictment, or, generally speaking, the number of x’s per y, where the x’s are a class of things some or all of which are connected with another class of things, their y’s, I term relative numbers. Of the two classes of things to which a relative number refers, that one of which it is a number may be called its relate, and that one per which the numeration is made may be called its correlate.
Probability is a kind of relative number; namely, it is the ratio of the number of arguments of a certain genus which carry truth with them to the total number of arguments of that genus, and the rules for the calculation of probabilities are very easily derived from this consideration. They may all be given here, since they are extremely simple, and it is sometimes convenient to know something of the elementary rules of calculation of chances.
RULE I. Direct Calculation.—To calculate, directly, any relative number, say for instance the number of passengers in the average trip of a street-car, we must proceed as follows:
Count the number of passengers for each trip; add all these numbers, and divide by the number of trips. There are cases in which this rule may be simplified. Suppose we wish to know the number of inhabitants to a dwelling in New York. The same person cannot inhabit two dwellings. If he divide his time between two dwellings he ought to be counted a half-inhabitant of each. In this case we have only to divide the total number of the inhabitants of New York by the number of their dwellings, without the necessity of counting separately those which inhabit each one. A similar proceeding will apply wherever each individual relate belongs to one individual correlate exclusively. If we want the number of x’s per y, and no x belongs to more than one y, we have only to divide the whole number of x’s of y’s by the number of y’s. Such a method would, of course, fail if applied to finding the average number of street-car passengers per trip. We could not divide the total number of travelers by the number of trips, since many of them would have made many passages.
To find the probability that from a given class of premises, A, a given class of conclusions, B, follow, it is simply necessary to ascertain what proportion of the times in which premises of that class are true, the appropriate conclusions are also true. In other words, it is the number of cases of the occurrence of both the events A and B, divided by the total number of cases of the occurrence of the event A.
RULE II. Addition of Relative Numbers.—Given two relative numbers having the same correlate, say the number of x’s per y, and the number of z’s per y; it is required to find the number of x’s and z’s together per y. If there is nothing which is at once an x and a z to the same y, the sum of the two given numbers would give the required number. Suppose, for example, that we had given the average number of friends that men have, and the average number of enemies, the sum of these two is the average number of persons interested in a man. On the other hand, it plainly would not do to add the average number of persons having constitutional diseases to the average number over military age, and to the average number exempted by each special cause from military service, in order to get the average number exempt in any way, since many are exempt in two or more ways at once.
This rule applies directly to probabilities. Given the probability that two different and mutually exclusive events will happen under the same supposed set of circumstances. Given, for instance, the probability that if A then B, and also the probability that if A then C, then the sum of these two probabilities is the probability that if A then either B or C, so long as there is no event which belongs at once to the two classes B and C.
RULE III. Multiplication of Relative Numbers.—Suppose that we have given the relative number of x’s per y; also the relative number of z’s per x of y; or, to take a concrete example, suppose that we have given, first, the average number of children in families living in New York; and, second, the average number of teeth in the head of a New York child—then the product of these two numbers would give the average number of children’s teeth in a New York family. But this mode of reckoning will only apply in general under two restrictions. In the first place, it would not be true if the same child could belong to different families, for in that case those children who belonged to several different families might have an exceptionally large or small number of teeth, which would affect the average number of children’s teeth in a family more than it would affect the average number of teeth in a child’s head. In the second place, the rule would not be true if different children could share the same teeth, the average number of children’s teeth being in that case evidently something different from the average number of teeth belonging to a child.
In order to apply this rule to probabilities, we must proceed as follows: Suppose that we have given the probability that the conclusion B follows from the premise A, B and A representing as usual certain classes of propositions. Suppose that we also knew the probability of an inference in which B should be the premise, and a proposition of a third kind, C, the conclusion. Here, then, we have the materials for the application of this rule. We have, first, the relative number of B’s per A. We next should have the relative number of C’s per B following from A. But the classes of propositions being so selected that the probability of C following from any B in general is just the same as the probability of C’s following from one of those B’s which is deducible from an A, the two probabilities may be multiplied together, in order to give the probability of C following from A. The same restrictions exist as before. It might happen that the probability that B follows from A was affected by certain propositions of the class B following from several different propositions of the class A. But, practically speaking, all these restrictions are of very little consequence, and it is usually recognized as a principle universally true that the probability that, if A is true, B is, multiplied by the probability that, if B is true, C is, gives the probability that, if A is true, C is.
There is a rule supplementary to this, of which great use is made. It is not universally valid, and the greatest caution has to be exercised in making use of it—a double care, first, never to use it when it will involve serious error; and, second, never to fail to take advantage of it in cases in which it can be employed. This rule depends upon the fact that in very many cases the probability that C is true if B is, is substantially the same as the probability that C is true if A is. Suppose, for example, we have the average number of males among the children born in New York; suppose that we also have the average number of children born in the winter months among those born in New York. Now, we may assume without doubt, at least as a closely approximate proposition (and no very nice calculation would be in place in regard to probabilities), that the proportion of males among all the children born in New York is the same as the proportion of males born in summer in New York, and, therefore, if the names of all the children born during a year were put into an urn, we might multiply the probability that any name drawn would be the name of a male child by the probability that it would be the name of a child born in summer, in order to obtain the probability that it would be the name of a male child born in summer. The questions of probability, in the treatises upon the subject, have usually been such as to relate to balls drawn from urns, and games of cards, and so on, in which the question of the independence of events, as it is called—that is to say, the question of whether the probability of C, under the hypothesis B, is the same as its probability under the hypothesis A, has been very simple; but, in the application of probabilities to the ordinary questions of life, it is often an exceedingly nice question whether two events may be considered as independent with sufficient accuracy or not. In all calculations about cards it is assumed that the cards are thoroughly shuffled, which makes one deal quite independent of another. In point of fact the cards seldom are, in practice, shuffled sufficiently to make this true; thus, in a game of whist, in which the cards have fallen in suits of four of the same suit, and are so gathered up, they will lie more or less in sets of four of the same suit, and this will be true even after they are shuffled. At least some traces of this arrangement will remain, in consequence of which the number of “short suits,” as they are called—that is to say, the number of hands in which the cards are very unequally divided in regard to suits—is smaller than the calculation would make it to be; so that, when there is a misdeal, where the cards, being thrown about the table, get very thoroughly shuffled, it is a common saying that in the hands next dealt out there are generally short suits. A few years ago a friend of mine, who plays whist a great deal, was so good as to count the number of spades dealt to him in 165 hands, in which the cards had been, if anything, shuffled better than usual. According to calculation, there should have been 85 of these hands in which my friend held either three or four spades, but in point of fact there were 94, showing the influence of imperfect shuffling.
According to the view here taken, these are the only fundamental rules for the calculation of chances. An additional one, derived from a different conception of probability, is given in some treatises, which if it be sound might be made the basis of a theory of reasoning. Being, as I believe it is, absolutely absurd, the consideration of it serves to bring us to the true theory; and it is for the sake of this discussion, which must be postponed to the next number, that I have brought the doctrine of chances to the reader’s attention at this early stage of our studies of the logic of science.
NOTE*
1910 Aug.† On reperusing this article after the lapse of a full generation, it strikes me as making two points that were worth making. The better made of the two had been still better made ten years before in my three articles in the Speculative Review, Vol II. (W. T. Harris, Editor).18 This point is that no man can be logical whose supreme desire is the well-being of himself or of any other existing person or collection of persons.
The other good point is that probability never properly refers immediately to a single event, but exclusively to the happening of a given kind of event on any occasion of a given kind. So far all is well. But when I come to define probability, I repeatedly say that it is the quotient of the number of occurrences of the event divided by the number of occurrences of the occasion. Now this is manifestly wrong; for probability relates to the future; and how can I say how many times a given die will be thrown in the future? To be sure I might, immediately after my throw, put the die in strong nitric acid, and dissolve it; but this suggestion only puts the preposterous character of the definition in a still stronger light. For it is plain, that if probability be the ratio of the occurrences of the specific event to the occurrences of the generic occasion, it is the ratio that there would be in the long run, and has nothing to do with any supposed cessation of the occasions. This long run can be nothing but an endlessly long run; and even if it be correct to speak of an infinite “number,” yet (infinity divided by infinity) has certainly, in itself, no definite value.
But we have not yet come to the end of the flaws in the definition, since no notice whatever has been taken of two conditions which require the strictest precautions in all experiments to determine the probability of a specific event on a generic occasion.* Namely in the first place we must limit our endeavours strictly to counting occurrences to the right genus of occasion and carefully resist all other motives for counting them, and strive to take them just as they would ordinarily occur. In the next place, it must be known that the occurrence of the specific event on one occasion will have no tendency to produce or to prevent the occurrence of the same event upon any other of the occurrences of the generic occasion. In the third place, after the probability has been ascertained, we must remember that this probability cannot be relied upon at any future time unless we have adequate grounds for believing that it has not too much changed in this interval.
I will now give over jeering at my former inaccuracies, committed when I had been a student of logic for only about a quarter of a century, and was naturally not so well-versed in it as now, and will proceed to define probability. I must promise that we, all of us, use this word with a degree of laxity which corrupts and rots our reasoning to a degree that very few of us are at all awake to. When I say our “reasoning,” I mean not formal reasonings only but our thoughts in general, so far as they are concerned with any of those approaches toward knowledge which we confound with probability. The result is that we not only fall into the falsest ways of thinking, but, what is often still worse, we give up sundry problems as beyond our powers,—problems of gravest concern, too,—when, in fact, we should find they were not in a bit so, if we only rightly discriminated between the different kinds of imperfection of certitude, and if we had only once acquainted ourselves with their different natures. I shall in these notes endeavor to mark the three ways of falling short of certainty by the three terms probability, verisimilitude or likelihood, and plausibility.19 Just at present I propose to deal only with Probability; but I will so far characterize Verisimilitude and Plausibility as mark them off as being entirely different from Probability. Beginning with Plausibility, I will first endeavour to give an example of an idea which shall be strikingly marked by its very low degree of this quality. Eusapia Palladino had been proved to be a very clever prestigiateuse and cheat, and was visited by a Mr. Carrington, who I suppose to be so clever in finding out how tricks are done, that it is highly improbable that any given trick should long baffle him.20 In point of fact he has often caught the Palladino creature in acts of fraud. Some of her performances, however, he cannot explain; and thereupon he urges the theory that these are supernatural, or, as he prefers to phrase it, “supernormal.” Well, I know how it is that when a man has been long intensely exercized and over-fatigued by an enigma, his common-sense will sometimes desert him; but as for me, it seems to me that the Palladino has simply been too clever for him, as no doubt she would be for me. The theory that there is anything “supernormal,” or super anything but super-chérie in the case, seems to me as needless as any theory I ever came across. That is to say, granted that it is not yet proved that women who deceive for gain receive aid from the spiritual world, I think it more plausible that there are tricks that can deceive Mr. Carrington than that the Palladino woman has received such aid. By Plausible, I mean that a theory that has not yet been subjected to any test, although more or less surprising phenomena have occurred which it would explain if it were true, is in itself of such a character as to recommend it for further examination or, if it be highly plausible, justify us in seriously inclining toward belief in it, as long as the phenomena be inexplicable otherwise.
I will now give an idea of what I mean by likely or verisimilar. It is to be understood that I am only endeavouring so far to explain the meanings I attach to ‘plausible’ and to ‘likely’ as this may be an assistance to the reader in understanding the meaning I attach to probable. I call that theory likely which is not yet proved but is supported by such evidence, that if the rest of the conceivably possible evidence should turn out upon examination to be of a similar character, the theory would be conclusively proved. Strictly speaking, matters of fact never can be demonstrably proved, since it will always remain conceivable that there should be some mistake about it. For instance, I regard it as sufficiently proved that my name is Charles Peirce and that I was born in Cambridge, Massachusetts in a stone colored wooden house in Mason Street.21 But even of the part of this of which I am most assured—that of my name, —there is a certain small probability that I am in an abnormal condition and have got it wrong. I am conscious myself of occasional lapses of memory about other things; and though I well remember,—or think I do,—living in that house at a tender age, I do not in the least remember being born there, impressive as such a first experience might be expected to be. Indeed, I cannot specify any date on which any certain person informed me I had been born there; and it certainly would have been easy to deceive me in the matter had there been any serious reason for doing so; and how can I be so sure as I surely am that no such reason did exist. It would be a theory without plausibility; that is all.
The history of science, particularly physical science, in contradistinction to natural science,—or, as I usually, though inadequately phrase the distinction, the history of nomological in contradistinction to classificatory science,—this history ever since I first seriously set myself, at the age of thirteen, in 1852, in the study of logic,22 shows only too grievously how great a boon could be any way determining and expressing by numbers the degree of likelihood that a theory had attained,—any general recognition, even among leading men of science, of the true degree of significance of a given fact, and of the proper method of determining it. I hope my writings may, at any rate, awaken a few to the enormous waste of effort it would save. But any numerical determination of likelihood is more than I can expect.
The only kind of reasoning which can render our conclusions certain,—and even this kind can do so only under the proviso that no blunder had been committed in the process,—attains this certainty by limiting the conclusion (as Kant virtually said, and others before him) to facts already expressed and accepted in the premisses. This is called necessary, or syllogistic reasoning. Syllogism, not confined to the kind that Aristotle and Theophrastus studied, is merely an artificial form in which it may be expressed, and it is not its best form, from any point of view. But the kind of reasoning which creates likelihoods by virtue of observations may render a likelihood practically certain,—as certain as that a stone let loose from the clutch will, under circumstances not obviously exceptional, fall to the ground,23—and this conclusion may be that under a certain general condition, easily verified, a certain actuality will be probable, that is to say, will come to pass once in so often in the long run. One such familiar conclusion, for example, is that a die thrown from a dice box will with a probability of one-third, that is, once in three times in the long run, turn up a number (either tray or size) that is divisible by three. But this can be affirmed with practical certainty only if by a “long run” be meant an endless series of trials, and (as just said) infinity divided by infinity gives of itself an entirely indefinite quotient. It is therefore necessary to define the phrase. I might give the definition with reference to the probability, p, where p is any vulgar fraction, and in reference to a generic condition, m, and a specific kind of event, n. But I think the reader will follow me more readily, if in place of the letter, m, (which in itself is but a certain letter, to which is attached a peculiar meaning, that of the fulfillment of some generic condition,) I put instead the supposition that a die is thrown from a dice-box; and this special supposition will be as readily understood by the reader to be replaceable by any other general condition along with a simultaneous replacement of the event, that a number divisible by three is turned up, and at the same time with the replacement of one third by whatever other vulgar fraction may be called for when some different example of a probability is before us. I am, then, to define the meaning of the statement that the probability that if a die be thrown from a dice box it will turn up a number divisible by three is one third. The statement means that the die has a certain “would-be;” and to say that a die has a “would-be” is to say that it has a property, quite analogous to any habit that a man might have. Only the “would-be” of the die is presumably as much simpler and more definite than the man’s habit, as the die’s homogeneous composition and cubical shape is simpler than the nature of the man’s nervous system and soul; and just as it would be necessary, in order to define a man’s habit, it would be needful to describe how it would lead him to behave and upon what sort of occasion; albeit this statement would by no means imply that this habit consists in that action, so to define the die’s “would-be,” it is necessary to say how it would lead the die to behave on an occasion that would bring out the full consequences of the would-be; and this statement will not of itself imply that the “would-be” of the die consists in such behaviour.
Now in order that the full effect of the die’s “would-be” may find expression, it is necessary that the die should undergo in an endless series of throws from the dice-box, the result of no throw having the slightest influence upon the result of any other throw, or, as we express it, the throws must be independent each of every other.
It will be no objection to our considering the consequences of the supposition that the die is thrown in an endless succession of times, and that with a finite pause after each throw, that such an endless series of events is impossible, for the reason that the impossibility is merely a physical, and not a logical, impossibility, as was well illustrated in that famous sporting event in which Achilles succeeded in overtaking the champion tortoise, in spite of his giving the latter the start of a whole stadion. For it having been ascertained, by delicate measurement, between a mathematical point between the shoulder blades of Achilles (marked on the limit between a red, a green, and a violet sector of a stained disk) and a similar point on the carapace of the tortoise, that when Achilles arrived where the tortoise started, the latter was just 60 feet 8 inches and 
inch further on, which is just one tenth of a stadion, and that when Achilles reached that point the tortoise was still 6 feet and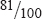 
inch in advance of him, and finally that, both advancing at a perfectly uniform rate, the tortoise had run just 67 feet 5 inches when he was overtaken by Achilles, it follows that the tortoise progressed at just one tenth the speed of Achilles, the latter running a distance in stadia of 1.111111111, so that he had to traverse the sum of an infinite multitude of finite distances, each in a finite time, and yet covered the stadion and one ninth in a finite time. No contradiction, therefore, is involved in the idea of an endless series of finite times or spaces having but a finite sum, provided there is no fixed finite quantity which every member of an endless part of that series must each and every one exceed.
The reader must pardon me for occupying any of his time with such puerile stuff as that 0.1111 =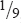 
; for astounding as it seems, it has more than once happened to me that a gentleman has come to me, every one of them not merely educated men, but highly accomplished, men who might well enough be famous over the civilized world, if fame were anything to the purpose, but men whose studies had been such that one would have expected to find each of them an adept in the accurate statement of arguments, and yet each has come and has undertaken to prove to me that the old catch of Achilles and the tortoise is a sound argument. If I tell you what after listening to them by the hour, I have always ended by saying, it may serve your turn on a similar occasion. I have said, “I suppose you do not mean to say that you really believe that a fast runner cannot, as a matter of fact, overtake a slow one. I therefore conclude that the argument which you have been unable to state, either syllogistically or in any other intelligible form, is intended to show that Zeno’s reasoning about Achilles and the tortoise is sound according to some system of logic which admits that sound necessary reasoning may lead from true premisses to a false conclusion. But in my system of logic what I mean by bad necessary reasoning is precisely an argument which might lead from true premisses to a false conclusion, —just that and nothing else. If you prefer to call such reasoning a sound necessary argument, I have no objection in the world to your doing so; and you will kindly allow me to employ my different nomenclature. For I am such a plain, uncultured soul that when I reason I aim at nothing else than just to find out the truth.
To get back, then, to the die and its habit,—its “would-be”—I really know no other way of defining a habit than by describing the kind of behaviour in which the habit becomes actualized. So I am obliged to define the statement that there is a probability of one third that the die when thrown will turn up either a three or a six by stating how the numbers will run when the die is thrown.
But my purpose in doing so is to explain what probability, as I use the word, consists in. Now it would be no explanation at all to say that it consists in something being probable, so I must avoid using that word or any synonym of it. If I were to use such an expression, you would very properly turn upon me and say, “I either know what it is to be probable, in your sense of the term, or I do not. If I don’t how can I be expected to understand you until you have explained yourself; and if I do what is the use of the explanation?” But the fact that the probability of the die turning up a three or a six is not sure to produce any determinate upon the run of the numbers thrown in any finite series of throws. It is only when the series is endless that we can be sure that it will have a particular character.
Even when there is an endless series of throws, there is no syllogistic certainty,—no “mathematical” certainty (if you are more familiar with this latter phrase,)—that the die will not turn up a six obstinately at every single throw. It might be that if in the course of the endless series, some friends should borrow the die to make a pair for a game of backgammon, there might be nothing unusual in the behaviour of the lent die, and yet when it was returned and our experimental series was resumed where it had been interrupted, the die might return to turning up nothing but six every time. I say it might, in the sense that it would not violate the principle of contradiction if it did. It surely would not, however, unless a miracle were performed; and moreover if such miracle were worked, I should say (since it is my use of the term probability that we have supposed to be in question,) that during this experimental series of throws, the die took on an abnormal,—a miraculous,—habit. For I should think that the performance of a certain line of behaviour throughout an endless succession of occasions, without exception, very decidedly constituted a habit. There may be some doubt about this; for owing to our not being accustomed to reason in this way about successions of events which are endless in the sequence and yet are completed in time, it is hard for me quite to satisfy myself what I ought to say in such a case. But I have reflected seriously upon it, and though I am not perfectly sure of my ground, (and I am a cautious reasoner,) yet I am more that what you would understand by “pretty confident,” that supposing one to be in a condition to assert what would surely be the behaviour in any single determinate respect, of any subject throughout an endless series of occasions of a stated kind, he ipso facto knows a “would-be,” or habit, of that subject. It is very true, mind you, that no collection whatever of single acts, though it were ever so many grades greater than a simple endless series, can constitute a would-be, nor can the knowledge of single acts, whatever their multitude, tell us for sure of a would-be. But there are two remarks to be made; 1st, that in the case under consideration a person is supposed to be in a condition to assert what surely would be the behaviour of the subject throughout the endless series of occasions,—a knowledge which cannot have been derived from reasoning from its behaviour on the single occasions; and 2nd, that that which in our case renders it true, as stated, that the person supposed “ipso facto knows a would-be of that subject,” as not the occurrence of the single acts, but the fact that the person supposed “was in condition to assert what would surely be the behaviour of the subject throughout an endless series of occasions.”*
I will now describe the behaviour of the die during the endless series of throws, in respect to turning up numbers divisible by three. It would be perfectly possible to construct a machine that would automatically throw the die and pick it up, and continue doing so as long as it was supplied with energy. It would further be still easier to design the plan of an arrangement whereby a hand should after each throw move over an arc graduated so as indicate the value of the quotient of the number of throws of three or six that had been known since the beginning of the experiment, divided by the total number of throws since the beginning. It is true that the mechanical difficulties would become quite insuperable before the die had been thrown many times; but fortunately a general description of the way the hand would move will answer our purposes much better than would the actual machine, were it ever so perfect.
After the first throw, the hand will go either to 0 = 
or to 1 = 
; and there it may stay for several throws. But when it once moves, it will move after every throw, without exception, since the denominator of the fraction at whose value it points will always increase by 1, and consequently the value of the fraction will be diminished if the numerator remains unchanged, as it will be increased in case the numerator is increased by 1, these two being the only possible cases. The behaviour of the hand may be described as an excessively irregular oscillation, back and forth, from one side of ⅓ to the other. I will actually throw a die, record the throws and put dots on squared paper, each square one way representing a unit of the numerator and each square the other way representing a unit of the denominator. Then straight lines to the origin or corner of the squared surface will represent the positions of the hand, so that you will have a sort of picture of its motion[.]*
NOTES
1. Peirce opens the sixth article, “Deduction, Induction, and Hypothesis,” by stating “the chief business of the logician is to classify arguments.”
2. Jacobus Henricus van ’t Hoff (1852–1911), Dutch chemist.
3. Francis Bacon, Novum Organum, Bk. 1, Aph. 55 and Bk. 2, Aph. 27.
4. The (mathematical) theme of continuity plays a central role throughout Peirce’s philosophical career.
5. Peirce discusses the issue of the classification of arguments at the beginning of the sixth Illustrations paper (see chapter 6 below).
6. The Law of Error originated with Karl Gauss. Lambert Adolphe Quetelet (1797–1874) applied the law to his theory of the average man in Sur l’homme et le développement de se facultés: ou Essai de physique sociale (Paris: Bachelier, 1835). Quetelet’s views influenced Sir Francis Galton in Hereditary Genius: An Inquiry Into Its Laws and Consequences (London: Macmillan, 1869); see esp. appendix. Later, in 1886, Galton would famously say that the Law of Error: “reigns with serenity and in complete self-effacement amidst the wildest confusion. The huger the mob and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason” (Natural Inheritance [London: Macmillan, 1889], 66). For Peirce’s recent technical work in this area, see his 1870 “On the Theory of Errors of Observations” (W3, sel., 42; see also sel. 41).
7. In a 26 January 1909 letter to William Edward Story, Peirce writes:
Here is a definition which pleases me: To say that a certain event has a probability, p, means that in an endless series of independent occasions, on each of which the event either occurs or does not, if a tally be kept and a new value of the proportion of occasions on which the event has occurred since the beginning of the series be calculated at every new occasion, then, if there be one value and one value only of this proportion which never ceases to recur, while every other value will some time occur for the last time, that value is the probability of the event. Of course it is assumed that the general conditions do not alter during the whole series. The probability is the value that would never cease to recur if the general conditions were to remain the same.
8. The entries for the first three meanings of the term probability in the Century Dictionary are Peirce’s (CD:4741).
9. John Locke, An Essay Concerning Human Understanding, Bk. 4, Ch. 15 “Of Probability,” sect. 1.
10. Ibid.
11. Peirce found Parmenides’s statement in Bk 1, Pt 1, Ch 1, §C1, Anmerkung 1 of Hegel’s Wissenshaft der Logik. See also W2:317, where Peirce criticizes Scotus Erigena’s binary approach in De divisione naturae, by using Parmenides’s claim.
12. John Venn, Logic of Chance (London: Macmillan, 1866). For Peirce’s review of that book, see W2, sel. 8.
13. Hence, for Peirce, no probabilistic argument can be given for the origin of the universe—universes, as he puts it in “The Probability of Induction,” are simply not as plentiful as blackberries. Nonetheless, Peirce develops a view where the universe develops from (absolute) chance. See esp. “Evolutionary Love” (W8, sel. 30).
14. The Martingale or doubling-up system is a betting strategy that became popular in eighteenth-century France; it also inspired the Gamblers Fallacy: the mistaken assumption that departures from what occurs on average or in the long run will be corrected in the short run.
15. See Peirce’s discussion of the method of science in “The Fixation of Belief,” with notes.
16. In “Evolutionary Love” (W8, sel. 30) Peirce criticizes the doctrine of self-interest espoused by economists, dismissively calling it “the gospel of greed,” while developing an alternative.
17. See 1 Corinthians 13. Paul uses the Greek agape for charity—the unselfish and unconditional love for others. For Peirce’s view on agape, and his doctrine of agapism, see esp. “Evolutionary Love” (W8, sel. 30).
18. These are the three papers Peirce published in 1868 in the Journal of Speculative Philosophy, edited by William Torrey Harris (W2, sel. 22–23).
19. Peirce makes the same trifold distinction in his letter to Paul Carus written later that month, which is included below as chapter 9.
20. Eusapia Palladino (1854–1918) was an Italian spiritualist medium. In 1908, the American Society for Psychical Research sent Hereward Carrington (1880–1958) to Naples to investigate her psychic abilities. Carrington described his encounter in Eusapia Palladino and her Phenomena (New York: B.W. Dodge & Co., 1909), and invited her to the US where he organized a tour for her.
21. The Peirce family resided from 1834 till 1845 at 11 Mason Street (Peirce was born in 1839). For a more extensive autobiographical account, see e.g. W8, sel. 12 and the accompanying editorial annotations.
22. Peirce is here referring to his discovery of his brother’s copy of Richard Whately’s Elements of Logic.
23. In the fourth Lowell Lecture of 1903, Peirce uses this as an example to show that thirdness is really operative in nature (CP 5.93–95).
24. Peirce is referring to “The Logic of Relatives,” Monist 7 (January 1897): 161–217; note that this was written fourteen years earlier, not nineteen years earlier.
I. That a science begins to be really accurate from the moment when it receives a quantitative treatment. II. The theory of probabilities is logic quantitatively considered. III. The vagueness, uncertainty, & error which have infested this theory. IV. The conception of probability made clear. V. The rules of the calculus. VI. All the difficulties disappear. VII. It is not a formularization of natural good sense, but is superior thereto. VIII. The use of scientific reasoning. Indeterminacy of the probability. This is essential; when the probability is determined we have nothing but a species of deduction. IX. How are synthetical judgments à priori possible? The question which exploded the Leibnizian philosophy. The question how are synthetical judgments possible? makes another great step in philosophy. X. Practical importance of the question. Abbé Gratry makes the thing miraculous. XI. Solution of the question. XII. New conception of Knowledge. XIII. Rule of reasoning.
In the original papers in the Popular Science Monthly of March and April, 1878, of which the present essay is a revision, I contented myself with applying the “common observation” that “a science first begins to be exact when it gets quantitatively treated.” Now this is, as I called it, “an observation.” But observation only supplies us with individual facts: it does not, by itself alone, supply a reason for the necessity of the facts observed. It may be a fact that any science takes a higher science as soon as it becomes quantitative, or, what comes to the same thing, so far as observation can show, that any science as it matures is led to pay more and more heed to quantities; for naturally we first remark the rough discriminations of quality and later the finer differences of quantity. Each of these two forms of interpreting the observable facts represents, I do not doubt, a side of the truth that the other leaves unexpressed. When we come to slight degrees of difference we resort to quantity, simply as a convenient means of expressing and of finding slight dissimilarities; but moreover quantitative expressions always tend to stimulate our attention to small distinctions. But it certainly is not a universal truth that progress in a science will render it more attentive to quantity; for it has not been so with nineteenth-century mathematics. […]
Such studies have been made in our generation of the general laws of chemistry that the reader may well be surprised to find it spoken of as a merely classificatory science. Yet that the chemists could not be so affected at the time of the original publication of this Essay is shown by the fact that only a few months previously van ’t Hoff2 had put forward the general law of massaction as a new discovery of his own. The fact that it had really been several times already announced as a newly discovered law only fortifies the evidence that chemists were not yet accustomed to think of general laws as belonging to their science, although of course there had been a few such since the early years of modern [science.]
I am satisfied by considerable search after pertinent facts that no distinction between different allied sciences can represent any truth of fact other than a difference between what habitually passes in the minds, and moves the investigations of the two general bodies of cultivators of those sciences at the time to which the distinction refers.