14 BRUTE-FORCE SEARCH YOUR WAY TO A GOOD STRATEGY
It is not being suggested that we should design the strategy in our own image. Rather it should be matched to the capacities and weakness of the computer. The computer is strong in speed and accuracy and weak in analytical abilities and recognition. Hence, it should make more use of brutal calculation than humans.
—Claude Shannon1
SEARCH FOR PLAYING GAMES
In the first chapter of this book we saw that the automata of the 18th century operated on the same principles as mechanical clockwork. Using only mechanical components—pulleys, gears, levers, and so on—they could perform amazing feats, like playing the harpsichord (a piano-like instrument), writing legible sentences, and making detailed illustrations with a pencil in their hand. They did this by following programs encoded within their clockwork.
Throughout this book, we’ve encountered computer programs that can emulate a wide variety of human-like behaviors, and in the next two chapters we’ll take a closer look at computer programs that have been developed to play games like chess and Go better than the best human players. These game-playing automata were implemented as modern, digital computer programs; but, like their mechanical ancestors, modern computers still follow programs.
In fact, the computer programs that play games like chess and Go could be replicated perfectly with only physical devices. These mechanical computers, sometimes called mechanical Turing machines, can be built out of only wooden components and powered by a hand crank. Such a wooden computer might need to be extraordinarily large—so large that it might take impractically large investments to build and power—but at least in theory, it’s possible.2
If you take a moment to ponder this, the whole premise that a wooden device powered by a hand crank could play a competitive game of chess is extraordinary. This was, after all, the appeal of the Mechanical Turk. How is it that such devices could not only play these games of strategy well; but that they could play them so well that they’ve beat the best human players? This is the central question you should hold in your mind throughout this chapter, as we explore the way in which machines can be programmed to play games of strategy. One of the key features of these machines is a form of foresight that they use to anticipate how the game will play out many moves into the future. To see how this works, let’s start with a simple game, a game for which the program only needs to anticipate its own moves: the classic game of Sudoku.
SUDOKU
Sudoku is a game in which the sole player must fill in the blank spaces (cells) on a 9 × 9 grid with the numbers 1 through 9. For each game of Sudoku, the puzzle creator partially fills some subset of the cells, so that before play begins the grid looks something like the one in figure 14.1.
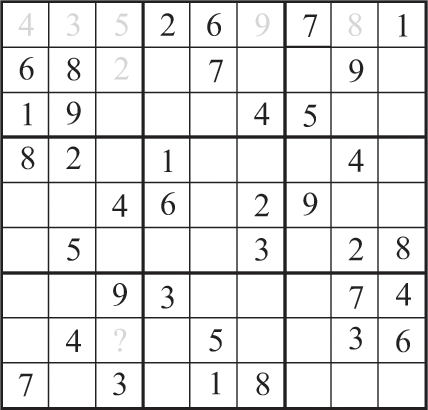
The goal of the Sudoku player is to place a number in each blank square, so that each row has each of the numbers 1 through 9, each column has each of the numbers 1 through 9, and each of the nine 3 × 3 subset grids has each of the numbers 1 through 9.
Humans approach this game by filling in one square at a time, with some combination of guesswork and the process of elimination. For example, we might notice that the third square in the first row can’t be any number except 5, so we would write “5” into that square and move on.
Some cells are a bit more difficult: at first glance, the third cell in the second-from-bottom row could be 1, 2, or 8. So we might focus on some other squares first, in the hope that doing so will narrow down the possibilities by the time we come back to that cell later; or else we might pencil-in one of these numbers—say, 8—and see where that takes us. The puzzle above is relatively easy because it doesn’t need much of this guesswork. In the more difficult puzzles, it’s impossible to proceed without some amount of guessing.
Sudoku became popular in the 1990s largely because of a mild-mannered New Zealander named Wayne Gould. Gould designed a computer program that could develop Sudoku puzzles, which he then distributed for free to newspapers all over the world. Gould’s program could develop Sudoku puzzles at different levels of difficulty: some, like the one above, were predictably easy even for novice Sudoku players, while others were predictably challenging for experienced Sudoku players. Perhaps cleverer than Gould’s computer program was his marketing strategy: he gave his puzzles to the newspapers for free. In return, they advertised his computer program and his books, which the Sudoku players devoured; through this arrangement he sold over four million copies of his books.3
Although Sudoku can be challenging to play, it’s not very difficult to write a computer program to solve Sudoku puzzles. Software engineers in Silicon Valley have been asked to do this during job interviews, and just about every introductory class in artificial intelligence teaches the key tool you need to solve a puzzle like this: search algorithms.
We’ve seen that self-driving cars use search algorithms to find paths through large maps and to plan ways to park in empty parking spots, and we saw that speech-recognition software uses search algorithms to find transcriptions of recorded speech. The way we would use a search algorithm to solve Sudoku is similar, except that instead of searching for a sequence of steps to take to move across a map, the program must search for a sequence of numbers to fill up the board.
In Sudoku, there are trillions upon trillions of possible board configurations. A computer program designed to solve Sudoku will search through these board configurations, iterating through many of them until it finds a fully populated board that is also a legal Sudoku layout. In the board above, there are 45 blank spaces, so the search algorithm must search through many different ways to fill all these spaces with numbers until it finds some configuration that works.
To search through these combinations, a search algorithm would reason about the Sudoku board as being in different states. The state of the board is described precisely by the set of numbers currently on the board. As the search algorithm fills in a certain number on the board, it moves from one state to another—to a state with one fewer blank space. At other times, the search algorithm might remove a number from the board—to a state with one more blank space.
There are many possible ways a search algorithm might wind through these states, and it’s really we humans—the computer’s programmers—who decide how the search algorithm should do this. We might program the computer to try every possible value for the first empty slot—the one in the top, left corner of the board—fill it in, and then consider each of these nine new states. For each of these nine states, the program would choose one of the values 1 through 9 for the next empty slot, and so on. Once the algorithm has filled in the 45 missing numbers, it can then test whether the board configuration is legal. If it’s not legal, it will need to backtrack to change some number it set previously and then continue forward again, repeating this until it finds a combination that works.
You can think of these states as being connected in a tree structure, where two states are connected if the search algorithm can move between them by filling in (or removing) a number. I show such a “search tree” in figure 14.2, except that I’ve simplified the tree to search through a 2 × 2 grid instead of a 9 × 9 grid, and so that it only uses the numbers 1 through 3 to fill in the grid, instead of the numbers 1 through 9. This search tree has 81 different states at the bottom, which means the diagram is too small for you to see much detail, so I also show a subset of this tree (but larger) in figure 14.3.

A search tree to find all ways to fill a 2 × 2 grid with the numbers 1 through 3. The number of states to search through grows quickly with each level of the tree, and there are 34 = 81 states at the bottom of this tree. A Sudoku board with 45 empty spots would have an unfathomable 945 states at the bottom of the tree.
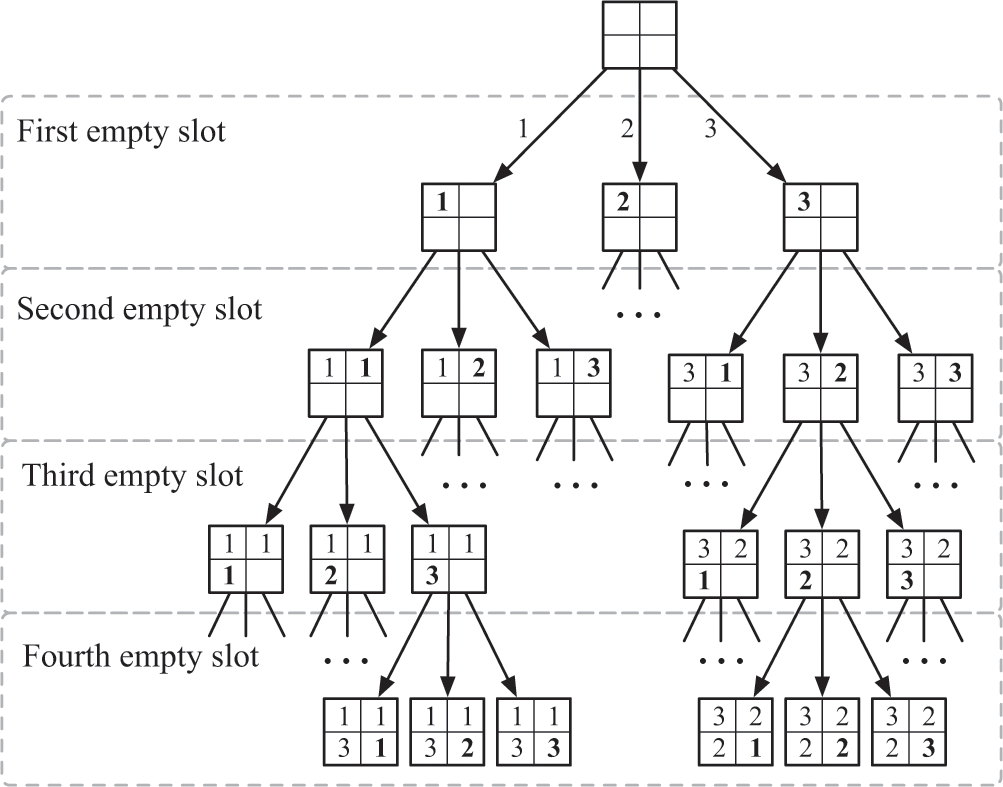
A subset of the search tree in figure 14.2, showing only selected states in the tree. At each level of the tree, the algorithm selects the next empty square and attempts to fill it in with each of the numbers 1 through 3 (shown in bold). The algorithm fills the spot with one of these values, descends to the next level, and attempts to fill in the next number.
Notice that a computer algorithm to search through a tree like this doesn’t need to make any “smart” decisions. It just needs to be consistent in how it descends through the tree. At any level of the tree, the computer just tries to fill in the next empty slot with the next number it hasn’t tried yet, starting from 1, and then it moves into that state to fill in the remaining squares by repeating the same process. On any given level, if it has tried a 1 for the next empty slot—and then tried all possible values for the remaining empty slots without success—it replaces that 1 with a 2 and then tries all combinations of the remaining slots again, and so on. As it tries these combinations, it essentially enumerates all of the possible ways for the 45 empty spots to be filled with the numbers 1 through 9, until it finds one that works.
I’d like to reiterate two observations I’ve already made. First, how exactly the algorithm moves through these states is up to the programmer. Second, a search tree like the ones in figures 14.2 and 14.3 gives the computer a methodical way to visit each state. There is no discretion an algorithm like this has in choosing which states to visit. As the computer searches through these states, it follows a simple, prescriptive algorithm—exactly something a wooden machine with a hand crank could do.
THE SIZE OF THE TREE
Unfortunately, a “brute-force” approach like this would also be impractical because it requires the computer to consider an exponential number of states. As in chapters 9 and 10, where I discuss neural networks, I mean “exponential” in the mathematical sense: for each level deeper we go into the Sudoku tree, the number of states grows by a factor of 9. Just two levels deep, as in figure 14.4, there are 81 states in the tree. If we look 45 levels deep, the number of states is about 1 followed by 43 zeros. This would be far too many states to evaluate within a reasonable amount of time even if we had an army of people turning hand cranks on wooden machines, let alone a large cluster of computers.

The number of states just two levels into the Sudoku search tree is 9 × 9 = 81. Because the number of states grows by a factor of 9 with each level in the tree, we must use a pruning algorithm to narrow the search down.
Does it help that we don’t need to enumerate all possible states to find the solution? For example, for the Sudoku board we saw earlier, we only need to try 36 percent of these combinations before finding one that works. Unfortunately, 36 percent of 1043 is 1042.6, which is still an impossibly large number.
We can fix this by “pruning” branches of the search tree, cutting the search short on a branch if we know that the branch could never lead to a valid Sudoku solution. So when we’re trying to figure out which number to put into an empty spot, we still consider each of the values 1 through 9, but we only “descend” into a state if selecting that number would lead to a valid Sudoku layout. I show how a search tree for this algorithm would look in figure 14.5.

A “pruned” search tree to find the values in a Sudoku board. Most branches are cut short because they would lead to a Sudoku board that couldn’t lead to a valid Sudoku layout.
Figure 14.5 is hardly a “tree” all: it’s more like a search “beam”! As you can see, there are a couple of false starts, but the algorithm doesn’t need to branch out too much at each level. Instead of having nine branches at each level, the pruned search tree usually has just one. If we’re lucky, we might only check about nine boards for most levels of the tree, and we could throw most of them away after finding that they’re illegal. This would eliminate all but one branch at most levels before descending. This would be about 9 × 45 boards we need to evaluate—a measly 405 states. This is small enough that you could run this search algorithm quickly with a computer from the 1970s.
THE BRANCHING FACTOR
The amount by which a search tree grows at each level is sometimes called its branching factor or branching ratio. The branching factor was 9 in the first, un-pruned Sudoku search tree and close to 1 in the pruned search tree. The branching factor varies by the initial layout of a Sudoku board, and the difficulty of a Sudoku puzzle for a human depends heavily on that puzzle’s branching factor. When Wayne Gould invented his program to create Sudoku boards, he was certainly aware of this: a game of Sudoku must strike the right balance in its branching factor. It can’t be so low that the game feels mechanical, and it can’t be so high that the game feels frustrating.
UNCERTAINTY IN GAMES
Solitary games like Sudoku tend to be less interesting from the perspective of AI research because there’s no uncertainty in them: the search path and the actions the player can make are well defined from the first turn all the way to the end. One thing that makes games more interesting is uncertainty. Uncertainty can show up when there’s some amount of randomness involved—as with any game where you roll dice—or when there’s more than one player—as in a game like chess.
To see how the game play changes when there’s some amount of uncertainty, let’s look at a simple game, which I’ll call “You-pick-this-then-flip-a-coin,” in figure 14.6.

In this game, you pick a direction to go from the start position—either up or down—and then flip a coin to see where you go from there. You then need to pay me whatever value you end up on (sorry, but this isn’t a very fun game for you). Take a moment to look at this diagram to figure out what your strategy for the first move is going to be.
To reason about this game, you might have taken an average of the two upper-most outcomes, and compared this with the average of the two lower-most outcomes, and decided that, on average, you’re best off choosing the higher branch, because you would pay me less on average. If you’re risk-averse, you might have reasoned differently: you would have noticed that $10 is the worst possible outcome and chosen the lower branch to avoid that outcome. Regardless of which strategy you took, the key observation is that you made your decision by looking at the end values and working your way backward to the starting decision.
Two-player games also have uncertainty, but in some sense they have less uncertainty for any one player because the other player’s choices are somewhat predictable. Consider the game in figure 14.7, which I’ll call “You-pick-this-then-I-pick-that.”
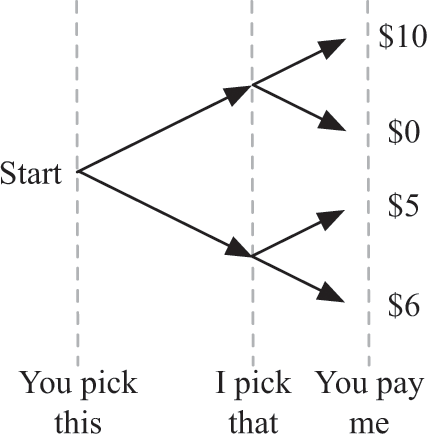
In this game, as before, you make the first up-or-down choice; then I choose whether to go up or down from there. After we’ve each made a choice, you again pay me the amount we end up at. Take another moment to look at the diagram in figure 14.7 to figure out your decision before you read further.
Again, this isn’t a very fun game for you, because I always win; but you do have a greater ability to predict the outcome, so your choice is easier. You know that I will always choose the highest number among my options—either $10 or $6—so you would choose “down,” since that will lead to you paying me only $6. As with the You-pick-this-then-flip-a-coin game, you started at the end and moved backward to decide which action to take.
In a game like chess, where the players take many turns, you would use the same approach to find the best strategy in the game, except that you must anticipate the outcome of many more decisions over the course of the game. The search tree will branch out massively within a few moves, as in figure 14.8, but even more so than can be shown in the figure. In this figure, gray dots at the end represent the outcome that you win, while white dots represent the outcome that I win. To figure out which move you should make on your turn, you’d again reason from the end, working your way backward. At each level, you would either predict which action I would take so I have the highest chances of winning, or select an action for yourself that would maximize your chances at winning. In this game, it is possible for you to win, provided that you make the right choices.
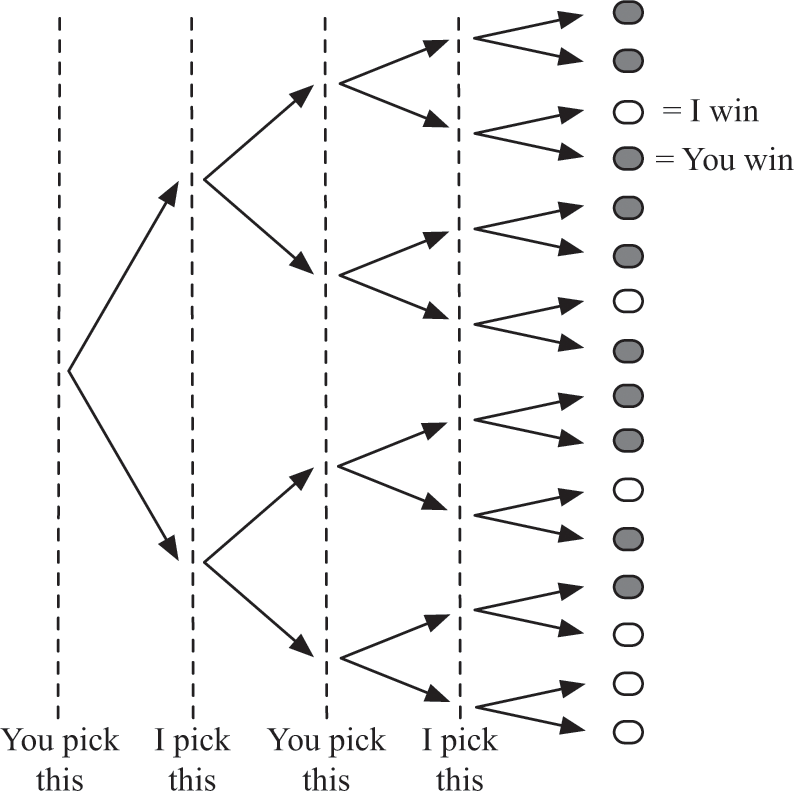
A multilayer search tree representing choices in a two-player game. Each level of the tree represents a single player’s choice between two actions. Gray dots at the end represent the outcome that you win, while white dots represent the outcome that I win.
If we wanted to program a computer to play this game, we would use a search algorithm just as in Sudoku, but we would write the program to anticipate which moves you and I would make at each level of the search tree. It must start out by searching deep into the tree. Once the program has descended in its search to the end of the game, it then works in reverse: it looks at each move I might make as my final move, anticipates that I would only make a move that would allow me to win, if such a move exists, and assumes that that is my choice. Once it has done that, the algorithm can ignore the final layer of the tree, because it knows the outcome of my move. In the next-higher level, the algorithm anticipates which move you would choose. You would choose a move that guarantees that you would win, if such a move exists. Once the program has figured out which move you would take, it can figure out who will win from there, and it can ignore all levels of the search tree below that. And so the program would proceed, moving backward in the tree, predicting which move either one of us would make, until it hits the beginning of the search tree, which is the current layout of the board. Once it gets to the beginning, it can tell you what move you should make to guarantee that you win. We would say that this algorithm anticipates that each player will be rational, that is, that each will act in his or her own best interest and by thinking ahead. It is possible to assume each player is rational when we can search through the entire tree. Just as you figured out the best move for each player by starting from the end of the tree, the program would do the same, in a predictable way.
The tree above is, of course, much simpler than a game of chess. In the tree above, the branching factor is 2, with four moves (called “plies”) in the game. Master chess players work through games that have, on average, a branching factor of 30 to 40 and an average of 40 moves per game.4 This leads to a search tree that is far too large for a computer to search through without a lot more pruning.5 The number of states we would need to search through could easily exceed the number 1 followed by 59 zeros.
Could we resolve this by using a fast-enough computer? Not really. The exponential growth rate of states as we descend into the search tree is a problem that transcends technology: it will always be prohibitively expensive to evaluate all of these states. Even if we could build a computer that could evaluate all board states up to 40 levels deep in a reasonable amount of time—say, over the course of two minutes—this computer would grind to a halt on searches just two levels deeper, where there are 40 × 40 = 1,600 times as many states to evaluate, so that the computer would need over two days to crunch through its states. And this is in a search tree that’s already been pruned in the way we pruned the Sudoku tree: these 30 to 40 moves per turn in chess are legal moves. So we need another way to prune this tree if we’re going to solve chess with computers.
CLAUDE SHANNON
If you’ve ever visited the quaint, Midwest town of Gaylord, Michigan, there’s a good chance you’ve seen the bronze bust of Claude Shannon. Shannon was a mathematician well known for his work in the field of information theory, which provides an elegant way to measure the amount of information—in a very literal sense—contained in a message.
The intuition around Shannon’s idea of information revolved around how exceptional a message is. If I told you that my cat meows, I wouldn’t be giving you very much information: you know that most cats make this sound. However, if I told you that my cat barks, this would be higher-information, because most cats don’t bark. And if I told you ten different (unrelated) facts like this, then I would be giving you ten times as much information.
Shannon encoded this intuition into a framework for reasoning about information. He did this by formalizing the idea of uncertainty: information is what you gain by removing that uncertainty. Shannon’s ideas have led to a vast and beautiful branch of mathematics commonly known as information theory. Ideas from information theory have been used to help us to understand a wide variety of things, such as the theoretical limits of how much information we can send in electronic messages. This is the same idea used in the word-overlap scorer from Watson: that scorer weighted words by how much information they conveyed: words like “scorpion” and “Čavić” convey more information than “almost” and “one.”
Shannon’s work on information theory is extremely important in the field of machine learning, but he is less well known for an academic paper he wrote in 1949 about how to create computer programs to play chess. Years before computers were household commodities, Shannon made some simple but thoughtful suggestions about how to write algorithms to play chess that have become commonplace in the field of AI. One of his core suggestions was the idea of an evaluation function.
EVALUATION FUNCTIONS
An evaluation function is a test that can be applied to a game state to predict which player will win if each player plays rationally after that. A perfect evaluation function for the search tree in figure 14.8 will tell you who will win, starting from each game state. You can see what a perfect evaluation function for this game would look like in figure 14.9, where I’ve colored each state based on who will win. A computer algorithm using this evaluation function doesn’t need to search all the way to the end of the tree to figure out which move to make: it just needs to search one or two levels deep to peek at the evaluation function to decide which move to make.

A multilayer search tree in which each state is colored with the result of an evaluation function. This evaluation function is perfect: it describes which player will win the game from each state, provided that each player plays perfectly. In practice, most evaluation functions are approximate.
Usually it’s impossible to create a perfect evaluation function, and we must resort to using an approximate evaluation function instead. If you’ve played chess, you’ve probably used an approximate evaluation function to decide your moves. Without even thinking about it, you probably assigned a rough value to each piece on the board: a queen is worth more than a knight, which is worth more than a pawn, and so on; and your opponent’s queen is worth more to them than their knight, and so on.
As Shannon explained, a computer’s evaluation function for chess might assign explicit weights to these pieces: a queen might be worth 9, a bishop worth 3, a knight 3, and a pawn 1; and the value to a player of having a set of pieces on the board is the sum of these pieces’ values.6 The numbers I’ve listed here are arbitrary—and probably wrong—but they capture some of our intuition. If you have a chance to capture your opponent’s queen but need to sacrifice a bishop in the process, it’s very possibly still a good move. If you can capture your opponent’s queen without losing any pieces of your own, that’s all for the better. Formalizing this into a more rigorous evaluation function, you might use a weighted sum of how many pieces of each type you have, minus a weighted sum of your opponent’s pieces, like this:7
(100K+ 9Q + 5R + 3B + 3N + 1P) – (100Ko + 9Qo + 5Ro + 3Bo + 3No + 1Po)
If you used this—which, by the way, is an example of a classifier—as an evaluation function, then it would help you to predict who will win the game based on how many of each type of piece is on the board.
This is just a simple example of an evaluation function, but evaluation functions like it can be extraordinarily powerful if you add enough features. Deep Blue, a powerful chess-playing system built by IBM, used an evaluation function; but whereas we used 12 features in our evaluation function, they used over 8,000 features!8
What might some of these additional features be? Many of them were esoteric, but they could roughly be broken up into two categories: material features—that is, features to describe which pieces were on the board, like the ones above—and positional features—features that describe where these pieces are on the board. For example, one of your pawns is worth much more if it is near your opponent’s side of the board because it is more likely to turn into a queen. And indeed, at least one version of Deep Blue preferred to advance pawns toward the opposite side of the board for this reason. Positional features are also necessary for computer chess. This became clear when Deep Blue played one of its games against the then-reigning chess champion Garry Kasparov.9
Kasparov is one of the greatest chess players to have ever lived. Intense and full of energy, he described playing chess as “controlling chaos.”10 When asked in 1988 whether a computer could beat a human grandmaster by the year 2000, Kasparov’s answer was simple. “No way, and if any Grandmaster has difficulty playing computers, I would be happy to provide my advice.”11 In one game he played with Deep Blue, Kasparov built up a significant strategic advantage against Deep Blue. The poor computer had no idea that it was losing until it was too late: Deep Blue’s evaluation function, focused on material advantage, underestimated Kasparov’s own positional advantage.12
How would you use an evaluation function in practice? One approach is to search to a fixed depth in the tree, run the evaluation function on each game state at that depth, and then treat the result of the evaluation function as if it were the outcome of the game, as in figure 14.10. You don’t need to search 40 levels deep in a game like chess: you might only search 6 or 12 levels deep, and then you’d use the evaluation function to decide which states are the most promising. Even though you may not come anywhere close to the end of the game with just six moves, the hope is that you’ll have a much more accurate idea of who will have an advantage at that depth.
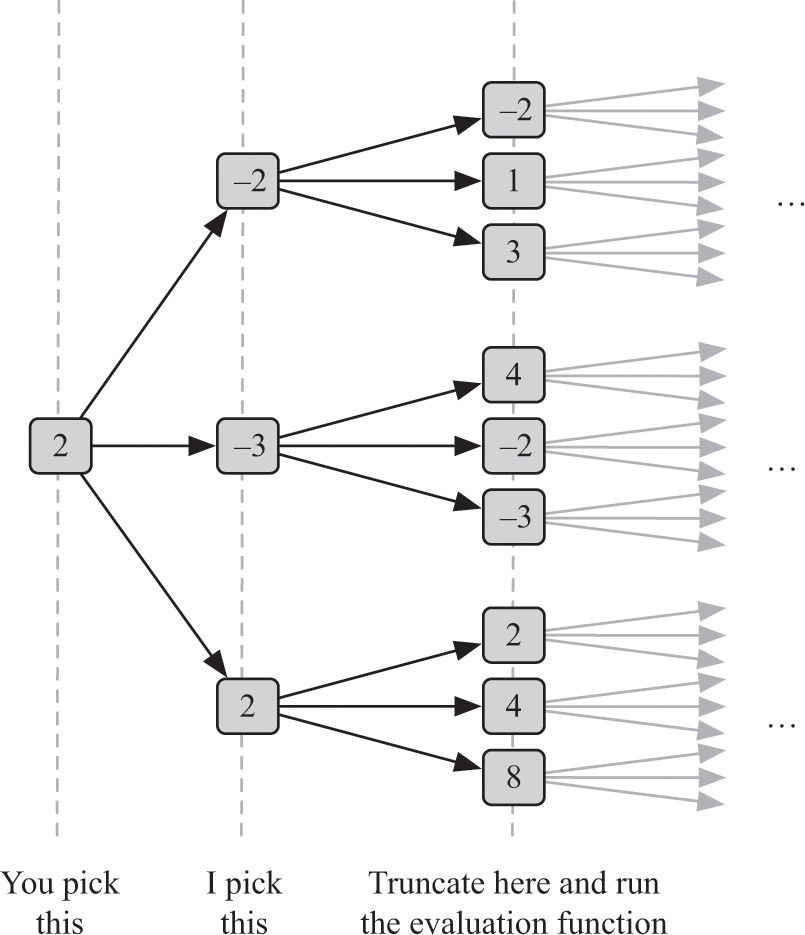
Using an evaluation function to search to a fixed depth in a two-player game.
Evaluation functions can also be used to prune the search tree in other ways. One way to do this is with an approach called alpha-beta pruning. In alpha-beta pruning, you strategically prune based on what you’ve observed so far in the search tree. Let’s say that you’re figuring out your next move in a game of chess against me. After looking at the first move you might make—move A—you’ve determined that it’s pretty good according to the evaluation function, considering all of my counter-moves to your move A, your counter-counter-moves, and so-on.
At this point you could stop searching, but you realize that you might be able to find an even better move, perhaps move B or move C. So you look at these moves too. With the very next move you consider (move B), you immediately notice that I could make a counter-move that will let me win the game. There’s no point in looking at move B any further, since you know that I will always choose the best move for myself. I wouldn’t choose any counter-move to move B that would be any worse than that for me. So you can stop considering move B altogether and move on to evaluating move C. This is the essence of alpha-beta pruning: cutting your search short when you know a certain branch on the search tree won’t lead to any better moves than one you’ve found already.
Alpha-beta pruning isn’t limited to just the top layers of the search tree: it can be applied at any level of the tree. Its effectiveness depends on the order in which you search through the search tree, but it can be very effective even if you don’t prioritize your search. It was also one of the methods used by IBM’s chess-playing Deep Blue.13
DEEP BLUE
IBM’s Deep Blue was the computer that proved world chess champion Garry Kasparov wrong in his 1988 prediction that no computer could defeat a grandmaster by the year 2000. Within a year of his prediction, a computer built by a little-known team of graduate students at Carnegie Mellon defeated a chess grandmaster for the first time in history.14 As their computer and its descendants gradually improved over the following decade, they grew more and more competitive, toppling grandmaster after grandmaster.
Deep Blue originated with this group of graduate students who had begun working on computer chess mostly for fun, largely basing their system on custom hardware designed by Feng-hsiung Hsu, the founding member of the project. Using hardware to play chess wasn’t uncommon at the time, even though these chess machines could sometimes be the size of a small office refrigerator.15 But by implementing Deep Blue in hardware, Hsu observed, they could get about a hundred-times speedup compared with the same algorithm implemented purely in software.16 Deep Blue leaned heavily on the ability this hardware gave it to quickly search through its tree. Distributed across 30 separate computers, Deep Blue used 480 custom chess chips to blaze through about 126 million positions per second.17
But the team behind Deep Blue learned that brute-force search up to a certain depth with an evaluation function wasn’t enough. They found that chess masters could anticipate moves in a much deeper beam than a search algorithm that searched up to a fixed depth. They did use an evaluation function with a limited-depth tree, and they did use alpha-beta pruning, but Hsu was skeptical of clever pruning methods and search tricks, at least in their hardware. Instead of using clever tricks to prune their search tree, Hsu and the team favored a different method to address the high branching factor: something called a singular extension.18
In contrast to pruning methods, which selectively cut off certain search paths, singular extensions selectively extend certain search paths. For example, if you move your pawn into a position that threatens my king, I will make some move to defend my king. Such moves have the property that they’re clearly among best possible move I could make—sometimes the only possible move I could make—and when Deep Blue could identify them, it would selectively extend its search in that direction, with a branching factor of close to 1 along that extension.19
Unlike DeepMind’s Atari-playing agent, which could play many different games, Deep Blue was designed specifically to play chess. The majority of the features in Deep Blue’s evaluation function were hand-selected and hand-created, which stands in sharp contrast to most of the statistical machines in this book—although the team did use some data-driven tuning to select the weights in their evaluation function. Deep Blue also used an “opening book” to select good strategic moves near the beginning of the game and an “endgame” database to select moves near the end of the game.20
JOINING IBM
As Feng-hsiung Hsu began developing the chess programs that eventually culminated in Deep Blue, he began to recruit his fellow graduate students to help out.21 A few years into the project, IBM got wind of the students’ chess-playing efforts. By one account, the seed for the idea was planted with a vice president during a conversation in a men’s restroom. The conversation, if you allow for some narrative liberties, went roughly like this:22
Friend: Super Bowl commercials are an expensive way to do marketing, aren’t they?
VP: They sure are.
Friend: Oh, by the way, have you heard about this CMU group’s chess-playing computer? No? Perhaps IBM could hire this team, and they could beat the best chess player in the world. That sort of marketing could be good for business, and maybe cheaper, huh?
VP: Interesting …
IBM eventually acquired the core group of CMU students working on the project. The students cut themselves an attractive deal when they joined IBM: they negotiated that they be given the mandate to build the “ultimate chess machine.” They asked that they have the flexibility to do things on their own, without the likes of Dilbert’s pointy-haired boss ordering them around.23 They got their wish, along with some other benefits of working within IBM, including the deep pockets that would enable them to build the final version of Deep Blue and to attend competitions, and help from IBM’s marketing team to manage their game against Garry Kasparov.24
By 1997, within a decade of Garry Kasparov’s prediction that no computer could beat a grandmaster by 2000, the researchers’ line of chess-playing computers culminated in the final version of Deep Blue. In a six-game match, the computer managed to defeat Garry Kasparov himself, the first professional match Kasparov had ever lost. As Hsu wrote:
Yes, you read it right. Garry had never lost a single chess match in his professional life before the 1997 rematch. … Some were concerned that Garry would react angrily to losing a match. The IBM team was asked … specifically not to smile during the closing ceremony, especially if Deep Blue won the match.25
SEARCH AND NEURAL NETWORKS
So, why we didn’t we use an approach like this—that is, a search algorithm—to play Atari games? Could we have designed a search algorithm to play a game like Breakout or Space Invaders? Although I’m reluctant to say the answer is a categorical no, there are a few challenges we’d face if we tried to do this.
In chess and Sudoku, the states are obvious: they describe the positions of chess pieces or numbers on the game board. The positions on the board and the rules of the game are well defined, so it’s easy to encode the states and the transitions between them into a search tree. But remember that DeepMind wanted an agent that could play many different games. It’s unclear what the “states” in a search tree should even look like for Atari games. Should a state in the search tree for an Atari game represent the unique arrangement of pixels on the screen? That would result in far more states than we faced for chess or Sudoku. An even bigger problem is that we have no idea how to move from one state to another as we search through the state space. It’s difficult for a search algorithm to anticipate the future of the game if we don’t even know how the states are connected to each other!
The role of a search algorithm when playing games is to help the agent find a path from its current state to a state with the highest likelihood of a good outcome. In chess, we search for states deep within the tree for which the evaluation function has a high value, and then we take an action that gets us one step closer to that state.
Reinforcement learning with a neural network gives us a different way to accomplish the same goal. The role of reinforcement learning when playing games is to orient the agent toward states with future rewards by telling it which actions will move it toward those states. Reinforcement learning essentially turns the problem from a search problem (which might be much harder) into a “hill-climbing” problem, where it can move, step by step, toward more promising states.
Sometimes hill-climbing algorithms don’t work. They don’t work well when the algorithm leads you to the top of a low hill when there are much higher hills around, separated from you by valleys. DeepMind faced this problem with games like Montezuma’s Revenge, where it hadn’t explored enough of the landscape to figure out where the bigger hills were; so it was stuck on one of these low hills.26 A search algorithm, in contrast, might be able to search through a wider landscape, to get you past those valleys. The deeper we can search into the game tree—in theory, at least—the more likely we are to find a good action for the agent.
Is it possible to use a hybrid of these two approaches? That is, could we use a search algorithm to search deeply into the tree when possible, and then use a very sophisticated evaluation function, like the one we used for Atari, in a sort of search / neural-network hybrid?
TD-GAMMON
Gerald Tesauro, an IBM researcher who eventually worked on Watson’s wagering strategy for Jeopardy!, used an approach exactly like this when he developed a program to play backgammon in the early and mid-1990s. Backgammon, like chess, is a two-player game in which players move their pieces around on a board. It involves a dice roll in addition to a small set of player actions, so its branching factor is a few hundred for each ply (remember, a ply is a single move by one player).27
Tesauro programmed his agent to use reinforcement learning, just as DeepMind did for its Atari agent. Also like DeepMind, Tesauro designed his agent to use a neural network. Its architecture was the “simple” neural network architecture we saw before, with an input layer, an output layer, and a single hidden layer:
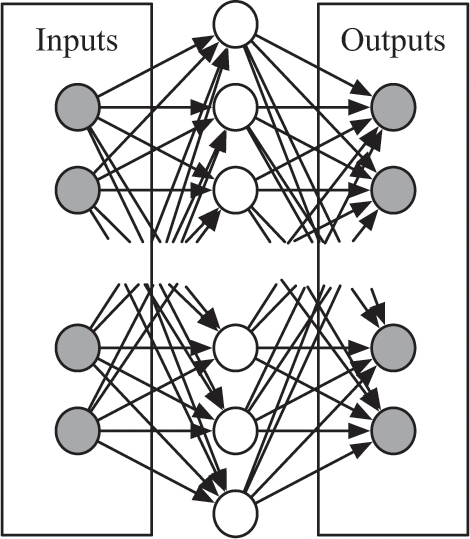
Figure 14.11
The input layer to Tesauro’s backgammon network encoded the position of each player’s pieces on the board as well as some handcrafted features Tesauro had created. The output layer represented the four possible outcomes the network aimed to learn: player 1 wins, player 2 wins, player 1 wins by a lot (called a “gammon”), or player 2 wins by a lot. As you can see, between the input and output layers was a hidden middle layer. In Tesauro’s experiments, this hidden layer worked well with anywhere from 40 to 160 neurons.
Tesauro’s algorithm was a hybrid between search and reinforcement learning, in that it searched out two or three plies before using its neural network to run the evaluation function.28 Remember: Tesauro could use the search option because the states and transitions in backgammon are well defined. In an early version of his backgammon-playing algorithm, Tesauro trained the neural network using reinforcement learning with games played by expert humans. This “supervised” algorithm worked okay, but it wasn’t great.
This changed when Tesauro let the neural network play against itself, which exposed it to a virtually unlimited amount of training data, the same benefit the Atari-playing agent had when it played millions of Atari games in its virtual world, the Arcade Learning Environment. After playing some 1.5 million games against itself, Tesauro’s search-plus-neural-network hybrid could play competitively against the best human players. (It may very well be better than the best human players by the time you’re reading this.) It has even taught the professional backgammon community new strategies, upending conventional wisdom about the game.29
Tesauro’s pitting of the backgammon neural network against itself became a famous story in the field of artificial intelligence, but the method wasn’t widely known outside of the AI and backgammon communities. The game-playing AI programs that became known to the public were the ones that made national headlines, like Deep Blue, Watson, and eventually AlphaGo, which defeated two Go world champions in 2016 and 2017.
LIMITATIONS OF SEARCH
The ideas behind Deep Blue and Tesauro’s backgammon program were the foundation for the algorithms that eventually enabled AlphaGo to play the strategy game Go, but these ideas on their own weren’t enough. A computer playing chess can lean heavily on brute-force search through hundreds of millions of moves per second along with a fairly simple evaluation function to prune away most of the search tree. Deep Blue’s 8,000-feature evaluation function may not sound simple, but the features in it were largely interpretable by humans. These things were together enough to push a computer algorithm up to and then past the frontier of human chess-playing ability.
Go is different. The branching factor for Go is nearly 10 times as high as the branching factor for chess, and the evaluation function for Go must be much more sophisticated than the one to play chess. As we’ll see in the next chapter, the ideas necessary for a computer to play Go competitively didn’t even exist when Tesauro developed his backgammon-playing agent and when Deep Blue beat Garry Kasparov in 1997. It would take two decades of new ideas and hardware improvements to bring computer Go agents within reach of the best humans.