5 NETFLIX AND THE RECOMMENDATION-ENGINE CHALLENGE
The Netflix prize contest will be looked at for years by people studying how to do predictive modeling.
—Chris Volinsky, senior scientist at AT&T Labs and member of Team BellKor1
A MILLION-DOLLAR GRAND PRIZE
As robotics departments were busy in 2006 preparing their cars for the DARPA Urban Challenge the following year, Netflix made an announcement to the budding data science community about their own Grand Prize: they were looking for teams that could create movie recommendation engines, and they were willing to pay $1 million to the best team.
When Netflix made their announcement, their streaming video business didn’t yet exist; the company operated as a physical DVD rental service.2 Customers could request DVDs from Netflix, and Netflix would send these DVDs to them by mail. But customers needed to give up one of their current DVDs to receive the next one, and the new DVD might take days to reach them. A bad selection could ruin days of quality movie-watching time, so customers tended to be careful about how they made their requests. This is where Netflix’s desire to recommend movies came in.
As part of their service, Netflix allowed their customers to rate individual movies on an integer scale of 1 star (worst) to 5 stars (best). Netflix hoped to use these ratings to help customers decide which movies they should rent. After announcing the competition, Netflix released a dataset consisting of 100 million of these star-ratings, collected from 1998 to 2005, to the research community.3 The first team to create a recommendation algorithm that improved on Netflix’s own algorithm by 10 percent would win the grand prize.4
This dataset was a godsend to full-time and casual data scientists, and they approached the problem with gusto.5 Within the first week some teams beat Netflix’s own recommendation engine by 1 percent.6 Within the first year, 20,000 teams had registered, some 2,000 of which submitted entries to the competition.7
THE CONTENDERS
The contenders for the prize were a ragtag group, but one three-person team maintained a strong position on the leaderboard. This team was BellKor, made up of three research scientists from AT&T Labs (one of them moved to Yahoo! in the course of the competition), whose expertise in the field of networks and recommendation systems equipped them with excellent skills for the project.8 Another team, ML@UToronto, consisted of a group of well-known neural network researchers from the University of Toronto.9 The members included Geoffrey Hinton, widely seen as one of the fathers of neural networks.
Not everyone in the competition had a PhD. One of the underdog teams with only three undergraduate members—two computer-science students and one of their roommates, a math student—came from Princeton University. The two computer science students were soon headed to top PhD programs to study machine learning, although one of them would stick around to work in Princeton’s psychology department for a year. The math student was on his way to trade interest rate derivatives at JP Morgan. The young, overachieving trio named their team after the first movie listed in their dataset: Dinosaur Planet.10 In spirit, they were similar to a couple of Hungarian graduate students who named their team Gravity.
The competition also included a variety of even less-credentialed contestants. Eventually a two-person team named Pragmatic Theory popped up. This French-Canadian duo had been working on the project in their spare time. One of them had set up shop in his kitchen, working from 9 p.m. to midnight while his kids were asleep. Having had no experience in the field of collaborative filtering, they were modest in their self-assessment: “Two guys, absolutely no clue.”
The list of contestants went on, thousands upon thousands long, including dabblers from seemingly disparate fields like psychology. And although these teams were competing with each other, they would find themselves collaborating during the competition. In fact, as we’ll see, it would have been virtually impossible for a team unwilling to learn from and collaborate with other teams to have succeeded in the competition. In the next two chapters, we’ll follow the journeys of several of these teams in their quest for the $1 million prize.
HOW TO TRAIN A CLASSIFIER
You may be wondering why I’ve included chapters about movie recommendations in this book. Are movie-recommendation engines really a major AI breakthrough?
Imagine the reception to Vaucanson’s Flute Player had it been able to accurately recommend books or songs to members of the audience based solely on what else they liked. The public would have been equally as floored. Indeed, a recommendation engine is an algorithm that aims to capture the preferences that make us human. As we’ll see in this chapter, recommendation engines can model human preferences so well that they can rival lawmakers at their most important job: voting on legislation. It certainly wouldn’t stretch credulity to suggest that they’ve already had a far bigger impact on our economy than self-driving cars and chess-playing computer programs, as they power online commerce.
There’s also another, more important reason I’ve included the Netflix Prize in this book. Some of what happened during the competition, including how the contestants approached the problem and with what tools, will directly inform how we look at other breakthroughs in this book. As we’ll see, the ideas poured into the competition touched on just about every theme we’ll see later.
In that vein, let’s look back for a moment at one of the building blocks of Stanley, the self-driving car from Stanford that we discussed a couple of chapters ago. Stanley depended heavily on machine learning, which enabled it to stay on the road and to perceive the world around it. As we saw, Sebastian Thrun and his team drove Stanley around while its sensors collected data from the surrounding environment. They then used that data to train a classifier to detect whether different types of ground were safe for the car to drive on. We glossed over some of the details about how Stanley’s drivable-ground classifier worked, but knowing how classifiers work is important if we’re going to understand how movie recommendations—and the neural networks we’ll see in later chapters—work. These classifiers operate on a principle as simple as that of a physical gear or lever, except that, instead of transforming energy to produce a useful result, they transform data to produce a useful result. Let’s go over those details now.
Imagine that you’re editing a cookbook called The World’s Best Recipes for Kids. For this cookbook, you’ll collect recipes that appear on the website Bettycrocker.com. You have a simple decision to make for each recipe: is it, or is it not, a recipe you should include in the kids’ cookbook?
One way to answer this question would be to prepare each recipe you found on the website, feed it to your kids, and ask them for their opinion. But if there were 15,000 recipes on this website, then even at a healthy clip of 9 new recipes per day, you’d be cooking for over four years. How could you determine which recipes are good for kids without a huge investment of time and energy?
A machine-learning student would eagerly tell you how to solve the problem: you could train a classifier! In the field of machine learning, a classifier provides a way to automatically figure out whether an item (like a recipe) belongs to a certain category—like “recipes that are appropriate for kids,” as opposed to “recipes that are inappropriate for kids.”
To use a classifier for this task, you first need to decide which characteristics of a recipe are likely to distinguish between the ones that are good for kids and the ones that are bad for kids. You can use your creativity and judgment here, but some things might stand out as particularly helpful in making that distinction. Users on the Betty Crocker website can provide star ratings of the recipes, and these are probably correlated with the recipes kids like, so you can use those ratings as one of these distinguishing characteristics. You also want to prefer recipes that are easy to prepare and easy to understand, for example, because they require a small number of steps or only a few ingredients. You may also want to consider the number of grams of sugar (kids like sugar) and the number of grams of vegetables (kids don’t like vegetables).
In machine learning, we call these distinguishing characteristics features. The magic happens when we combine these features into a single “recipe score” that describes how good a recipe is. The simplest way to combine them—and the way you can assume they’re always combined in other classifiers in this book—is by taking a weighted average, where we use weights that summarize how important we think each feature is in the final score. Take a moment to look at how I’ve applied this to the recipe “Holiday Baked Alaska” in figure 5.1.11

By applying a classifier to the recipe “Holiday Baked Alaska” we can see whether it would be good for kids. The weights stay fixed, and the details (and hence the recipe score) change for each recipe. “Holiday Baked Alaska” details are from the Betty Crocker website (see notes).
Why combine the features with a weighted average? It might seem arbitrary, and you’ve probably guessed (correctly) that machine-learning researchers have figured out a million other ways we could combine these features into a score. But this way of doing it is simple, straightforward, and easy to reason about. It’s by far the most important “statistical gear” that makes up all of the automata in this book. And remember that this is just a building block: we want it to be simple, since we’ll be combining it with other building blocks, and since we’ll want to be able to understand what we’ve built.
To get a classifier from the weighted average, we just need to pick a threshold—let’s just say “0” to be concrete—and call everything with a score above that threshold a good recipe and everything below it a bad recipe. According to the classifier in figure 5.1, Holiday Baked Alaska would be a very good recipe to add to the kids’ cookbook, even though it’s a bit complicated, because its other benefits—lots of sugar and no vegetables—make up for that.
If you’re using machine learning to fit the classifier, you’d use data to figure out the weights for each feature and possibly to pick the threshold. You might collect this data by asking your kids to prepare some recipes and keeping track of how much they liked each one. Then you’d use a standard formula from statistics to estimate these weights from this data. You’ve probably already seen this formula (and promptly forgotten it) in high school, where you learned it as fitting the best line through a bunch of points (x, y) on a piece of paper. Here you use the same formula, except that you have more than one x-coordinate for each y-coordinate.
Once you’ve fit this classifier’s weights using a handful of recipes—say, 100 recipes instead of 15,000—then you can have a computer run this classifier over the remaining 14,900 recipes to predict whether each one is good or bad. You could pick the top 200 recipes out of those 15,000 for your book according to this classifier, try them to make sure they’re good, keep the best ones, and then you’d be all set.
With the skill of fitting a classifier in hand, now, let’s turn back to the Netflix Prize to see how we can use it to recommend movies.
THE GOALS OF THE COMPETITION
What criteria should Netflix use to recommend movies to its viewers? What should its goals in recommending movies be? Clive Thompson pondered these questions in an article he wrote for the New York Times Magazine back in 2008, as the competition was underway.12 Should Netflix’s movie-recommendation service aim to recommend “safe bets” that you’re very likely to enjoy, he asked, even if it doesn’t push you out of your comfort zone? Or should it fill the role of that quirky movie-store clerk, taking bets to suggest movies that you may absolutely love, while running a risk of suggesting a movie that you’ll think is a dud?13
At traditional video stores at the time, new and popular movies accounted for the majority of rentals; these stores could lean on this limited selection to make it easier to recommend movies. Netflix was different: 70 percent of their rentals were independent or older “backlist” titles. With such a large collection, and with a long delay between rentals, Netflix depended on Cinematch, its own movie-recommendation system, for its ability to recommend movies to its users. Improving Cinematch was important to the company’s bottom line, because they risked losing customers who watched too few Netflix movies or who disliked a movie they had waited a few days to see: those viewers were the most at risk of canceling their subscriptions.14
So Netflix’s own engineers worked and worked to improve their Cinematch recommendation algorithm. When they couldn’t improve Cinematch any more, they decided to host the Netflix Prize, offering the $1 million to the first team that could beat their own algorithm by 10 percent. As Netflix CEO Reed Hastings pointed out, paying out the grand prize wasn’t really a risk for them: the financial benefits in having better movie recommendations could far exceed the cost of the prize.15 Even a small improvement in their recommendations could lead to big wins overall, because it was multiplied across the hundreds of millions of recommendations they made per day.16 And in case none of the teams ever reached the 10 percent target, Netflix would also offer Progress Prizes: if the contestants made enough progress each year, the best team would be offered $50,000. Netflix attached just one condition to these prizes: the winner needed to publish the details of their recommendation algorithm.
Netflix made the task simple for their contestants by offering them a clear, objective target. The contestants needed to predict how many stars certain customers assigned to specific movies on specific dates. Netflix would evaluate the performance of each team by computing the average squared difference between their predicted ratings and the actual ratings the customers gave on a secret dataset that the contestants would never see.17
Whenever a team submitted some predictions to Netflix, Netflix measured the team’s performance on the secret dataset and updated their scores on a public leaderboard that was closely followed by other teams and journalists.18 It was technically possible for a team to still “peek” at these ratings by submitting a lot of predictions to be evaluated on this dataset, but Netflix was clever enough to have also stashed away yet another secret dataset that would never be revealed to the contestants. This double-secret dataset would only be used at the very end of the competition to evaluate the top candidates.
A GIANT RATINGS MATRIX
Given that the Netflix competition focused exclusively on customers’ movie ratings, it’s helpful to reason about the Netflix Prize by looking at the problem as a gigantic matrix of ratings. I show a small sample from this matrix (with made-up numbers) in figure 5.2.

Some examples of star ratings that Netflix customers might have made on various movies. Netflix provided some of the ratings in the matrix (shown as numbers). Competitors needed to predict some of the missing recommendations (shown as question marks).
This matrix was immense: it provided ratings for 17,770 separate movies and 480,189 separate users.19 Netflix provided some customers’ ratings on some movies, and it asked contestants to predict some of the missing ratings (these are the question marks in the grid). Despite its size, only 1 percent of the matrix had any numbers at all: naturally most Netflix customers never rated most movies.
So where should the contestants begin?
Early into the competition, most of the top competitors converged on very similar approaches to analyze these ratings. The members of team BellKor—the team with researchers from AT&T and Yahoo!—noted the importance of starting with a simple “baseline” model to explain away the most basic trends in the ratings matrix. BellKor’s baseline model began with two components. The first applied just to movies; we might call it the “E.T. effect.”20 The E.T. effect measured the popularity of a movie regardless of who was rating it. In the Netflix dataset, for example, the least popular movie was Avia Vampire Hunter, a low-budget movie about a woman who hunts poorly costumed vampires. Avia had 132 ratings on Netflix, with an average rating of just 1.3 out of 5 stars. One of two reviews on Amazon.com said the following about the movie:
I should be paid for watching this trash. It was made in someones [sic] backyard with a hand held camera. Don't order it. It is the worst movie, if you can call it that, that I have ever seen!!! If I knew before hand, you couldn't give it to me free of charge.
At the other extreme, the most popular movie was the extended edition of the fantasy Lord of the Rings: The Return of the King, which had 73,000 ratings in the Netflix dataset, with a respectable average of 4.7 out of 5 stars. Its Amazon.com reviews were also overwhelmingly positive; here is one review on Amazon.com for this movie:
SOOOO GOOOOD! If you have never seen The Lord of the Rings Trilogy, I HIGHLY recommend it. It is an excellent trilogy. I especially love the extended editions …
Although this review is more about the trilogy than the movie, it’s clear that people like it. And the movie’s negative reviews on Amazon.com tended to be more about the format of the video or the seller of the video, not the movie itself.
Another part of BellKor’s baseline model, which we might call the “Scrooge effect,” aimed to capture whether Netflix users rated movies with a glass-half-empty mentality or a glass-half-full mentality. Some users assigned 1-star ratings to all the movies they rated; but most were somewhere in-between. Whether these viewers were trying to be objective wasn’t relevant, but the fact that such trends existed in the data meant that teams like BellKor needed to capture them.
With the two effects BellKor outlined—the E.T. effect and the Scrooge effect—we can begin piecing together a rudimentary recommendation engine. BellKor combined the E.T. effect, the Scrooge effect, and an overall bias term—which described the average movie rating across all movies and customers—into a single model using a classifier like the one we created for our World’s Best Recipes for Kids book. In this simple model, they learned a weight for each movie, a weight for each user, and the intercept. With such a “recommendation engine,” BellKor could recommend the best movies to Netflix’s users—a decent start in the absence of any other information.
The problem with this recommendation engine is that it would always recommend the same exact shows to all users—specifically, The Lord of the Rings and other popular DVDs, like the first season of Lost and the sixth season of The Simpsons. It couldn’t produce personalized recommendations. If Netflix used this approach to recommend movies to each user, then it would never satisfy Netflix users who only like foreign films, cult classics, or kids’ movies. It would be decent for everybody but great for nobody.
And it really is the case that most people aren’t well served by a one-size-fits-all system. The US Air Force discovered this when they were trying to understand what was causing so many airplane crashes in the 1950s. Cockpits had been built since the 1920s to match the average measurements of American men, but Lt. Gilbert Daniels, a scientist who studied the problem, discovered that most men aren’t average. As Todd Rose explains in his book The End of Average:
Out of 4,063 pilots, not a single airman fit within the average range on all 10 dimensions. One pilot might have a longer-than-average arm length, but a shorter-than-average leg length. Another pilot might have a big chest but small hips. Even more astonishing, Daniels discovered that if you picked out just three of the ten dimensions of size—say, neck circumference, thigh circumference and wrist circumference—less than 3.5 percent of pilots would be average sized on all three dimensions. Daniels’s findings were clear and incontrovertible. There was no such thing as an average pilot. If you’ve designed a cockpit to fit the average pilot, you’ve actually designed it to fit no one.21
Based upon these findings, Daniels recommended that the cockpits be adjusted so that they could be personalized to the pilots, a recommendation the Air Force adopted:
By discarding the average as their reference standard, the air force initiated a quantum leap in its design philosophy, centred on a new guiding principle: individual fit. Rather than fitting the individual to the system, the military began fitting the system to the individual. In short order, the air force demanded that all cockpits needed to fit pilots whose measurements fell within the 5-percent to 95-percent range on each dimension.
They designed adjustable seats, technology now standard in all automobiles. They created adjustable foot pedals. They developed adjustable helmet straps and flight suits.
Once these and other design solutions were put into place, pilot performance soared, and the US Air Force became the most dominant air force on the planet. Soon, every branch of the American military published guides decreeing that equipment should fit a wide range of body sizes, instead of standardized around the average.22
We need to determine the equivalent of adjustable seats for the Netflix recommendation engine so that it can be customized for each user. We need something that can capture the Terminator effect: the fact that some Netflix users—but not all of them—like science-fiction and action movies, and that other users like kids’ movies, that some users like both, and that some like neither. To capture the Terminator effect, most teams converged on a method known as matrix factorization.
MATRIX FACTORIZATION
Matrix factorization relies on the fact that the giant ratings matrix in figure 5.2 has a lot of redundant information. People who liked Futurama tend to like The Simpsons, and people who liked Shrek tend to like its spinoff, Puss in Boots. That there would be redundant information in this matrix isn’t such a crazy idea—after all, the very premise that we can offer personalized recommendations assumes that there are predictable patterns in peoples’ ratings.
To see the key insight behind matrix factorization, let’s assume for the moment that we can summarize movies and users with just a handful of numbers apiece. For each movie, those numbers might just represent its possible genres: Is it an action movie, a comedy, a thriller, or some combination of these? We could represent each movie as a short, ordered list of numbers: 1 where it fits a certain genre and 0 where it doesn’t.
We could also do the same thing for Netflix user preferences: 1 if the user likes the genre, –1 if the user doesn’t like it, and 0 if the user doesn’t care about it. If the user really likes or dislikes a genre, we might use more extreme numbers, like 1.5 or −2.2. Don’t worry for the moment about where we get this information about our movies and users. For now, just assume that we can find which movies belong to which genres from public sources like Wikipedia and the Internet Movie Database (IMDb), and that we can simply use a survey to ask people which genres they like.
Once we’ve described each movie and person in our database with these descriptive numbers, we’d like to use them to predict whether any one person likes a given movie. Let’s try to predict whether the director Steven Spielberg likes Jurassic Park. That movie is mostly science fiction and adventure, so let’s say it has a 1 for those two genres and 0 for everything else. And let’s say that Steven Spielberg really likes science fiction (1.2), sort-of likes adventure and comedy movies (0.6 and 0.5), and dislikes horror movies (−1.2). How should we combine these numbers to predict whether he likes Jurassic Park?
One simple way is to take the numbers describing whether Jurassic Park falls into each genre, multiply those by how much Steven Spielberg likes those genres, and then add these products up to get a score that describes how much he likes Jurassic Park (see figure 5.3). I’m making no promises that this is the “best” way to combine these numbers, but if you’re willing to suspend your disbelief for a moment, you’ll probably agree that this should at least point us in the right direction.
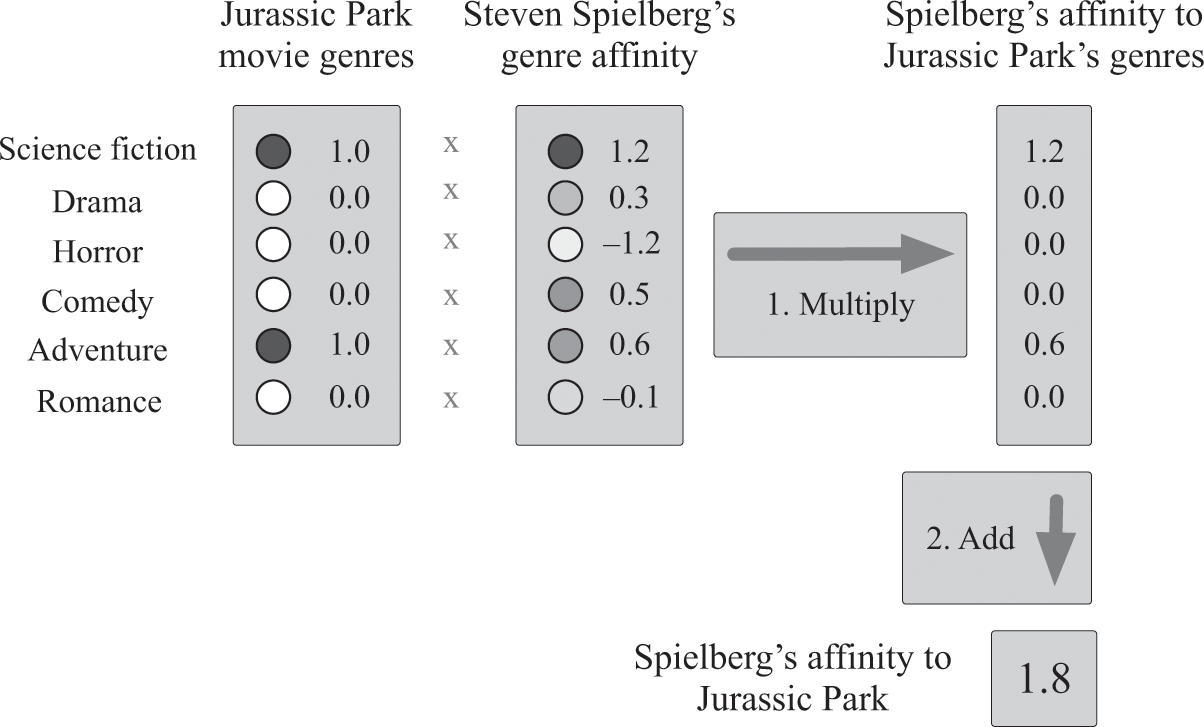
A test to determine whether Steven Spielberg would like the movie Jurassic Park. Here, we can assume Jurassic Park falls into two genres: science fiction and adventure. Steven Spielberg tends to like science fiction movies, comedies, and adventures, and tends not to like horror movies, as indicated by his genre affinities. We combine these into a score by multiplying together the genre scores, which are 0 or 1, with Spielberg’s affinities for those genres, and adding the results together. The result is a fairly high “affinity” score describing how much Spielberg likes Jurassic Park.
In a nutshell, this is matrix factorization. This is the most important algorithm we’ll see for making personalized recommendations, and here’s the key intuition I want you to internalize about it: this algorithm assumes that we’ve summarized each movie with a few numbers and each user with a few numbers, and it provides a way—precisely the way I showed you in figure 5.3—to combine these sets of numbers into a score to describe how much any user will like any movie. This is called matrix factorization because, the way the math works out, it’s equivalent to approximating the original, gigantic ratings matrix in figure 5.2 as the matrix product of two or more much smaller matrices—its factors—which encode exactly the numbers we’ve used to describe the movies and users.23
If you compare figure 5.3 with figure 5.1, you’ll notice that we’ve created a classifier in both. In figure 5.1 the features are recipes and the weights are kids’ preferences; in figure 5.3 the features are movies’ genres and the weights are Mr. Spielberg’s movie preferences. This hand-built classifier gives us personalized recommendations for Steven Spielberg.
As you might imagine, we can do better if we learn these weights from data. If Mr. Spielberg has rated movies on Netflix, we could use those ratings and the genres of the movies he’s rated to learn his movie preferences automatically. This is exactly the same thing we did when we trained the classifier to find good recipes for kids, except that now we’re training a classifier to make movie recommendations for Steven Spielberg. This classifier will only work for Steven Spielberg, but it’s trivial to repeat this process for each Netflix user. Using each user’s past movie ratings, we could automatically create a classifier for everyone, without needing to directly ask them which genres they like.
It turns out that we can improve these predictions even more. To see how, look again at figure 5.3. Notice that Jurassic Park’s genres are fixed to either 0 or 1. I chose these numbers by looking at IMDb, but we can improve our predictions by learning about movies’ genres from data. Instead of requiring that Jurassic Park be described by either 0 or 1, we could represent it with numbers that we’ve learned from users’ ratings of the movie, applying the exact same approach we used to learn Steven Spielberg’s preferences for different genres.
Why bother learning movies’ genres from data when we already know the actual genres for each movie? We do this because we have no reason to believe that the genre labels selected by humans are the best way to summarize movies for the task of making movie recommendations. Fixed genres are too coarse a way to describe movies; and in fact, we have plenty of evidence that movie genres are fluid. Movies like Jurassic Park illustrate this perfectly: Jurassic Park was both a science-fiction film and an adventure film, but it also had some elements of comedy and some elements of horror. So it should have at least a little weight for these latter genres. And some genres are too coarse: comedy movies might be dry, slapstick, or raunchy; and each type of comedy might draw vastly different audiences. Genres are a useful way for movie store clerks and other people to describe movies, but they don’t tend to be very useful for predicting how much people will like them, at least compared to what we can learn from the data.24 We can actually predict movie ratings much better if we ignore “real” movie genres altogether and just use the artificial ones we’ve machine-learned from the ratings matrix.25
In fact, as Chris Volinsky of BellKor pointed out, none of the data that came from outside the ratings matrix during his team’s experiments seemed to be very useful in predicting ratings. They tried a bunch of things—movie genre, which actors were in the movie, what the movie’s release date was, and so on—but nothing seemed to help. Chris’s intuition was that the dataset of movie ratings was so large and so rich that peoples’ ratings told you all you really needed to know about who would like a movie. Knowing how thousands of different people voted on a movie could tell you more about that movie than any amount of external knowledge ever could. The ratings for a movie are like its digital fingerprint, and matrix factorization provides a compact but excellent summary of that fingerprint.
If we repeatedly alternate between these two steps—that is, learning movies’ genres while holding users’ affinities for those genres fixed, and then estimating users’ affinities for those genres while holding the genres fixed, then our recommendations will get better and better until eventually the genres stop changing. At that point, we’ll have learned a set of weights for each user and another set of weights for each movie that we can multiply together and sum up to provide rich, personalized recommendations for each user-movie pair. This is what most data scientists mean when they refer to matrix factorization, and this alternating process of relearning the genres and genre affinities from data is how they often compute the matrix factorization.
As we learn these artificial genres with this alternating method, they’ll diverge from the original genres we started with. By the time we’re done, they might not look like the original genres at all, but they’ll still often be interpretable.
The way I’ve described matrix factorization just now probably isn’t the way you’d hear about matrix factorization in a college class. Often when researchers talk about matrix factorization to other people, they draw up an image of the movies in the ratings matrix forming a point cloud, where movies with similar ratings are near one another and movies with very different ratings tend to be farther apart. In fact, it’s easy to create such a cloud from the matrix, although it’s difficult to visualize, because each movie-point has 480,189 coordinates: one for each of the 480,189 users’ ratings for the movie.
But just like the matrix, this cloud has a lot of redundant information. Matrix factorization takes the high-dimensional cloud of movies and collapses it down into a lower-dimensional cloud that still captures the trends we care about—namely, that similar movies cluster near one another, while different movies tend to settle farther apart from one another. In the new space, each movie might be described with only half a dozen or a hundred numbers apiece—exactly the numbers we’d find with the alternating method above.
Matrix factorization and its brethren are often the first approach researchers try when they’re working with any data that can be put into a large matrix.26 For example, political scientists use matrix factorization to understand how lawmakers vote on legislation. If we place US lawmakers’ votes on different bills into a giant matrix and apply matrix factorization to it, we can summarize each lawmaker and each piece of legislation very well with just one or two numbers apiece.27 In one two-year period, for example, it was possible to explain 98 percent of the votes coming out of the House of Representatives by using just a single number to describe each lawmaker, and this number turns out to explain their political party. If you use this number to place lawmakers along the real line, Democrats and Republicans are usually perfectly separated. Matrix factorization tells us that US congresspersons’ voting is, quite literally, one-dimensional.
THE FIRST YEAR ENDS
Armed with tools like matrix factorization to capture the Terminator effect, and combining them with models that captured the Scrooge effect and the E.T. effect, the top teams made considerable progress toward the Netflix Prize. By the end of the first year, the top teams were around 8 percent better than Netflix’s own Cinematch algorithm. This wasn’t enough for them to win the grand prize, but it was more than enough to guarantee that some team would be eligible for the $50,000 Progress Prize. The Progress Prize was to be awarded annually, which meant that the contestants faced a fast-approaching deadline.
Among the top teams as the deadline approached was BellKor, whose members were the researchers from AT&T Labs and Yahoo!, and who had held the lead throughout most of the first year. But earlier in the game, the top of the leaderboard had changed frequently. The neural network researchers from the University of Toronto were near the top for a bit, and they produced an influential paper with a model that was used by other teams, including BellKor. But the three Princeton students making up Dinosaur Planet, free for the summer, had been working aggressively to challenge BellKor.28 And another team of young upstarts—the two Hungarian graduate students from the team Gravity—was challenging the Princeton students for second place.
Then, on October 21, 2007, one day before the first year’s deadline, the ground shifted. The two teams that had been hanging around second and third place—Dinosaur Planet and Gravity—formed an alliance. They combined their models, submitting the average of their models’ scores to the leaderboard, and suddenly they were in first place. BellKor had just one day to try to regain its position to claim the Progress Prize. Although they didn’t realize it yet, this was also the beginning of a phenomenon that would shape the rest of the competition.