7 TEACHING COMPUTERS BY GIVING THEM TREATS
Why don’t we have robots that can tidy the house or clean up after the kids? It’s not because we’re not mechanically capable—there are robots that could do that. But the problem is that every house, every kitchen, is different. You couldn’t pre-program individual machines, so it has to learn in the environment it finds itself in.
—Demis Hassabis, founder of DeepMind1
DEEPMIND PLAYS ATARI
In early 2014, as Google’s self-driving car project was humming along, the company was on an acquisition spree, gobbling up a variety of artificial intelligence and robotics companies. During this spree they acquired a small and mysterious company named DeepMind for over $500 million. At the time, DeepMind had only about 50 employees. Its website appeared to consist of a single webpage listing its founders and two email addresses.
Google holds an all-hands meeting at the end of every week called TGIF. The founders and other leaders of the company use the meeting to make announcements and to share details on projects within its various organizations. A number of months after Google acquired DeepMind, word spread around the company that DeepMind would be presenting at TGIF. Everyone at Google could finally learn what the secretive unit had been working on this whole time.
DeepMind explained at the meeting that they had figured out how to let a computer program teach itself how to play a wide variety of Atari games, including classic games like Space Invaders and Breakout. After DeepMind allowed their program to play millions of games, it often became far better than human players.
DeepMind then gave a demonstration to the audience, showing them a video of its program playing Space Invaders, a game in which the player must move a spaceship around the bottom of the screen to shoot aliens before the aliens make their way down to the bottom (you might recognize screenshots of this game and of Breakout in figures 7.1a and 7.1b).

Two of the Atari games played by DeepMind’s agent: Space Invaders (top) and Breakout (bottom).
As the audience looked on intently, the program played the game impeccably. Every shot it fired hit a target. As the game’s round neared its end, a single alien remained. The computer fired one stray shot, as the alien was moving step by step away from the missile and toward the right side of the screen. The humans in the room relaxed slightly: maybe this AI wasn’t a threat to their existence after all.
And then, as the audience continued to look on, the alien bounced off the side of the screen and began moving back toward the screen’s center. The program’s strategy became clear. The alien moved directly into the trajectory of the stray missile and was destroyed. The computer had won a flawless game. The room erupted in cheers.
Why was the audience of Googlers so excited? Hadn’t IBM created Deep Blue to defeat the Garry Kasparov, the world’s best chess player nearly two decades earlier, in 1997? Hadn’t Watson defeated the Jeopardy! champion Ken Jennings in 2011? Didn’t Google’s engineers already know about its self-driving cars, which had traveled nearly 700,000 autonomous miles on the road? If self-driving cars were possible, why was everyone impressed that a computer could beat a simple video game, when computers had been playing video games competitively for years?
The computer program was so impressive because it had learned how to play the game without any human guidance. Earlier breakthroughs had involved a high degree of human judgment and tweaking for the algorithms to work. With the self-driving car, a human needed to carefully develop the features for detecting drivable terrain and then tell the car that it could drive on that terrain. A human needed to manually create the finite state machines in the self-driving car’s Monopoly board module. Self-driving cars had not learned how to drive on their own by trial and error.
In contrast, the DeepMind program was never told by a programmer that tapping the joystick left would make the spaceship move left, or that hitting the button would shoot a missile, or even that shooting a missile at an alien would destroy the alien and earn it points. The only inputs to the Atari-playing agent were the raw pixels on the screen—their red, green, and blue colors—and the current score.2 Even more impressively, DeepMind used the same program to learn how to play all of 49 Atari games—the majority of which it learned to play well—with no hand-tuning whatsoever. All that the program needed was the time to practice each game. DeepMind did this with an idea called reinforcement learning, a field of artificial intelligence devoted to giving computer programs the ability to learn from experience.
REINFORCEMENT LEARNING
In this chapter and the next I’ll explain the key intuition behind how DeepMind used reinforcement learning to master these Atari games.3 Computer programs that use this technique learn to do things when they receive occasional rewards or punishments; so to train them, we just need to program them to seek these incentives—and then we need to give them these incentives when they’ve done something we want them to do (or not do) again. Just as your dog will learn to follow your commands when you give him a treat, a program that learns by reinforcement learning—the lingo for such a program in the AI community is agent—will also learn to follow your commands.
Reinforcement-learning agents may seem too smart to be automata, but, as we’ll see in the next two chapters, they still follow deterministic programs. Once the Atari-playing agent had been trained, for example, the agent just needed to look at the four most-recent screenshots from an Atari game (see figure 7.2). After looking at these screen shots, it evaluated a mathematical function to select a joystick action: left, right, or press the “fire” button, for example. It then repeated this process, over and over again, looking at the recent screenshots of the game and selecting an action based on what it saw, until the game was over. As you might guess, though, the magic wasn’t in how it played the game: as I just explained, that part was simple. The real magic was in how it learned to play the game—and in how it perceived what was happening on the screen. In this chapter we’ll begin with the first of those questions: How can an agent learn which actions to take given its past experience?
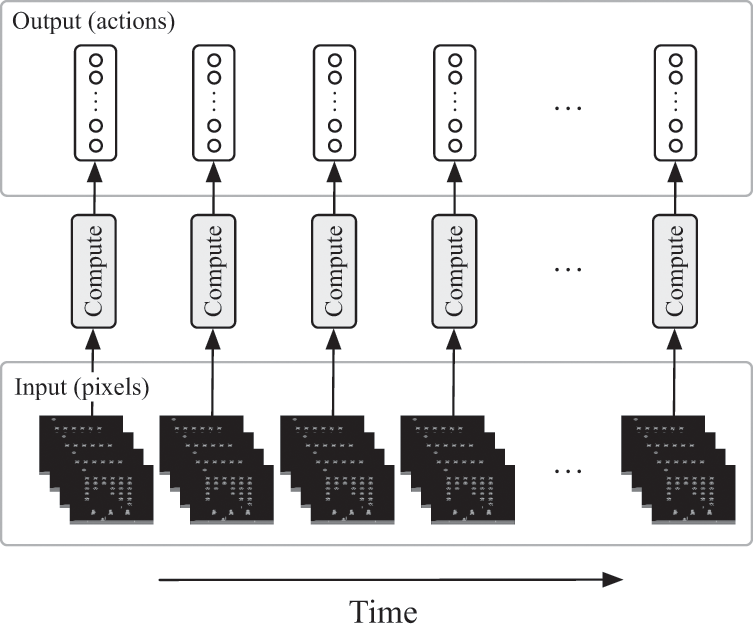
DeepMind’s Atari-playing agent ran continuously. At any given moment, it would receive the last four screenshots’ worth of pixels as an input, and then it would run an algorithm to decide on its next actions and output its action.
I’ll use a virtual game of golf to illustrate how reinforcement learning works. With this game of golf, which we’ll play on the course shown in figure 7.3a, the goal of the agent is to hit the golf ball into the hole in as few strokes as possible. We’re interested in designing an agent that can “learn” in which direction it should swing to get it closer to the hole when it’s in different parts of the golf course. Should it aim north, east, south, or west? To teach the agent, we will train it until it has enough experience to play golf on its own. At that point, it will be able to select on its own the direction in which it should to aim to make progress toward the hole, no matter where it is on the course.
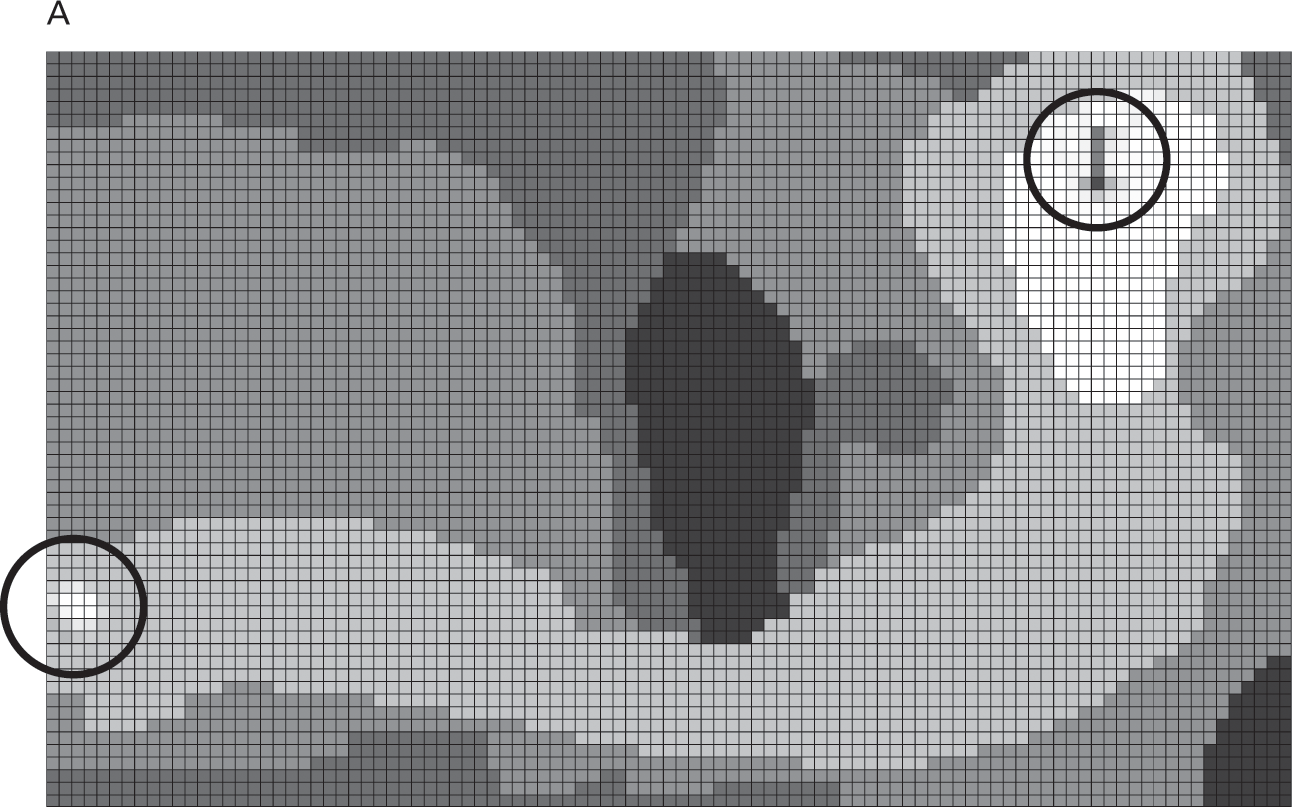
The golf course used in the reinforcement-learning example. Terrain types, ranging from light grey to dark black: the green (least difficult), fairway, rough, sand trap, and water hazard (most difficult). The starting point is on the left, and the goal is in the top-right corner.
Are we overcomplicating things? Do we really need to use reinforcement learning to tell the agent where to aim on the golf course? Couldn’t we just program the agent to aim directly toward the hole? As you’ll see in the next section, that’s not a viable option because there will be many obstacles in the way. Instead, the agent will need to make subtle adjustments to its swings depending on where it is on the course. Reinforcement learning won’t just be a tool for the job; it will be the tool for the job.
INSTRUCTIONS TO THE AGENT
You, the agent, will play golf on the course shown in figure 7.3a. You can aim your swing in any of the cardinal directions (north, east, south, or west) or halfway between these (northeast, southeast, northwest, or southwest). If you succeed in hitting the ball, it will move one square in the direction you aimed, as in figure Figure 7.3b, and your hope is to use as few strokes as possible to get the ball into the hole. Note also that this is a humongous golf course, so it might take 150 strokes or so to play a full round.
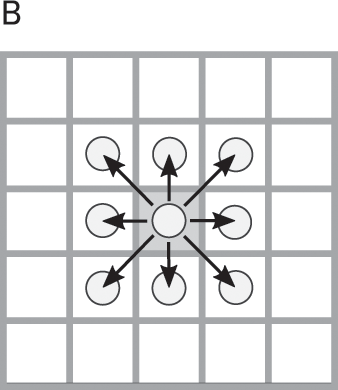
Your goal is to hit the ball from the start position into the hole in as few swings as possible; the ball moves only one square (or zero squares) per swing.
Two more things will make this game of golf interesting. First, and most importantly, there are explosive mines all over the place, as shown in figure 7.3c. You know where these mines are as you play the game—and they stay fixed every time you play the game—but you must avoid stepping on them at all costs.

The golf course also has explosive mines, each of which is marked with an x. You must avoid hitting these.
The mines wouldn’t be a problem if you could aim perfectly, so I’m going to add a final rule to make this game more difficult: the ball will not always move in the direction you swing. Sometimes it will end up in a different cell adjacent to you, and sometimes it may not move at all. You could attribute this to whatever you want—maybe it’s wind, or maybe it’s a bad swing. You don’t know details of how it moves when you swing—there’s some randomness involved—but you suspect that the ball is more difficult to hit on difficult terrain like rough than on easy terrain like green; these are all details you need to learn from experience. From easiest to most difficult, the types of terrain are green, fairway, rough, and sand trap. There is also a water hazard. If you hit the ball into the water hazard, you’ve wasted a stroke and need to retry from your last place on the course.
What should your strategy be to get the ball into the hole in as few strokes as possible? Should you aim directly for the hole no matter where you are, crossing the sand trap if need be? Should you try to stay on the fairway and the green so you can maintain control of the ball? And how far from the mines should you stay to remain safe?
PROGRAMMING THE AGENT
The answer to these questions will depend on a lot of factors, but even if the agent doesn’t have this information, we can still teach it a good strategy if we let it play for a while and give it rewards at the right times. How do we train the agent? We will offer it an immediate reward of a chocolate bar (for a value of 1) whenever it has reached the end position—the hole at the end of the golf course—at which time the game ends. If the agent steps on a mine, we will punish it with an electric shock that is equal to a reward of minus one-half a chocolate bar (value of –1/2). For stepping onto any other square, we’ll neither give it a reward nor punish it.
The more interesting and technically challenging question we need to answer is: How can we create an agent that can learn from these rewards? We can’t just give the agent chocolate bars and expect it to do what we want. We also need it to know that chocolate bars are worth seeking.
There are two observations that will help us to answer this question. The first relates to how we let the agent store its model of the world. The model must summarize the agent’s experience in a way that it can use to make future decisions. Let’s have the agent store its model of the world in a giant cube of numbers, like the one in figure 7.4.
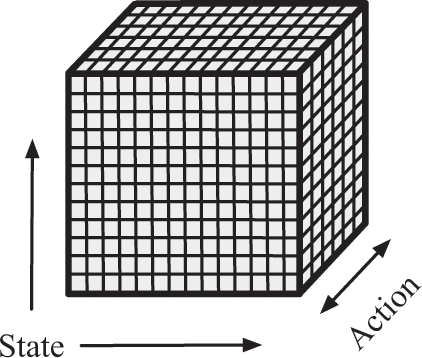
Each cell of this cube will store a number that tells the agent the expected “value”—that is, how much chocolate it should expect to receive—for taking certain actions from different positions on the course. Each time the agent needs to decide which action to take, it looks up all eight actions for its current position—those actions form a “stack” of values going straight through the cube—and then it selects whichever action has the highest value. After taking this action, the agent will find itself in another state—possibly a state it didn’t expect to find itself in—and it will repeat the same process. If the cube already has the correct values filled in, this strategy seems like it could work, and it’s simple enough that we could encode it even with a physical device, to create a mechanical automaton. But this still begs the question: How do we figure out which values go into each cell of the cube?
To answer that question, we need to make another key observation, this time about what the values in the cube should represent. Note that if the agent moves to a state that’s not the end goal, the agent receives no chocolate bar. This is problematic because a lack of rewards conveys little sense of progress to the agent. We might say that the “landscape” of rewards in the golf course is too flat. If the agent followed rewards blindly in this environment, it would struggle to make progress. This brings us to the final observation we need to design a reinforcement-learning agent: even when the agent receives no chocolate bar from some state, it still has the opportunity to eventually reach the chocolate bar from that state. The values in the cube should represent, at least intuitively, this opportunity.
One property we want in designing this idea of “opportunity” for the agent is that the agent should prefer to receive chocolate bars sooner rather than later. This makes intuitive sense: if your dog is across the room and you hold out your hand with a treat for your dog, he will immediately bound over to you. Provided that you’ve already trained your dog to do some tricks, he will sit and roll over, maybe even before you’ve given him the commands to do so. Your dog is behaving in a way that will earn him a treat as soon as possible. If the dog has a choice between doing something to get the treat now and doing the same thing to get the treat in thirty seconds, he will do what it takes to get it now. However we decide to define this idea of “opportunity,” our hope is that this preference for chocolate bars sooner rather than later will fall out naturally from that definition.
We can formalize this idea of opportunity—again, the opportunity is the value we want represented by each cell of the cube—by defining it as the total of all future chocolate bars the agent can expect to receive, adjusted for how long it will take the agent to receive those bars. A chocolate bar far into the future should be worth less than a chocolate bar now. This time-adjustment works a lot like how you would value money. Let’s say you could put a $10 bill into a change machine for $10 in quarters. If the machine had a delay of one day—that is, you put in your $10 today and get $10 in quarters tomorrow, you probably wouldn’t think it’s a good tradeoff, because you’ve given up the ability to spend that money in the meantime and because there’s some uncertainty that you’ll be able to recover it tomorrow. So maybe you’d be willing to put just $8 into the machine today to get your $10 in quarters tomorrow. If the machine had a two-day delay, you’d be even less willing to put in money today—maybe you’d be willing to put, say, just $6.40 into the machine. The longer you need to wait to receive some reward, the lower the value you’ll typically assign to that reward. Researchers call this idea temporal discounting (but I’ll just call it time adjustment from now on).
To program an agent to seek out the opportunity to earn chocolate bars, then, we will need to develop a way to fill in each cell of the cube with an estimate of the total of all chocolate the agent should expect for taking an action, adjusted for how long it will take to receive each payout of chocolate in the future.4 Actions with high values in the cube suggest more chocolate, earlier chocolate, more frequent chocolate, or some combination of these; while actions with low values suggest smaller, fewer, or later chocolate bars. An agent in a certain state faced with a choice between an action that offers a time-adjusted reward of 2.5 pounds of chocolate, and another action that offers a time-adjusted reward of 1.5 pounds of chocolate, should choose the first one.
This time adjustment gives the agent a chance at making progress toward the hole when the majority of the actions it takes lead to no chocolate bars. It turns the flat landscape faced by the agent into a hilly landscape, where the reward is at the peak of a mountain. The agent doesn’t actually do any complex planning: at each step it simply needs to “follow the gradient” in an effort to reach the top of the mountain.
This time adjustment also gives us a knob to adjust for the agent. This knob controls the tradeoff between having the agent seek an immediate reward and having it take a path that might postpone the reward for an even bigger reward later. Usually the way we apply this time adjustment is by multiplying the reward by a fixed amount between 0 and 1 for every unit of time—every hour, second, or day, for example—the agent needs to wait to receive its reward. This multiplier changes the reward landscape the agent sees, and it controls how much willpower the agent has: if it’s close to 0, the agent will tend to think very short-term, taking whatever chocolate it can get as soon as possible, even if that means giving up chocolate down the road. If this number is close to 1, the agent will be willing to give up short-term chocolate in favor of even more chocolate later.5
HOW THE AGENT SEES THE WORLD
One obvious difference between a dog and DeepMind’s Atari-playing agent—aside from the fact that dogs aren’t supposed to eat chocolate—is that the dog lives in the real world, while the Atari-playing agent lives in a simulated, virtual world. Instead of sitting or begging for treats, the Atari agent’s actions are limited to whichever joystick actions it can play in the game. And instead of using its eyes, ears, and nose to perceive the world around it, the Atari agent must perceive its world by looking at the pixels on the screen and tasting the virtual treats we give it. When DeepMind designed the agent, they needed some way to link what was happening in the game with what the agent perceived. How could they do this in a simple, coherent way that made their agent easy to reason about?
Fortunately for DeepMind, researchers at the University of Alberta had created a platform called the Arcade Learning Environment, which enabled them to let the agent move around in its Atari universe. The environment was built on top of an Atari emulator—that is, a program that mimics the behavior of an Atari console—and the environment pulled information directly from these games’ computer memory.6 By using the Arcade Learning Environment, DeepMind could simply “look up” the inputs to its agent—the pixels and the current score—to present them as sensory input to their agent, and send the agent’s commands to the environment to be interpreted as joystick actions. The Arcade Learning Environment then dealt with the messy details of simulating the Atari world correctly.
NUGGETS OF EXPERIENCE
From everything we’ve seen so far, we still don’t have a concrete way to fill in the values of the action-value cube. We know that each value of the cube should represent the time-adjusted chocolate the agent will receive in the future, and we know that to create an agent to use these values, we need to program it to select the action with the highest value for whichever state it’s in; but it’s not clear how to compute the values that go into the cube in the first place.
If we had perfect information about the game—such as how likely we are to hit the ball in a certain direction on each area of the course—then we could use some mathematical formulas from the field of reinforcement learning to compute the values of the entire cube without ever having the agent play a game. But perfect information is a luxury we don’t have. In the golf game, as with Atari games, we don’t even know how likely we are to end up in different states after performing an action.
DeepMind resolved this problem by having their agent learn the values in the cube by trial and error. At first, their agent chose completely random actions so it could learn from experience which state-action pairs tended to be followed by rewards. Using a trick from the field of reinforcement learning called off-policy learning, the agent learned a good strategy for its games even though it stumbled around randomly. Then, as the agent gained experience, it began to prefer actions that weren’t random.
Let’s apply an off-policy learning algorithm to the golf game. First we let the agent play through a game, selecting random actions each time it needs to make a move. This will generate a sequence of state-action pairs, as in the left panel of figure 7.5. After the agent has played through the game, we need to update the values in the action-value cube using what the agent experienced during the game.
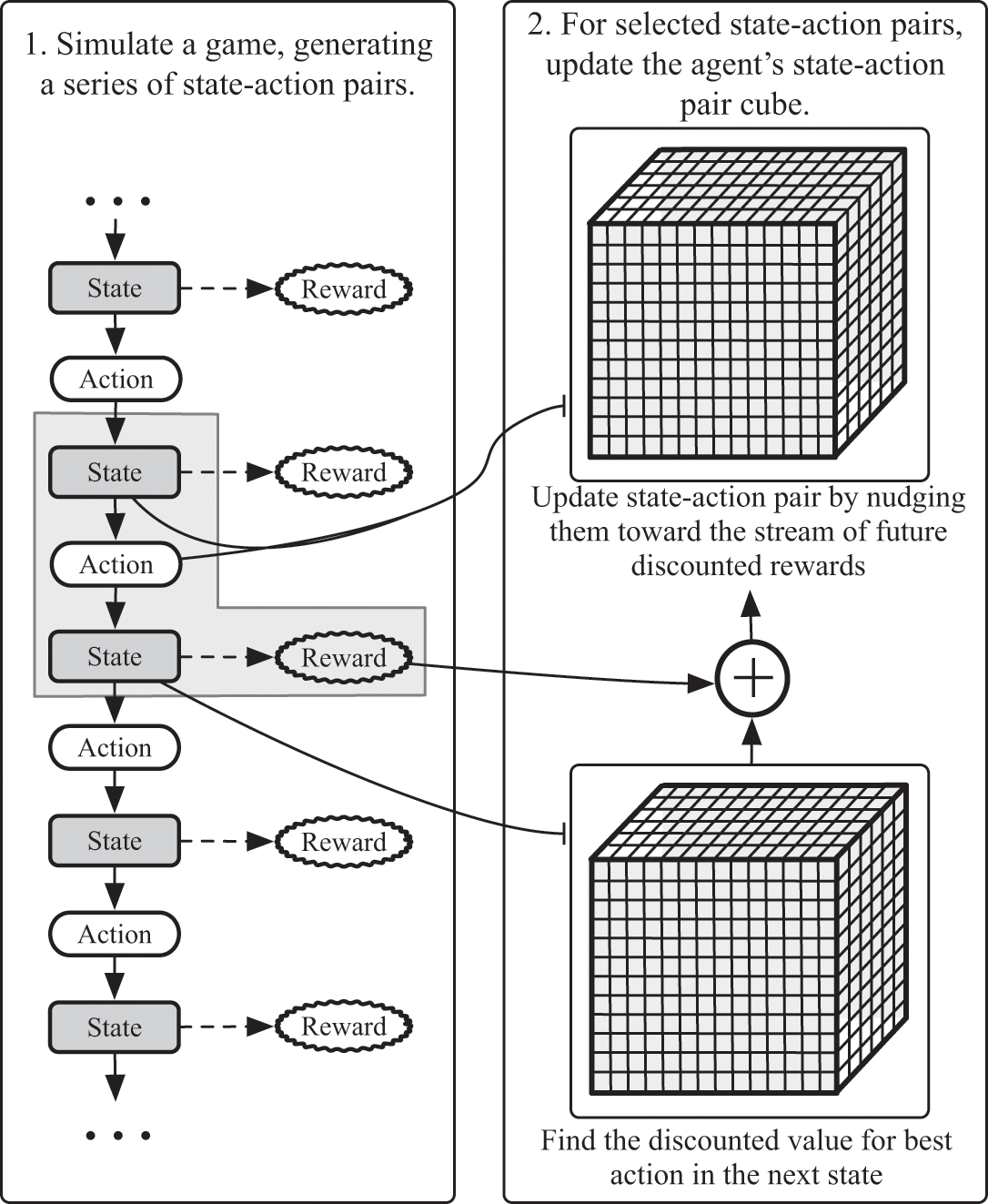
One way to train a reinforcement-learning agent is with simulation. First the agent plays through a game to generate a series of state-action pairs and rewards, as shown in the left panel. Next, as shown in the right panel, the agent’s estimate of future rewards for taking different actions when it’s on a given state is updated using the state-action pairs experienced by the agent. This particular method is sometimes called “temporal difference, or TD, learning.”
We can summarize the agent’s experience by breaking it into chunks, each of which has several bits of information: what state it was in when it selected and performed an action, which action it chose (north, northeast, east, and so on), which state it ended up in after it made its action, and whether it earned or lost any chocolate when it reached the next state. You can see such a chunk outlined in the left side of figure 7.5. The agent will learn everything it needs to from these “nuggets” of experience.
We need some way to update the value of the action-value cube to incorporate each of these nuggets. If the agent ended up at its final destination—the hole—after experiencing some state-action pair, we nudge the value of that state-action pair in the cube a little bit toward the reward of 1. We don’t set it to 1; we just nudge it a little bit toward 1. If a state-action pair led to a spot on the course with an explosive mine, we nudge the value of the state-action pair a bit toward –1/2. Otherwise, we nudge the value of the state-action pair closer to 0. When I use the word “nudge,” I’m using the term casually, but reinforcement learning offers a mathematically precise way to adjust these values that agrees well enough with the intuitive meaning of the word.
This is enough to teach the agent about the rewards it will see immediately after its action. But remember: we want the action-value cube to represent the time-adjusted stream of all future chocolate, since we want the agent to pick actions that will move it toward chocolate even when it is far away. We need some way to estimate the stream of chocolate the agent will see after this action. And herein lies the secret to training the agent: since we already know from the experience-nugget the state in which the agent ended up after choosing some action, we can look this information up in the cube itself!
More specifically, since we already know that the agent’s strategy is to select the best action for whichever state it’s in, then we can figure out exactly which action a clever agent will take after the experience-nugget. Because we know—by definition—that the cube stores the amount of time-adjusted chocolate the agent will receive for that next action, we can use that information to update the current state-action pair.
Since that action (and its chocolate) are one step into the future, we time-adjust the chocolate the agent will receive for that future action, and then we nudge our original state-action pair toward the value of that time-adjusted chocolate. To train the agent, we repeat this process for the states the agent visited during its game, and then we repeat this process for many games.
This self-referential trick might set off some alarm bells in your head. When we first start training the agent, the numbers in the cube will be garbage. Combine this with the fact that the agent starts out by selecting random actions, and it’s hard to believe it could possibly learn a good strategy. Doesn’t garbage in equal garbage out? It’s true that the values in the action-value cube will start out very bad at first, and the initial changes we make to the cube won’t be very helpful. But the quality of learning will gradually improve over time.
There’s an important assumption I’ve made about the world hidden in the way I’ve described how the agent populates and uses the action-value cube. Here is the assumption: in anticipating the agent’s future, the only state that’s relevant is its current state. This doesn’t mean that its past states and actions don’t matter: they might have been important in getting the agent to its current state. But once we know the agent’s current state, we can forget about everything before that, because we assume its current state captures all of the history that’s relevant in anticipating its future. This is often called a Markovian assumption. While simple, the Markovian assumption enables us to update the action-value cube with experience nuggets that link the past to the future, so that the values in the action-value cube themselves link the past to the future. This is how, with each game the agent plays, the cube’s values will become a little more accurate. The cells of the cube will improve in a virtuous cycle, as they change from “bad” to “good” to “great.”
In each game of golf, the sequence of states the agent visits form a “trajectory” on the golf course. You can see what some of these trajectories look like in figures 7.6a and 7.6b. At first, on the top, the agent moves around completely randomly, and it takes many strokes to reach the hole at the end. With a few games, the agent can bumble toward the hole at the end of the course. Once it has played through a few thousand games, however, it moves precisely around the mines. In the lower half of the figure, you can see that the agent is even able to anticipate and steer to avoid the mines far in advance of reaching them. Once the agent has learned a perfect strategy, it still bumbles a bit: there’s no way for it to avoid the randomness it faces in each swing. But the agent has become optimal in a different way: it learns to anticipate the mines long in advance of reaching them.

Trajectories (white paths) made by the golf-playing agent. (a): a trajectory made by the agent after playing 10 games. (b): a trajectory made by the agent after playing 3,070 games.
PLAYING ATARI WITH REINFORCEMENT LEARNING
The method I describe in this chapter is one of the most common ways reinforcement learning is used in practice. In this method, the agent moves around from state to state by selecting different actions, and we give the agent rewards—chocolate—when it has done something we approve of. When it needs to perform an action, the agent references its action-value cube: it looks up which actions it can make, selects the one with the highest time-adjusted reward stream—and performs that action, moving to a different state and possibly receiving another reward as a result. When we want to train the agent, we let it play many games and then we use its “nuggets” of experience to update its action-value cube.
It’s possible to play golf with this action-value cube because there were 60 × 100 = 6,000 states in the golf course and 6,000 × 8 = 48,000 cells in the action-value cube. That’s a lot of cells, but it’s not so many that we can’t accurately estimate the values in this cube by telling the agent to bumble around randomly for a while.
Unfortunately the method I’ve just described wouldn’t work if we wanted an agent that could play Atari. The problem is that the action-value cube needs to be many orders of magnitude larger for the Atari-playing agent than it is for our golf-playing agent.
As we saw at the beginning of the chapter, DeepMind considered the state in an Atari game to be the arrangement of the pixels on the screen for the past four screenshots.7 For a game like Space Invaders, the action-value cube would need to keep track of many trillions of states.8 The approach we used to estimate the values in the action-value cube when we played golf—learning by choosing actions randomly—wouldn’t have worked, because we would need to play far too many games to fill up the action-value cube with reasonable values.
This may sound like just a technicality, but it’s a very real limitation.9 Even if we had enough time to fill up the cube, or even if we only needed to fill up a fraction of the cube, its size would also push up against the memory limits of computers. The cube for most Atari games would simply be too big.
DeepMind needed some other way to represent the information we put into the action-value cube. The tool they turned to was neural networks.