‘Physics is hard.’ Remarks such as these have been heard by teachers and students of physics innumerable times. Physics of course has its own object of study, its own ways of organising its knowledge and its own ways of expressing its knowledge. In this sense, it is its own unique discipline. But this does not mark physics as different from any other academic subject; every discipline has its intricacies and idiosyncrasies, and every subject has its detractors and its devotees. Nonetheless, physics seems to be regularly positioned as an exceptional case in the academic world. It is often said to be the most fundamental of the sciences, one upon which all others are based (e.g. Feynman et al. 1964, Young and Freedman 2012); this perhaps can be taken to mean that it shares many of the characteristics of the others sciences, but also maintains its own distinctive features. Biglan (1973), for example, classifies physics as a pure science, along with geology, chemistry and botany, but he positions it as the ‘hardest’ of the pure sciences. Kolb (1981) characterises it as a reflective (non-applied) discipline, like geography, bacteriology and biochemistry, but he portrays it as the most ‘abstract’ of the reflective disciplines. And those following Bernstein (1999) identify it with other natural sciences as a discipline that develops generalised theories and integrates empirical phenomena, but they regularly use physics as the exemplar of such a discipline (Maton and Muller 2007, O’Halloran 2007, Martin 2011).
There is thus a sense that physics is both a natural science, and as such shares many of the features of the natural sciences; but at the same time physics is in some sense the most ‘sciencey’ of the natural sciences. Exactly how this recurrent characterisation of physics arises, however, is not clear. We might even ask whether it is truly the case that physics maintains a special position within the sciences? And if so, what gives rise to this special position? Questions such as these go to the heart of the disciplinary organisation of physics and so are not born of idle curiosity. They hold strong significance for the development of educational programs that acknowledge and target disciplinary knowledge. If disciplines vary in the way they organise their knowledge, vary in the discourse they use to construe this knowledge and vary in the means of judging and comparing competing knowledges, the pedagogic approach for teaching these disciplines must take this into account.
To investigate how physics manages its apparently special knowledge structure, this book examines its discourse in classrooms, in textbooks and in student work. What is immediately apparent when considering this discourse is the large emphasis on mathematics and images throughout almost all contexts. Figure 1.1 shows a typical page from a senior high school exam paper and marked student response involving two graphs, multiple equations and a number of stretches of language.
This page is typical of physics texts throughout the data set used for this study (described in Appendix C). Indeed Parodi (2012), in his quantitative study of textbooks across multiple academic disciplines, suggests that of the basic sciences, physics is by far the most reliant on mathematics, while still utilising to a large degree images such as graphs and diagrams to present information. Based on these findings, Parodi suggests that physics is the most predominately graphic-mathematical of the disciplines he studied. This amplifies the characterisation of physics by Biglan as the ‘hardest’ of the pure sciences and by Kolb as the most abstract of the non-applied disciplines, and reinforces its exceptional form. Parodi’s study also reinforces the findings of Lemke’s (1998) survey of articles in the prestigious physics research journal Physical Review Letters. Within this corpus, Lemke found that on average, around four images and equations occurred per page (2.7 equations, 1.2 images); this is significantly higher than the rate of images and equations in the corresponding journal for the biological, earth and space sciences, Science, or for medicine, Bulletin of the New York Academy of Medicine (Lemke 1998: 89).1 Images and equations are thus clearly regular features of physics’ discourse.
In order to understand the discourse of physics, then, it is necessary to comprehend the full range of resources involved—language, mathematics and images, as well as gesture, demonstration apparatus, various symbolic formalisms and numerous others. This book moves in this direction by considering mathematics, images and language as crucial components of the discourse and knowledge of physics. It thus offers a more exhaustive analysis of physics texts than would be possible if our gaze was restricted solely to language. In addition, a detailed study of each resource makes it possible to understand why each is used. The pervasiveness of each resource throughout physics across a broad range of levels in schooling and in research suggests that each plays a crucial role in developing the knowledge of physics. By taking each resource seriously and considering their roles in detail, we can begin to understand their functionality for organising this knowledge. More specifically, we can investigate whether the particularly predominant use of mathematics and images plays any role in the distinctive knowledge structure that physics maintains.
Before we can investigate these resources, however, we need a common method for understanding them. Scientific language, for example, has a long
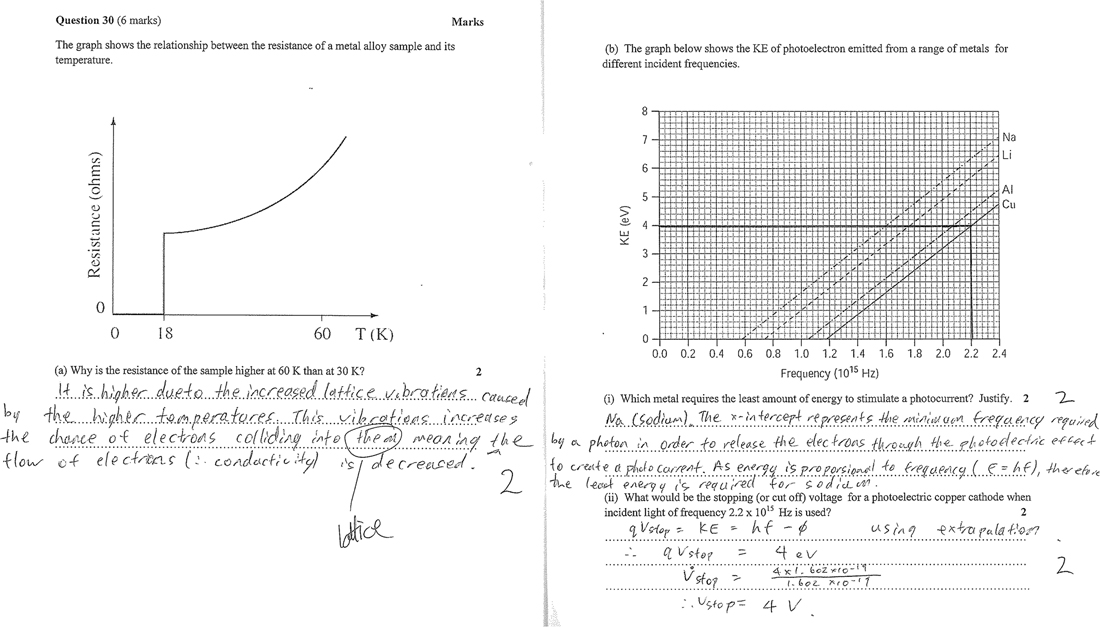
Figure 1.1 Mathematics, image and language in a high school exam
history of research in linguistics. For example, in the tradition of SFL and the agnate approach of Social Semiotics, there have been several decades of research into its peculiarities (e.g. Huddleston et al. 1968, Lemke 1990, Halliday and Martin 1993, Martin and Veel 1998, Halliday 2004). These studies and the educational programs developed from them have been based upon elaborate and wide-ranging descriptions of language developed by Halliday, Martin and colleagues (consolidated in Halliday and Greaves 2008 for phonology, Halliday and Matthiessen 2014 for lexicogrammar, Martin 1992 for discourse semantics, and Martin and Rose 2008 for register and genre). These descriptions were not necessarily developed with science or education explicitly in mind (though some did arise in relation to these considerations), but were built with an eye to the range of variation across different contexts and the extrinsic functionality that language serves. Nonetheless, they have proven immensely useful to many researchers who wish to study the language of science in addition to its other applications. These descriptions are being continually developed and improved as further avenues of research come to light.
In recent decades, descriptions drawing on SFL have been developed for modalities of communication alongside language. Kress and van Leeuwen’s (1990) and O’Toole’s (1994) grammars of images, and O’Halloran’s (1996, 2005) description of mathematics, to name a few, have widened our gaze and allowed us to understand these resources as meaning-making systems in their own right. These and related descriptions have fostered the growing field of multimodality and have encouraged scholars to take seriously the roles of extra-linguistic semiotic resources. Some of these descriptions, however, require further development in order to achieve the comprehensiveness and robustness of the descriptions of English mentioned earlier. For example, O’Halloran’s description of mathematics has yet to be fully systematised and the range of variation in mathematical symbolism has not yet been fully mapped. Further, for images, there still remain significant areas yet to be fully developed, including a more thorough exploration of abstract graphs and the highly complex diagrams used in the sciences to explain physical phenomena. Before we can understand the functionality of these resources and their role in building the knowledge in physics, we need an understanding of what they can and cannot do in various contexts. This requires thorough descriptions to map the choices available and the typical text patterns in each context.
One challenge we need to face is that the various models of semiotic resources produced to date (whether focused on language, image, mathematics, gesture, film, sound or space), rarely begin from the same starting point. Each description tends to make its own assumptions and develops according to its own criteria. Moreover, with the exception of linguistic studies, descriptions tend to have little explicit discussion of the principles guiding them. If we are looking to compare the functionality of various resources and determine why they are used, this becomes an issue. With different starting points and different methods of development, it is often difficult to determine whether similarities or differences apparent in resources are due to the intrinsic nature of these resources or simply due to the informing theory and descriptive methodology. Just as the classification of species in biology or the explanation of phenomena in physics needs to be based on systematic principles, so does the description and comparison of resources in semiotics. By way of facing this challenge, this book proposes principles for description based on Systemic Functional theory that provide a basis for systematic and thorough descriptions of semiotic resources. These principles offer a method through which descriptions can bring out each resource’s intrinsic and unique functionality, rather than assuming categories developed from other resources. They will also underpin a detailed description of mathematical symbolism that explores the range of variation and the detailed potential available across contexts. And they will be used to generate larger theoretical architecture that allows a comparison of the broader functions of resources.
This book thus incorporates two components. The first is descriptive: it develops a comprehensive formalised description of mathematical symbolism both at the micro level of its grammar and at the broader level of text patterns arising from its interaction with language. In doing so, it illustrates a set of descriptive principles that can be applied widely as a shared basis for semiotic description. In addition, it considers images, language and mathematics in terms of the meanings they can make and their unique functionality in the discourse of physics. The second component of the book uses these descriptions to investigate the knowledge of physics. It shows how physics manages to build abstract theory while maintaining its grasp on the empirical world, and highlights the crucial role that language, mathematics and images each play in this. The book thus investigates the knowledge of physics by examining the semiotic resources that organise it.
This book is organised into seven chapters. Following an introduction to SFL in the rest of this chapter, Chapters 2–6 progressively build the descriptive component of the book by steadily widening its gaze. Chapter 2 begins with a focus on language’s role in organising physics, Chapters 3 and 4 continue this monomodal focus with a study of mathematics, Chapter 5 widens its scope by considering mathematics and language together and Chapter 6 brings images into the picture to contrast their role with that of mathematics and language. As the descriptive lens broadens, the book increasingly focuses on the overall knowledge of physics and the role each resource plays in its structure. The final chapter brings each component of the book together to underscore the interplay between the descriptive and knowledge-building foci, as well as their implications for the broader field of semiotics and our understanding of knowledge. Throughout the book, we will see that each resource—language, mathematics and image—plays a crucial part in construing physics’ knowledge.
Before moving onto the language of physics, it is first useful to introduce the model of language underpinning this book—SFL. SFL is a multifaceted theory of language with a large an interconnected architecture. It considers language in its social context and describes it in terms of both the functions it plays and the possible options available in any situation. It is by far the most elaborated component of the broader field of Systemic Functional Semiotics and is the basis for most of the theoretical principles and descriptive mechanics in broader Systemic Functional theory. As will be argued in the next chapter, most Systemic Functional descriptions of semiotic resources other than language have taken their lead from the work on English by Halliday and his colleagues. It is thus important to understand the architecture of language from the perspective of SFL in order to understand how accounts of non-linguistic semiotic resources have been developed. This section will focus on four main dimensions of language in SFL known as stratification, metafunction, rank and axis.
Stratification
SFL views language as a stratified system involving three levels (strata), known as discourse semantics, lexicogrammar and phonology/graphology (Martin and Rose 2007). Discourse semantics is concerned with meanings made through entire texts (beyond the clause). Lexicogrammar is concerned with meanings made within clauses, sentences and other elements that make up the grammar of language such as groups/phrases, words and morphemes. Phonology (for spoken language) and graphology (for written language) are concerned with the sounds (phonology) and letters/punctuation (graphology) that realise the meanings made by discourse semantics and lexicogrammar. Every instance of language necessarily makes a choice from each of phonology/graphology, lexicogrammar and discourse semantics, and every stratum contributes its own meanings. This means that choices made in discourse semantics are realised by and affect the choices in lexicogrammar, and choices in lexicogrammar are realised by and affect choices in phonology/graphology.
When looking at texts, it is clear that the way we use language changes depending on the context. To see this, SFL proposes further strata above language. In Martin’s model (1999), two further strata, register and genre, coordinate choices in language. Genre is the highest stratum and describes a text’s global social purpose (Rose and Martin 2012). Genres tend to unfold in distinct stages and coordinate the meanings at the stratum below, termed register. Register encompasses three variables: field, tenor and mode (Martin 1992). Field is concerned with what is happening in a social activity, tenor is concerned with the relationship between participants and mode is concerned with the role language plays in the situation (Martin and Rose 2008). The strata of language in context are represented in Figure 1.2 as co-tangential circles.
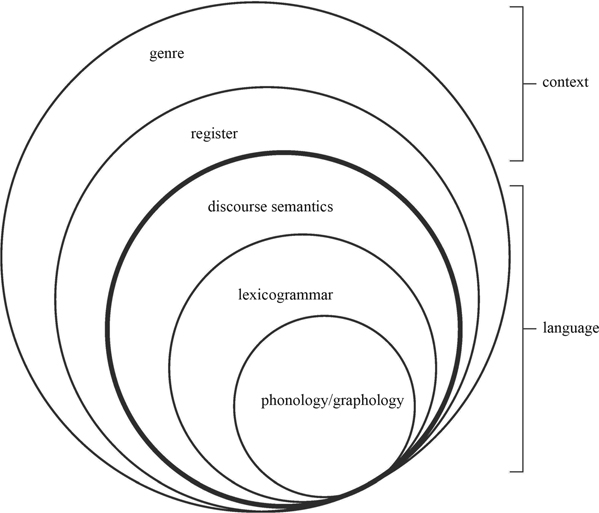
Figure 1.2 Language and context in SFL, adapted from Martin (1999)
Crucially for this book, genre and register are not strata of language. Rather, they are semiotic systems in their own right expressed through language. In Hjelmslev’s (1943) terms, genre and register are connotative semiotics, while language is a denotative semiotic (Martin 1992). As connotative semiotics, genre and register have language as their expression plane, whereas language, as a denotative semiotic, has its own expression plane—phonology or graphology. This connotative/denotative distinction is important for Chapters 5 and 6, where mathematics, language and image are viewed from the perspective of a shared system of genre (Chapter 5) and the register variable field (Chapter 6). By positing a semiotic system above language (genre and register), the regular uses of mathematics, language and image in physics can be explained.
Metafunction
Cross-cutting strata, SFL proposes that language makes three broad types of meaning, known as ideational, interpersonal and textual meanings (Halliday 1969, 1973, 1994). Ideational meanings construe the outside world and in some sense organises our knowledge of reality. Interpersonal meanings enact our social relationships which organises our sociality. And textual meanings organise language’s information flow and salience, giving language its textuality. In addition, ideational meanings are regularly distinguished into two subtypes, known as the experiential and logical meanings. The experiential component is said to construe our experience of the outside world, while the logical component organises the large set of iterative relations between different elements of this experience. These different types of meanings are referred to as metafunctions and are reflected in different components of the grammatical systems of languages.
The metafunctional distribution of meanings in language coordinates with a three-way distinction of register at the level of context, into field, tenor and mode (Halliday 1970, 1978). Field is the variable concerned with the ‘content’ of what is being said and so tends to coordinate ideational meanings in language. Tenor is the variable concerned with the social relations encoded through language and so tends to coordinate interpersonal meanings. Mode is the variable concerned with the role of language in any situation and so tends to coordinate textual meanings. This relation between the components of register and the metafunctions of language relates the extrinsic functionality of language (its roles and use in social interaction) to the intrinsic functionality of language (its internal functional organisation). This register-metafunction ‘hook-up’ suggests that language is as it is because of the functions it has evolved to do (Martin 1991). The metafunction-register relation is presented in Figure 1.3.
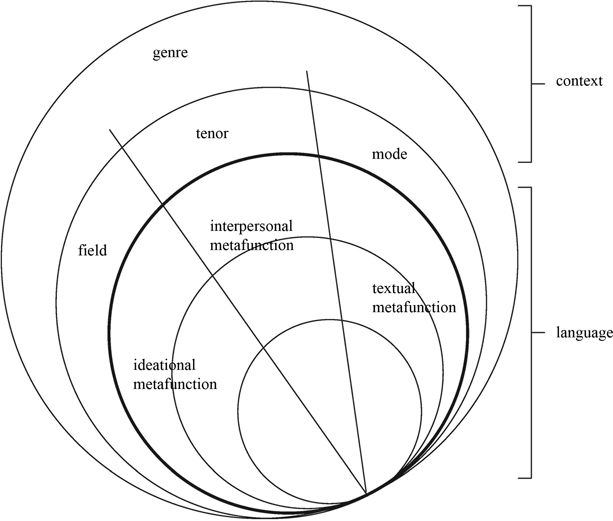
Figure 1.3
Metafunctions in language and context, adapted from Martin (1999)
Halliday’s notion of metafunction arises from his work on the grammatical organisation of language. In developing this model, Halliday observed that there are different components in the grammar that are made up of relatively discrete bundles of systems. As Halliday (1978: 187) puts it, ‘within one component there is a high degree of interdependence and mutual constraint, whereas between components there is very little: each one is relatively independent of the others.’
In addition, Halliday (1979) suggests that each metafunction tends to be realised by its own type of structure. Ideational meanings tend to be realised by particulate structures, where each element is clearly distinguished from the others with sharp, discrete boundaries. For example, the TRANSITIVITY system in English involves functions such as Actor, Process and Goal, where the boundaries between each are relatively clear-cut (Halliday and Matthiessen 2014). For example, in I kicked the habit, I realises the function Actor, kicked realises the function Process, and the habit realises the function Goal; each element is relatively discrete and clearly distinguished. On the other hand, interpersonal meanings tend not be realised by discrete elements, but by prosodic structures where meanings cut across multiple units. For example, negation in English is not restricted to a single element in an clause, but rather is realised across a function known as the Finite and any subsequent indefinite deixis in other elements—e.g. I won’t eat any vegetables anywhere (c.f. the positive I will eat some vegetables somewhere) (Martin 2008). The choice of negation necessitates particular choices across multiple elements. Finally, textual meanings are realised by periodic structures whereby text is ordered into peaks and troughs of informational salience. At clause rank, this is represented in English through the thematic prominence at the beginning of the clause (labelled Theme) and the intonationally marked newness prominence typically placed at the end of the clause (labelled New) (Halliday and Matthiessen 2014). These structures can be represented as in Figure 1.4.
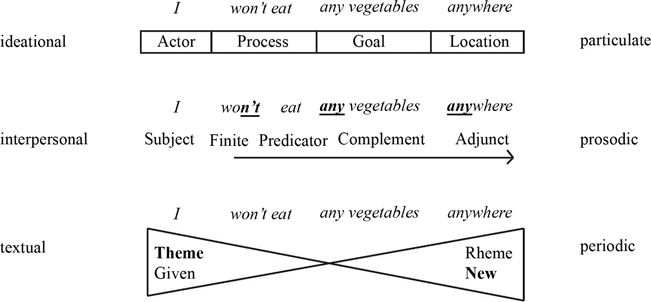
Figure 1.4
Types of structure for each metafunction
For this book, the most pertinent structures are particulate structures. These are associated with the ideational and field-based meanings developed in physics and form the core of the grammatical organisation of mathematics. For the discussion in Chapter 3, 4 and 5 it is important to further distinguish two subtypes of particulate structure, which Halliday (1965) calls multivariate and univariate structures. These types of structure are associated with the two components of the ideational metafunction—multivariate with the experiential component, univariate with the logical component (Halliday 1979).
Multivariate structures involve multiple variables that normally occur only once (Halliday 1965). For example, the TRANSITIVITY structure of the English clause, We saw him, is a multivariate structure involving three different functions in sequence Senser (We) ^ Process (saw) ^ Phenomenon (him) (Halliday and Matthiessen 2014; sequence is indicated by a caret ^. Non-sequenced functions are indicated by a dot •). In contrast, univariate structures involve a single variable that can be repeated (often indefinitely). For example, the clause complex The Cronulla Sharks lost Michael Ennis last year and this year they lost Ben Barba involves two clauses (underlined) linked by and (a coordinating conjunction, also known as paratactic extension Halliday and Matthiessen 2014). In principle, any number of elements could be related in this way, creating very complex sequences. Finally, univariate structures can either be paratactic, where each element is of the same status (such as the clause complex mentioned earlier), or hypotactic where one element is dependent on another. An example of a hypotactic structure is the clause complex after buying Ennis, Cronulla bought Maloney. In this complex, the clause buying Ennis is dependent on Cronulla bought Maloney in the sense that it cannot occur on its own. It is common in Systemic Functional descriptions for multiple structures to be mapped onto the same unit. For example, the English clause in Figure 1.4 has structures arising from TRANSITIVITY (Actor ^ Process ^ Goal ^ Location), MOOD (Subject ^ Finite ^ Predicator ^ Complement ^ Adjunct), THEME (Theme ^ Rheme) and INFORMATION (Given ^ New).
In addition to multivariate and univariate structures, Martin (1992) offers a third type of particulate structure to account for discourse relations. These structures account for, for example, relations deriving from taxonomies where multiple elements are mutually dependent on each other. Martin’s example considers the relation between robot and model in the short text:
I’m not pleased with this robot, but that model looks fine.
(1992: 24)
In this example, robot is a subordinate of model (that is, robot is a type of model in this case). This sets up a cohesive tie in the text, whereby model and robot enter into the same taxonomy and thus hold some relation in the text. This relation is of mutual interdependence; model is as dependent on robot for its role in helping the text cohere as robot is on model. Following Lemke (1985), Martin terms these relations covariate structures.
The multivariate, univariate and covariate distinction will be used through the grammatical description of mathematics in the following chapters and so will be reviewed when they become relevant. Each type of structure is associated with a particular bundle of systems in the grammar, and will be used in developing a metafunctional model for mathematics. Figure 1.5 presents the different types of structure relevant for this book (following Martin 1992, covariate and univariate structures are grouped together as interdependency structures).
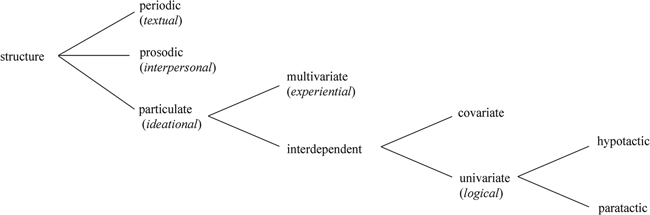
Figure 1.5
Types of structure and their associated metafunction
Rank and Nesting
Within strata, SFL proposes a second set of levels known as ranks. Ranks form a constituency hierarchy whereby every rank is made up of one or more units of the rank below it (Halliday 1963). In English phonology for example, there are four ranks: the tone group is the highest rank and contains one or more feet, which in turn contain one or more syllables, which in turn contain one or more phonemes (Halliday 1963, 1994). At the higher stratum of lexicogrammar, English also has four ranks. Clauses contain groups (or phrases), groups/phrases contain words and words contain morphemes (Halliday and Matthiessen 2014). A rank scale’s constituency organisation is what distinguishes it from strata. Strata are related in terms of abstraction; this means that a unit on a higher stratum is not compositionally related to a unit in another stratum (e.g. a morpheme in the grammar does not consist of phonemes in phonology, Hockett 1961). In contrast, by definition, the units in a rank scale will necessarily be related through a part-whole relation (Halliday 1961). For example, the clause The second Saints album contains 13 tracks can be divided into three functions: Carrier (The second Saints album), Process (contains) and Attribute (13 tracks). Each of these functions are realised by a single unit at the rank of group/phrase. The Carrier is realised by a nominal group (The second Saints album), the Process is realised by a verbal group (contains) and the Attribute is realised by another nominal group (13 tracks). Each of these groups is in turn realised by another set of functions, which are then realised by words, and the words then have their own internal structure, which are finally realised by morphemes.
The rank scale is organised through a constituency hierarchy involving multivariate structures (Huddleston 1965). However, in addition to the rank scale, univariate structures can also produce additional depth in a process commonly known as layering or nesting (Halliday 1965). This arises from the fact that (in English) every rank can complex into indefinitely large sequences: just as clauses can become clause complexes (The Cronulla Sharks lost Michael Ennis last year and this year they lost Ben Barba), groups and phrases can also form group/phrase complexes (e.g. the hydrogen atom and the helium ion), words can form word complexes (hydrogen and helium) and morphemes can form morpheme complexes (pre- and post-discovery). Through this iterative structure, complexes of units can form single elements within larger complexes, producing further depth. Halliday (1965) illustrates this through the nominal group complex soup, a main dish, sweet or cheese and biscuits, and coffee. This complex sets up a univariate structure with four immediate elements: (1) soup, (2) a main dish, (3) sweet or cheese and biscuits and (4) coffee. However, the third element contains two further elements: (1) sweet and (2) cheese and biscuits. And cheese and biscuits in turn contain two more elements: (1) cheese and (2) biscuits. This sets up three layers arising from its univariate structure:
|
soup, a main dish, sweet or cheese and biscuits and coffee
|
| layer 1 |
soup
|
a main dish
|
sweet or cheese and biscuits
|
coffee
|
| layer 2 |
|
|
sweet cheese and biscuits
|
|
| layer 3 |
|
|
cheese biscuits
|
|
The nesting in this case all occurs at the same rank; the entire complex would function as a whole within a clause (e.g. The menu today is soup, a main dish, sweet or cheese and biscuits, and coffee). As discussed in the previous section, univariate structures (and the nesting that arises from them) are associated with the logical metafunction. This metafunction, including its univariate structure and nesting underpin much of the grammatical organisation of mathematics, and so will be discussed in more detail in Chapter 3.
Axis: System and Structure
Finally, underpinning each of the dimensions of rank, strata and metafunction is the dimension of axis. Axis involves the complementarity of system and structure. Systems organise the large array of choices available in language. Formally, these systems are known as the paradigmatic axis and arrange features in opposition to each other. For example, in the system of MOOD there is a choice between a declarative clause that generally gives statements, such as It’s all too beautiful, and an interrogative clause that generally gives questions, such as Is it all too beautiful?. The paradigmatic axis arranges the multitude of choices available in any language or other semiotic resource.
Complementing this, each choice in a system is realised by a particular configuration in structure. These structures are known as the syntagmatic axis, and involve elements called functions (shown within initial capitals). For example, both declarative and interrogative clauses involve the functions Subject and Finite. In distinguishing between these two types of clause, the order of the Subject and Finite is reversed: for declaratives, the Subject comes before the Finite, as in It (Subject) is (Finite) is all too beautiful, while for interrogatives, the Finite comes before the Subject, as in Is (Finite) it (Subject) all too beautiful?
The systems and structures that make up the dimension of axis are formalised in SFL using system networks. A simplified MOOD network is shown in Figure 1.6.
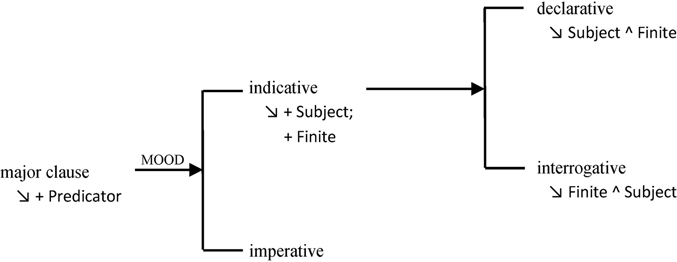
Figure 1.6
Simplified system network of MOOD, adapted from Halliday and Matthiessen (2014)
Read from left to right, this network indicates that the system concerns major clauses (major clause are described as the entry condition for the system). The downward slanting arrow ↘ indicates a realisation statement giving the structure for major clauses. In this case, a major clause is realised by the insertion of a Predicator (indicated by +). To the right, MOOD gives the name of the system (systems are shown in small caps) and the large square bracket indicate that if a major clause is chosen, then either indicative or imperative must be chosen. These options are known as features and are written entirely in lower case. If indicative is chosen, then a Subject and a Finite is inserted, and the choice of declarative or interrogative arises. If declarative, then the Subject is sequenced before the Finite; if interrogative, then the Finite comes before the Subject. Systems further to the right are described as being more ‘delicate’ than those to the left.
Figure 1.6 illustrates a series of ‘either/or’ choices shown by square brackets. In addition to these, system networks can also show simultaneous systems (both/and choices) through curly brackets. This allows multiple systems to occur at the same time and is the mechanism through which SFL models multiple strands of independent variation. Figure 1.7 illustrates a simplified account of the three simultaneous systems of MOOD, TRANSITIVITY and THEME.
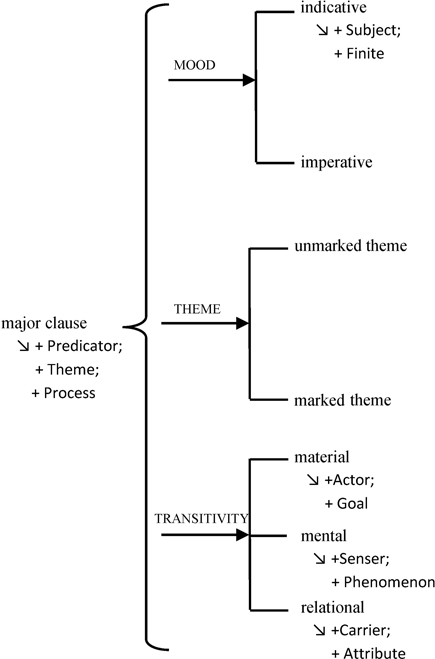
Figure 1.7
Simultaneous systems of MOOD, TRANSITIVITY and THEME
This network says that for all major clauses, a choice must be made from each of the systems of MOOD, THEME and TRANSITIVITY and that choices from each system are independent of choices from every other system. That is, for any feature in the TRANSITIVITY system (mental, material or relational), any feature from the THEME or MOOD system can be chosen. The structures that arise from the choices in these systems are then mapped onto each other.
Finally, systems may be recursive, whereby a choice in one feature can be repeated indefinitely. Figure 1.8 exemplifies this for a simplified network of English clause complexing.
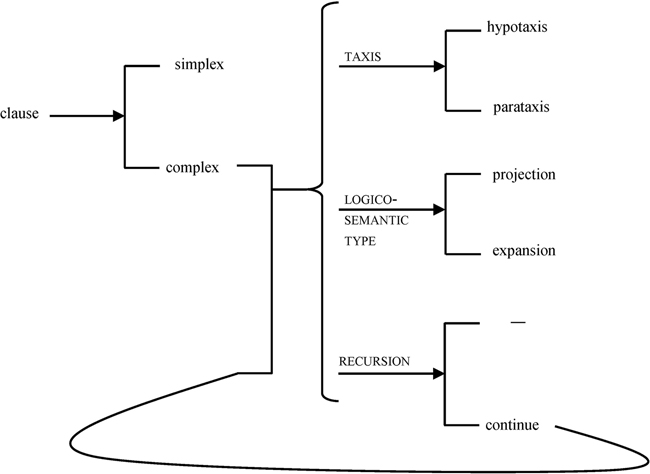
Figure 1.8
Recursive system, adapted from Halliday and Matthiessen (2014)
This system indicates that if the feature complex is chosen, a choice must be made from each of the systems of TAXIS, LOGICO-SEMANTIC TYPE and RECURSION. Within the RECURSION system the wiring emanating from the feature continue indicates that if this feature is chosen another choice from each of these systems is needed. This offers an indefinitely recursive loop with any number of choices available until the feature ‘—’ (glossed as stop) is chosen. As this system is indefinitely recursive, it is realised by an indefinitely iterative structure—a univariate structure. As mentioned earlier, recursive systems such as this and the univariate structures that realise them are associated with the logical metafunction. We will see in Chapters 3, 4 and 5 that recursive systems permeate the description of mathematics, and so form an important component of this book. The full set of conventions for system networks is outlined in Appendix A.
The systems and structures constituting the dimension of axis play a pivotal role in the architecture of Systemic Functional descriptions. Indeed Martin (2013) argues that the paradigmatic and syntagmatic axes are the theoretical primitives of Systemic Functional theory from which metafunction, rank and strata can be derived. This is a powerful claim and will be explored in more detail in relation to descriptive issues in the broader field of Systemic Functional Semiotics. First, however, the next chapter will consider the role of language in physics and its role in building physics knowledge. We will see language enables physics to reorganise our everyday experience into uncommon-sense knowledge and that this allows physics to build large swathes of interconnected meanings.
Bernstein, B. (1999) Vertical and Horizontal Discourse: An Essay. British Journal of Sociology of Education. 20:2. 157–173.
Biglan, A. (1973) The Characteristics of Subject Matter in Different Academic Areas. Journal of Applied Psychology. 57:3. 195–203.
diSessa, A. A. (2006) A History of Conceptual Change Research: Threads and Fault Lines. In K. Sawyer (ed.) Cambridge Handbook of the Learning Sciences. Cambridge: Cambridge University Press. 265–281.
Georgiou, H., Maton, K. and Sharma, M. (2014) Recovering Knowledge for Science Education Research: Exploring the “Icarus Effect” in Student Work. Canadian Journal of Science, Mathematics and Technology Education. 14:3. 252–268.
Halliday, M. A. K. (1961) Categories of the Theory of Grammar. Word. 17. 241–292.
Halliday, M. A. K. (1963) The Tones of English. Archivum Linguisticum. 15:1. 1–28.
Halliday, M. A. K. (1965) Types of Structure. In J. R. Martin and Y. J. Doran (eds.) (2015) Grammatics. Volume 1 in Critical Concepts in Linguistics: Systemic Functional Linguistics. London: Routledge. 227–241.
Halliday, M. A. K. (1969) Options and Functions in the English Clause. Brno Studies in English. 8. 81–88.
Halliday, M. A. K. (1970) Language Structure and Language Function. In J. Lyons (ed.) New Horizons in Linguistics. Hammondsworth: Penguin. 140–165.
Halliday, M. A. K. (1973) Explorations in the Functions of Language. London: Edward Arnold.
Halliday, M. A. K. (1978) An Interpretation of the Functional Relationship between Language and Social Structure. In Language as Social Semiotic. London: Edward Arnold. 183–192.
Halliday, M. A. K. (1979) Modes of Meaning and Modes of Expression: Types of Grammatical Structure, and Their Determination by Different Semantic Functions. In D. J. Allerton, E. Carney and D. Hollcroft (eds.) Function in Context in Linguistic Analysis: A Festschrift for William Haas. London: Cambridge University Press. 57–79.
Halliday, M. A. K. (1994) Introduction to Functional Grammar. 2nd ed. London: Edward Arnold.
Halliday, M. A. K. and Greaves, W. S. (2008) Intonation in the Grammar of English. London: Equinox.
Halliday, M. A. K. and Matthiessen, C. M. I. M. (2014) Halliday’s Introduction to Functional Grammar. London: Routledge.
Halliday, M. A. K. and Martin, J. R. (1993) Writing Science: Literacy and Discursive Power. London: Falmer.
Hjelmslev, L. (1943) Prolegomena to a Theory of Language. Translated by F. J. Whitfield (1961). Madison: University of Wisconsin Press.
Hockett, C. F. (1961) Linguistic Elements and Their Relations. Language. 37:1. 29–53.
Hood, S. (2010) Appraising Research: Evaluation in Academic Writing. London: Palgrave Macmillan.
Huddleston, R. D. (1965) Rank and Depth. Language. 41:4. 574–586.
Huddleston, R. D., Hudson, R. A., Winter, E. O. and Henrici, A. (1968) Sentence and Clause in Scientific English. Report on The Linguistics Properties of Scientific English. Communication Research Centre, Department of General Linguistics, University College London.
Kolb, D. A. (1981) Learning Styles and Disciplinary Differences. In A. Chickering (ed.) The Modern American College. San Francisco: Jossey-Bass. 232–255.
Kress, G. and van Leeuwen, T. (1990) Reading Images. Geelong: Deakin University Press.
Lemke, J. L. (1985) Ideology, Intertextuality, and the Notion of Register. In J. D. Benson and W. S. Greaves (eds.) Systemic Perspectives on Discourse: Volume 1. Norwood, NJ: Ablex. 275–294.
Lemke, J. L. (1990) Talking Science: Language, Learning and Values. Norwood, NJ: Ablex.
Lemke, J. L. (1998) Multiplying Meaning: Visual and Verbal Semiotics in Scientific Text. In J. R. Martin and R. Veel (1998). 87–113.
Martin, J. R. (1991) Intrinsic Functionality: Implications for Contextual Theory. Social Semiotics. 1:1. 99–162.
Martin, J. R. (1992) English Text: System and Structure. Amsterdam: John Benjamins.
Martin, J. R. (1999) Modelling Context: A Crooked Path of Progress in Contextual Linguistics. In M. Ghadessy (ed.) Text and Context in Functional Linguistics. Amsterdam: John Benjamins. 25–61.
Martin, J. R. (2008) What Kind of Structure: Interpersonal Meaning and Prosodic Realisation Across Strata. Word. 59:2. 113–143.
Martin, J. R. (2011) Bridging Troubled Waters: Interdisciplinary and What Makes it Stick. In F. Christie and K. Maton (eds.) Disciplinarity: Linguistic and Sociological Perspectives. London: Continuum. 35–61.
Martin, J. R. (2013) Systemic Functional Grammar: A Next Step into the Theory: Axial Relations. [Chinese translation and extensions by Wang Pin and Zhu Yongsheng]. Beijing: Higher Education Press.
Martin, J. R. and Doran, Y. J. (2015) (eds.) Language in Education. Volume V in Systemic Functional Linguistics: Critical Concepts in Linguistics. London: Routledge.
Martin, J. R. and Rose, D. (2007) Working with Discourse. 2nd ed. London: Continuum.
Martin, J. R. and Rose, D. (2008) Genre Relations: Mapping Culture. London: Equinox.
Martin, J. R. and Veel, R. (1998) (eds.) Reading Science: Critical and Functional Perspectives on Discourses of Science. London: Routledge.
Maton, K. (2014) Knowledge and Knowers: Towards a Realist Sociology of Education. London: Routledge.
Maton, K. and Muller, J. (2007) A Sociology for the Transmission of Knowledges. In F. Christie and J. R. Martin (eds.) Language, Knowledge and Pedagogy: Functional Linguistic and Sociological Perspectives. London: Continuum. 14–33.
Metropolitan East Disadvantaged Schools Program (1994) Writing a Descriptive Response: A Unit of Work for Junior Secondary Visual Arts. Sydney: Metropolitan East Disadvantaged Schools Program.
Metropolitan East Disadvantaged Schools Program (1995a) Summary of Secondary School Text Types in Science. Sydney: Metropolitan East Disadvantaged Schools Program.
Metropolitan East Disadvantaged Schools Program (1995b) Literacy in Visual Arts: A Unit of Work Focussing on Reading and Writing Descriptions. Sydney: Metropolitan East Disadvantaged Schools Program.
O’Halloran, K. (1996) The Discourses of Secondary School Mathematics. PhD Thesis. Department of Communication Studies. Murdoch University, Western Australia.
O’Halloran, K. (2005) Mathematical Discourse: Language, Symbolism and Visual Images. London: Continuum.
O’Halloran, K. (2007) Mathematical and Scientific Forms of Knowledge: A Systemic Functional Multimodal Grammatical Approach. In F. Christie and J. R. Martin (eds.) Language, Knowledge and Pedagogy: Functional Linguistic and Sociological Perspectives. London: Continuum. 205–238.
O’Toole, M. (1994) The Language of Displayed Visual Art. Plainsboro, NJ: Associated University Presses.
Parodi, G. (2012) University Genres and Multisemiotic Features: Accessing Specialized Knowledge through Disciplinarity. Fórum Linguístico. 9:4. 259–282.
Rose, D. and Martin, J. R. (2012) Learning to Write, Reading to Learn: Genre, Knowledge and Pedagogy in the Sydney School. London: Equinox.
Veel, R. (2008) The Write It Right Project: Linguistic Modelling of Secondary School and the Workplace. In R. Whittaker, M. O’Donnell and A. McCabe (eds.), Language and Literacy: Functional Approaches. London: Continuum. 66–92.
Young, H. D. and Freedman, R. A. (2012) Sears and Zemansky’s University Physics with Modern Physics. 13th ed. San Francisco: Pearson.







