1
Overview of Programming and Problem Solving
KNOWLEDGE GOALS
 To understand what a computer program is.
To understand what a computer program is.
 To understand what an algorithm is.
To understand what an algorithm is.
 To learn what a high-level programming language is.
To learn what a high-level programming language is.
 To understand the compilation and execution processes.
To understand the compilation and execution processes.
 To learn the history of the C++ language.
To learn the history of the C++ language.
 To learn what the major components of a computer are and how they work together.
To learn what the major components of a computer are and how they work together.
 To learn about some of the basic ethical issues confronting computing professionals.
To learn about some of the basic ethical issues confronting computing professionals.
SKILL GOALS
To be able to:
 List the basic stages involved in writing a computer program.
List the basic stages involved in writing a computer program.
 Describe what a compiler is and what it does.
Describe what a compiler is and what it does.
 Distinguish between hardware and software.
Distinguish between hardware and software.
 Choose an appropriate problem-solving method for developing an algorithmic solution to a problem.
Choose an appropriate problem-solving method for developing an algorithmic solution to a problem.
1.1 Overview of Programming
Content removed due to copyright restrictions
What a brief definition for something that has, in just a few decades, changed the way of life in industrialized societies! Computers touch all areas of our lives: paying bills, driving cars, using the telephone, shopping. In fact, it would be easier to list those areas of our lives that are not affected by computers.
It is sad that a device that does so much good is so often maligned and feared. How many times have you heard someone say, “I’m sorry, our computer fouled things up” or “I just don’t understand computers; they’re too complicated for me”? The very fact that you are reading this book, however, means that you are ready to set aside prejudice and learn about computers. But be forewarned: This book is not just about computers in the abstract. This is a text to teach you how to program computers.
What Is Programming?
Much of human behavior and thought is characterized by logical sequences. Since infancy, you have been learning how to act, how to do things. You have also learned to expect certain behavior from other people.
A lot of what you do every day, you do automatically. Fortunately, it is not necessary for you to consciously think of every step involved in a process as simple as turning a page by hand:
1. Lift hand.
2. Move hand to right side of book.
3. Grasp top-right corner of page.
4. Move hand from right to left until page is positioned so that you can read what is on the other side.
5. Let go of page.
Think how many neurons must fire and how many muscles must respond, all in a certain order or sequence, to move your arm and hand. Yet you do it unconsciously.
Much of what you do unconsciously you once had to learn. Watch how a baby concentrates on putting one foot before the other while learning to walk. Then watch a group of three-year-olds playing tag.
On a broader scale, mathematics never could have been developed without logical sequences of steps for solving problems and proving theorems. Mass production never would have worked without operations taking place in a certain order. Our whole civilization is based on the order of things and actions.
We create order, both consciously and unconsciously, through a process we call programming. This book is concerned with the programming of one of our tools, the computer.
Programming Planning or scheduling the performance of a task or an event.
Computer A programmable device that can store, retrieve, and process data.
Just as a concert program lists the order in which the players perform pieces, so a computer program lists the sequence of steps the computer performs. From now on, when we use the words programming and program, we mean computer programming and computer program.
Computer program A sequence of instructions to be performed by a computer.
Computer programming The process of planning a sequence of steps for a computer to follow.
The computer allows us to do tasks more efficiently, quickly, and accurately than we could by hand—if we could do them by hand at all. To use this powerful tool, we must specify what we want done and the order in which we want it done. We do this through programming.
How Do We Write a Program?
A computer is not intelligent. It cannot analyze a problem and come up with a solution. Instead, a human (the programmer) must analyze the problem, develop a sequence of instructions for solving the problem, and then communicate it to the computer. What’s the advantage of using a computer if it can’t solve problems? Once we have written the solution as a sequence of instructions for the computer, the computer can repeat the solution very quickly and consistently, again and again. The computer frees people from repetitive and boring tasks.
To write a sequence of instructions for a computer to follow, we must go through a two-phase process: problem solving and implementation (see FIGURE 1.1).
Problem-Solving Phase
1. Analysis and specification. Understand (define) the problem and what the solution must do.
2. General solution (algorithm). Develop a logical sequence of steps that solves the problem.
3. Verify. Follow the steps exactly to see if the solution really does solve the problem.
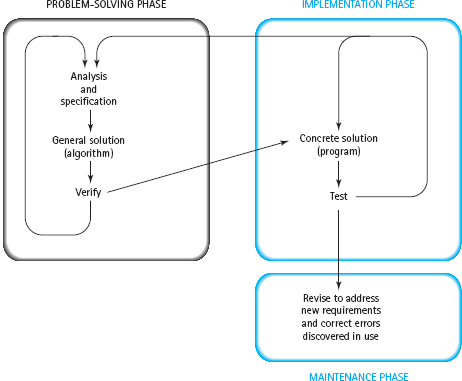
FIGURE 1.1 Programming Process
Implementation Phase
1. Concrete solution (program). Translate the algorithm into a programming language.
2. Test. Have the computer follow the instructions, then manually check the results. If you find errors, analyze the program and the algorithm to determine the source of the errors, and then make corrections.
Once a program has been written, it enters a third phase: maintenance.
Maintenance Phase
1. Use. Use the program.
2. Maintain. Modify the program to meet changing requirements or to correct any errors that show up in using it.
This series of stages is known as the waterfall model of software development. Other development models exist that are used in different situations. For example, the spiral model involves developing an initial specification of the problem, programming a portion of the solution, having the client evaluate the result, and then revising the specification and repeating the process until the client is satisfied. The spiral model is appropriate when a problem is not well defined initially or when aspects of the problem are changing during the development. Solutions to scientific or engineering research problems are often developed using the spiral model. We use the waterfall model throughout this book because it is well suited for solving the kinds of clearly defined problems that you’ll encounter in an introductory programming course.
What Is an Algorithm?
The programmer begins the programming process by analyzing the problem and developing a general solution called an algorithm. Understanding and analyzing a problem take up much more time than Figure 1.1 implies. These steps are the heart of the programming process.
Algorithm A step-by-step procedure for solving a problem in a finite amount of time.
If our definitions of a computer program and an algorithm look similar, it is because all programs are algorithms. A program is simply an algorithm that has been written for a computer.
An algorithm is a verbal or written description of a logical sequence of actions. We use algorithms every day. Recipes, instructions, and directions are all examples of algorithms that are not programs.
When you start your car, you follow a step-by-step procedure. The algorithm might look something like this:
1. Insert the key.
2. Depress the brake pedal.
3. Make sure the transmission is in Park (or Neutral).
4. Turn the key to the start position.
5. If the engine starts within six seconds, release the key to the ignition position.
6. If the engine doesn’t start in six seconds, release the key and gas pedal, wait ten seconds, and repeat Steps 3 through 6, but not more than five times.
7. If the car doesn’t start, call the garage.
Without the phrase “but not more than five times” in Step 6, you could be trying to start the car forever. Why? Because if something is wrong with the car, repeating Steps 3 through 6 over and over again will not start it. This kind of never-ending situation is called an infinite loop. If we leave the phrase “but not more than five times” out of Step 6, the procedure does not fit our definition of an algorithm. An algorithm must terminate in a finite amount of time for all possible conditions.
Suppose a programmer needs an algorithm to determine an employee’s weekly wages. The algorithm reflects what would be done by hand:
1. Look up the employee’s pay rate.
2. Determine the number of hours worked during the week.
3. If the number of hours worked is less than or equal to 40, multiply the number of hours by the pay rate to calculate regular wages.
4. If the number of hours worked is greater than 40, multiply 40 by the pay rate to calculate regular wages, and then multiply the difference between the number of hours worked and 40 by 1.5 times the pay rate to calculate overtime wages.
5. Add the regular wages to the overtime wages (if any) to determine total wages for the week.
The steps the computer follows are often the same steps you would use to do the calculations by hand.
After developing a general solution, the programmer tests the algorithm, walking through each step mentally or manually. If the algorithm doesn’t work, the programmer repeats the problem-solving process, analyzing the problem again and coming up with another algorithm. Often the second algorithm is just a variation of the first. When the programmer is satisfied with the algorithm, he or she translates it into a programming language. We use the C++ programming language in this book.
Programming language A set of rules, symbols, and special words used to construct a computer program.
What Is a Programming Language?
A programming language is a simplified form of English (with math symbols) that adheres to a strict set of grammatical rules. English is far too complicated a language for today’s computers to follow. Programming languages, because they limit vocabulary and grammar, are much simpler.
Although a programming language is simple in form, it is not always easy to use. Try giving someone directions to the nearest airport using a vocabulary of no more than 45 words, and you’ll begin to see the problem. Programming forces you to write very simple, exact instructions.
Translating an algorithm into a programming language is called coding the algorithm. The product of that translation—the program—is tested by running (executing) it on the computer. If the program fails to produce the desired results, the programmer must debug it—that is, determine what is wrong and then modify the program, or even the algorithm, to fix it. The combination of coding and testing an algorithm is called implementation.
There is no single way to implement an algorithm. For example, an algorithm can be translated into more than one programming language, and each translation produces a different implementation. Even when two people translate the same algorithm into the same programming language, they are likely to come up with different implementations (see FIGURE 1.2). Why? Because every programming language allows the programmer some flexibility in how an algorithm is translated. Given this flexibility, people adopt their own styles in writing programs, just as they do in writing short stories or essays. Once you have some programming experience, you will develop a style of your own. Throughout this book, we offer tips on good programming style.
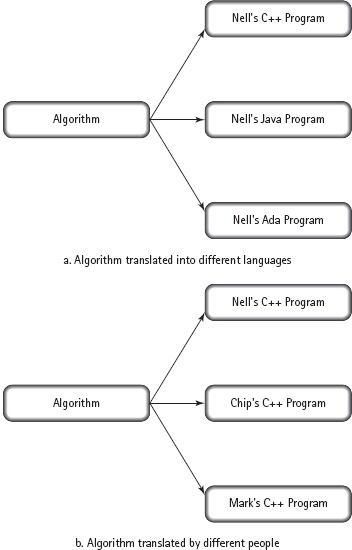
FIGURE 1.2 Differences in Implementations
Some people try to speed up the programming process by going directly from the problem definition to coding the program (see FIGURE 1.3). A shortcut here is very tempting and at first seems to save a lot of time. However, for many reasons that will become obvious to you as you read this book, this kind of shortcut actually takes more time and effort. Developing a general solution before you write a program helps you manage the problem, keep your thoughts straight, and avoid mistakes. If you don’t take the time at the beginning to think out and polish your algorithm, you’ll spend a lot of extra time debugging and revising your program. So think first and code later! The sooner you start coding, the longer it takes to write a program that works.
Once a program has been put into use, it may become necessary to modify it. Modification may involve fixing an error that is discovered during the use of the program or changing the program in response to changes in the user’s requirements. Each time the program is modified, the problem-solving and implementation phases must be repeated for those aspects of the program that change. This phase of the programming process, which is known as maintenance, actually accounts for the majority of the effort expended on most programs. For example, a program that is implemented in a few months may need to be maintained over a period of many years. Thus it is a cost-effective investment of time to develop the initial problem solution and program implementation carefully. Together, the problem-solving, implementation, and maintenance phases constitute the program’s life cycle.
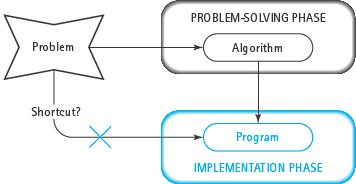
FIGURE 1.3 Programming Shortcut?
In addition to solving the problem, implementing the algorithm, and maintaining the program, documentation is an important part of the programming process. Documentation includes written explanations of the problem being solved and the organization of the solution, comments embedded within the program itself, and user manuals that describe how to use the program. Most programs are worked on by many different people over a long period of time. Each of those people must be able to read and understand your code.
Documentation The written text and comments that make a program easier for others to understand, use, and modify.
After you write a program, you must give the computer the information or data necessary to solve the problem. Information is any knowledge that can be communicated, including abstract ideas and concepts such as “the earth is round.” Data is information in a form the computer can use—for example, the numbers and letters making up the formulas that relate the earth’s radius to its volume and surface area. Data can represent many kinds of information, such as sounds, images, video, rocket telemetry, automobile engine functions, weather, global climate, interactions of atomic particles, drug effects on viruses, and so forth. Part of the programming process involves deciding how to represent the information in a problem as data.
Information Any knowledge that can be communicated.
Data Information in a form a computer can use.
THEORETICAL FOUNDATIONS
Binary Representation of Data

In a computer, data are represented electronically by pulses of electricity. Electric circuits, in their simplest form, are either on or off. A circuit that is on represents the number 1; a circuit that is off represents the number 0. Any kind of data can be represented by combinations of enough 1s and 0s. We simply have to choose which combination represents each piece of data we are using. For example, we could arbitrarily choose the pattern 1101000110 to represent the name “C++.”
Data represented by 1s and 0s are in binary form. The binary, or base-2, number system uses only 1s and 0s to represent numbers. (The decimal, or base-10, number system uses the digits 0 through 9.) The word bit (short for binary digit) refers to a single 1 or 0. Thus the pattern 1101000110 has ten bits. A binary number with three bits can represent 23, or eight, different patterns. The eight patterns are shown here, together with some examples of base-2 arithmetic:

A ten-digit binary number can represent 210 (1024) distinct patterns. Thus you can use your fingers to count in binary from 0 to 1023! A byte is a group of eight bits; it can represent 28 (256) patterns. Inside the computer, each character (such as the letter A, the letter g, the digit 7, a question mark, or a blank) is usually represented by either one or two bytes.2 For example, in one scheme 01001101 represents M and 01101101 represents m (look closely—the third bit from the left is the only difference). Groups of 16, 32, and 64 bits are generally referred to as words (the terms “short word” and “long word” sometimes are used to refer to 16-bit and 64-bit groups, respectively).
The process of assigning bit patterns to pieces of data is called coding—the same name we give to the process of translating an algorithm into a programming language. The names are the same because the first computers recognized only one language, which was binary in form. Thus, in the early days of computers, programming meant translating both data and algorithms into patterns of 1s and 0s. The resulting programs looked like messages in a secret code that were being passed from the programmer to the computer. It was very difficult for one programmer to understand a program written by another programmer. In fact, after leaving a program alone for a while, many programmers could not even understand their own programs!
The patterns of bits that represent data vary from one family of computers to another. Even on the same computer, different programming languages may use different binary representations for the same data. A single programming language may even use the same pattern of bits to represent different things in different contexts. (People do this, too: The four letters that form the word tack have different meanings depending on whether you are talking about upholstery, sailing, sewing, paint, or horseback riding.) The point is that patterns of bits by themselves are meaningless. Rather, it is the way in which the patterns are used that gives them their meaning. That’s why we combine data with operations to form meaningful objects.
Fortunately, we no longer have to work with binary coding schemes. Today, the process of coding is usually just a matter of writing down the data in letters, numbers, and symbols. The computer automatically converts these letters, numbers, and symbols into binary form. Still, as you work with computers, you will continually run into numbers that are related to powers of 2—numbers such as 256, 32,768, and 65,536. They are reminders that the binary number system is lurking somewhere in the background.
QUICK CHECK

1.1.1 What do we call a sequence of instructions that is executed by a computer? (p. 2)
1.1.2 Is a computer capable of analyzing a problem to come up with a solution? (p. 3)
1.1.3 How does an algorithm differ from a computer program? (p. 4)
1.1.4 Describe the three important phases of the waterfall model we must go through to write a sequence of instructions for a computer. (p. 3–4)
1.1.5 How does a programming language differ from a human language? (p. 5)
Answers to Quick Check questions are given at the end of each chapter.
1.2 How Does a Computer Run a Program?
In the computer, all data, whatever its form, is stored and used in binary codes—that is, as strings of 1s and 0s. Instructions and data are stored together in the computer’s memory using these binary codes. If you were to look at the binary codes representing instructions and data in memory, you could not tell the difference between them; they are distinguished only by the manner in which the computer uses them. This scheme makes it possible for the computer to process its own instructions as a form of data.
When computers were first developed, the only programming language available was the primitive instruction set built into each machine, the machine language, or machine code.
Machine language The language, made up of binary-coded instructions, that is used directly by the computer.
Even though most computers perform the same kinds of operations, their designers choose different sets of binary codes for each instruction. Thus the machine code for one computer is not the same as the machine code for another computer.
When programmers used machine language for programming, they had to enter the binary codes for the various instructions, a tedious process that was prone to error. Moreover, their programs were difficult to read and modify. In time, assembly languages were developed to make the programmer’s job easier.
Assembly language A low-level programming language in which a mnemonic is used to represent each of the machine language instructions for a particular computer.
Instructions in an assembly language are in an easy-to-remember form called a mnemonic (pronounced nee-MAHN-ik). Typical instructions for addition and subtraction might look like this:

Although assembly language is easier for humans to work with, the computer cannot directly execute the instructions. One of the fundamental discoveries in computer science is that, because a computer can process its own instructions as a form of data, it is possible to write a program to translate the assembly language instructions into machine code.
Such a program is called an assembler. The name comes from the fact that much of what an assembler does is to look up the pieces of an instruction in a table to find the corresponding binary code (such as ADD = 1001, R1 = 001, R3 = 011, R5 = 101), and then assemble these binary coded pieces of the instruction into a complete machine language instruction (1001 001 011 101). The assembler also puts the instructions together in the specified sequence to create a complete program.
Assembler A program that translates an assembly language program into machine code.
Assembly language is a step in the right direction, but it still forces programmers to think in terms of individual machine instructions. Eventually, computer scientists developed high-level programming languages. These languages are easier to use than assembly languages or machine code because they are closer to English and other natural languages (see FIGURE 1.4).
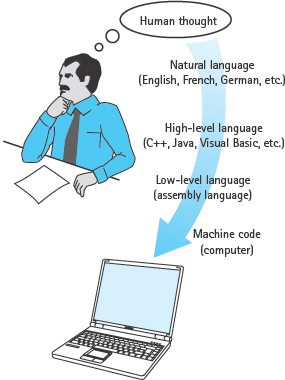
FIGURE 1.4 Levels of Abstraction
A program called a compiler translates programs written in certain high-level languages (C++, Java, Visual Basic, and Ada, for example) into machine language. If you write a program in a high-level language, you can run it on any computer that has the appropriate compiler. This is possible because most high-level languages are standardized, which means that an official description of the language exists.
Compiler A program that translates a high-level language into machine code.
A program in a high-level language is called a source program. To the compiler, a source program is just input data. It translates the source program into a machine language program called an object program (see FIGURE 1.5). If there are errors in the program, the compiler instead generates one or more error messages indicating the nature and location of the errors.
Source program A program written in a high-level programming language.
Object program The machine language version of a source program.
One benefit of using standardized high-level languages is that they allow you to write portable (or machine-independent) code. As Figure 1.5 emphasizes, a single C++ program can be used on different machines, whereas a program written in assembly language or machine language is not portable from one computer to another. Because each computer has its own machine language, a machine language program written for computer A will not run on computer B.
It is important to understand that compilation and execution are two distinct processes. During compilation, the computer runs the compiler program. During execution, the object program is loaded into the computer’s memory unit, replacing the compiler program. The computer then runs the object program, doing whatever the program instructs it to do (see FIGURE 1.6).
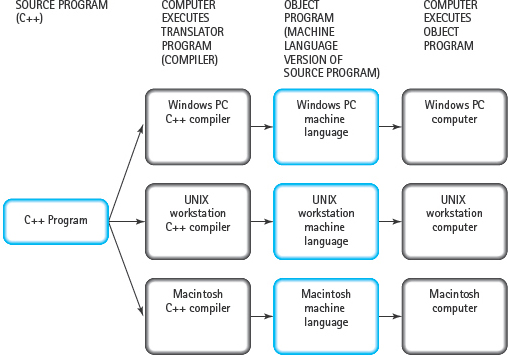
FIGURE 1.5 High-Level Programming Languages Allow Programs to Be Compiled on Different Systems
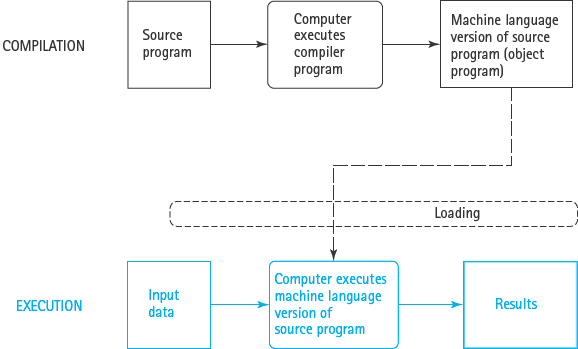
FIGURE 1.6 Compilation and Execution
BACKGROUND INFORMATION
Compilation Versus Interpretation

Some programming languages—LISP, Prolog, and many versions of BASIC, for example—are translated by an interpreter rather than by a compiler. An interpreter translates and executes each instruction in the source program, one instruction at a time. In contrast, a compiler translates the entire source program into machine language, after which execution of the object program takes place. The difference between compilation and interpretation is like the difference between translating a book of poetry into another language (say, translating Goethe’s Faust from German to English) and having a human interpreter provide a live interpretation of a dramatic reading of some poems.
The Java language uses both a compiler and an interpreter. First, a Java program is compiled not into a particular computer’s machine language, but rather into an intermediate code called bytecode. Next, a program called the Java Virtual Machine (JVM) takes the bytecode program and interprets it (that is, translates a bytecode instruction into machine language and executes it, translates the next instruction and executes it, and so on). Thus, a Java program compiled into bytecode is portable to many different computers, as long as each computer has its own specific JVM that can translate bytecode into the computer’s machine language.
What Kinds of Instructions Can Be Written in a Programming Language?
The instructions in a programming language reflect the operations a computer can perform:
 A computer can transfer data from one place to another.
A computer can transfer data from one place to another.
 A computer can input data from an input device (a keyboard or mouse, for example) and output data to an output device (a screen, for example).
A computer can input data from an input device (a keyboard or mouse, for example) and output data to an output device (a screen, for example).
 A computer can store data into and retrieve data from its memory and secondary storage (parts of a computer that we discuss in the next section).
A computer can store data into and retrieve data from its memory and secondary storage (parts of a computer that we discuss in the next section).
 A computer can compare two data values for equality or inequality.
A computer can compare two data values for equality or inequality.
 B computer can perform arithmetic operations (addition and subtraction, for example) very quickly.
B computer can perform arithmetic operations (addition and subtraction, for example) very quickly.
Programming languages require that we use certain control structures to express algorithms as programs. There are four basic ways of structuring statements (instructions) in most programming languages: sequentially, conditionally, repetitively, and with subprograms (see FIGURE 1.7). A sequence is a series of statements that are executed one after another. Selection, the conditional control structure, executes different statements depending on certain conditions. The repetitive control structure, called a loop, repeats statements while certain conditions are met. The subprogram allows us to structure a program by breaking it into smaller units. Each of these ways of structuring statements controls the order in which the computer executes the statements, which is why they are called control structures.
Imagine you’re driving a car. Going down a straight stretch of road is like following a sequence of instructions. When you come to a fork in the road, you must decide which way to go and then take one or the other branch of the fork. This is what the computer does when it encounters a selection control structure (also called a branch) in a program. Sometimes you have to go around the block several times to find a place to park. The computer does the same sort of thing when it encounters a loop in a program.
A subprogram is a process that consists of multiple steps. Every day, for example, you follow a procedure to get from home to work. It makes sense, then, for someone to give you directions to a meeting by saying, “Go to the office, then go four blocks west” without specifying all the steps you have to take to get to the office. Subprograms allow us to write parts of our programs separately and then assemble them into final form. They can greatly simplify the task of writing large programs.
What Is Software Maintenance?
In the life cycle of a program, the maintenance phase accounts for the majority of a typical program’s existence. As we said earlier, programs are initially written in a fairly short time span, and then are used for many years after. The original designers develop the program to meet a set of specifications, and they cannot possibly foresee all the ways that the program will be used in the future. Decisions that were made in the initial implementation may prove to be inadequate to support some future use, and a new team of programmers may then be called in to modify the program. After going through many modifications, the code may become so complicated that it is difficult to identify the purpose of some of the original instructions.
For example, at the turn of the millennium, the software industry faced a major maintenance effort known collectively as the “Y2K Problem.” For much of the preceding 50 years, programmers had been encoding dates with a two-digit integer representing the year, as shown here:
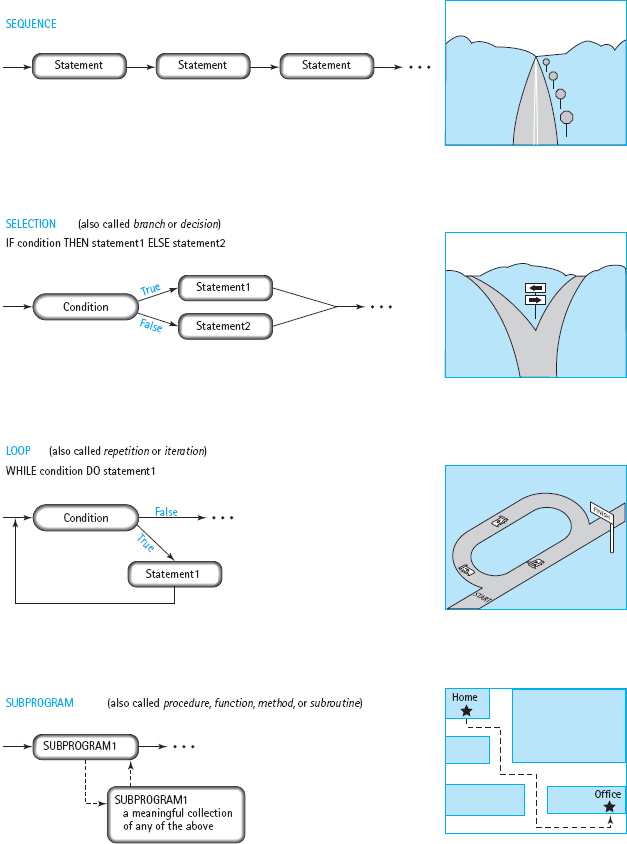
FIGURE 1.7 Basic Control Structures of Programming Languages

There was no way for these programs to make the transition to the new millennium and be able to distinguish a year such as 2005 from 1905. There were dire predictions for the failure of much of our modern infrastructure, such as the shutdown of the electric power grid, telecommunication networks, and banking systems.
In the end, the software industry spent billions of dollars finding all of the places where programs used a two-digit year and changing the code to use four digits. Some of this code dated back to the 1960s, and the original programmers were not available to help with the conversion. A new generation of programmers had to read and understand the programs well enough to make the necessary changes.
While the rest of the world was celebrating New Year’s Eve in 1999, many of these programmers were sitting at their computers, watching nervously as the date ticked over to 2000, just in case they had missed something. A few problems were encountered, but the vast majority of computers made the transition without skipping a beat.
In retrospect, it is easy to find fault with the decisions of the original programmers to use a two-digit date. But at the time, computers had very small memories (in the 1960s, a large computer had only 65,000 bytes of main memory), and saving even a byte or two in representing a date could make the difference between a working program and one that wouldn’t fit in memory. None of those programmers expected their code to be used for 40 years. It is impossible to know which programming decisions are being made today that will turn out to be problematic in the future.
Successive attempts to extend the capabilities of a program will often produce errors because programmers fail to comprehend the ways that earlier changes to the program will interact with new changes. In some cases, testing fails to reveal those errors before the modified program is released, and it is the user who discovers the error. Then, fixing the bugs becomes a new maintenance task and the corrections are usually done hastily because users are clamoring for their software to work. The result is code that is even harder to understand. In time, the software grows so complex that attempts to fix errors frequently produce new errors. In some cases the only solution is to start over, rewriting much of the software anew with a clean design.
SOFTWARE MAINTENANCE CASE STUDY: An Introduction to Software Maintenance
The preceding discussion is intended to illustrate the importance of developing skills not just in writing new code, but also in working with existing code. These Software Maintenance Case Study sections walk you through the process of typical maintenance tasks. Unlike the Problem-Solving Case Study sections, where we begin with a problem, solve it, and then code a program, here we begin with a program and see how to understand what it does before making some change.
Let’s start with something extremely simple, just to get a sense of what we’ll be doing in future Software Maintenance Case Study sections. We keep this example so simple that you don’t even have to know anything about C++ to follow what’s happening. But in following our steps through this process, you’ll get a sense of what’s involved in working with programs.
MAINTENANCE TASK: Enter the “Hello World” application program, changing it to output “Hello Universe” instead.
EXISTING CODE
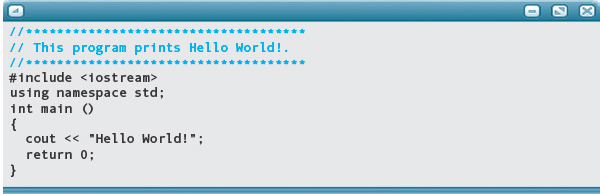
DISCUSSION: The classic first application that is written by many beginners is generically known as “Hello World.” Its sole purpose is to print out a greeting from the computer to the programmer, and then quit. There are many variations of the message, but the traditional one is “Hello World!” Here, we are being asked to change the existing message to “Hello Universe!”
Looking at this code, you can immediately see the message, enclosed in quotes. Your first temptation would be to just change the word “World” to “Universe”. (Even without knowing any C++, you’re already programming!) In a simple case like this, that strategy may be adequate; with a larger application, however, such an approach could result in the creation of more problems. With any maintenance effort, we must first observe and record the current behavior of the application. If it isn’t working initially, you may think that your changes are the source of a preexisting problem and spend many hours in a futile attempt to fix the problem by correcting your changes.
Thus the first step in this maintenance task is to enter the application exactly as it is written and run it to ensure that it works. Unless you’ve written programs before, it is hard to appreciate how precisely you must type C++ code. Every letter, every capitalization, every punctuation mark is significant. There are exceptions, which we’ll see later, but for now, it is good practice to enter this application exactly as it appears here. For example, can you spot the error in the following version of the code that fails to run? All you have to do is compare it, letter by letter, with the preceding version, to find the difference.3
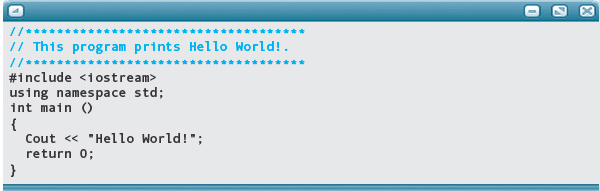
Once we are sure that the program works as claimed, we can change it with the knowledge that any new problems are associated with our modifications.
Entering an application involves typing it into the computer with an editor, which is just a program that lets us record our typing in a file. A word processor is an example of an editor. Most programming systems use a specialized code editor that has features to help us enter programs. For example, a code editor will indent the lines of an application automatically in a pattern similar to what is shown in the preceding example, and it may color-code certain elements of the program to help us locate them more easily.
Depending on the programming system that you are using, you may need to begin by creating a new “project,” which is the system’s way of organizing the information it keeps about your application. Typically, creating a new project involves selecting the “New Project” item from the File menu of the programming system, and then entering a name for the project in a dialog box that appears.
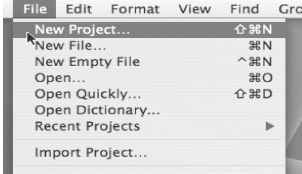
In another programming system, you may need to create a new file directory manually and tell the editor to store your code file there. There are too many different C++ programming systems for us to show them all here. You should consult the manual or help screens for your particular system to learn the specifics.
Once you type the application into the editor window, you need to save it (with another menu selection) and then run it. Here’s what happens when we try to run the erroneous version of Hello World. A red mark appears in the margin next to the line with the offending name, and the error message, “error: ‘Cout’ was not declared within this scope” appears on another screen.
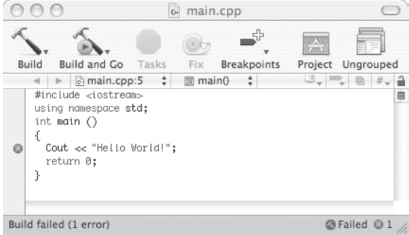
Every programmer gets these kinds of error messages at some time. Very few of us are perfect typists! Rather than being afraid of seeing such messages, we just come to expect them, and are pleasantly surprised on the rare occasions when we discover that we’ve entered a long stretch of code without typos. Usually, we enter some code, look it over carefully for mistakes, and run it to see if the computer finds any more. We then use the error messages to help us find remaining typos and fix them. Here’s what happens when the application is at last correct:

Now we know that the program works as advertised, and we can start changing it. Of the seven lines in this application, the first three and the sixth are general instructions that appear in almost all programs. The braces are a form of punctuation in a C++ application. It is the fifth line that is specific to this problem.
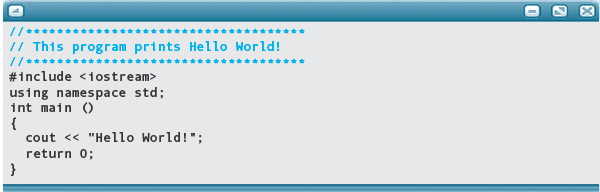
Now, let’s try making our change, substituting “Universe” for “World”—in two places. We must also change the documentation. Here’s the revised application, with “Universe” substituted for “World”.
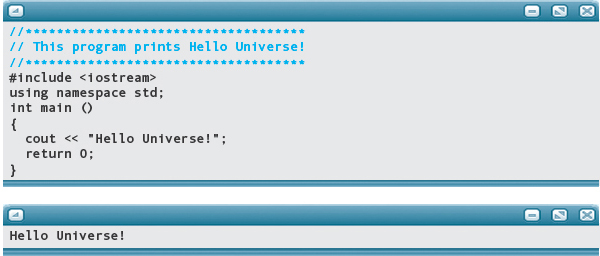
Is that it? Could it really be as simple as changing one word? Well, actually no. We edited our existing Hello World code file, and when we saved it, we overwrote the existing application, so we no longer have the original code. It’s always a good idea to keep the working version of a program separate from a new version. That way, we have a working baseline to compare against the new version. And if things really go wrong with our modifications, we have a place to go back to, and start over.
To correct this situation, we really should have created a new project, perhaps called HelloUniverse, and copied the code from our existing project into the new one. Then we can edit the fifth line, and save the change without affecting the original.
Software Maintenance Tips
1. Check that the existing code works as claimed.
2. Make changes to a copy of the existing code.
3. A maintenance task isn’t necessarily complete once the desired functionality has been achieved. Change related aspects of the program to leave clean, consistent code for the next programmer who has to do maintenance.
4. Keeping backup copies of code is also useful in developing new programs. Before making any significant change in a program that you’re developing, save a copy of the current version so that you can go back to it if necessary.
QUICK CHECK

1.2.1 What is the input and output of a compiler? (p. 11)
1.2.2 Which of the following tools translates a C++ program into machine language: editor, operating system, compiler, or assembler? (pp. 10–11)
1.2.3 What are the four basic ways of structuring statements in most programming languages? (p. 13)
1.2.4 What happens when a program encounters a selection statement during execution? (p. 13)
1.2.5 What happens when a program encounters a loop statement during execution? (p. 13)
1.2.6 What are subprograms used for? (p. 13)
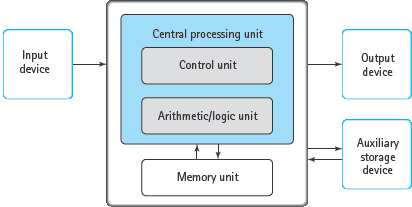
FIGURE 1.8 Basic Components of a Computer
1.3 What’s Inside the Computer?
You can learn a programming language, including how to write programs and how to run (execute) these programs, without knowing much about computers. But if you know something about the parts of a computer, you can better understand the effect of each instruction in a programming language.
Most computers have six basic components: the memory unit, the arithmetic/logic unit, the control unit, input devices, output devices, and auxiliary storage devices. FIGURE 1.8 is a stylized diagram of the basic components of a computer.
The memory unit is an ordered sequence of storage cells, each capable of holding a piece of data. Each memory cell has a distinct address to which we refer so as to store data into it or retrieve data from it. These storage cells are called memory cells, or memory locations.4 The memory unit holds data (input data or the product of computation) and instructions (programs), as shown in FIGURE 1.9.
Memory unit Internal data storage in a computer.
The part of the computer that follows instructions is called the central processing unit (CPU). The CPU usually has two components. The arithmetic/logic unit (ALU) performs arithmetic operations (addition, subtraction, multiplication, and division) and logical operations (comparing two values). The control unit controls the actions of the other components so that program instructions are executed in the correct order.
Central processing unit (CPU) The part of the computer that executes the instructions (program) stored in memory; made up of the arithmetic/logic unit and the control unit.
Arithmetic /logic unit (ALU) The component of the central processing unit that performs arithmetic and logical operations.
Control unit The component of the central processing unit that controls the actions of the other components so that instructions (the program) are executed in the correct sequence.
For us to use computers, there must be some way of getting data into and out of them. Input/output (I/O) devices accept data to be processed (input) and present data values that have been processed (output). A keyboard is a common input device. Another is a mouse, a pointing device. Trackpads and touch screens are also used as pointing devices. A liquid crystal display (LCD) screen is a common output device, as are printers. Some devices, such as a connection to a computer network, are used for both input and output.
Input/output (I/O) devices The parts of the computer that accept data to be processed (input) and present the results of that processing (output).
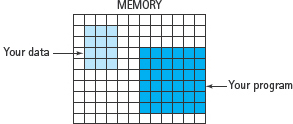
FIGURE 1.9 Memory
For the most part, computers simply move and combine data in memory. The many types of computers differ primarily in the size of their memories, the speed with which data can be recalled, the efficiency with which data can be moved or combined, and limitations on I/O devices.
When a program is executing, the computer proceeds through a series of steps, the fetch–execute cycle:
1. The control unit retrieves (fetches) the next coded instruction from memory.
2. The instruction is translated into control signals.
3. The control signals tell the appropriate unit (arithmetic/logic unit, memory, I/O device) to perform (execute) the instruction.
4. The sequence repeats from Step 1.
Computers can have a wide variety of peripheral devices attached to them. An auxiliary storage device, or secondary storage device, holds coded data for the computer until we actually want to use the data. Instead of inputting data every time, we can input it once and have the computer store it onto an auxiliary storage device. Whenever we need to use this data, we can tell the computer to transfer the data from the auxiliary storage device to its memory. An auxiliary storage device therefore serves as both an input device and an output device. Typical auxiliary storage devices are disk drives and flash memory. A disk drive uses a thin disk made out of magnetic material. A read/write head containing an electromagnet travels across the spinning disk, retrieving or recording data in the form of magnetized spots on the surface of the disk. A flash memory is a silicon chip containing specialized electronic switches that can be locked into either the on or off state, representing a binary 1 or 0, respectively. Unlike normal computer memory, flash memory retains its contents when the power is turned off. Flash is typically used to transfer data between computers, and to back up (make a copy of) the data on a disk in case the disk is ever damaged.
Peripheral device An input, output, or auxiliary storage device attached to a computer.
Auxiliary storage device A device that stores data in encoded form outside the computer’s main memory.
Other examples of peripheral devices include the following:
 Scanners, which “read” visual images on paper and convert them into binary data
Scanners, which “read” visual images on paper and convert them into binary data
 CD-ROM (compact disc–read-only memory) disks, which can be read (but not written)
CD-ROM (compact disc–read-only memory) disks, which can be read (but not written)
 CD-R (compact disc–recordable), which can be written to once only but can be read many times
CD-R (compact disc–recordable), which can be written to once only but can be read many times
 DVD-ROM (digital versatile disc–read-only memory), which has greater storage capacity than CDs, and is often used to store video
DVD-ROM (digital versatile disc–read-only memory), which has greater storage capacity than CDs, and is often used to store video
 Modems (modulator/demodulators), which convert back and forth between binary data and signals that can be sent over conventional telephone lines
Modems (modulator/demodulators), which convert back and forth between binary data and signals that can be sent over conventional telephone lines
 Audio sound cards and speakers
Audio sound cards and speakers
 Microphones and electronic musical instruments
Microphones and electronic musical instruments
 Game controllers
Game controllers
 Digital cameras
Digital cameras
Together, all of these physical components are known as hardware. The programs that allow the hardware to operate are called software. Hardware usually is fixed in design; software is easily changed. In fact, the ease with which software can be manipulated is what makes the computer such a versatile, powerful tool.
Hardware The physical components of a computer.
Software Computer programs; the set of all programs available on a computer.
In addition to the programs that we write or purchase, some programs in the computer are designed to simplify the user/computer interface, making it easier for humans to use the machine. The interface between user and computer is a set of I/O devices—for example, a keyboard, mouse, and screen—that allow the user to communicate with the computer. We work with the keyboard, mouse, and screen on our side of the interface boundary; wires attached to these devices carry the electronic pulses that the computer works with on its side of the interface boundary. At the boundary itself is a mechanism that translates information for the two sides.
User/computer interface A connecting link that translates between the computer’s internal representation of data and representations that humans are able to work with.
When we communicate directly with the computer, we are using an interactive system. Interactive systems allow direct entry of programs and data and provide immediate feedback to the user. In contrast, batch systems require that all data be entered before a program is run and provide feedback only after a program has been executed. In this text we focus on interactive systems, although in Chapter 4 we discuss file-oriented programs, which share certain similarities with batch systems.
Interactive system A system that allows direct communication between user and computer.
The set of programs that simplify the user/computer interface and improve the efficiency of processing is collectively called system software. It includes the compiler as well as the operating system and the editor (see FIGURE 1.10). The operating system manages all of the computer’s resources. It can input programs, call the compiler, execute object programs, and carry out any other system commands. The editor is an interactive program used to create and modify source programs or data.
Operating system A set of programs that manages all of the computer’s resources
Editor An interactive program used to create and modify source programs or data.
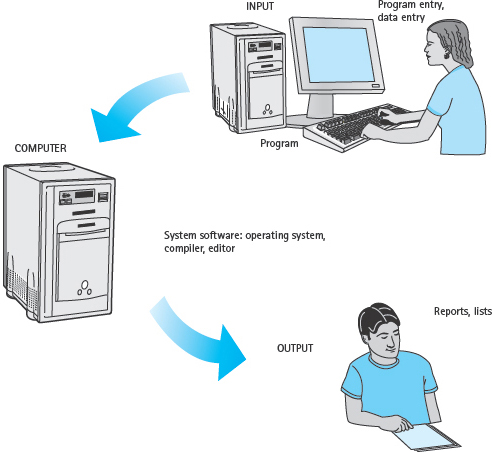
FIGURE 1.10 User/Computer Interface
Although solitary (standalone) computers are often used in private homes and small businesses, it is very common for many computers to be connected together, forming a network. A local area network (LAN) is one in which the computers are connected by wires or a wireless router and must be reasonably close together, as in a single office building. In a wide area network (WAN) or long-haul network, the computers can be far apart geographically and communicate through phone lines, fiberoptic cable, and other media. The most well-known long-haul network is the Internet, which was originally devised as a means for universities, businesses, and government agencies to exchange research information. The Internet exploded in popularity with the establishment of the World Wide Web, a system of linked Internet computers that support specially formatted documents (web pages) that contain text, graphics, audio, and video.
BACKGROUND INFORMATION
What Makes One Computer Faster Than Another?

The faster a computer is, the more quickly it responds to our commands and the more work it can do in less time. But which factors affect the speed of a computer? The answer is quite complex, but let’s consider some of the essential issues.
In computer advertising you often see numbers such as 3.2 GHz, and the ads clearly want you to believe that this is an important contributor to speed. But what does it really mean? The abbreviation GHz is short for gigahertz, which means billions of cycles per second. What’s cycling at this speed is the pulse of the computer—an electrical signal called the clock, which generates a continuous sequence of precisely regulated on/off pulses that are used to coordinate all of the actions of the other circuitry within the computer. It’s called a clock because it bears a similarity to the steady ticking of a mechanical clock. But if you want a better sense of what it does, think of it like the rhythmic swinging of an orchestra conductor’s baton, which keeps all of the instruments playing in time with each other. The clock ensures that all the components of the computer are doing their jobs in unison. It’s clear that the faster the clock, the faster the components work. But that’s just one factor that affects speed.
Clock An electrical circuit that sends out a train of pulses to coordinate the actions of the computer’s hardware components, The speed of the clock is measured in Hertz (cycles per second).
Although we have described the fetch–execute cycle as if the computer always fetches just one instruction at a time and executes that instruction to completion before fetching the next one, modern computers are not so simple. They often fetch and execute multiple instructions at once (for example, most can simultaneously do integer and real arithmetic, while retrieving values from memory). In addition, they start fetching the next instruction from memory while executing prior instructions. The number of instructions that the computer can execute simultaneously also has a significant effect on speed.
Different computers also work with data in chunks of different sizes. The computer in a microwave oven may work with 8 bits at a time, whereas a smartphone computer typically handles 32 bits at once. Higher-performance machines work with data in units of 64 bits. The more data the computer can process at once, the faster it will be, assuming that the application has need of working with larger quantities of data. The computer in the microwave is plenty fast enough to do its job—your popcorn would not pop any faster if it had a 64-bit processor!
It is not uncommon to see, for example, a 1.8 GHz, 64-bit computer that can process many instructions at once, which is significantly faster than a 3.6 GHz, 32-bit computer that handles fewer instructions in parallel. The only way to accurately judge the speed of a computer is to run an application on it, and measure the time it takes to execute.
Other major hardware factors that affect speed are the amount of memory (RAM) and speed of the hard disk. When a computer has more memory, it can hold more programs and data in its memory. With less memory, it must keep more of the programs and data on the hard disk drive, shuffling them between disk and memory as it needs them. The hard disk takes as much as a million times longer to access than RAM, so you can see that a computer with too little RAM can be slowed down tremendously. Disks themselves vary significantly in the speed with which they access data.
Software also affects speed. As we will see in later chapters, problems can be solved more or less efficiently. A program that is based on an inefficient solution can be vastly slower than one that is more efficient. Different compilers do a better job of translating high-level instructions into efficient machine code, which also affects speed. Operating systems also vary in their efficiency. The raw speed of the hardware is masked by the overall efficiency of the software. As a programmer, then, you can have a strong influence on how fast the computer seems to be.
QUICK CHECK

1.3.1 What are the six basic components most computers have? (p. 20)
1.3.2 What two important types of data are held by the memory unit? (p. 20)
1.3.3 What do we call the combination of the control unit and the arithmetic/logic unit? (p. 20)
1.3.4 What is the general term that we use to refer to the physical components of the computer? (p. 21)
1.3.5 What are the steps taken by the computer’s fetch–execute cycle? (p. 21)
1.4 Ethics and Responsibilities in the Computing Profession
Every profession operates with a set of ethics that help to define the responsibilities of its practitioners. For example, medical professionals have an ethical responsibility to keep information about their patients confidential. Engineers must protect the public and environment from harm that may result from their work. Writers are ethically bound not to plagiarize, and so on.
The computer can affect people and the environment in dramatic ways. As a consequence, it challenges society with new ethical issues. Some existing ethical practices apply to the computer, whereas other situations require new rules. In some cases, it will be up to you to decide what is ethical.
Software Piracy
Computer software is easy to copy. But just like books, software is usually copyrighted—it is illegal to copy software without the permission of its creator. Such copying is called software piracy.
Software piracy The unauthorized copying of software for either personal use or use by others.
Copyright laws exist to protect the creators of software (and books and art) so that they can make a profit. A major software package can cost millions of dollars to develop, which is reflected in its purchase price. If people make unauthorized copies of the software, then the company loses sales.
Software pirates sometimes rationalize their theft with the excuse that they’re just making one copy for their own use. It’s not as if they’re selling a bunch of bootleg copies, after all. Nevertheless, they have failed to compensate the company for the benefit they received. If thousands of people do the same thing, the losses can add up to millions of dollars, which leads to higher prices for everyone.
Computing professionals have an ethical obligation to not engage in software piracy and to try to stop it from occurring. You should never copy software without permission. If someone asks to copy some software that you have, you should refuse to supply it. If someone says that he or she just wants to “borrow” the software to “try it out,” tell the person that he or she is welcome to try it out on your machine but not to make a copy.
This rule isn’t restricted to duplicating copyrighted software; it includes plagiarism of all or part of code that belongs to anyone else. If someone gives you permission to copy some of his or her code, then, just like any responsible writer, you should acknowledge that person with a citation in the comments.
Privacy of Data
The computer enables the compilation of databases containing useful information about people, companies, and so on. These databases allow employers to issue payroll checks, banks to cash a customer’s check at any branch, the government to collect taxes, and mass merchandisers to send out junk mail. Even though we may not care for every use of databases, they generally have positive benefits. However, they can also be used in negative ways.
For example, a car thief who gains access to a state’s motor vehicle database could print out a “shopping list” of car models together with their owners’ addresses. An industrial spy might steal customer data from a company database and sell it to a competitor. Although these are obviously illegal acts, computer professionals face other situations that are not as clearly unethical.
Suppose your job includes managing the company payroll database, which includes the names and salaries of the firm’s employees. You might be tempted to poke around in the data and see how your salary compares to others—but this act is an unethical invasion of your associates’ right to privacy. Any information about a person that is not clearly public should be considered confidential. An example of public information is a phone number listed in a telephone directory. Private information includes any data that has been provided with an understanding that it will be used only for a specific purpose (such as the data on a credit card application).
A computing professional has a responsibility to avoid taking advantage of special access that he or she may have to confidential data. The professional also has a responsibility to guard that data from unauthorized access. Guarding data can involve such simple things as shredding old printouts, keeping backup copies in a locked cabinet, using passwords that are difficult to guess, and implementing more complex measures such as file encryption.
Use of Computer Resources
A computer is an unusual resource because there is no significant physical difference between a computer that is working and one that is sitting idle. By contrast, a car is in motion when it is working. Thus to use a car without permission requires taking it physically—stealing it. However, someone can make unauthorized use of a computer without physically taking it, by using its time and resources.
For some people, theft of computer resources is a game. The thief doesn’t really want the resources, but likes the challenge of breaking through a computer’s security system. Such people may think that their actions are acceptable if they don’t do any harm. Whenever real work is displaced by such activities, however, harm is done. If nothing else, the thief is trespassing. By analogy, consider that even though no physical harm may be done by someone who breaks into your bedroom and takes a nap while you are away, that is certainly disturbing to you because it poses a threat of harm.
Other thieves have malicious intentions and destroy data. Sometimes they leave behind programs that act as time bombs, causing harm later. Another destructive kind of program is a virus—a program that replicates itself, with the goal of spreading to other computers, usually via email or shared files. Some viruses may be benign, merely using up some resources. Others can be destructive. Incidents have occurred in which viruses have cost millions of dollars in data losses. In contrast to a virus, which is spread by contact between users, a worm exploits gaps in a computer’s security, hijacking it to search the Internet for other computers with the same gaps. When a computer is taken over and used for some other purpose, such as sending spam email, it is called a zombie.
Virus Malicious code that replicates and spreads to other computers through email messages and file sharing, without authorization, and possibly with the intent of doing harm.
Worm Malicious code that replicates and spreads to other computers through security gaps in the computer’s operating system, without authorization, and possibly with the intent of doing harm.
Zombie A computer that has been taken over for unauthorized use, such as sending spam email.
Harmful programs such as these are collectively known as malware. Now that spam accounts for the majority of worldwide email traffic, some viruses have attempted to extort money from their victims, and zombies have been used to shut down parts of the Internet, the effects of malware on the computing industry are significant.
Malware Software written with malicious purposes in mind.
Computing professionals should never use computer resources without permission. We also have a responsibility to help guard computers to which we have access by watching for signs of unusual use, writing applications without introducing security loopholes, installing security updates as soon as they are released, checking files for viruses, and so on.
Software Engineering
Humans have come to depend greatly on computers in many aspects of their lives. That reliance is fostered by the perception that computers function reliably; that is, they work correctly most of the time. However, the reliability of a computer depends on the care that is taken in writing its software.
Errors in a program can have serious consequences, as the following examples of real incidents involving software errors illustrate:
 An error in the control software of the F-18 jet fighter caused it to flip upside down the first time it flew across the equator.
An error in the control software of the F-18 jet fighter caused it to flip upside down the first time it flew across the equator.
 A rocket launch went out of control and had to be blown up because a comma was typed in place of a period in its control software.
A rocket launch went out of control and had to be blown up because a comma was typed in place of a period in its control software.
 A radiation therapy machine killed several patients because a software error caused the machine to operate at full power when the operator typed certain commands too quickly.
A radiation therapy machine killed several patients because a software error caused the machine to operate at full power when the operator typed certain commands too quickly.
Even when software is used in less critical situations, errors can have significant effects. Examples of such errors include the following:
 An error in your word processor causes your term paper to be lost just hours before it is due.
An error in your word processor causes your term paper to be lost just hours before it is due.
 An error in a statistical program causes a scientist to draw a wrong conclusion and publish a paper that must later be retracted.
An error in a statistical program causes a scientist to draw a wrong conclusion and publish a paper that must later be retracted.
 An error in a tax preparation program produces an incorrect return, leading to a fine for the taxpayer.
An error in a tax preparation program produces an incorrect return, leading to a fine for the taxpayer.
Programmers have a responsibility to develop software that is free from errors. The process that is used to develop correct software is known as software engineering.
Software engineering The application of traditional engineering methodologies and techniques to the development of software.
Software engineering has many aspects. The software life cycle described at the beginning of this chapter outlines the stages in the development of software. Different techniques are used at each of these stages. We address many of these techniques in this text. In Chapter 4, we introduce methodologies for developing correct algorithms. We discuss strategies for testing and validating programs in every chapter. We use a modern programming language that enables us to write readable, well-organized programs, and so on. Some aspects of software engineering, such as the development of a formal, mathematical specification for a program, are beyond the scope of this text.
QUICK CHECK

1.4.1 How can you help to keep confidential data private? (p. 25)
1.5 Problem-Solving Techniques
You solve problems every day, often unaware of the process you are going through. In a learning environment, you usually are given most of the information you need: a clear statement of the problem, the necessary input, and the required output. In real life, the process is not always so simple. You often have to define the problem yourself and then decide what information you have to work with and what the results should be.
After you understand and analyze a problem, you must come up with a solution—an algorithm. Earlier we defined an algorithm as a step-by-step procedure for solving a problem in a finite amount of time. Although you work with algorithms all the time, most of your experience with them is in the context of following them. You follow a recipe, play a game, assemble a toy, take medicine. In the problem-solving phase of computer programming, you will be designing algorithms, not following them. This means you must be conscious of the strategies you use to solve problems so as to apply them effectively to programming problems.
Ask Questions
If you are given a task orally, you ask questions—When? Why? Where?—until you understand exactly what you have to do. If your instructions are written, you might put question marks in the margin, underline a word or a sentence, or in some other way indicate that the task is not clear. Your questions may be answered by a later paragraph, or you might have to discuss them with the person who gave you the task.
These are some of the questions you might ask in the context of programming:
 What do I have to work with—that is, what is my data?
What do I have to work with—that is, what is my data?
 What do the data items look like?
What do the data items look like?
 How much data is there?
How much data is there?
 How will I know when I have processed all the data?
How will I know when I have processed all the data?
 What should my output look like?
What should my output look like?
 How many times will the process be repeated?
How many times will the process be repeated?
 What special error conditions might come up?
What special error conditions might come up?
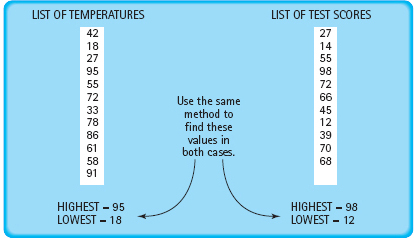
FIGURE 1.11 Look for Things That Are Familiar
Look for Things That Are Familiar
Never reinvent the wheel. If a solution exists, use it. If you’ve solved the same or a similar problem before, just repeat your solution. People are good at recognizing similar situations. We don’t have to learn how to go to the store to buy milk, then to buy eggs, and then to buy candy. We know that going to the store is always the same; only what we buy is different.
In programming, certain problems occur again and again in different guises. A good programmer immediately recognizes a subtask he or she has solved before and plugs in the solution. For example, finding the daily high and low temperatures is really the same problem as finding the highest and lowest grades on a test: You want the largest and smallest values in a set of numbers (see FIGURE 1.11).
Solve by Analogy
Often a problem may remind you of a similar problem you have seen before. You may find solving the problem at hand easier if you remember how you solved the other problem. In other words, draw an analogy between the two problems. For example, a solution to a perspective-projection problem from an art class might help you figure out how to compute the distance to a landmark when you are on a cross-country hike. As you work your way through the new problem, you may come across things that are different than they were in the old problem, but usually these are just details that you can deal with one at a time.
Analogy is really just a broader application of the strategy of looking for things that are familiar. When you are trying to find an algorithm for solving a problem, don’t limit yourself to computer-oriented solutions. Step back and try to get a larger view of the problem. Don’t worry if your analogy doesn’t match perfectly—the only reason for using an analogy is that it gives you a place to start (see FIGURE 1.12). The best programmers are people who have broad experience solving all kinds of problems.
Means-Ends Analysis
Often the beginning state and the ending state are given; the problem is to define a set of actions that can be used to get from one to the other. Suppose you want to go from Boston, Massachusetts to Austin, Texas. You know the beginning state (you are in Boston) and the ending state (you want to be in Austin). The problem is how to get from one to the other. In this example, you have lots of choices. You can fly, walk, hitchhike, ride a bike, or whatever. The method you choose depends on your circumstances. If you’re in a hurry, you’ll probably decide to fly.
FIGURE 1.12 Analogy
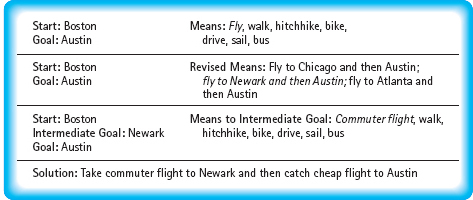
FIGURE 1.13 Means-Ends Analysis
Once you’ve narrowed down the set of actions, you have to work out the details. It may help to establish intermediate goals that are easier to meet than the overall goal. Suppose there is a really cheap, direct flight to Austin out of Newark, New Jersey. You might decide to divide the trip into legs: Boston to Newark, and then Newark to Austin. Your intermediate goal is to get from Boston to Newark. Now you just have to examine the means of meeting that intermediate goal (see FIGURE 1.13).
The overall strategy of means-ends analysis is to define the ends and then to analyze your means of getting between them. This process translates easily to computer programming. You begin by writing down what the input is and what the output should be. Then you consider the actions a computer can perform and choose a sequence of actions that can transform the data into the results.
Divide and Conquer
We often break up large problems into smaller units that are easier to handle. Cleaning the whole house may seem overwhelming; cleaning the rooms one at a time seems much more manageable. The same principle applies to programming: We can break up a large problem into smaller pieces that we can solve individually (see FIGURE 1.14). In fact, the functional decomposition and object-oriented methodologies, which we describe in Chapter 4, are based on the principle of divide and conquer.
The Building-Block Approach
Another way of attacking a large problem is to see if any solutions for smaller pieces of the problem exist. It may be possible to put some of these solutions together end to end to solve most of the big problem. This strategy is just a combination of the look-for-familiar-things and divide-and-conquer approaches. You look at the big problem and see that it can be divided into smaller problems for which solutions already exist. Solving the big problem is just a matter of putting the existing solutions together, like mortaring together blocks to form a wall (see FIGURE 1.15).
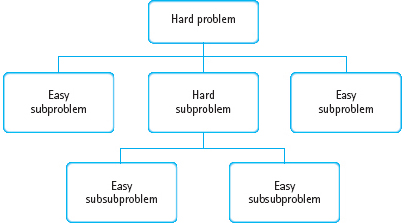
FIGURE 1.14 Divide and Conquer
Merging Solutions
Another way to combine existing solutions is to merge them on a step-by-step basis. For example, to compute the average of a list of values, we must both sum and count the values. If we already have separate solutions for summing values and for counting values, we can combine them. But if we first do the summing and then do the counting, we have to read the list twice. We can save steps if we merge these two solutions: Read a value, add it to the running total, and add 1 to our count before going on to the next value. Whenever the solutions to subproblems duplicate steps, think about merging them instead of joining them end to end. (See FIGURE 1.16.)
Mental Blocks: The Fear of Starting
Writers are all too familiar with the experience of staring at a blank page, not knowing where to begin. Programmers have the same difficulty when they first tackle a big problem. They look at the problem and it seems overwhelming.
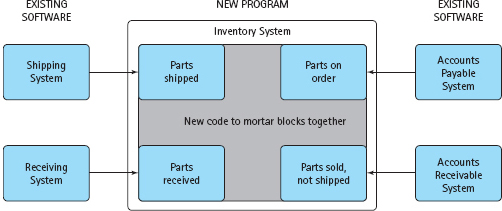
FIGURE 1.15 Building-Block Approach
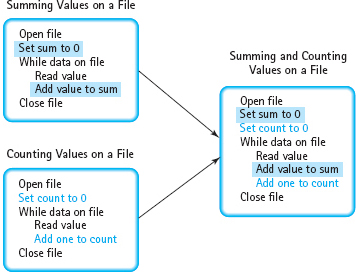
FIGURE 1.16 Merging Solutions
Remember that you always have a way to begin solving any problem: Write it down on paper in your own words so that you understand it. Once you paraphrase the problem, you can focus on each of the subparts individually instead of trying to tackle the entire problem at once. This process gives you a clearer picture of the overall problem. It helps you see pieces of the problem that look familiar or that are analogous to other problems you have solved, and it pinpoints areas where something is unclear and you need more information.
As you write down a problem, you tend to group things together into small, understandable chunks, which may be natural places to split the problem up—to divide and conquer. Your description of the problem may collect all of the information about data and results into one place for easy reference. Then you can see the beginning and ending states necessary for means-ends analysis.
Most mental blocks are caused by a failure to really understand the problem. Rewriting the problem in your own words is a good way to focus on the subparts of the problem, one at a time, and to understand what is required for a solution.
Algorithmic Problem Solving
Coming up with a step-by-step procedure for solving a particular problem is not always a cut-and-dried process. In fact, it is usually a trial-and-error process requiring several attempts and refinements. We test each attempt to see if it really solves the problem. If it does, great. If it doesn’t, we try again. Solving any nontrivial problem typically requires a combination of the techniques we’ve described.
Remember that the computer can only do certain things (see page 13). Your primary concern, then, is how to make the computer transform, manipulate, calculate, or process the input data to produce the desired output. If you keep in mind the allowable instructions in your programming language, you won’t design an algorithm that is difficult or impossible to code.
In the Problem-Solving Case Study that follows, we develop a program to determine whether a year is a leap year. This case study typifies the thought processes involved in writing an algorithm and coding it as a program, and it shows you what a complete C++ program looks like.
BACKGROUND INFORMATION
The Origins of C++

In the late 1960s and early 1970s, Dennis Ritchie created the C programming language at AT&T Bell Labs. At the time, a group of people within Bell Labs were designing the UNIX operating system. Initially, UNIX was written in assembly language, as was the custom for almost all system software in those days. To escape the difficulties of programming in assembly language, Ritchie invented C as a system programming language. C combines the low-level features of an assembly language with the ease of use and portability of a high-level language. UNIX was reprogrammed so that approximately 90% was written in C and the remainder in assembly language.
People often wonder where the cryptic name “C” came from. In the 1960s, a programming language named BCPL (Basic Combined Programming Language) had a small but loyal following, primarily in Europe. From BCPL, another language arose with its name abbreviated to B. For his language, Dennis Ritchie adopted features from the B language and decided that the successor to B naturally should be named C. So the progression was from BCPL to B to C.
In 1985, Bjarne Stroustrup, also of Bell Labs, invented the C++ programming language. To the C language he added features for data abstraction and object-oriented programming (topics we discuss later in this book). Instead of naming the language D, the Bell Labs group, following a humorous vein, named it C++. As we see later, ++ signifies the increment operation in the C and C++ languages. Given a variable x, the expression x++ means to increment (add one to) the current value of x. Therefore, the name C++ suggests an enhanced (“incremented”) version of the C language.
In the years since Dr. Stroustrup invented C++, the language began to evolve in slightly different ways in different C++ compilers. Although the fundamental features of C++ were nearly the same in all companies’ compilers, one company might add a new language feature, whereas another would not. As a result, C++ programs were not always portable from one compiler to the next. The programming community agreed that the language needed to be standardized, so a joint committee of the International Standards Organization (ISO) and the American National Standards Institute (ANSI) began the long process of creating a C++ language standard. After several years of discussion and debate, the ISO/ANSI language standard for C++ was officially approved in mid-1998. Most of the current C++ compilers support the ISO/ANSI standard (hereafter called standard C++).
Although C originally was intended as a system programming language, both C and C++ are widely used today in business, industry, and personal computing. C++ is powerful and versatile, embodying a wide range of programming concepts. In this book you will learn a substantial portion of the language, but C++ incorporates sophisticated features that go well beyond the scope of an introductory programming course.
QUICK CHECK

1.5.1 Who invented the C++ programming language? (p. 32)
1.5.2 When would you use the building-block approach to solve a problem? (pp. 29–30)
1.5.3 What does it mean to use divide and conquer to solve a problem? (p. 29)
1.5.4 What is the overall strategy of means-ends analysis? (p. 29)
1.5.5 Which problem-solving technique should be used as an alternative to the building-block approach when we want to save steps? (p. 30)
Problem-Solving Case Study
Leap Year Algorithm
PROBLEM: You need to write a set of instructions that can be used to determine whether a year is a leap year. The instructions must be very clear because they will be used by a class of fourth graders who have just learned about multiplication and division. They plan to use the instructions as part of an assignment to determine whether any of their relatives were born in a leap year. To check that the algorithm works correctly, you will code it as a C++ program and test it.
DISCUSSION: The rule for determining whether a year is a leap year is that a year must be evenly divisible by 4, but not a multiple of 100. When the year is a multiple of 400, it is a leap year anyway. We need to write this set of rules as a series of steps (an algorithm) that can be followed easily by the fourth graders.
First, we break this into major steps using the divide-and-conquer approach. There are three obvious steps in almost any problem of this type:
1. Get the data.
2. Compute the results.
3. Output the results.
What does it mean to “get the data”? By get, we mean read or input the data. We need one piece of data: a four-digit year. So that the user will know when to enter the value, we must have the computer output a message that indicates when it is ready to accept the value (this is called a prompting message, or a prompt). Therefore, to have the computer get the data, we have it do these two steps:
Get Data
Prompt the user to enter a four-digit year
Read the year
Next, we check whether the year that was read can be a leap year (is divisible by 4), and then we test whether it is one of the exceptional cases. Our high-level algorithm is as follows:
Is Leap Year
IF the year is not divisible by 4
then the year is not a leap year
ELSE check for exceptions
Clearly, we need to expand these steps with more detailed instructions, because neither the fourth graders nor the computer knows what “divisible” means. We use means-ends analysis to solve the problem of how to determine when something is divisible by 4. Our fourth graders know how to do simple division that results in a quotient and a remainder. We can tell them to divide the year by 4, and if the remainder is zero, then it is divisible by 4. Thus the first line is expanded into the following:
Is Leap Year revised
Divide the year by 4
IF the remainder is not 0
then the year is not a leap year
ELSE check for exceptions
Checking for exceptions when the year is divisible by 4 can be further divided into two parts: checking whether the year is also divisible by 100 and whether it is further divisible by 400. Given how we did the first step, this is easy:
Checking for exceptions
Divide the year by 100
IF the remainder is 0
then the year is not a leap year
Divide the year by 400
IF the remainder is 0
then the year is a leap year
These steps are confusing by themselves. When the year is divisible by 400, it is also divisible by 100, so we have one test that says it is a leap year and one that says it is not. What we need to do is to treat the steps as building blocks and combine them. One of the operations that we can use in such situations is to check when a condition does not exist. For example, if the year is divisible by 4 but not by 100, then it must be a leap year. If it is divisible by 100 but not by 400, then it is definitely not a leap year. Thus the third step (check for exceptions when the year is divisible by 4) expands to the following three tests:
Checking for exceptions revised
IF the year is not divisible by 100
then it is a leap year
IF the year is divisible by 100 but not by 400
then it is not a leap year
IF the year is divisible by 400
then it is a leap year
We can simplify the second test because the check for being divisible by 100 is just the opposite of the first test—if the subalgorithm determines that year is not a leap year in the first test, it can return to the main algorithm, conveying this fact. The second test will then be performed only if the year is actually divisible by 100. Similarly, the last test is really just the “otherwise” case of the second test. If the second test did not return, then we know that the year has to be divisible by 400. Once we translate these simplified tests into steps that the fourth graders know how to perform, we can write the subalgorithm that returns true if the year is a leap year and false otherwise. Let’s call this subalgorithm IsLeapYear, and put the year it is to test in parentheses beside the name.
IsLeapYear(year)
Divide the year by 4 |
|
IF the remainder isn’t 0
RETURN with false |
(We know the year is not a leap year) |
| |
|
Divide the year by 100 |
(To get to this step, the year must be divisible by 4) |
IF the remainder isn’t 0
RETURN true |
(We know the year is a leap year) |
| |
|
Divide the year by 400 |
(To get to this step, the year must be divisible by 100) |
IF the remainder isn’t 0
RETURN false |
(We know the year is not a divisible-by-400 leap year) |
|
(To get to this point, the year is divisible by 400) |
RETURN true |
(The year is a divisible-by-400 leap year) |
The only piece left is to write the results. If IsLeapYear returns true, then we write that the year is a leap year; otherwise, we write that it is not a leap year. Now we can write the complete algorithm for this problem.
Main Algorithm
Prompt the user to enter a four-digit year
Read the year
IF IsLeapYear(year)
Write year is a leap year
ELSE
Write year is not a leap year
Not only is this algorithm clear, concise, and easy to follow, but once you have finished the next few chapters, you will see that it is easy to translate into a C++ program. We present the program here so that you can compare it to the algorithm. You do not need to know how to read C++ programs to begin to see the similarities. Note that the symbol % is what C++ uses to calculate the remainder, and whatever appears between // and the end of the line is a comment that is ignored by the compiler.

Here is the input and the output of a test run:

 Summary
Summary
We think nothing of turning on the television and sitting down to watch it. The television is a communication tool we use to enhance our lives. Computers are becoming as common as televisions, just a normal part of our lives. And like televisions, computers are based on complex principles but are designed for easy use.
Computers are dumb; they must be told what to do. A true computer error is extremely rare (usually due to a component malfunction or an electrical fault). Because we tell the computer what to do, most errors in computer-generated output are really human errors.
Computer programming is the process of planning a sequence of steps for a computer to follow. It involves a problem-solving phase and an implementation phase. After analyzing a problem, we develop and test a general solution (algorithm). This general solution becomes a concrete solution—our program—when we write it in a high-level programming language. The sequence of instructions that makes up our program is then compiled into machine code, the language the computer uses. After correcting any errors (“bugs”) that show up during testing, our program is ready to use.
Once we begin to use the program, it enters the maintenance phase. Maintenance involves correcting any errors discovered while the program is being used and changing the program to reflect changes in the user’s requirements.
Data and instructions are represented as binary numbers (numbers consisting of just 1s and 0s) in electronic computers. The process of converting data and instructions into a form usable by the computer is called coding.
A programming language reflects the range of operations a computer can perform. The basic control structures in a programming language—sequence, selection, loop, and subprogram—are based on these fundamental operations. In this text, you will learn to write programs in the high-level programming language called C++.
Computers are composed of six basic parts: the memory unit, the arithmetic/logic unit, the control unit, input and output devices, and auxiliary storage devices. The arithmetic/logic unit and control unit together are called the central processing unit. The physical parts of the computer are called hardware. The programs that are executed by the computer are called software.
System software is a set of programs designed to simplify the user/computer interface. It includes the compiler, the operating system, and the editor.
Computing professionals are guided by a set of ethics, as are members of other professions. Copying software only with permission, including attribution to other programmers when we make use of their code, guarding the privacy of confidential data, using computer resources only with permission, and carefully engineering our programs so that they work correctly are among the responsibilities that we have.
Problem solving is an integral part of the programming process. Although you may have little experience programming computers, you have lots of experience solving problems. The key is to stop and think about which strategies you use to solve problems, and then to use those strategies to devise workable algorithms. Among those strategies are asking questions, looking for things that are familiar, solving by analogy, applying means-ends analysis, dividing the problem into subproblems, using existing solutions to small problems to solve a larger problem, merging solutions, and paraphrasing the problem to overcome a mental block.
The computer is used widely today in science, engineering, business, government, medicine, consumer goods, and the arts. Learning to program in C++ can help you use this powerful tool effectively.
 Quick Check Answers
Quick Check Answers
The Quick Checks are intended to help you decide if you’ve met the goals set forth at the beginning of each chapter. If you understand the material in the chapter, the answer to each question should be fairly obvious. After reading a question, check your response against the answers listed at the end of the chapter. If you don’t know an answer or don’t understand the answer that’s provided, turn to the page(s) listed at the end of the question to review the material.
1.1.1 A computer program. 1.1.2 No, a computer is not intelligent. A human must analyze the problem and create a sequence of instructions for solving the problem. A computer can repeat that sequence of instructions over and over again. 1.1.3 An algorithm can be written in any language, to be carried out by a person or a processor of any kind. A program is written in a programming language, for execution by a computer. 1.1.4 The Problem-Solving phase focuses on understanding the problem and developing a general solution, the Implementation phase translates the algorithm into a computer program, and the Maintenance phase emphasizes the use and maintenance of a computer program. 1.1.5 A programming language has a very small vocabulary of words and symbols, and a very precise set of rules that specify the form and meaning of valid language constructs. 1.2.1 The compiler inputs a source program written in a high-level language, and outputs an equivalent program in machine language. Some compilers also output a listing, which is a copy of the source program with error messages inserted. 1.2.2 Compiler. 1.2.3 sequentially, conditionally, repetitively, and subprograms. 1.2.4 It will execute different statements depending on certain conditions. 1.2.5 The program repeats statements while a certain condition is met. 1.2.6 They allow us to write parts of a program separately. 1.3.1 the memory unit, the arithmetic/logic unit, the control unit, input devices, output devices, and auxiliary storage devices. 1.3.2 The memory unit holds data that is input to the program or the result of computation and the program instructions. 1.3.3 The central processing unit. 1.3.4 Hardware. 1.3.5 (1) fetch an instruction, (2) the instruction is translated into control signals, (3) the control signals tell the computer how to execute the instruction, and (4) repeat this sequence starting at (1). 1.4.1 Use passwords that are difficult to guess, and change them periodically. Encrypt stored data. Ensure that data storage media are kept in a secure area. 1.5.1 Bjarne Stroustrup at Bell Laboratories. 1.5.2 When you see that a problem can be divided into pieces that may correspond to subproblems for which solutions are already known. 1.5.3 We can break up a large problem into smaller pieces that we can solve individually to make it easier to handle. 1.5.4 The overall strategy of means-ends analysis is to define the ends and then to analyze your means of getting between them. 1.5.5 Merging solutions.
 Exam Preparation Exercises
Exam Preparation Exercises
1. Match the following terms to their definitions, given below:
a. Programming
b. Computer
c. Algorithm
d. Computer program
e. Programming language
f. Documentation
g. Information
h. Data
i. A programmable device that can store, retrieve, and process data.
ii. Information in a form a computer can use.
iii. A sequence of instructions to be performed by a computer.
iv. A set of rules, symbols, and special words used to construct a computer program.
v. Planning or scheduling the performance of a task or event.
vi. Any knowledge that can be communicated.
vii. The written text and comments that make a program easier for others to understand, use, and modify.
viii. A step-by-step procedure for solving a problem in a finite amount of time.
2. List the three steps in the problem-solving phase of the software life cycle.
3. List the steps in the implementation phase of the software life cycle.
4. If testing uncovers an error, to which step in the software life cycle does the programmer return?
5. Explain why the following series of steps isn’t an algorithm, and then rewrite the steps to make a valid algorithm:
Wake up.
Go to school.
Come home.
Go to sleep.
Repeat from first step.
6. Match the following terms with their definitions, given here:
a. Machine language
b. Assembly language
c. Assembler
d. Compiler
e. Source program
f. Object program
i. A program that translates a high-level language into machine code.
ii. A low-level programming language in which a mnemonic is used to represent each of the instructions for a particular computer.
iii. The machine language version of a source program.
iv. A program that translates an assembly language program into machine code.
v. The language, made up of binary coded instructions, that is used directly by the computer.
vi. A program written in a high-level programming language.
7. What is the advantage of writing a program in a standardized programming language?
8. What does the control unit do?
9. The editor is a peripheral device. True or false?
10. Memory (RAM) is a peripheral device. True or false?
11. Is it a case of software piracy if you and a friend buy a piece of software together and install it on both of your computers? The license for the software says that it can be registered to just one user.
12. Match the following problem-solving strategies to the descriptions below:
a. Ask questions.
b. Look for things that are familiar.
c. Solve by analogy.
d. Means-ends analysis.
e. Divide and conquer.
f. Building-block approach.
g. Merging solutions.
i. Break up the problem into more manageable pieces.
ii. Gather more information to help you discover a solution.
iii. Identify aspects of the problem that are similar to a problem in a different domain.
iv. Combine the steps in two or more different algorithms.
v. Identify aspects of the problem that you’ve solved before.
vi. Join existing problem solutions together.
vii. Look at the input, output, and available operations and find a sequence of operations that transform the input into the output.
 Programming Warm-Up Exercises
Programming Warm-Up Exercises
1. In the following algorithm for making black-and-white photographs, identify the steps that are branches (selection), loops, or references to subalgorithms defined elsewhere.
a. Mix developer according to instructions on package.
b. Pour developer into tray.
c. Mix stop bath according to instructions on package.
d. Pour stop bath into tray.
e. Mix fixer according to instructions on package.
f. Pour fixer into tray.
g. Turn off white lights and turn on safelight.
h. Place negative in enlarger and turn on.
i. Adjust size of image and focus, and then turn off enlarger.
j. Remove one piece of printing paper from paper safe and place in enlarging easel.
k. Turn enlarger on for 30 seconds and then off.
l. Place paper in developer for 1 minute, stop bath for 30 seconds, and fixer for 1 minute.
m. Turn on white lights and inspect the first print, and then turn off white lights.
n1. If first print is too light:
Remove one piece of paper from paper safe, place on easel, and expose for 60 seconds to create a too-dark print. Then place in developer for 1 minute, stop bath for 30 seconds, and fixer for 1 minute.
n2. If first print is too dark:
Remove one piece of paper from paper safe, place on easel, and expose for 15 seconds to create a too-light print. Then place in developer for 1 minute, stop bath for 30 seconds, and fixer for 1 minute.
n3. If first print is about right:
Remove one piece of paper from paper safe, place on easel, and expose for 60 seconds to create a too-dark print. Then place in developer for 1 minute, stop bath for 30 seconds, and fixer for 1 minute. Remove one piece of paper from paper safe, place on easel, and expose for 15 seconds to create a too-light print. Then place in developer for 1 minute, stop bath for 30 seconds, and fixer for 1 minute.
o. Analyze too-light and too-dark prints to estimate base exposure time, and then identify highlights and shadows that require less or more exposure and estimate the necessary time for each area.
p. Remove one piece of paper from paper safe, place on easel, and expose for base exposure time, covering shadow areas for estimated time, and then cover entire print except for highlight areas, which are further exposed as estimated. Then place print in developer for 1 minute, stop bath for 30 seconds, and fixer for 1 minute.
q. Analyze print from Step p and adjust estimates of times as appropriate.
r. Repeat Steps p and q until a print is obtained with the desired exposure.
s. Document exposure times that result in desired print.
t. Remove one piece of paper from paper safe, place on easel, and expose according to documentation from Step s. Then place in developer for 1 minute, stop bath for 30 seconds, and fixer for 4 minutes. Place print in print washer.
u. Repeat step t to create as many prints as needed.
v. Wash all prints for 1 hour.
w. Place prints in print dryer.
2. Write an algorithm for brushing teeth. The instructions must be very simple and exact because the person who will follow them has never done this activity before, and takes every word literally.
3. Identify the steps in your solution to Exercise 2 that are branches, loops, and references to subalgorithms defined elsewhere.
4. Change the algorithm in Exercise 1 so that 10 properly exposed prints are created each time it is executed.
 Case Study Follow-Up
Case Study Follow-Up
1. Use the algorithm in the leap year case study to decide whether the following years are leap years.
a.1900
b.2000
c.1996
d.1998
2. Given the algorithm from the leap year case study with the lines numbered as follows:
1. |
Divide the year by 4 |
|
2. |
IF the remainder isn’t 0 |
|
3. |
RETURN false |
(We know the year is not a leap year) |
4. |
Divide the year by 100 |
(To get to this step, year must be divisible by 4) |
5. |
IF the remainder isn’t 0 |
|
6. |
RETURN true |
(We know the year is a leap year) |
7. |
Divide the year by 400 |
|
8. |
IF the remainder isn’t 0 |
|
9. |
RETURN false |
(We know the year is not a divisible-by-400 leap year) |
10. |
RETURN true |
(The year is a divisible-by-400 leap year) |
Indicate which line of the algorithm tells you whether the date is a leap year in each of the following cases.
a.1900 Line =
b.1945 Line =
c.1600 Line =
d.1492 Line =
e.1776 Line =
3. How would you extend the leap year algorithm to tell you when a year is a millennium year (a multiple of 1000)?
4. Use the leap year algorithm to determine whether you were born in a leap year.
5. Extend the leap year algorithm so that it tells you when the next leap year will be, if the input year is not a leap year.
6. Compare the algorithm for determining the leap year with the C++ program that is shown in the Problem-Solving Case Study. Using the numbering scheme for the algorithm from Question 2, decide which line (or lines) of the algorithm corresponds to which line (or lines) of the program shown here.
 Line Number
Line Number

 To understand what a computer program is.
To understand what a computer program is. To understand what an algorithm is.
To understand what an algorithm is. To learn what a high-level programming language is.
To learn what a high-level programming language is. To understand the compilation and execution processes.
To understand the compilation and execution processes. To learn the history of the C++ language.
To learn the history of the C++ language. To learn what the major components of a computer are and how they work together.
To learn what the major components of a computer are and how they work together. To learn about some of the basic ethical issues confronting computing professionals.
To learn about some of the basic ethical issues confronting computing professionals.










 A computer can transfer data from one place to another.
A computer can transfer data from one place to another.



















 Summary
Summary