14
Dynamic Data and Linked Lists
KNOWLEDGE GOALS
 To understand the concept of a linked data structure.
To understand the concept of a linked data structure.
 To understand the difference between deep and shallow copy operations.
To understand the difference between deep and shallow copy operations.
 To know and understand the four member functions that should be present in any class that manipulates dynamic data.
To know and understand the four member functions that should be present in any class that manipulates dynamic data.
SKILL GOALS
To be able to:
 Create, access, and destroy dynamic data.
Create, access, and destroy dynamic data.
 Create linked data structures.
Create linked data structures.
 Manipulate data in a linked structure.
Manipulate data in a linked structure.
 Distinguish between a reference variable and a pointer variable.
Distinguish between a reference variable and a pointer variable.
In Chapter 10 we looked at pointer types and reference types. A variable of one of these types does not contain a data value; it contains the memory address of another variable or structure. We focused on understanding how to create and manipulate pointers to static data defined in our C++ programs. The true power of pointers, however, becomes apparent with the introduction of dynamic data. Dynamic data allows programs to operate over data structures without a predetermined size and lifetime. Dynamic data structures can grow and shrink over the execution time of a program providing the ultimate in flexibility that can be both efficient in time and space. It is the creation and manipulation of dynamic data that we emphasize here by studying the linked list dynamic data structure.
14.1 Dynamic Data
In Chapter 9, we described two categories of program data in C++: static data and automatic data. Any global variable is static, as is any local variable explicitly declared as static. The lifetime of a static variable is the lifetime of the entire program. In contrast, an automatic variable—a local variable not declared as static—is allocated (created) when control reaches its declaration and is deallocated (destroyed) when control exits the block in which the variable is declared.
With the aid of pointers, C++ provides a third category of program data: dynamic data. Dynamic variables are not declared with ordinary variable declarations; instead, they are explicitly allocated and deallocated at execution time by means of two special operators, new and delete. When a program requires an additional variable, it uses new to allocate the variable. When the program no longer needs the variable, it uses delete to deallocate it. The lifetime of a dynamic variable is, therefore, the time between the execution of new and the execution of delete. The advantage of being able to create new variables at execution time is clear: We don’t have to create any more variables than we actually need.
Dynamic data Variables created during execution of a program by means of special operations. In C++. These operations are new and delete.
Allocating Dynamic Data
The new operation has two forms, one for allocating a single variable and one for allocating an array. Here is the syntax template:
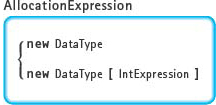
The first form is used for creating a single variable of type DataType. The second form creates an array whose elements are of type DataType; the desired number of array elements is given by IntExpression.
Here is an example that demonstrates both forms of the new operation:

Normally, the new operator does two things: It creates an uninitialized variable (or an array) of the designated type, and it returns the address of this variable (or the base address of an array). It is this address that is stored into the pointer variable. If the computer system has run out of space in which to store dynamic data, however, the program terminates with an error message. In Chapter 16, we show how to test for this condition and keep the program from terminating.
Variables created by new are said to reside on the free store (or heap), a region of memory set aside for dynamic variables. The new operator obtains a chunk of memory from the free store and, as we will see, the delete operator returns it to the free store.
Free store (heap) A pool of memory locations reserved for allocation and deallocation of dynamic data.
A dynamic variable is unnamed and cannot be addressed directly. Instead, it must be addressed indirectly through the pointer returned by the new operator. Following is an example of creating dynamic data and then accessing the data through pointers.

FIGURE 14.1 pictures memory after the effect of executing this code segment. Note that the contents of the struct to which patientPtr points have not been changed. What patientPtr points to was stored in the array, not a copy of the pointer.
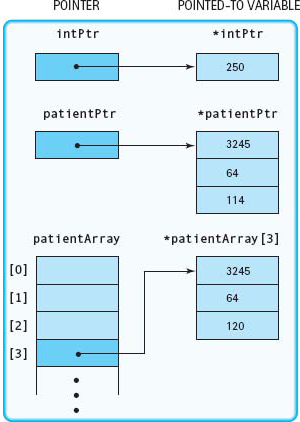
Figure 14.1 Picture of Memory After Execution of Code Segment
Deleting Dynamic Data
Dynamic data can (and should) be destroyed at any time during the execution of a program when it is no longer needed. The built-in operator delete is used to destroy a dynamic variable. The delete operation has two forms: one for deleting a single variable, the other for deleting an array.
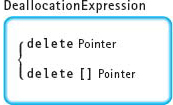
Using the previous example, we can deallocate the dynamic data pointed to by intPtr, patientPtr, and patientArray with the following statements:
delete intPtr; |
Returns the int variable pointed to by intPtr to the free store to be used again |
delete patientPtr; |
Returns the struct variable pointed to by patientPtr to the free store to be used again |
delete [] patientArray |
Returns the array pointed to by patientArray to the free store to be used again |
After execution of these statements, the values pointed to by intPtr, patientPtr, and patientArray are undefined; that is, they may or may not still contain the deallocated data. Before using these pointers again, you must assign new values to them (that is, store new memory addresses into them).
Until you gain experience with the new and delete operators, it is important to pronounce the statement
delete intPtr;
accurately. Instead of saying, “Delete intPtr,” it is better to say, “Delete the value to which intPtr points.” The delete operation does not delete the pointer; it deletes the pointed-to value.
When using the delete operator, you should keep two rules in mind:
1. Applying delete to the NULL pointer does no harm; the operation simply has no effect.
2. Excepting Rule 1, the delete operator must only be applied to a pointer value that was obtained previously from the new operator.
The second rule is important to remember. If you apply delete to an arbitrary memory address that is not in the free store, the result is undefined and could prove to be very unpleasant.
The new operator lets you create variables only as they are needed. When you are finished using a dynamic variable, you should delete it. It is counterproductive to keep dynamic variables when they are no longer needed—a situation known as a memory leak. If a memory leak is permitted to occur too often, you may run out of memory.
Memory leak The loss of available memory space that occurs when dynamic data is allocated but never deallocated
Let’s look at another example of using dynamic data.
Here is a more detailed description of the effect of each statement:
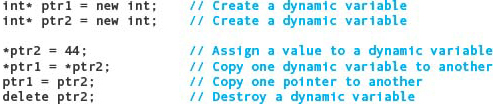
int* ptr1 = new int;
int* ptr2 = new int; |
Creates a pair of dynamic variables of type int and stores their locations into ptr1 and ptr2. The values of the dynamic variables are undefined even though the pointer variables now have values (see FIGURE 14.2A). |
*ptr2 = 44; |
Stores the value 44 into the dynamic variable pointed to by ptr2 (see FIGURE 14.2B). |
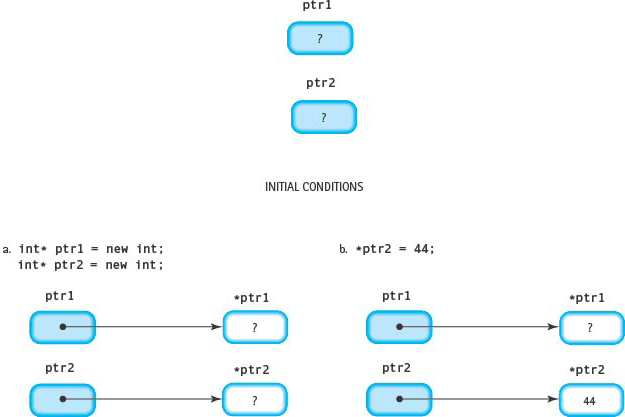
Figure 14.2A and B Results from Sample Code Segment
*ptr1 = *ptr2; |
Copies the contents of the dynamic variable *ptr2 to the dynamic variable *ptr1 (see FIGURE 14.2C). |
ptr1 = ptr2; |
Copies the contents of the pointer variable ptr2 to the pointer variable ptr1 (see FIGURE 14.2D). |
delete ptr2; |
Returns the dynamic variable *ptr2 back to the free store to be used again. The value of ptr2 is undefined (see FIGURE 14.2E). |
In FIGURE 14.2d, notice that the variable pointed to by ptr1 before the assignment statement is still there. It cannot be accessed, however, because no pointer is pointing to it. This isolated variable is called an inaccessible object. Leaving inaccessible objects on the free store should be considered a logic error and is a cause of memory leaks.
Inaccessible object A dynamic variable on the free store without any pointer pointing to it.
Notice also that in FIGURE 14.2e ptr1 is now pointing to a variable that, in principle, no longer exists. We call ptr1 a dangling pointer. If the program later dereferences ptr1, the result will be unpredictable. The pointed-to value might still be the original one (44), or it might be a different value stored there if that space on the free store has been reused.
Dangling pointer A pointer that points to a variable that has been deallocated.
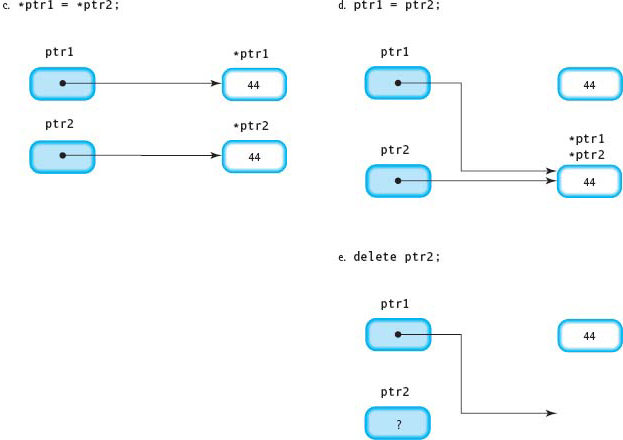
Figure 14.2c, D, and E Results from Sample Code Segment
Both situations shown in FIGURE 14.2e—an inaccessible object and a dangling pointer—can be avoided by deallocating *ptr1 before assigning ptr2 to ptr1, and by setting ptr1 to NULL after deallocating *ptr2.

FIGURE 14.3 shows the results of executing this revised code segment.
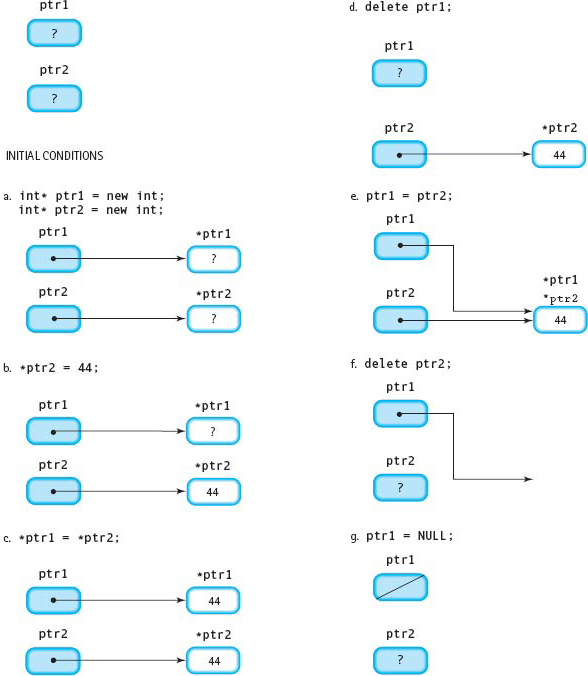
Figure 14.3 Results from Sample Code Segment After It Was Modified
Constants and Dynamic Data
There is another way to avoid the inaccessible object problem. Just as C++ allows us to define constants of other simple types, so a pointer can be made constant. In the following declaration, patientPtr is a constant pointer that is initialized to the address of a dynamic memory location representing a struct of type PatientRec:
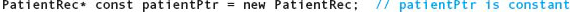
Once this code is executed, patientPtr will always point to the same location. We can change the values stored in that location by dereferencing patientPtr, but we cannot assign a new value to patientPtr itself. That is, we cannot make it point to another place in memory. As a result, the location it points to can never become inaccessible. When we apply delete to a constant pointer, we can be assured that we are deleting precisely what was originally allocated, thereby preventing a memory leak.
In the next section we look at the use of pointers in another form of list implementation.
QUICK CHECK

14.1.1 What is the keyword that we use in writing a C++ allocation expression? (pp. 718–719)
14.1.2 What is the keyword that we use in writing a C++ deallocation expression? (pp. 720–721)
14.1.3 What is dynamic data? (p. 718)
14.1.4 What are the two things the new operator does? (p. 719)
14.1.5 Where do variables created by new reside? (p. 719)
14.1.6 What does the delete operator do in terms of the free store? (p. 719)
14.2 Sequential Versus Linked Structures
As we pointed out in Chapter 13, many problems in computing involve lists of items. In that chapter, we implemented the List ADT using an array to store the items in the list. The size of an array is fixed, but the number of items in the list varies.
If the list we are implementing is a sorted list—one whose components must be kept in ascending or descending order—certain operations are efficiently carried out using an array representation. For example, searching a sorted list for a particular value is done quickly by using a binary search. However, inserting and deleting items from a sorted list are inefficient operations when we are using an array representation. To insert a new item into its proper place in the list, we must shift the array elements down to make room for the new item (see FIGURE 14.4). Similarly, deleting an item from the list requires that we shift up all the array elements following the one to be deleted.
When insertions and deletions will occur frequently, there is a better data representation for a list: the linked list. A linked list is a collection of items, called nodes, that can be scattered about in memory, not necessarily in consecutive memory locations. Each node, typically represented as a struct, consists of two members:
Linked list A list in which the order of the components is determined by an explicit link member in each node, rather than by the sequential order of the components in memory.
 A component or item member, which contains one of the data values in the list
A component or item member, which contains one of the data values in the list
 A link member, which gives the location of the next node in the list
A link member, which gives the location of the next node in the list

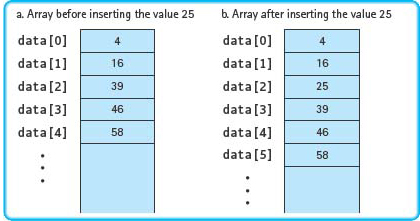
Figure 14.4 Inserting into a Sequential Representation of a Sorted List
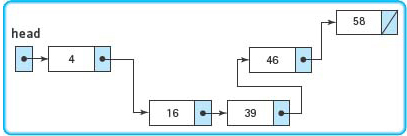
FIGURE 14.5 Linked List
FIGURE 14.5 shows an abstract diagram of a linked list. An arrow is used in the link member of each node to indicate the location of the next node. The slash (/) in the link member of the last node signifies the end of the list. A separate named variable points to the first node in the list; this pointer is called the external pointer to the list. This variable is not a pointer within the linked list; rather, its purpose is to give the location of the first node. The identifier “head” is sometimes used to refer to the external pointer to a list.
External pointer A pointer that points to the first node in a linked list.
Accessing the items in a linked list is a little like playing the children’s game of treasure hunt—each child is given a clue to the hiding place of the next clue, and the chain of clues eventually leads to the treasure.
As you look at FIGURE 14.5, you should observe two things. First, we have deliberately arranged the nodes in random positions. We have done so to emphasize the fact that the items in a linked list are not necessarily in adjacent memory locations (as they are in the array representation of FIGURE 14.4). Second, you may already be thinking of pointers when you see the arrows in the figure—and you would be right.
QUICK CHECK

14.2.1 Why is it often more space efficient to implement a list using pointers rather than with an array? (p. 708)
14.2.2 Which member do we need in addition to the data members of a struct to use the struct as a node in a linked list? (p. 709)
14.2.3 What is the primary difference between an array and a linked list? (pp. 708–709)
14.2.4 What frequently occurring operations are more efficient for a linked list representation? (p. 725)
14.2.5 What is an external pointer? (p. 726)
14.3 Creating a Dynamic Linked List: A Walk-Through Example
In this section we walk through the creation of an example linked list so that we can see how the process works in one specific case. We represent the list as a linked structure whose nodes are dynamically allocated on the free store; the link member of each node contains the memory address of the next dynamic node. In this data representation, called a dynamic linked list, the arrows in the diagram of FIGURE 14.5 really do represent pointers (and the slash in the last node is the NULL pointer). We access the list with a pointer variable that holds the address of the first node in the list. This pointer variable, named head in FIGURE 14.5, is called the external pointer or head pointer. Every node after the first node is accessed by using the link member in the node before it.
Dynamic linked list A linked list composed of dynamically allocated nodes that are linked together by pointers.
External (head) pointer A pointer variable that points to the first node in a dynamic linked list.
Such a list can expand or contract as the program executes. To insert a new item into the list, we allocate more space from the free store. To delete an item, we deallocate the memory assigned to it. We don’t have to know in advance how long the list will be (that is, how many items it will hold). The only limitation is the amount of available memory space. Data structures built using this technique are called dynamic data structures.
Dynamic data structure A data structure that can expand and contract during execution.
To create a dynamic linked list, we begin by allocating the first node and saving the pointer to it in the external pointer. We then allocate a second node and store the pointer to it into the link member of the first node. We continue this process—allocating a new node and storing the pointer to it into the link member of the previous node—until we have finished adding nodes to the list.
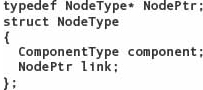
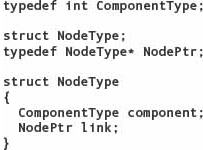
Let’s look at how we can use C++ pointer variables to create a dynamic linked list of float values. We begin with the following declarations:
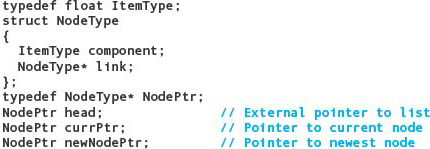
The order of these declarations is important. The Typedef for NodePtr refers to the identifier NodeType, so the declaration of NodeType must come first. (Remember that C++ requires every identifier to be declared before it is used.) Within the declaration of NodeType, we would like to declare link to be of type NodePtr, but we can’t because the identifier NodePtr hasn’t been declared yet. However, C++ allows forward (or incomplete) declarations of structs, classes, and unions:

The advantage of using a forward declaration is that we can declare the type of link to be NodePtr just as we declare head, currPtr, and newNodePtr to be of type NodePtr.
Given the preceding declarations, the following code fragment creates a dynamic linked list with the values 12.8, 45.2, and 70.1 as the components in the list:

Let’s go through each of these statements, describing in words what is happening and showing the linked list as it appears after the execution of the statement.
head = new NodeType; |
A dynamic variable of type NodeType is created.
The pointer to this new node is stored into head. Variable head is the external pointer to the list we are building. |
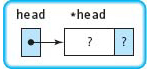
head→component = 12.8; |
The value 12.8 is stored into the component member of the first node. |
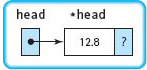
newNodePtr = new NodeType; |
A dynamic variable of type NodeType is created.
The pointer to this new node is stored into newNodePtr. |

newNodePtr→component = 45.2; |
The value 45.2 is stored into the component member of the new node. |

head→link = newNodePtr; |
The pointer to the new node containing 45.2 in its component member is copied into the link member of *head. Variable newNodePtr still points to this new node. The node can be accessed either as *newNodePtr or as *(head→link). |
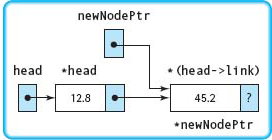
currPtr = newNodePtr; |
The pointer to the new node is copied into currPtr. Now currPtr, newNodePtr, and head→link all point to the node containing 45.2 as its component. |
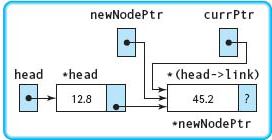
newNodePtr = new NodeType; |
A dynamic variable of type NodeType is created. The pointer to this new node is stored into newNodePtr. |
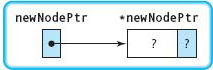
newNodePtr→component = 70.1; |
The value 70.1 is stored into the component member of the new node. |
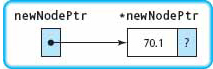
currPtr→link = newNodePtr; |
The pointer to the new node containing 70.1 in the component member is copied into the link member of the node that contains 45.2. |
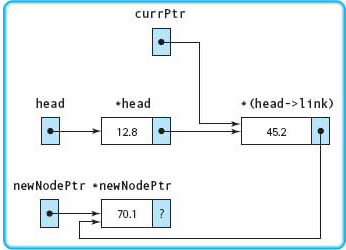
newNodePtr→link = NULL; |
The special pointer constant NULL is stored into the link member of the last node in the list. When used in the link member of a node, NULL means the end of the list. NULL is shown in the diagram as a slash (/) in the link member. |
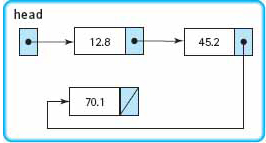
currPtr = newNodePtr; |
currPtr is updated to point to the last node in the list (not shown). |
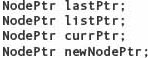
We would like to generalize this algorithm so that we can use a loop to create a dynamic linked list of any length. In the algorithm, we used three pointers:
1. head, which was used in creating the first node in the list and became the external pointer to the list.
2. newNodePtr, which was used in creating a new node when it was needed.
3. currPtr, which was updated to always point to the last node in the linked list.
When building any dynamic linked list by adding each new node to the end of the list, we always need three pointers to perform these functions. The algorithm that we used is generalized here to build a linked list of ten integer values from the standard input device.

Here is a program that implements this algorithm and prints the values in the order in which they were read. The part of the code that creates the linked list is highlighted. We cover how to print the list later in the chapter
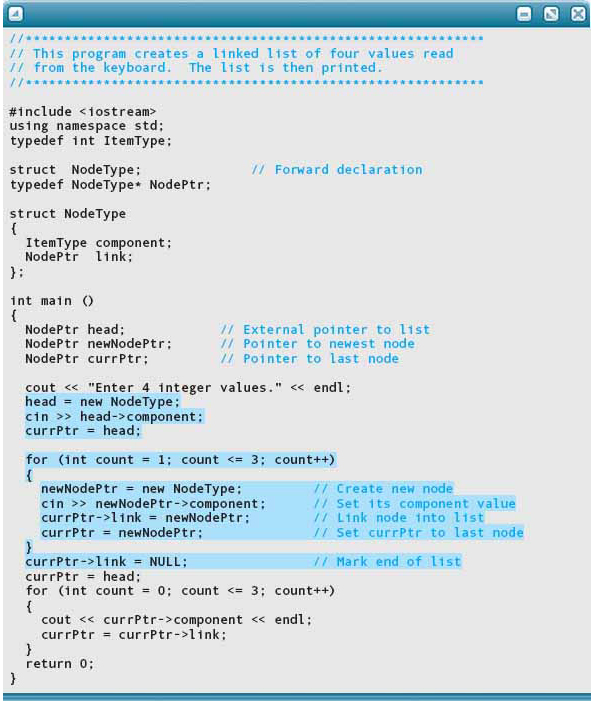
Here is a sample run:
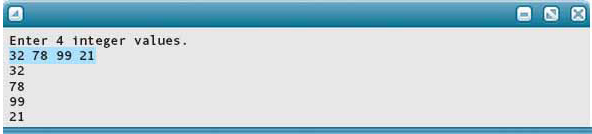
Let’s do a code walk-through and see just how this algorithm works.
head = new NodeType; |
A variable of type NodeType is created. The pointer is stored into head. Variable head will remain unchanged as the pointer to the first node (that is, head is the external pointer to the list). |
cin >> head→component; |
The first number is read into the component member of the first node in the list. |
currPtr = head; |
currPtr now points to the last node (the only node) in the list. |
for (…) |
A count-controlled loop is used to read four integer values. |
{ |
The loop begins. |
newNodePtr = new NodeType; |
Another variable of type NodeType is created, with newNodePtr pointing to it. |
cin >> newNodePtr→component; |
The current input value is stored into the component member of the newly created node. |
currPtr→link = newNodePtr; |
The pointer to the new node is stored into the link member of the last node in the list. |
currPtr = newNodePtr;
} |
currPtr is again pointing to the last node in the list.
The loop body repeats. |
currPtr→link = NULL; |
The link member of the last node is assigned the special end-of-list value NULL. |
Here is the linked list that results when the program is run with the data 32, 78, 99, and 21 as input. The final values are shown for the auxiliary variables.

QUICK CHECK

14.3.1 What is a dynamic linked list? (p. 727)
14.3.2 What is a dynamic data structure? (p. 727)
14.3.3 What do we use to get access to the first node in a dynamic linked list? (p. 727)
14.3.4 Consider the task of adding a new node to a linked list of integers that already contains a single node. Describe the process of adding this new node to the existing linked list. (pp. 731–733)
14.4 Dynamic Implementation of ADT List
Now that we have looked at two examples of creating a dynamic linked list, let’s examine the algorithms that process nodes in a linked list. We need to be able to insert a node into a list, delete a node from a list, search for a node, and traverse the list. For each of these operations, we make use of the fact that NULL is in the link member of the last node. NULL can be assigned to any pointer variable; it means that the pointer points to nothing. Its importance lies in the fact that we can compare the link member of each node to NULL, thereby determining when we have reached the end of the list.
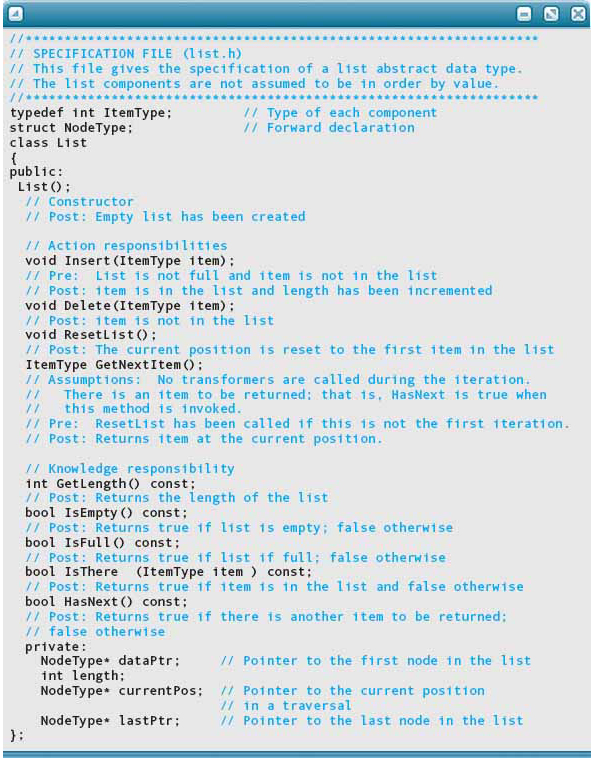
As we develop these algorithms, we do so in the context of the ADT List. Here are the prototypes for the class List, which form the specification for the data type.

In the class declaration, notice that the preconditions and postconditions of the member functions mention nothing about linked lists. The abstraction is a list, not a linked list. The user of the class is interested only in manipulating lists of items and does not care how we implement a list. If we decide to use a different implementation, the same public interface remains valid.
The private data in the array-based implementation of Chapter 13 consisted of a data array, a length field, and a currentPos field that held the current position for a traversal of the list. What would be the equivalent in a linked implementation? The array and the current position would be replaced with pointers.

Do we need to make other changes to the specification file for our new implementation? Yes, we must include a forward declaration for NodeType so that the private variable dataPtr can be specified. In the spirit of information hiding, we place the complete declaration of NodeType into the implementation file List.cpp. Now let’s look at the linked implementation for the class, beginning with the constructor and the action responsibilities.
Creating an Empty Linked List
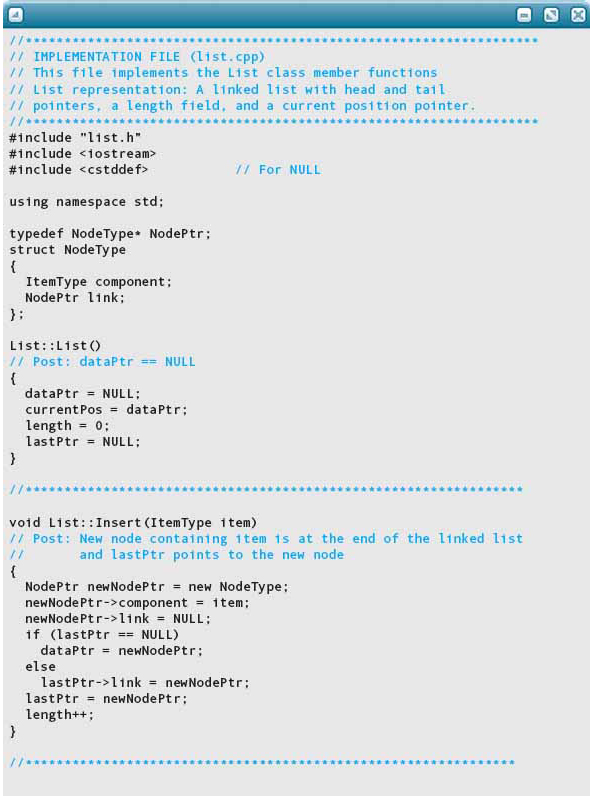
To create a linked list with no nodes, all that is necessary is to assign the external pointer the value NULL. For the List class, the appropriate place to do this is in the class constructor. currentPos and length must also be set. length should be set to 0—but what about currentPos? This data field should be initialized to point to the first item in the list: dataPtr.
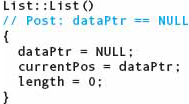
As we discussed in Chapter 13, the implementation documentation (the preconditions and postconditions appearing in the implementation file) is often stated differently from the abstract documentation (located in the specification file). Specification documentation is written in terms that are meaningful to the user of the ADT; implementation details should not be mentioned. In contrast, implementation documentation can be made more precise by referring directly to variables and algorithms in the implementation code. In the case of the List class constructor, the abstract postcondition simply states that an empty list (not a linked list) has been created. By comparison, the implementation postcondition
// Post: dataPtr == NULL
is stated in terms of how this is done.
Inserting into a Linked List
A function for inserting a component into a linked list must have an argument: the item to be inserted. The phrase inserting into a linked list could mean inserting the component as the first node, inserting the component as the last node, or inserting the component into its proper place according to some ordering (alphabetic or numeric). The list specification says nothing about order, however, so either of the first two meanings would be acceptable. In the case of the array-based list, we assumed the first meaning because inserting an item at the beginning of the list would have been grossly inefficient. In the case of a linked implementation, the logical place to insert an item is at the beginning of the list, because this place is directly accessible via the external pointer. If we want to insert an item at the end of the linked list, either we have to keep an additional pointer to the last node in the list or we must search for the end of the list with each insertion.
Because we are now providing an alternative implementation to an existing class, we want a traversal of the two implementations to be identical. Thus we implement the second meaning: The new item goes at the end of the list. What about the option of inserting the component in its proper place? That’s the difference between an unordered list and a sorted list. We examine sorted lists later.
As we noted, there are two ways of managing insertion at the end of a linked list. We choose the approach of keeping a pointer to the last item in the list because it is faster than searching for the end of the list. Thus we add the data field lastPtr to our class private data. Our list now has the following general form:
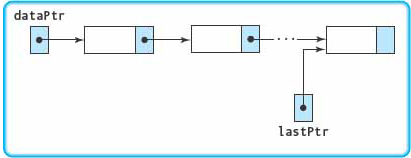
To what do we initialize lastPtr? We initialize lastPtr to NULL: The list is empty, so there is no last node. We insert the new node at the end and reset lastPtr to point to that node. This algorithm is very similar to the one we just used to build a list of four numbers.
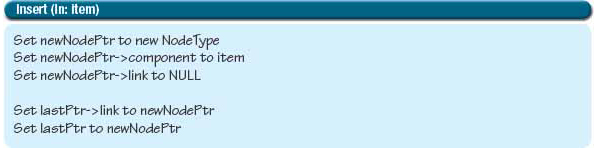
Before we code this algorithm, we need to look at the end conditions. Does this algorithm work if the list is empty? No, it doesn’t. Trying to access lastPtr→link when lastPtr is NULL will cause the program to crash. We need to make inserting into an empty list be a special case. If lastPtr is NULL, we need to set both dataPtr and lastPtr to the new node. Here is the revised algorithm:
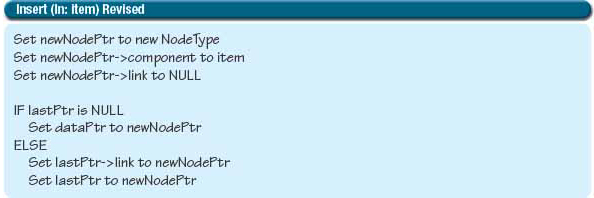
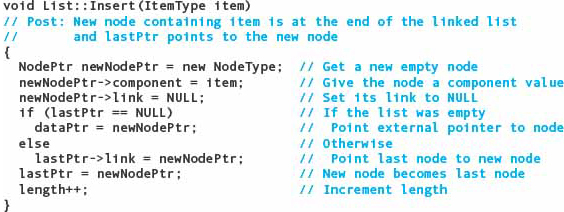
Have we forgotten anything else? Yes—length must be incremented when an item is inserted. This algorithm is coded in the following function:
Traversals of a Linked List
Many of the following list algorithms require a traversal—that is, going through the list node by node. Before considering the rest of the functions, let’s examine the simple traversal of the four-element list that we used in the sample program in Section 14.3.

In this code segment, the traveling pointer currentPtr is initialized to head, the first node in the list. This code segment goes through the nodes, printing the component part of each. When count == 3, currPtr is equal to NULL, and each element has been examined.
Do not confuse this internal traversal with the external traversal that a client would undertake using ResetList, HasNext, and GetNextItem. The preceding code segment illustrates the style of traversal that would be performed by a member function that needs to run through part or all of the list. However, because our linked list won’t be fixed in size, we’ll use a While loop instead of a For loop.
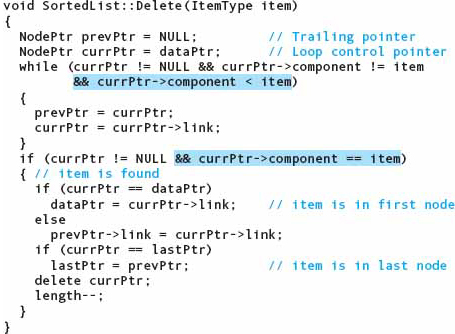
Deleting from a Linked List
To delete an existing node from a linked list, we must loop through the nodes until we find the node we want to delete. The postcondition says only that the item is not in the list; there is no precondition. Thus the item may be in the list or it may not be. However, we do know (by the precondition on Insert) that the list contains at most one copy of the item. Thus our search needs two ending conditions: The item is found or the end of the list is found. Here is the loop for the algorithms:
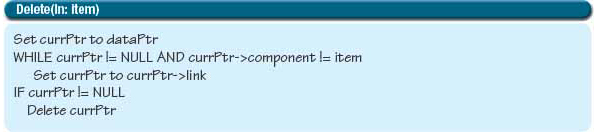
If item is in the list, at this point currPtr→component equals item. To delete the node, we must set the link portion of the node before it to its link field.
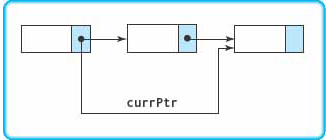
But we don’t have access to the link field of the node before currPtr! Therefore, we must keep track of two nodes in this loop: currPtr and the node before it. Let’s call it prevPtr. We must initialize prevPtr to NULL. Here is the revised algorithm:

Are there any end conditions that we missed? If the node to be deleted is the first node, we must update dataPtr. If the node to be deleted is the last node, we must update lastPtr. If the node to be deleted is the only node in the list, both dataPtr and lastPtr must be updated. These tests must be done before the deletion is made.

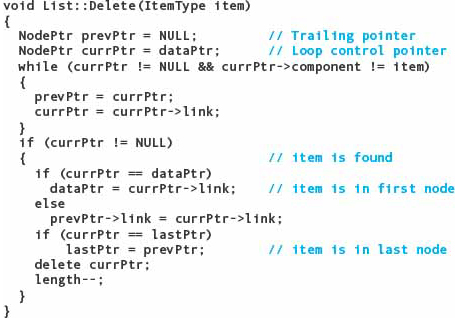
As a walk-through example to check our algorithm, let’s delete the node whose component is 20. The structure is shown below, with the nodes labeled as they are when the While statement is reached.
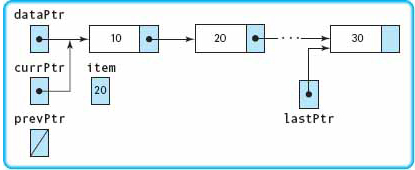
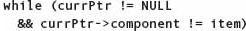
|
currPtr is not NULL and 10 is not equal to 20, so the loop body is entered. |

|
The trailing pointer points to the first node.
The current pointer points to the second node. |
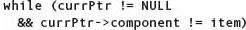
|
currPtr is not NULL but 20 equals 20, so the loop is exited. |
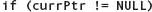
|
currPtr is not NULL so the item is found. |
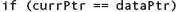
|
currPtr is not equal to dataPtr so the item is not in the first node. |
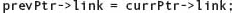
|
The node with the item is unlinked. |
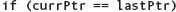
|
The item is not in the last node. |
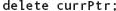
|
The node is deallocated. |
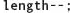
|
The length of the list is decremented. |
If the value to be deleted is in the first node, the node is unlinked by setting dataPtr to the link field of the first node. If the value to be deleted is in the last node, lastPtr is reset to the current last node (prevPtr).
Resetting the List
This function initializes currentPos for a traversal. The constructor sets it originally; this function must reset it to point to the head of the list: dataPtr.

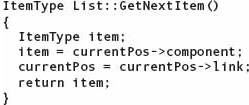
Getting the Next Item
This algorithm is identical to the one in the array-based list implementation. We return the contents of the node pointed to by currentPtr and then set currentPtr to point to the next node. We don’t have to worry about dereferencing the NULL pointer, because the precondition for the function states that there is another item to be returned.
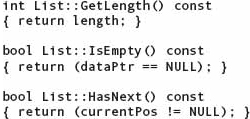
Now we have finished looking at all the action responsibilities, leaving only the knowledge responsibilities to examine. Three of these are so straightforward that we show the code with no explanation: GetLength, IsEmpty, and HasNext.
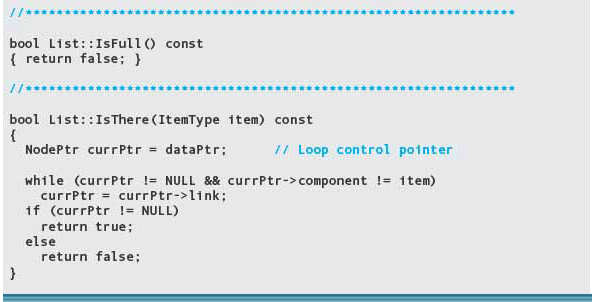
Testing for the Full Linked List
Theoretically, a linked list cannot be full. However, there is a possibility that the list might be so long that the heap runs out of memory to supply to the new operator. We show how to handle this situation in Chapter 16 when we cover exceptions. Until then, we just let function IsFull return false.

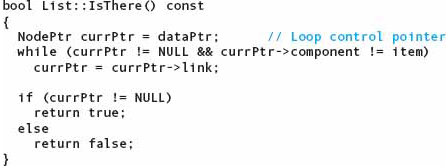
Searching the List
We actually looked at this algorithm when we were searching the list for an item to delete. In fact, we can use the first part of the code directly. However, because we are not deleting a component, we do not need the pointer to the previous node.
Now we need to collect these functions in an implementation file and write a driver to test them. As this is an alternative implementation of a class, we can use the same driver that we used to test the array-based list implementation.
Here is the specification file:
Here is the implementation file:

The same driver was used with this implementation, and here is the output. If you look back to the last chapter, you will see the output is identical.
QUICK CHECK

14.4.1 What are the general steps necessary to insert a new node into a linked list following a specific node? (pp. 736–737)
14.4.2 What are the general steps necessary to delete a node from a linked list following a specific node? (pp. 738–739)
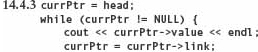
14.4.3 Write C++ code to traverse from beginning to end a linked list whose first element is pointed to by the variable head printing out the value of each node. Assume that each node consists of a variable called value for the value and link for the link to the next node. (pp. 737–738)
14.4.4 What does the IsFull method of a linked list return and why? (p. 741)
14.5 Destructors and Copy-Constructors
Classes whose objects manipulate dynamic data on the free store should provide three special operations: a constructor, a destructor, and a copy-constructor. You are familiar with constructors; now we look at the other two operations.
Destructor
The purpose of the destructor is to deallocate the nodes in a dynamic linked list when a List class object is destroyed. Without a destructor, the linked list would be left behind on the free store, still allocated but inaccessible. The code for the destructor is easy to write. We just traverse the list, deleting nodes as we go along. Note that the destructor is defined exactly like a constructor except that it has a tilde (~) before the class name.

Shallow Versus Deep Copying
When we introduced arrays, we said that you could assign one array to another, but you wouldn’t get what you expect. That’s because you would just be copying the address of one array into another, not the contents of the array. The same is true of a linked list. After the following operations
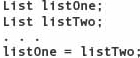
listOne just points to the first node of listTwo. With the built-in assignment operator (=), assignment of one class object to another copies only the class members; it does not copy any data pointed to by the class members. See FIGURE 14.6.
The result is called a shallow copy operation: The pointer is copied, but the pointed-to data is not. Shallow copying is perfectly fine if none of the class members are pointers. In the preceding example, length, currentPos, and lastPtr are copied as you would expect. But if one or more members are pointers to dynamic data, then shallow copying may not give the results you expect. Only the external pointer to the list (dataPtr) is copied into listOne, not the list to which it points. Thus there is only one copy of the linked list, not two as you would expect when copying one instance to another. In addition, the dynamic data originally pointed to by the listOne object has been left inaccessible. See Figure 14.6.
Shallow copy An operation that copies one class object to another without copying any pointed-to data.
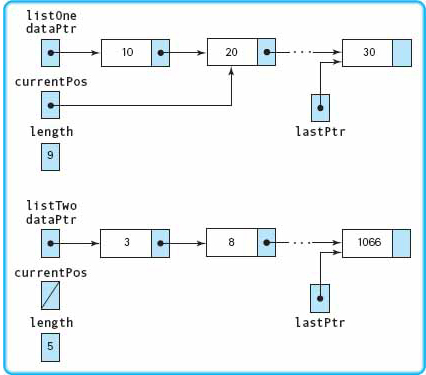
FIGURE 14.6 Shallow Copy (Initial State)
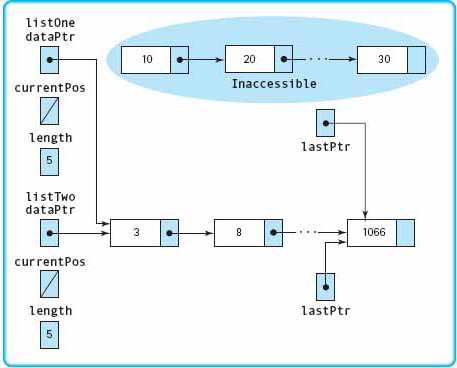
FIGURE 14.6 Shallow Copy After Executing listOne = listTwo;
What we really want is a deep copy operation—one that duplicates not only the class members, but also the pointed-to data.
Deep copy An operation that not only copies one class object to another, but also makes copies of any pointed-to data.
Copy-Constructor
As we have just discussed, the built-in assignment operator (=) leads to a shallow copy when class data members point to dynamic data. The issue of deep versus shallow copying also can crop up in another context: initialization of one class object by another. C++ defines initialization to mean the following:
1. Initialization in a variable declaration:
Name name1(“Kenneth”, “Charles”, “Smith”); Name name2 = name1;
2. Passing a copy of an argument to a parameter (that is, passing by value)
3. Returning an object as the value of a function:
return someObject;
By default, C++ performs such initializations using shallow copy semantics. In other words, the newly created class object is initialized via a member-by-member copy of the old object without regard for any data to which the class members may point. Both name1 and name2 point to the same three strings; they do not each point to separate copies of the strings.
To handle this situation, C++ supports a special kind of constructor known as a copy–constructor. In a class declaration, its prototype has the following form:

Notice that the function prototype does not use any special words to suggest that this is a copy-constructor. You simply have to recognize the pattern of symbols: the class name followed by a parameter list, which contains a single const reference parameter of its own type:
const SomeClass&
The copy-constructor is more challenging to write than the destructor. Before we look at this task, we must stress the importance of providing a copy-constructor whenever we also provide a destructor. Pretend that List doesn’t have a copy-constructor, and suppose that a client passes a class object to a function using pass by value. (Remember that passing an argument by value sends a copy of the value of the argument to the function.) Within the function, the parameter is initialized to be a copy of the caller’s class object, including the caller’s value of the private external pointer to the list. At this point, both the argument and the parameter are pointing to the same dynamic linked list. When the client function returns, the class destructor is invoked for the parameter, destroying the only copy of the linked list. Upon return from the function, the caller’s linked list has disappeared!
By providing a copy-constructor, we ensure deep copying of an argument to a parameter whenever a pass by value occurs. The implementation of the copy-constructor, shown next, employs a commonly used algorithm for creating a new linked list as a copy of another: We set up the external pointer to the new list and copy the first node. We then use a While loop to traverse the original list, copying each node and linking the copy into the new list.

If a copy-constructor is present, the default method of initialization (member-by-member copying) is circumvented. Instead, the copy-constructor is implicitly invoked whenever one object is initialized by another.
In summary, the default operations of assignment and initialization may be dangerous when objects point to dynamic data on the free store.1 Member-by-member assignment and initialization cause only pointers to be copied, not the pointed-to data. If a class allocates and deallocates dynamic data, it almost certainly needs the following suite of member functions to ensure deep copying of dynamic data:

QUICK CHECK

14.5.1 If you want to copy all of the pointed-to data in a struct or class, should you use deep or shallow copying? (p. 746)
14.5.2 Two of the ways that C++ defines initialization are initialization in a variable declaration and passing an argument by value. What is the third way that C++ defines initialization? (pp. 748–749)
14.5.3 Every class that manipulates dynamic data should have a constructor, a destructor, and which other member function? (p. 746)
14.5.4 What is a copy constructor? (p. 748)
14.6 Sorted Linked List
As we saw in the array-based list implementation, the only operations that differ between an unsorted list and a sorted list are the insert operation and the delete operation. The same is true in the linked implementation.
To insert a component into its proper place in a sorted list, we must loop through the nodes until we find where the component belongs. Because the SortedList class keeps components in ascending order, we can recognize where a component belongs by finding the node that contains a value greater than the one being inserted. Our new node should be inserted directly before the node with that value; therefore, we must keep track of the node before the current one so that we can insert our new node. We use a pointer prevPtr to point to this previous node as we did in the delete operation.
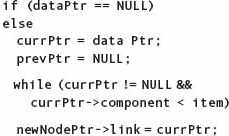
What are the special cases? When the list is empty, when the value to be inserted is less than the first, and when the value to be inserted is greater than the last. Let’s check for the empty list before we enter the loop. When the loop exits, there are two cases: If the current pointer is NULL, the node is inserted at the end; otherwise, the node is inserted between the trailing pointer and the current pointer. This method leads to the following algorithm:

The following function implements our algorithm with these changes incorporated:
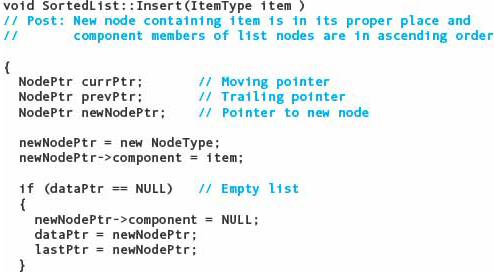

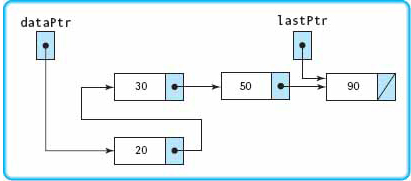
Let’s go through this code for each of the three cases: inserting at the beginning (item is 20), inserting in the middle (item is 60), and inserting at the end (item is 100). Each insertion begins with the following list:
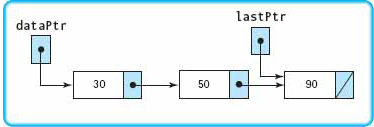
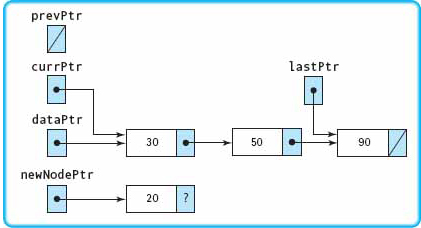
The next diagram shows the status after initialization. The only thing that changes is the value in the component field of newNodePtr.
Insert(20)

|
These two statements create and initialize the new node. |
|
List is not empty.
Set up for traversal.
Because 20 is less than 30, the expression is false and the loop body is not entered.
link member of *newNodePtr now points to *currPtr. |
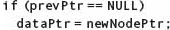
|
Because prevPtr is NULL, the then-clause is executed and 20 is inserted at the front of the list. |
Insert(60) (pick up with loop)

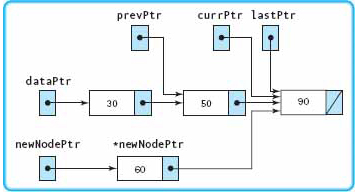
|
Because 30 is less than 60, this expression is true and the loop body is repeated. Pointer variables are advanced. |
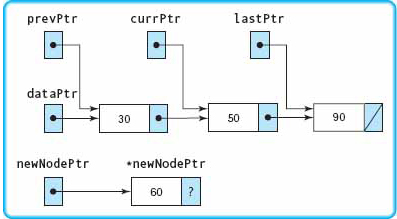

|
Because 50 is less than 60, the expression is true and the loop body is repeated. Pointer variables are advanced. |
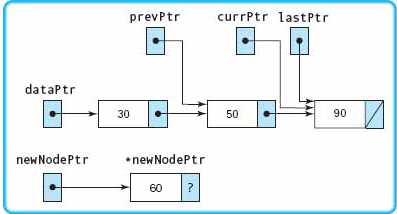

|
Because 90 is not less than 60, the expression is false and the loop body is not repeated. |
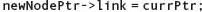
|
link member of *newNodePtr now points to *currPtr. |
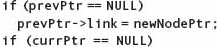
|
Because the node is not inserted as the first component, the else-clause is executed.
Because the node is not inserted as the last component, no further action is taken. |
Insert(100)
We do not repeat the first part of the search, but pick up the walk-through where prevPtr is pointing to the node whose component is 50, and currPtr is pointing to the node whose component is 90.

|
Because 90 is less than 100, this expression is true and the loop body is repeated.
The pointer variables are advanced. |
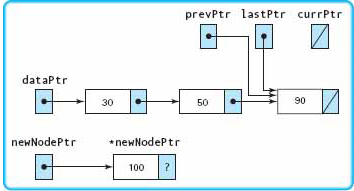

|
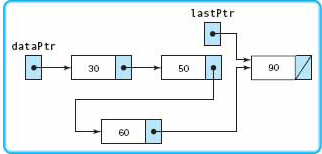
Because currPtr equals NULL, the expression is false and the loop body is not repeated. NULL is copied into the link member of *newNodePtr. |

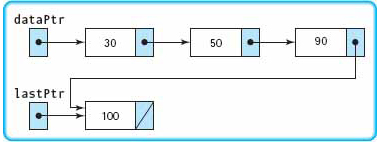
|
Because the node is not inserted as the first component, the else-clause is executed. The node is inserted at the end, so lastPtr is updated. |
Deleting from a Linked List
To delete an existing node from a linked list, we have to loop through the nodes until we find the node we want to delete. In fact, the function written for the unordered list would work just fine here. However, we can determine that the item is not present when we pass a value that is greater than the one we are deleting. Thus the While expression needs an additional test (which we show as shaded).
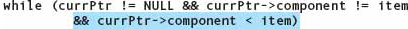
Now there are two conditions that indicate that the item is not there: currPtr is NULL or currPtr→component < item. Here is the coded function with the changes shaded:
Let’s see what happens when we delete the node whose component is 30. The structure is shown below, with the nodes labeled with their state when the While statement is reached. Because the While and If expressions are so long, we show only the part of the expression responsible for the result.
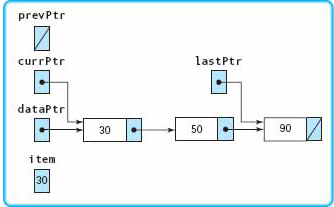
Delete(30)
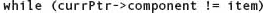
|
The item is found so the loop is not entered. |

|
The item is found.
The node is the first one.
The external pointer points to the second node. |

|
The node is not the last.
*currPtr is returned to the heap.
The length of the list is decremented. |
Delete(50)
The picture is the same except that item contains 50.

|
All of the expressions are true so the loop is entered.
Pointers are moved forward. |

|
The node does contain the item to be deleted, so the loop is not entered again. |

|
The item is found.
The node is not the first one.
The node with 30 is linked to the node with 90. |

|
The node is not the last.
*currPtr is returned to the heap.
The length of the list is decremented. |
We leave the walk-through of the other cases as an exercise. We could use this same technique to improve the efficiency of IsThere. We leave its reimplementation as an exercise.
QUICK CHECK

14.6.1 What are the special cases for inserting a node into a sorted linked list? (p. 751)
Problem-Solving Case Study
Creating a Sorted List of Entry Objects
PROBLEM: Create a sorted list of time/name pairs ordered by time.
DISCUSSION: We already have a Name class, a TimeOfDay class, and an Entry class made up of Name and TimeOfDay objects. (See Chapter 12.) We have two List classes, one unordered and one sorted. Because the list is to be returned in order by time, we must use the sorted list. It looks like the solution to this problem involves simply putting building blocks together, where the building blocks are classes. We can use each of these classes directly, except for the List class.
The List class is a list of ItemType objects in which ItemType is set by a Typedef statement. In the case study in Chapter 13, we used the List class to hold a list of integers. Here we have a list of Entry objects, which should be ordered by time. That’s okay; we have a SortedList class we can use. Uh oh, on second thought, it really isn’t okay: The SortedList operations compare items using the relational operators, but our TimeOfDay class only supports a ComparedTo function that returns values of RelationType. If we are going to have a sorted list of objects of class Entry, we must add to the class a ComparedTo function that compares TimeOfDay objects. Then we need to change the SortedList implementation to use the ComparedTo operation instead of the relational operators.
As it stands now, there is only one parameterized constructor for class Entry, which takes parameters representing the separate parts of a name and time, so that it can build Name and TimeOfDay objects internally. Let’s include a second parameterized constructor that takes already instantiated objects as parameters. Here are the prototypes for the new functions:

SORTED LIST: Is our current SortedList class useless? No; we must rewrite the functions that require comparisons: Insert, Delete, and IsThere. We replace the relational operators with the ComparedTo function from the Entry class, thereby specializing the list. But we can directly use the operations that do not require a comparison.
Is there some way that we could avoid this specialization and have a linked list that works for many different types? Yes—several advanced features of C++ will allow us to solve this problem by creating a general list. We look at one of them in Chapter 16.
Do we really need to change Delete? Our problem doesn’t indicate that we need to delete an appointment, but we should anticipate such an operation in the future. Note that “item” is of class Entry, and our comparisons are based on time, so ComparedTo in class Entry just calls ComparedTo in class TimeOfDay. IsThere should also be changed because the client needs to be sure the item isn’t in the list before inserting it.
Insert(In: item)
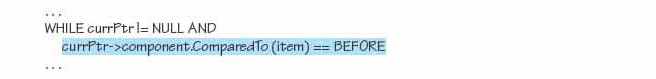
Delete(In: item)

We must remember to add to the specification file the Typedef statement that equates itemtype with Entry.
DRIVER: The calls to the SortedList functions to implement the tasks currently go into the driver. When we incorporate what we have done here into the bigger task, the driver will become part of the class that manipulates a day’s events. We need to create Entry objects and insert them into the sorted list. We must precede each insertion with a test to be sure the item is not already present in the list. We should try to insert one copy to be sure IsThere works correctly. Here is the driver program:

Output:

Testing and Debugging
One common error—leaving inaccessible objects on the free store—usually results from either a shallow copy operation or incorrect use of the new operator. In FIGURE 14.6, we showed how the built-in assignment operator causes a shallow copy; the dynamic data object originally pointed to by one pointer variable remains allocated but is inaccessible. Misuse of the new operator also can leave dynamic data inaccessible. For example, execution of the code fragment

creates an inaccessible object: the dynamic variable containing 38.5. The problem is that we assigned a new value to floatPtr in the last statement without first deallocating the variable it pointed to. To guard against this kind of error, examine every use of the new operator in your code. If the associated variable currently points to data, delete the pointed-to data before executing the new operation.
Finally, dangling pointers are a source of errors and can be difficult to detect. One cause of dangling pointers is the deallocation of a dynamic data object that is pointed to by more than one pointer. Figures 14.2d and 14.2e picture this situation. A second cause of dangling pointers is returning a pointer to an automatic variable from a function. The following function, which returns a function value of type int*, is erroneous:

Remember that automatic variables are implicitly created at block entry and implicitly destroyed at block exit. The preceding function returns a pointer to the local variable n, but n disappears as soon as control exits the function. The caller of the function, therefore, receives a dangling pointer. Dangling pointers are hazardous for the same reason that uninitialized pointers are hazardous: When your program dereferences incorrect pointer values, it will access memory locations whose contents are unknown.
Testing and debugging a linked structure are complicated by the fact that each item in the structure contains not only a data portion but also a link to the next item. Algorithms must correctly account for both the data and the link.
Testing and Debugging Hints
1. A function must not return a pointer to automatic local data; otherwise, a dangling pointer will result.
2. If ptrA and ptrB point to the same dynamic data object, the statement
delete ptrA;
makes ptrB become a dangling pointer. You should now assign the value NULL to ptrB rather than leave it dangling.
3. Deallocate dynamic data when it is no longer needed. Memory leaks can cause you to run out of memory space.
4. Inaccessible objects—another cause of memory leaks—are caused by
a. Shallow copying of pointers that point to dynamic data. When designing C++ classes whose data members point to dynamic data, be sure to provide a deep copy operation and a copy-constructor.
b. Using the new operation when the associated variable already points to dynamic data. Before executing new, use delete to deallocate the data that is currently pointed to.
5. Make sure that the link member in the last node of a dynamic linked list has been set to NULL.
6. When visiting the components in a dynamic linked list, test for the end of the list in such a way that you don’t try to dereference the NULL pointer. On many systems, dereferencing the NULL pointer will cause a run-time error.
7. Be sure to initialize the external pointer to each dynamic data structure.
8. Do not use
currPtr++;
to make currPtr point to the next node in a dynamic linked list. The list nodes are not necessarily in consecutive memory locations on the heap.
9. Keep close track of pointers. Changing pointer values prematurely may cause problems when you try to access the pointed-to variable.
10. If a C++ class that points to dynamic data has a class destructor but not a copy-constructor, do not pass a class object to a function using pass by value. A shallow copy will occur, and both the parameter and the argument will point to the same dynamic data. When the function returns, the parameter’s destructor is executed, destroying the argument’s dynamic data.
11. The delete operator must be applied to a pointer whose value was previously returned by new. Also, the delete operation leaves the value of the pointer variable undefined; do not use the variable again until you have assigned a new value to it.
12. A function must not return a pointer to automatic local data; otherwise, a dangling pointer will result.
 Summary
Summary
A powerful use of pointers is to create dynamic variables. While a pointer variable can be declared at compile time, the data to which the pointer points is only created at run time. The built-in operator new creates a variable on the free store (heap) and returns the address of that variable, for storage in a pointer variable. A dynamic variable is not given a name, but rather is accessed through a pointer variable.
The use of dynamic data saves memory space because a variable is created only when it is needed at run time. When a dynamic variable is no longer needed, it can be deallocated (using delete) and the memory space can be reused. Use of dynamic data can also save machine (computing) time when large structures are being sorted. With this approach, we simply rearrange the pointers to the large structures, rather than the large structures themselves.
When C++ class objects point to data on the free store, it is important to distinguish between shallow copy and deep copy operations. A shallow copy of one class object to another copies only the pointers and results in two class objects pointing to the same dynamic variable. A deep copy results in two distinct copies of the pointed-to data. Classes that manipulate dynamic data usually require a complete collection of support routines: one or more constructors, a destructor (for cleaning up the free store), a deep copy operation, and a copy-constructor (for deep copying during initialization of one class object by another).
Dynamic data structures grow and contract during run time. They are made up of nodes that contain two kinds of members: (1) the component and (2) one or more pointers to nodes of the same type. The pointer to the first node is saved in a variable called the external pointer to the structure.
A linked list is a data structure in which the components are logically next to each other, rather than physically next to each other as they are in an array. A linked list can be represented as a collection of dynamic nodes, linked together by pointers. The end of a dynamic linked list is indicated by the special pointer constant NULL. Common operations on linked lists include inserting a node, deleting a node, and traversing the list (visiting each node from first to last).
In this chapter, we used linked lists to implement lists. Linked lists are also used to implement many data structures other than lists. The study of data structures forms a major topic in computer science. Indeed, entire books have been written and courses developed to cover the subject. A solid understanding of the fundamentals of linked lists is a prerequisite to creating more complex structures.
 Quick Check Answers
Quick Check Answers
14.1.1 new 14.1.2 delete 14.1.3 Variables created during execution of a program by means of special operators. In C++, these operators are new and delete. 14.1.4 It creates an uninitialized variable (or array) and returns the address of this variable. 14.1.5 free store or heap. 14.1.6 It returns allocated memory to the free store. 14.2.1 Because pointers allow us to dynamically create the list to be only as long as necessary. 14.2.2 A pointer to the next node in the list. 14.2.3 A linked list is a collection of items that can be scattered about in memory where as an array is a sequential collection of items that reside in consecutive memory locations. 14.2.4 insert and delete 14.2.5 A pointer that points to the first node in a linked list. 14.3.1 A linked list composed of dynamically allocated nodes that are linked together by pointers. 14.3.2 A data structure that can expand and contract during execution. 14.3.3 The external head pointer. 14.3.4 Set the pointer of the existing node in the linked list to point to the new node. 14.4.1 Allocate a new node. Assign the value from the node pointer of the current node to the node pointer of the new node. Assign the node pointer of the current node to equal the address of the new node. Assign any data members to the new node as appropriate. 14.4.2 Assign the value of the node pointer of the current node to a temporary pointer. Assign the value of the node pointer from the node pointed to by the node pointer field of the current node to the node pointer field of the current node. (Assign the address of the node following the one to be deleted to the node pointer of the current node.) Delete the data associated with the temporary pointer.
14.4.4 It always returns false because a linked list cannot be full. 14.5.1 Deep copying. 14.5.2 Returning an object as the value of a function. 14.5.3 A copy constructor. 14.5.4 A constructor that is specifically designed to construct a new object based on an old object using deep copy semantics. 14.6.1 When the list is empty, when the value to be inserted is less than the first, and when the value to be inserted is greater than the last.
 Exam Preparation Exercises
Exam Preparation Exercises
1. Match the following terms with the definitions given below.
a. Pointer type
b. Indirect addressing
c. Direct addressing
d. Reference type
e. Shallow copy
f. Deep copy
i. Accessing a variable using its name
ii. Assigning the value of one object to another object, including the duplication of any pointed-to data
iii. Accessing a variable using an address stored in a pointer
iv. A simple type that can only be initialized with the address of a variable
v. A simple type that can be assigned the address of a variable
vi. Assigning the value of one object to another without duplicating any pointed-to data
2. Match the following terms with the definitions given below.
a. Heap
b. Memory leak
c. Inaccessible object
d. Dangling pointer
e. Destructor
f. Dynamic data
i. The loss of available space that occurs when dynamic data is not deallocated properly
ii. The area of memory used for allocation and deallocation of dynamic data
iii. An object that has been allocated but has no pointer pointing to it
iv. Variables created with the new operation
v. A pointer that points to a deallocated object
vi. A member function invoked when an object goes out of scope
3. When an object goes out of scope, its pointer variables are automatically deleted, but their pointed-to values are not automatically deleted. True or false?
4. Does delete return the pointer variable to the heap or the pointed-to data?
5. What happens to the pointer(s) and pointed-to data in an object if the object goes out of scope without applying delete to the corresponding pointer(s)?
6. What is wrong with the following code segment?

7. What is wrong with the following code segment?

8. The copy-constructor for class faxLog should have one parameter. What should the type of this parameter be?
9. Why is it a problem if you perform a shallow copy of one object to another object and then delete the first object and all of its pointed-to dynamic data?
10. Which kind of member function does the following heading declare?
˜phoneTree();
11. Applying delete to the NULL pointer produces an error message. True or false?
12. In the following expression, index is a pointer to an array and book is a member of a struct of type libraryRecord:
index[12] → book[5]
What is the type of the components that are contained in the array that index points to?
13. Define the following terms:
a. Node
b. Component member
c. Link member
d. Current pointer
14. We only need an external pointer for a dynamic linked list. With an array-based list, we can find the head automatically. True or false?
15. Using a forward declaration of the node pointer type allows us to avoid using an anonymous type to declare the link field within the struct representing the node. True or false?
16. Which value does each of the following expressions access? The variable names have the same meanings as we have used them elsewhere in this chapter.
a. currPtr→link
b. currPtr→component
c. currPtr→link→component
d. currPtr→link→link
e. currPtr→link→link→component
f. head→link→link→link→component
17. a. Which special state of a list does the condition listPtr == NULL test for?
b. Which special condition does the expression currPtr == NULL test for?
18. What are the algorithmic steps for inserting a new node into a sorted linked list?
19. What are the algorithmic steps for deleting the successor of the current node, assuming that the current node is not the last node in the list?
20. For each of the following operations, decide which is faster: a direct array representation of a list or a linked representation of a list.
a. Inserting near the front of the list
b. Deleting the last element of the list
c. Accessing the nth element
d. Searching for an item in a sorted list
21. Why does the following code segment produce a compiler error? What is missing from the declarations?
22. For each of the following, decide whether a direct array implementation or a dynamic linked list representation would be the best choice. Assume that memory capacity is limited and that good speed of execution is desirable.
a. A list of CD titles in a personal library, with not more than 500 albums. CDs are rarely deleted and added occasionally, and the most frequent operation on the list is to search for a specific title.
b. A list of shipping orders to be processed. The orders are inserted as they come in, and they are deleted as they are shipped out. The list can be quite large just before the December holidays, but may be nearly empty in January. The list is occasionally searched for a specific item, to check its status.
c. An itinerary of customer visits for a salesperson. Visits may be added anywhere within the itinerary, and they are deleted from the head after they have been completed. The itinerary can be of any length.
23. What does the following code do?

a. Increments the contents of atlas.
b. Increments the contents of number.
c. Increments the contents of both atlas and number.
d. Adds 2 to number.
e. Produces a dangling pointer.
24. What does the following code do?

a. Increments the contents of weathervane.
b. Increments the contents of number.
c. Increments the contents of both weathervane and number.
d. Adds 2 to number.
e. Produces a dangling pointer.
25. What does the following code do?

a. Increments the contents of finger.
b. Increments the contents of number.
c. Increments the contents of both finger and number.
d. Adds 2 to number.
e. Produces a dangling pointer.
 Programming Warm-Up Exercises
Programming Warm-Up Exercises
1. Extend the Sorted Linked List described in this chapter to include an additional method called Split. The Split method takes a single parameter that is the type of the element contained in the list and will search the list until it finds a matching element. If it finds a matching element it should return a new Linked List of the elements that start with the matching element until the end of the original linked list. The original Linked List should be modified such that the element before the matching element becomes the last element in the list. If the element is not found Split should return NULL. You should reuse all the NodeType nodes in the original linked list in the linked list that is returned.
2. Declare a pointer variable structPointer and initialize it to point to a struct variable called newPhone, of type Phone, that has three int fields called country, area, and number. Also write the declaration of the Phone type. Then write assignment statements to indirectly store the values 1, 888, and 5551212, respectively, into these fields.
3. Write a Boolean value-returning function called ShallowCompare that takes two variables of type structPointer, as defined in Exercise 2, and returns true if they point to the same struct and false otherwise.
4. Write a Boolean value-returning function called DeepCompare that takes two variables of type structPointer, as defined in Exercise 2, and returns true if the structs that they point to have identical values in their corresponding fields.
5. Write a For loop that scans through a dynamically allocated int array, pointed to by a variable called dataPtr, keeping track of the greatest value in a static int variable max. The array contains 100 values. At the end of the loop, the array should be deleted.
6. Wrap the For loop written in Exercise 5 in an int-returning function called Greatest that takes the array and its size as parameters and returns the value in max after the array is deleted. Be sure to change the loop to work with the given array size rather than the constant 100.
7. Write an int-returning function that prompts the user for the number of values to be entered, creates an int array of that size, and reads that many values into it. The function then passes this array to the Greatest function defined in Exercise 6, and returns the result from that function as its own result. Call the new function GetGreatestlnput.
8. A class called Circuit has two private dynamic array data members called source and sink. Write a destructor for the class that ensures that the dynamic data is destroyed.
9. Write a code segment that checks whether the pointer oldValue actually points to a valid memory location. If it does, then its contents are assigned to newValue. If not, then newValue is assigned a new int variable from the heap.
10. Write a code segment that checks whether the pointers oldValue and newValue point to different locations. If they do, then delete the value pointed to by oldValue; otherwise, do nothing.
11. Given the dynamic linked implementation of a linked list shown below, write expressions that do the following, assuming that currPtr is somewhere in the middle of the list:
a. Access the component member of the first list element.
b. Advance currPtr to point to the next element.
c. Access the component member of the next element (the one that follows the current element).
d. Access the component member of the element that follows the next element.
12. Given the declarations in Exercise 11, write a code segment that creates a new node, assigns the value 100 to the component member, links listPtr to the new node, and sets currPtr to also point to the node.
13. Given the declarations in Exercise 11, and the fact that the first node has been inserted into the list as in Exercise 12, write a code segment that creates a new node with the component value equal to 212 and inserts this node at the end of the list, updating any pointers as necessary.
14. Given the declarations in Exercise 11, assume that the list has a large collection of members and that currPtr is somewhere in the middle of the list. Write a code segment to insert a new node with the component value of 32 following the node pointed to by currPtr, and update currPtr to point to the new node.
15. Given the declarations in Exercise 11, assume that the list has a large collection of members and that currPtr is somewhere in the middle of the list. Write a code segment to remove the node following the node pointed to by currPtr and reinsert it at the head of the list.
16. Given the declarations in Exercise 11, write a void function that sorts the elements of the list in ascending order. The sort algorithm will scan the list, keeping a pointer to the lowest value seen thus far. When the end of the list is reached, the lowest value will be removed from that point and inserted at the end of a new list. After all of the elements have been moved from the original list to the new sorted list, change listPtr and currPtr to point to the first element of the new list. That way, when the function returns, the client code will simply see the list as having been sorted.
17. Given the code for the sorted delete operation on page 739, walk through the following deletions.
a. Delete from an empty list.
b. Delete 20 from the list on page 740.
c. Delete 30 from the list on page 740.
18. Write the code for the sorted version of IsThere.
 Programming Problems
Programming Problems
1. Imagine you have been asked by a first grade teacher to create a hangman game for her students to help them with spelling and word recognition. In the game of hangman you are first presented with a list of blanks representing unknown letters of a hidden word. You must then guess a letter to see if that letter exists in the word. If it does, the blank that corresponds to the guessed letter is then displayed along with blanks for the letters that have not been guessed yet. If you guess a previously guessed letter you get to try again. If you guess wrong you incrementally move toward being hung. You have eight bad guesses until you lose the game. To represent the different states of “being hung” we will use the values PLATFORM, HEAD, BODY, LEFT_ARM, RIGHT_ARM, LEFT_LEG, RIGHT_LEG, and HUNG. To implement the game you should use the Linked List ADT to represent the word being guessed. Each element in the list should be an object of type Slot that stores the letter of the word and a boolean that indicates if the letter is to be displayed or if a blank should be displayed. The Slot class should provide the appropriate observer and mutator methods for accessing and manipulating a slot. You should use a second linked list to represent the letters that have already been guessed and an enumeration to represent the states of the game. Your program should keep asking the user for another guess until either the entire word has been guessed or the state of the game is HUNG. After each guess, the program should display the current state of the word to be guessed, the list of characters already guessed, and the state of the game.
2. You are working for your state’s motor vehicle registry, and it has been discovered that some people in the driver’s license database have multiple records. The license records are stored in alphabetical order on a set of files, one file per letter in the alphabet. The first file is licensesa.dat, and the last is licensesz.dat. For this problem, we’ll just focus on getting the program to work for the licensesa.dat file. Each record consists of a license number (an eight-digit integer), a name, and an address, all on a single line. For the purposes of this problem, the name and address can be stored in a single string because they are not processed separately. The license number and the corresponding string should be kept together in a struct.
Use the functions of the SortedList class to create a list of numbers that contains no duplicates. If a duplicate is found in the data file, write the contents of the original entry (first one encountered) and the contents of any duplicates in the file on file duplicates.dat.
3. You’re working for a company that wants to take client contact information as it is entered by a salesperson from a stack of business cards that he or she has collected, and output the information to a file (contacts.dat) in alphabetical order. The program should prompt the salesperson for each of the following values for each card:
Last name
First name
Middle name or initial
Title
Company name
Street address
City
State
ZIP code
Phone number
Fax number
Email address
After the data are entered for each card, the user should be asked if there is another card to enter. Each card should be inserted into a sorted list, whose key is the last name. After all the data are entered, iterate through the list, writing each card onto file contacts.dat. Use the SortedList modified in the Problem-Solving Case Study.
4. You are working for a company that has a collection of files, each of which contains information from business cards. The files are created by another program (see Problem 3 for a description of what this program outputs). The company would like to merge the files into a single file, sorted alphabetically by last name. The user should be prompted to enter the names of the files, until a file name of “done” is entered. Once all of the data has been input, the sorted data should be written back out to a file called mergedcontacts.dat.
5. Create a new List ADT where duplicates are allowed. Define the delete operation to delete all copies of an item. Implement both an unordered version of the list and a sorted version.
6. Use the sorted list version defined and implemented in Problem 5 to solve Problem 2.
7. Use the sorted list version defined and implemented in Problem 5 to solve Problem 4.
 Case Study Follow-Up
Case Study Follow-Up
1. We did not discuss a copy-constructor or a destructor for the revised SortedList class. Would these functions have to be changed to use ComparedTo? Explain.
2. The classes in this case study have been built up over several chapters. Does this process demonstrate functional decomposition or object-oriented design? Explain.
3. Outline the next step in constructing an appointment calendar.
 To understand the concept of a linked data structure.
To understand the concept of a linked data structure. To understand the difference between deep and shallow copy operations.
To understand the difference between deep and shallow copy operations. To know and understand the four member functions that should be present in any class that manipulates dynamic data.
To know and understand the four member functions that should be present in any class that manipulates dynamic data.









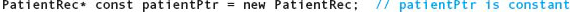

 A component or item member, which contains one of the data values in the list
A component or item member, which contains one of the data values in the list

































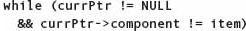

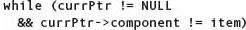
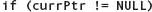
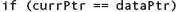
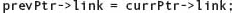
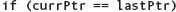
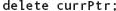
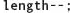
























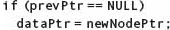






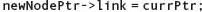

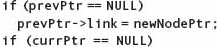






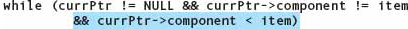


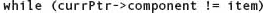







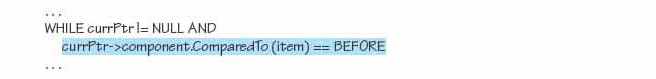





 Summary
Summary







