

In order to understand calculus, you need to know what a “limit” is. A limit is the value a function (which usually is written “f(x)” on the AP exam) approaches as the variable within that function (usually “x”) gets nearer and nearer to a particular value. In other words, when x is very close to a certain number, what is f(x) very close to? As far as the AB test is concerned, that’s all you have to know about evaluating limits. There’s a more technical method that you BC students have to learn, but we won’t discuss it until we have to—at the end of this chapter.
Let’s look at an example of a limit: What is the limit of the function f(x) = x2 as x approaches 2? In limit notation, the expression “the limit of f(x) as x approaches 2” is written like this: 
![]() f(x). In order to evaluate the limit, let’s check out some values of
f(x). In order to evaluate the limit, let’s check out some values of 
![]() f(x) as x increases and gets closer to 2 (without ever exactly getting there).
f(x) as x increases and gets closer to 2 (without ever exactly getting there).
When x = 1.9, f(x) = 3.61.
When x = 1.99, f(x) = 3.9601.
When x = 1.999, f(x) = 3.996001.
When x = 1.9999, f(x) = 3.99960001.
As x increases and approaches 2, f(x) gets closer and closer to 4. This is called the left-hand limit and is written: 
![]() f(x). Notice the little minus sign!
f(x). Notice the little minus sign!
What about when x is bigger than 2?
When x = 2.1, f(x) = 4.41.
When x = 2.01, f(x) = 4.0401.
When x = 2.001, f(x) = 4.004001.
When x = 2.0001, f(x) = 4.00040001.
As x decreases and approaches 2, f(x) still approaches 4. This is called the right-hand limit and is written like this: 
![]() f(x). Notice the little plus sign!
f(x). Notice the little plus sign!
We got the same answer when evaluating both the left- and right-hand limits, because when x is 2, f(x) is 4. You should always check both sides of the independent variable because, as you’ll see shortly, sometimes you don’t get the same answer. Therefore, we write that 
![]() x2 = 4.
x2 = 4.
We didn’t really need to look at all of these decimal values to know what was going to happen when x got really close to 2. But it’s important to go through the exercise because, typically, the answers get a lot more complicated. Let’s do a few examples.
The approach is simple: Plug in 5 for x, and you get 25.
Example 2: Find 
![]() x3.
x3.
Here the answer is 27.
There are some simple algebraic rules of limits that you should know. These are:

![]() Kf(x) = k
Kf(x) = k 
![]() f(x)
f(x)
Example: 
![]()
If 
![]() f(x) = L1 and
f(x) = L1 and 
![]() g(x) = L2, then
g(x) = L2, then 
![]() [f(x) + g(x)] = L1 + L2
[f(x) + g(x)] = L1 + L2
Example: 
![]()
If 
![]() f(x) = L1 and
f(x) = L1 and 
![]() g(x) = L2, then
g(x) = L2, then 
![]() [f(x) · g(x)] = L1 · L2
[f(x) · g(x)] = L1 · L2
Example: 
![]()
Plug in 0, and you get 0.
So far, so good. All you do to find the limit of a simple polynomial is plug in the number that the variable is approaching and see what the answer is. Naturally, the process can get messier—especially if x approaches zero.
Example 4: Find 
![]() .
.
If you plug in some very small values for x, you’ll see that this function approaches ∞. And it doesn’t matter whether x is positive or negative, you still get ∞. Look at the graph of y = 
![]() :
:


On either side of x = 0 (the y-axis), the curve approaches ∞.
Example 5: Find 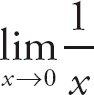
![]() .
.
Here you have a problem. If you plug in some very small positive values for x (0.1, 0.01, 0.001, and so on), you approach ∞. In other words, 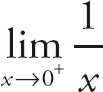
![]() = ∞. But, if you plug in some very small negative values for x (−0.1, −0.01, −0.001, and so on) you approach –∞. That is,
= ∞. But, if you plug in some very small negative values for x (−0.1, −0.01, −0.001, and so on) you approach –∞. That is, 
![]() = −∞. Because the right-hand limit is not equal to the left-hand limit, the limit does not exist.
= −∞. Because the right-hand limit is not equal to the left-hand limit, the limit does not exist.


You can see that on the left side of x = 0, the curve approaches –∞, and on the right side of x = 0, the curve approaches ∞. There are some very important points that we need to emphasize from the last two examples.
Why do we state the limit in Example 4 but not for Example 5? Because when we have 
![]() , the function is always positive no matter what the sign of x is and thus the function has the same limit from the left and the right. But when we have
, the function is always positive no matter what the sign of x is and thus the function has the same limit from the left and the right. But when we have 
![]() , the function’s sign depends on the sign of x, and you get a different limit from each side.
, the function’s sign depends on the sign of x, and you get a different limit from each side.
Let’s look at a few examples in which the independent variable approaches infinity.
(1) If the left-hand limit of a function is not equal to the right-hand limit of the function, then the limit does not exist.
(2) A limit equal to infinity is not the same as a limit that does not exist, but sometimes you will see the expression “no limit,” which serves both purposes. If 
![]() f(x)= ∞, the limit, technically, does not exist.
f(x)= ∞, the limit, technically, does not exist.
(3) If k is a positive constant, then 
 = ∞,
= ∞, 
 = −∞, and
= −∞, and 
![]() does not exist.
does not exist.
(4) If k is a positive constant, then 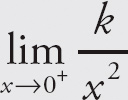
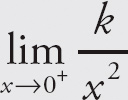 = ∞,
= ∞, 
 = ∞, and
= ∞, and 
 = ∞.
= ∞.
As x gets bigger and bigger, the value of the function gets smaller and smaller. Therefore, 
![]() = 0.
= 0.
Example 7: Find 
![]() .
.
It’s the same situation as the one in Example 6; as x decreases (approaches negative infinity), the value of the function increases (approaches zero). We write the following:

![]() = 0
= 0
We don’t have the same problem here that we did when x approached zero because “positive zero” is the same thing as “negative zero,” whereas positive infinity is different from negative infinity.
Here’s another rule.
If k and n are constants, |x| > 1, and n > 0, then 
![]() = 0, and
= 0, and 
![]() = 0.
= 0.
Example 8: Find 
![]() .
.
When you have variables in both the top and the bottom, you can’t just plug ∞ into the expression. You’ll get 
![]() . We solve this by using the following technique:
. We solve this by using the following technique:
When an expression consists of a polynomial divided by another polynomial, divide each term of the numerator and the denominator by the highest power of x that appears in the expression.
The highest power of x in this case is x1, so we divide every term in the expression (both top and bottom) by x, like so


Now when we take the limit, the two terms containing x approach zero. We’re left with 
![]() .
.
Example 9: Find 
 .
.
Divide each term by x2. You get
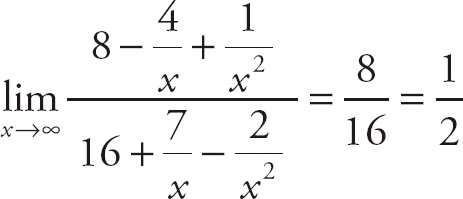
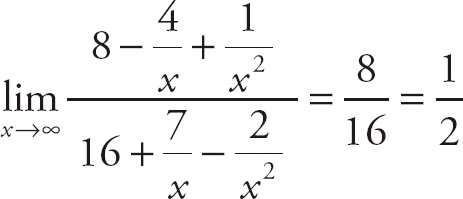
Example 10: Find 
 .
.
Divide each term by x10.
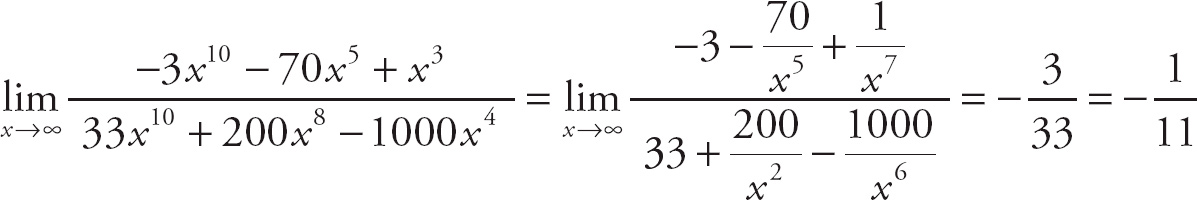
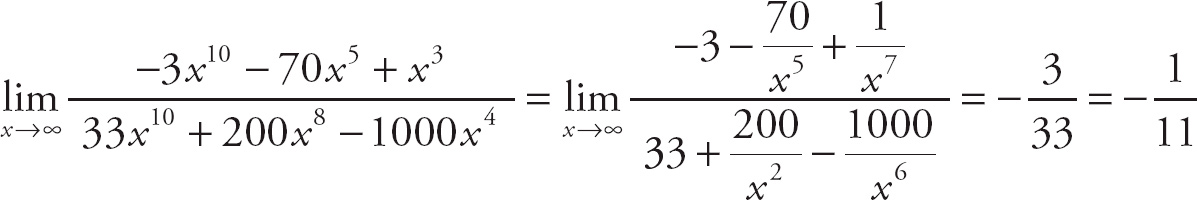
The other powers don’t matter, because they’re all going to disappear. Now we have three new rules for evaluating the limit of a rational expression as x approaches infinity.
(1) If the highest power of x in a rational expression is in the numerator, then the limit as x approaches infinity is infinity.
Example: 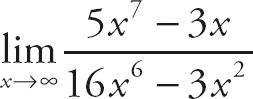
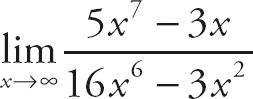 = ∞
= ∞
(2) If the highest power of x in a rational expression is in the denominator, then the limit as x approaches infinity is zero.
(3) If the highest power of x in a rational expression is the same in both the numerator and denominator, then the limit as x approaches infinity is the coefficient of the highest term in the numerator divided by the coefficient of the highest term in the denominator.
Example: 

At some point during the exam, you’ll have to find the limit of certain trig expressions, usually as x approaches either zero or infinity. There are four standard limits that you should memorize—with those, you can evaluate all of the trigonometric limits that appear on the test. As you’ll see throughout this book, calculus requires that you remember all of your trig from previous years.
Rule No. 1: 
![]() = 1 (x is in radians, not degrees)
= 1 (x is in radians, not degrees)
This may seem strange, but if you look at the graphs of f(x) = sin x and f(x) = x, they have approximately the same slope near the origin (as x gets closer to zero). Because x and the sine of x are about the same as x approaches zero, their quotient will be very close to one. Furthermore, because 
![]() cos x= 1 (review cosine values if you don’t get this!), we know that
cos x= 1 (review cosine values if you don’t get this!), we know that 
![]() tan x =
tan x = 
![]() = 0.
= 0.
Now we will find a second rule. Let’s evaluate the limit 
![]() . First, multiply the top and bottom by cos x + 1. We get
. First, multiply the top and bottom by cos x + 1. We get 
 . Now simplify the limit to:
. Now simplify the limit to: 
 . Next, we can use the trigonometric identity sin2 x = 1 − cos2 x and rewrite the limit as:
. Next, we can use the trigonometric identity sin2 x = 1 − cos2 x and rewrite the limit as: 
 . Now, break this into two limits:
. Now, break this into two limits: 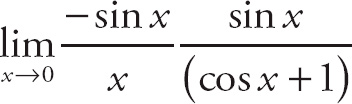
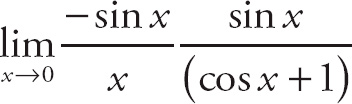 . The first limit is −1 (see Rule No. 1) and the second is 0 (why?), so the limit is 0.
. The first limit is −1 (see Rule No. 1) and the second is 0 (why?), so the limit is 0.
Rule No. 2: 
![]() = 0
= 0
Example 11: Find 
![]() .
.
Use a simple trick: Multiply the top and bottom of the expression by 3. This gives us: 
![]() . Next, substitute a letter for 3x; for example, a. Now, we get the following:
. Next, substitute a letter for 3x; for example, a. Now, we get the following:

Example 12: Find 
![]() .
.
Now we get a bit more sophisticated. First, divide both the numerator and the denominator by x, like so
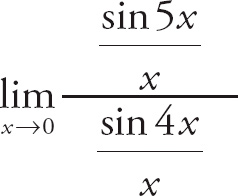
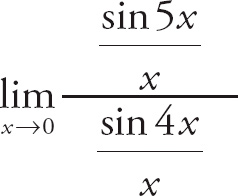
Next, multiply the top and bottom of the numerator by 5, and the top and bottom of the denominator by 4, which gives us


From the work we did in Example 11, we can see that this limit is 
![]() .
.
Guess what! You have two more rules!
Rule No. 3: 
![]() = a
= a
Rule No. 4: 
![]()
Example 13: Find 
![]() .
.
Using trigonometric identities, you can replace (1 – cos2x) with sin2x.
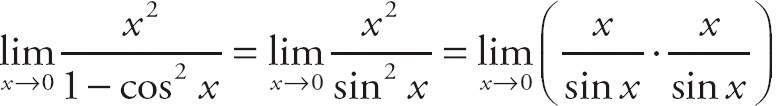
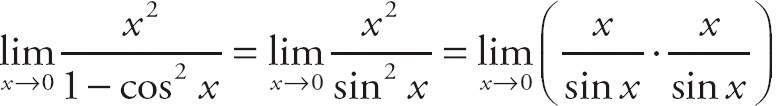 = 1 · 1 = 1
= 1 · 1 = 1Here are other examples for you to try, with answers right beneath them. Give ’em a try, and check your work.
PROBLEM 1. 
![]() .
.
Answer: If you plug in 3 for x, you get 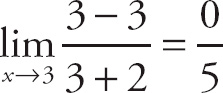
![]() = 0.
= 0.
PROBLEM 2. Find 
![]() .
.
Answer: The left-hand limit is: 
![]() = −∞
= −∞
These two limits are not the same. Therefore, the limit does not exist.
PROBLEM 3. Find 
 .
.
Answer: The left-hand limit is: 
 = ∞
= ∞
The right-hand limit is: 
 = ∞
= ∞
These two limits are the same, so the limit is ∞.
PROBLEM 4. Find 
![]() .
.
Answer: If you plug −4 into the top and bottom, you get 
![]() . You have to factor the top into (x+2)(x+4) to get this:
. You have to factor the top into (x+2)(x+4) to get this: 

Now it’s time to cancel like terms: 
 =
= 
![]() (x + 2) = −2.
(x + 2) = −2.
PROBLEM 5. Find 
 .
.
Answer: Divide each term by x2.
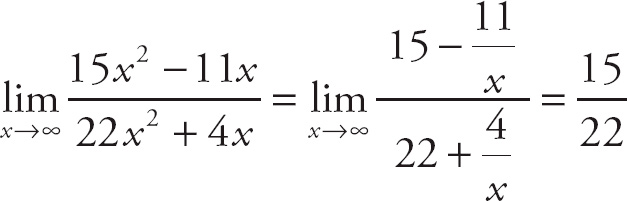
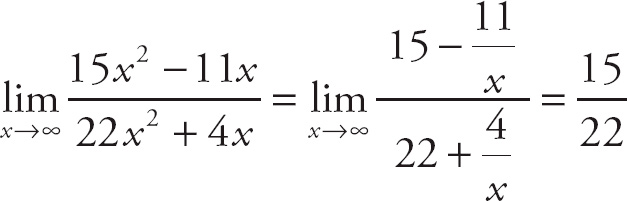
PROBLEM 6. Find 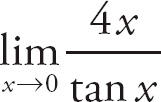
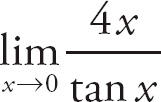 .
.
Answer: Replace tan x with 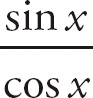
![]() , which changes the expression into
, which changes the expression into
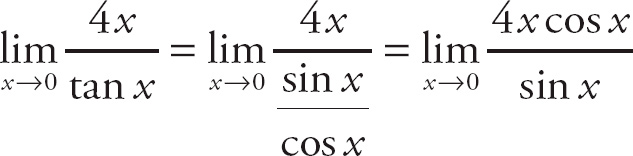
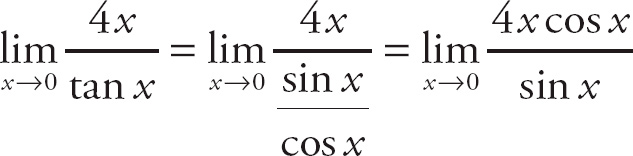
Because 
![]() = 1, the
= 1, the 
![]() = 1 as well. Thus, because
= 1 as well. Thus, because 
![]() = 1 and
= 1 and 
![]() = 1, the answer is 4.
= 1, the answer is 4.
PROBLEM 7. Find 
 .
.
Answer: First, expand and simplify the numerator.

Next, factor h out of the numerator and the denominator.

Taking the limit you get: 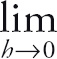
![]() (10 + h) = 10.
(10 + h) = 10.
Try these 30 problems to test your skill with limits. The answers are in Chapter 23.
1. 
![]() (x2 − 5x −11) =
(x2 − 5x −11) =
2. 
 =
=
3. 
![]() π2 =
π2 =
4. 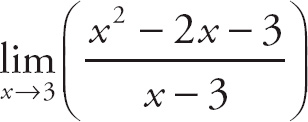
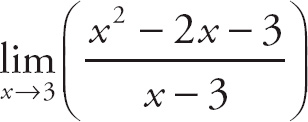 =
=
5. 
 =
=
6. 
 =
=
7. 
 =
=
8. 
 =
=
9. 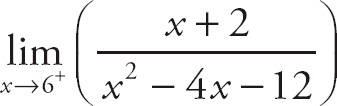
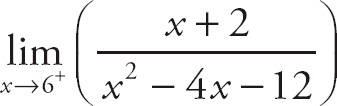 =
=
10. 
 =
=
11. 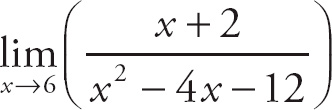
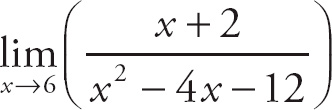 =
=
12. 
 =
=
13. 
 =
=
14. 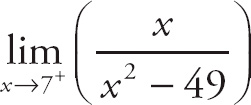
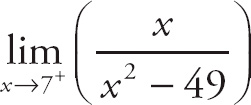 =
=
15. 
 =
=
16. 
![]() =
=
17. Let f(x) = 

Find: (a) 
![]() f(x); (b)
f(x); (b) 
![]() f(x); and (c)
f(x); and (c) 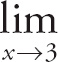
![]() f(x)
f(x)
18. Let f(x) = 

Find: (a) 
![]() f(x); (b)
f(x); (b) 
![]() f(x); and (c)
f(x); and (c) 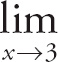
![]() f(x)
f(x)
19. Find 
![]() 3cos x.
3cos x.
20. Find 
![]() .
.
21. Find 
![]() .
.
22. Find 
![]() .
.
23. Find 
![]() .
.
24. Find 
![]() sinx.
sinx.
25. Find 
![]() .
.
26. Find 
 .
.
27. Find 
 .
.
28. Find 
 .
.
29. Find 
![]() .
.
30. Find 
 .
.