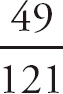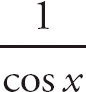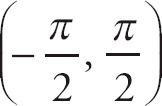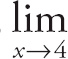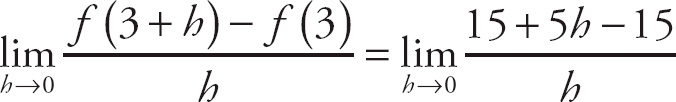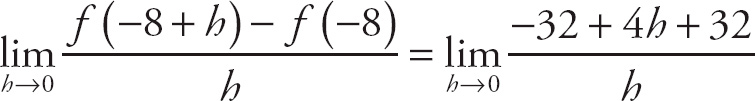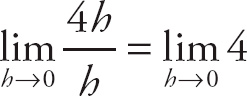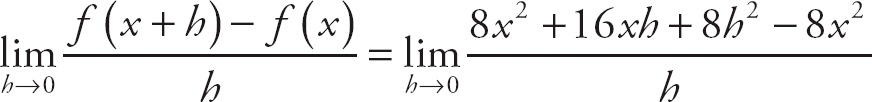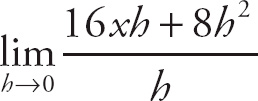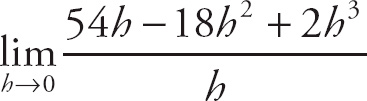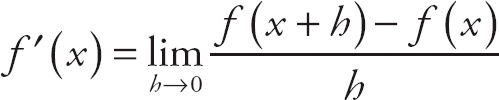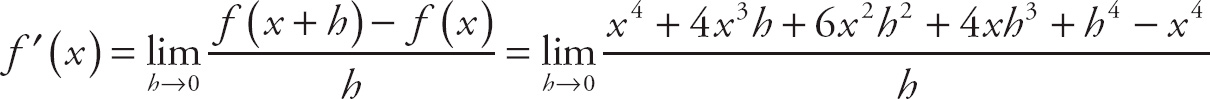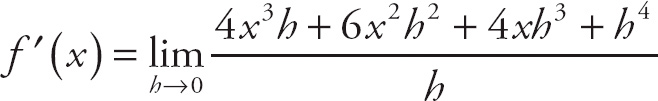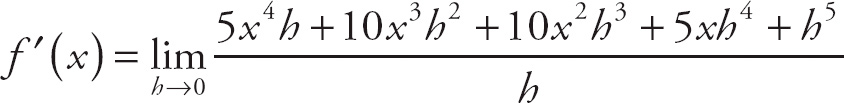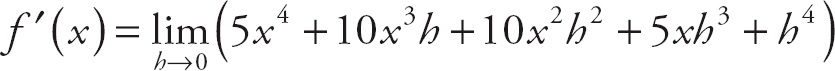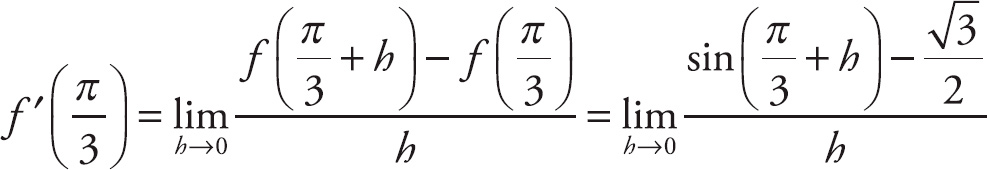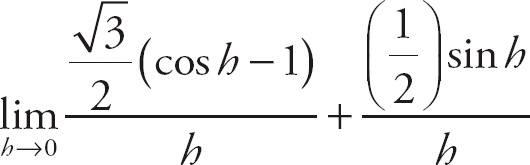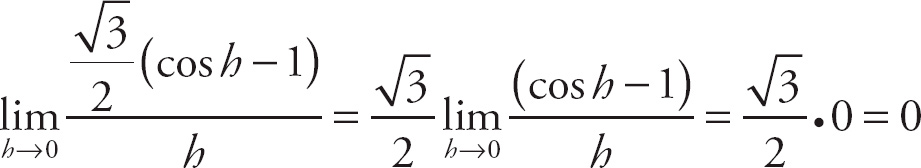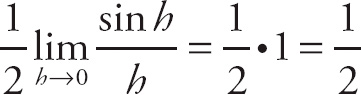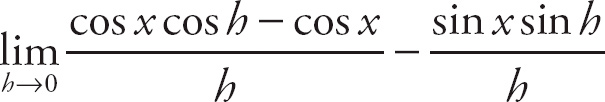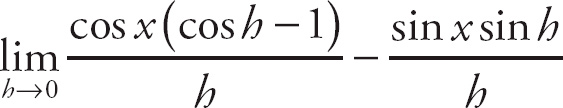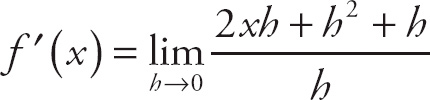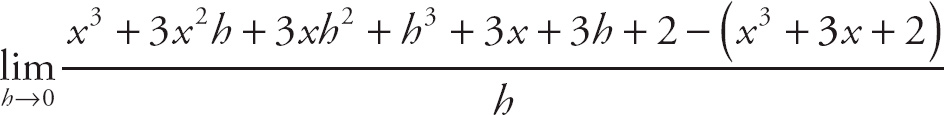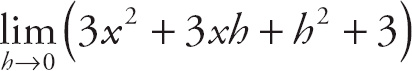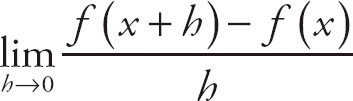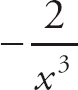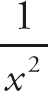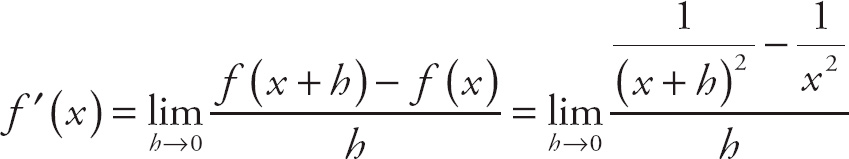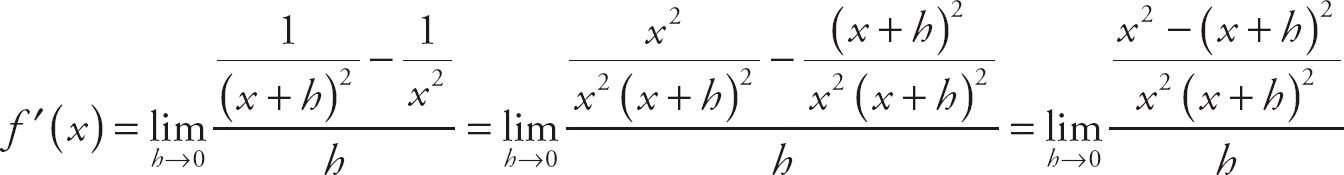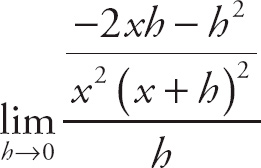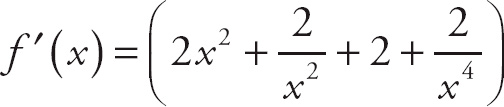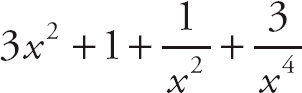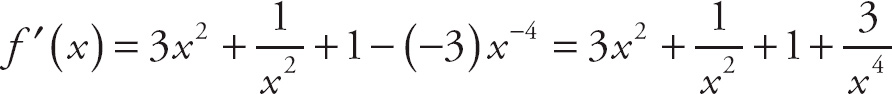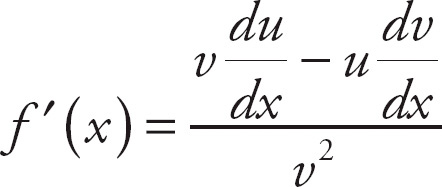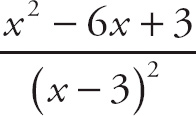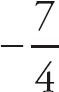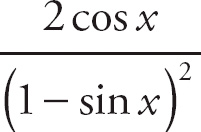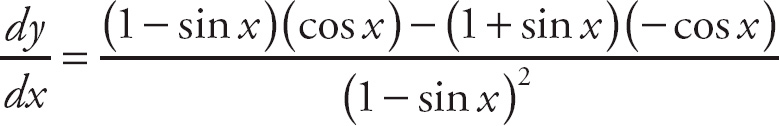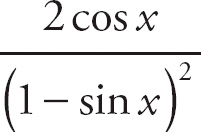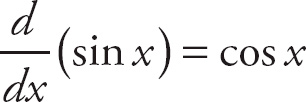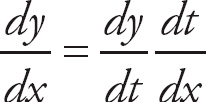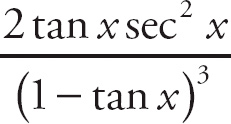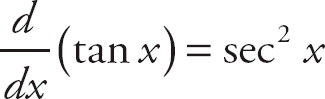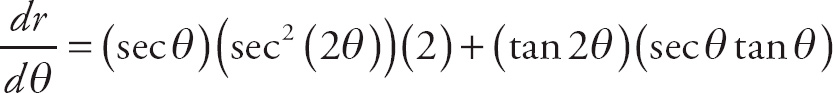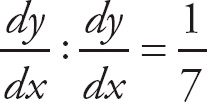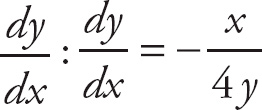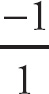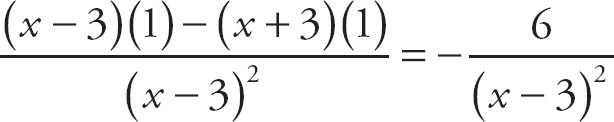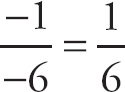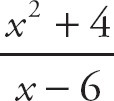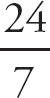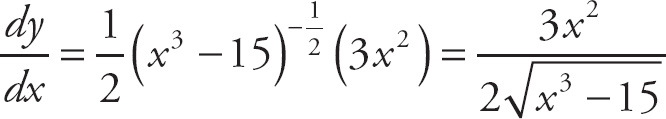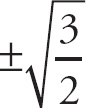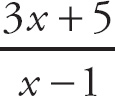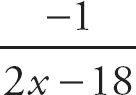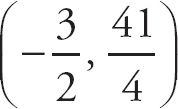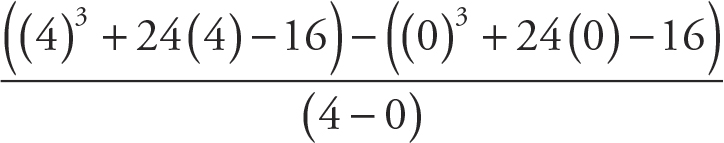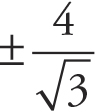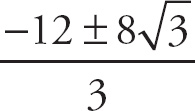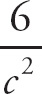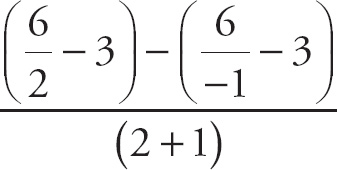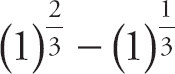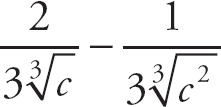1. 13
To find the limit, we simply plug in 8 for x: 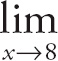
![]() (x2 − 5 x − 11)= (82 − (5)(8) − 11) = 13.
(x2 − 5 x − 11)= (82 − (5)(8) − 11) = 13.
To find the limit, we simply plug in 5 for x: 
 =
= 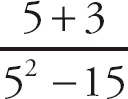
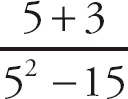 =
= 
![]() =
= 
![]() .
.
3. π2
To find the limit, we would plug in π for x, but there is no x in the limit. So the limit is simply π2.
4. 4
If we plug in 3 for x, we get 
![]() , which is indeterminate. When this happens, we try to factor the expression in order to get rid of the problem terms. Here we factor the top and get:
, which is indeterminate. When this happens, we try to factor the expression in order to get rid of the problem terms. Here we factor the top and get: 
 =
= 
 . Now we can cancel the term x − 3 to get
. Now we can cancel the term x − 3 to get 
![]() (x+1). Notice that we are allowed to cancel the terms because x is not 3 but very close to 3. Now we can plug in 3 for x:
(x+1). Notice that we are allowed to cancel the terms because x is not 3 but very close to 3. Now we can plug in 3 for x: 
![]() (x+1) = 3 + 1 = 4.
(x+1) = 3 + 1 = 4.
5. 0
Here we are finding the limit as x goes to infinity. We divide the top and bottom by the highest power of x in the expression: 
 =
= 
 . Next, simplify the top and bottom:
. Next, simplify the top and bottom: 
 . Now, if we take the limit as x goes to infinity, we get
. Now, if we take the limit as x goes to infinity, we get 
 =
= 
![]() = 0.
= 0.
6. + ∞
Here we are finding the limit as x goes to infinity. We divide the top and bottom by the highest power of x in the expression, which is x4: 
 =
= 
 . Next, simplify the top and bottom:
. Next, simplify the top and bottom: 
 . Now, if we take the limit as x goes to infinity, we get
. Now, if we take the limit as x goes to infinity, we get 
 =
= 
![]() = ∞.
= ∞.
Here we are finding the limit as x goes to infinity. We divide the top and bottom by the highest power of x in the expression, which is x4: 
 =
= 
 . Next, simplify the top and bottom:
. Next, simplify the top and bottom: 
 . Now, if we take the limit as x goes to infinity, we get
. Now, if we take the limit as x goes to infinity, we get 
 =
= 
![]() =
= 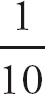
![]() .
.
Here we are finding the limit as x goes to infinity. We divide the top and bottom by the highest power of x in the expression, which is x2. Notice that, under the radical, we divide by x4 because 
![]() = x2:
= x2: 
 =
= 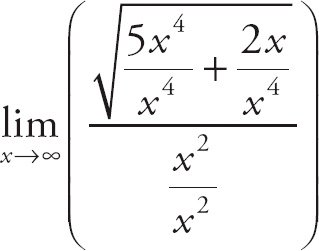
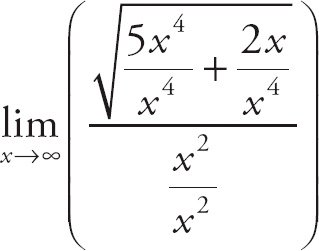 . Next, simplify the top and bottom:
. Next, simplify the top and bottom: 
 . Now, if we take the limit as x goes to infinity, we get
. Now, if we take the limit as x goes to infinity, we get 
 =
= 
 =
= 
![]() .
.
9. +∞
Here we have to think about what happens when we plug in a value that is very close to 6, but a little bit more. The top expression will approach 8. The bottom expression will approach 0, but will be a little bit bigger. Thus, the limit will be 
![]() , which is +∞.
, which is +∞.
10. −∞
Here we have to think about what happens when we plug in a value that is very close to 6, but a little bit less. The top expression will approach 8. The bottom expression will approach 0 but will be a little bit less. Thus, the limit will be 
![]() , which is −∞.
, which is −∞.
11. The limit Does Not Exist.
In order to evaluate the limit as x approaches 6, we find the limit as it approaches 6+ (from the right) and the limit as it approaches 6– (from the left). If the two limits approach the same value, or both approach positive infinity or both approach negative infinity, then the limit is that value, or the appropriately signed infinity. If the two limits do not agree, the limit “Does Not Exist.” Here, if we look at the solutions to problems 9 and 10, we find that as x approaches 6+, the limit is +∞, but as x approaches 6–, the limit is −∞. Because the two limits are not the same, the limit Does Not Exist.
12. 1
Here we have to think about what happens when we plug in a value that is very close to 0, but a little bit more. The top and bottom expressions will both be positive and the same value, so we get 
 .
.
13. −1
Here we have to think about what happens when we plug in a value that is very close to 0, but a little bit less. The top expression will be negative, and the bottom expression will be positive, so we get 
 .
.
14. +∞
Here we have to think about what happens when we plug in a value that is very close to 7, but a little bit more. The top expression will approach 7. The bottom expression will approach 0 but will be a little bit positive. Thus, the limit will be 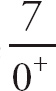
![]() , which is +∞.
, which is +∞.
15. The limit Does Not Exist.
In order to evaluate the limit as x approaches 7, we find the limit as it approaches 7+ (from the right) and the limit as it approaches 7– (from the left). If the two limits approach the same value, or both approach positive infinity or both approach negative infinity, then the limit is that value, or the appropriately signed infinity. If the two limits do not agree, the limit “Does Not Exist.” Here, if we look at the solutions to problem 14, we see that as x approaches 7+, the limit is +∞. As x approaches 7–, the top expression will approach 7. The bottom will approach 0, but will be a little bit negative. Thus, the limit will be 
![]() , which is −∞. Because the two limits are not the same, the limit Does Not Exist.
, which is −∞. Because the two limits are not the same, the limit Does Not Exist.
16. +∞
In order to evaluate the limit as x approaches 7, we find the limit as it approaches 7+ (from the right) and the limit as it approaches 7– (from the left). If the two limits approach the same value, or both approach positive infinity or both approach negative infinity, then the limit is that value, or the appropriately-signed infinity. If the two limits do not agree, the limit “Does Not Exist.” Here we see that as x approaches 7+, the top expression will approach 7. The bottom expression will approach 0 but will be a little bit positive. Thus, the limit will be 
![]() , which is +∞. As x approaches 7–, the top expression will again approach 7. The bottom will approach 0 but will be a little bit positive. Thus, the limit will be
, which is +∞. As x approaches 7–, the top expression will again approach 7. The bottom will approach 0 but will be a little bit positive. Thus, the limit will be 
![]() , which is +∞. Because the two limits are the same, the limit is +∞.
, which is +∞. Because the two limits are the same, the limit is +∞.
17. (a) 4; (b) 5; (c) The limit Does Not Exist.
(a) Notice that f(x) is a piecewise function, which means that we use the function f(x) = x2 − 5 for all values of x less than or equal to 3. Thus, 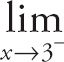
![]() f(x) = 32 − 5 = 4.
f(x) = 32 − 5 = 4.
(b) Here we use the function f(x) = x + 2 for all values of x greater than 3. Thus, 
![]() = 3 + 2 = 5.
= 3 + 2 = 5.
(c) In order to evaluate the limit as x approaches 3, we find the limit as it approaches 3+ (from the right) and the limit as it approaches 3– (from the left). If the two limits approach the same value, or both approach positive infinity or both approach negative infinity, then the limit is that value, or the appropriately signed infinity. If the two limits do not agree, the limit “Does Not Exist.” Here, if we refer to the solutions in parts (a) and (b), we see that 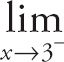
![]() f(x) =4 and
f(x) =4 and 
![]() f(x) =5. Because the two limits are not the same, the limit Does Not Exist.
f(x) =5. Because the two limits are not the same, the limit Does Not Exist.
18. (a) 4; (b) 4; (c) 4
(a) Notice that is a piecewise function, which means that we use the function f(x) = x2 − 5 for all values of x less than or equal to 3. Thus, 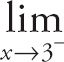
![]() = 32 − 5 = 4.
= 32 − 5 = 4.
(b) Here we use the function f(x) = x + 1 for all values of x greater than 3. Thus, 
![]() f(x) = 3 + 1 = 4.
f(x) = 3 + 1 = 4.
(c) In order to evaluate the limit as x approaches 3, we find the limit as it approaches 3+ (from the right) and the limit as it approaches 3– (from the left). If the two limits approach the same value, or both approach positive infinity or both approach negative infinity, then the limit is that value, or the appropriately signed infinity. If the two limits do not agree, the limit “Does Not Exist.” Here, if we refer to the solutions in parts (a) and (b), we see that 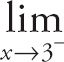
![]() f(x) = 4 and
f(x) = 4 and 
![]() f(x) = 4. Because the two limits are the same, the limit is 4.
f(x) = 4. Because the two limits are the same, the limit is 4.
Here, if we plug in 
![]() for x, we get
for x, we get 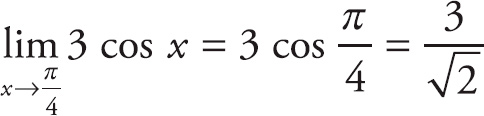
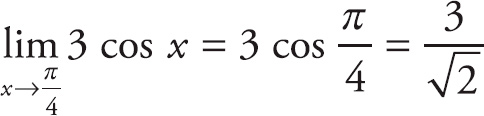 .
.
20. 0
Here, if we plug in 0 for x, we get 
![]() .
.
21. 3
Remember Rule No. 1, which says that 
![]() . If we want to find the limit of its reciprocal, we can write this as
. If we want to find the limit of its reciprocal, we can write this as 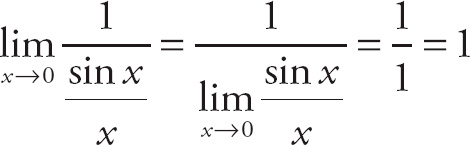
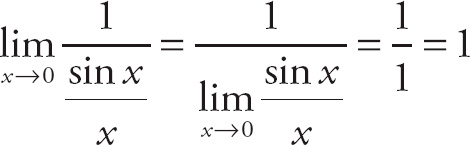 . Here, if we plug in 0 for x, we get
. Here, if we plug in 0 for x, we get 
 = (3)(1) = 3.
= (3)(1) = 3.
Remember Rule No. 4, which says that 
![]() . Here
. Here 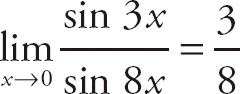
![]() . If we want to evaluate the limit the long way, first we divide the numerator and the denominator of the expression by x:
. If we want to evaluate the limit the long way, first we divide the numerator and the denominator of the expression by x: 
 . Next, we multiply the numerator and the denominator of the top expression by 3 and the numerator and the denominator of the bottom expression by 8. We get
. Next, we multiply the numerator and the denominator of the top expression by 3 and the numerator and the denominator of the bottom expression by 8. We get 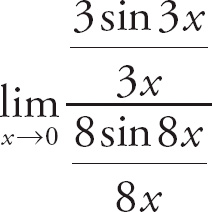
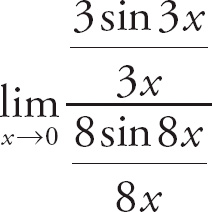 . Now, we can evaluate the limit:
. Now, we can evaluate the limit: 
 .
.
Here, we can rewrite the expression as 
 . Remember Rule No. 4, which says that
. Remember Rule No. 4, which says that 
![]() . Here,
. Here, 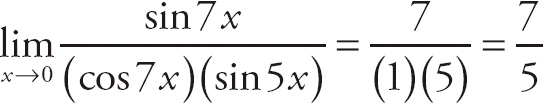
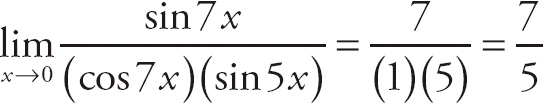 . If we want to evaluate the limit the long way, we first divide the numerator and the denominator of the expression by x:
. If we want to evaluate the limit the long way, we first divide the numerator and the denominator of the expression by x: 
 . Next, we multiply the numerator and the denominator of the top expression by 7 and the numerator and the denominator of the bottom expression by 5. We get
. Next, we multiply the numerator and the denominator of the top expression by 7 and the numerator and the denominator of the bottom expression by 5. We get 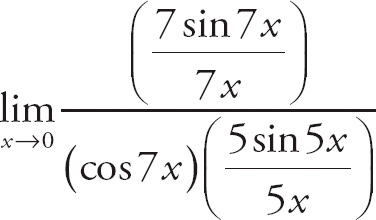
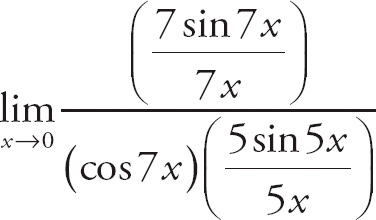 . Now, we can evaluate the limit:
. Now, we can evaluate the limit: 
 .
.
24. The limit Does Not Exist.
The value of sin x oscillates between −1 and 1. Thus, as x approaches infinity, sin x does not approach a specific value. Therefore, the limit Does Not Exist.
25. 0
Here, as x approaches infinity, 
![]() approaches 0. Thus,
approaches 0. Thus, 
![]() .
.
26. 0
Here, use the trigonometric identity sin2 x = 1 − cos2 x to rewrite the bottom expression: 
 . Next, we can break up the limit into
. Next, we can break up the limit into 
 . Remember that
. Remember that 
 and that
and that 
![]() as well. Now we can evaluate the limit:
as well. Now we can evaluate the limit: 
 = (1)(1)(0) = 0.
= (1)(1)(0) = 0.
We can break up the limit into 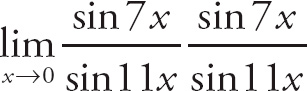
![]() . Remember Rule No. 4, which says that
. Remember Rule No. 4, which says that 
![]() . Here
. Here 
![]() . If we want to evaluate the limit the long way, we first divide the numerator and the denominator of the expressions by x:
. If we want to evaluate the limit the long way, we first divide the numerator and the denominator of the expressions by x: 
 . Next, we multiply the numerator and the denominator of the top expression by 7 and the numerator and the denominator of the bottom expression by 11. We get
. Next, we multiply the numerator and the denominator of the top expression by 7 and the numerator and the denominator of the bottom expression by 11. We get 
 . Now, we can evaluate the limit:
. Now, we can evaluate the limit: 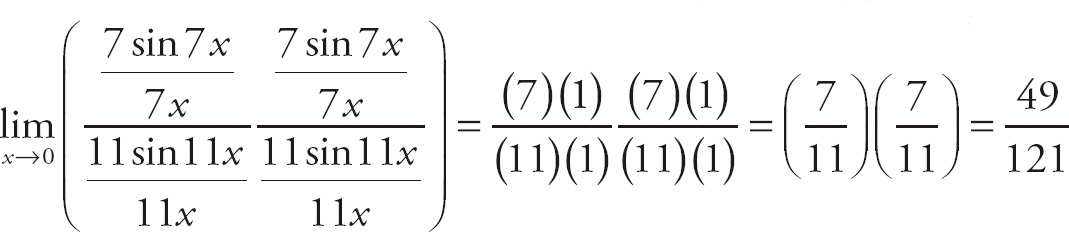
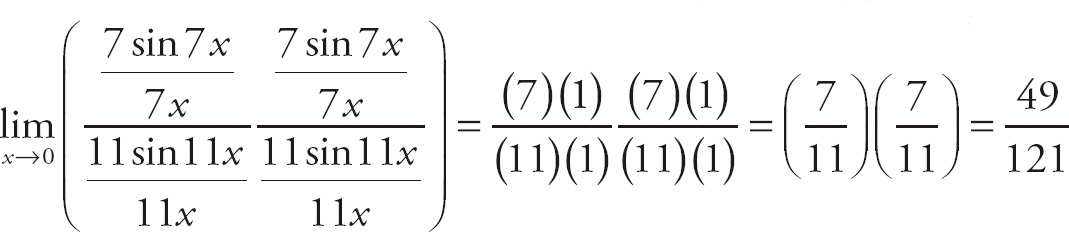 .
.
28. 6
Notice that if we plug in 0 for h, we get 
![]() , which is indeterminate. If we expand the expression in the numerator, we get
, which is indeterminate. If we expand the expression in the numerator, we get 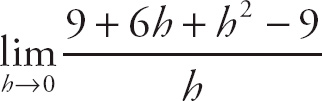
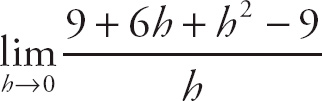 . This simplifies to
. This simplifies to 
 . Next, factor h out of the top expression:
. Next, factor h out of the top expression: 
 . Now, we can cancel the h and evaluate the limit to get
. Now, we can cancel the h and evaluate the limit to get 
 (6+h) = 6 + 0 = 6.
(6+h) = 6 + 0 = 6.
29. cos x
Notice that if we plug in 0 for h, we get 
![]() , which is indeterminate. Recall that the trigonometric formula sin (A + B) = sin A cos B + cos A sin B. Here, we can rewrite the top expression as
, which is indeterminate. Recall that the trigonometric formula sin (A + B) = sin A cos B + cos A sin B. Here, we can rewrite the top expression as 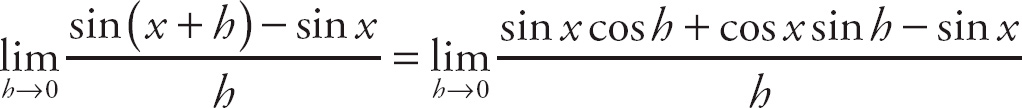
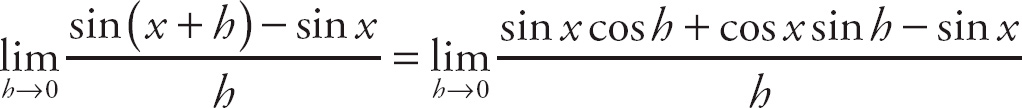 . We can break up the limit into
. We can break up the limit into 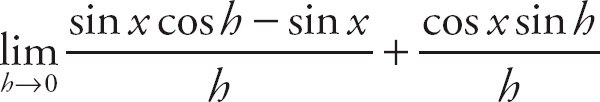
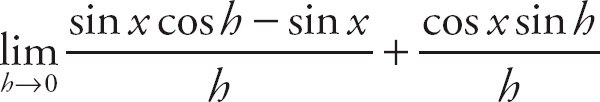 . Next, factor sin x out of the top of the left-hand expression:
. Next, factor sin x out of the top of the left-hand expression: 
 . Now, we can break this into separate limits:
. Now, we can break this into separate limits: 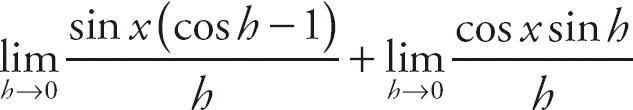
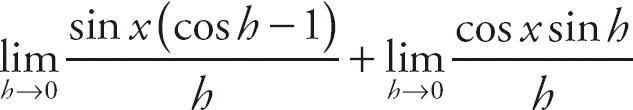 . The left-hand limit is
. The left-hand limit is 
 . The right-hand limit is
. The right-hand limit is 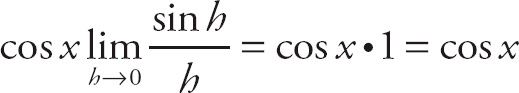
![]() . Finally, combine the left-hand and right-hand limits:
. Finally, combine the left-hand and right-hand limits: 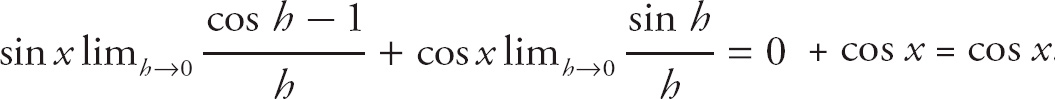
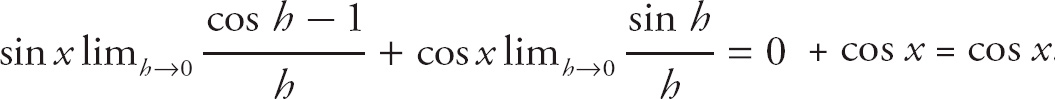 .
.
Notice that if we plug in 0 for h, we get 
![]() , which is indeterminate. If we combine the two expressions on top with a common denominator, we get
, which is indeterminate. If we combine the two expressions on top with a common denominator, we get 
 . We can simplify the top expression, leaving us with:
. We can simplify the top expression, leaving us with: 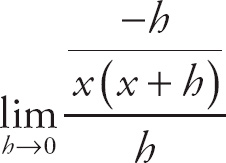
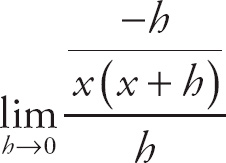 . Next, simplify the expression into:
. Next, simplify the expression into: 
 . We can cancel the h to get
. We can cancel the h to get 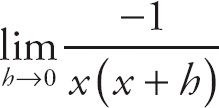
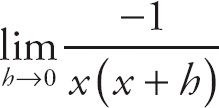 . Now, if we evaluate the limit we get
. Now, if we evaluate the limit we get 
 .
.