
By now, it should be easy for you to take the derivative of an equation such as y = 3x5 – 7x. If you’re given an equation such as y2 = 3x5 – 7x, you can still figure out the derivative by taking the square root of both sides, which gives you y in terms of x. This is known as finding the derivative explicitly. It’s messy, but possible.
If you have to find the derivative of y2 + y = 3x5 – 7x, you don’t have an easy way to get y in terms of x, so you can’t differentiate this equation using any of the techniques you’ve learned so far. That’s because each of those previous techniques needs to be used on an equation in which y is in terms of x. When you can’t isolate y in terms of x (or if isolating y makes taking the derivative a nightmare), it’s time to take the derivative implicitly.
Implicit differentiation is one of the simpler techniques you need to learn to do in calculus, but for some reason it gives many students trouble. Suppose you have the equation y2 = 3x5 – 7x. This means that the value of y is a function of the value of x. When we take the derivative, 
![]() , we’re looking at the rate at which y changes as x changes. Thus, given y = x2 + x, when we write
, we’re looking at the rate at which y changes as x changes. Thus, given y = x2 + x, when we write

![]() = 2x + 1
= 2x + 1
we’re saying that “the rate” at which y changes, with respect to how x changes, is 2x + 1.
Now, suppose you want to find 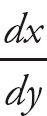
![]() . As you might imagine
. As you might imagine
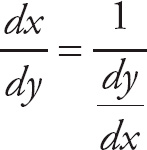
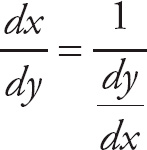
So here, 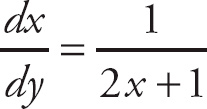
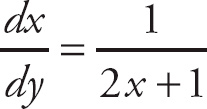 . But notice that this derivative is in terms of x, not y, and you need to find the derivative with respect to y. This derivative is an implicit one. When you can’t isolate the variables of an equation, you often end up with a derivative that is in terms of both variables.
. But notice that this derivative is in terms of x, not y, and you need to find the derivative with respect to y. This derivative is an implicit one. When you can’t isolate the variables of an equation, you often end up with a derivative that is in terms of both variables.
Another way to think of this is that there is a hidden term in the derivative, 
![]() , and when we take the derivative, what we really get is
, and when we take the derivative, what we really get is
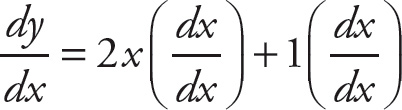
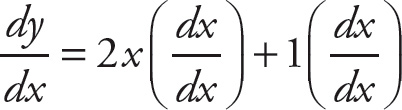
A fraction that has the same term in its numerator and denominator is equal to 1, so we write

![]() = 2x(1) + 1(1) = 2x + 1
= 2x(1) + 1(1) = 2x + 1
Every time we take a derivative of a term with x in it, we multiply by the term 
![]() , but because this is 1, we ignore it. Suppose however, that we wanted to find out how y changes with respect to t (for time). Then we would have
, but because this is 1, we ignore it. Suppose however, that we wanted to find out how y changes with respect to t (for time). Then we would have


If we wanted to find out how y changes with respect to r, we would have
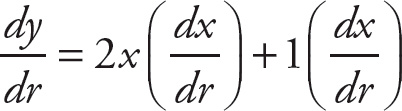
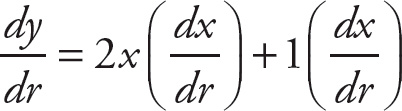
and if we wanted to find out how y changes with respect to y, we would have
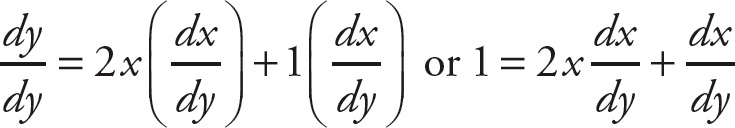
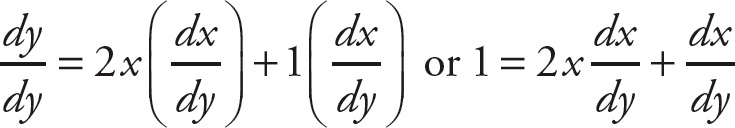
This is how we really do differentiation. Remember the following:
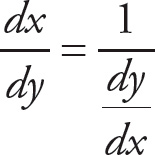
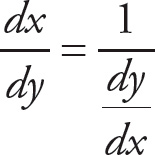
When you have an equation of x in terms of y, and you want to find the derivative with respect to y, simply differentiate. But if the equation is of y in terms of x, find 
![]() and take its reciprocal to find
and take its reciprocal to find 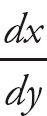
![]() . Go back to our original example.
. Go back to our original example.
y2 + y = 3x5 – 7x
To take the derivative according to the information in the last paragraph, you get

Notice how each variable is multiplied by its appropriate 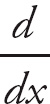
![]() . Now, remembering that
. Now, remembering that 
![]() = 1, rewrite the expression this way:
= 1, rewrite the expression this way: 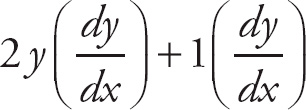
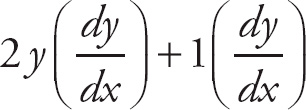 = 15x4 − 7.
= 15x4 − 7.
Next, factor 
![]() out of the left-hand side:
out of the left-hand side: 
![]() (2y + 1) = 15x4 − 7.
(2y + 1) = 15x4 − 7.
Isolating 
![]() gives you
gives you 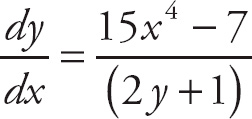
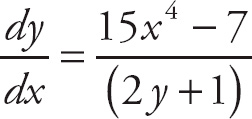 .
.
This is the derivative you’re looking for. Notice how the derivative is defined in terms of y and x. Up until now, 
![]() has been strictly in terms of x. This is why the differentiation is “implicit.”
has been strictly in terms of x. This is why the differentiation is “implicit.”
Confused? Let’s do a few examples and you will get the hang of it.
Example 1: Find 
![]() if y3 – 4y2 = x5 + 3x4.
if y3 – 4y2 = x5 + 3x4.
Using implicit differentiation, you get


Remember that 
![]() = 1:
= 1: 
![]() (3y2 − 8y) = 5x4 + 12x3.
(3y2 − 8y) = 5x4 + 12x3.
After you factor out 
![]() , divide both sides by 3y2 – 8y.
, divide both sides by 3y2 – 8y.
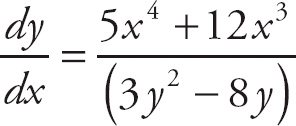
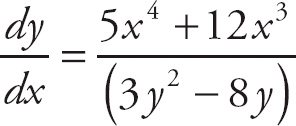
Note: Now that you understand that the derivative of an x term with respect to x will always be multiplied by 
![]() , and that
, and that 
![]() = 1, we won’t write
= 1, we won’t write 
![]() anymore. You should understand that the term is implied.
anymore. You should understand that the term is implied.
Example 2: Find 
![]() if sin y2 – cos x2 = cos y2 + sin x2.
if sin y2 – cos x2 = cos y2 + sin x2.
Use implicit differentiation.
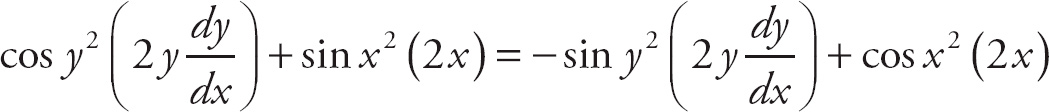
Then simplify.
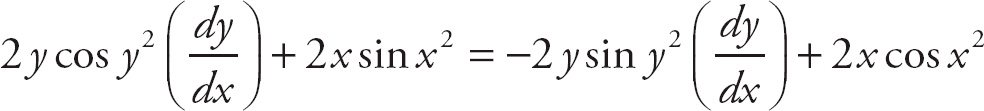
Next, put all of the terms containing 
![]() on the left and all of the other terms on the right.
on the left and all of the other terms on the right.
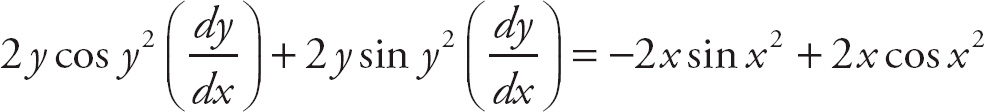
Next, factor out 
![]() .
.

![]() (2y cos y2 + 2y sin y2) = −2x sin x2 + 2x cos x2)
(2y cos y2 + 2y sin y2) = −2x sin x2 + 2x cos x2)
And isolate 
![]() .
.


This can be simplified further to the following:
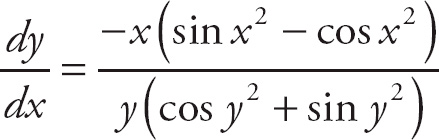
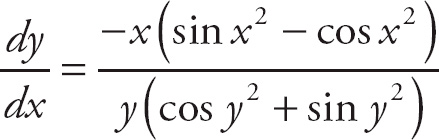
Example 3: Find 
![]() if 3x2 + 5xy2 – 4y3 = 8.
if 3x2 + 5xy2 – 4y3 = 8.
Implicit differentiation should result in the following:
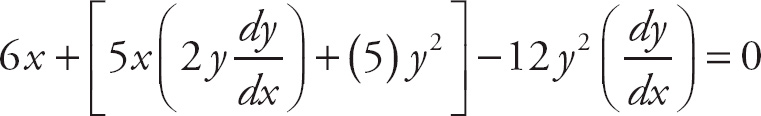
6x + 10xy
![]() + 5y2 − 12y2
+ 5y2 − 12y2
![]() = 0
= 0
Next, put all of the terms containing 
![]() on the left and all of the other terms on the right.
on the left and all of the other terms on the right.
10xy
![]() − 12y2
− 12y2
![]() = −6x − 5y2
= −6x − 5y2
Next, factor out 
![]() .
.
(10xy − 12y2)
![]() = −6x − 5y2
= −6x − 5y2
Then, isolate 
![]() .
.
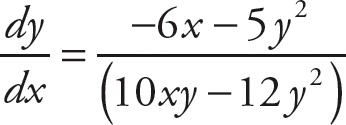
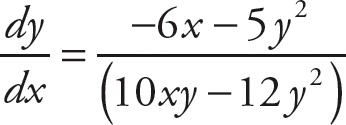
Example 4: Find the derivative of 3x2 − 4y2 + y = 9 at (2, 1).
You need to use implicit differentiation to find 
![]() .
.
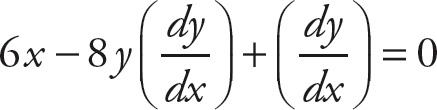
Now, instead of rearranging to isolate 
![]() , plug in (2, 1) immediately and solve for the derivative.
, plug in (2, 1) immediately and solve for the derivative.
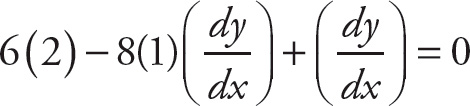
Simplify: 12 − 7 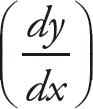
![]() = 0, so
= 0, so 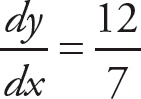
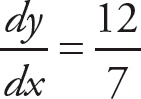
Getting the hang of implicit differentiation yet? We hope so, because these next examples are slightly harder.
Example 5: Find the derivative of 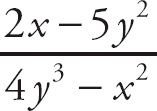
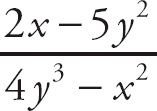 = −x at (1, 1).
= −x at (1, 1).
First, cross-multiply.
2x − 5y2 = −x(4y3 − x2)
Distribute.
2x – 5y2 = −4xy3 + x3
Take the derivative.
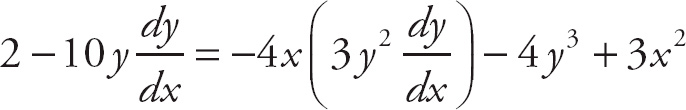
Do not simplify now. Rather, plug in (1, 1) right away. This will save you from the algebra.
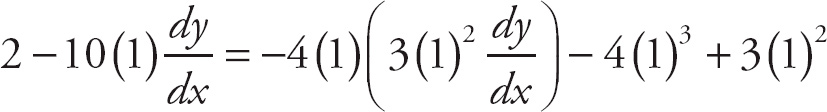
Now solve for 
![]() .
.
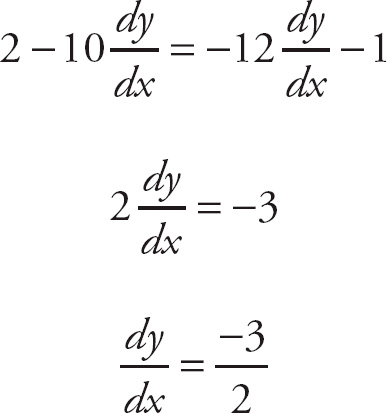
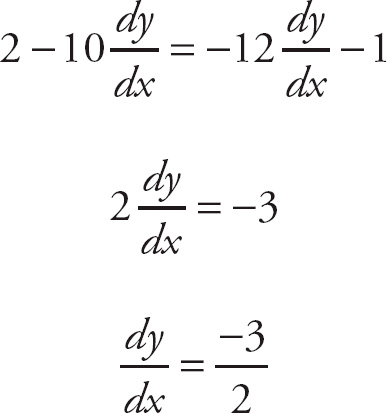
Sometimes, you’ll be asked to find a second derivative implicitly.
Example 6: Find 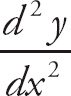
![]() if y2 + 2y = 4x2 + 2x
if y2 + 2y = 4x2 + 2x
Differentiating implicitly, you get
2y
![]() + 2
+ 2
![]() = 8x + 2
= 8x + 2
Next, simplify and solve for 
![]() .
.
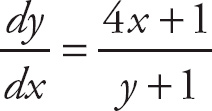
Now, it’s time to take the derivative again.
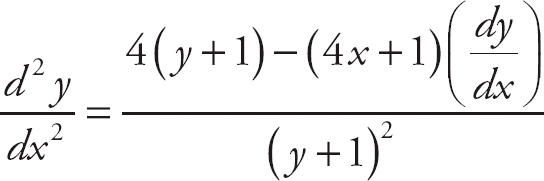
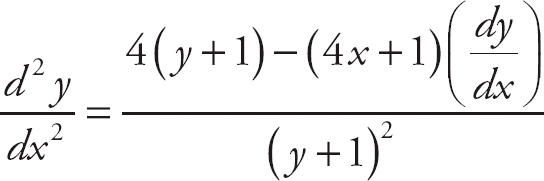
Finally, substitute for 
![]() .
.


Try these solved problems without looking at the answers. Then check your work.
PROBLEM 1. Find 
![]() if x2 + y2 = 6xy.
if x2 + y2 = 6xy.
Answer: Differentiate with respect to x.
2x + 2y
![]() = 6x
= 6x
![]() + 6y
+ 6y
Group all of the 
![]() terms on the left and the other terms on the right.
terms on the left and the other terms on the right.
2y
![]() − 6x
− 6x
![]() = 6y − 2x
= 6y − 2x
Now factor out 
![]() .
.

![]() (2y − 6x) = 6y − 2x
(2y − 6x) = 6y − 2x
Therefore, the first derivative is the following:
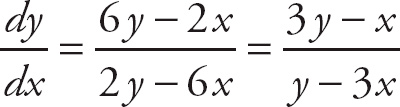
PROBLEM 2. Find 
![]() if x – cos y = xy.
if x – cos y = xy.
Answer: Differentiate with respect to x.
1 + sin y
![]() = x
= x
![]() + y
+ y
Grouping the terms, you get
sin y
![]() − x
− x
![]() = y − 1
= y − 1
Now factor out 
![]() .
.

![]() (siny − x) = y − 1
(siny − x) = y − 1
The derivative is

PROBLEM 3. Find the derivative of each variable with respect to t of x2 + y2 = z2.
Answer: 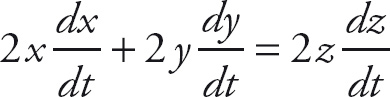
![]()
PROBLEM 4. Find the derivative of each variable with respect to t of V = 
![]() πr2h.
πr2h.
Answer: 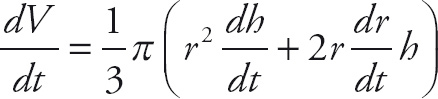
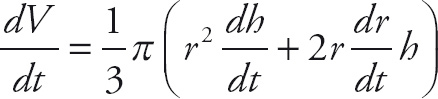
PROBLEM 5. Find 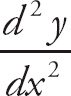
![]() if y2 = x2 − 2x.
if y2 = x2 − 2x.
Answer: First, take the derivative with respect to x.
2y
![]() = 2x − 2
= 2x − 2
Then, solve for 
![]() .
.
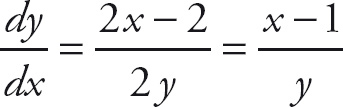
The second derivative with respect to x becomes
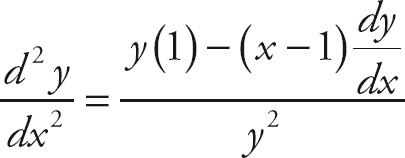
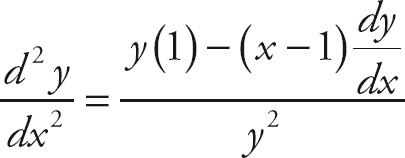
Now substitute for 
![]() and simplify.
and simplify.
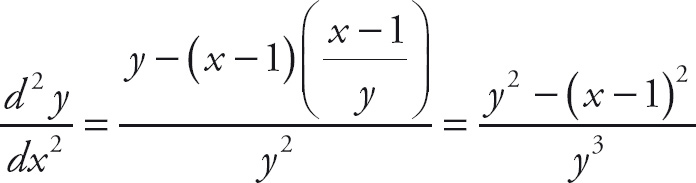
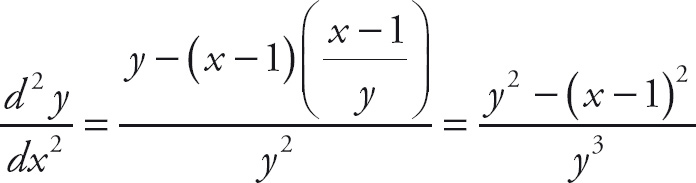
Use implicit differentiation to find the following derivatives. The answers are in Chapter 23.
1. Find 
![]() if x3 − y3 = y.
if x3 − y3 = y.
2. Find 
![]() if x2 − 16xy + y2 = 1.
if x2 − 16xy + y2 = 1.
3. Find 
![]() at (2, 1) if
at (2, 1) if 
![]() = 3.
= 3.
4. Find 
![]() if cos y − sin x = sin y − cos x.
if cos y − sin x = sin y − cos x.
5. Find 
![]() if 16x2 − 16xy + y2 = 1 at (1, 1).
if 16x2 − 16xy + y2 = 1 at (1, 1).
6. Find 
![]() if
if 
![]() = 2y2 at (1, 1).
= 2y2 at (1, 1).
7. Find 
![]() if x sin y + y sin x =
if x sin y + y sin x = 
![]() at
at 
 .
.
8. Find 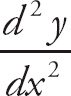
![]() if x2 + 4y2 = 1.
if x2 + 4y2 = 1.
9. Find 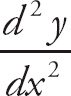
![]() if sin x + 1 = cos y.
if sin x + 1 = cos y.
10. Find 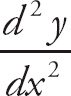
![]() if x2 − 4x = 2y − 2.
if x2 − 4x = 2y − 2.