
FROM HUNTER-GATHERERS TO HERDERS
According to historians there are five main stages involved in a society becoming ‘civilized’. The first stage is the ability to make and control fire – Homo sapiens and their ancestors have been creating fires for approximately half a million years. The second stage is the cultivation of crops, which really requires the help of domesticated animals. The Neolithic Revolution, which occurred in independent locations across the globe approximately 10,000 years ago, saw humans begin to stay in one place, grow crops and domesticate and rear livestock.
The first shepherds would have needed a method for counting their animals, so it seems obvious that they would have been good at counting. Or would they? Equally, the first farmers would have needed a method of working out what time of year it was so they knew when to plant their seeds – surely more numbers were involved here?
The Neolithics used a system called pebble counting. In order to count their herds of sheep the shepherds placed one counter – perhaps a pebble or a fruit pip – in a bag for each member of the flock. To find out if all of the animals in the herd were safe the shepherds then removed a pip for each sheep counted. If by the time they got through all of the sheep they still had pips remaining they knew then that one or more of the sheep had been lost. Hopefully, if they were half-decent shepherds, this number would have been one of the low numbers (1–10), which we now know hunter-gatherers were equipped to deal with. The farmers would have used a similar system to count from a key event, such as the rains beginning, or the birds flying south, to let them know when to plant their crops.
The economy takes shape
Surplus is an inevitable consequence of agriculture and the domestication of animals. Once there was an excess of food, early civilizations could start to trade their surplus, which in turn promoted the idea of value. This is the third sign of civilization – the idea of an economy; of goods being bartered or sold. Naturally, they needed a way to cart around their surplus of goods, so the fourth sign of civilization is the wheel, which seemed to be widespread by c. 4000 BC.
THE DAWN OF THE ACCOUNTANTS
With a reliable surplus of food it then became possible for some people to fill their time doing things other than finding or growing food in order to survive. By c. 3000 BC towns and cities were filled with such people. These large urban societies needed organizing in order to function properly, and the ability to count large numbers was key to this. The need also arose for these new, large numbers to be recorded – and hence written – for the first time. Among the myriad flagship new professions that arose – craftsmen, soldiers, farmers, merchants – a new literate class – the scribe – was to be found; almost certainly many of these scribes were numerate accountants and – inevitably – tax collectors.
The Bronze Age
The fifth sign of a civilization is the use and working of metals, which started at approximately the same time as the first towns and cities arose. The easiest metal to work is copper, which is used to make bronze. Hence we call this period in history the Bronze Age.
Most of the earliest civilizations developed around the fertile areas near rivers, where the land was suitable for farming and raising livestock. Three notable civilizations that arose during this period, and about which we know a great deal, were:
1. The Mesopotamians: a collective name for the Sumerians, Akkadians, Babylonians and Assyrians. They lived in the Middle East from c. 3000 BC.
2. The Ancient Egyptians: the baddies in the Old Testament. They were based along the River Nile from c. 3000 BC.
3. The Mayans: from Central America. Their earliest stages of development began c. 1500 BC; they entered a stage of development similar to the Mesopotamians and Egyptians after AD 250.
As some cities rose in importance and began to dominate the surrounding area, either economically or by strength of arms, certain regions began to adopt the most effective numbers system. Unfortunately the early records from many such cultures have not survived, perhaps because these people were sited next to large rivers that flooded often. But if we take a quick look at some of the highlights of the archaeological findings that have survived from each civilization, we gain some idea of an evolution of written numbers and number systems from our earliest urbanite ancestors.
Mesopotamia means ‘between rivers’ in Ancient Greek, and refers to the cultures that sprang up between the Tigris and Euphrates rivers in present-day Iraq – a very fertile area of land often called the Cradle of Civilization. Despite their early beginnings, we know a fair amount about the Mesopotamians because they performed all of their writing on clay tablets, which are hardy enough to withstand repeated soakings.
Clay tablets, however, are not easy to write on. The Mesopotamians began with a pictographic language, when the written symbol for a word is a stylized picture of the thing being described. However, drawing decent images in thick wet clay is tricky, so they took to using the end of a wedge-shaped stylus (a rod-like implement with a pointed end) to make marks.
Number system
The Mesopotamian’s number system was base 60 (also referred to as sexagesimal), which means they counted in blocks of 60 rather than in blocks of 10, as we do today. Lots of numbers go into 60 (mathematicians would say 60 has many factors), which makes it a convenient number with which to do arithmetic. We still see a few reminders of it today – 60 seconds in a minute and 60 minutes in an hour hark back to the Babylonians.
Cunningly, their number system contained only one symbol, made using the end of a stylus:
They would use up to nine of these symbols. They would show a 10 by rotating the stylus by 90 degrees to get a slightly different symbol:
![]()
So the number 47 would look like this:

The Mesopotamians could write up to the number 59 in this way, using a sub-column for each of the tens and units digits. To write numbers larger than 59, they would write a new number alongside the tens and units (just as we can go as high as 9 in one column before we have to move on to the next one). Whereas our columns follow the pattern units, tens, hundreds, thousands, etc., according to our way of thinking the Mesopotamians’ columns went units, sixties, three-thousand six-hundreds, two-hundred and sixteen-thousands. A Mesopotamian would think of our number 437 as being 7 lots of 60 (7 × 60 = 420) plus 17, which they would write like this:
Zero interest
Although this seems like a pretty decent number system, not unlike our own, there were a couple of problematic areas. The first problem was that until c. 500 BC the Mesopotamians had no symbol for zero, which means they had no way of showing an empty column. For example, if I write down 205, the zero tells you that I mean two-hundred and five, and nothing else. The Mesopotamian number system was flawed because empty columns in the middle or at the end of a number were missing. For example:

This looks like 60 + 10 = 70. But there could be an empty column in the middle, in which case the number would be 3600 + 0 + 10 = 3610. Or there could be an empty column at the end, in which case we would have 216000 + 60 + 0 = 216060 – quite a large difference. Apparently, Mesopotamians tended to rely on the context in which the numbers were used in order to read them in the most reasonable way.
Many people consider the abacus to have been the ancient world’s version of the electronic calculator. In fact, the counting frame with beads – which most people think of when they hear the word abacus – is a relatively modern piece of technology, first made popular in China after AD 1000.
The word ‘abacus’ is thought to come from the Hebrew word for ‘dust’, and the first abacuses were simply that – a board or level surface strewn with dust that could be used as a scratch pad for calculations. Eventually the dust was replaced by a board with tokens that could be placed in columns to allow for the addition of large numbers without having to be able to count higher than ten.
Later, the Romans used pebbles or, in Latin, calculi (from which we get the words calculus and calculation). In England, we called the tokens ‘counters’, which is why shops had a counter-top to put their counting board on.
Multiplication madness
The second problem arose when the Mesopotamians tried to multiply numbers together. Whichever way you multiply using our decimal system, you need to have memorized your times tables up to 9 x 9 (because 9 is the highest digit we have). However, according to the Mesopotamian system, you needed to know your times tables up to 59 x 59! We think they used a few key times tables, written on small tablets, to help, but even so their times-table tests at school must have been a nightmare.
Archaeologists have found many hundreds of clay tablets littered with Mesopotamian mathematics. It seems the Mesopotamians were able to use fractions, to work out the areas of rectangles and triangles, and to solve quite complicated equations. My favourite fact is that many tablets found appear to have been maths homework! But maybe you need to be a maths teacher to appreciate that ...
ANCIENT EGYPTIAN MATHEMATICS
The Ancient Egyptians were a talented lot. In addition to building the pyramids, many of which are still standing over 4,000 years later, they also turned their hands to committing the written word to papyrus, a paper-like material made from interwoven reeds. Papyrus was a much more forgiving material to write on than the clay tablets the Mesopotamians were using further north. As such, unlike the Mesopotamians, the Ancient Egyptians were not limited to using a single symbol. However, because papyrus rots, especially if it gets wet, it does mean that a vast majority of the writing of Ancient Egypt has been destroyed over time.
It also seems that the Egyptians were not limited to one writing system.
Egypt is famous for its hieroglyphics – pictograms they carved on to their monuments, and which remained a complete mystery until French soldiers unearthed the Rosetta Stone in 1799.
Hieroglyphics were the Ancient Egyptian equivalent of calligraphy – decorative writing for use only on wedding invitations and inscriptions. The Egyptians had another writing system called hieratic, which they used for everyday stuff – a much easier and faster way to write script that scribes would then use for their calculations.
Hieroglyphic numbers had symbols for 1, 10, 100, 1000, etc., which the Ancient Egyptians would combine to make the required number:

So if an Egyptian wanted to refer to Rameses’ 1,234 chariots on his latest obelisk, he would have used the following symbols:
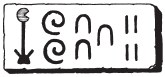
Because they added up the symbols in order to generate a total, the Egyptians could write the symbols in any order and direction they pleased – a handy tool when they wanted to be decorative.
The hieratic number system was a little more complicated because it used different symbols for each unit, each ten, each hundred and each thousand. The symbols for 40 and 50, for example, bore no relation to each other. It seems that this system relied on the fact that the scribes would be familiar with the symbols and would be able to perform calculations either in their heads, or by converting to the hieroglyphic system for tricky sums.
The business of numbers
Three important sources of mathematical information were left behind from Ancient Egypt: the Rhind Papyrus, the Moscow Mathematical Papyrus and the Berlin Papyrus. All three documents contained mathematical problems in arithmetic and geometry, alongside, interestingly, the first written information about pregnancy tests.
From these three sources we have learned that the Egyptians used fractions. However, they only used fractions that had a numerator of 1 – that is, the number on the top of the fraction could only be 1. They would talk about more complicated fractions by adding these unit fractions together. So, for example, they would think of ¾ as ½ + ¼. Although slightly cumbersome, this method stood the test of time – unit fractions were still used by mathematicians in medieval times.
The pyramid builders obviously had a pretty good grasp of geometry; the papyri contain detail about how they set about making these ancient structures. The pyramids were made with stacks of stone blocks in layers, and the steepness of a pyramid depended on the size of the overlap between two layers – the larger the overlap, the steeper the pyramid. The Egyptians devised a series of methods to work out what size of overlap was needed for different gradients. It has also been suggested the Egyptians had some idea of Pythagoras’ theorem (see here), which would have enabled them to work out the third length of a right-angled triangle if they knew the length of the other two sides.
There are, of course, many more far-fetched theories regarding the Ancient Egyptians, including the super-high technology they appropriated from the legendary island of Atlantis (or from aliens, or time travellers...). I cannot say whether such things were true, but I do know the Egyptians were pretty clever fellows.
A Tall Order
The fact about the Ancient Egyptians that I always find most extraordinary is that the Great Pyramid, which was completed c. 2560 BC, was the tallest building in the world until the central towers of Lincoln Cathedral were raised in AD 1311 – that’s the best part of 4,000 years!
By the first millennium AD Mayan civilization had reached a level of cultural and mathematical development similar to the Mesopotamians and the Egyptians. They declined somewhat as time went by, but when the Spanish conquistadores arrived in the early 1500s the Mayans had managed to recapture their previous levels of sophistication.
Born in isolation
The Mayans left behind a raft of evidence that demonstrated how they conducted their mathematics, but unfortunately virtually all of it was destroyed when the Spanish invaders arrived and sought to convert the region’s heathens to Catholicism. The Dresden Codex is one of three surviving examples of Mayan writing. Although it was badly damaged during the Second World War, the book still contains a great deal of insight into the Mayan development of mathematics. Many surviving monuments in modern-day Mexico and Guatemala contain numerical information, such as dates, inscribed upon them.
Unlike the cross-pollination that occurred between the Mesopotamian and Egyptian cultures, the Mayans developed in complete isolation. They also failed to fulfil the last two criteria of ‘civilization’: they did not possess the wheel, perhaps because there were no beasts of burden in the parts of Central America where they lived; they also did not seem to be able to smelt metal. However, despite technically still existing in the Stone Age, the Mayans were able to build great cities, some of which contained populations of over 50,000 people.
So, what of their mathematics? The Dresden Codex is concerned only with astrology and astronomy, so everything we know about the Mayans’ mathematics is shone through this lens.
The Mayans used a base-20 system, within which lay a base-5 system (much like the Mesopotamians’ base-60 and base-10 system).

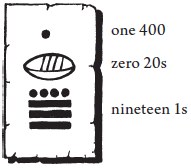
Like modern mathematics, Mayan mathematics had a grasp of place value: the value attached to the position of each digit. Unlike modern mathematics, Mayan mathematics placed numbers in vertical stacks, with the highest place value positioned at the top. Because the Mayans counted in groups of twenties, each level in the stack was twenty times the value of the level below. From the bottom it went something like this: 1s, 20s, 400s, 8000s, etc. So our number 8577 is one 8000, one 400, eight 20s and seventeen 1s, which in Mayan looked like this:
The Mayans had a symbol for an empty level in the stack, e.g. they possessed a concept of zero, which avoided the confusion faced by the Mesopotamians. So the number 419 (one 400, zero 20s and nineteen 1s) looked like this:
The Mayan calendar
As the information contained in The Dresden Codex would attest, the Mayans’ way of life was governed by astrology. Ritual human sacrifice was an integral part of Mayan culture and was thought to aid the continuation of the Mayan people’s cosmology.
Tasked with working out which rites were necessary to appease the gods, high-ranking priests were responsible for interpreting the positions of the sun, the moon and Venus. They developed a system of several different calendars, which the Mayans used in parallel. They possessed a 365-days-a-year civil calendar called the Haab, which comprised 18 months of 20 days each, plus 5 ‘nameless’ unlucky days, called Uayeb, to make up the full total.
The Mayans’ main calendar was called the Tzolk’in, which worked on a 260-day cycle. The Mayans devised a 13-day week and believed that 20 gods were each associated with a day of the year, and so 13 × 20 = 260 days in a cycle. The Tzolk’in was their everyday calendar, which they used to keep the date.
The 260-day cycle and the 365-day year would start together every 18,980 days, after 73 260-day cycles or 52 ‘vague’ years, as they were called. Fifty-two years was considered to be a good, long life in those days, so in order to record anything longer than this the Mayans used yet another calendar – the Long Count. This calendar was used for recording dates of important events, such as kings dying or volcanoes erupting; these were the dates they chiselled on to temples and statues using their stone tools. Considering their 360-day year (ignoring the Uayeb, the 5 nameless days – they did not want to bring bad luck to their monuments!) the Mayans, as base-20 people, deduced that 20 of those years made something called a k’atun, and 20 k’atuns comprised a b’ak’tun. A b’ak’tun was approximately 395 years. The Mayans needed a starting point for their dates – much as we use the birth of Christ for ours – which they decreed was 3114 BC. All important dates were measured forward from that point.
It just so happens that the current b’ak’tun finishes in December 2012. Some people believe the Mayans, in their infinite wisdom, predicted the world would end on this date. However, these people don’t realize the Mayans did in fact have a few more dates up their sleeves (if they had sleeves, that is) and that their calendar could be extended up to 367 million years. So I wouldn’t worry about the world ending just yet.
The Mesopotamian, Egyptian and Mayan cultures had many things in common. Mathematically speaking, their work with numbers was functional, a means to an end – whether that end was taxation, working out when the next eclipse was due or how to build a pyramid. Maths was certainly never performed for its own sake. The Mesopotamians and the Egyptians did amass a large body of knowledge, which our next civilization – the Ancient Greeks – built upon.
Since ancient times the idea that a year comprises 365 ¼ days has been well accepted. This system worked well for the Roman Empire after Julius Caesar instigated the Julian calendar in 45 BC. They even had a leap day every 4 years too.
But things started to get a little off kilter when it was observed that fixed points in the year, such as equinoxes and solstices, did not occur on the same day each year as time progressed. The reason for this is that a year is actually eleven minutes shy of that quarter day – not a great deal of difference, but over hundreds of years it built up to become quite an error.
By the sixteenth century the error had totalled ten days, which Pope Gregory XIII wouldn’t stand for. The majority of the Catholic countries in Europe changed to the new Gregorian calendar, which got things back on track. Britain, as ever, mistrusted this newfangled European enterprise and stuck with the old calendar until 1752, by which point we had to jump from 2 September to 14 September. The Russians kept the old calendar until the communist October Revolution in 1918, which, according to the new calendar, actually happened in November.