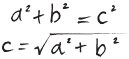
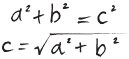
Now it’s time to move on to the Classical period, when the great empires of the Greeks and, later, the Romans dominated vast swathes of the known world. Their respective legacies were huge and their ways of doing pretty much anything were adopted and used for many hundreds of years after their demise.
Because we have only recently been able to translate and understand the cultures of the Mesopotamians and the Ancient Egyptians, it was for a long time believed the Greeks had been responsible for the ancient world’s greatest discoveries and inventions.
The philosophies of Socrates (c. 470–399 BC), Plato (427–347 BC) and Aristotle (384–322 BC), whose influence as mathematicians is explored later in this chapter (see here), were so significant that their modes of thought, minus their pagan beliefs, were later used by Christian theologists to expound their doctrine. So it is no wonder that these three philosophers of Ancient Greece were held in awe for so long in Europe – their ideas, cobbled together with stories from the Bible, were held to be the literal truth, and to disagree with them publicly was unwise.
However, despite their influence, I think they developed some quite strange ideas.
Illogical logic
The first philosophers (which means ‘lovers of wisdom’ in Greek) were often generalists because at that time they did not possess the specializations of science and the humanities that we do today. Some of these philosophers used logic in its purest sense against clear evidence to the contrary. Zeno of Elea (c. 490–430 BC) developed a series of paradoxes to help explain that motion was impossible. He argued, logically, that the great war hero Achilles could never catch up with a tortoise because, having started the race 100 metres ahead, the tortoise would always be making slow progress as Achilles tried in vain to catch up. Zeno also suggested that an arrow fired from a bow was stationary because it could not be in two places at once. During its flight the arrow is constantly occupying a whole bit of space, and is therefore, in that instant, motionless. This reductio ad absurdum method was given credence because it ‘proved’ that we should not trust the evidence of our senses, which were imperfect, whereas reasoning and logic were considered to be flawless. Hmmm.
Greek mathematics
Because the Greeks were so interested in pure logic, they had a keen interest in maths for its own sake.
The Ancient Greeks split mathematics into two camps: arithmetic and logistics. Arithmetic, what we today call pure mathematics – the study of abstract ideas rather than simple sums – was the sole preserve of intellectuals, the equivalent of today’s post-graduates. However, logistics, performing calculations, was an inferior trade that was better left to numerate slaves.
The Greeks used two number systems. The first, in use from c. 500 BC, was the forerunner to the Roman system (see here), only it used Greek letters rather than Latin: I for 1, ∏ for 5, Δ for 10, and so on.
The second system, which replaced the first by c. 100 BC, was still based on the letters of the alphabet. The first ten letters, alpha (α) to iota (ι) represented numbers 1 to 10. After this point the letters went up in tens, so the eleventh letter, kappa (κ), stood for 20, and so on until rho (ρ), which stood for 100. The remainder of the alphabet then went up in hundreds. So the number 758 looked like ψνη. This number system still didn’t allow for calculations to be performed with the numbers themselves, so we believe that sums would still have been carried out using counters. Despite the limitations of these numbers, they were used in Europe for over 1,000 years.
The Greek Alphabet

The Greeks, with the body of knowledge they acquired from their forebears in Egypt, Mesopotamia and elsewhere, wrote down and formalized many mathematical concepts that have been in use ever since, and which we will now explore.
One of the first Greek philosophers, Thales (pronounced Thay-leez) hailed from present-day Turkey. Often considered to have been the first true scientist, at some point around 600 BC Thales began to try to explain what he saw around him in terms of natural phenomena, rather than through the actions of deities.
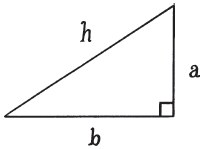
When it came to mathematics, Thales was, like many Ancient Greeks, interested in geometry. He understood the principle of similar triangles and used it to predict the height of the pyramids.

The two triangles on the preceding page are similar triangles because their angles are the same, and therefore their sides must be in proportion to each other. Thales was able to determine the height of a pyramid by measuring the length of its shadow. He waited until his own shadow was the same length as his height to measure the pyramid’s shadow in order to determine how tall it was.
PYTHAGORAS (c. 570–c. 490 BC)
Pythagoras’ name is instantly recognizable because his theorem has been taught to students of mathematics the world over. Because he left no written works behind, everything we know about Pythagoras was written long after he died. He founded a religious movement called Pythagoreanism, hence much that was written about him, embellished over time, assumed a decidedly mystical tinge. Among other things, Pythagoras is described as having a thigh made of gold and the ability to be in two places at once.
The theorem
Today Pythagoras is best known for his theorem for working out the hypotenuse (the longest side, the side opposite the right angle) of a right-angled triangle. In words, Pythagoras’ theorem is described as:
But it’s much pithier to say:
h2 = a2 + b2
Pythagoras wasn’t the first to explore the theorem. The Ancient Egyptians had investigated this idea, and the Mesopotamians too – some of their homework tablets were Pythagoras-type questions (see here). We know from several different sources that, as a young man, Pythagoras travelled extensively around the Mediterranean, and possibly even further afield, to gather knowledge, so it seems he had plenty of opportunity to glean this information from elsewhere.
So why is the theorem named after him? Because Pythagoras was the first Greek identified with the concept. And, since we were unable to read hieroglyphics or cuneiform until recently, it was assumed Pythagoras must have worked the theorem out independently.
Another legend associated with Pythagoras is that he was the first person to work out the relationship between a length of string and the note it produces when plucked. He also noted that if the lengths of two strings were in a whole number ratio to each other then a harmonious chord was produced.

Pythagoras is also often attributed to the discovery of the Platonic solids and the golden mean, both of which were recorded by Plato (see here).
Pythagoreanism
Pythagoras’ religious cult was a somewhat bizarre group. Its members favoured an ascetic lifestyle by avoiding talking and following a vegetarian diet. They were a highly secretive group – the revelation of a cult secret was punishable by death. Pythagoreans were also very exclusive, and managed to antagonize the inhabitants of nearby towns enough for the populace to burn down their meeting place, killing many of the cult’s members in the process.
Central to the Pythagoreans’ doctrine was the idea that numbers were divine. They also believed that all numbers could be written as fractions. One notable legend centres on an unfortunate fellow called Hippasus, a Pythagorean who was pretty certain he had come across numbers that could not be written as fractions. In some of the more fanciful legends, Pythagoras asks Hippasus to take a boat out to sea with him to discuss his heretical ideas – only Pythagoras comes back. An alternative version sees Hippasus being drowned by the gods for his crimes against holy numbers.
An irrational discovery
Whatever the circumstances of Hippasus’ sticky end, he may have been one of the first people to discover irrational numbers – numbers that cannot be written as a fraction, and whose decimal equivalent goes on for ever without repeating.
See if you can follow some good ol’ Greek reductio ad absurdum (see here) to see why √2 must be an irrational number.
√2 is the square root of 2 – the number that when multiplied by itself gives an answer of 2.
√2 = 1.4142135623...
If √2 can be written as a fraction, let’s say it is x/y in its lowest terms.
If x/y is in its lowest terms x and y cannot both be even because if they were even you would be able to divide both x and y by 2, so they could not have been in their lowest terms to start with.
If you square everything you get 2 = x2/y2. This means that x2 must be twice y2 and so x2 must be even because it is two times something. This in turn means x must be even because odd x odd = odd.
If x is even then y must be odd because, as you might recall, x/y was in its lowest terms and the two, therefore, cannot both be even.
If x is even, then it must be divisible by 2. So let’s say x = 2 × w.
If x = 2 × w and x2 must be twice y2, then 4w2 = 2y2, so 2w2 = y2, and so y2 must be even because it is twice something. It follows that y must be even, which conflicts with our earlier deduction that y must be odd!
If x is even, then y must also be even. But we said it must be odd. So √2 ≠ x/y so √2 cannot be written as a fraction.
SOCRATES (c. 470–399 BC), PLATO (427–347 BC) AND ARISTOTLE (384–322 BC)
Three of Ancient Greece’s most renowned philosophers, Socrates, Plato and Aristotle are often mentioned together because Socrates taught Plato, who in turn taught Aristotle. They were hugely influential to Western thought because, essentially, they were responsible for inventing it.
Socrates
While he did not contribute to mathematics directly, Socrates did supply a way of thinking about problems, called the Socratic method, which provided a logical framework for solving mathematical conundrums. Using the Socratic method, a difficult problem could be broken down into a series of smaller, more manageable pieces; by working through these smaller challenges the inquirer would eventually reach a solution to the main problem. Although Socrates generally used this method to solve ethical questions, it is equally useful for mathematical and scientific problems.
Plato’s dialogues
Plato was a student of Socrates’, and is well known for writing a series of works called the Socratic Dialogues, which use a fictional discussion between Socrates and a range of other people to set forth ideas and philosophies; a little like reading a fictional transcript of a lesson, with a student questioning the ideas put forth by his teacher.
In one such dialogue, Timaeus, written in c. 360 BC, Plato discusses several important mathematic and scientific ideas.
Plato’s solids
The elements is the first topic addressed in Timaeus. Today modern atomic theory tells us that there are over 100 elements that can be combined to create all known substances. In his dialogue Plato was the first to propose that the four elements – fire, air, water and earth – each assume a specific shape. We name the shapes of these elements the Platonic solids in his honour.
The Platonic solids are 3D shapes (polyhedrons) whose faces are made up of regular (all sides and angles are equal) 2D shapes (polygons). For example, a triangle-based pyramid made up of equilateral triangles is a Platonic solid called a tetrahedron.
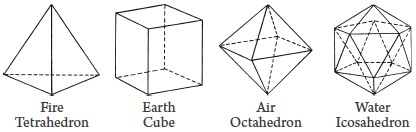
These four elements, much like the elements we know today, could be combined to make any substance. There is one other Platonic solid – the twelve-sided dodecahedron– which was not an element, but which represented the shape of the universe.

Going for gold
Another important concept discussed in Timaeus is the golden mean, sometimes called the golden ratio or golden section.
The golden mean is the optimum position between two extremes, and it’s also a number: 1.6180339887... – one of those irrational numbers the Pythagoreans were not very keen on. Much like √2, the golden mean cannot be written as a fraction because its decimal continues for ever without repeating. This is inconvenient when it comes to writing the number down, so mathematicians use the symbol φ (the Greek letter phi) to represent it.
Another irrational number that has its own Greek letter is 3.14159265...: π, which you will remember from learning about circles at school. We get π by dividing a circle’s circumference (its perimeter) by its diameter (the distance across the circle through the centre). It doesn’t matter what the size of the circle is, you always get the same value: π. φ has a similar geometrical provenance.
If a line is divided into a longer part and a shorter part, and if the total length (x + y) divided by x gives the same value as x ÷ y then the line has been split into the golden ratio. As with π, the length of the line doesn’t matter – to get it to work you find that x ÷ y = 1.618... = φ.
The same idea works with shapes too. The Ancient Greeks considered a rectangle with its longer side φ times longer than its shorter side to be the most aesthetically pleasing rectangle possible.

It is often said that many important examples of sculpture and architecture are made using the golden mean.
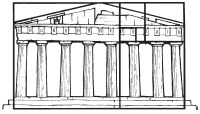
The Parthenon was designed according to the golden mean. Its length and height and the space between the columns were designed in perfect proportion to one other.
The son of the doctor at the court of the kings of Macedon, Aristotle was a nobleman who became a hugely influential philosopher. He was taught by Plato and later became a teacher at Plato’s Academy, and he contributed ideas on a whole host of subjects, from politics and ethics to physics and zoology. So wide-ranging were his skills, it has been suggested Aristotle knew everything it was possible to know. Indeed, his influence extended through to the philosophy of the modern world.
Zero Option
Aristotle let things slip in his treatment of numbers. He felt that a number only really had meaning if it was an amount of something: a pile. In Aristotle’s eyes, 10 apples, 1 apple, ½ an apple and 1/10 of an apple were all valid numbers. However, if you do not have an apple, you have nothing to pile up or count – zero, as far as Aristotle was concerned, was not a number.
Aristotle is known chiefly for his logic, a series of works that comprised the earliest-known study of the theory of logic. His theories have since split into many different branches, some highly mathematical, others more philosophical.
Aristotle’s work in mathematics and science focused on explaining the way things behave by describing them rather than using numbers and equations. He was among the first to explain the motion of objects (a subject we today call kinetics, from the Greek for ‘movement’). Aristotle’s descriptions acknowledged that time and space are not arranged in indivisible chunks but are continuous, which allowed him to show that Zeno of Elea’s ideas were flawed and that Achilles would have been able to catch up with the tortoise!
EUCLID (c. 325–c. 265 BC)
While little is known about the Greek mathematician Euclid, we do know that he was active in Alexandria in Egypt under Greek rule, and is notable for having penned a groundbreaking book called Elements. Certainly one of the most important maths books of all time, Euclid’s Elements was considered essential reading for any scholar well into the nineteenth century.
Elementary proof
Although Euclid drew on the ideas of others, he was one of the first mathematicians to produce work that used mathematical logic in order to prove theories. This idea of proof is one of the foundations of mathematics.
Elements covers much of geometry and ideas about numbers, including prime numbers and other number sequences, and all of Euclid’s geometrical constructions were made using only a pair of compasses and a straight edge.
It is split into thirteen books, each of which starts with definitions of words to help make it clear what Euclid means when he refers to words such as point, line, straight, surface, etc. Euclid then sets out a list of axioms or statements that are evidently true, such as ‘all right angles are equal to each other’ and ‘if A=B and A=C, then B=C’.
The next section of the Elements is called ‘Propositions’, in which Euclid proposes a method of how to carry out a mathematical task. For example, in Proposition 1 of Book 1 Euclid shows how to draw an equilateral triangle (all the sides are the same length and all the angles are equal to 60°), and he then goes on to prove that the triangle is, in fact, equilateral.
ERATOSTHENES (276–195 BC)
It would be wrong to talk too much about prime numbers without mentioning multi-disciplined mathematician Eratosthenes, who hailed from a Greek city in modern-day Libya. He was responsible for many great intellectual endeavours, including calculating the earth’s circumference to a surprising degree of accuracy and coining the word ‘geography’, which means ‘drawing the earth’ in Ancient Greek. Mathematically, Eratosthenes’ greatest contribution is the Sieve of Eratosthenes.
Before we look at the sieve let us first contemplate prime numbers: numbers that have only two factors – themselves and 1. Hence 13 is a prime number because 1 and 13 are the only numbers that divide into it without leaving a remainder. 9 is not prime, because it can be divided by 1, 3 and 9, which means it has three factors. 1 is also not a prime number because it has only one factor.
Prime numbers are important for two reasons:
1. Any whole number or integer greater than 1 can be written as a chain of multiplied prime numbers. For example, the numbers between 20 and 30 can be written as follows:
20 = 2 × 2 × 5
21 = 3 × 7
22 = 2 × 11
23 = 23 (prime)
24 = 2 × 2 × 2 × 3
25 = 5 × 5
26 = 2 × 13
27 = 3 × 3 × 3
28 = 2 × 2 × 7
29 = 29 (prime)
30 = 2 × 3 × 5
There is only one way of doing this for each number so it seems to me, at least, that primes are the equivalent of DNA for numbers.
Fundamentals
The idea that any whole number greater than 1 can be expressed as the unique product of a chain of multiplied prime numbers is called the fundamental theorem of arithmetic.
2. They are very mysterious – there is no pattern to prime numbers, and there is no formula that will produce them. To this day the nature of prime numbers is still under intensive study by mathematicians.
Eratosthenes’ sieve works using a very simple principle to help find prime numbers up to a certain limit. 2 is the first prime number. Anything that 2 goes into cannot be prime, because it would then have 2 as a factor as well as itself and 1.
If we set ourselves a limit of 100, we could highlight 2 as a prime and then eliminate all the numbers that have 2 as a factor: 4, 6, 8, etc. up to 100. If we use a grid we can shade them in to generate a pattern:
You don’t even need to be brilliant at your two-times table to do this – you could just count on 2 each time and shade in each square you land on.
After you’ve shaded in all the multiples of 2 you move on to the next unshaded number, which also happens to be the next prime number: 3. We highlight 3 as a prime and then eliminate all the multiples of 3, some of which have already been eliminated in the first round. The next unshaded number is 5, which again is also prime. As before, highlight that and then eliminate the multiples of 5.
As you move along, the next unshaded number must be prime because none of the prime numbers that went before it could go into it. If you keep on repeating this process eventually you’ll have a completed sieve. Turn to page 55 to see what this looks like.
Euclid’s theorem demonstrated that there are infinitely many prime numbers. We know that any number can be made by multiplying a chain of prime numbers together; thanks to our sieve, we also now know all of the prime numbers under 100. How can we be sure there are more? Let’s use the Sieve of Eratosthenes to investigate.
If you multiply all the primes together you generate a number. This next number will either be a prime number or it won’t. If the next number in sequence is a prime then we have a new prime number.
However, if the next number isn’t prime there must be a prime number that we don’t already know of that goes into making it – therefore there’s another prime number somewhere.
So, whatever happens, we either have a new prime number or know there is an unknown prime number that is less than or more than our number. No matter how large we make the sieve, there is always another prime number that is not on it, therefore there must be an infinite number of primes.
You can make the sieve as big as you like in order to work out higher and higher prime numbers. There are no hard calculations to do, but it is quite a tedious process – something a Greek mathematician would probably have left to an educated slave.
ARCHIMEDES (287–212 BC)
Archimedes was a friend of Eratosthenes and he hailed from the city of Syracuse in present-day Sicily. He was famous as a scientist and engineer: he invented the Archimedes screw for pumping liquids and raising grain, which is still in use today. Archimedes is also said to have defended Syracuse from Roman warships by directing an intense ray of light from the sun towards the approaching soldiers, setting their vessels alight.
Archimedes’ contributions to mathematics are no less impressive, even if they are less well known. He worked out a value for π by noting that, as a polygon accrues more sides, it gets closer and closer to becoming a circle. π is defined as a circle’s circumference divided by its diameter. It is hard to measure the curved edge of a circle accurately, but easy to measure the straight sides of a polygon to find the perimeter. By approximating a circle as a polygon with a certain number of sides, Archimedes was able to find a value for π by dividing the polygon’s perimeter by the distance across the polygon. Archimedes performed this calculation with a polygon that had up to 96 sides. During his investigations he came up with a value of between 3.143 and 3.140 for π, which is pretty close to its actual value: 3.1415...
Archimedes hit upon an important idea with this method of exhaustion – the idea that if an approximation is performed accurately enough it becomes indistinguishable from the true answer. This idea has been used in many other areas of mathematics, perhaps most noticeably in the calculus of Newton (see here) and Leibniz (see here) almost 2000 years later.
Archimedes proved other important results, including that the area of a circle is π multiplied by the radius squared. He also proved that the volume of a sphere is 2/3 the volume of the cylinder that it is able to fit into. Archimedes was so pleased with his discovery he had a sculpture of the sphere and cylinder erected on his tomb.
Archimedes died at the hands of a Roman soldier while working at his desk. Legend suggests Archimedes was so absorbed in his work he failed to respond to the soldier’s orders that he come with him. Insulted, the soldier killed Archimedes, and presumably faced the wrath of his commanding officer, who would have regarded the slain intellectual as a highly valuable scientific asset.
With the death of Archimedes we come to the end of Ancient Greece, when its territories were consolidated into the emerging Roman Empire. The mathematical legacy of the Greeks is long lasting and most people today will have encountered the discoveries made by many of the mathematicians mentioned in this chapter. I think the Ancient Greeks’ greatest contribution was to invent mathematics as a rich and diverse subject, moving it beyond the basic necessity of numeracy and arithmetic, the functional tools of an economy. They created a subject that would become the language of science and which would eventually allow humanity to create scientific ideas from first principles, basing discoveries on a concept rather than from fudging equations and formulae to match observations. Without this mode of thinking Sir Isaac Newton would have been unable to conduct much of his pioneering work.