
The Greek mainland was conquered by the Romans in 146 BC, and the empire reached its zenith 200 years later, occupying a vast area that covered the entirety of the Mediterranean on all sides.
A PRACTICAL PEOPLE
Discipline was a central aspect of Roman life, which extended to its education system. The wealthier young Romans were taught basic arithmetic, most likely at home, but the main thrust of their education was to understand the workings of their own society. Oration was seen as the pinnacle of education, along with physical training for boys, who would go on to do military service, and home economics for girls, who were in charge of running their homes.
In terms of higher mathematics, it appears that very little was taught to the Romans when compared to their Greek predecessors. The Romans were a far more practical people, focusing their attentions on developments in engineering and medicine; practicality is not the best mindset for exploring mathematics for its own sake.
A spanner in the works
The Roman number system, inherited from the Greeks, didn’t help matters. Roman numerals rely on the position they sit within a string of letters, which makes it very difficult to use them in arithmetic.
The basic Roman numerals are:
I: one
V: five
X: ten
L: fifty
C: one hundred
D: five hundred
M: one thousand
The Romans wrote their numbers with the largest starting from the left. Therefore, in order to read a Roman numeral you have to add up the numbers from left to right. For example:
MMMDCLXVII would be 1000+1000+1000+500+100 +50+10+5+1+1 = 3667
However, the Romans devised a useful shortcut for using when the value of a number was close to the value of the next letter. The method involved putting a letter out of sequence, which indicated it should be subtracted from the next letter in sequence.
For example, in longhand the number 999 should be written DCCCCLXXXXVIIII, but with the shortcut it could be written as IM. However, there seemed to be no written rules, and the Romans, it seems, didn’t like having an I before an M or a C if they could avoid it. Therefore, 999 would more likely have be written as CMXCIX which gives (1000 - 100) + (100 - 10) + (10 - 1) = 900 + 90 + 9 = 999. Needless to say, having more than one way to write a number did not make life easy!
Alexandria
The Roman Empire subsumed the old Greek Empire and, as such, the Greek mathematical tradition continued. It focused in Alexandria, Egypt, a remarkable centre of learning that had been founded in 331 BC by the leader of the Greeks, Alexander the Great, as he conquered his way East across Europe and Asia.
HERO (10–70 AD)
An Alexandrian scientist and mathematician, Hero is most famous for detailing a primitive steam engine, and for perhaps being the first person to harness wind power on land with the aid of a windmill.
Hero also made two significant contributions to mathematics:
1. He came up with a formula for working out the area of a triangle that only requires the lengths of the sides of the triangle.
2. He devised a way of working out square roots: a number that when multiplied by itself gives a specific quantity.
Hero’s formula
There are many ways to work out the area of a triangle. Most of us were taught at school that:
area of triangle = ½ × base × height
For this formula you need to choose which side is the base and then work out the height of the triangle, which, if it’s non-right-angled, may not be one of the other two sides:
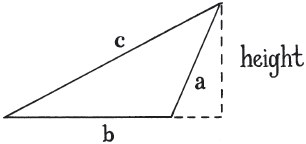
Hero’s formula removed the need both to choose a base and to measure the height, although perhaps at the expense of simplicity:
area of triangle with sides of length a, b and c = ¼ × √[(a2 + b2 + c2)2 - 2(a4 + b4 + c4)]
The root of the problem
Hero’s method for working out square roots involved using a formula to generate a new value; this new value would then be put back into the formula and the process would be repeated a number of times with the answer getting closer to the true value.
This technique is called iteration – another important development in mathematics. For example, if you wanted to work out the square root of 2, which, as we saw earlier, is an irrational number – one which cannot be written as a fraction and whose decimal goes on for ever without repeating (see here) – Hero’s method would work like this:
new value = ½ × (old value + R ÷ old value)
where R is the number you want to know the square root of. The first time you use the formula there is no ‘old value’, so you have to take a guess. The square root of 2 must be between 1 and 2, because 1 × 1 = 1 and 2 × 2 = 4 and 2 lies between 1 and 4. Let’s opt for the middle value, 1.5, and see what happens:
new value = ½ × (1.5 + 2 / 1.5) = 1.41666666...
You can now repeat this process using 1.41666 as your old value:
new value = ½ × (1.41666 + 2 / 1.41666) = 1.414215686
new value = ½ × (1.414215686 + 2 / 1.414215686) = 1.41423562
new value = ½ × (1.41423562 + 2 / 1.41423562) = 1.41423562
At this point you should notice that the old value and new value are the same, so our work here is done – and this is indeed the square root of 2, accurate to 8 decimal places.
If you wanted to work out the square root of another number you would start with a different R. It’s important to note that if you make R a negative number the formula does not work. For example, if you make R = -2 and have 1 as your first guess you get:
This process continues for ever without ever settling on a value. Why? Because negative numbers cannot have a square root – a negative number multiplied by a negative number always gives a positive answer. Hence the formula is searching for something that does not exist!
Hero did, however, postulate that it could be possible for a negative number to have a square root, if you use a bit of imagination (see here).
DIOPHANTUS (c. 200–c. 284 AD)
A resident of Alexandria from c. 250 AD, Diophantus is sometimes referred to as the ‘Father of Algebra’ because of his contribution to solving equations. While today thoughts of algebra conjure up a process of replacing numbers with letters, Diophantus did not adhere to this principle. Before true symbolic algebra was invented, mathematicians were forced to write out equations longhand.
These days it’s very easy to write a simple algebraic equations, such as: 3a + 4a2. However, Diophantus’ method would have been far more laborious, involving something along the lines of: ‘three multiplied by the unknown number added to four times the unknown number multiplied by itself.’ This made solving equations a tricky process, both in terms of writing and reading them.
An imaginary triangle
Diophantus was interested in Pythagoras’ theorem. He noticed something strange when he tried to work out the sides of a right-angled triangle with a perimeter of 12 and an area of 7. It produced an equation that could not be solved, indicating a triangle with those specific dimensions cannot exist. However, Diophantus remarked that if negative numbers could have square roots he would be able to solve the equation – which would mean the triangle would then exist. Much later, these numbers were called imaginary numbers (see box here), because in order to get round the problem you have to imagine that there is a number, represented by the symbol ‘i’, that is the square root of -1.
Triple the fun
His interest in Pythagoras’ theorem also sparked another mathematical mystery that would take hundreds of years to solve. Diophantus was interested in Pythagorean triples, which are solutions to the theorem that are whole numbers. For example:
32 + 42 = 52
52 + 122 = 132
82 + 152 = 172
In his great work Arithmetica, Diophantus included instructions on how to find such numbers. In 1637 French mathematician Pierre de Fermat wrote in the margin of his copy of Arithmetica that it was not possible to find the Pythagorean triples where the numbers were raised to any power other than 2. He finished with a tantalizing comment that was to tease mathematicians for years to come: ‘I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.’
These innocuous words started a 350-year challenge to solve what became known as Fermat’s last theorem.
Although we know very little about Diophantus’ life, a charming riddle, sometimes known as ‘Diophantus’ Epitaph’, associated with him provides a brief overview of his days on this earth. The riddle was first noticed in a puzzle book by the Greek philosopher Metrodorus some time in the sixth century AD.
‘Here lies Diophantus,’ the wonder behold.
Through art algebraic, the stone tells how old:
‘God gave him his boyhood one-sixth of his life,
One twelfth more as youth while whiskers grew rife;
And then yet one-seventh ere marriage begun;
In five years there came a bouncing new son.
Alas, the dear child of master and sage
After attaining half the measure of his father’s life
chill fate took him. After consoling his fate by the
science of numbers for four years, he ended his life.’
Can you work out how old Diophantus was when he died?
Hypatia (c. 370–415 AD)
The Alexandrian mathematician, philosopher and astronomer Hypatia was the daughter of Theon, a mathematician who produced an edition of Euclid’s Elements. He educated his daughter in the same way as his sons, which exposed Hypatia to the rich philosophical heritage of her Greek ancestors.
Hypatia was a teacher specializing in the philosophies of Plato and Aristotle, and as part of this she developed her own ideas in mathematics, physics and astronomy. She edited her father’s editions of Euclid’s and Diophantus’ works, using her teacher’s eye to help the reader understand the more difficult sections.
Hypatia is widely considered to have been the first woman to make contributions to mathematics and science, although few of her original works survive. She dressed in scholar’s robes rather than in female dress, and chose to navigate the city unaccompanied, often driving her own chariot, which at the time was considered very unladylike. Hypatia also stood for what by then the Christian Romans considered to be a pagan religion. Her lectures, which were open to all comers, regardless of race or religion, were targeted by Christians and led to riots. This discrimination reached an inevitably bloody conclusion, and in March AD 415 Hypatia was brutally attacked and murdered by a Christian mob.
THE END OF THE ROMANS
The Roman Empire began to disintegrate in c. AD 380. In the absence of the sizeable bureaucratic machine and enforced discipline the Romans had instilled, Western Europe entered what is sometimes referred to as the Dark Ages: a period when little intellectual development occurred. Allegedly.