

The Renaissance began in Italy as early as the twelfth century and witnessed great advances in all fields of intellectual endeavour. It sparked a new-found interest in the culture of the classical civilizations, which made an appreciation for – not to mention an investment in – science, culture and philosophy, the done thing among the wealthy patrons of fourteenth-century Europe.
The initial epicentre of the Renaissance was Florence, Italy, where a wealthy merchant family, the Medicis, became sponsors of art and culture. One artist who benefited from their philanthropy was Leonardo da Vinci.
Legendary for his talent in almost every field of intellectual pursuit, da Vinci was equally adept in the arts and the sciences. His superior ability and imagination enabled him both to paint the Mona Lisa and to invent flying machines, among other extraordinary feats.
Perfectly proportioned
Da Vinci was also a keen anatomist, perhaps out of a desire to bring an element of realism to his art. He was very interested in the relative proportions of the human body, and his famous drawing of the Vitruvian Man demonstrates his understanding.

The name of the picture harks back to a Roman architect called Vitruvius. He believed the proportions of the human body are naturally pleasing to the eye, which led him to design his own buildings along similar proportions. Vitruvius considered the navel to be the natural centre of a man’s body. He believed a square and a circle drawn over an image of a man with his legs and arms outstretched would represent the natural proportions of the body. Many artists tried to draw human figures that adhered to Vitruvius’ proportions, but all looked somehow misshapen. Da Vinci, however, discovered the correct drawing could be made if the centre of the circle and the centre of the square are positioned differently.
A Helping Hand
Although da Vinci himself was not a trained mathematician, he did spend time receiving instruction from Luca Pacioli, a highly regarded maths teacher and accountant. Da Vinci created many drawings of solids for one of Pacioli’s books, and his technical expertise with perspective helped to make the diagrams clear.
NICOLAUS COPERNICUS (1473–1543)
A Polish astronomer, Nicolaus Copernicus was one of the first to propose the heliocentric model of the universe: the earth is not the centre of the universe; it does, in fact, orbit the sun. While this was not a mathematical discovery in itself, the way in which Copernicus devised his theory had significant implications for mathematics and science.
The march of science
According to the Bible, the earth was the centre of the universe, which was a perfectly reasonable, if slightly self-important, assumption to have made. After all, both the sun and the moon appear to orbit the earth every day; indeed, all other objects in the night sky appear to do the same.
However, an exploration into the world of astronomy soon revealed problems with this assumption. For example, there are times when the planets appear to move in reverse, which could not be explained if the earth is stationary.
Scientists at the time worked empirically, which means they made observations of phenomena and then came up with an explanation to fit what had been observed. But Copernicus did something that was considered very backward by scientists at the time – he first came up with a theory about how the solar system might work and then tested it against observations, using mathematics as his main tool.
While Copernicus’s heliocentric model did not cause much of a stir at the time, his way of working theoretically was one of the first examples of a new way of conducting modern scientific methods.
JOHN NAPIER (1550–1617)
A Scottish nobleman, John Napier was responsible for inventing a new kind of abacus called Napier’s bones. He also discovered logarithms.
Napier’s table
Logarithms are very important in many fields of mathematics and Napier’s book Description of the Wonderful Rule of Logarithms was quickly adopted by those who had to conduct such calculations on a regular basis. It took Napier an astonishing twenty years to perform the calculations required for the tables of logarithms in the book – that’s some dedication.
The logarithm of a number is the number we have to raise ten by in order to generate that number. For example:
The logarithm of 100 is 2 because 100 = 102
The logarithm of 1000 is 3 because 1000 = 103
The shorthand for writing this would be log (1000) = 3
We can find logarithms for numbers that are not whole powers of ten too:
log (25) = 1.39794 because 25 = 101.39794
We can also find the logarithm for numbers using any number, not just 10, as a base:
log5 (25) = 2 because 25 = 52
Natural logarithms (see here) are logarithms with a base of e, which is a very special number in mathematics that allows many difficult calculus problems to be solved.
Logarithms today are computed using a calculator or computer, but originally they were worked out either by hand or using Napier’s tables. Before desktop calculators became commonplace people would use logarithms and a slide rule (see here)to perform difficult calculations.
Napier’s bones
Napier also devised a faster and more convenient way of performing multiplication, based on a lattice method that Fibonacci had learned from the Arabs.
Napier’s bones was a useful tool that consisted of a set of sticks engraved with numbers, and each stick had a times table written on it, from 2 times the number up to 9 times the number:
If you wanted to multiply 567 by 3, for example, you would collect together the three sticks that match the large number and then highlight the third row:
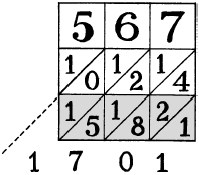
You then add the diagonal rows shown on the bones in order to calculate the answer.
Napier was also one of the first people to use the decimal point. Although the Hindu-Arabic numeral system was in common use across Europe by this point, a standard way of writing fractions was yet to be formalized. Because Napier needed a concise way to write them for his log tables, he adopted the Hindu-Arabic decimal fractions we use today.
WILLIAM OUGHTRED (1574–1660)
An English mathematician and teacher, William Oughtred continued Napier’s work on logarithms. He is credited with inventing the slide rule, a calculating device that allowed the user to multiply large numbers together using a ruler marked with logarithmic scales (see here), which meant the answer to the multiplication could simply be read off the ruler. Slide rules were used by scientists, engineers and mathematicians up until electronic calculators became commonplace in the 1970s.
The slide rule works because of the law of logarithms:
log (a × b) = log (a) + log (b)
Let’s test this out using some easy numbers:
log (10 × 1000) = log (10) + log (1000)
= 1 + 3
= 4
From this we know that 10 × 1000 = 104 = 10000.
Therefore, if you want to multiply two numbers together you can ‘take the log’ of each number, add them together and then raise ten by this number. Before the slide rule, you would have had to look up this answer in a big, expensive book of tables – so the slide rule was a remarkably convenient development for mathematicians and scientists.
Rather than spacing out successive markings along an axis by adding on the same value each time, a logarithmic scale spaces them out by a multiple (normally of 10) each time. For example, a graph with a normal linear scale would go 0, 1, 2, 3; a graph with a logarithmic scale would go 0, 1, 10, 100. The graphs of y=10x shown below are with a linear and logarithmic scale respectively.

Born in France, René Descartes was an important philosopher, perhaps best known for coining the statement ‘I think, therefore I am’.
A different equation
Descartes was a sickly child and was allowed to sleep in every morning to recuperate, which became a lifelong habit. Apparently, during one such lie-in Descartes was watching a fly walk across the ceiling and wondered how he might be able to describe accurately the position of the fly at any given time. He realized that if he mapped out the ceiling with a square grid he could use what we now call coordinates to record exactly where the fly was positioned.
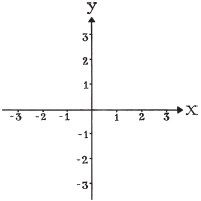
These Cartesian graphs proved to be incredibly useful in mathematics because they linked the fields of geometry and algebra. Equations could now be drawn on a set of numbered axes, which allowed them to be investigated more easily by sight, rather than solving them algebraically.
Cartesian geometry encouraged mathematicians to think about the graphical properties of equations, such as whether or not the lines of equations are parallel. To find out whether lines are parallel you need to work out their gradient. If two lines have the same gradient they must be parallel. Only the simplest linear equations are a straight line, which makes their gradients straightforward to work out. Curves, however, have a changing gradient, but thanks to Descartes’ breakthrough the way was paved for Isaac Newton and Gottfried Wilhelm Leibniz to discover calculus (see here).
The Proof of the Matter
Descartes’ philosophy also assumed a mathematical bent because he believed the universe was set out according to mathematical rules. For example, in his book Meditations on First Philosophy, Descartes discards any beliefs he holds that are unproven, and then builds his philosophy of the way in which reality works without recourse to anything other than proven fact. This sceptical viewpoint is one of the ideas that underpins modern science and makes mathematics the scientist’s most powerful and productive tool.
A French lawyer, Pierre de Fermat spent his spare time pursuing his love of mathematics. Although he did not publish any of his ideas when he was alive, he did share them in letter form with his mathematical contemporaries. Frustratingly, however, Fermat seldom found it necessary to provide proof for his work.
Fermat worked in many areas of mathematics, but the area for which he is famed is number theory: the study of integers (whole numbers) and the attempt to find integer solutions to equations.
Fermat is famous for his ‘last theorem’, which he wrote in his copy of Diophantus’ Arithmetica, and which was discovered by his son after his death (see here). Fermat was also interested in perfect numbers (see box here) and primes.
In their prime
Fermat devised a method of testing whether or not a number is prime that relies on an algebraic trick known as the difference of two squares. This says that:
a2 - b2 = (a + b)(a - b)
A perfect number is a number whose factors (not including the number itself) add up to make the number.
For example, 6 is a perfect number (the first one, in fact) because the factors of 6 are 1, 2 and 3 and 1 + 2 + 3 = 6
Perfect numbers are rare – the next one is 28, followed by 496 and then 8128. The fifth perfect number is 33,550,336.
Numbers whose factors add up to less than the number are called deficient numbers. For example, 8’s factors are 1, 2 and 4, which have a sum of 7, so 8 is deficient.
Numbers whose factors add up to more than the number are called abundant numbers, e.g. the sum of 12’s factors are: 1 + 2 + 3 + 4 + 6 = 16.
In the case of some abundant numbers, no combination of its factors will make up the number. These numbers are called weird numbers. For example, 24 is not a weird number because we can add its factors together (2, 4, 6 and 12) to make 24. The first weird number is 70 – we cannot add any combination of its factors 1, 2, 5, 7, 10, 14 and 35 to get a total of 70.
For example, if a = 8 and b = 5:
82 - 52 = (8 + 5)(8 - 5)
64 - 25 = 13 × 3
39 = 39![]()
Fermat needed to test odd numbers (because 2 is the only even prime) to see if they were prime. He made the number he was testing, n, equal to the difference of two squares:
n = a2 - b2
which means that:
n = (a + b)(a - b)
This shows that n is two numbers multiplied together, in which case n cannot be a prime number unless (a + b) = n and (a - b) = 1.
Fermat took the first statement and rearranged it:
a2 - n = b2
This meant that he could pick a starting value for a, square it and subtract n and see if he was left with a perfect square which is easily identifiable. If b2 was not a perfect square he would increase his starting value by one and try again until he either found numbers for a and b that worked or got to a point where a × b was larger than n.
BLAISE PASCAL (1623–62)
Educated by his father, Blaise Pascal was a French prodigy who worked in the fields of mathematics, physics and religion. His precocious talent saw his first mathematical paper published at the tender age of sixteen.
Speeding things up
Pascal’s father was a tax collector during a time of war in Europe, which made his job a somewhat onerous endeavour. Pascal sought to help his father by developing the first mechanical calculator – a machine known as a ‘Pascaline’, designed to add and subtract numbers. After he’d created a number of prototypes, Pascal’s finished product comprised a box with a series of numbered dials on its front and with a digit displayed above each dial. Numbers to be added were ‘dialled’ into the machine and the result would be displayed.
Unfortunately, the Pascaline was very expensive to make and was therefore seen as more of a deluxe executive toy than a useful mathematical device. But Pascal’s contribution to mathematics should not be underestimated – he paved the way for Leibniz and others to develop more effective mechanical calculators and, eventually, modern computing.
Pascal was also interested in games of chance and gambling. His work with his acquaintance Pierre de Fermat (see here) led to the field of mathematics we now call probability. In probability, we talk about an event (e.g. rolling a die) having a certain number of outcomes (rolling a 1, 2, 3, 4, 5 or 6 has six outcomes). Each outcome has a probability – for our die, each outcome is equally likely – which is expressed as a fraction (1/6), and the sum of the probabilities of all the events must add up to one. Probability is part of the branch of mathematics called statistics, which has a wide variety of applications in science and economics.
Under pressure
As a scientist, Pascal was fascinated with the notion of a vacuum. At the time, many scientists conformed to the view expounded by Aristotle: vacuums cannot exist; you cannot have emptiness because ‘nature abhors a vacuum’. However, Pascal noticed that if you place a glass beaker upside down in liquid (he used mercury) and then pull it out, there is a small gap at the top of the up-ended beaker that somehow holds up the column of liquid below it. He reasoned that this could only be a vacuum and that it must provide some sort of suction force to hold up the liquid.
Pascal went on to conduct more experiments on pressure within liquids and as a result the unit of pressure is called the Pascal (Pa) in his honour.
In 1654 Pascal had a profound religious experience and it changed the course of his life. He subsequently devoted himself to an ascetic existence and focused on writing theological commentaries. He used his knowledge of probability to expound a reason for assuming God exists, now known as Pascal’s wager:
You cannot tell whether God does or does not exist through logic.
If you believe that he exists and he does not, you lose nothing.
If you believe that he does not exist and he does, you lose an eternal afterlife.
Therefore, there is nothing to lose and possibly infinite reward to be had from believing in God and nothing to gain from not believing in him.
So, on balance, you may as well believe God exists.
One of the greatest scientists of his era, Isaac Newton hailed from Lincolnshire and wrote one of the most important books ever to be written: The Mathematical Principles of Natural Philosophy, often known by a shortened version of its Latin name Principia Mathematica. In the book Newton essentially rewrites the laws of physics that govern the way objects move and react to forces exerted on them. With his laws, Newton was able to explain the motion of the planets and prove conclusively that the sun sits at the centre of the solar system.
Scientifically, Newton’s insight was to recognize gravity as a force that is caused by the earth’s mass, and his ability to understand intuitively how objects would behave when the earth’s gravity was not present. Newton’s critics saw gravity, which acts invisibly and at a distance, as some kind of demonic force and that Newton, an alchemist, was obviously in league with such forces. However, Newton’s Law of Universal Gravitation and his Equations of Motion were perfectly sufficient to allow us to send men to the moon three hundred years later.
Change afoot
Mathematically, Newton’s greatest achievement is calculus, which was also developed independently by Gottfried Leibniz at approximately the same time. Calculus is a tool used today in a range of different disciplines to describe and predict change. Building on the work of Descartes (see here), calculus can be split into two main branches.

We can see that for every square the line moves to the right (the positive direction) the line goes up two squares. The gradient of the line, therefore, is 2.
However, not all equations give straight lines. Any equation with x2, x3 or higher powers produces a curved line:
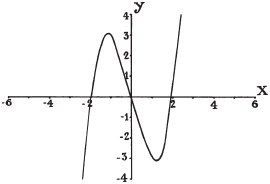
The gradient of this line constantly changes. However, the gradient of the tangent – the line that meets the curve at a point – is the same as the gradient of the line at that point:
Differentiation lets us find a formula for the gradient of the line at any point so we no longer need to draw the tangent, which eliminates an area prone to error.
If we have the formula for the gradient at any point, we can find the places where the gradient is zero. These are called the turning points of the equation and finding them can be very helpful. Many problems in mathematics, banking and business involve finding the maximum or minimum values of an equation – differentiation lets us find these points. Scientists have also found that many phenomena are governed by differential equations. For example, Newton’s Second Law, force = mass x acceleration, is derived by differentiating momentum.
2. The other branch of calculus is integration, which is concerned with finding the area between a curve and the x axis:
Again, drawing the graph might enable us to estimate the area under the curve, and there are various numerical methods that allow us to calculate an approximation of the area. One method would be to divide the area into thin rectangular strips and add each area together:

As you increase the number of rectangles you get closer to the actual value. Newton and Leibniz took this one stage further. They imagined the rectangles became infinitely thin, in which case you get the true value of the area.
You can use this method if you want to calculate the precise area of the shape under a curve. As with differentiation, there are many scientific laws that rely on integration.
Back to the Beginning
It turns out that integrating and differentiation are the inverse of each other, which means that integrating an equation and then differentiating it again takes you back to the original equation. This is known as the Fundamental Theorem of Calculus. Mathematicians use it to help them perform calculus on more difficult equations.
GOTTFRIED LEIBNIZ (1646–1716)
A mathematician and philosopher from Saxony, in the present-day state of Germany, Gottfried Leibniz was the son of a philosophy professor who died when Leibniz was just six years old. Leibniz inherited his father’s extensive library, through which he gained much knowledge, after first having taught himself Latin so he could read the books. Leibniz began his working life as a lawyer and diplomat, and, while on secondment in Paris, he met a Dutch astronomer called Christiaan Huygens, who assisted him in his learning of science and mathematics.
Things turn ugly
Leibniz is important for several reasons, although, perhaps unfortunately, he is mainly remembered for the bitter dispute he had with Isaac Newton over the invention of calculus. Newton was based in Cambridge and Leibniz in Paris, where both men devised the concept of calculus independently of each other. Newton began work on calculus as early as 1664 but he failed to publish his findings. That responsibility was left to Leibniz, who published his first paper on the subject in 1684.
The argument centred on whether or not Leibniz had been exposed to Newton’s prior work. No evidence exists to prove whether or not Leibniz did have access to Newton’s work, and there is no reason to assume that Leibniz could not have come up with calculus independently. However, he died with the matter still unsettled.
Leibniz and Newton developed different notations for calculus and both are used in different areas of mathematics. Leibniz’s is perhaps more commonly used.
To evaluate the area shown on the graph you would use Leibniz’s notation to write:
Which is shorthand for: ‘integrate x2 between x=1 and x=2 with respect to x’.
If you wanted to find the gradient of the line at a point you would need to use differentiation, for which the notation is:

A new dawn
Leibniz was also instrumental in a new field of mathematics that was emerging at the time: computing. In our Hindu-Arabic numeral system, each column in a number is 10 times larger than the one on its right – a decimal system. Leibniz was interested in a way of writing numbers in which each column is twice the value of the column on its right – a binary system. The binary system required only the digits 0 and 1, and the columns have values of 1, 2, 4, 8, 16, etc., doubling each time. So the decimal number 13 would be written as 1101:
Digit: 1 1 0 1 because 8 + 4 + 1 = 13
This system seems quite peculiar but it has the advantage of using only two digits, which makes calculations easier. The binary system would later become very important for electronics and computers.
Number Punching
Leibniz also pioneered the ‘Stepped Reckoner’, one of the first mechanical calculators that could perform multiplication and division. It was a very intricate machine and the complex system of gears could be unreliable, but as manufacturing technology improved over time the Stepped Reckoner went from strength to strength, and Leibniz’s ideas were used for hundreds of years, well into the twentieth century.
JOHANN BERNOULLI (1667–1748) AND JACOB BERNOULLI (1654–1705)
The Bernoulli brothers were Swiss mathematicians. Although they both pursued alternative professions – Johann was trained in medicine and Jacob as a minister – both siblings loved mathematics, especially the calculus of Leibniz. The Bernoulli brothers were able to push on with the fledgling field of calculus and became proficient in its use, turning it from an intellectual and political curiosity into a useful mathematical tool. They were also fiercely competitive with each other, which spurred on their discoveries even more.
Arch rivalry
One example of the Bernoulli brothers’ rivalry stemmed from the problem of the catenary curve: the shape produced by a rope or chain when it hangs from both ends. A mathematical equation of this shape had eluded mathematicians up to this point. Jacob proposed the problem in 1691; Johann, with some assistance from Leibniz and the Dutch mathematician Christiaan Huygens, then went on to solve it. Catenary curves have important applications in bridge building and in architecture because arches that follow an upside-down catenary curve are the strongest.
In everyone’s interest
Jacob also discovered something interesting when he looked at a problem involving compound interest. Jacob noticed that if you had £100 in a bank account that paid 10% interest per annum, the way the interest is paid throughout the year affects the total money you will have at the end of the year. Compound interest payments add to the principal sum of money in a bank account, which increases the interest you earn year after year:
|
Interest Calculation |
Total |
|
|
10% paid at end of year |
100 × 1.1 |
£110 |
|
5% every six months |
(100 × 1.05) × 1.05 |
£110.25 |
|
2.5% every 3 months |
((((100 × 1.025) × 1.025) × 1.025) ×1.205) |
£110.38 |
|
Daily interest |
|
£110.51 |
Admittedly, the changes are not making a vast difference to your balance, a fact that most banks rely on. Of greater significance was Jacob’s investigation into instances when interest is paid continuously, in tiny amounts, over the entire year. He discovered that if your interest rate is x (e.g. x=0.045 for a rate of 4.5%) at the end of a year you would have 2.718281x times what you started with. I have rounded the 2.718281 – it is in fact an irrational number, like π, that goes on for ever without repeating.
Napier made reference to this number in his work with logarithms, and it also plays a very important role in calculus, as exemplified by our next mathematician.
LEONHARD EULER (1707–83)
Euler (rhymes with ‘boiler’ rather than ‘ruler’) was a Swiss mathematician who had originally intended on becoming a priest. However, while at university he met Johann Bernoulli, who recognized Euler’s extraordinary mathematical talent and managed to persuade Euler senior to allow his son to transfer to studying maths.
An increase in power
Euler’s contributions to mathematics and science were far-reaching. The number 2.718281..., discovered by Jacob Bernoulli in relation to his compound interest problem, also turned up in Euler’s work on calculus.
When you integrate to find the area under a graph you need to increase the power of x by one. For example, if your graph is y=x2, the integral is 1/3 x3 – the power of x has gone up by one. If you’re faced with something slightly more tricky, let’s say y = 1/x4, there is a handy rule of powers that can help you:
1/xn = x-n
So y=1/x4 becomes y=x-4, and when you increase the power by one your answer will be something to do with x-3, which is 1/x3.
But what happens if your graph is y = 1/x?
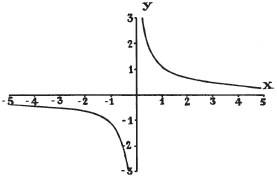
This is the same as x-1, but if you increase the power by one you get x0. Anything to the power of zero is 1, implying that, no matter which section of the graph you look at, the area will be the same. This doesn’t make sense!
Well, it turns out, through a complicated system of algebra developed by Euler, that the area is equal to the natural logarithm of x. A natural logarithm is similar to a normal logarithm, but its base is the number 2.7818281... There is a sizeable family of equations that can only be integrated or differentiated using natural logs, and the 2.7818281 was known as ‘e’ for Euler’s number.
Returning to the area under the graph, if you wanted to know the area between x=1 and x=4, you would need to work out:
area = loge 4 - loge 1
As ‘loge’ turns up so often in calculus, it is denoted by ln and you will find this button on all good scientific calculators.
area = ln 4 - ln 1 = 1.386 (to 3 decimal places)
A bridge too far
Euler’s work on ‘The Seven Bridges of Königsberg’ contributed to methods of simplifying maps. Königsberg was the old Prussian name for the city of Kaliningrad in that strange bit of Russia that sits between Poland and Lithuania. The city is centred on an island, which straddles a river. Seven bridges connect the two sides of the island at various locations:
A popular Sunday afternoon pastime for the residents of Königsberg was to attempt to walk over all seven bridges and return to their starting place without having to use the same bridge twice. Not one person ever managed it, but Euler was the first to tackle the problem mathematically. He redrew the map as a network:
Euler counted the number of routes into and out of each node or intersection on his network. He then reasoned that you would have to walk into and out of each node as you made your way around the map, so you needed each node to have an even number of routes. All the nodes in Königsberg have an odd number, so it is impossible to complete the challenge. Networks where all the nodes have even numbers are known as eulerian. A semi-eulerian network is one that possesses two nodes with an odd number; if you start at one odd node and finish at the other you can complete the network without repeating yourself, as with the following famous example:
Euler was also interested in what are known as complex numbers. These are numbers that are made up of two parts, one real (i.e. any number between plus and minus infinity) and one imaginary.
Diophantus had the first inklings of imaginary numbers (see here), but it wasn’t until the sixteenth century and the arrival of two Italian mathematicians, Niccolò Fontana Tartaglia and Gerolamo Cardano, that the study of imaginary numbers really took off. Tartaglia and Cardano discovered that some equations only generate an answer if you are prepared to allow negative numbers to have square roots – which can’t happen with real numbers, because a negative multiplied by a negative gives a positive.
Descartes coined the term ‘imaginary’ – even though such numbers don’t exist, you can permit them to exist in your imagination in order to find answers to previously unsolvable equations.
The letter i is used to denote the square root of minus 1: √-1
This allows you to reference the square root of any negative number:
√ -49 = √(49 × -1) = √49 × √-1 = 7i
Despite these numbers being imaginary, they have many practical applications, especially in electronics and electrical engineering.
This way of simplifying and thinking about maps and routes had implications for cartography. It’s also an important part of decision mathematics, the branch of mathematics that many businesses rely on for planning delivery routes and other logistical operations.
The many faces of geometry
Euler worked in three-dimensional geometry too. He discovered there is a relationship between the number of corners (or vertices), edges and faces of a polyhedron (a three-dimensional shape with flat faces, like a cube or a pyramid):
vertices – edges + faces = 2
Mathematical Perfection
Euler devised an equation now known as Euler’s identity (an identity is an equation that is always true no matter what value you use for the unknown), which is said to be the most beautiful and elegant mathematical equation. It relates to complex numbers, but unfortunately its meaning is beyond the scope of this book. Here is the equation in all its glory:
eiπ + 1 = 0
Its subjective mathematical beauty arises from the fact that it uses five of the most important numbers in mathematics: e, i, π, 1 and 0.
A cube has 8 vertices, 12 edges and 6 faces: 8 – 12 + 6 = 2

A tetrahedron (triangular-based pyramid) has 4 vertices, 6 edges and 4 faces: 4 – 6 + 4 = 2

A dodecahedron (12-sided polyhedron) has 20 vertices, 30 edges and 12 faces: 20 – 30 + 12 = 2
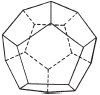
A truncated icosahedron (the combination of hexagons and pentagons used to make a football) has 60 vertices, 90 edges and 32 faces: 60 – 90 + 32 = 2

Euler also teamed up with Daniel Bernoulli (1700–82, son of Johann, nephew of Jacob) to work in applied mathematics. They considered the forces acting on beams in buildings and how the forces would make the beams bend – a very useful tool in engineering applications.
Mathematician Christian Goldbach (1690–1764), in a letter to Euler about the nature of prime numbers, wrote what has become known as Goldbach’s conjecture:
‘Every even whole number greater than 2 can be written as the sum of two prime numbers.’
For example, 10 can be made up from 5 + 5 and 28 is 11 + 17.
In mathematics, ideas are split into three categories:
1. Propositions are statements that may or may not be true. Euclid proposed many in his Elements that he then showed to be true.
2. When a proposition has been shown to be true in all possible cases, it is said to be a theorem, like Pythagoras’ – it works for all right-angled triangles.
3. A conjecture is a proposition that holds the middle ground – mathematicians believe it to be true but have not yet been able to prove it is always true.
Although Goldbach’s conjecture has been checked as far as 4,000,000,000,000,000,000 without finding a counter-example, it is still only a conjecture rather than a theorem. Very picky, these mathematicians!
Carl Gauss was born into a poor family in Germany in 1777 but it soon became apparent that he possessed an extraordinary intellect and a special ability in mathematics in particular.
According to legend, when Gauss was at school he continually annoyed his maths teacher by completing his work far faster than the rest of his class. Exasperated, Gauss’ teacher finally told him to add together all the numbers from 1 to 100, thinking that might give him some peace.
Gauss immediately stated the correct answer: 5050.
Gauss was not a lightning calculator; he had instantaneously seen a shortcut. If you repeat the series, but backward, it can be seen that all the terms add up to 101:

Gauss then quickly worked out that 100 terms of 101 gives 10100, but as this is twice the sum we actually want, he halved it to give the answer 5050.
When Gauss was at university he was interested in the classical geometry of the Ancient Greeks, but new developments in mathematics meant it was now possible to prove geometric theories using algebra, rather than graphically. Gauss proved that it was possible to draw a regular polygon (all sides of equal length and all interior angles of equal size) with 5, 17 or 257 sides using only a pair of compasses and a straight edge.
Back to the beginning
Gauss furthered Euler’s initial work in a branch of number theory called modular arithmetic, in which numbers are allowed up to a certain value, after which they wrap-around and start again. The twenty-four-hour clock is an example of modular arithmetic – after 23:59 we start again at 00:00.
Much like normal arithmetic, in modular arithmetic you need to define what your highest number can be. In normal arithmetic we work in tens, but our highest digit is one less than this: 9. If we are working in modulo 8 we can only use the digits from 0 to 7. This means that 8 would be 0 in modulo 8 because we start again from zero after we reach 7. Likewise, 15 would be 7 in modulo 8 because 15 = 8 + 7 but the 8 counts as 0. Mathematicians would write this as:
In certain circumstances, if you divide two numbers you may be more interested in the remainder (what’s left over) than the quotient (the answer to the division). This is where modular arithmetic can be useful, because a number’s value in a particular modulo is the same as the remainder if you were dividing it. For example:
75 ÷ 8 = 9 remainder 3
75 ≡ 3 (mod 8)
If you wanted to check whether a number was prime, you could see whether the number was ever equal to zero in successive modulos, which is something that computers are good at.
A magnificent spread
Gauss’ work naturally moved into prime numbers, which remain one of the greatest mysteries in mathematics. Gauss made a conjecture, now called the prime number theorem (it is a theorem because it has since been proven, (see here), about the way in which prime numbers are spread out. Although we do not have a formula for making prime numbers, Gauss noticed that the higher up through the numbers you go, on average the more spread out the prime numbers become. He wrote:
number of primes less than x ≈ x / lnx
The symbol ≈ means ‘is roughly equal to’ and the symbol ln means ‘natural logarithm’. Therefore:
number of primes less than 1000 ≈ 1000 / ln 1000 ≈ 145
number of primes less than 10000 ≈ 10000 / ln 10000 ≈ 1086
This shows that, although we made x ten times larger, there are fewer than eight times as many primes. This trend continues as we make x bigger, so primes become fewer the higher we count.
Uneven distribution
Gauss also made an important contribution to statistics by being the first person to introduce the normal distribution. This bell curve applies to all manner of real-world situations such as animals’ heights and weights, marks in examinations, measurements made in scientific experiments and so on.
If you measured the height of every thirteen-year-old boy in the country, you could work out the average or mean height (worked out by adding up all of the data and dividing by how many data there were). You could then look at the percentage of the boys in a certain height bracket and you would find that most of them were within a certain distance from this mean. As you move away from the mean, either higher or lower, you find that there are fewer and fewer boys. Thinking in terms of percentages like this is the same as thinking in terms of probabilities, and so the normal distribution is said to be a probability density function:
The shape of the graph shows what we know to be true. Think about your own friends. Unless you hang out with professional basketball players, most of your friends are clustered around an average or normal height for their gender, and you probably know far fewer very tall and very short people.
The idea of IQ (intelligence quotient) is an example of a score that has been standardized using the normal distribution. An IQ score of 100 is the mean, and a 15-mark interval is called the standard deviation, which is a measure of how spread out the marks are. As a result of the equation of the line used for the normal distribution, it turns out that over 68% of scores are within one standard deviation of the mean, so nearly 70% of people will have an IQ of between 85 and 115. Over 95% of people are within two standard deviations, scores of 70 to 130. Over 99.7% of people are within three standard deviations, scores of 55 to 145. Mensa, a society for people with high IQs, has an entrance test intended to select people who have an IQ higher than 98% of the population, which corresponds to an IQ of just under 131.
An equation (such as y + 3 = 10) is something we can try to solve in order to find out if there are any values that satisfy the equation. Linear equations, where the unknown has an index of 1 (i.e. it is not squared or cubed), have only one answer. Equations that incorporate squares, or cubes, or higher can have more than one answer, but equally may have no answer. For example, there is no real number x that works in x2 = -6.
In formulae (such as Einstein’s E = mc2 or average speed = distance ÷ time) we can substitute values for the letters in order to solve the equation. For example, if you travelled 200 kilometres in 4 hours, you would get the following:
Average speed = 200 ÷ 4 = 50 km / hour
An identity is something that is always true for any value of the unknowns. Gauss invented the triple-bar symbol, ≡, to show this. For example:
(y + 2)(y - 3) ≡ y2 - y - 6
This is an identity because it works for any value of y. Say I make y = 7:
(7 + 2)(7 - 3) = 72 - 7 - 6
9 × 4 = 49 - 13
36 = 36![]()