MATHEMATICAL COMMENTARY
1. Properties of position and of form and geometrical transformations
If we are to believe Ibn al-Haytham, the first part of The Knowns included concepts and propositions ‘that none of the ancients has set out, and they have not set out anything of this kind’.4 Exactly what does this novelty that is claimed by an eminent mathematician, who is always rigorous and circumspect, consist of? And in fact, before even setting out on a detailed commentary on this part, we should note that Ibn al-Haytham considers two closely connected areas: sets of points and point by point transformations. In this research, Ibn al-Haytham’s principal concern is to identify the non-variable elements of the figure, those of geometrical loci, and those that do vary, those of shape, of position or of magnitude. The majority of the propositions in this part concern properties of position and of shape. Ibn al-Haytham is in fact looking for rectilinear or circular loci that provide answers to problems that associate with each point of a locus already given – a straight line or a circle – a new point, found by a transformation of the known locus into the locus we seek. These transformations are displayed explicitly in cases where we have a homothety, a similarity or a translation. In other cases, the transformations, although present, are not identified. In fact, some of them are birational transformations of order 2. Moreover, we need to remember, an essential difference between the two types of transformation we have mentioned above: whereas homotheties, similarities and translations can act on all the points in the plane, the quadratic birational transformations employed by Ibn al-Haytham act only from a curve to a curve.
This difference is perhaps the reason why Ibn al-Haytham did not explicitly discuss the second type of transformation, despite its being present in his work.
We may also note that it often happens that Ibn al-Haytham does not enter into any discussion about the existence of solutions and their number. It would be very naïve to suppose that such discussions, which are often easy, were beyond Ibn al-Haytham’s capacity; their absence, seen also in other books (for example in the Completion of the Work on Conics), is simply an indication of the fact that Ibn al-Haytham did not feel obliged, on every occasion, to enter into a discussion and to carry it through to the end.
Let us take the propositions of this part one by one.
Proposition 1.1. — Any point B situated at a given distance d from a fixed point A lies on the circle with centre A and radius d.
Fig. 2.1.1
Ibn al-Haytham devotes all this part of his work to plane geometry and deliberately concerns himself only with straight lines and circles; he begins by characterising the circle as the locus of a point equidistant from a fixed point.
He stresses the fact that a circle is determinate in position and magnitude when the centre and the radius are known. He distinguishes the invariant elements – a fixed point, a known distance – from the variable elements – positions of the point B. Here we see the beginnings of the idea of drawing the figure in a continuous motion; this idea will reappear throughout the text.
The following three propositions are designed to show the characteristics of homothety and similarity.
Proposition 1.2. — Let there be a given circle (C, R) and a given point B ∈(C, R). The locus of the point D such that 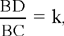 , a given ratio, and that CB̂D = α, a given angle, is a circle (C, r) concentric [with the given one]. This latter circle is the transform of (C, R) in a similarity with centre C, ratio k1 and angle α1 which can be deduced from R, k and α. Ibn al-Haytham shows that the point D is the image of the point B in this similarity with centre C, ratio
, a given ratio, and that CB̂D = α, a given angle, is a circle (C, r) concentric [with the given one]. This latter circle is the transform of (C, R) in a similarity with centre C, ratio k1 and angle α1 which can be deduced from R, k and α. Ibn al-Haytham shows that the point D is the image of the point B in this similarity with centre C, ratio 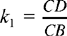 and angle BCD = α1. The given values k1, α1 are known because the triangle BCD, in which the angle at B and the ratio of the sides enclosing this angle are known, is of known shape.
and angle BCD = α1. The given values k1, α1 are known because the triangle BCD, in which the angle at B and the ratio of the sides enclosing this angle are known, is of known shape.
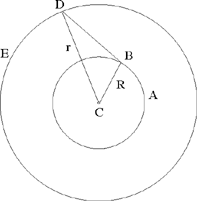
Fig. 2.1.2
Proposition 1.3. — Let there be a circle (E, R), an arbitrary given point C ≠ E and an arbitrary point A ∈ (E, R). The locus of the point D ∈[C, A] such that 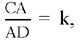 , a given ratio, is a circle (G, R1). This circle is the transform of the circle (E, R) in the homothety h
, a given ratio, is a circle (G, R1). This circle is the transform of the circle (E, R) in the homothety h 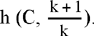 .
.
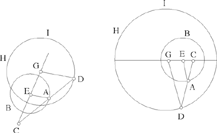
Fig. 2.1.3
Ibn al-Haytham proves the converse and defines the homothety.
Note: Al-Qūhī had studied this problem in his text Two Geometrical Problems (Mas’alatayn handasiyyatayn)5 and it is highly likely that Ibn al-Haytham knew this text by al-Qūhī, as well as many others written by his eminent predecessor. A comparison of the two texts is of interest.
In this third problem of The Knowns, Ibn al-Haytham studies the homothetic figure of a circle with given centre E and radius r. The problem has two parts:
First part: Ibn al-Haytham takes a point C that can lie inside or outside the circle and chooses a ratio k. A point A describes a circle (E, r1). Ibn al-Haytham studies the geometrical locus of the point D of the straight line CA defined by the given ratio 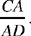
In the argument, it is the ratio 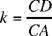 that is used. Now
that is used. Now
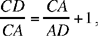
so the ratio 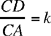 is known.
is known.
Ibn al-Haytham draws DG ∥ EA where G lies on CE and deduces
1) 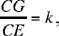 so G is a known point; CG = k · CE.
so G is a known point; CG = k · CE.
2) 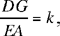 so the length DG is known; DG = k · r1.
so the length DG is known; DG = k · r1.
So the point D lies on the circle (G, r2) where r2 = k · r1.
Second part: Let there be two circles (E, r1) and (G, r2) and a point C on the straight line EG such that 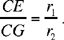
For any straight half line from C that cuts (E, r1) in A and (G, r2) in D, we have
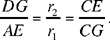
From this we deduce that DG ∥ AE; hence
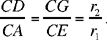
The ratio 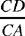 is the same for any straight half line from C; the same is true for the ratio
is the same for any straight half line from C; the same is true for the ratio 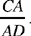
When the point C lies outside the circle with centre E, the position of the circle with centre G depends on the value of the given ratio. The two circles may cut one another, as in the figure, or touch, or lie entirely outside one another. The argument is the same in all these cases for the figure.
The two parts of Ibn al-Haytham’s proposition correspond to the first two propositions of the treatise by al-Qūhī, but in reverse order. However, whereas Ibn al-Haytham presents a single argument in regard to the given point C, whether it lies inside or outside the given circle, in his first two propositions al-Qūhī supposes that C lies inside the given circle; the homothetic circles then lie one inside the other. In a third proposition in his text, he considers the case in which the given point lies outside the given circle. The proof is, however, unchanged. The order of the argument presented by Ibn al-Haytham is more ‘natural’ and his proof is more concise than those of al-Qūhī. On his proof, Ibn al-Haytham does not make use of the endpoints of the diameters on the straight line CE, whereas al-Qūhī considered them in his first proposition in order to introduce the second circle. The reasoning is slightly different. Ibn al-Haytham draws DG ∥ EA and from this deduces the equalities between ratios that lead to the conclusion, whereas al-Qūhī starts from an equality between ratios from which he deduces that the two straight lines are parallel and there are other equalities between ratios, and he reaches the conclusion in the same way.
Finally, we may note that in the case where the centre of homothety lies outside the given circle, al-Qūhī proves that the tangent drawn from the centre of homothety to the first circle is also a tangent to the second circle. Ibn al-Haytham, for his part, studies the problem of the common tangents in a general manner in Proposition 2.24 of The Knowns. The point of intersection of a common tangent with the straight line through the centres is a centre of homothety.
Proposition 1.4. — Let there be a given circle (C, R), an arbitrary given point D ≠ C and a variable point E lying on the circle (C, R). The locus of a point G such that 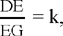 a given ratio and that DÊG = α, a given angle, is a circle. This last is the transform of the circle (C, R) in a similarity with centre D, with ratio k1 and angle β which can be deduced from the data for the problem.
a given ratio and that DÊG = α, a given angle, is a circle. This last is the transform of the circle (C, R) in a similarity with centre D, with ratio k1 and angle β which can be deduced from the data for the problem.
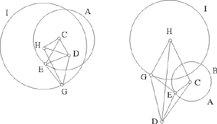
Fig. 2.1.4
Ibn al-Haytham proves the converse proposition and thus defines the similarity.
Proposition 1.5. — Let there be a given straight line BC, a given arbitrary point A, A ∉BC, and a variable point D on BC. The locus of the point E such that 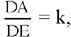 a given ratio, and AD̂E = α, a given angle, is a straight line. That straight line is the transform of the straight line BC in a similarity with centre G such that AG ⊥BC, with ratio k1 and angle α. The ratio k1 is deduced from what is given.
a given ratio, and AD̂E = α, a given angle, is a straight line. That straight line is the transform of the straight line BC in a similarity with centre G such that AG ⊥BC, with ratio k1 and angle α. The ratio k1 is deduced from what is given.
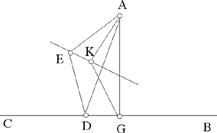
Fig. 2.1.5
Proposition 1.6. — Given two points A and B and an angle α, the locus of the point C such that AĈB = α in a half-plane defined by the straight line AB is an arc of a circle. This arc is called the subtending arc that contains the angle α.
Let C be a point that has the properties in the problem and let D be the centre of the circle circumscribed about the triangle ABC, then AD̂B = 2α, 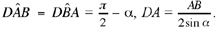 . The point D and
the length DA are determined by what is given. So
C ∈ C (D, DA).
. The point D and
the length DA are determined by what is given. So
C ∈ C (D, DA).
Fig. 2.1.6a
Notes:
1) The straight line AB cuts the circle into two arcs:

only the first arc is a solution.
2) If a point C has the properties required in the problem, the point symmetrical to it with respect to AB is a solution. The point C lies on the arc AEB or on the arc AE1B.
3) Conversely, any point C on the arc AEB or on the arc AE1B satisfies AĈB = α.
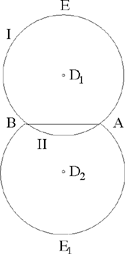
Fig. 2.1.6b
4) This proposition is a preparation for the following proposition, in which we investigate homotheties of a circle in a homothety whose centre is the centre of that circle.
We may note that in this property Ibn al-Haytham makes use of the relation between the angle at the centre and the inscribed angle.
Proposition 1.7. — Given the subtending arc obtained in Proposition 1.6, the locus of the point D ∈[AC) such that 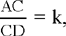 a given ratio, is the arc homothetic to the subtending arc in the homothety
a given ratio, is the arc homothetic to the subtending arc in the homothety 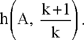
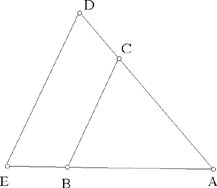
Fig. 2.1.7
Note: The point C lies on the subtending arc of the angle α constructed on AB, and 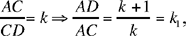 , so D is the image of C in the homothety h (A, k1). So D lies on the subtending arc of the angle α constructed on the segment AE such that E is the image of B in the homothety h(A, k1).
, so D is the image of C in the homothety h (A, k1). So D lies on the subtending arc of the angle α constructed on the segment AE such that E is the image of B in the homothety h(A, k1).
On the extension of AB Ibn al-Haytham constructs the point E such that 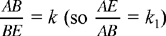 and, with the help of homothetic triangles, he proves that the angle ADE = α; so he has reduced this to the previous proposition, that is to considering the subtending arc.
and, with the help of homothetic triangles, he proves that the angle ADE = α; so he has reduced this to the previous proposition, that is to considering the subtending arc.
Proposition 1.8. — The locus of a point equidistant from two given points A and B is the perpendicular bisector of AB.
Here Ibn al-Haytham is using the third case for the equality of angles in triangles, Elements I.8.
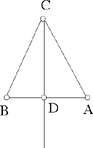
Fig. 2.1.8
Proposition 1.9. — Let A and B be two given points and k ≠ 1 a given ratio. The locus of a point C such that 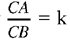 is a circle the endpoints of whose diameter are the points that divide AB in the given ratio k and thus form a harmonic range with A and B.
is a circle the endpoints of whose diameter are the points that divide AB in the given ratio k and thus form a harmonic range with A and B.
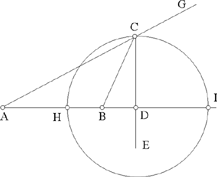
Fig. 2.1.9
Ibn al-Haytham also proves the converse: any point of the circle we have found gives a solution to the problem.
The circular locus that we find is usually called Apollonius’ circle.
Proposition 1.10. — Let A and B be two given points such that the segment AB = l, and let S be a given area. The locus of a point C such that the area (ABC) = S is formed by two straight lines parallel to AB whose distance from AB is equal to 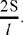
Fig. 2.1.10
Proposition 1.11. — Let there be two equal circles with centres E and G, then the circle with centre G is the transform of the circle with centre E under the translation EG, from E towards G, let it be 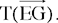 .
.

Fig. 2.1.11
Proposition 1.12. — The transform of a circle under a translation is an equal circle.
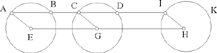
Fig. 2.1.12
Let us return to Ibn al-Haytham’s formulation:
Let there be two equal circles (E, R), (G, R) and an arbitrary straight line parallel to EG that cuts the circles in A and C respectively, such that AC = EG; if a point I on the extension of AC satisfies 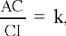 a given ratio, then I lies on a circle equal to the given circles.
a given ratio, then I lies on a circle equal to the given circles.
Let H be the point of EG defined by 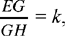 then H is a known point.
then H is a known point.
We have AC = EG and consequently CI = GH; so the quadrilateral (HICG) is a parallelogram, hence HI = GC = R and I ∈ (H, R).
Note: In other words, the hypothesis can be expressed in the form
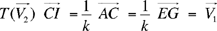
or in the form
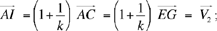
the point I is derived from C in the translation 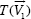 or from A in the
translation
or from A in the
translation 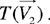 .
.
Proposition 1.13. — Let there be a given segment [AB], a given point C ∉ AB and a variable point D ∈ [AB]. The locus of a point E on [CD)
such that 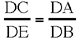 is a straight half line [Bx) ∥ CA.
is a straight half line [Bx) ∥ CA.
In other words, the equation 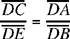 defines the transformation of [BA] into the straight half line [Bx).
defines the transformation of [BA] into the straight half line [Bx).
This transformation is the homography which leaves B unchanged and transforms A into the point at infinity of CA and the point at infinity of (BA) into the point where (Bx) meets the straight line parallel to (BA) that passes through C.
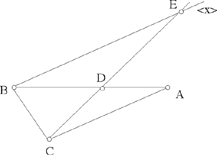
Fig. 2.1.13
Let us use coordinate geometry for this transformation by taking (BA) as the axis for the abscissa and (Bx) as the axis for the ordinate. The coordinates of the points concerned are: B (0,0); A(a,0); C(a, c); D(x,0); E(X, Y).
The equation of CD can be written
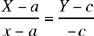
and the condition
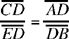
projected onto the axis (BA) can be written
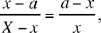
that is X = 0, which defines the straight line (Bx). We then have
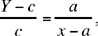
that is
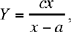
an expression of the homographic transformation. In the case considered by Ibn al-Haytham, since 0 ≤ x ≤ a, y ∈ [0, ∞[.
Notes:
1) If x becomes infinite, the condition becomes the identity –1 = –1 which does not lead to a determinate value of X; so the straight line Y = c parallel to (BA) and passing through C must be taken to be a singularity as a component part of the locus as a whole; it corresponds to a single point of (BA), the point at infinity.
2) Ibn al-Haytham determines the locus by considering, for a fixed position of D on BA, the homothety with centre D that transforms A into B; this homothety transforms C into E, so it transforms the straight line AC into the straight line BE, which is thus parallel to AC. Since AC is known and B is known, the straight line BE is known. We have a variable homothety, different for each point D.
Let us return to the equation 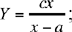 if we fix x while leaving c
variable, we effectively define a homothety with centre D, and ratio
if we fix x while leaving c
variable, we effectively define a homothety with centre D, and ratio 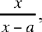 transforming the straight line CA into BE.
transforming the straight line CA into BE.
Since Ibn al-Haytham provides no explanations in his short proof, and since the preceding propositions concern homotheties, it is reasonable to suppose that this latter interpretation is the most appropriate one for the text and that Ibn al-Haytham did not think about homographic transformation.
Proposition 1.14. — Let there be a given segment [AB], a given point C ∉ AB and a variable point D ∈ [AB]. The locus of a point E ∈ [C, D) such that CD · DE = AD · DB is an arc of the circle circumscribed about the triangle ABC.
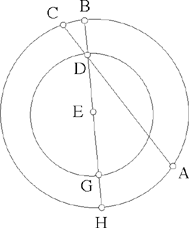
Fig. 2.1.14
Ibn al-Haytham transforms the condition for the problem into a relation of proportions 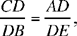 which makes the triangles ADE and CBD similar to one another; thus the angle AEC is equal to the known angle CBD and E lies on the corresponding subtending arc.
which makes the triangles ADE and CBD similar to one another; thus the angle AEC is equal to the known angle CBD and E lies on the corresponding subtending arc.
We may note that with each point D of AB there is associated a point E of the circle that is the locus; thus we define a correspondence between the straight line AB and this circle. The converse is also true: with each point E of the subtending arc, we can associate the point D in which CE cuts AB; the triangles AED and CBD remain similar because they have two corresponding equal angles, so the equation CD · DE = AD · DB is satisfied.
Let us use coordinate geometry for the relationship between AB and the circle. We take as axes the straight line AB and the perpendicular to AB that passes through C; the coordinates of the points we are concerned with can be written: A(a, 0); B(b, 0); C(0, c); D(x, 0); E (X, Y). We have 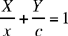 because C, D, E are collinear and the condition for the problem can be written:
because C, D, E are collinear and the condition for the problem can be written:
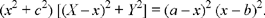
We have
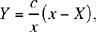
so
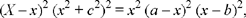
which gives
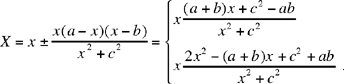
We next have
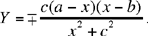
We note that this transformation is a rational application of degree 2 or 3 depending on which sign we choose. The case considered by Ibn al-Haytham corresponds to the upper sign.
Moreover,
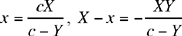
and
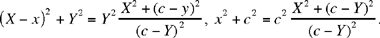
The condition for the problem thus reduces to
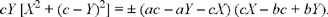
In the case considered by Ibn al-Haytham, the first member is negative (c > 0, Y < 0) while the product in the second member has the sign of (a – x)(x – b), which is positive; so we must choose the lower sign.
When we make Y = c in the equation, we note that the equation is satisfied identically; so we can take Y – c as a factor. We write the equation as:
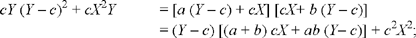
or
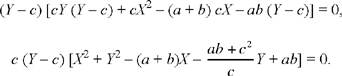
The first factor Y – c corresponds to the line parallel to AB that passes through C; this straight line is a singularity in the locus, the image of the unique point at infinity of the straight line AB. The second factor gives the equation of the circle circumscribed about the triangle ABC.
In the transformation in which AB becomes this circle, the points A and B are fixed and the point at infinity of the line AB becomes the point (a + b, c) where the line parallel to AB that passes through C meets the circle.
The upper sign would have given a cubic curve that does not correspond to any of the cases considered in this treatise.
If we extend the construction by taking a point D that does not lie on the straight line AB, we find an irrational transformation of the plane into itself.
Propositions 1.15 and 1.16. — Let there be a given circle C and two given points A and B lying outside C. If two straight lines from A and B cut one another in a point H inside C such that 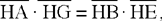 , then CD ∥ AB and (A, B, G, E) are concyclic.
, then CD ∥ AB and (A, B, G, E) are concyclic.
In fact, in Proposition 1.15, Ibn al-Haytham proves that if A, B, G, E lie on the same circle, then AB ∥ CD; in Proposition 1.16, he establishes that if AB ∥ GE, then A, B, C, D lie on the same circle.
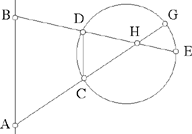
Fig. 2.1.15
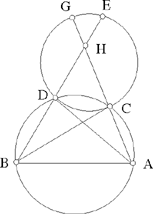
Fig. 2.1.16
Proposition 1.17. — Let there be two given points A and B lying outside a given circle; two straight lines from A and B cut one another in C on the circle and cut it again in D and E. If 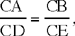 then we either have AD · DC = BE · EC, or the ratio
then we either have AD · DC = BE · EC, or the ratio 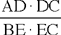 is known.
is known.
Let PA and PB be the powers of the points A and B with respect to the circle, PA > 0, PB > 0; we have AC · AD = PA and BC · BE = PB
Let us write k for the ratio 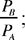 by hypothesis we have
by hypothesis we have
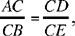
hence
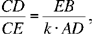
that is
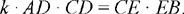
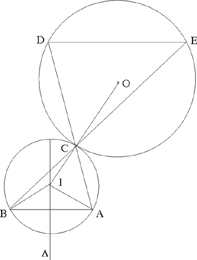
Fig. 2.1.17a
Note: The hypothesis  implies DE ∥ AB. But if a line parallel to AB cuts the circle in D and E, the point of intersection C of the straight lines AD and BE is not in general a point on the circle. From Proposition 1.16, it can lie inside the circle.
implies DE ∥ AB. But if a line parallel to AB cuts the circle in D and E, the point of intersection C of the straight lines AD and BE is not in general a point on the circle. From Proposition 1.16, it can lie inside the circle.
Proposition 1.17 thus appears to be a special case of Proposition 1.16 in which the points D, C, H are coincident.
For a point C to satisfy the conditions in Proposition 1.17, it must be the point of contact of a circle that passes through A and B and is tangent to the given circle. In the text, Ibn al-Haytham supposes we have an external contact.
If I is the centre of the required circle, O the centre of the given circle and R its radius, we have IO − IA = R and IA = IB.
If I exists, it is at the intersection of Δ, the perpendicular bisector of AB, and ℋA, the branch around A of the hyperbola with foci O and A.
So we can have two points, one point or no point C that is a solution to the problem.
We may also note that in the case where Δ, the perpendicular bisector of AB, passes through the centre of the circle (PA = PB and k = 1), Δ cuts the circle in C1 and C2. The point C1 is a solution to the problem, whereas the point C2 is not.
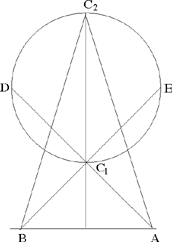
Fig. 2.1.17b
Proposition 1.18. — Let there be two circles touching internally at A. A straight line that passes through an arbitrary point D of the smaller circle cuts the greater circle in B and G; if D is a variable point on the smaller circle, then  is known.
is known.
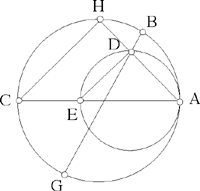
Fig. 2.1.18
The straight line AD cuts the greater circle in H. We have DB · DG = DA · DH, hence

but
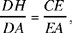
hence
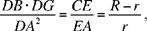
where R and r are the radii of the greater circle and the smaller circle respectively.
Note: The two circles correspond to one another in the homothety 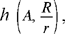
hence
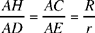
and consequently
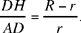
Proposition 1.19. — Let there be two circles touching internally at A. The tangent to the smaller circle at an arbitrary point D cuts the greater circle in two points, let B be one of them. When D varies, the ratio 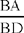 is constant.
is constant.
Let AGC be the common diameter and E the point of intersection of AB and the smaller circle. We have
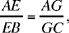
hence
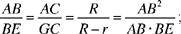
but
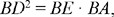
hence
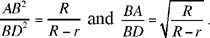
If BD cuts the greater circle again in H, we prove in the same way that
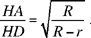
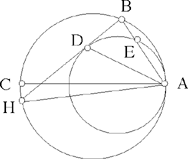
Fig. 2.1.19
So we have
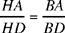
and consequently
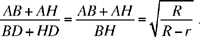
We may note that the two circles correspond to one another in the homothety 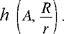
Note: In Propositions 1.18 and 1.19, we consider a variable point on a given circle and two straight lines that pass through this point, in each case we study a ratio associated with these straight lines and we prove that it is constant and can be expressed in terms of what we are given.
Propositions 1.20 and 1.21 each concern two circles that touch internally. These circles again correspond to one another in a homothety which has as its centre the point of contact and as its ratio the ratio of the radii. These propositions shed light on the reasons for including the preceding propositions. Thus, Proposition 1.20 is a corollary to Proposition 1.19, while Proposition 1.21 is a consequence of Proposition 1.18.
Proposition 1.20. — Let there be two circles touching internally at the point A, AGC their common diameter, the straight line BDH touching the smaller circle at D; let us join AD and let us extend it to I on the greater circle. The point I, the point of intersection of AD and the greater circle, is the mid point of the arc subtended by the tangent at D.
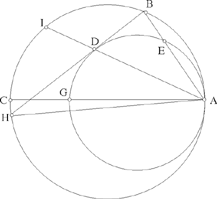
Fig. 2.1.20
From Proposition 1.19, we have

so AD is the bisector of the angle BAH inscribed in the greater circle, so I is the mid point of the arc HB.
Proposition 1.21. — Let there be two circles touching at A, AEC their common diameter; we put 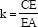 If a variable straight line that passes through E cuts the smaller circle in D and the greater one in B and G, then
If a variable straight line that passes through E cuts the smaller circle in D and the greater one in B and G, then
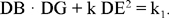
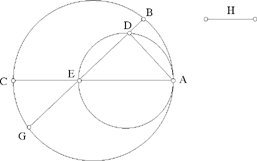
Fig. 2.1.21
From Proposition 1.18, we have
so
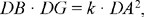
hence
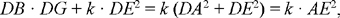
hence the result, where
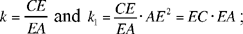
so k and k1 are known and we can express them in terms of R (the radius of the greater circle) and r (radius of the smaller circle):
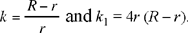
Propositions 1.22 and 1.23 concern loci of points. In Proposition 1.22, we use a metric property to determine the locus of the point; this proposition serves as a lemma for Proposition 1.23.
Proposition 1.22. — Let there be a circle with centre G and diameter AC and two points E and D on this diameter such that GE = GD. For any point B lying on the circle, we have
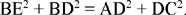

Fig. 2.1.22
In other words, let there be a line segment AC with mid point G, let E and D be two points on this segment such that GE = GD; the sum of the squares of the distances from an arbitrary point B on the circle with diameter AC to the points E and D is constant. The converse is true (compare Proposition 1.23); the locus of a point B that satisfies (*) is a circle with centre G and diameter the segment AC.
The proof given by Ibn al-Haytham is valid for any point B on the circle.
Proposition 1.23. — Let A and B be two fixed points and ℓ a given length. The locus of a point C such that CA2 + CB2 = ℓ2, and AĈB is acute, is a circle whose centre is the mid point of AB and whose radius is known.
If the angle C is acute, it is necessary that the given length ℓ satisfies the relation ℓ > AB in order for the triangle ABC to exist.
Let us put ℓ2 – AB2 = d2; let E be a point such that 2EA · EB = d2 and let G be such that AG = EB. Let us draw the circle with diameter GE and let us prove that it passes through C.
If C does not lie on the circle, the bisector of the angle ACB cuts the circle in H and I, then, from Proposition 1.22, we have
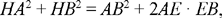
so
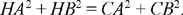
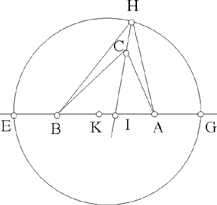
Fig. 2.1.23
But AĈI being acute implies that HĈB and HĈA are obtuse, hence HB > CB and HA > CA, hence HA2 + HB2 > CA2 + CB2, which is impossible.
Notes:
1) The argument by reductio ad absurdum is valid if the point C is taken to lie inside or outside the circle.
2) From Proposition 1.22, we can calculate the radius of the circle. Let K be the centre, we have seen that
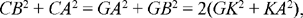
hence
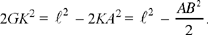
Proposition 1.24. — Let AC be an arbitrary chord in a given circle, if the point D of that chord is such that
(*) 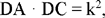 where k is given,
where k is given,
then D lies on a known circle.
In other words: the locus of a point D that has a given power k2 with respect to a given circle (E, R) is part of a concentric circle (E, R∲). The radius R∲ can be found from k and R:
If D lies inside the circle, we have k2 = R2 – Ra => Ra = R2 – k2.
If D lies outside the circle, we have k2 = Ra – R2 => Ra = R2 + k2.
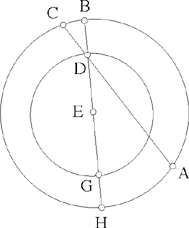
Fig. 2.1.24
Let E be the centre of the circle, ED cuts the circle in B and H, we have
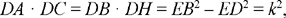
so ED2 = R2 – k2. But ED is constant for given k, so D lies on the circle 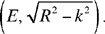
2. Invariant properties of geometrical loci and geometrical transformations
In the second and final part of The Knowns, Ibn al-Haytham deals with concepts and propositions, he writes, ‘of the same kind as what was set out by Euclid in his book the Data, although nothing in this part is to be found in the book the Data’.6 This declaration gives us to understand that in the Data Euclid dealt with only a particular class of knowns and that Ibn al-Haytham returns to the study of them to complete Euclid’s book with new propositions that Euclid had not thought of. So for Ibn al-Haytham his distant predecessor also considered only a certain class of invariant properties of the figures. What we have is an a posteriori interpretation of the presence of this book by Euclid in the ‘domain of analysis’ as Pappus has set its boundaries in the preamble to the seventh book of his Mathematical Collection. In any case, in this part of his work Ibn al-Haytham investigates certain invariant properties of rectilinear and circular loci.
He employs a multiplicity of methods, some of which are close to those of Euclid. Geometrical transformations appear mainly in the form of homotheties in similar divisions. The last proposition finds the centres of homothety for two given circles; it is thus presented as the procedure that is the converse of that in Proposition 1.3.
He starts with a group of five propositions in which he tries to find a straight line that passes through a known point and has a property P. In the first proposition of this group, he deals with finding a straight line that passes through a known point A and cuts a known circle between B and C in such a way that BA/BC = k, a known ratio. The construction of this straight line reduces to constructing a second point as the intersection of two lines: two circles in the first proposition, a circle and a straight line in the third, two straight lines in the fourth and the fifth. As for the second proposition, it reduces to the first one. We may note that all of these are construction problems, the second one being a neusis.
Proposition 2.1. — From a given point A outside a circle, we draw a straight line that cuts the circle in B and C (where B lies between A and C). If 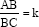 , where k is a given ratio, then the straight line is known in position.
, where k is a given ratio, then the straight line is known in position.
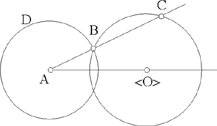
Fig. 2.2.1
So we are concerned with finding a straight line that passes through a BA known point A and cuts a known circle in B and C such that 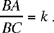 .
.
The power of A with respect to the circle (O, R) is known;
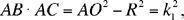 which is known.
which is known.
We have
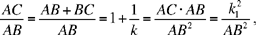
hence
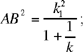
the length AB is determined by the data for the problem; let AB = d. Consequently B ∈ C (A, d), so it lies at the intersection of two circles C (O, R) and C (A, d).
Note: Ibn al-Haytham does not prove here that the point B exists. The circles C (O, R) and C (A, d) cut one another if and only if
(1) 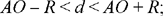
but
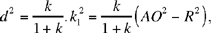
hence (1) may be written
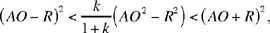
hence
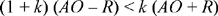
and
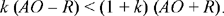
The second condition is always satisfied, and it remains to satisfy

We have
• AO < (2k + 1) R, there exist two straight lines symmetrical with respect to AO that give a solution to the problem.
• AO = (2k + 1) R, there exists a straight line that gives a solution to the problem, that is AO.
• AO < (2k + 1) R, there does not exist any straight line that gives a solution to the problem.
Proposition 2.2. — From a known point we draw to a circle known in position a straight line that cuts off a known segment from the circle, then the line is known in position.
This is how Ibn al-Haytham states the second proposition.
We may note that from the definitions in Book III of the Elements (Definitions 6, 7, 8 and 11), as well as Proposition 23 of the same book, or the Definitions 7 and 8 and Propositions 88 and 89 of the Data, the segment of the circle is known if we know its base and the inscribed angle with its vertex on the arc of the circle that is a boundary of the segment.
In a known circle, a known inscribed angle is associated with a chord of known length. So, to say that a segment of a given circle is known reduces to saying that its base is known. In Elements III.34 Euclid gives a construction for this base. Ibn al-Haytham’s problem may be rewritten as follows:
From a point A we draw a straight line that cuts a known circle in B and C; if the chord BC is of known length, then the straight line BC is known in position.
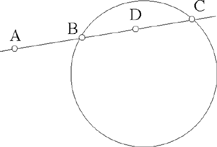
Fig. 2.2.2
The power of the point A with respect to the circle is known, let ABAC = k2.
Let us put BC = 2 BD = 2ℓ (where D is the mid point of BC).
But if A lies outside the circle, we have

If, on the other hand, A lies inside the circle (a case not considered by Ibn al-Haytham, whose purpose is clearly to get back to the previous proposition), we have AD2 = ℓ2 – k2.
So the length AD is known. From it we deduce 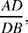 then
then 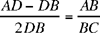 and we have returned to the previous case.
and we have returned to the previous case.
Proposition 2.3. — Let A, B, C be three known points and D a point on the segment BC; if  a given ratio, then the straight line AD is known in position.
a given ratio, then the straight line AD is known in position.
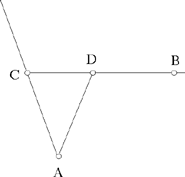
Fig. 2.2.3
By hypothesis we have two known points A and C and 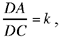 so from Proposition 9, D lies on a circle whose centre is a point of AC. So if D exists, it is at the intersection of this circle and the segment CB. The point D is known, as is the point A; so AD is known.
so from Proposition 9, D lies on a circle whose centre is a point of AC. So if D exists, it is at the intersection of this circle and the segment CB. The point D is known, as is the point A; so AD is known.
Proposition 2.4. — Let there be a known point A and two straight half-lines that are parallel and in opposite directions [CB) and [DE). Let us suppose that a straight line from A cuts the straight half-lines in H and G HP respectively. if 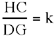 is a known ratio, the straight line AG is known.
is a known ratio, the straight line AG is known.
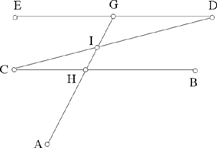
Fig. 2.2.4a
We suppose that A does not lie on the straight line CD. Let I be the point of intersection of AG and DC, we have
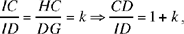
because I lies between C and D.
So the point I is known and consequently the straight line AI is also known.
Comment: In the statement of this problem, Ibn al-Haytham first makes it clear that BC and DE are ‘two parallel straight lines known in magnitude and in position’. So we are dealing with segments. On the straight lines CB and DE, the points H and G such that 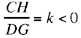 correspond to one another in a homothety in which the image of D is C. So the centre of this homothety is the point I such that
correspond to one another in a homothety in which the image of D is C. So the centre of this homothety is the point I such that 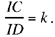 . So for given k, k < 0 the point I exists and it is unique, I ∈ [CD]. It follows that if A ∉ [CD], the straight line AIcuts the straight lines CB and DE respectively in H and G such that
. So for given k, k < 0 the point I exists and it is unique, I ∈ [CD]. It follows that if A ∉ [CD], the straight line AIcuts the straight lines CB and DE respectively in H and G such that
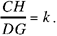 . Note that, in this book, when we write k < 0 we always mean that the segments in a ratio have opposite senses.
. Note that, in this book, when we write k < 0 we always mean that the segments in a ratio have opposite senses.
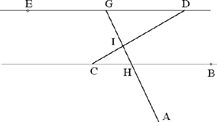
Fig. 2.2.4b
But if H and G must belong to the segments [CB] and [DE] respectively, the straight line AI does not give a solution to the problem except when A is in the smaller of the angles BIC and DIE, or in the angle that is opposite it at its vertex (the hatched area).

Fig. 2.2.4c
Proposition 2.5. — Let there be a point A, a segment BC and an arbitrary point D on this segment. If AD + CD = ℓ, a known length, then the straight line AD is known.
Let us put BC = ℓ1; we have BD + DC = ℓ1 and AD + DC = ℓ.
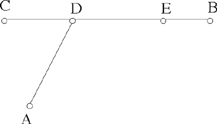
Fig. 2.2.5
If ℓ = ℓ1, then AD = BD, so, from Proposition 1.8, D∈A, the perpendicular bisector of AB. The point D must lie at the intersection of the segment BC and Δ.
Note: We may note that if AB ┴ BC, then Δ ‖ BC, and the point D does not exist. On the other hand, it can happen that the point of intersection of A and BC does not lie on the segment BC.
If ℓ1 < ℓ, then DB < AD. Let E be such that BE =ℓ1-ℓ= BD – AD; so the point E is known and ED = DA. If the point D exists, it thus lies on the perpendicular bisector of EA and on the segment EC; it is then known and the straight line AD is also known.
We may add the same note as before.
If ℓ1 > ℓ, the argument takes the same form. We then have E lying beyond B.
In Propositions 2.6, 2.7 and 2.8, we go on to the construction of a point by using the intersection of a straight line and a circle. We are in fact dealing with two straight lines that each pass through a known point and have a property P; they are determined by a second point, which is constructed as in the preceding group of propositions by the intersection of two lines – here a straight line and a circle (a subtending arc). We encounter the same procedure later on, in Problems 2.21 and 2.22.
The two Problems 2.6 and 2.7 can be written: Let there be a straight line Δ and two points A and B, to find a point E on A such that:
(6) ÂEB = α, a known angle
(7) 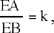 a known ratio.
a known ratio.
In the two cases, E ∈ Δ and E ∈ E (a circle). The problem can have 0, 1 or 2 solutions.
In Problem 2.8, we again take a straight line A and two fixed points E and G, and we try to find H∈D such that EH } HG = k which is known. The point H lies on a subtending arc and the problem again has 0, 1 or 2 solutions.
In the three Problems 2.6, 2.7 and 2.8, there is a finite number of pairs of straight lines that provide solutions to the problem; whereas in Problem 9, as we shall see, there is an infinite number of such pairs of straight lines.
Proposition 2.6. — Let there be two fixed points A and B and a straight line CD. Let there be a point E ∈ CD such that AEB = α, a known angle, then the segments AE and BE are known.
If the point E exists, it lies at the intersection of the straight line CD and the subtending arc that contains the angle α constructed on AB, from Proposition 1.6; so we can have 0, 1 or 2 solutions.
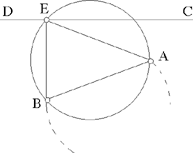
Fig. 2.2.6
We are dealing with the intersection of a straight line and two arcs that are symmetrical with respect to AB.
Proposition 2.7. — Let there be two fixed points A and B and a fixed AE straight line CD. Let there be a point E ∈ CD such that 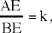 a known ratio. The two straight lines AE and BE are then known.
a known ratio. The two straight lines AE and BE are then known.
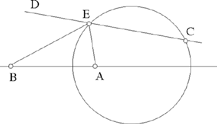
Fig. 2.2.7
If the point E exists, it lies at the intersection of the straight line CD and a circle determined by the data for the problem, from Proposition 1.9; here again we can have 0, 1 or 2 solutions.
Proposition 2.8. — Let there be AB and CD two parallel straight lines, E and G two fixed points on AB. Let there be a point H on CD such that EH · HG = k, a known product. The segments EH and GH are then known in position and in magnitude.
Let us suppose the point H is known. There exists a point I on AB such that GĤI = GÊH. The triangles IHG and HEG are similar, hence
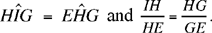
So we have
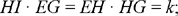
since EG is known, we have
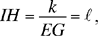 a known length.
a known length.
Let us put in a straight line DB perpendicular to the two known parallel lines: the distance DB = d is known.
If d = ℓ, then IH ⊥. AB, so HÎG is a right angle and consequently EĤG is a right angle.
If d > ℓ; let DL = ℓ, the circle (D, ∓) cuts AB at the point K, DK = HI = ∓; then the two straight lines DK and HI are either parallel or anti-parallel. In the first case: HÎG = DK̂B, a known angle, and consequently EĤG = DK̂B a known angle.
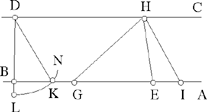
Fig. 2.2.8a
Fig. 2.2.8b
In the second case (when the lines are anti-parallel), the two straight lines DK and HI cut one another in a point M (Figs 2.2.8c and 2.2.8d); we have MÎK = IK̂M = DK̂B, a known angle, so the angles HIG and EHG are again known.
Fig. 2.2.8c
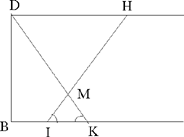
Fig. 2.2.8d
So in all cases, EĤG= α is known.
If the point H exists, it lies at the intersection of the subtending arc that contains the angle α constructed on EG and the straight line DC; then it is known and the straight lines EH and GH are again known.
Notes:
1) The point H lies on a line parallel to EG, the triangle HEG has a known area S. Now
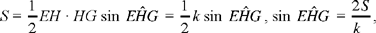
so EHG = a, an angle determined by the data for the problem.
2) The problem considered is plane because the straight line CD is parallel to EG. If we do not make this hypothesis, we are dealing with a solid problem, as is proved by the following formulation in terms of coordinate geometry:
As coordinate axes we take the straight line EG and the perpendicular bisector of EG. The coordinates of G and E are (−a, 0) and (a, 0) respectively. The equation of the straight line CD is of the form αx + βy = γ and the condition for the problem can be written
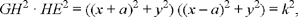
or
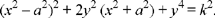
We eliminate j by using the equation for CD:

an equation of the fourth degree in x.
In the case considered, where the straight lines are parallel, we have α = 0 and the preceding equation reduces to:
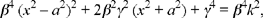
or
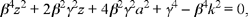
if we putz = x2 – a2.
Proposition 2.9. — Let there be two parallel straight lines AB and CD, and two known points E and G on AB. From these points are drawn two straight half lines that cut CD in I and K and cut one another in H beyond CD. If the area of the triangle HGE is known, then the segment KI is of known length.
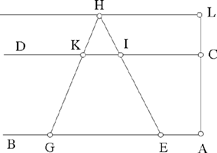
Fig. 2.2.9
Since the triangle HEG has a known area and a fixed base EG, the height from H is of constant length h; so the locus of H is a straight line parallel to AB. Let L be its intersection with the perpendicular AC, the lengths LA and LC are known and we have
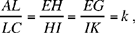
a ratio that does not depend on the position of H.
Then we have
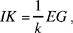
where IK is of known length.
Note: Let us put EG = a and let us use d and h respectively to designate the distance between the two parallel lines and the height of the triangle HEG of given area S.
The statement assumes that h<d, that is 2S > ad. We have
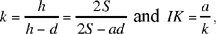
hence
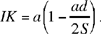
If h > d, 2S > ad, the locus of the point H lies between the straight lines AB and CD and we have
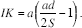
Thus, the locus of the point H is a straight line Δ ‖ EG; the distance 25 between the two straight lines is 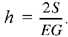 To each point H of Δ there EG corresponds a segment IK of constant length on DC.
To each point H of Δ there EG corresponds a segment IK of constant length on DC.
Proposition 2.10. — In the general case, being given two points A and B and two angles α and β defines a triangle.
Notes:
1) We suppose the angles to be on the same side of AB:
• if their sum is two right angles, the straight lines are parallel;
• if their sum is not two right angles, the straight lines cut one another on one or the other side of AB. The point of intersection C is unique. The data define a unique triangle, because A and B are fixed. The three sides are then known and the ratios of these sides two by two are also known.
2) If a triangle T has known angles, if we take points A and B we can construct a triangle ABC which is similar to it. The ratios of the sides two by two are then known. The triangle T is determinate, up to similarity. If a side of Tis known, Tis then determinate, up to isometry.
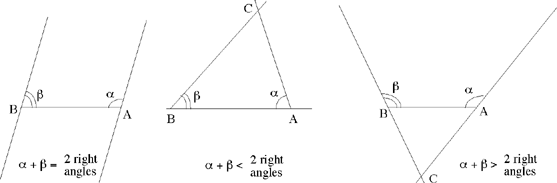
Fig. 2.2.10
In this proposition, Ibn al-Haytham first proves that being given one side of a triangle and two angles adjacent to that side allows us to construct the triangle. He makes two comments on this: one on isometric triangles that he uses in Proposition 2.12, the other on similar triangles that he uses in Proposition 2.11, in which a straight line that passes through a given point and has a property P is characterised by the angle it makes with a given straight line.
We may note that Ibn al-Haytham’s investigation in Proposition 2.10 resembles what Euclid did in Propositions 39 and 40 of the Data, where we again find the construction of a triangle in which three elements are known; these are three sides in Proposition 39 and three angles in Proposition 40.
Proposition 2.11. — Let there be a given triangle ABC and a given point D on the extension of BC. If a straight line from D cuts AB in E and AC in G such that 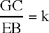 is a known ratio, then the straight line DEG is known.
is a known ratio, then the straight line DEG is known.
The parallel to AC drawn through B cuts DE in H. The points C, B, D are known, hence
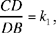 a known ratio,
a known ratio,
and we have
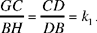
But 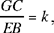 by hypothesis, hence
by hypothesis, hence

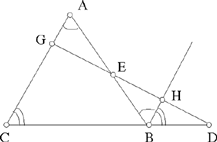
Fig. 2.2.11
Moreover, EB̂H = BÂC, a known angle. The triangle EBH is determinate up to similarity, so the angle BHE is known, and consequently the angle BHD is also known.
But HB̂D = AĈB, a known angle, so the angle BDH is known, so the straight line DHG is known, and the points G and E also.
Note: We are dealing with the construction of a straight line that passes through a given point; the line is defined by an angle.
The problem does not always have a solution. Let us put BC = a, AC = b,BA = c,BD = d,EB = x, CG = y, where y/x = k.
In the triangles EBD, CGD and AGE, we have
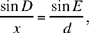 (2)
(2) 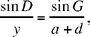 (3)
(3) 
From (1) and (2) we obtain
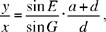
and taking account of (3)

hence

hence
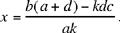
We must have 0 < x < c, which requires 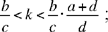 these inequalities also imply that 0 < y < b.
these inequalities also imply that 0 < y < b.
If this double condition is satisfied, the problem has a unique solution.
Proposition 2.12. — Let there be a given circle, a given straight line CD outside this circle and a tangent to the circle at a point B which meets CD in E. If the length BE is equal to a given length, then the segment BE is known in position.
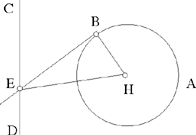
Fig. 2.2.12
Let E (H, BH) be the circle, BE = d and r = BH given lengths. The triangle HBE, with a right angle at B, is determinate up to isometry, so HE = d1 is a known length. So the point E lies on E (H, d1) and it also lies on the given straight line CD. So the angle HEB is known, the straight line EB is thus known.
Notes:
1) There are two tangents that correspond to the point E of the straight line DC.
2) To establish the existence of the point E, we have 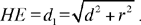 . Let h be the distance from H to the given straight line; we have the following cases:
. Let h be the distance from H to the given straight line; we have the following cases:
d1 < h, the problem has no solution;
d1 = h, the problem has one solution;
d1 < h, the problem has two solutions.
3) Ibn al-Haytham does not use Pythagoras’ theorem in finding HE, but proves that from the data for the problem the triangle HBE, in which we know an angle, the right angle, and the lengths of two sides, is determinate up to isometry. This confirms that this research, just like the Data of Euclid, in no way belongs to the domain of algebra.
The construction of point E can be carried out by means of straightedge and compasses.
4) So the problem reduces to constructing E using the intersection of the given straight line and a circle whose centre is known. The radius of the circle is found from what we are given.
The same will be true for a whole group of problems, numbered from 12 to 16.
Proposition 2.13. — Let there be a given circle E (H, HB) and a given straight line CD lying outside the circle. Let us join a point B on the circle to a point E on CD in such a way that BÊC = α, a known angle and BE = d, a known length; then the straight line BE is known in position.
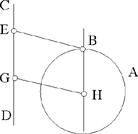
Fig. 2.2.13a
Let H be the centre of the circle, let us put HK to CD. Let the point G on CD be such that HĜC known, as is the length HG,

To characterise the point G, here – as in Proposition 2.17 and Proposition 2.23 – Ibn al-Haytham uses Proposition 1.6, that is the subtending arc. It is simpler to note that, with the perpendicular dropped from H on CD, HG makes an angle  if
if 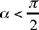 or
or 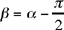 if
if 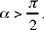 .
.
In both cases, G exists and it is unique.
In regard to the numbers of solutions, there are several cases to consider:
If d1 = d, then HGEB is a parallelogram, because HG = EB and HG ‖ EB, so BH ‖ CD. The point B lies at the intersection of the circle and the parallel to CD drawn through H. There are two solutions.
If d1 > d, then the straight line HB meets the given straight line; let the point of intersection be C. The point B lies between H and C. We have
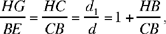
hence
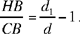
Now HB = r, the radius of the circle, so
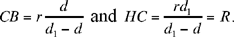
So the point C lies at the intersection of the given straight line and the circle E (H, R). The point C exists if and only if
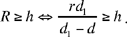
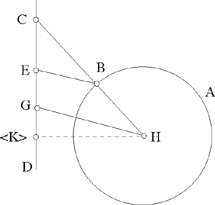
Fig. 2.2.13b
But 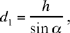 , so the condition can be written d sin α ≥ h – r.
, so the condition can be written d sin α ≥ h – r.
When we find C, we deduce B and BE ‖ HG from it.
If d1 < d, the straight line HB meets the given straight line, but we have that H lies between B and C. In this case we have
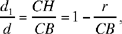
hence
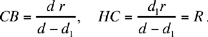
The condition R ≥ h gives
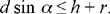

Fig. 2.2.13c
To summarise, this problem has a unique solution if
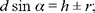
it has two solutions if
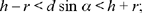
and it has no solution if d sin a lies outside the interval [h- r,h + r].
This problem also reduces to the construction of a point C using the intersection of the given straight line and a circle with known centre; the radius is deduced from what we were given.
Proposition 2.14. — Let there be two parallel straight lines AB and CD and a point E lying between them. Let there be a straight line that passes through E and cuts AB and CD in H and G respectively.
If EG · EH = k, then EG is known in position.
The given straight lines correspond to one another in a homothety with centre E. Ibn al-Haytham’s argument sets out from a point I on AB, chosen arbitrarily, and uses that property.
If the distances from E to the straight lines AB and AC are called α and β respectively, the ratio of the homothety has the absolute value β/α.
If the straight line EG exists, we have
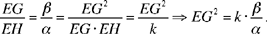
Fig. 2.2.14
The circle with centre E and radius 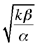 does not cut the straight line CD unless
does not cut the straight line CD unless 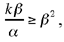 that is unless k ≤ αβ. Thus, if
that is unless k ≤ αβ. Thus, if
k > α/β, the problem does not have a solution;
k = α/β, the problem has one solution G0H0 ⊥ AB;
k > α/β, the problem has two solutions symmetrical with respect to G0H0.
This problem also reduces to constructing a point G using the intersection of a given straight line and a circle with a known centre; the radius of the circle is deduced from what we are given.
Proposition 2.15. — Let there be a triangle ABC, determinate up to isometry. If a point D on the base satisfies
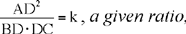
then the straight line AD is known in position.
If the straight line AD exists, it cuts the circle % the circle circumscribing (ABC), again in G; the points G and A lie on opposite sides of BC; hence
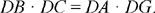
The condition (1) becomes
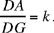
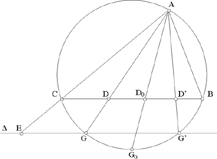
Fig. 2.2.15
Let E be the point of AC beyond C such that 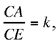 then the required
point G lies on Δ, the parallel to BC that passes through E, and it lies on the circle. So G exists if Δ cuts the circle.
then the required
point G lies on Δ, the parallel to BC that passes through E, and it lies on the circle. So G exists if Δ cuts the circle.
Let G0 be the mid point of the arc CB, the straight line AG0 is the bisector of the angle A; let D0 be the point in which it cuts the base and let 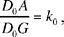 a known ratio.
a known ratio.
If k > k0, the problem does not have a solution.
If k = k0, the problem has one solution, AD0, the bisector of the angle BAC.
If k < k0, the problem has two solutions. The corresponding points G and G’ are such that the arc CG is equal to the arc BG’ so the two straight lines AD and AD’ are symmetrical with respect to the bisector AD0.
Note: In the statement of the problem, Ibn al-Haytham writes ‘triangle whose sides and angles are known’. The position of the triangle is not given. On the conclusion, he writes ‘I say that the straight line AD is known in position’. This refers to the position of AD with respect to the triangle.
This problem is reduced to that of constructing a point G using the intersection of the given circle and a straight line deduced from what we have been given.
Proposition 2.16. — Let there be two given straight lines AB and AC, and a point D lying inside the salient angle BAC. If a straight line that passes through D cuts AB in E and AC in G such that 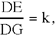 a known ratio, then the segment EG is known.
a known ratio, then the segment EG is known.
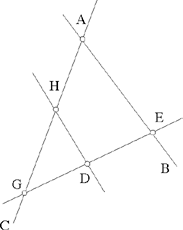
Fig. 2.2.16
The line parallel to AB that passes through D cuts AC in H and we have
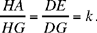
So with every value of k there is associated a point G and consequently a straight line GD which cuts AB in E (G # H, so GD is not parallel to AB).
In Propositions 2.13, 2.14, 2.15 and 2.16, Ibn al-Haytham uses parallel straight lines and Thales– theorem; he finds homothetic triangles as well as nomothetic straight lines.
Proposition 2.17. — Let there be two straight lines AB and AC, and a point D in the salient angle BAC. If a straight line that passes through D cuts AB in E and AC in G such that DE · DG = k2, then the segment EG is known.
Let us suppose that the straight line GE exists; let H lie on the extension of AD and be such that DA ‖ DH = k2; the points A and H lie on opposite sides of D. We have
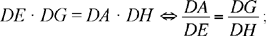
so the triangles DAE and DĜH are similar and consequently DĜH = EÂD= a, a known angle. So the point G lies on the subtending arc for the angle α constructed on the segment DH. But G also lies on the straight line AC. So the point G exists if the straight line AC and the subtending arc cut one another, and we could have 0, 1 or 2 solutions.
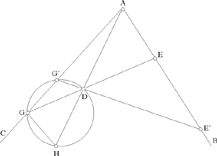
Fig. 2.2.17
With the point G that provides a solution to the problem there is associated a segment GE known in length and position.
Proposition 2.18. — Let A, C and D be three known points on a circle such that 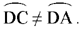 . If a straight line that passes through D cuts the arc AC which does not contain D in a point B such that
. If a straight line that passes through D cuts the arc AC which does not contain D in a point B such that  a known ratio, then the segment DB is known (in position and magnitude).
a known ratio, then the segment DB is known (in position and magnitude).
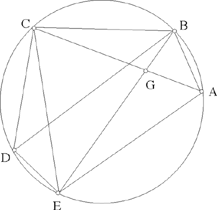
Fig. 2.2.18
Let us suppose the problem has been solved. If E is the mid point of the arc CDA, we have CB̂E = EB̂A = CÂE. Moreover, BĈA = BÊA, the triangles ABE, GBC and EGA are similar two by two:
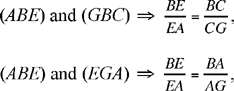
hence
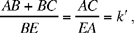
so
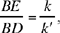
a known ratio (because A, C and E are known points).
So we have

because
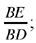
So in the triangle EBD, we know the angle EBD and the ratio 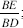 this BD, triangle is determinate up to similarity and thus its other angles are known. So the straight line DB makes a known angle with the straight line DE. The point B lies at the intersection of that straight line and the given circle. The points B and D need to lie on opposite sides of AC if B is to provide a solution to the problem. If this is so, the segment BD is determined by its two endpoints.
this BD, triangle is determinate up to similarity and thus its other angles are known. So the straight line DB makes a known angle with the straight line DE. The point B lies at the intersection of that straight line and the given circle. The points B and D need to lie on opposite sides of AC if B is to provide a solution to the problem. If this is so, the segment BD is determined by its two endpoints.
To summarise, we are concerned with three given points A, C, D that are not collinear and a circumscribed circle (ADC); the problem is to construct a point B on the arc AC such that 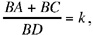 a known ratio. Ibn al-Haytham constructs B as the point of intersection of the given circle and a straight line.
a known ratio. Ibn al-Haytham constructs B as the point of intersection of the given circle and a straight line.
Proposition 2.19. — Let there be a given angle xAy and in this a straight half line Az. For any straight line Δ that cuts Ax in B, Ay in C and Az in D, we have
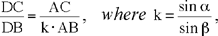
where α = xÂy and β = yÂz, known angles.
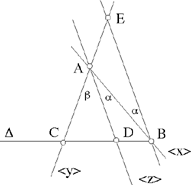
Fig. 2.2.19
First we may note that Ibn al-Haytham does not mention the special case α = β; in which case Az is the bisector and in any triangle ABC we then have
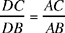 (in this case k = 1).
(in this case k = 1).
Let us now look at the general case.
For an arbitrary point B on Ax, let us draw an arbitrary straight line which cuts Ay in C and Az in D, and a straight line parallel to Az which cuts the extension of Ay in E. The triangle AEB has two angles known; it is EA determinate up to similarity. So we have 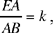 a ratio which does not depend on the angles that are given. In fact,
a ratio which does not depend on the angles that are given. In fact,
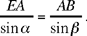
Moreover,
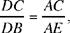
hence
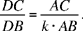
Notes:
1) From this property we immediately deduce: Three concurrent straight lines Ax, Ay, Az determine similar divisions on two parallel lines.
Let there be points D, B, C lying on Δ and D1, B1, C1 on Δ1. If Δ ∥ Δ1, we have
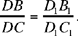
2) The property established in this proposition is a generalisation of the property of the point of intersection of the internal bisector of an angle of a triangle ABC with the base.
The following proposition is the converse of this.
Proposition 2.20. — If the angles of a triangle ABC are known and if D is a point of [BC] such that 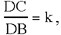 a known ratio, then the straight line AD makes known angles with AB and AC.
a known ratio, then the straight line AD makes known angles with AB and AC.
The triangle ABC is determinate up to similarity, so 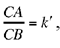 a known ratio,
a known ratio, 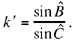
Let E be a point on the extension of AC such that
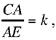 a known ratio. The straight line BE is parallel to the required straight line, because
a known ratio. The straight line BE is parallel to the required straight line, because
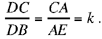
But the triangle EAB is determinate up to similarity, because
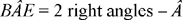
and
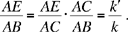
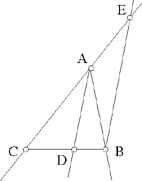
Fig. 2.2.20a
So the angle AEB is known and consequently the angle CAD is also known.
Notes:
1) Starting from Proposition 2.20, we prove that:
if on two parallel straight lines Δ and Δ1 we have the similar ranges D, B, C and D1, B1, C1 such that 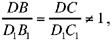 then the three straight lines BB1, CC1, DD1 are concurrent.
then the three straight lines BB1, CC1, DD1 are concurrent.
This is the converse of Proposition 2.19.
Propositions 2.19 and 2.20 state that if three straight lines are concurrent, they cut off similar ranges on two parallel straight lines, and conversely.7
This configuration reminds us of Desargues: in his version the points D and D1 do not lie on BC and B1C1. The straight lines BC and B1C1 are parallel and the same holds for BD and B1D1; of BB1, CC1 and DD1 are concurrent, DC and D1C1 are parallel, and conversely.8
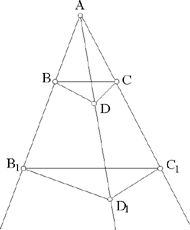
Fig. 2.2.20b
The case examined by Ibn al-Haytham is a degenerate limit of the configuration in Desargues.
Proposition 2.21. — Let there be a given circle, a given chord AB and a triangle ABC inscribed in the circle. If this triangle has a given area, the point C is known, then the straight lines AC and BC are also known.
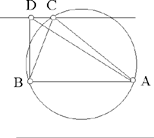
Fig. 2.2.21a
Here Ibn al-Haytham returns to the proof of the second proposition of the first part about triangles with given area and with one given side; he deduces from this that the point C lies on a chord parallel to AB. As in Proposition 2.10, the point C lies on one or other of the two parallel straight lines equidistant from AB. Now by hypothesis C lies on the circle.
Notes:
The problem can have 0, 1, 2, 3 or 4 solutions.
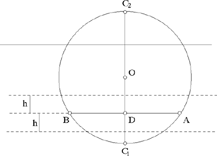
Fig. 2.2.21b
Let D be the mid point of AB and O the centre of the circle. Let us put AB = 2a, OA = R, OD = d; we have R2 = a2 + d2. If S is the area given for the triangle ABC, its height is h = S/a.
The perpendicular bisector of AB cuts the circle in C1 and C2 and we have
hence
h < R ? d the problem has four solutions
h = R ? d the problem has three solutions
R − d < h < R + d the problem has two solutions
h = R + d the problem has one solution
h > R + d the problem has no solution.
The problem reduces to that of constructing the point C using the intersection of the given circle and a straight line deduced from what was given, using the method that was set out in Proposition 1.10.
Proposition 2.22. — Let there be a circle and two known points A and B on this circle. If C is a point on the circle such that CA · CB = k2, a known ratio, then C is known and thus the straight lines CA and CB are also known.
This proposition reduces to the preceding one, because
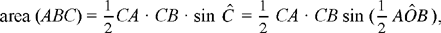
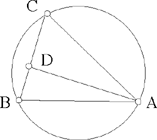
Fig. 2.2.22
where AÔB is the angle at the centre.
Now CA · CB = k2 is known, and
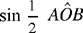 does not depend on the position of the point C on the circle, so area (ABC) = S is known. Ibn al-Haytham makes this clear in his proof:
does not depend on the position of the point C on the circle, so area (ABC) = S is known. Ibn al-Haytham makes this clear in his proof:
Let us suppose that C is known; let AD ⊥ BC, then the triangle ADC has known angles and
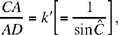
hence
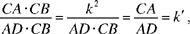
hence
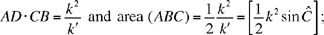
so we have returned to the preceding problem and there can be 0, 1, 2, 3 or 4 solutions for the point C.
Note: This problem is like Problem 2.8, with a circle instead of two parallel straight lines. In both cases, the area of the triangle is fixed by the data.
Proposition 2.23. — We are given a circle and a straight line CD. If a straight line cuts the circle in A and B and the straight line CD in E in such a way that
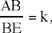 a known ratio, and BÊC = α, a known angle, then the straight line AB is known, so the segment AB is known.
a known ratio, and BÊC = α, a known angle, then the straight line AB is known, so the segment AB is known.
Let us suppose that the straight line AB is known. Let H be the centre of the circle and HI ⊥ AB, then I is the mid point of AB and
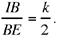
Let G be a point on CD such that HĜC = α; G exists and is unique, and HG is parallel to the required straight line. Let us put HG = ℓ.
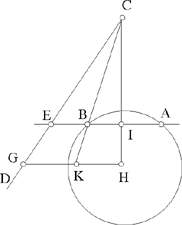
Fig. 2.2.23a
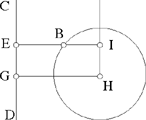
Fig. 2.2.23b
If HI ∥ DC, which implies 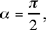 then IE = HG = ℓ. But
then IE = HG = ℓ. But 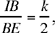 hence
hence
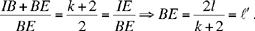
So we return to Proposition 2.13 with BE = ℓ′ and
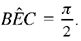
If 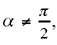 HI cuts the straight line CD at the known point C. The straight line CB cuts HG in K and we have
HI cuts the straight line CD at the known point C. The straight line CB cuts HG in K and we have 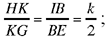 so, from Proposition 2.20, the straight line CK is known in position and the point B lies at the intersection of this straight line and the circle. We then draw the perpendicular from B to CH, which gives us the points E and A. So the points A, B and E are known.
so, from Proposition 2.20, the straight line CK is known in position and the point B lies at the intersection of this straight line and the circle. We then draw the perpendicular from B to CH, which gives us the points E and A. So the points A, B and E are known.
We have just seen that this proposition reduces to Proposition 2.13 or to Proposition 2.20 depending on the given angle, and this reduces to the construction of a point by means of a given circle and a straight line.
Comment: We can restate this proposition as follows: Let there be a circle C (H, R) and a straight line xy that lies outside it. To find on xy a point E so that a straight half-line Ez cuts the circle in A and B such that xÊz = α and 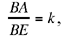 both known.
both known.
The analysis of this problem leads to similar ranges I, B, E and H, K, G if 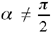 and to equal ranges of
and to equal ranges of 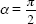
The synthesis begins from the data, which allow us to construct K and G.
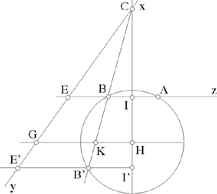
Fig. 2.2.23c
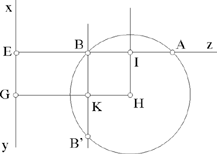
Fig. 2.2.23d
If 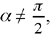 we know C. The required point B ∈ C ∩ KC, from which we deduce Ez, and thus A. The problem can have 0, 1 or 2 solutions.
we know C. The required point B ∈ C ∩ KC, from which we deduce Ez, and thus A. The problem can have 0, 1 or 2 solutions.
If 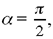 the point C does not exist and the required point B is given by the intersection of the circle and the perpendicular to HG at K, hence there are 0, 1 or 2 solutions.
the point C does not exist and the required point B is given by the intersection of the circle and the perpendicular to HG at K, hence there are 0, 1 or 2 solutions.
Proposition 2.24. — Let there be two circles lying outside one another, equal or unequal. If a straight line is a common tangent to the two circles, it is known.
We may note that the figures provided in the text show circles that lie outside one another; this condition is not necessary in investigating the external common tangent.
1. External common tangents
Let there be C1 (E, EA) and C2 (G, GD) two circles, and A and D the points of contact. So in this case we have
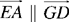 and in the same sense.
and in the same sense.
1.1. Equal circles
AEDG is a rectangle that can be constructed immediately, we have AD = EG; so AD is known.
What we have is a translation 
Fig. 2.2.24a
1.2 Unequal circles
The straight lines DA and GE cut one another in H which lies beyond E and we have 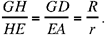 So the point H is known.
So the point H is known.
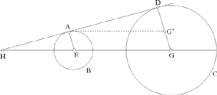
Fig. 2.2.24b
What we have is a homothety 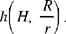
2. Internal common tangent
2.1. Equal circles
The reasoning is the same.
This time what we have is a central symmetry h (H, − 1).
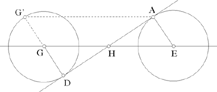
Fig. 2.2.24c
2.2. Unequal circles
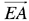 and
and 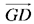 are parallel and have opposite senses, AD cuts EG in H between E and G and we have
are parallel and have opposite senses, AD cuts EG in H between E and G and we have
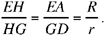 So the point H is known.
So the point H is known.
What we have is a homothety
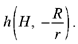
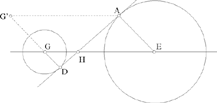
Fig. 2.2.24d
In all cases, the construction of the tangent reduces to the construction of a point, for example D. In 1.1, the point D is at the intersection of the given straight line EG and the perpendicular, and in the other cases, it is at the intersection of the given circle with centre G and the circle with diameter GH.
________________
5 See mss Cairo, Dār al-Kutub, 40, fols 206v–208r; Istanbul, Aya Sofya 4830, fols 171r–173r and also 4832, fols 123v–125r.
7 Piero della Francesca (c. 1412–1492) gives a version of this theorem in his treatise on perspective, De prospectiva pingendi, Book 1, Section 8. See J. V. Field, ?When is a proof not a proof? Some reflections on Piero della Francesca and Guidobaldo del Monte’, in R. Sinisgalli (ed.), La Prospettiva: Fondamenti teorici ed esperienze figurative dall’Antichità al mondo moderno, Florence, 1998, pp. 120?32, figs pp. 373?5; and J. V. Field, Piero della Francesca: A Mathematician’s Art, New Haven and London, 2005.
8 See Girard Desargues, Exemple de l’une des manieres universelles du S. G. D. L. touchant la pratique de la perspective sans emploier aucun tiers point, de distance ni d’autre nature, qui soit hors du champ de l’ouvrage, Paris, 1636, pp. 11?12; translation J. V. Field and J. J. Gray, The Geometrical Work of Girard Desargues, London and New York, 1987, pp. 158?60 (French text, pp. 200?1).