In the name of God, the Compassionate the Merciful
TREATISE BY AL-ḤASAN IBN AL-ḤASAN IBN AL-HAYTHAM
On the Knowns
Knowledge is an opinion which does not change, and opinion is belief in a certain notion. So knowledge is belief in a certain notion, as it is, and it is, moreover, a belief that does not change, as when we believe that the whole is greater than the part. But belief cannot occur without there being someone who believes, and a notion that is believed. Now belief cannot be unchanging except if the notion that is believed does not change. If this is so, then knowledge is belief in a notion that does not admit of change. A known is the notion in which one believes that does not admit of change, and the person who knows is the one who believes a notion that does not admit of change. On the other hand, believing notions that change cannot be considered to be knowledge, because these latter are not fixed according to one single attribute, as when one believes that Zayd is standing upright: it is possible that he is not standing upright at the moment when we believe [this], and that he is standing upright at other moments. So if we situate it in time, as when we believe that Zayd is standing upright at this time, or that he was standing upright at some particular moment, our belief can be true; if one is certain that it is a true belief, its being called ‘knowledge’ will come about as a metaphor, since it [the belief] resembles knowledge on account of the correctness of the belief. But knowledge, itself, does not, in truth, admit of change at any moment. If knowledge is a belief, and if belief can occur only for someone who believes, then knowledge can occur only when there is a person who knows.
Further, belief in a notion that does not admit of change may be divided into two kinds1: on one hand, when we believe a notion that does not change, while knowing that this notion does not change; on the other hand, when we believe a notion that does not change, without knowing that it does not change. Believing a notion is indeed separate from belief in whether this notion changes or not. Someone who believes a notion which does not change, while knowing that it does not change, has knowledge of that notion. Moreover, he knows that he has knowledge of it, because in believing that notion that does not admit of change, he has knowledge of that notion, and in knowing that it does not admit of change, he knows that he has knowledge of it. But someone who believes a notion that does not change, without knowing that it does not change, has knowledge of that notion, but does not know that he has knowledge of it, because he does not know if this notion admits of change or not. And someone who believes with this kind of belief believes a notion without proof or necessity, but by hearsay and imitation, taking it on trust, or by intuition. It is legitimate to say that he has knowledge of that notion, because he believes a notion that does not admit of change, which is the definition of knowledge.
Knowledge is divided into two parts: knowledge in actu, and knowledge in potentia. Knowledge is in actu when it has become a belief for someone who believes; knowledge is in potentia when it can become a belief for someone who believes.
If knowledge is a belief, [and] if belief cannot occur without someone who believes and a notion that is believed, that is to say the known, and if knowledge is divided into two parts, knowledge in actu and knowledge in potentia, then the known is also divided into two parts: a known in actu and a known in potentia. A known in actu has become known by someone who has knowledge of it; a known in potentia is one that can become known by someone who has knowledge of it. But we have shown that a known is a notion that does not admit of change; notions that do not admit of change are thus divided into two parts: some are beliefs for someone who believes; the others can be beliefs for someone who believes. These two parts can be known only if the notions belonging to these two parts do not themselves admit of change. If all of what we have said is true, a known is in truth any notion that does not admit of change, whether or not it is believed by someone who believes.
All known notions are divided up into two kinds: one is concerned with quantity and the other is not concerned with quantity. Our treatise will deal only with known notions that are concerned with quantity.
Quantity is divided up into two parts: one is discrete quantity and the other is continuous quantity. Discrete quantity is divided up into two parts, which are: the letters of words and numbers. Continuous quantity is divided up into five parts, which are: line, surface, solid, weight and time.
The known notions contained in this treatise are those concerning letters of words, those which concern number, those which concern lines, those which concern surfaces, those which concern solids, those which concern weights and those which concern time.
The notions which concern the letters of words are divided into three parts: one is concerned with the essence of the letters; another is concerned with the quantity of the number of the letters – that part reduces to what concerns number; and the third part is that which concerns the arrangements of the letters and the combinations of them among themselves, which are words.
The notions concerning number are divided up into four parts: one concerned with the essence of number; another concerned with the quantity of number; the third concerned with the properties of number, [such] as those that concern numbers that are perfect, abundant or deficient, squares, cubes or numbers like them which are properties of the nature of number; the fourth part is concerned with the association of numbers one with another as in commensurability, ratios, augmentation, diminution and <the relation> of the whole and the part.
Notions concerning lines are divided up into seven parts: one is concerned with the essence of a line; another is concerned with the endpoint of a line which is a point; the third is concerned with the figure of a line; the fourth is concerned with magnitudes of lines; the fifth is concerned with positions of lines, that is to say their situation2 – that part is divided up into seven parts: one is the position of the line with respect to fixed points, the second is the position of the line with respect to a single fixed point, the third is the position of the line with respect to a moving point or with respect to <several> moving points, the fourth is the position of the line with respect to a fixed line, the fifth is the position of the line with respect to a moving line, the sixth is the position of the line with respect to a fixed surface, and the seventh is the position of the line with respect to a moving surface. The sixth part of the first system of division is concerned with ratios of magnitudes of lines, one to another, and the seventh part is concerned with the composition of a group of these lines when some of them meet with one another.
Notions concerned with surfaces are divided up into parts like those into which the notions concerned with lines are divided up, except the one that is concerned with endpoints, because the boundaries of surfaces are lines.
In the same way, notions concerned with solids are divided up into parts, like those into which notions concerned with surfaces were divided up, except for the last part, which is concerned with composition, because composition of solids arises only from composition of the positions of their surfaces; similarly, positions of solids with respect to anything one can use to situate them are the positions of the surfaces of the solids.
Notions concerned with weights are divided up into three parts: one is concerned with the essence of weight, the next is concerned with magnitudes of weights and the third is concerned with the ratios of weights one to another.
Notions concerned with time are divided up into three parts: one is concerned with the essence of time, the second is concerned with the magnitude of time and the third is concerned with ratios of intervals of time one to another.
The known concerned with the essence of the letters of a word, that is the ordinary letters used in all languages, and whose forms and sound do not change from one language to another. The essence of the letters of a word is, in fact, the separate sounds, used in the words of dialogues and conversations, in all languages; but the words of the languages are different, depending on the difference in character of the people who speak these languages, and all the different words, in all the different languages, there are combined letters. Among the composite letters, some are common to all the languages, the others are peculiar to one language, and not to another. What is common to all the languages has a form and figure that do not change; so this is known because it does not change in all the words there are in all the languages. Among these letters, what is not common [to all languages] has a form that can change in the [different] languages; some of them are to be found in some languages and are not to be found in the other languages, and some are found in one of the languages with a [particular] property and in another language they have another property. Thus, for the letters of a word, the known concerned with the essence of the letters is the letters that are common to all the languages.
As was mentioned earlier, the known concerned with the number of the letters reduces to that concerned with the quantity of the number.
As for the known concerned with the arrangement of letters and the combination of letters one with another, this is the words used in all languages. In fact, words are letters put together, combined with one another, but not every combination of letters is a word used in a language, further, the majority of the combinations of letters do not make a word that is used. The forms and the arrangement in the words that are used do not change, but any word that is used in a language always takes the same shape and does not change in the language in which it is used. As for the known concerned with the combination of letters in a word, this is the words used in all languages.
As for the known concerned with the essence of number, it is merely unity. In fact, the essence of number is unity and what is generated from repeating it. Every number involves nothing more than unity and repetition. In a number the repetition is not [always] one and the same repetition, but a repetition that increases and that decreases, so it is touched by change, whereas unity is not susceptible of change in any way. So the known concerned with the essence of number is only unity.
The known concerned with the quantity of a number is that every number has a finite plurality, which does not change either by increasing or by decreasing. This type of number is subdivided into two parts: one is where the number is limited by necessity and the other is where it is limited by hypothesis. What is limited by necessity is as in the number of the planets, the number of the orbs, the number of the elements, and similar things, that is to say any numbers for which the counted numbers3 neither increase nor decrease. If the thing that is numbered neither increases nor decreases, then its number does not change either by increasing or by decreasing, but number does not undergo change except by increasing and decreasing. If the numbered does not lend itself either to increasing or to decreasing, its number does not lend itself either to increasing or to decreasing, this part of number is that which applies to a quantity limited by necessity. As for the other part, it is that limited by hypothesis, that is to say that in his imagination, or in a numerical problem that he poses by hypothesis, a human being gives himself a certain number; he supposes that it does not change, or he assumes determinate numbers in the world of sensation and in existence; thus, by way of hypothesis, he will have taken a number that does not change. It is in these two ways that the quantity of a number is known.
The known concerned with the properties of numbers, such as the properties of a square, of a cube, of a surface, of a solid, of a perfect number, of an abundant number, of a deficient number and numbers like them, it is the form of each of these numbers from which its properties have been constituted, as the form of the square from which its properties have been constituted, that is to say as the product of a number with itself. The known notion of a square concerned with the properties of the square is the product of a number with itself. This notion is [to be found] in every square and it is a notion that does not change for any square, despite a change in the sides of the squares and change in the sizes of the squares; every property of every square is, in fact, constituted from the multiplication of a number, which is its side, by itself. Similarly, the form of the cube, from which its properties are constituted, is the multiplication of a number by what is obtained by multiplying it by itself. Similarly, the form of a surface is the multiplication of a number by a number. Similarly, the form of a solid is the multiplication of a number by what is obtained from the multiplication of a number by a number. The form of a perfect number is that it is equal to the sum of its aliquot parts. The form of an abundant number is that the sum of its aliquot parts exceeds it. The form of a deficient number is that the sum of its aliquot parts is less than it. Similarly, every number like this has a form from which its properties are constituted. The known for any number that has a property or properties is the form it has from which its property or properties are constituted, because this form does not change in any of the numbers of that species, despite a change in its quantity and change in its aliquot parts and its sides.
The known concerned with the combination of numbers with one another is divided up into six parts: one of them – and it is the first – is the equality of every unity, in every number, to every unity, in every number; the second part is that every number is a multiple of every unity that is in it, and a multiple of every unity in every number that is combined with it; the third part is that two arbitrary numbers are commensurable through unity and that unity measures each of them; the fourth part is that any number is [one] of the parts of any number that is combined with it; the fifth part is that two different arbitrary numbers are such that one is greater than the other and that other is smaller than the first. These notions hold for all numbers and do not change for any numbers. As for the sixth part, that is ratios; every numerical ratio is between two numbers; a numerical ratio is the measure of the quantity of the number expressed in terms of the quantity of the number with which its ratio is set up. A known ratio is the ratio of two numbers one to the other, whose quantity is known, as well as the ratio of two numbers that are equimultiples of two numbers whose quantity is known, or of parts, in equal number, of two numbers whose quantity is known, or two homologous parts of two numbers whose quantity is known. Two arbitrary numbers are the two smallest numbers in their ratio or are equimultiples of the two smallest numbers in their ratio; two arbitrary numbers, that are the two smallest numbers in their ratio, in fact measure two numbers in the ratio of equality: the smaller measures the smaller and the greater measures the greater. It is possible that two other numbers that are equimultiples of the two smallest numbers in their ratio measure the two numbers that are measured.4 If this is the case, then two arbitrary numbers, which are not the two smallest numbers in their ratio, are equimultiples of the two smallest numbers in their ratio, because they are measured by the two smallest numbers in their ratio; it is possible that these two numbers are equimultiples of multiples of the two smallest numbers in their ratio. If the two numbers which are the measure are known, then the ratio of one to the other is known and it is the ratio of the two numbers that are measured; the ratio of two numbers that are measured, one to the other, will then be known even if their quantities are not known. But if the quantity of the two numbers that are measured is known, then the ratio of the two numbers that are measures, one to the other, is also known, because the ratio of the parts is equal to the ratio of their equimultiples. So the known ratio is the ratio of two numbers, one to the other, whose quantity is known; it is the ratio of two numbers, which are multiples of two numbers whose quantity is known; it is the ratio of two homologous parts of two numbers of known plurality, and it is the ratio of two numbers which are equal parts of two numbers whose plurality is known. In general, the known numerical ratio is that of two numbers of known quantity, or is equal to the ratio of two numbers of known quantity. So the known in a known numerical ratio is the quantity of each of the two numbers in the ratio one to the other – if each of them is known – or the quantity of two known numbers which are in their ratio.
As for the known concerned with the essence of a line, it is that the line is a length without breadth, because this notion applies to all lines and does not change for any of them. The length of a line and its figure change with the lines, since, for lines, there are straight lines, circular ones, [and] curves with different kinds of curvature. So the known concerned with the essence of a line is that the line is a length without breadth.
The known concerned with an endpoint of a line, which is a point, is made up of two notions: one relates to its essence, that is to say that it is not divisible, and the other to its position, that is to say its distance from another point or points that exist in the imagination, if this distance or these distances do not change. This notion is divided up into three parts: one is that this point, itself of known position, is fixed, and that the point or the points that exist in the imagination are also fixed and that none of them moves with any sort of motion; the second part is that the point that exists in the imagination is fixed, whereas the point of known position is free to move about the fixed point, with a circular motion, and the distance between them [sc. the two points] does not change; and the third part is that the point of known position is at a distance that does not change from a point that exists in the imagination or is at distances that do not change from points that exist in the imagination and are such that the two points, or all the points, are free to move with one equal motion, all together, and that the distances that lie between the point of known position and the points, do not change. These two notions are known and concerned with a point which is the endpoint of a line.
As for the known concerned with the figure of the line, it is the notion which constitutes the essence of the line; for the straight line, it is its two endpoints, plus the fact of being the shortest distance. In fact, a straight line is the distance there is between its two endpoints, on condition that this distance is the shortest distance between its two endpoints; so what constitutes its essence is its two endpoints, because it is its two endpoints which delimit the distance that there is between them. If we make the further demand of the distance that it shall be the shortest, this distance will be a straight line. The known notion concerned with the figure of the straight line which does not change for any of the straight lines, is the two endpoints, plus the fact of being the shortest. As for a circular line, what constitutes its essence is the circular surface of which the line is the boundary; but what constitutes the essence of that circular surface is the centre together with the distance between the centre and the circumference. So what constitutes the essence of the circular line – and is its prime constituent – is its centre and the distance between the line and its centre. The known notion concerned with the figure of the circular line is the centre and the semidiameter. If the magnitude of the semidiameter does not change, the circular line is a whole circle or an arc of a circle, whether the arc or the circumference of the circle is convex or concave. As for curved lines that can have a known figure, these are the ones which are in an arrangement, an order, and a notion which constitutes their essence and which does not change for any line their [various] species. For a curved line, the known notion concerned with its figure is the notion which constitutes its essence. So a line of known figure is a line for which the notion that constitutes its essence is known.
As for the known concerned with magnitudes of lines, it is the value of the length of the line. But we have knowledge of the value of the length of the line from the fact that we have knowledge of the distance there is between its two endpoints, while knowing the figure of the line. Thus, a finite line of known magnitude is one for which the distance between its two endpoints does not change, that is to say does not increase or decrease, and which is such that its figure does not change. In fact, there is an infinity of lines with different figures between two points, each of which [lines] is called a distance, and we cannot imagine any one of them by imagining only its two endpoints, apart from the straight line, because it is the shortest line to join two points. But since the form of linearity is established in the imagination, and the figure of linearity is no different from one straight line to another and it does not change, accordingly a straight line of known magnitude is one for which the shortest distance between its two endpoints does not change.
A circular line is also the distance between its two endpoints if it is an arc; but it is not the shortest distance and, in addition, its magnitude is not limited by its two endpoints because it is possible that, between its two endpoints, there are many circular lines of different magnitudes, none being equal to any other nor having a ratio to it; in consequence, the magnitude of a circular line will not be known unless its semidiameter is known, that is to say unless the magnitude of the latter does not change. But if its semidiameter is known, then its figure will be known because its semidiameter is what constitutes its essence. A finite circular line has a known magnitude only if the distance between its two endpoints is of known magnitude – that is to say the straight line which is its chord – and if, in addition, its figure is known.
Similarly, a curved line is of known magnitude only if its figure is known, but its figure will not be known unless we know the notion which constitutes its essence, because between two points there are many curved lines, none being equal to any other nor having a ratio to it. So, a finite curved line is of known magnitude only if the distance between its two endpoints – that is to say the straight line that is its chord – is of known magnitude and if, in addition, the figure of the curved line is known.
A finite line of known magnitude is one for which the distance between its two endpoints is of known magnitude and one whose figure is also known.
A circular line which is a whole circle and which is of known magnitude is one whose semidiameter is of known magnitude, because, if its semidiameter is of known magnitude, then the magnitude of the circular line does not change and its figure does not change.
A curved line, if it is closed,5 is of known magnitude only if the distance from each point taken on the line to its centre, or to a fixed point that lies inside it, is of known magnitude, that is to say the straight lines.
As for the known concerned with the position of a line with respect to fixed points, it is the distances from the points, which are on the line, to each of the two [fixed] points, or more than two fixed points. If these distances do not change, and if the line that has this property is a line which does not move with any kind of motion, except for increasing and decreasing,6 then it does not change its position, but changes only its magnitude. A line which does not move with any kind of motion is known in position with respect to fixed points, because if the distance from each point taken on the line to each of the two [fixed] points, or more than two fixed points, is a distance which does not change, then this line does not move with any kind of motion, whether the line is straight, circular or of an arbitrary figure. If the line moves along a rectilinear path, the distance of each of its points changes with respect to any fixed point, whether the line is straight or not straight. Similarly, if the line moves along a curvilinear path or if it moves along a circular path, then the points that lie on the line can preserve the distance between each of them and a single point if the line is moving round that single point. As for the remaining fixed points, the distances between them and the points that lie on the line change in every case.
A line of known position with respect to fixed points is a line which does not move with any kind of motion, except for increasing and decreasing, and it is one for which the distances from points that lie on it to each of the two [fixed] points, or more than two fixed points, are distances that do not change. The line that has this property is said to be known in position absolutely, without any condition or addition, whether the line is straight or not straight. A straight line known in position absolutely is one that does not move with any kind of motion, except for increasing and decreasing. A circular line known in position absolutely is one whose centre known in position, and whose semidiameter is of known magnitude.7 As for the known for this line, it is the distances between the points that lie on it and the fixed points, because these distances do not change.
As for the known concerned with the position of a line with respect to a single fixed point, it is the distances between each point taken on the line and the fixed point, if the distances do not change. The line that has this property is said to be known in position with respect to the fixed point, and this line is not known in position absolutely, because the line can preserve the distances that lie between it and the fixed point, even if it is moving; in fact, this line can move round the fixed point in such a way that the distances between the points on it and the fixed point do not change; indeed if we join its two endpoints to the fixed point with two straight lines and if the triangle generated by the line and the two straight lines drawn from its two endpoints to the fixed point is put in motion about the fixed point, then the distances between the points that lie on the line and the fixed point do not change, and the line will, however, be in motion, whether the line is straight or not straight. If the line is a circumference of a circle and is in motion about its centre, then the distances from points that lie on it, to the fixed point, which is its centre, do not change. So a straight line known in position with respect to a single fixed point is the line for which the distances from the points that lie on it to the fixed point are distances which do not change, whether the line is fixed, immobile or mobile, rotating about the fixed point and whether the line is straight or not straight.
As for the known concerned with the position of a line with respect to a moving point or to moving points, it is the distances between each point taken on the line and the moving point or moving points, if the distances between the points are known and if the line moves with a motion equal to the motion of the moving point or moving points, and in the direction in which the point or points move. A line known in position with respect to a moving point or moving points is a line for which distances from its points to the moving point or the moving points are distances which do not change, and which [sc. the line] moves, despite this, with a motion equal to the motion of the moving point or the moving points, and in the direction of their motion, whether the line is straight or not straight.
The known concerned with the position of a line with respect to a fixed line is the angle enclosed by that line and the fixed line, if the two lines intersect, and it is the angle formed if we extend these two lines until they meet one another – if the two lines are ones which can meet one another – and if they do not intersect. A line known in position with respect to a fixed line is – if the two lines are such that they can intersect one another – a line which encloses a known angle with the fixed line, whether the line known in position is also fixed and does not move with any kind of motion, or whether it is moving, but at the same time preserving the form of the angle enclosed by the line known in position itself and the fixed line to which it is compared.
A straight line known in position with respect to a fixed line, if it cuts the fixed line or if it can cut it, is a straight line which encloses a known angle with the fixed line; it can be fixed motionless or it can move as a whole, while preserving the angle, or it can increase or decrease. A straight line that has this property does not, in fact, change in position with respect to the fixed line, because the angle enclosed by the two <lines> does not change, whether the fixed line is straight or not straight. The known for the position of this line is the known angle.
A circular line of known position with respect to a fixed line – if the fixed line cuts it or can cut it if it is extended indefinitely – is the circular line which encloses with the fixed line a known angle; it can be fixed, motionless or in motion about its centre, its centre being fixed, motionless, whether the fixed line is straight or not straight, or in motion along the fixed line, but with the angle enclosed by the two lines not changing. This can take place if the fixed line is straight or circular. The position of the circular line that has this property does not change with respect to the fixed line because the angle between it and the fixed line does not change; the known is the angle.
If the line does not cut the fixed line or cannot cut it, it will then be of known position with respect to the fixed line when, once it has been cut by a straight line which makes a known angle with one of the two lines, this latter encloses a known angle with the other line, whether the line of known position is fixed, motionless or in motion, while preserving the form of the angle formed between it and the line that cuts it, when that is possible for it. What is known for the line that has this property is the two angles formed by the intersection of each of the two lines with the line that cuts them.
A curved line of known position with respect to a fixed line is a line which does not move with any kind of motion, whether the fixed line is straight or not straight, or the curved line that is moving with respect to the fixed line, if the fixed line is straight or circular, and whether the point on the curved line which lies on the straight or circular line does not change, and if the angle enclosed by it and the straight or circular line does not change; this, if the curved line cuts the fixed line. If it does not cut it, it will be of known position if its relation with the straight line which cuts it, as well as the fixed line in accordance with two known angles, is the relation described earlier in regard to the fixed line.
The known concerned with the position of the line with respect to a moving line is the known, in the preceding paragraph, without any difference between them concerning the angles or the division <into cases>. The only difference between this line and the preceding line is that the line to which the position is referred is fixed for the first line, whereas it is moving for the latter one, and that, with respect to that reference line, the line moves with its own motion and in the direction of the motion of the latter line, whether the line of known position is straight or not straight.
The known concerned with the position of the line with respect to a fixed surface is the right angle, if the line is perpendicular to the fixed surface or to the plane tangent to the fixed surface at the endpoint of the perpendicular, if the fixed surface is convex or concave, or the angle enclosed by that line and the perpendicular drawn from a point on the line, perpendicular to the surface or perpendicular to the plane tangent to the fixed surface at the endpoint of the perpendicular, if the angle is known. The line known in position with respect to a fixed surface is the perpendicular erected on the fixed surface or on the plane tangent to the fixed surface at the foot of the perpendicular, or the one that encloses a known angle with the perpendicular, whether the line known in position is fixed, motionless or in motion with respect to the fixed surface, while preserving the right angle or the known [angle]. The known is the angle.
The known concerned with the position of a line with respect to a moving surface is the known in the preceding paragraph, that is to say the angle. The only difference between this line and the preceding line is that the surface to which the position of the line is referred is fixed for the first line, and is in motion for the latter, and that the line, whose position is referred to the surface, moves with a motion equal to its motion and in the direction of its motion, whether the line is straight or nor straight. A line known in position with respect to a moving surface is a line perpendicular to the moving surface or to the plane tangent to the moving surface at the foot of the perpendicular, or a line which encloses with the perpendicular drawn from a point of the line, perpendicular to the moving surface or to the plane tangent to the moving surface at the endpoint of the perpendicular, a known angle, if the line is moving with a motion equal to the motion of the surface and in the direction of this motion.
The known concerned with ratios of magnitudes of lines, the one to the other, includes two notions: one is the figure of the two lines one of which is referred to the other; the second is the quantity of each of the two lines; in fact, of two lines, one cannot have a ratio to the other, and there cannot be a ratio between the two lines, unless they are of the same species and what constitutes their essence is the same notion, as [when there are] two straight lines or two arcs of the same circle or of two equal circles. It is for only these two species of line that there can be ratios between the magnitudes of individuals. As for the species of lines, other than those two, there is no ratio between their magnitudes. So the known ratio between the lines is the one between two straight lines or two circular lines of the same species, and such that the magnitude of each of them is known, or one that is equal to the ratio of two lines of their species such that the magnitude of each of them is known. The known of two straight or circular lines that are of the same species, and whose ratio one to the other is known, is the magnitude of each of the two lines, if each of them is known, or the magnitude of each if the two lines of known magnitude, [lines] for which the ratio of one to the other is equal to the ratio of the two lines for which the ratio of one to the other is known. The two lines for which the ratio of one to the other is known are straight lines or circular <lines>, for which the magnitude of each of them is known, or the magnitude of each of the two lines of known magnitude for which the ratio of one to the other is equal to the ratio of two lines whose ratio one to the other is known. The known ratio between two lines is that between two known lines, because the ratios between the known magnitudes does not change, it being given that, for known magnitudes, their magnitudes do not change, so the magnitude of one does not change when it is measured by the magnitude of the other.
The known concerned with figures made up of lines that meet one another is their form. It is a notion made up of their angles and their magnitudes, measured one by another, <measures> that are the ratios of one to another, if the sides are straight lines or arcs of equal circles. If the angles of a figure are known – that is to say that they do not change – if we know that they do not change and if the ratio of the quantity of each of the sides to each of the sides that remain is a known ratio, then the form of the figure does not change, whether the magnitude of each of the sides is known and does not change or whether the magnitudes of the sides change, while preserving the ratios between them and the angles that they form, whether all the sides are straight or whether all the sides are circular, <belonging to> equal circles, or whether some of them are straight and the others circular, if the ratios of those that are straight to the straight ones do not change and if the ratios of the circular ones to the circular ones do not change. A figure of known form, enclosed by straight lines or arcs of equal circles, is one whose angles are known and one in which the ratios of the sides one to another are known.
Figures of known form, made up of curved lines, are those in which only the angles are known because there cannot be ratios between the magnitudes of the curved lines, except when they are equal, because the parts of a curved line are not measured by a single magnitude, and none of them can be superposed on another and the parts of one of them do not have similar forms, but, on the contrary, two parts of the same curved line always have different forms. A figure enclosed by curved lines or by lines some of which are curved is thus of known form, if only its angles are known.
The known concerned with the essence of a surface is that the surface is only a length and a width, because this notion holds for all surfaces and does not change in any of them. As for the quantity of the length of the surface, of its width and of its shape, it changes from one surface to another, because surfaces have different figures and shapes, in regard to their plane <shape>, their being convex and their being concave. The known concerned with the essence of surfaces is that a surface is only a length and a width.
The known concerned with the figure of a surface, that is to say the shape of the surface, is the notion that constitutes its essence; so for a plane surface the latter is the edges which enclose it, in addition to its smallness because a plane surface is the smallest surface enclosed by its edges. The known notion concerned with the figure of a plane surface that does not change for any plane surface, is the edges of the surface [together] with its smallness.
What constitutes the essence of a spherical surface is the spherical solid; what constitutes the essence of the spherical solid is its centre and its semidiameter, so what constitutes the essence of the spherical surface, which is the primary cause, is its centre and its semidiameter, whether the spherical surface is a complete sphere or a portion of a sphere, convex or concave.
As for non-spherical convex or concave surfaces, which can be of known figure, they are those that have a [spatial] arrangement, ordered and have a notion that constitutes their essence and ones that do not change in any of their species. The known notion for a non-spherical convex or concave surface which is concerned with its figure is the notion that constitutes its essence. So a surface of known shape is one for which the notion that constitutes its figure is known.
The known concerned with the magnitudes of surfaces is the quantity of the area of the surface, if the area of the surface does not change either by increasing or by decreasing. So a surface of known magnitude is the surface such that the quantity of its area does not change. As for what the area of a surface is and how to have knowledge of the area of a surface, we have set it out in our book On Measurement,8 [where] we have explained it in an exhaustive manner, and it is not appropriate to explain, in this book, how to <find> the area.
The known concerned with the position of a surface with respect to fixed points is the distances from each point taken on the surface to two fixed points, or more than two fixed points, if these distances do not change. A surface that has this property is a surface that does not move with any kind of motion, apart from increasing and decreasing; this, in fact, does not change its position, but changes its magnitude because, if the distances from the points that lie on the surface to two [fixed] points, or more than two fixed points, are distances that do not change, then the surface does not move with any kind of motion, whether the surface is plane, convex or concave. In fact, if the surface moves along a rectilinear path or along a curvilinear path, then it is necessary that the distances between its points and the fixed points change; but if it moves along a circular path,9 then it is possible for it to preserve the distances between its points and only one point among the fixed points, if the surface moves around this single point. A surface of known position with respect to fixed points is thus one which does not move with any kind of motion, except for increasing and decreasing. A surface that has this property is said to be known in position absolutely, unconditionally, whether the surface is plane, convex or concave.
The known concerned with a position of the surface with respect to a single fixed point is the distances between each point taken on the surface and the fixed point, if these distances do not change. A surface that has this property is said to be of known position with respect to the fixed point; this surface will not be known in position absolutely because the distances between points of this surface and the fixed point can be known without their magnitudes changing, even if the surface moves when its motion is around this fixed point. A surface of known position with respect to a single fixed point is thus a surface for which the distances from its points to the fixed point are distances that do not change, whether the surface is fixed, motionless or in motion along a circular path around the fixed point, [and] whether the surface is plane, convex or concave.
The known concerned with a position of a surface with respect to a moving point is the distances which lie between the points of the surface and the moving point, if the distances are known; the surface moves with a motion equal to the motion of the point, and in the direction of its motion. A surface of known position with respect to a moving point is a surface for which the distances from its points to the moving point are known distances, if, in addition, the surface moves with a motion the same as that of the moving point, and in the direction of its motion, whether the surface is plane, convex or concave. It is the same for a surface of position known with respect to moving points.
The known concerned with the position of a surface with respect to a fixed line is a right angle, if the line is perpendicular to the surface or perpendicular to the plane tangent to the surface at the endpoint of the perpendicular, if the surface is convex or concave, or the angle enclosed by the fixed line and the perpendicular drawn from the point on the fixed line, perpendicular to the surface or to the plane tangent to the surface at the endpoint of the perpendicular. A surface of known position with respect to a fixed line is thus a surface to which the fixed line is perpendicular, or perpendicular to the plane tangent to the surface at the foot of the perpendicular, or the surface such that the fixed line encloses a known angle with the perpendicular, whether the surface is plane, convex or concave, [and] whether the surface is fixed, immobile or in motion along a circular path around the fixed line. So the known is the angle. This case is similar to that of the line [considered] with respect to a fixed surface.
The known concerned with the position of a surface with respect to a moving line is the same known as that in the paragraph before this one, that is to say the angle. The only difference between this surface and the pre ceding surface is that the reference line for the position of the preceding surface was fixed and immobile, whereas the reference line for the position of this surface is moving, and that, in addition, the surface moves with a motion equal to its motion and in the direction of its motion, whether the surface moves with that motion alone or whether it moves with this motion while [also] moving with a circular motion about the moving line. So a surface of known position with respect to a moving line is the surface to which the moving line is perpendicular, or perpendicular to the plane tangent to the surface at the endpoint of the perpendicular, or the surface such that the perpendicular to the surface or to the plane that is tangent to it encloses a known angle with the moving line and is such that the surface moves with a motion equal to the motion of the moving line and in the direction of its motion, or moves with this motion or also with a circular motion about the moving line; the known is the angle.
The known concerned with the position of a surface with respect to a fixed surface is the angle at which the two surfaces cut one another, if this angle is known, that is to say the angle enclosed by the two lines drawn in the two surfaces from a point on the [line of] intersection, [lines] that cut one another, if these two lines are perpendicular to the [line of] intersection, this when the two surfaces are plane. If the two surfaces are not plane, then the surface will be of known position with respect to the other surface if the surface10 which cuts them and which is perpendicular to each of them gives rise, at the intersection, to a known angle enclosed by the two intersections generated by the surface perpendicular to the two surfaces, the angle will be at a known point of the intersection, this if the two surfaces cut one another; if the two surfaces do not cut one another and one does not meet the other, then one will be known in position with respect to the other if each of them is known in position with respect to the surface11 which cuts both of them and which is perpendicular to each of them, the known for each of these surfaces will be the known angle or the two known angles. So a surface known in position with respect to a fixed surface is the surface that encloses a known angle with the fixed surface at the intersection of the two surfaces, or that encloses a known angle at the intersection of the surface of known position and the surface that is perpendicular to it and perpendicular to the fixed surface.
The known concerned with the position of a surface with respect to a moving surface, is like <the known for> a position of the surface we have already mentioned. The only difference between the two is that the reference surface for the position was fixed for the first surface, whereas it is moving for this latter surface, and that the surface of known position moves with a motion equal to its motion and in the direction of its motion. A surface of known position with respect to a moving surface is thus one which encloses a known angle with the moving surface, at the intersection between the two surfaces, or one which encloses a known angle at its intersection with the surface that is perpendicular to it and perpendicular to the moving surface, if the moving surface moves with a motion equal to the motion of the reference surface for its position, and in the direction of its motion.
As for the known concerned with ratios of magnitudes of surfaces the one to the other, there are two notions; one is the figure of the two surfaces, one of which is referred to the other, the second is the quantity of each of the two surfaces, that is to say the area of each of them. In fact, for two arbitrary surfaces, one does not necessarily have a ratio to the other, and there is not necessarily a ratio between the two surfaces, except if they are of the same species and if the notion that constitutes their essence is the same, as for two plane surfaces or two spherical surfaces from the same sphere or from two equal spheres. It is for these two species of surface only that there can be ratios between magnitudes of the individuals belonging to them. The known for two plane surfaces or spherical [ones] of the same species, whose ratio one to another is known, is thus the magnitude of each of the two surfaces – if each of them is known – or the magnitude of each of two surfaces of known magnitude, whose ratio one to another is equal to the ratio of the two surfaces, whose ratio one to another is known. So two surfaces whose ratio one to another is known are two plane or spherical surfaces for which the magnitude of each is known; or the magnitude of each of two surfaces of known magnitude, whose ratio one to another is equal to the ratio of the two known surfaces, one to another. A known ratio between two surfaces is one which is between two surfaces of known magnitude, because the ratios between known magnitudes do not change; it being given that the magnitudes are known, their magnitudes do not change, so the magnitude of one does not change when it is measured by the other.
The known concerned with figures made up of surfaces which meet one another, which are solids, are the shapes of surfaces that meet one another. So if each of the surfaces that enclose the solid is of known shape, then the solid is of known shape. So a solid figure of known shape is one which is enclosed by surfaces of known shape, whether each of these surfaces is of known magnitude or is not of known magnitude, on condition that it preserves its shape.
The known concerned with the essence of a solid is that it has three dimensions, because this notion is to be found in all solids and does not change in any of them. As for the quantity of the length of the solid, of its width and of its depth, it changes depending on the solids. Similarly, the figures of solids change depending on the solids. So the known concerned with the essence of a solid is that it has three dimensions.
The known concerned with the figure of a solid is the notion that constitutes the figure of the solid, that is to say its boundaries which are the surfaces that enclose it. So a solid of known figure is one for which the surface or the surfaces which enclose it are of known figure.
The known concerned with magnitudes of solids is the quantity of the volume of the solid, if the quantity of the volume of the solid does not change, either by increasing or by decreasing. So a solid of known magnitude is one such that the quantity of its volume does not change.
The known concerned with positions of solids with respect to fixed points or to one fixed point, or to a point or points that move, to a fixed straight line or to a moving straight line, to a fixed surface or to a moving surface, is the positions of the surfaces of the solids with respect to these things, so it is the positions of the surfaces which we have already discussed, because if the position of the surface of the solid is known, that is to say that it does not change, then the position of the solid does not change. So a solid of known position is one whose surface or surfaces are of known position, whatever thing it is to which the position has been referred.
The known concerned with ratios of magnitudes of solids one to another, is thus the magnitude of each of the two solids, one of which bears a ratio to the other, if each of them is known, or it is the magnitude of each of two solids of known magnitude, whose ratio one to another is equal to the ratio of the two solids whose ratio one to another is known.
The known concerned with the essence of a weight is the force that moves [it] towards the centre of the Universe, because that notion does not change for any weight. It is this force which is called weight.
The known concerned with magnitudes of weights is the quantity of the weight. But the quantity of the weight is known by its ratio to the size of the measure12 by which the size of weights is measured is known: the raṭl, the manā, the mithqāl and the weight of darāhim13 and things like them. If the ratio of the quantity of the weight to the size of the weight of the measure is a known ratio, then the magnitude of the weight is known, as it does not change because of the fact that the weight of the measure does not change and the known ratio does not change; so this ratio is a numerical ratio. Now, we have proved earlier how a numerical ratio is known. But the ratios of weights can be non-numerical ratios, these are the irrational ratios which are ratios of an actual weight that does not change to an actual weight that does not change, without either of the two weights having a [numerical] ratio to the measure. It remains that what we use for weights is only a numerical ratio. So a weight of known magnitude is one for which the ratio of its quantity to the size of the weight of the measure is a known ratio.
The known concerned with ratios of magnitudes of weights one to another is the quantity of each of the two weights, one of which is compared with the other, if each of them is of known magnitude, or it is the magnitude of each of the two weights of known magnitude, whose ratio to one another is equal to the ratio of the two weights whose ratio one to another is known.
The known concerned with the essence of time is the interval that elapses between two instants, because the essence of the interval does not change for arbitrary times, but it is the magnitudes of the times which differ.
The known concerned with the magnitude of time, that is the quantity of time, and the quantity of time is known in relation to the motion of the celestial sphere, because the revolution14 of the celestial sphere is the measure15 by which we measure time. So a time of known magnitude is the time whose ratio to the revolution of the celestial sphere is a known ratio.
The known concerned with ratios of the parts of time one to another is the quantity of each of two times, one of which is compared with the other, if each of them is of known magnitude; or it is the magnitude of each of two times of known magnitude, whose ratio one to another is equal to the ratio of the two times whose ratio one to another is known.
These notions which we have set out are all the knowns which are concerned with quantity in a detailed and precise manner. We are not aware of any predecessor who has given details of them in this way and made them precise in this fashion. These notions are pieces of knowledge each of which stands up in its own right and anyone who seeks to understand the sciences that deal in truths needs to know them. These notions are, in addition, the rules and premises used to solve mathematical problems; the solution of mathematical problems is completed only with their help.
For solving these problems, we may need other notions of the same kind as those in The Knowns which were not mentioned by Euclid in his book devoted to Data, and which were not mentioned by any of [our] predecessors. We set them out in this treatise so that this treatise may gather together all that has not been mentioned by [our] predecessors regarding knowns.
The notions that we set out now are divided into two parts; one of the two parts concerns notions that have not been mentioned by any of [our] predecessors, these [predecessors] have not mentioned anything of the kind; the second part is of the kind of thing that Euclid mentioned in the Data, though without anything about them being mentioned in the book of the Data.
For this let us introduce premises constructed on what we said earlier in this book of The Knowns, so that we could use it later on, following the premises.
We have already reminded ourselves that a known ratio is one which is between two known magnitudes or two magnitudes in the ratio of two known magnitudes. If this is so, then by composition of the separated known ratio, it will be known because the known ratio that has been isolated is equal to the ratio of two known magnitudes, one to the other; so by composition of the ratio that has been isolated, it will become equal to the ratio of the sum of two known magnitudes to one of them. But the sum of two known magnitudes is a known magnitude; so by composition of the known ratio that has been isolated, it will become equal to the ratio of two known magnitudes, one to the other; it is a known ratio. Similarly, by separation of a known composed ratio, it will become known, because its separation will be equal to the ratio of two known magnitudes composed, if they are separated. The same holds for a known ratio, if it is inverted.
Similarly, if we have a known ratio between two magnitudes and if one of the two magnitudes is known, it follows that the other is known, because a known ratio is one that exists between two known magnitudes. So the ratio of one known magnitude to the other magnitude is equal to the ratio of two known magnitudes, one to the other. But the ratio that exists between two known magnitudes does not change, thus the ratio of the known magnitude to the other magnitude is a ratio that does not change. So the second magnitude does not change, because if it changed, the ratio of a known magnitude to it would change, because the true nature of a ratio is to measure the quantity of a magnitude against the quantity of a magnitude. So if the quantity of a known magnitude does not change and its ratio to the other magnitude does not change, then the quantity of the other magnitude does not change. Thus, for two magnitudes such that the ratio of one to the other is known, if one is known, then the other is known.
Similarly, if we have two straight lines of known magnitude which enclose a known angle, then the straight line which joins their two endpoints is of known magnitude and with each of the two straight lines [it] encloses a known angle. Yet it is of known magnitude, since its two endpoints do not change – because they are the endpoints of two straight lines of known magnitude – and since the position of one with respect to the other does not change. But the line encloses a known angle with each of the two straight lines, since the distance to each of the two endpoints from each point of the other straight line does not change, accordingly the position of the straight line which joins the two endpoints does not change with respect to each of the two straight lines, because if the distance from each of the endpoints of the straight line to a single point does not change, then the distance from each point of the straight line to this point does not change. It follows that the position of the straight line that joins the two endpoints with respect to each of the two straight lines does not change. So, if the position of the straight line that joins the two endpoints does not change with respect to each of the two straight lines, then it encloses a known angle with each of the two straight lines. It follows also that the ratio of the sides of the triangle that is formed, one to another, is known, because their magnitudes are known.
Similarly, we have already reminded ourselves that a straight line known in position absolutely is one that does not move with any kind of motion, except increasing and decreasing; and that a circular line known in position absolutely is one whose centre is known and whose semidiameter is known. If this is so, it does not move with any kind of motion. The same holds for any line known in position absolutely which does not move with any kind of motion. It follows that if two lines known in position absolutely cut one another, then the point of intersection is known in position, because it does not undergo displacement, or change, whether the two lines are straight, circular, curved or of two different species.
Similarly, we have already reminded ourselves that a straight line of known magnitude is one whose length does not increase or decrease and its magnitude does not change. It follows that a straight line known in magnitude and in position is one that does not change by any kind of change.
Similarly, we have already reminded ourselves that a straight line of known position with respect to another straight line is one that encloses a known angle with the other straight line.
These notions were proved by Euclid in his book the Data using methods different from those we have set out here. We have proved them from knowns that we have given earlier in this book, in order that this book shall have no need of what Euclid set out in his book the Data.
Now that we have introduced these premises, let us begin by proving the notions that we have decided to include in this book, and which are needed for solving the problems, which divide up into two parts, as we have shown.
FIRST PART
These are the notions that none of the ancients has set out, and they have not set out anything of this kind.
– 1 – If from a point of known position we draw a straight line of known magnitude, then its endpoint will lie on the circumference of a circle of known position.
Example: Let there be a point A of known position; we draw from this point the straight line AB which is of known magnitude.
I say that the point B lies on the circumference of a circle known in position.
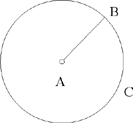
Fig. II.2.1.1
Proof: Let us make point A a centre and with the distance AB let us draw a circle; let the circle be BC. Since the circle BC has a centre known in position, the surface of the circle does not move in any way; and since the semidiameter of the circle is of known magnitude, the position of its circumference does not change in any way. So the circumference of the circle BC is known in position, so the point B lies on the circumference of a circle known in position, which is the circle BC. This is what we wanted to prove.
– 2 – If from the centre of a circle known in magnitude and in position we draw, as far as its circumference, a straight line which is then inclined at a known angle, and is such that the ratio of the first straight line to the second is known, then the endpoint of the second straight line lies on the circumference of a circle of known position.
Example: Let there be the circle AB, known in magnitude and in position, whose centre is C; from the point C we draw the straight line CB which is turned to lie along the straight line BD, so that the angle CBD is known and the ratio of CB to BD is known.16
I say that the point D lies on the circumference of a circle of known position.
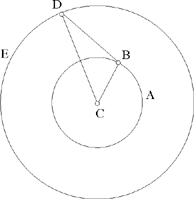
Fig. II.2.1.2
Proof: The circle AB is known in magnitude and in position, so the straight line CB is of known magnitude and its ratio to BD is known, so the straight line BD is of known magnitude, as has been proved in the premises. But since angle DBC is known, the straight line BD is known in position with respect to the straight line CB; since the straight line CB is of known magnitude, the position of the point B with respect to the point C is a known position that does not change; the same holds for the position of the point D with respect to the point B. Now, since the position of the point D with respect to the point B does not change – that is to say that one does not move away from or towards the other – similarly the position of the point B with respect to the point C does not change, and the angle CBD does not change – that is to say that, with respect to the straight line BC, the straight line BD does not incline in any direction – and similarly, with respect to the straight line BD, the straight line CB does not turn in any direction, then the position of the point D with respect to the point C does not change. We join CD; it will be of known magnitude because the position of its two endpoints, one with respect to the other, does not change. But since the point C is known in position and the straight line CD is of known magnitude, the point D will lie on the circumference of a circle known in position, as has been proved in the preceding proposition. We make C a centre and with distance CD we draw the circle DE, then it will be known in position, and thus the point D will lie on the circumference of a circle known in position. This is what we wanted to prove.
– 3 – In the plane of a circle of known magnitude and position, if from a known point, that is not its centre, we draw a straight line to meet the circumference of the circle and if we extend it so that the ratio of the first straight line to the second straight line is known, then the endpoint of the second straight line lies on the circumference of a circle known in position. Example: Let there be a circle AB known in magnitude and in position, and the known point C which is in the plane of the circle, but which is not at its centre; from the point C we draw the straight line CA as far as the circumference of the circle and we extend it to [the point] D such that the ratio of CA to AD is known.
I say that the point D lies on the circumference of a circle of known position.
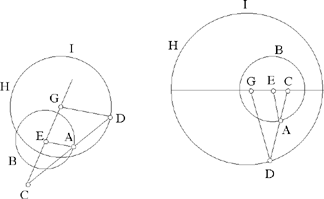
Fig. II.2.1.3
Proof: We mark off the centre of the circle, let it be E, and we join CE; it will be of known magnitude because its two endpoints are known. We extend it in the direction of E, we join EA in our imagination, and we imagine DG parallel to the straight line AE; so the ratio of GD to EA will be equal to the ratio of DC to CA and equal to the ratio of GC to CE and the ratio of DA to AC will be equal to the ratio of GE to EC. But the ratio of DA to AC is known because the ratio of CA to AD is known, so the ratio of GE to EC is known; now EC is of known magnitude, so GE is of known magnitude and GC is of known magnitude,17 as has been proved in the premises, so the ratio of GC to CE is known as has also been proved in the premises. Now the ratio of GC to CE is equal to the ratio of GD to EA, so the ratio of GD to EA is known and EA is of known magnitude, so the straight line GD is of known magnitude. We make point G a centre and with distance GD we draw a circle, let it be the circle DHI; the circle DHI is then known in magnitude and in position because its centre is of known position and its semidiameter is of known magnitude, so the point D lies on the circumference of a circle known in position. This is what we wanted to prove.
Starting out from this proof, we prove that: if an arbitrary straight line from the point C cuts two circles AB and HI, then the ratio of its two parts, one to the other, is equal to the ratio of the two parts of the straight line CD one to the other, because for every straight line [drawn] from the point C and which cuts the two circles, if from the two centres E and G we draw two straight lines to the two points of intersection, then the ratio of the two straight lines drawn from the two centres to the two points of intersection, one to the other, is equal to the ratio of GC to CE; these two straight lines will thus be parallel,18 and the ratio of the two parts of the straight line which cuts the two circles, one to the other, is then equal to the ratio of the two parts of the straight line CD one to the other.
– 4 – In the plane of a circle known in magnitude and in position, if from a point of known position, which is not the centre, we draw a straight line to the circumference of the circle, which is inclined at a known angle, in such a way that the ratio of the first straight line to the second is known, then the endpoint of the second straight line will lie on the circumference of a circle known in position.
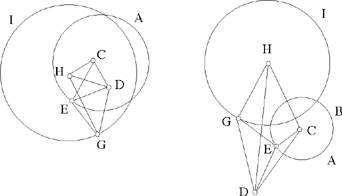
Fig. II.2.1.4
Example: Let there be a circle AB of known magnitude and position whose centre is C, and the point D of known position, DE comes out from it and is inclined at a known angle which is the angle DEG, in such a way that the ratio of DE to EG is known.
I say that the point G lies on the circumference of a circle known in position.
Proof: We join DC, it will be known in magnitude and in position because its two endpoints are known in position. We make the angle DCH equal to the known angle DEG; we make the ratio of DC to CH equal to the known ratio of DE to EG and we join the two straight lines CH and DG, then the two triangles DCH and DEG are similar, so the angle CDH is equal to the angle EDG, so the angle HDG is equal to the angle CDE and the ratio of CD to DH is equal to the ratio of ED to DG. But since the straight line DC is of known magnitude and position and the angle DCH is known, the straight line DH will be known in position. Since the ratio of DC to CH is known and the straight line DC is of known magnitude, the straight line CH is of known magnitude. Since the two straight lines DC and CH are known in magnitude and position, and since the angle DCH is known, the straight line DH will be known in magnitude and in position, because its two endpoints do not change. We join CE and HG. Since the ratio of CD to DH is equal to the ratio of ED to DG, the ratio of CD to DE will be equal to the ratio of HD to DG. But the angle CDE is equal to the angle HDG, so the triangle CDE is similar to the triangle HDG and the ratio of DC to CE is equal to the ratio of DH to HG. But the ratio of CD to DE is known, because they are both of known magnitude, so the ratio of DH to HG is known. But DH is of known magnitude, so the straight line HG is of known magnitude and the point H is known, because it is the endpoint of the straight line CH of known magnitude and position. With centre H and distance HG let us draw a circle GI, then it will be known in magnitude and in position, because its centre is known in position and its semidiameter is of known magnitude. So the point G lies on the circumference of a circle known in position, which is the circle GI. By this same proof, we [can] prove this proposition for the case in which the straight line DC passes through the point E. This is what we wanted to prove.
By an analogous proof, we prove that for every straight line from the point D which ends on the circumference of the circle AB and which is inclined at an angle equal to the angle DEG, in such a way that the ratio of the first straight line to the second straight line is equal to the ratio of DE to EG, the endpoint of the second straight line will lie on the circumference of the circle GI, [at the position] where there is the point E with respect to the circle AB, because the proof of this results in the straight line which joins the point H to the endpoint of the second straight line being equal to the straight line HG. It necessarily follows that, for every straight line from the point D which ends on the circumference of the circle AB, a straight line which is inclined at an angle equal to the angle DEG and which ends on the circle GI, the ratio of the two straight lines, one to the other, will always be equal to the known ratio of DE to EG.
– 5 – If, from a point of known position, we draw to a straight line known in position a straight line which is inclined at a known angle, in such a way that the ratio of the first straight line to the second is known, then the endpoint of the second straight line will lie on a straight line known in position.
Example: Let there be a point A of known position and the straight line BC of known position; from the point A we draw the straight line AD which is inclined at a known angle, say the angle ADE, so that the ratio of AD to DE is a known ratio.
I say that the point E lies on a straight line known in position.
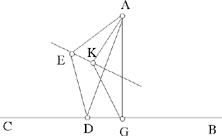
Fig. II.2.1.5
Proof: From the point A we draw a perpendicular to the straight line BC, let it be AG. Since the straight line BC is known in position and the point A is known in position, the distances between the point A and each point of the straight line BC do not change and the straight line AG is the shortest distance between the point A and the straight line BC, so the straight line AG does not change and the point G does not change; so the straight line AG is of known magnitude, because it does not change. Now, the point A is known in position, the straight line AG does not change and the point G does not change, so the straight line AG is known in magnitude and in position. We make the angle AGK equal to the angle ADE and we make the ratio of AG to GK equal to the known ratio of AD to DE, then the straight line GK is of known magnitude because AG is of known magnitude. Now, since the angle AGK is known, the straight line GK is known in position because the straight line AG is known in position – in fact if the position of the straight line GK changed, the angle KGA would change – so the straight line GK is known in magnitude and in position. So the point K does not change and the point A does not change. We join AK, it will be known in magnitude and in position and the angle GAK will be known, as has been proved in the premises. We join AE. Since the ratio of AG to GK is equal to the ratio of AD to DE and the angle AGK is equal to the angle ADE, the triangle ADE will be similar to the triangle AGK. So their angles are equal, so the angle DAE is equal to the angle GAK and the ratio of DA to AE is equal to the ratio of GA to AK. We join KE. Since the angle DAE is equal to the angle GAK, the angle GAD is equal to the angle KAE. Since the ratio of GA to AK is equal to the ratio of DA to AE, the ratio of GA to AD is equal to the ratio of KA to AE. Since the angle GAD is equal to the angle KAE and the ratio of GA to AD is equal to the ratio of KA to AE, the triangle KAE is similar to the triangle GAD. So the angle AKE is equal to the angle AGD; but the angle AGD is a right angle, so the angle AKE is a right angle. But the straight line AK is known in magnitude and in position and the angle AKE is a right angle, so the straight line KE is known in position – in fact, if its position changed, the right angle would change; but since the angle is a right angle, the position of the straight line KE does not change. So the straight line KE is known in position and the point E lies on the straight line KE, so the point E lies on a straight line known in position, which is the straight line KE. This is what we wanted to prove.
– 6 – If, from two points known in position, we draw two straight lines which meet one another in a point and which, at this point, enclose a known angle, then this point lies on the circumference of a circle known in magnitude and in position.
Example: Let there be two points A and B known in position, from which we draw two straight lines AC and BC, in such a way that the angle ACB is known.
I say that the point C lies on the circumference of a circle known in magnitude and in position.
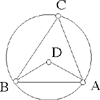
Fig. II.2.1.6
Proof: We join AB and we imagine a circle circumscribed about the triangle ACB, let the circle be ACB; and let its centre be D. We join AD and BD, then the angle ADB is known, because it is double the angle ACB; there remain the two known angles DAB and DBA which are equal because the two straight lines AD and BD are equal, so the angle BAD is known and the straight line AB is known in magnitude and in position because its two endpoints are known. So the straight line AD is known in position because its point A is known and the angle BAD is known – if its position changed, the angle BAD would change. Similarly, we [can] prove that the straight line BD is known in position, so each of the straight lines AD and BD is known; neither of the two straight lines AD and BD moves with any kind of motion; the point D, which is the point of intersection, thus does not change in any way;19 so the point D is known in position and the point A is known in position, so the straight line AD is known in magnitude, and the straight line BD is also. So each of the two straight lines DA and BD is known in magnitude and in position and the point D is the centre of the circle ACB. So the circle ACB is known in magnitude and in position and the point C lies on the circumference of this circle. So the point C lies on the circumference of a circle known in magnitude and in position, which is ACB. This is what we wanted to prove.
– 7 – If, from two points known in position, we draw two straight lines which meet one another in a point and which enclose a known angle, if we then extend one of the two straight lines in such a way that the ratio of the first straight line to its extended part is a known ratio, then the endpoint of the second straight line lies on the circumference of a circle known in position.
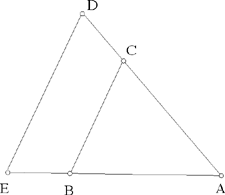
Fig. II.2.1.7
Example: Let there be the two points A and B known in position, from which we draw two straight lines AC and BC which meet one another at the point C, in such a way that the angle ACB is known. We then extend the straight line AC to D in such a way that the ratio of AC to CD is a known ratio.
I say that the point D lies on the circumference of a circle known in position.
Proof: We join AB, thus it will be of known magnitude and position because its endpoints are known; we extend it in the direction of B to E and we make the ratio of AB to BE equal to the known ratio of AC to CD; BE will thus be known in magnitude. But it is known in position because it lies on the extension of the straight line AB, known in position. So the whole straight line AE is known in magnitude and in position; its endpoints, which are A and E, are known. We join DE, thus it is parallel to the straight line CB because the ratio of AB to BE is equal to the ratio of AC to CD. So the angle ADE is equal to the known angle ACB, so the angle ADE is known. So, from the two points A and E known in position, we have drawn the two straight lines AD and ED which enclose a known angle, which is the angle ADE. So the point D lies on the circumference of a circle known in position, as has been proved in the preceding proposition. This is what we wanted to prove.
– 8 – If, from two points known in position, we draw two straight lines which meet one another in a point, in such a way that they are equal, then the point where they meet lies on a straight line known in position.
Example: Let there be the two points A and B known in position, for which we draw the two straight lines AC and BC which meet one another at the point C in such a way that they are equal.
I say that the point C lies on a straight line known in position.
Fig. II.2.1.8
Proof: We join the straight line AB, thus it will be known in magnitude and in position because its two endpoints do not change. Let us divide it into two halves at the point D; so the point D is known because it does not change. We join CD. Since the two straight lines AD and DC are <respectively> equal to the two straight lines BD and DC and the base AC is equal to the base BC, accordingly the angle ADC is equal to the angle BDC, so they are right angles. So the straight line DC is known in position, because the two angles which are on either side of this straight line do not change; and the point D does not change, so the point C lies on a straight line known in position, which is the straight line DC. This is what we wanted to prove.
– 9 – If, from two points of known position, we draw two straight lines which meet one another in a point, in such a way that the ratio of one to the other is known and there is a ratio of a greater to a smaller, then the point where they meet lies on the circumference of a circle known in position.
Example: Let there be the two points A and B known in position, from which we draw the two straight lines AC and BC which meet one another at the point C, in such a way that the ratio of AC to CB is known, and it is a ratio of a greater to a smaller.
I say that the point C lies on the circumference of a circle known in position.
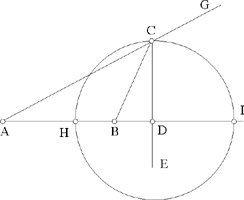
Fig. II.2.1.9
Proof: We join AB and we extend it in the direction of B to D; we imagine AC extended in the direction of C to G and we imagine the angle ACE equal to the angle CBD. Since AC is greater than CB, the angle CBA will be greater than the angle CAB; now, since the angle ACE is equal to the angle CBD, the angle ECG is equal to the angle CBA, so the angle ECG is greater than the angle CAB; now the angle ACE is common, so <the sum> of the two angles ECG and ACE is greater than <the sum> of the two angles CAB and ACE; now <the sum> of the angles ECG and ACE is equal to two right angles, so the two angles CAB and ACE <have a sum> less than two right angles, so the two straight lines AB and CE meet; let them meet at the point D. Thus, the two triangles ACD and CBD are similar because the angle ACD is equal to the angle CBD and the angle CDB is common, and there remains the angle CAD [which is] equal to the angle BCD. So the ratio of AD to DC is equal to the ratio of CD to DB and is equal to the ratio of AC to CB. But the ratio of AC to CB is known, so the ratio of AD to DC is known and the ratio of CD to DB is known. But the ratio of AD to DB is equal to the ratio of the square of AD to the square of DC, and the ratio of the square of AD to the square of DC is known, because the ratio of AD to DC is known, so the ratio of AD to DB is known. We make DH equal to DC, then the ratio of AD to DH is known, the ratio of HD to DB is known, and there remains the ratio of AH to HB [which is] known. But since the ratio of AD to DB is known, the ratio of AB to BD is known; but AB is of known magnitude, so the straight line BD is of known magnitude; now point B on it is known, so the point D is known. Since the ratio of AD to DH is known and AD is of known magnitude, accordingly DH is of known magnitude. But DH is equal to DC. We make D a centre and with distance DH we draw a circle, so it passes through the point C; let the circle be HCI. So the circle HCI is known in magnitude and in position because its centre is known in position, being the point D, and its semidiameter is of known magnitude, being the straight line DH. So the point C lies on the circumference of a circle known in position, which is the circle HCI. This is what we wanted to prove.
Starting out from this proof, we prove that for two straight lines from two points A and B, which meet in a point that lies on the circumference of the circle HCI, the ratio of one to the other is equal to the ratio of AC to CB; and this because if, from the two points A and B, we draw two straight lines which meet one another in [D], an arbitrary point on the circumference of the circle HCI and if, from the point D, we then draw a straight line to this point, two triangles are formed whose [common] vertex is this point, and which are such that the ratio of AD to the straight line extended from the point D to this point is equal to the ratio of this straight line to the straight line DC. Accordingly, the two triangles are similar and the ratio of one of the straight lines to the other is equal to the ratio of AD to DH which is equal to the ratio of AC to CB. So for two straight lines drawn from the two points A and B and which meet one another in a point on the circumference of the circle HCI, the ratio of one to the other is equal to the ratio of AC to CB.
– 10 – If, from two points of known position, we draw two straight lines which meet one another in a point, and if we join the two points with a straight line in such a way that the triangle that is formed is of known magnitude, then the point where they meet lies on a straight line known in position.
Example: Let there be two points A and B, known in position, from which we draw the two straight lines AC and BC which meet at the point C, in such a way that the triangle ACB is of known magnitude.
I say that the point C lies on a straight line known in position.20
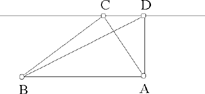
Fig. II.2.1.10
Proof: We join AB, it will be of known magnitude, and we draw the straight line AD at a right angle [to AB]; so the straight line AD is known in position because the angle BAD does not change and its point A does not change. We make the area enclosed by these two straight lines BA and AD equal to double the triangle ACB of known magnitude; this is possible. So AD will be of known magnitude, because if its magnitude changed, the area enclosed by the two straight lines BA and AD would change; but this area does not change, because it is of known magnitude. So the straight line AD is known in magnitude and known in position, and its point A is known, so the point D is known. We join BD, so the triangle BDA is known in magnitude and it is equal to the triangle ACB. We join DC, so it will be parallel to the straight line AB because the two triangles ACB and ADB are equal and their two bases are equal,21 thus the angle ADC is a right angle, the straight line AD is known in magnitude and in position and its point D is known; so the straight line DC is known in position and the point C lies on a straight line known in position. This is what we wanted to prove.
– 11 – If, between two equal circles, we draw a straight line parallel to the one that joins the centres of these two circles, in such a way that its endpoints are in two similar directions,22 then this straight line is equal to the straight line between the two centres.
Example: Let there be the two circles AB and CD whose centres are E and G; we join EG and we draw the straight line BC parallel to the straight line EG.
I say that the straight line BC is equal to the straight line EG.
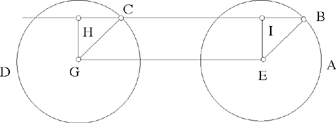
Fig. II.2.1.11
Proof: We join the two straight lines EB and GC, they will be equal; we erect the two perpendiculars EI and GH, they will be equal and parallel. But the two straight lines EB and GC are equal and are in two similar directions with respect to the two perpendiculars EI and GH; so they are parallel, because the two triangles BEI and CGH are equal, so the angle EBI is equal to the angle GCH,23 and the straight line BI will be equal to the straight line CH; IC is common, so the straight line BC is equal to the straight line IH; but the straight line IH is equal to the straight line EG, so the straight line BC is equal to the straight line EG. This is what we wanted to prove.
– 12 – If, between two equal circles known in magnitude and in position, we draw a straight line parallel to the straight line that joins their centres; if we then extend it in one of the two directions and if we put its ratio to the extended part, a known ratio, then the endpoint of the second straight line lies on the circumference of a circle known in position.
Example: Let there be two equal circles AB and CD, known in magnitude and in position, and let their centres be E and G; we join EG, we draw the straight line AC parallel to the straight line EG and we extend it to I, in such a way that the ratio of AC to CI is a known ratio.
I say that the point I lies on the circumference of a circle known in magnitude and in position.
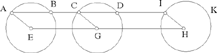
Fig. II.2.1.12
Proof: We extend the straight line EG and we put the ratio of EG to GH equal to the known ratio of AC to CI. So the straight line GH will be known in magnitude because the straight line EG is known in magnitude, from what has been proved in the premises. Now the point G is known, so the point H is known. We join HI and GC. Since AC is parallel to the straight line EG and it is equal to it, and since the ratio of AC to CI is equal to the ratio of EG to GH, the straight line CI is equal to the straight line GH and it is parallel to it, so the straight line HI is equal to the straight line GC and is parallel to it. But the straight line GC is known in magnitude, so the straight line IH is known in magnitude and the point H is known. We take H as a centre and with distance HI we draw the circle IK; it will be known in magnitude and in position, so the point I will lie on the circumference of a circle known in magnitude and in position, which is the circle IK. This is what we wanted to prove.
– 13 – If, from a known point, we draw to a straight line known in magnitude and in position a straight line which cuts it, [and] if we then extend it in such a way that the ratio of the first straight line to the second straight line is equal to the ratio of the two parts of the straight line known in magnitude and in position, then the endpoint of the second straight line lies on a straight line known in position.

Fig. II.2.1.13
Example: Let there be a straight line AB known in magnitude and in position and a known point C; from the point C, we draw to the straight line AB the straight line CD, which we extend to E in such a way that the ratio of CD to DE is equal to the ratio of AD to DB.
I say that the point E lies on a straight line known in position.
Proof: We join AC, it is known in magnitude and in position. We join BE. Since the ratio of CD to DE is equal to the ratio of AD to DB,24 the straight line BE is parallel to the straight line AC. But the straight line AC is known in magnitude and in position and the straight line AB is known in position, so the angle CAB is known and it is equal to the angle ABE, so the angle ABE is known. Now, the straight line AB is known in position and its point B is known, so the straight line BE is known in position and the point E lies on a straight line known in position, which is the straight line BE. This is what we wanted to prove.
– 14 – If, from a known point, we draw to a straight line known in magnitude and in position a straight line which cuts it; if we then extend this straight line, in such a way that the product of the first part and the second is equal to the product of the two parts of the straight line known in magnitude and in position, one with the other, then the endpoint of the second straight line lies on the circumference of a circle known in position.
Example: Let there be the straight line AB known in magnitude and in position, and the known point C; from the point C we draw the straight line CD which we extend to E, in such a way that the product of CD and DE is equal to the product of AD and DB.
I say that the point E lies on the circumference of a circle known in position.
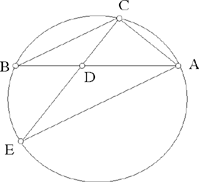
Fig. II.2.1.14
Proof: We join AC, CB and AE; the ratio of CD to DB is equal to the ratio of AD to DE and the two angles at the point D are equal, so the two triangles AED and CBD are similar and the angle AEC is equal to the angle CBD. We draw a circle to circumscribe the triangle ABC, thus it passes through the point E; let the circle be ACBE. Since the two points A and C are known, the straight line AC is known in magnitude and in position; and since the points A, B and C are known, the angle ABC is known; but since the angle ABC is known and the two points A and C are known, the circle ACBE is known in magnitude and in position, as has been proved in Proposition 6 of this treatise. So the point E lies on the circumference of a circle known in magnitude and in position. This is what we wanted to prove.
– 15 – If from two known points we draw two straight lines to a circle known in magnitude and in position, if they cut one another in a point inside the circle and if they are extended to end on the circumference of the circle, in such a way that the product of the two parts of one of the two straight lines, one with the other, is equal to the product of the two parts of the other straight line, one with the other; if, with a straight line, we join the first two points in which the two straight lines cut the circle, then this straight line is parallel to the straight line that joins the first two points.
Example: Let there be two points A and B known in position and the circle CDEG known in magnitude and in position; from the two points A and B we draw two straight lines ACHG and BDHE which cut one another at the point H – the point H being inside the circle – in such a way that the product of AH and HG is equal to the product of BH and HE. We join CD and AB.
I say that the straight line CD is parallel to the straight line AB.
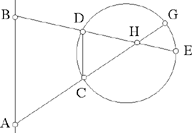
Fig. II.2.1.15
Proof: The product of AH and HG is equal to the product of BH and HE, so the ratio of AH to HB is equal to the ratio of EH to HG. But the product of CH and HG is equal to the product of DH and HE,25 so the ratio of EH to HG is equal to the ratio of CH to HD. In consequence, the ratio of AH to HB is equal to the ratio of CH to HD, the triangle AHB is thussimilar to the triangle CHD, so their angles are equal, so the straight line CD is parallel to the straight line AB. This is what we wanted to prove.
– 16 – If from two known points we draw two straight lines to <the circumference of> a known circle, if they cut one another in a point inside the circle and if, at the point of intersection, they divide one another in the same ratio, then the first two points in which the two straight lines cut the circle lie on the circumference of a circle that passes through the two known points.
Example: Let there be two points A and B from which we draw, to a circle CDGE, the two straight lines ACHG and BDHE, which cut one another at the point H, in such a way that the ratio of AH to HG is equal to the ratio of BH to HE.
I say that the two points C and D lie on the circumference of a circle which passes through the two points A and B.
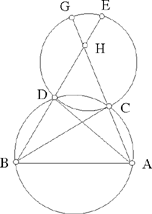
Fig. II.2.1.16
Proof: We join AD and BC. Since the ratio of AH to HG is equal to the ratio of BH to HE, the ratio of AH to HB is equal to the ratio of GH to HE. But the ratio of GH to HE is equal to the ratio of DH to HC because the product of CH and HG is equal to the product of DH and HE, so the ratio of AH to HB is equal to the ratio of DH to HC. Now, the angle AHB is common to the two triangles AHD and BHC, so the two triangles AHD and BHC are similar and the angle HDA is equal to the angle HCB; so the angle ADB is equal to the angle ACB. We imagine a circle circumscribed about the triangle ACB, it passes through the point D, let the circle be ACDB. The two points C and D lie on the circumference of a circle that passes through the two points A and B. This is what we wanted to prove.
– 17 – If from two points known in position we draw two straight lines to a circle known in magnitude and in position, if they meet one another on the circumference of the circle, if they also reach as far as the circumference of the circle and if they divide one another in the same ratio, then the ratio of the product of one of the two straight lines and the part of it that lies inside the circle to the product of the other straight line and the part of it that lies inside the circle is a known ratio.26
Example: Let there be two known points A and B and the circle CDE known in magnitude and in position; from the two points A and B we draw the two straight lines ACD and BCE which cut one another at the point C, in such a way that the ratio of AC to CD is equal to the ratio of BC to CE.
I say that either the product of AD and DC is equal to the product of BE and EC or its ratio to it is a known ratio.
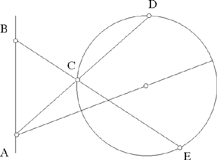
Fig. II.2.1.17
Proof: The point A is known and the circle is known in magnitude and in position, so the straight line drawn from the point A to the centre of the circle CDE and which ends on its circumference is known in magnitude and in position and the part of it that lies outside the circle is of known magnitude because its point of intersection with the circumference of the circle is known; the product of the whole straight line and the part of it that lies inside the circle is thus known, since it is enclosed27 by two known straight lines. But the product of this straight line and the part of it that lies outside the circle is equal to the product of DA and AC, so the product of DA and AC is known. Similarly, we [can] prove that the product of EB and BC is known. So these two products28 are known. Either they are equal, or the ratio of one to the other is known. So the ratio of AC to CB is equal to the ratio of EB to AD or to a straight line whose ratio to AD is known. But the ratio of AC to CB is equal to the ratio of DC to CE, so the ratio of DC to CE is equal to the ratio of EB to AD or to a straight line whose ratio to AD is known. If the ratio of DC to CE is equal to the ratio of EB to AD, then the product of AD and DC is equal to the product of BE and EC; if it is equal to the ratio of EB to a straight line whose ratio to AD is known, then the ratio of the product of AD and DC to the product of BE and EC is known. This is what we wanted to prove.
– 18 – For two known circles that are tangent, one inside the other, if we draw a straight line that cuts the two circles in whatever way, and if we join the point of intersection of the smaller circle to the point of contact with a straight line, then the ratio of the product of the two parts of the straight line that cuts the greater circle, one with the other, to the square of the straight line that joins the point of intersection and the point of contact, is known.
Example: Let there be two circles ABC and ADE tangent at the point A; we draw the straight line BDG which cuts the two circles and we join AD.
I say that the ratio of the product of BD and DG to the square of DA is known.
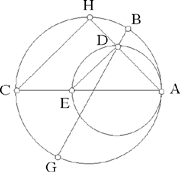
Fig. II.2.1.18
Proof: We draw the common diameter to the two circles, let the diameter be AEC; we extend AD to H and we join DE and HC. The two angles ADE and AHC are right angles, so the straight line DE is parallel to the straight line CH. So the ratio of HD to DA will be equal to the ratio of CE to EA. But the ratio of HD to DA is equal to the ratio of the product of HD and DA to the square of DA, so the ratio of the product of HD and DA to the square of DA is equal to the ratio of CE to EA. But the product of HD and DA is equal to the product of BD and DG, so the ratio of the product of BD and DG to the square of DA is equal to the ratio of CE to EA. Now the ratio of CE to EA is known because each of them is known. So the ratio of the product of BD and DG to the square of DA is known. This is what we wanted to prove.
And at this point it becomes clear that if a straight line is drawn from a point of contact and if it cuts the two circles, then it is divided by the smaller circle in a known ratio, let it be the ratio of AE to EC.
– 19 – For two known circles tangent internally, if we draw a straight line touching the smaller circle, which ends on the greater circle, and if we draw a straight line from the point of contact of the two circles to the endpoint of the tangent straight line, then its ratio to the tangent straight line is known.
Example: Let there be two circles ABC and ADG tangent at the point A; we draw the straight line DB tangent to the smaller circle and we join AEB.
I say that the ratio of AB to BD is known.

Fig. II.2.1.19
Proof: We draw the common diameter, which is AGC, thus the ratio of AG to GC is known and is equal to the ratio of AE to EB,29 so the ratio of AE to EB is a known ratio. So the ratio of AB to BE is known and the ratio of the square of AB to the product of AB and BE is known. But the product of AB and BE is the square of BD, so the ratio of the square of AB to the square of BD is known and is equal to the known ratio of AC to CG; so the ratio of AB to BD is known. This is what we wanted to prove.
If we draw BD in the other direction to H and if we join AH, we [can] prove, as has been shown earlier, that the ratio of AH to HD is known, that the ratio of the square of AH to the square of HD is equal to the ratio of AC to CG, and thus that the ratio of AB to BD is equal to the ratio of AH to HD. This is what we wanted to prove.
Starting from this, we prove that the ratio of the sum of the two straight lines BA and AH to the straight line BH is known.
– 20 – Let us draw the circle again. We draw the straight line BDH tangent to the smaller circle, we join AD and we extend it to I.
I say that the point I divides the arc BIH into two halves.
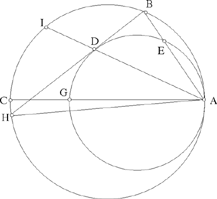
Fig. II.2.1.20
Proof: We join AB and AH; then the ratio of AB to BD is equal to the ratio of AH to HD. By permutation, the ratio of BA to AH will then be equal to the ratio of BD to DH. So the straight line AD has divided the angle BAD into two halves, so the angle BAD is equal to the angle DAH and the arc BI is equal to the arc IH. This is what we wanted to prove.
– 21 – Let there be two known circles tangents internally; if from their point of contact we draw the common diameter and if from the endpoint of the diameter on the smaller circle we draw a straight line which cuts the smaller circle, then it is divided into two parts such that the product of one and the other plus a square, whose ratio to the square of the straight line inside the smaller circle is a known ratio, is known in magnitude.

Fig. II.2.1.21
Example: Let there be two circles ABC and ADE tangent at the point A; we draw the diameter AEC and from the point E we draw the straight line EDBG.
I say that the product of GD and DB plus a square, whose ratio to the square of DE is known, is known in magnitude.
Proof: We join AD; then the ratio of the product of GD and DB to the square of DA is equal to the known ratio of CE to EA. Let the ratio of the square of the straight line H to the square of the straight line DE be equal to the ratio of CE to EA; the ratio of the product of GD and DB, plus the square of H, to <the sum> of the squares of AD and DE is thus equal to the ratio of CE to EA. But <the sum> of the two squares of AD and DE is equal to the square of AE because the angle ADE is a right angle. So the ratio of the product of GD and DB, plus the square of H, to the square of AE is equal to the ratio of CE to EA which is equal to the ratio of the product of CE and EA to the square of EA, so the product of GD and DB, plus the square of H, is equal to the product of CE and EA which is known. But the ratio of the square of H to the square of DE is known, because it is equal to the ratio of CE to EA. The product of GD and DB plus a square, whose ratio to the square of DE is known, is thus known in magnitude. This is what we wanted to prove.
– 22 – If in a circle known in magnitude and in position, we draw a diameter known in position on which we take two points on either side of the centre, such that their distances to the centre are two equal distances, and if from these two points we draw two arbitrary straight lines that meet one another in a point on the circumference of the circle, then the sum of their two squares is known and is equal to the sum of the squares of the two parts of the diameter.
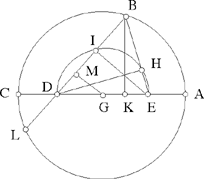
Fig. II.2.1.22
Example: Let there be a circle ABC known in magnitude and in position, in which we draw the diameter AC known in position; let its centre be G; on the diameter we take two points E and D, we put EG equal to DG and we draw the two straight lines EB and DB.
I say that the sum of the squares of the two straight lines EB and DB is equal to the sum of the squares of the two known straight lines AD and DC.
Proof: On the straight line ED we draw a semicircle; let the semicircle be HI; let it cut the two straight lines at the points H and I.30 We join EI, DH and we draw the perpendicular BK. Since the arc EHID is a semicircle, the angle EHD is a right angle and the angle EID is a right angle. But since BK is perpendicular, the angle BKD is a right angle, so the circle circumscribed about the triangle BKD passes through the point H. So the product of DE and EK is equal to the product of BE and EH. But since each of the angles BKE and BIE is a right angle, the circle circumscribed about the triangle BKE passes through the point I, so the product of BD and DI is equal to the product of ED and DK, so the square of ED is equal to the product of BE and EH, plus the product of BD and DI. We extend BD to L and we draw the perpendicular GM, then M divides DI into two halves and divides BL into two halves. So the straight line BI is equal to the straight line DL and the product of DB and BI is equal to the product of BD and DL. But the product of BD and DL is equal to the product of AD and DC. So the product of DB and BI is equal to the product of AD and DC. But the product of EB and BH is equal to the product of DB and BI. The product of EB and BH, plus the product of DB and BI, is thus equal to twice the product of AD and DC. The sum of the products31 of BE and EH, of BD and DI, of DB and BI and of EB and BH is equal to the square of ED, plus twice the product of AD and DC. But the sum of these four products32 is the sum of the squares of EB and of DB. So the sum of the squares of EB and DB is equal to the square of ED, plus twice the product of AD and DC.33 Twice the product of AD and DC is equal to twice the product of EC and CD. But twice the product of EC and CD, plus the square of ED, is equal to the square of EC, plus the square of CD which is equal to the square of AD, plus the square of DC. So the sum of the squares of EB and BD is equal to the sum of the squares of AD and DC which are known. This is what we wanted to prove.
Whatever the position we have given to the two straight lines EB and DB, the sum of their squares is equal to the sum of the squares of the two parts of the diameter, and the proof for all positions is the one that we have set out and differs only in regard to differences in the position of the two points H and I. It is in fact possible for one of the two straight lines EB and BD to be a tangent to the smaller circle at the endpoint of its diameter or to cut the other half of the semicircle of the smaller circle. For each of these positions, the sum of the squares of the two straight lines EB and DB will be equal to the sum of the squares of the two parts of the diameter.
– 23 – If from two points we draw two straight lines which meet in a point and enclose an acute angle in such a way that the sum of their squares is known, then the point where they meet lies on the circumference of a circle known in magnitude and in position.
Example: From two points A and B we draw two straight lines AC and BC which meet one another at the point C and which enclose an acute angle that is the angle ACB, and are such that the sum of their squares is known.
I say that the point C lies on the circumference of a circle known in magnitude and in position.

Fig. II.2.1.23
Proof: We join AB; it is known and its square will be smaller than the sum of the squares of AC and CB because the angle ACB is acute; the excess <of the sum> of the squares of AC and CB over the square of AB is known. We put twice the product of AE and EB equal to the excess <of the sum> of the squares of AC and CB over the square of AB. We put AG equal to BE and on GE as diameter we draw a circle; let it be the circle GHE.
I say that the circle GHE passes through the point C.
If it does not pass through the point C, then we divide the angle ACB into two halves with the straight line CI. We extend IC to H and we join AH and HB, then the [sum of the] squares of AH and HB exceeds the square of AB by twice the product of AE and EB, as has been proved in the previous proposition. But the [sum of the] squares of AC and CB exceeds the square of AB by twice the product of AE and EB, so <the sum> of the squares of AH and HB is equal to <the sum of> the squares of AC and CB. But the angle ACI is acute, so the angle HCA is obtuse, so the straight line HA is greater than the straight line AC. Similarly, we [can] prove that the straight line HB is greater than the straight line BC. So the two straight lines AH and HB are greater than the two straight lines AC and CB. <The sum of> the squares of the two straight lines AH and HB is greater than <the sum of> the squares of AC and CB; but they are equal, which is impossible. So the point C lies on the circumference of the circle GHE and the circle GHE is known in magnitude and in position, because its diameter, which is GE, is known in magnitude and in position. So the point C lies on the circumference of a circle known in magnitude and in position. This is what we wanted to prove.
– 24 – If, in a circle known in magnitude and in position, we draw an arbitrary chord which we divide into two parts in such a way that the product of one of the two parts and the other is known, then the point of division lies on the circumference of a circle known in position and in magnitude.
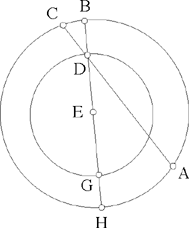
Fig. II.2.1.24
Example: Let there be a circle ABC known in magnitude and in position in which we draw the arbitrary chord AC which we divide at the point D, in such a way that the product of AD and DC is known.
I say that the point D lies on the circumference of a circle known in magnitude and in position.
Proof: Indeed, let us name the centre of the circle, say as the point E. We join ED and we extend it in both directions to B and H, then the product of HD and DB is equal to the product of AD and DC.34 But the product of AD and DC is known, so the product of HD and DB is known. But the diameter HB is known, so half of it, which is EB, is known; there remains the square of ED, which is known, so the straight line ED is known.
We make E a centre and with the known distance ED we draw a circle, let the circle be DG. So the circle DG is known in magnitude and in position because its centre is known in position and its semidiameter is of known magnitude. So the point D lies on the circumference of a circle known in magnitude and in position. This is what we wanted to prove.
SECOND PART
The work in this part is of the same kind as what was set out by Euclid in his book the Data, although nothing in this part is to be found in the book the Data.
– 1 – If, from a known point, we draw to a circle known in magnitude and in position, a straight line which cuts the circle; if the point lies outside the circle and if the ratio of the part that is outside [the circle] to the part that lies inside the circle is a known ratio, then the straight line is known in position.
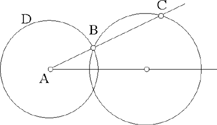
Fig. II.2.2.1
Example: Let there be a known point A and a circle BC known in magnitude and in position; we draw the straight line ABC in such a way that the ratio of AB to BC is known.
I say that the straight line ABC is known in position.
Proof: The point A is known and the circle BC is known in magnitude and in position, so the straight line drawn from the point A to the centre of the circle, and which ends on its circumference, is known in magnitude and in position; the part which lies outside the circle is of known magnitude, so the product of CA and AB is of known magnitude and the ratio of CA to AB is known; but it is equal to the ratio of the product of CA and AB to the square of AB. So the square of AB is known and the straight line AB is of known magnitude. But the point A is known, so the point B lies on the circumference of a circle known in position, as has been proved in the first proposition of this book; let the circle be BD. The circle BD is known in position and the circle BC is known in position, so the point B is known and the point A is known, so the straight line AB is known in position, so the straight line ABC is known in position. This is what we wanted to prove.
– 2 – If, from a known point, we draw to a circle known in position, a straight line which cuts off from the circle a known segment,35 then the line is known in position.
Example: Let there be a known point A and a circle BC known in position; we draw the straight line ABC in such a way that the segment BC is known.
I say that the straight line ABC is known in position.
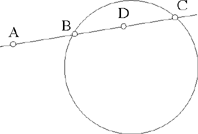
Fig. II.2.2.2
Proof: The point A is known, so the product of CA and AB is known. But since the segment BC is known and the circle is known, the straight line BC is known.36 So the straight line BC is known and the product of CA and AB is known. The ratio of twice the product of CA and AB to the square of BC is thus known. We divide BC into two halves at the point D, then the ratio of the product of CA and AB to the square of BD is known, so the ratio of the square of AD to the square of DB is known. So the ratio of AD to DB, that is DC, is known. So the ratio of AC to CB is known, so the ratio of AB to BC is known. But the point A is known and the circle BC is known, so the straight line ABC is known in position. This is what we wanted to prove.
– 3 – If, from a known point, we draw to a straight line known in magnitude and in position, a straight line such that its ratio to what it cuts off from the <first> straight line is a known ratio, then the straight line that has been drawn is known in position.
Example: Let there be a known point A and a straight line BC known in magnitude and in position; we draw the straight line AD in such a way that the ratio of AD to DC is a known ratio.
I say that the straight line AD is known in position.
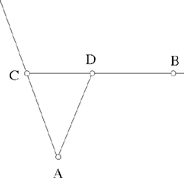
Fig. II.2.2.3
Proof: The two points A and C are in fact known and the ratio of AD to DC is known, so the point D lies on the circumference of a circle known in position, as has been proved in Proposition 9 of this treatise. So the point D lies on the circumference of a circle known in position and it lies on the straight line BC [which is] known in position; so the point D is known and the point A is known, so the straight line AD is known in position. This is what we wanted to prove.
– 4 – If, from a known point, we draw to two parallel straight lines known in magnitude and in position, a straight line which cuts off two alternate straight lines,37 in such a way that the ratio of one to the other is known, then the straight line that is drawn is known in position.
Example: Let there be a known point A and two straight lines BC and DE known in position38 and parallel; we draw the straight line AHG in such a way that the ratio of HC to DG is known.
I say that the straight line AG is known in position.

Fig. II.2.2.4
Proof: We join DC, it is known in magnitude and in position because its two endpoints are known, and it cuts the straight line HG; let it cut it at the point I. So the ratio of CI to ID is known, so the ratio of CD to DI is known. But CD is known, so DI is known. But the point D is known, so the point I is known. But the point A is known, so the straight line AIG is known in position. This is what we wanted to prove.
– 5 – If, from a known point, we draw to a straight line known in position and in magnitude, a straight line such that, added to what it cuts off from the known straight line, <it gives a sum that is> known, then it is known in position.
Example: Let there be a known point A and a straight line BC known in magnitude and in position; we draw the straight line AD in such a way that AD plus DC is known.
I say that AD is known in position.
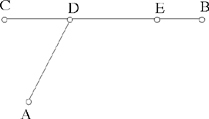
Fig. II.2.2.5
Proof: AD plus DC is a known <sum>; BD plus DC is a known <sum>, so either the two straight lines AD and DB are equal, or one is greater than the other by a known magnitude.
If they are equal, then from the two known points A and B we have drawn two equal straight lines AD and DB, so the point D lies on a straight line known in position, as has been proved in Proposition 8 of this treatise.
If one is greater than the other by a known magnitude, let BE be that excess; so BE is known, so the point E is known, and the straight line AD is equal to the straight line DE; so the two points A and E, from which we drew the two equal straight lines AD and DE, are known. So the point D lies on a straight line known in position and it lies on the straight line EC, which is known in position; so the point D is known. But the point A is known, so the straight line AD is known in position. This is what we wanted to prove.
– 6 – If, from two points known in position, we draw to a straight line known in position two straight lines that enclose a known angle, then they are known in position and in magnitude.
Example: Let there be two known points A and B and the straight line CD known in position; we draw two straight lines AE and BE which enclose a known angle; let it be the angle AEB.
I say that the two straight lines AE and BE are known in magnitude and in position.
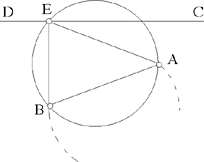
Fig. II.2.2.6
Proof: The two points A and B are known, from them we have drawn two straight lines AE and BE which enclose a known angle; then the point E lies on the circumference of a circle known in position, as has been proved in Proposition 6 of the first section of this treatise. So the point E lies on the circumference of a circle known in position; but it lies on the straight line CD known in position, so the point E is known. But each of the two points A and B is known, so the two straight lines AE and BE are known in magnitude and in position. This is what we wanted to prove.
– 7 – If, from two known points we draw, to a straight line known in position, two straight lines in such a way that the ratio of one to the other is known, then the two straight lines are known in position and in magnitude.
Example: Let there be two known points A and B and the straight line CD known in position; we draw the two straight lines AE and BE in such a way that the ratio of one to the other is known.
I say that each of the two straight lines AE and BE is known in magnitude and in position.
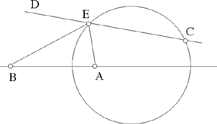
Fig. II.2.2.7
Proof: The point E lies on the circumference of a circle known in position, as has been proved in Proposition 9 of the first section of this treatise. But it lies on the straight line DC, so the point E is known and the two straight lines AE and BE are known in magnitude and in position. This is what we wanted to prove.
– 8 – If we have two parallel straight lines known in position, if we take two points on one [of them] and if we draw from these two points two straight lines which meet one another in a point on the other parallel straight line in such a way that the product of one of the two straight lines [we have] drawn and the other is known, then the two straight lines are known in magnitude and in position.
Example: Let there be two parallel straight lines AB and CD, known in position; on the straight line AB we take two points E and G and from these points we draw two straight lines EH and GH in such a way that the product of EH and HG is known.
I say that the two straight lines EH and GH are known in magnitude and in position.
Proof: We imagine an angle GHI equal to the angle HEG, then the straight line HI meets the straight line GA, because <the sum> of the two angles IHG and IGH is smaller than two right angles; let it meet it at the point I. The triangle IHG is then similar to the triangle HEG, so the angle HIG is equal to the angle EHG, the ratio of IG to GH is equal to the ratio of HG to GE and it is equal to the ratio of IH to HE, so the ratio of IH to HE is equal to the ratio of HG to GE and the product of HI and EG is equal to the product of EH and HG. But the product of EH and HG is known, so the product of IH and EG is known. But EG is known, so IH is known, because if two straight lines enclose a known area with a right angle and if one of the two straight lines is known, then the other straight line is known, because the magnitude of the area does not change and the angle of the area does not change, so the magnitude of the other straight line does not change, so the straight line IH is known. We take an arbitrary point on the straight line CD, let it be D; from the point D, at a right angle, which is the angle CDB, we draw the straight line DB; thus it will be known in position. But the straight line AB is known in position, so the point B is known, then the straight line DB is known in magnitude, so it is either equal to the straight line HI or smaller than it.

Fig. II.2.2.8a
Fig. II.2.2.8b
If it is equal, then the straight line HI is perpendicular and the angle HIG is a right angle. But it is equal to the angle EHG, so the angle EHG is a right angle. If the straight line DB is smaller than the straight line HI, we make the straight line DL equal to the straight line HI. We make D a centre and with distance DL we draw the circle LKN. So this circle is known in position. But the straight line AB is known in position, so the point K is known. We join DK, thus it is known in magnitude and in position, because the two points D and K are known; but the straight line DK is equal to the straight line HI; either they are parallel or they meet one another. If they are parallel, then the angle HIG is equal to the angle DKB. But the angle DKB is known, because the two straight lines DK and KB are known in position, so the angle HIG is known, so the angle EHG is known. And if the two straight lines IH and KD meet one another, let them meet one another at the point M. So the ratio of IM to MK is equal to the ratio of IH to KD; but IH is equal to KD, so IM is equal to MK, so the angle MIK is equal to the angle MKI; but the angle MKI is known, so the angle MIK is known, so the angle EHG is known.
In all cases, the angle EHG is thus known and the two points E and G are known, so the point H lies on the circumference of a circle known in position, as has been proved in Proposition 6 of the first section of this treatise. But the point H lies on the straight line CD which is known in position, so the point H is known, so each of the straight lines EH and GH is known in magnitude and in position. This is what we wanted to prove.
– 9 – If we have two parallel straight lines known in position, if we take two points on one of them and if from these two points we draw two straight lines which cut the second straight line, traverse it and meet one another in a point in such a way that the triangle that is formed is of known magnitude, then the straight line traversed by the two straight lines that start on the second parallel straight line is of known magnitude.
Example: Let there be two parallel straight lines AB and CD known in position; we take two arbitrary points on the straight line AB, which are the two points E and G, and from the two points E and G we draw two straight lines EIH and GKH which meet one another at the point H in such a way that the triangle EHG is known in magnitude.
I say that the straight line IK is known in magnitude.
Fig. II.2.2.9
Proof: The two points E and G are known, from them we have drawn the two straight lines EH and GH, and thus we have formed the triangle EHG which is known in magnitude; so the point H lies on a straight line known in position, parallel to the straight line EG, as has been proved in Proposition 10 of the first section of this treatise; let this straight line be the straight line LH. We draw the perpendicular ACL; it will thus be known in magnitude. Since the straight line AL is known in position and the straight line LH is known in position, accordingly the point L is known; but the point A is known, so the straight line AL is known in position and in magnitude.
Similarly, we [can] prove that the straight line LC is known in magnitude and in position; so the ratio of AL to LC is known and the ratio of EH to HI is known; the ratio of EG to IK is thus known and EG is known, so IK is known. So the straight line IK is known in magnitude. This is what we wanted to prove.
– 10 – If, from the endpoints of a straight line known in position, we draw two straight lines [that are] at two known angles and which meet one another in a point, then they are known in magnitude and in position.
Example: Let there be a straight line AB known in magnitude and in position; from its endpoints we draw the two straight lines AC and BC [that are] at two known angles, and which meet one another at the point C.
I say that the two straight lines AC and BC are known in magnitude and in position.
Fig. II.2.2.10
Proof: The straight line AB is known in position and its point A is known; we draw the straight line AC at a known angle, so the straight line AC is known in position. Similarly, the straight line BC is known in position. Each of the two straight lines AC and BC is thus known in position, so the point C is known. But the two points A and B are known, so each of the two straight lines AC and BC is known in magnitude and in position. This is what we wanted to prove.
If each of the straight lines AB, AC and BC is of known magnitude, then the ratio of each of them to one of the two others is known. We shall prove from this proof that for any triangle with known angles, the ratios of its sides, two by two,39 are known. In fact, if the angles of the triangle are known, if we take a straight line known in magnitude and in position and if from its endpoints we draw two straight lines at angles equal to two of the angles of the triangle whose angles are known, a triangle is formed whose sides are known; the ratios of its sides, two by two,40 are known, as has been proved in this proposition, and the triangle formed is similar to the triangle whose angles are known; it follows that the ratios of the sides of the triangle, two by two,41 [in the triangle] whose angles are known, are known.
– 11 – If we extend one of the sides of a triangle whose sides are known in magnitude and in position, if we take a known point on the extension and if from this point we draw a straight line that intersects the triangle and cuts off from its two sides two straight lines on the side towards its base in such a way that the ratio of one to the other is known, then the straight line is known in position.
Example: Let there be a triangle ABC whose sides are known in magnitude and in position; we extend one of its sides, which is BC; on the extension we take a point D and from the point D we draw the straight line DEG in such a way that the ratio of GC to EB is known.
I say that the straight line DEG is known in position.
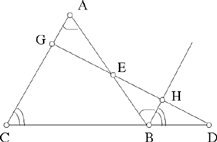
Fig. II.2.2.11
Proof: We draw the straight line BH parallel to the straight line AC; the ratio of GC to HB is thus equal to the ratio of CD to DB. But the ratio of CD to DB is known, because each of them is of known magnitude; so the ratio of GC to BH is known. But the ratio of GC to EB is known, so the ratio of EB to BH is known, since the ratios of GC, EB and HB, two by two,42 *are known ratios of three magnitudes, two by two, so the ratio of EB to BH is the known ratio of two magnitudes one to the other,*43 so the ratio of EB to BH is known and the angle EBH is known because it is equal to the angle BAC which is known, so the angle BHE is known as has been proved in the premises. So the angle BHE is known and the angle HBD is known because it is equal to the angle ACB; there then remains the angle HDB [which is] known, so the straight line DG is known in position and the straight line AC is known in position, so the point G is known and the point D is known, so the straight line DEG is known in magnitude and in position. This is what we wanted to prove.
– 12 – If we have a circle known in magnitude and in position and a straight line known in position and if we draw a straight line tangent to the circle, which ends on the straight line known in position, and which is known in magnitude, then it is known in position.
Example: The circle AB is known in magnitude and in position and the straight line DC is known in position; we draw the straight line BE tangent to the circle such that BE is known in magnitude.
I say that it is known in position.
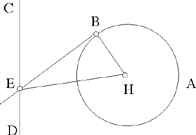
Fig. II.2.2.12
Proof: We mark off the centre of the circle, let it be H, and we join HB and HE. Since the circle is known in magnitude and in position, the straight line HB is known in magnitude. Since the straight line BE is a tangent, the angle HBE is a right angle. Since BE is known in magnitude, the ratio of the straight line HB to the straight line BE is known. Since the angle HBE is a right angle, the position of the straight line BE with respect to the straight line BH is known. Since the straight line HB is known in magnitude, and its ratio to the straight line BE is known and the angle HBE is a right angle, the angle HEB is known and the straight line HE is known in magnitude, as has been proved in the premises. Since the point H is known and the straight line HE is known in magnitude, the point E lies on the circumference of a circle known in position, as has been proved in the first proposition of this treatise. Since the point E lies on the circumference of a circle known in position and it lies on the straight line CD known in position, the point E is known. But the point H is known, so the straight line EH is known in position. But the angle HEB is known, so the straight line EB is known in position. This is what we wanted to prove.
– 13 – If we have a circle known in magnitude and in position and a straight line known in position, if from <the circumference> of the circle we draw a straight line to the straight line known in position which encloses a known angle with the latter and if the straight line we have drawn is known in magnitude, then it is known in position.
Example: Let there be a circle AB known in magnitude and in position and a straight line CD known in position; we draw the straight line BE which encloses with the straight line CD a known angle which is the angle BEC, in such a way that BE is known in magnitude.
I say that it is known in position.
Fig. II.2.2.13a
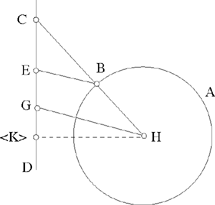
Fig. II.2.2.13b
Proof: We mark off the centre of the circle; let it be the point H. From the point H we draw a straight line HG which encloses with the straight line CD an angle equal to the known angle BEC, which is the angle HGC. We join HB; either it is parallel to CD or it meets it. If HB is parallel to the straight line CD, the area HBEG is a parallelogram. But since the point H is known and the angle HGC is known, the straight line HG is known in magnitude and in position, because if we take the point C as known, the two points H and C are known, the point G will thus lie on the circumference of a circle known in position. But it lies on the straight line CD known in position, so the point G is known and the point H is known; so the straight line HG is known in magnitude and in position. And if HB is parallel to CD, the angle GHB is known because it is equal to the known angle DGH; so the straight line HB is known in position and the circle AB is known in position, so the point B is known. But from this latter we have drawn the straight line BE at a known angle, which is the angle HBE, because it is equal to the angle HGE; so the straight line BE is known in position.
If the straight line HB meets the straight line CD – let it meet it at the point C – the ratio of HG to BE is then equal to the ratio of HC to CB. But the ratio of HG to BE is a known ratio because each of the two straight lines is known, so the ratio of HC to HB is known, the ratio of HB to BC is then known. But HB is known in magnitude, so the straight line BC is known in magnitude and, in consequence, the straight line HC is known in magnitude, so the point C lies on the circumference of a circle known in position and it lies on the straight line CD known in position; so the point C is known; and the point H is known, so the straight line HC is known in magnitude and in position. But the straight line HG is known in position, so the angle CHG is known. So the angle HBE is known and the straight line HB is known in position, so the straight line BE is known in position. This is what we wanted to prove.
– 14 – If, between two parallel straight lines known in position, we take a point from which we draw a straight line which cuts the two straight lines in such a way that the product of one of the two parts and the other is known, then the straight line is known in position.
Example: The two straight lines AB and CD are parallel and known in position; we take a point E between them and from the point E we draw the straight line EGH in such a way that the product of GE and HE is known in magnitude.
I then say that the straight line GH is known in position.
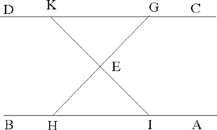
Fig. II.2.2.14
Proof: We take a point I on the straight line AB and we join EI; it will be known in magnitude and in position. We extend IE to K, so EK will be known in position. But the straight line CD is known in position, so the point K is known. But the point E is known, so the straight line EK is known in magnitude and in position, the ratio of IE to EK is then known and is equal to the ratio of HE to EG. So the ratio of HE to EG is known; in consequence, the ratio of the product of HE and EG to the square of EG is known; but the product of HE and EG is known, so the square of EG is known. So the straight line EG is known in magnitude, the point G thus lies on the circumference of a circle known in position; now it lies on the straight line CD, which is known in position; so the point G is known, so the straight line GEH is known in position. This is what we wanted to prove.
– 15 – Let there be a triangle with known sides and angles; if we draw a straight line from its vertex to its base, in such a way that the ratio of the square of the straight line [we have] drawn to the product44 of the two parts <cut off> on the base is a known ratio, then the straight line [we have] drawn is known in position.
Example: The triangle ABC has known sides and angles; we draw inside this triangle the straight line AD in such a way that the ratio of the square of AD to the product of BD and DC is a known ratio.
I say that the straight line AD is known in position.
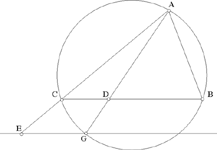
Fig. II.2.2.15
Proof: We circumscribe a circle about the triangle ABC; let the circle be ABC, and we extend AD to G; the product of AD and DG is then equal to the product of BD and DC. So the ratio of the square of AD to the product of AD and DG is known and is equal to the ratio of AD to DG. So the ratio of AD to DG is known; let it be equal to the ratio of AC to CE; so CE is known. We join EG, it will be parallel to the straight line CD and the angle AEG will be equal to the known angle ACD, so the angle AEG is known and the straight line CE is known in magnitude and in position; so the straight line EG is known in position; but the circle ABC is known in position, so the point G is known. But the point A is known, so the straight line AG is known in position and, in consequence, the straight line AD is known in position. This is what we wanted to prove.
– 16 – Let there be two straight lines which cut one another and which are known in position; if we take a point between them and we draw from this point a straight line which cuts the two straight lines known in position in such a way that the ratio of one of the two parts to the other is known, then the straight line is known in magnitude and in position.
Example: Let there be two straight lines AB and AC known in position and a given point D; from the point D we draw a straight line EDG in such a way that the ratio of ED to DG is known.
I say that the straight line EG is known in magnitude and in position.

Fig. II.2.2.16
Proof: We draw from the point D a straight line DH parallel to the straight line AB, then the angle DHG is equal to the known angle BAC and the straight line DH is thus known in position. But the straight line AC is known in position, so the point H is known and the straight line AH is known in magnitude. But the ratio of AH to HG is equal to the ratio of ED to DG which is known, so the ratio of AH to HG is known. But AH is known in magnitude, so the straight line HG is known in magnitude. But the point H is known, so the point G is known. But the point D is known, so the straight line GD known in magnitude and in position and its ratio to DE is known, so the straight line DE is known in magnitude; so the straight line GDE is known in magnitude and in position. This is what we wanted to prove.
– 17 – Let there be two straight lines which cut one another and which are known in position; if we take a point between them and we draw from this point a straight line which cuts the two straight lines known in position in such a way that the product of one of the two parts and the other is known, then the straight line is known in magnitude and in position.
Example: The two straight lines AB and AC are known in position and the point D is known; we draw the straight line DGE in such a way that the product of DE and DG is known.
I say that the straight line EG is known in magnitude and in position.
Proof: We join AD; it will be known in magnitude and in position. We put the product of AD and DH equal to the product of ED and DG which is known, then the product of AD and DH is known. But AD is known, so DH is known, as has been proved in Proposition 10 of the first section of this treatise. But the point D is known, so the point H is known. We join GH, so we shall have the ratio of AD to DE equal to the ratio of GD to DH; so the triangle DGH is similar to the triangle AED and the angle EAD is thus equal to the angle DGH; but the angle EAD is known, so the angle DGH is known. But the straight line DH is known in magnitude and in position, so the point G lies on the circumference of a circle known in position, as has been proved in Proposition 6 of the first section of this treatise.
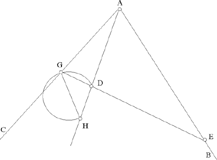
Fig II.2.2.17
But the point G lies on the straight line AC which is known in position, so the point G is known; but the point D is known, so the straight line DG is known in magnitude and in position, its product with DE is known, so the straight line DE is known in magnitude and in position and, in consequence, the straight line EDG is known in magnitude and in position. This is what we wanted to prove.
– 18 – Let there be a circle known in magnitude and in position in which we draw a chord which cuts off a known segment from it; if we then take a point on one of the two arcs, not its mid point; if from this point we draw a straight line to the other segment and if we join the two endpoints of the chord to the endpoint of the straight line with two straight lines in such a way that the ratio of the sum of these two straight lines to the first straight line is a known ratio, then the first straight line is known in magnitude and in position.
Example: Let there be the circle ABCD known in magnitude and in position; in this circle we draw the chord AC which cuts off a known segment from it; we take a point D on the arc ADC in such a way that the two arcs AD and DC are different, we draw the straight line DB and we join the two straight lines AB and CB in such a way that the ratio of the sum of the two straight lines AB and CB to the straight line DB is known.
I say that the straight line DB is known in magnitude and in position.

Fig II.2.2.18
Proof: We cut the arc ADC into two halves at the point E and we join AE, thus it will be known in magnitude and the triangle ABE will be similar to the triangle AEG, because the angle EAG is equal to the angle ABE; so the ratio of BE to EA is equal to the ratio of BA to AG which is equal to the ratio of the sum of AB and BC to AC and the ratio of BE to EA is equal to the ratio of the sum of AB and BC to AC; so the ratio of the sum of AB and BC to BE is equal to the known ratio of CA to AE, so the ratio of the sum of AB and BC to BE is known; but the ratio of the sum of AB and BC to BD is known, so the ratio of EB to BD is known. But the angle EBD is known, because the arc DE is known, so the angle EDB is known, as has been proved in the premises.45 But the straight line ED is known in magnitude and in position, so the straight line DB is known in position; but the circle ABC is known in position, so the point B is known, so the straight line DB is known in magnitude and in position. This is what we wanted to prove.
– 19 – Let there be a known angle of a triangle; from the known angle we draw a straight line which divides the known angle into two known parts, then the ratio of the two parts of the base, one to the other, is equal to the ratio of one of the sides which enclose the known angle to a straight line whose ratio to the remaining side is known.
Example: Let there be a triangle ABC whose angle BAC is known; we draw the straight line AD in such a way that one of the two angles BAD and DAC is known.46
I say that the ratio of CD to DB is known and that it is equal to the ratio of CA to a straight line whose ratio to AB is known.
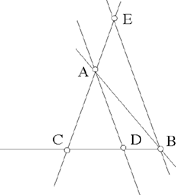
Fig II.2.2.19
Proof: We make the angle ABE equal to the known angle BAD, so the straight line BE will be parallel to the straight line AD. We draw the straight line CA to meet it; let it meet it at the point E. So the angle BEA will be equal to the known angle DAC. So each of the angles of the triangle ABE will be known, the ratios of its sides, two by two,47 are thus known, as has been proved in Proposition 10 of the second section of this treatise. So the ratio of EA to AB is known. But the ratio of CD to DB is equal to the ratio of CA to AE, so the ratio of CD to DB is equal to the ratio of CA to a straight line whose ratio to AB is known. This is what we wanted to prove.
– 20 – Let there be a triangle with known angles; from one of its angles we draw a straight line which divides its base in a known ratio, then this straight line is known in position.
Example: The triangle ABC has known angles and we draw the straight line AD in such a way that the ratio of CD to DB is known.
I say that the straight line AD is known in position.
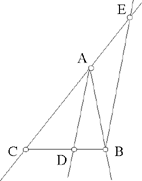
Fig II.2.2.20
Proof: We put the ratio of CA to AE equal to the ratio of CD to DB which is known. We join BE, it will be parallel to the straight line AD; so the angle BEA will be equal to the angle DAC. But since the angles of the triangle ABC are known, the ratio of CA to AB is known. But the ratio of CA to AE is known, so the ratio of BA to AE is known, because these two ratios can only be between three magnitudes, so the ratios of each of them to the two others are known. But since the ratio of BA to AE is known and the angle BAE is known, the triangle BAE has known angles, as was proved in the premises. So the angle BEA is known and it is equal to the angle DAC, so the angle DAC is known; in consequence, the straight line AD is known in position with respect to the straight line AC and to the straight line AB. So the straight line AD is known in position. This is what we wanted to prove.
– 21 – Let there be a circle known in magnitude and in position, we take two points on its circumference; if from these two points we draw two straight lines which meet one another in a point on the circumference of the circle, and if we join the two points with a straight line in such a way that the triangle that is formed is known in magnitude, then each of the two straight lines drawn from the two points is known in magnitude and in position.
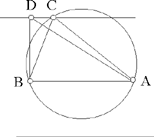
Fig II.2.2.21
Example: The circle ABC is known in magnitude and in position; on its circumference we take the two points A and B from which we draw the two straight lines AC and BC, and we join AB in such a way that the triangle ACB is known in magnitude.
I say that each of the two straight lines AC and BC is known in magnitude and in position.
Proof: From the point B we draw the straight line BD at a right angle and we construct the rectangle enclosed by the two straight lines AB and BD [to be] equal to double the triangle ACB which is known in magnitude. The straight line BD will thus be known in magnitude, because AB is known in magnitude. We join AD, so the triangle ADB will be equal to the triangle ACB. We join DC; DC will be parallel to the straight line AB. So the angle BDC is a right angle, so the straight line DC is known in position. But the circle ACB is known in position; accordingly the point C is known. But each of the two points A and B is known, so each of the straight lines AC and BC is known in magnitude and in position. This is what we wanted to prove.
– 22 – Let there be a circle known in magnitude and in position; we take two points on its circumference and we draw from these two points two straight lines which meet one another in a point on the circumference of the circle in such a way that their product with one another is known, then each of them is known in magnitude and in position.
Example: The circle ABC is known in magnitude and in position; we take the two points A and B on its circumference, from which we draw the two straight lines AC and BC in such a way that the product of AC and CB is known.
I say that each of the straight lines AC and BC is known in magnitude and in position.
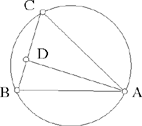
Fig II.2.2.22
Proof: We draw the perpendicular AD. Since the two points A and B are known, the segment ACB is known, so the angle ACB is known. But the angle ADC is a right angle, so the angles of the triangle ACD are known, so the ratio of CA to AD is known, and the ratio of the product of AC and CB to the product of AD and CB is known. But the product of AC and CB is known, so the product of AD and CB is known. Now the product of AD and CB is double the triangle ACB; so double the triangle ACB is known and, in consequence, the triangle ACB is known. But the two points A and B are known, so the point C is known, as has been proved in the preceding proposition; so each of the straight lines AC and BC is known in magnitude and in position. This is what we wanted to prove.
– 23 – Let there be a circle known in position and a straight line known in position; we draw a straight line which cuts the circle and which ends on the [first] straight line and is such that it is divided by the circumference of the circle in a known ratio and encloses with the [first] straight line a known angle, then this straight line is known in magnitude and in position.
Example: The circle AB is known in magnitude and in position and the straight line CD is known in position; we draw the straight line ABE in such a way that the ratio of AB to BE is known and the angle BEC is known.
I say that the straight line AB is known in magnitude and in position.

Fig II.2.2.23a
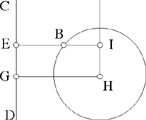
Fig II.2.2.23b
Proof: We mark off the centre of the circle, let it be the point H, and we draw the perpendicular HI; it divides AB into two halves, so the ratio of IB to BE is known. We draw HG such that the angle HGC is equal to the angle BEC which is known, then the straight line HG will be known in position, because if we make C a known point and we join HC, the point G lies on the circumference of a circle known in position, so the point G is known. But the point H is known, so the straight line HG is known in magnitude and in position. If the straight line HI is parallel to the straight line DC,48 then the straight line IE will be equal to the straight line HG, so it is known in magnitude. So the straight line BE is known in magnitude and the angle BEC is known, so the straight line BE is known in position, as has been proved in Proposition 13 of the second section of this treatise; in consequence, the straight line ABE is known in magnitude and in position.
If the straight line HI is not parallel to the straight line DC, it meets it; let it meet it at the point C. Since the angle CIE is a right angle, the angle CHG is a right angle and the straight line HG is known in magnitude and in position. But the straight line HI is known in position and the straight line CD is known in position, so the point C is known. We join CB and we extend it to K. So the ratio of HK to KG is equal to the ratio of IB to BE, which is known; the ratio of HK to KG is thus known. But the triangle HCG has known angles and from its vertex we drew the straight line CK which divided the straight line HG in a known ratio; so the straight line CK is known in position, as has been proved in Proposition 20 of the second section of this treatise. But the point K is known because it divides the known straight line HG in a known ratio. So from the point K we have drawn a straight line KC known in position, which cuts the known circle AB in a point B; so the point B is known. So we have drawn the straight line BE at a known angle; in consequence, BE is known in position since the point E lies on the circumference of a circle known in position; the point E is thus known. But the point B is known, so the straight line BE is known in magnitude and in position and its ratio to BA is known; so the straight line ABE is known in magnitude and in position. This is what we wanted to prove.
– 24 – Let there be two circles known in magnitude and in position; we draw a straight line tangent to the two circles; it is known in magnitude and in position.
Example: The two circles AB and CD are known in magnitude and in position; we draw a straight line AD which touches them.
I say that the straight line AD is known in magnitude and in position.
Proof: We mark off the two centres, let them be E and G, and we join EG. The circles AB and CD are either equal or different.
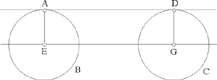
Fig II.2.2.24a
Let them first be equal, the straight line AD touches the two circles either in two similar directions as in the first figure49 or in two different directions as in the second figure. If the contact is as in the first figure, then we join EA and GD, so the two angles at the points A and D are right angles, so the two straight lines EA and GD are parallel and they are equal. Then the straight line AD is equal to the straight line EG and is parallel to it, so the angle GEA is a right angle, so the straight line EA is known in position; now, it is known in magnitude, so the point A is known. But the angle EAD is a right angle, so the straight line AD is known in position and it is equal to the straight line EG which is known in magnitude; so the straight line AD is known in magnitude and in position.

Fig II.2.2.24b
If the two circles AB and CD are different, then the two straight lines GD and EA are different50 and they are parallel, so the straight line DA meets the straight line GE in the direction towards the smaller circle – let it be the circle AB; let the straight lines meet at the point H. So the ratio of GH to HE is equal to the ratio of GD to EA. But the ratio of GD to EA is known, because each of these straight lines is known, so the ratio of GH to HE is known, so the straight line EH is known, the point H is consequently known, and the straight line HG is known in magnitude and in position. But the angle HDG is a right angle, so the point D lies on the circumference of a circle known in position, whose diameter is HG, and it [the point D] lies on the circumference of the circle CD known in position. So the point D is known. But the point H is known, so the straight line HD is known in magnitude and in position and the ratio of HD to DA is known, so the straight line AD is known in magnitude and in position. This is what we wanted to prove.
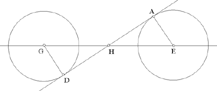
Fig II.2.2.24c
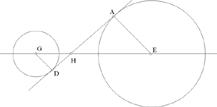
Fig II.2.2.24d
If the contact is in two different directions, as in this figure,51 we mark off the two centres; let them be E and G, and we join EG; so it will be known in magnitude and in position. We join EA and GD, the two angles at the two points A and D are then right angles and are in two different directions with respect to the straight line EG; the two points A and D will then lie to either side of the straight line EG. So the straight line AD cuts the straight line EG; let it cut it at the point H; so the two straight lines EA and GD will be parallel and the two triangles EAH and HDG are similar. So the ratio of EH to HG is equal to the ratio of EA to GD which is known, because each of the two straight lines EA and GD is known in magnitude. So the ratio of EH to HG is known and the straight line EG is known in magnitude, each of the two straight lines EH and HG is known in magnitude and the angle EAH is a right angle. So the point A lies on the circumference of a circle known in position whose diameter is EH and it is the circumference of the circle AB, so the point A is known. Similarly, we [can] prove that the point D is known.
So the straight line AD is known in magnitude and in position, whether the two circles are equal or unequal. This is what we wanted to prove.
The notions we have set out are notions that are of great use in solving geometrical problems. They are notions that none of our predecessors has set out. What we have set out regarding these notions is sufficient for our purpose, and here we end this treatise.
<The treatise on the> Knowns is completed.
Praise be to God, Lord of the worlds.
_______________
1 R. Rashed, Les Mathématiques infinitésimales du IXe au XIe siècle, vol. II: Ibn al-Haytham, London, 1993; English trans. Ibn al-Haytham and Analytical Mathematics. A History of Arabic Sciences and Mathematics, vol. 2, Culture and Civilization in the Middle East, London, 2012.
2 R. Rashed, Les Mathématiques infinitésimales du IXe au XIe siècle, vol. I: Fondateurs et commentateurs: Banū Mūsā, Thābit ibn Qurra, Ibn Sinān, al-Khāzin, al-Qūhī, Ibn al-Samḥ, Ibn Hūd, London, 1996; English trans. Founding Figures and Commentators in Arabic Mathematics, A History of Arabic Sciences and Mathematics, vol. 1, Culture and Civilization in the Middle East, London, 2012.
3 On this concept in Hobbes, see Opera philosophica quae latine scripsit omnia…, ed. Gulielmi Molesworth; especially his Elementorum philosophiae sectio prima de corpore, vol. II, London, 1839, pp. 98–9 and his Examinatio et emendatio mathematicae hodiernae, vol. IV, London, 1865, p. 76. See also the commentary by Martial Gueroult, as well as the similarities he establishes between the conception in Hobbes and, following him, that of Spinoza; Martial Gueroult, Spinoza, vol. II: L’âme, Paris, 1974, pp. 480–7.
5 See mss Cairo, Dār al-Kutub, 40, fols 206v–208r; Istanbul, Aya Sofya 4830, fols 171r–173r and also 4832, fols 123v–125r.
7 Piero della Francesca (c. 1412–1492) gives a version of this theorem in his treatise on perspective, De prospectiva pingendi, Book 1, Section 8. See J. V. Field, ‘When is a proof not a proof’ Some reflections on Piero della Francesca and Guidobaldo del Monte’, in R. Sinisgalli (ed.), La Prospettiva: Fondamenti teorici ed esperienze figurative dall’Antichità al mondo moderno, Florence, 1998, pp. 120–32, figs pp. 373–5; and J. V. Field, Piero della Francesca: A Mathematician’s Art, New Haven and London, 2005.
8 See Girard Desargues, Exemple de l’une des manieres universelles du S. G. D. L. touchant la pratique de la perspective sans emploier aucun tiers point, de distance ni d’autre nature, qui soit hors du champ de l’ouvrage, Paris, 1636, pp. 11–12; translation J. V. Field and J. J. Gray, The Geometrical Work of Girard Desargues, London and New York, 1987, pp. 158–60 (French text, pp. 200–1).
1 Lit.: parts.
2 We use this term to translate the Arabic term naṣba that is reguarly used to translate the Greek θέσιϛ.
3 See Aristotle, Physics, IV, chap. XI, 219b 7–10.
4 That is measured by the smallest.
5 Lit.: if it surrounds perfectly.
6 That is extension and shortening.
7 Compare Euclid, Data 6.
8 See Les Mathématiques infinitésimales, vol. III, chap. IV.
9 See the commentary in our discussion of the position of a line with respect to fixed points, p. 329.
10 Ibn al-Haytham does not indicate explicitly here whether we are concerned with a plane surface.
11 Idem.
12 Measure (miqyās): a unit chosen for measuring weight.
13 raṭl = 144 dirham = 450 gr.; manā = 2 raṭl = 2,130 dirham = 812,5 gr.; mithqāl = 4,464 gr.; dirham = 3,125 gr. See Walther Hinz, Islamische Masse und Gewichte umgerechnet ins metrische System, Leiden, 1955.
14 In the plural in the original.
15 The sidereal day, whose duration is that of a revolution of the celestial sphere, is taken as the unit of time.
16 In Euclid, Data 51, the triangle CBD is said to be ‘given in species’.
17 So the point G is known in position.
18 See commentary, pp. 310–12.
19 Ibn al-Haytham insists on the fact that the position of D is the same irrespective of the point C that is proposed as a solution of the problem.
20 Two straight lines parallel to AB provide a solution to the problem.
21 Euclid, Elements, I.39.
22 If a parallel to the line of centres cuts the circles, it cuts each of them in two points. With each of the two points of the first circle we can associate one or other of the two points of the second, and consequently two segments. Ibn al-Haytham makes it precise how to choose which points to associate.
23 The following gloss is found in the margin of manuscript [B]: ‘Known from the proof of Proposition 7 of Book VI of the Elements’.
24 The following gloss is found in the margin of manuscript [B]: ‘the two angles at D are equal, so the two triangles are similar from the Proof 6 of <Book> VI of the Elements, so the angle A is equal to the angle B’.
25 The power of a point inside a circle (Euclid, Elements, III.35).
26 The text seems to assume that the given points lie outside the circle.
27 The product of the lengths of two segments is the area of the rectangle ‘enclosed’ by the two segments.
28 Lit.: surfaces.
29 From the comment made at the end of Proposition 18.
30 The points H and I do not need to lie on the same semicircle of diameter ED. The argument remains valid.
31 Lit.: surfaces (suṭūḥ).
32 Lit.: surfaces.
33 The following gloss appears in the margin in manuscript [B]: ‘But, by Proof 7 of <Book> II of the Elements’.
34 Euclid, Elements, III.35.
35 Euclid, Definitions 7 and 8 of the Data.
36 Euclid, Data, 88 and 89.
37 Here ‘alternate’ is the translation of mutabādilayn, which refers to the two segments DG and CH which lie on either side of HG.
38 We need to assume that CB and DE are parallel segments and in contrary senses so that CH and DG will be so too. We may note that the points B and E play no part in what follows.
39 Lit.: the ones to the others.
40 Lit.: the ones to the others.
41 Lit.: the ones to the others.
42 Lit.: the ones to the others.
43 *...* In the text, we may read: ‘are the ratios of three known magnitudes, two by two, then the ratio of EB to BH is the ratio of two known magnitudes one to the other’.
44 Lit.: surface.
45 The comment made in the premises (p. 384) applies to a triangle in which we know two sides and the angle between them: so we necessarily know the ratio of these two sides. But here the result: ‘so the angle EDB is known’, derives from the fact that the triangle BDE is defined up to similarity (Euclid, Data, 51); so its other angles are known (Euclid, Elements, IV.6).
46 If one of these angles is known, the other is also known, because the angle BAC is known and AD is inside that angle.
47 Lit.: one to the other.
48 This happens if the known angle BEC is a right angle.
49 Ibn al-Haytham distinguishes between two cases for equal circles: an exterior common tangent (Fig. II.2.2.24a) and an interior common tangent (Fig. II.2.2.24c).
50 See Fig. II.2.2.24b.
51 See Figs II.2.2.24c and Figs II.2.2.24d