APPENDIX:

THE ARS INVENIENDI: THĀBIT IBN QURRA AND AL-SIJZĪ

 

 

 

It is because of Ibn Sinān’s research on analysis and synthesis in geometry, but also in opposition to it, that Ibn al-Haytham conceived of the art of analysis. It is also, as we have indicated, following on from the ars inveniendi proposed by al-Sijzī, and in opposition to it, that Ibn al-Haytham developed this art. We have seen that Ibn al-Haytham’s novel conception can be understood in the light of new demands in geometry.

But Ibn Sinān, and his successor al-Sijzī, both started out from a short essay by Thābit ibn Qurra. Thus, a historical picture emerges, or at least the parts of it that have survived the vicissitudes of time; it suggests that if we wish to get a clearer idea of where Ibn al-Haytham’s contribution fits in, we need to make a careful examination of the writings of Thabit ibn Qurra, Ibn Sinān and al-Sijzī. Studies of Ibn Sinān’s book and of his other works have already been carried out.¹ So there remain the essay by Thābit ibn Qurra and the treatise by al-Sijzī. It is to these last two works that the following pages will be dedicated, with the purpose of understanding how a new area of study emerged and how it developed before Ibn al-Haytham, so that we can take the measure of the step forward that he made.

I. THĀBIT IBN QURRA: AXIOMATIC METHOD AND INVENTION

We might say that in the beginning there was the translation of Euclid’s Elements. In the eyes of the mathematicians of the ninth century, as in those of their successors, this book was a model of organisation, but it rather rapidly became the source of a multitude of topics for reflection. There is a whole book to be written on this double part the Elements played in Arabic mathematics. Let us remind ourselves that hardly had the Elements been translated before they became the object of numerous commentaries that tried to describe the author’s intentions, to discuss the organisation of the work, to correct some of the propositions and to rewrite some of the proofs. This is how it happens that in the mid ninth century the famous philosopher al-Kindī wrote two books whose titles are particularly eloquent: On the Rectification of the Book by Euclid and On the Intentions of the Book by Euclid. Others, such as al-Jawharī, wrote commentaries on Euclid’s book, and were interested in some of the difficulties it presented, notably the question of the fifth postulate. Others again, such as al-Māhānī, wanted to replace proofs by reductio ad absurdum with direct proofs. We could indeed cite many more authors and book titles that bear witness to the central position occupied by the Elements, not only at the heart of mathematical activity, but also, more generally, in the intellectual life of the time. Mathematicians who were geometers, but also some who were algebraists, philosophers and intellectuals, quickly began to take an interest in the treatise, in its organisation, its order and its style. Among the intellectuals, we find a state official, a member of a dynasty of great administrators of the Empire: Ibn Wahb.² He was, no doubt, an alert reader of the Elements, and as such he raises the major question regarding the axiomatic method and discovery. In Ibn Wahb’s terms, the question takes the form: in his order of exposition of the propositions, Euclid has regard only to the requirements of proof, so he brings forward the position of certain propositions while he puts back others, irrespective of their significance. So, in the Elements, Euclid opted simply for syntactic order, ignoring semantics. This order, Ibn Wahb admits, is suitable for training an apprentice in geometry; but when it is a matter of carrying it through into research, what one has learned shows itself to be inadequate: we need another order, that of discovery. This question formulated by Ibn Wahb in the ninth century is brought up again centuries later by Petrus Ramus,³ Antoine Arnauld and Pierre Nicole,⁴ among many others.

But the fact that this topic is a perennial one is an indication of the intimate links it has with the actual style of the Elements, that is the axiomatic method (in Euclid’s sense, of course) that governs the work. The Elements, a model of organisation for mathematicians, not only in the ninth century but for more than two millennia, is also a model in the sense of being something to be imitated as well as representing an ideal. This double validity as establishing a norm derives from the application of the axiomatic method. But, in the context of Euclid’s work, this application is itself possible only insofar as the geometrical object – the figure – is the object of knowledge that is subordinate to hypotheses and to construction processes that take place in the imagination. The question of discovery might thus, in such a context, seem to be a meta-geometrical one. Discoveries would be at most a matter of circumstance, for the most part resulting from applying the axiomatic method to verifying a proof or to assessing the limits of its validity.

In any case, Ibn Wahb is writing to Ibn Qurra to ask him to devise a method, different from the axiomatic method, that is capable of meeting the requirements for discovery. So the intention is clear: to provide the reader, presumed to be familiar with the axiomatic method, with a second method that will allow him to discover new propositions and to carry out new constructions. It seems that Ibn Wahb’s decision was not actuated solely by Thābit ibn Qurra’s eminence as a geometer; Thābit also had first hand knowledge of the Elements because he had made a revised version of the third Arabic translation of the work, the translation by Isḥāq ibn Ḥunayn.

By way of replying to Ibn Wahb, Thābit ibn Qurra composed a short text – which is translated here.⁵ We may note, briefly, that this short work has a simple structure. In the first section, which is introductory, the author takes up the question of the axiomatic style of exposition employed in the Elements and that of the order which should be followed for discovery, and presents a classification of geometrical concepts. The second part, consisting of examples that provide illustrations for the first part, might thus be said to supply ‘exercises in invention’.

The first part of the essay opens with two interesting observations. Ibn Qurra’s immediate purpose is to think out the rules for a method that will lead to the discovery of new propositions and constructions, this for a mathematician who has a grasp of the axiomatic method and an adequate knowledge of mathematics. But Ibn Qurra does not stop there: the method must be applicable in ‘any apodeictic science’ (fī kull ‘ilm burhānī). So it is obvious that we are looking at a pragmatic approach. Moreover, it requires us to proceed by classifying concepts so as to be able to distinguish between different species, in order to group them together later into species and thus bear them all in mind when required. Now, to identify the different species, Ibn Qurra begins by distinguishing three kinds of geometrical investigation: geometrical constructions making use of instruments – for example using ruler and compasses for constructing an equilateral triangle; propositions referring to an unknown magnitude or state – for example to determine the area of a triangle whose sides are known, or to find a perfect number; and finally general statements concerning the nature of the object – or concerning a specific property of the object – for example, when the object is a triangle: the sum of its angles is equal to two right angles. Ibn Qurra points out that the first type requires a knowledge of the two others, but the converse is not true.

The first rule of the method is more or less self-evident: it consists of beginning by finding out which type or which grouping the concept we are looking for belongs to. But each of these three groupings includes principles and results established by means of these principles, together with some supplementary ones. By principle (aṣl), Ibn Qurra means something in the tradition of the Posterior Analytics (I, 10). It is, as he says, a matter of ‘common notions’, of postulates and definitions. For the latter, these are only the definitions that refer to the essence of the concept we seek. Once the mathematician has distinguished, for each of the preceding types, between axioms, postulates and definitions on the one hand and propositions on the other, he is in a position to ‘bring to mind’ all the ideas that are necessary for forming a conception of the required object: this is the second rule for the method.

The third rule, which Ibn Qurra does not identify by name, is analysis: to start from the necessary conditions for the required object, then work from the necessary conditions for these conditions, and so on. To illustrate this analysis, he examines three constructions in which, in each example, we see how to carry out the analysis. This choice of examples is influenced by a somewhat didactic purpose, as well as a particular interest in the form of analysis that is called ‘problematic’ in geometry. We may, however, note that by singling out the particular class of propositions that deal with determining a magnitude or a number, Ibn Qurra distances himself from the classic opposition between ‘theoretical analysis’ and ‘problematic analysis’.

As the first text on the method of discovery, the context of Ibn Qurra’s short essay sheds light on the emergence of the topic of discovery in mathematics which, in the work of his successors, will move away from its origins and will acquire a quite different scope. But the importance of this essay does not relate only to the fact that it contains the first discussion of this topic; it was also responsible for encouraging its readers to carry out further research in the light of the new mathematical insights it provided.

II. AL-SIJZĪ: THE IDEA OF AN ARS INVENIENDI

1. Introduction

To establish ‘a method intended for students, which includes all that is necessary for the solution of problems in geometry’.⁶ This is the expression used by Ibrāhīm ibn Sinān (296/909–335/946) when committing himself to fulfilling his grandfather’s promise, Thābit ibn Qurra. But the mathematical context has been in continual change since his time, following the path already mapped out by Thābit’s teachers, the Banū Mūsā. The effect of new research in the geometry of measurement and in the geometry of position and of shape, the emergence of a new mathesis from the impact of algebra, all these had, as Ibn Sinān himself tells us, spurred mathematicians into returning to the traditional question of analysis and synthesis, and, more generally, that of the philosophy of mathematics. As we have seen, Ibn Sinān’s intervention in this matter proved to be crucial: in the first known substantial treatment of analysis and synthesis, he works out a philosophical logic that allows him to combine an ars inveniendi with an ars demonstrandi.⁷ His contribution was soon extended to provide a proper theory of proof, in which questions of logic take centre stage: the reversibility of implications, auxiliary constructions, classification of propositions according to the number of variables and according to the number of conditions.

Ibn Sinān’s successors repeatedly took up the question of analysis and synthesis, either in the course of their technical mathematical works, or, following Ibn Sinan’s example, though from a different point of view, dedicating complete treatises to it. Such is the case for Ibn Sahl, al-Qūhī and Ibn al-Haytham, among many others. Nor was this line of research neglected by philosophers who took an interest in mathematics: al-Fārābī discusses it and Muḥammad ibn al-Haytham also pays attention to it. Which is to say that, at least from the mid tenth century onwards, we see the development of a new field of research in the philosophical logic of mathematics, or more generally in the philosophy of mathematics, a meeting place for professional mathematicians and philosophers of mathematics – a field of which ‘analysis and synthesis’, in their different forms, makes up the core. Now it is in exactly this domain that we come across al-Sijzī, and this is above all the context in which we must situate the book by him that concerns us here: To Smooth the Paths for Determining Geometrical Propositions.

Al-Sijzī lived almost a generation after Ibn Sinān; he knew the latter’s writings well, in particular the treatise on analysis and synthesis, which he had himself transcribed.⁸ He was also familiar with the writings of Thābit ibn Qurra,⁹ notably with Thābit’s short work on methods for determining geometrical problems, which he had addressed to Ibn Wahb: one of the manuscripts of this short work was indeed written out by al-Sijzī.¹⁰ So Thābit ibn Qurra and Ibrāhīm ibn Sinān provide us with the two clearest points of reference for assessing the place of al-Sijzī’s contribution.

Al-Sijzī’s text is much more fully developed than that of Ibn Qurra and its purpose is different. It remains true, of course, that they have in common elements of their vocabulary, their intention and their organisation, which makes it reasonable to suggest these books were the first source of al-Sijzī’s inspiration. His own book is also made up of two parts: a first part that is introductory, followed by a second that is devoted to examples. In addition to this similarity in form, we have another similarity: like Ibn Qurra, al-Sijzī deals only with geometry, to the exclusion of all other branches of mathematics – and in fact both of them set up geometry as the model for any apodeictic science. Finally, the intention that animated both of them was at once didactic and logical. This intention is, of course, not absent in Ibn Sinān, but in his work the didactic element took second place to the task of developing a theory of proof. In al-Sijzī’s case, and in some sense thanks to his having read Ibn Sinān, this project is transformed into a true ars inveniendi, something that did not occur in the work of Ibn Qurra. Here we need to look at the direction al-Sijzī is taking and the novelty of what he proposes to do. To make this clear, we must comment on his treatise in detail.

2. A propaedeutic to the ars inveniendi

The first part of al-Sijzī’s treatise opens with a propaedeutic to research into the methods that will form the main body of the ars inveniendi. This propaedeutic is itself made up of two short parts, in accordance with the author’s purposes for the work as a whole, which are both didactic and logical. Al-Sijzī starts with a theory of mathematical discovery, a sketchy one, certainly, but nevertheless one that contains the genesis of the psychology of mind (to use a later term) that is connected with the ars inveniendi. According to this theory, invention in geometry is the offspring of a ‘natural power’, of an innate gift and arduous training in principles as well as in methods and theorems. This latter is more important than having a gift, in the sense that, when the natural power is not at its height, it may happen that training will serve to remedy this relative weakness. However, the reverse is not true, since a natural power without training leads nowhere. Without training there is no invention. Under such conditions, there is room for a discipline to guide the geometer from training to discovery: this discipline is the ars inveniendi. That is to say that the need for this art is built into the didactic side of the discipline. So we are seeing a first manifestation of its being necessary.

The second part of the propaedeutic is concerned with the preliminary procedures for any method, the operations one must carry out before choosing one method or another. In taking this approach, al-Sijzī in fact starts out from the conception of training in geometry. As he conceives it, the part training plays in invention makes it necessary for the beginner in geometry to start by learning the theorems (al-qawānīn) proved in the Elements. This very natural demand nevertheless raises some questions, which al-Sijzī considers. It is, moreover, in connection with these that he touches on certain logico-philosophical problems some of which he will return to in a later text.¹¹ The first relates to logical ordering of proofs, the order adopted by Euclid in the exposition in the Elements. If we allow this same order for simple training, which al-Sijzī does, following the example of Thābit ibn Qurra, can we accept it as an ordering in training for research, that is training that leads to discovery? In either case, if we adopt a deductive system like that of Euclid, we should begin with the axioms (the common notions) rather than with theorems. Surely it is indeed more natural and more consistent to start with what is most basic. The more so because the theorems, as such, form part of what we are trying to establish. So the risk is that, if we start with the theorems, we may take the end for the means. To avoid this, it might be preferable to employ methods that begin from the axioms alone so as to determine the objects of research. In this treatise, once the question of the ordering appropriate for training in preparation for discovery has been raised, and once the didactic problem has been reduced to the logico-philosophical problem of the relations between axioms and theorems, al-Sijzī dismisses the possibility of following the order of proof, and recommends starting with the theorems. There are three reasons for this, with distinct origins. First of all, starting out with the axioms alone would lengthen the journey towards discovery to an unreasonable degree. In the second place, if we limit ourselves to only the axioms, it will be difficult, without theorems, to proceed to discovery. Finally, in his system, Euclid combined axioms and theorems in a balanced manner, which allows us to start out from the theorems he established. These arguments, which are summarily listed by al-Sijzī, essentially belong to programmatic and pragmatic logic. The problem itself is, as we have seen, much more significant, since it concerns the status of the theorem in a deductive system, when we are considering training designed to lead on to research and invention. As regards al-Sijzī’s preoccupations, this problem seems to lie in the background, sufficiently present for him to come back to it, but seen in a different light.

Al-Sijzī notes that, in a deductive system, a theorem is at once a lemma and a consequence. He describes this state as mushtabah, that is as ambiguous. There is also an additional difficulty: the chain of implications can be unlimited. So the question is to find how, under these conditions, there can be training in regard to theorems; it might perhaps be better to confine ourselves to axioms. Now it is at this very moment that al-Sijzī refers ‘to the equilibrium’ in Euclid’s exposition.

In this treatise, al-Sijzī gives only very brief answers to the questions that he himself raises. He refers to a fear of excessive length, to the difficulty and the equilibrium of Euclid’s exposition, all of which is no doubt significant, nevertheless leaves the discussion open. Further, he permits himself to relaunch the debate, since he returns to the question of axioms and theorems, more fully and in greater depth, in a later treatise, where he mentions the one we are concerned with here. This later treatise is his work on the asymptote,¹² where with the help of the pair ‘conceive – prove’ he works out a classification for mathematical propositions thus distinguishing and illuminating the connections between axioms and theorems. He distinguishes five classes, in order: (1) Propositions that can be conceived directly from axioms; (2) Propositions that can be conceived before we proceed to prove them, that is ones that are close to the axioms; (3) Propositions that can be conceived when we form the idea of how to prove them; (4) Propositions that can be conceived only once they have been proved; (5) Propositions that are difficult to conceive even after they have been proved.¹³ Thus, in returning to his own work, al-Sijzī shows us what he was interested in when he was writing his first treatise.

Thanks to this training, from the outset the geometer already has a store of theorems and lemmas, knows how to proceed, and is ready to embark upon research. The important question is to know how to put that readiness into action in such a way that it leads to discoveries. But, before deciding on a specific method, it is necessary to master a mass of faculties and knowledge that underlies all the methods. This underlying mass also includes, without distinction, many elements that are psychological and logico-philosophical.

Once he has recognised what kind of object he requires, as well its specific properties, the geometer must first of all bring to mind the lemmas and theorems that apply to that kind of object, or to a kind of object connected with it. This effort of imagining the lemmas and theorems is necessary for both the classes of object that together constitute geometry: constructions and propositions. Al-Sijzī accordingly proposes some rules to guide us in this search for lemmas and theorems. To establish these rules, he begins by distinguishing two classes of propositions. The first class consists of the propositions that are in themselves possible but which, because of a lack of preliminary results (lemmas), it is impossible for us to prove. This is the class to which the squaring of the circle belongs. In other words, as al-Sijzī will say later, for us these propositions are conceivable but not demonstrable. In the other class, there are propositions that can be proved, and in this case we can proceed according to the following rules:

1. For any proposition we think we can establish from a particular lemma, we can try to establish it by lemmas of the same class – that is ones that, at least, apply to the same objects – or to some of them.

2. Any proposition we think we can establish from a lemma, or from lemmas, we can establish from lemmas of that lemma, or of these lemmas.

3. Any proposition that we cannot establish from a series of successive lemmas could be established from many compound lemmas. Al-Sijzī later examines an example of this.

These rules are applicable to all the methods that the geometer should adopt, and around which al-Sijzī’s treatise is organised. However, the application of one or other of them is by no means automatic; it in fact demands preliminary work which involves the faculties of the intelligence. This is, indeed, the way that these faculties are introduced into the ars inveniendi. Now there are two characteristics that distinguish these faculties in al-Sijzī’s work: they belong to the intellect, and intelligence itself is not natural intelligence, but a power exercised in the art of geometry. All its faculties are, moreover, as it were formed by this art. Al-Sijzī lists them, and presents them at the head of the list of preliminary procedures. They are skill, intelligence informed by practice, and the faculty for calling to mind, instantly and simultaneously, the necessary conditions for the proposition we wish to establish. These three faculties are concomitants in al-Sijzī’s actual presentation.

Next in this preparation for applying the rules and methods comes learning all the theorems and lemmas necessary for the object we require, and to learn them exhaustively. The third demand requires that these truths already established become things counted among the intellectual faculties. At this stage, alongside the skill that comes directly from educated intelligence, al-Sijzī mentions, both intuition and cunning. By ‘intuition’, al-Sijzī here once again means intuition informed by the art. No doubt what we have is an act of thought which immediately grasps the object of knowledge, an act that does not require the intermediate deductions. Cunning, or the faculty for finding ingenious procedures, is itself also obviously the fruit of informed intelligence, of long practice and intense application.

These first three preparatory rules call upon all these considerations regarding intellectual faculties, thus introducing these faculties into the ars inveniendi. Exactly like his successors many years later, al-Sijzī obviously could not avoid these elements of a psychology of reason, the logic being what it was. The fourth and final rule is logical in nature: we are concerned with classifying theorems and lemmas according to what they have in common, their differences and their specific properties, that is the properties of the objects they apply to.

Once this propaedeutic work has been done, the geometer, knowing the rules that apply to all methods, is now in a position to make use of one of the following three methods: (1) the method of transformation; (2) ‘analysis and synthesis’; (3) ingenious procedures.

These methods are neither of the same nature, nor do they have the same power, but they can be combined. We may note that in this part, as in the remainder of the treatise, al-Sijzī comes up against a difficulty part of which we have already pointed out, and one which he could not surmount. He in fact formulates the logical problems in a mixed language, that of traditional modal logic and that of the theory of proportions; thus he speaks of necessary and impossible propositions. On the other hand, as we shall see later, when he speaks of the logical implications among mathematical propositions, he compares them to ratios in the theory of proportions. This is not a matter of criticising al-Sijzī for not knowing the work of George Boole, or of regretting that he did not think of using the language of algebra, but merely a matter of noting that his writing has an irremovable ambiguity, whose cause is to be found in the mixed form of expression. It seems that a psychology of reason being involved to form the basis of the ars inveniendi results in the absence of the logical language appropriate to discussion of the art of analysis. Later, Ibn al-Haytham would invent a new geometrical discipline, with the intention, among other things, of meeting this difficulty: the knowns.

3. The methods of the ars inveniendi and their applications

As we have seen, al-Sijzī proposes three methods. The four methods that he presents before them are recommended as propaedeutic to these final three: transformation, analysis and synthesis and ingenious procedures. We observe, however, that he presents all seven as on the same level, as if all of them carried the same weight. Further, his account of them is very brief, not to say incomplete. Transformation is merely named, ‘analysis and synthesis’ are cited in ordinary, that is standard, terms; as for the ingenious procedures, they appear in connection with a rather vague reference to Hero of Alexandria. All the same, al-Sijzī gives a clear explanation of his reason for this choice of exposition, distinguishing between two possible styles for presenting this material, styles which for him are complementary: one is general, indicative and not demonstrative; the second consists of examining examples and giving detailed proofs. It is in the course of carrying out this second process that al-Sijzī presents these methods, as it were in action. All the same, this does not completely explain why his earlier account was short and somewhat allusive.

If we examine al-Sijzī’s text more closely, we see that there is in fact only one method that is truly worthy of its title: ‘analysis and synthesis’. In this respect, al-Sijzī belongs to the tradition established by his predecessors and his contemporaries; but the task he has deliberately set himself is that of elaborating on this principal method by adding a group of special procedures, mathematical procedures, theoretical and practical. These special methods are intended to increase the power of the principal method in the making of discoveries and thus to make its application easier. Thus, transformation is a mathematical procedure that is theoretical in nature, ingenious procedures are of a technical and practical nature, and all of them are means of bringing analysis to its conclusion and making it easier to carry out. It is the combining special methods with the principal method, for the purpose we have just described, that marks a break with tradition and is due specifically to al-Sijzī. Let us explain.

As we have said, al-Sijzī’s purpose is to extend the power of analysis and synthesis by introducing theoretical and technical procedures. This is the approach he chose for instituting the ars inveniendi. It is in this context that he fully grasped the importance of point-to-point transformations in geometry, which had been used since al-Ḥasan ibn Mūsā,¹⁴ by giving them a name: al-naql.¹⁵ It is with this same aim that he develops various procedures that spring from the idea of one element varying while all the others remain fixed. Al-Sijzī in fact notices that there are two ways to investigate the properties of geometrical objects. The first consists of looking for what remains fixed when all the other properties vary – an investigation carried out by imagination based on the senses. In following the second approach, we take the required property as given and look for the lemmas that are necessary for it. The first approach, that of variation, is one that al-Sijzī not only finds interesting, but also one he goes on to employ in its various forms. The most obvious form is that where the varia include an element of a figure, in which all the other elements remain constant. It is, so to speak, the paradigmatic form of the procedure. There is also the variation of constructions using a fixed figure; then there is the variation of methods for establishing a fixed property, and, finally, the variation of lemmas for a fixed proposition. As for the second approach, it is none other than that of analysis, as a theoretical procedure. In fact, for al-Sijzī, analysis in turn can be looked at in two, inseparable, ways, but not always in an explicit way: a method of discovery on a par with other special methods, and in this sense it is a mathematical procedure; that is, it is the method of discovery, supported by all other procedures, such as transformation, ingenious procedures, variation, and so on. The boundaries that separate the two aspects of analysis are obviously not set solidly in place once and for all, but vary according to the complexity of what we seek to discover: for instance the number of lemmas, or the number of auxiliary constructions. Moreover, in the matter of appreciating the degree of this complexity, al-Sijzī calls upon not only the geometer’s skill and intelligence, but also his intuition. From this point onwards, intuition continues to play a central role, either alone, or in combination with reasoning, to assess the degree of difficulty and judge what will be the shortest way of finding the necessary lemmas.

Like his predecessors from Pappus and Proclus onwards, al-Sijzī distinguishes between two applications of analysis, depending on whether we have geometrical constructions or propositions that concern geometrical properties. Behind his brief explanations, we may recognise echoes of Ibn Sinan. Al-Sijzī does in fact point out, in passing, some problems raised and discussed in full by Ibn Sinān: the number of conditions or of lemmas; the number of solutions. But he passes over these logical problems, and does not discuss them. This hint confirms his intentions and also reflects the deliberate choice of a style of exposition that privileges explanation through, and with the help of, studies of examples of the methods, of combinations and applications of them. All we now need to do is to follow al-Sijzī in his choice.

3.1. Analysis and point-to-point transformation

The first example al-Sijzī discusses concerns a geometrical construction, in which he proceeds by analysis. He shows how employing point-topoint transformations makes the method simpler and discovery easier. So with the method of analysis he combines the geometrical procedure of transformation, obviously with the aim of increasing the power of the analysis.

It is, al-Sijzī writes, a matter of constructing a figure:

How to find two straight lines proportional to two given straight lines one of which is a tangent to a given circle and the other meets the circle and is such that, if it is drawn inside the circle, it passes through its centre?¹⁶

Let us proceed by analysis and let us suppose that the figure has been constructed. So we must find the necessary lemmas.

 

The problem is: given a circle CED with centre H and diameter CD, and a ratio 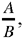to construct EG, a tangent to the circle, in such a way that the ratio 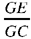is equal to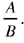

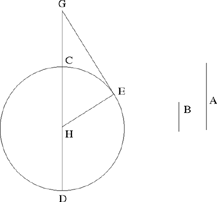
Fig. 1

The difficulty in this construction, pointed out by al-Sijzī himself, lies in the fact that the angle EGH of the triangle is unknown. To determine this angle, we construct an auxiliary figure IKMN similar to the figure GEHC. In other words, we try to find a triangle IKM with a right angle at K and a point N on the hypotenuse such that MN = MK and satisfying

 

 

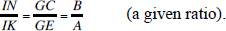
Since the straight line IK is known in position and magnitude, and B and A are two known magnitudes, the straight line IN is of known magnitude. So the point N lies on a circle with centre I and radius IN. The first figure in the manuscript illustrates this situation.

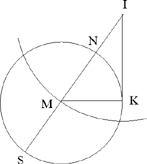
Fig. 2

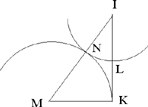
Fig. 3

To construct the point N, we choose a point L on the circle and we rotate the straight line IL about I until the distance from N, the new position of L, to M, the point of intersection of the extended line IN with KM, the perpendicular to IK at K, is equal to KM. The point L is then at the point N and we have NM = KM.

If we extend IN to the point S such that MS = MN = MK, we have IS · IN= IK², so IS is of known magnitude, as is 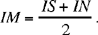So the point M lies at the intersection of the circle with centre I and radius IM and the perpendicular KM; from which we find the points N and S.

We take the point N on IM such that 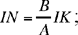it only remains to construct the triangle GEH similar to IKM with a ratio of similarity equal to 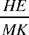(where HE is the radius of the given circle).

 

Thus, in essence the method consists of displacing the problem by supposing the segment IK is given and seeking to find the circle NKS that touches IK at K. We then return to the problem of the similarity. This is the sense of the term ‘transformation’ in the context of analysis.

 

Many mathematicians of the time had made use of a point-to-point transformation, when working by analysis and synthesis, among them some scholars well known to al-Sijzī, such as al-Qūhī. We may cite the example of the construction of the regular heptagon: we construct a triangle of type (1, 2, 4) or (1, 1, 5), or other types; then in the given circle we construct a triangle homothetic with one of them.¹⁷ This technique was to be employed several times by al-Sijzī’s successor, Ibn al-Haytham, and we meet it again later on, for example when Fermat finds a tangent to Descartes’ folium at 45° to its axis.

The essential point here is that of employing a point-to-point transformation in order to reduce a difficult problem, on which one is using analysis, to another problem that is less difficult. Thus, in this context, the point-to-point transformation serves two purposes: one mathematical (transformation of a figure) and the other logical (reduction to an easier problem). So we have increased the power of the analysis in two ways.

3.2. Analysis and variation of one element of the figure

Being always in search of techniques to make analysis more powerful, al-Sijzī proposes continuous variation of one element of the figure while all the other elements remain fixed. He illustrates this search for new techniques with a simple example: to establish a specific property of triangles, that of the sum of their angles being the same; to prove in a second stage that this sum is equal to two right angles.

Al-Sijzī takes an arbitrary triangle ABC; the side AB of the angle BAC is fixed, while the vertex C can vary continuously on the straight line AC.

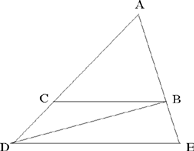
Fig. 4

If C comes to D where AD > AC, we have AD̂B < AĈB and AB̂D > AB̂C. We wish to establish that AD̂B + AB̂D = AĈB + AB̂C, or that CD̂B + CB̂D = AĈB, which comes to the same thing, since AB̂D = AB̂C + CB̂D.

We draw DE parallel to CB, and by Elements I.29 (a necessary premise at this point), AD̂E = AĈB, AÊD = AB̂C and BD̂E = DB̂C. Thus,

 

 

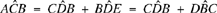
and consequently

 

 

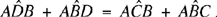
So the three angles of the two triangles ABC and ABD have the same sum. So al-Sijzī has established that if two triangles have a common angle, then the sum of their three angles is the same. From that we can establish that two arbitrary triangles have the same sum for their three angles; al-Sijzī does not even mention this.

Legendre gives an analogous argument, but without using I.29, to establish that if the sum of the angles of a single triangle is equal to two right angles (respectively, the sum is more than/less than two right angles), the same is true for any triangle.¹⁸

Al-Sijzī uses this same technique of the variation of one element of the figure to show that this sum is equal to two right angles. This time it is sufficient to consider a special triangle, here the isosceles right-angled triangle ABC. We draw BD parallel to AC; by Proposition I.29 of the Elements, we have

 

CB̂D = AĈB and AB̂D is a right angle.

 

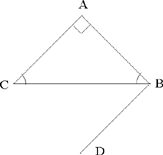
Fig. 5

We see that

 

 

It is clear that we can get to this result in the initial figure if we make the point D move away to infinity on AC, so that the side BD becomes parallel to AC. In the limit AD̂B collapses and AB̂D becomes the supplement of DÂB (as before by Elements I.29). This is very probably the approach that al-Sijzī took.

3.3. Analysis and variation of two methods of solution of a single problem

This time al-Sijzī gives an example in which the problem is kept fixed and the methods of solution are allowed to vary. Thus, there are many roads to discovery, and they are not equivalent: not only are some easier than others, but there are also some that are more elegant. To illustrate this procedure, al-Sijzī considers the division of a triangle into three parts in given ratios.

The problem here is to divide a given triangle ABC into three triangles ABH, ACH and BCH whose areas are in given ratios:

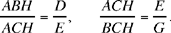
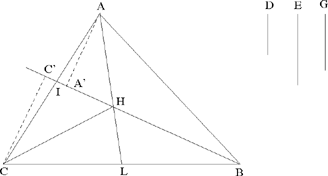
Fig. 6

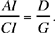We first note that the ratio of the areas of ABH and BCH is equal to the ratio ¹⁹ where I is the point of intersection of AC and the extension of BH. So we construct the point I on AC such that We know that H must lie on BI. It remains for us to choose H on BI in such a way that the ratio of the areas of ACH and ABH is equal to 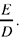Now this ratio is equal to the ratio 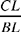where L is the point of intersection of BC and the extension of AH. So we construct L on BC such that 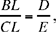where H is the point of intersection of BI and AL. We are carrying out an analysis of the problem; the synthesis is self evident and the text passes over it in silence.

Al-Sijzī proposes another method: we construct the ratio 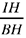in which the required point, H, divides BI; this ratio is equal to the ratio of the areas of triangles AIH and AHB. Now

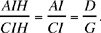
Let us divide the magnitude E into two parts X and Y such that the ratio

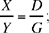
the ratio 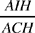is thus equal to 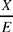(because ACH = AIH + CIH). Since

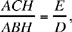
we see that

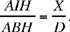
Accordingly

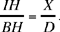
Which is what it was required to prove. Here again, the text presents only the analysis; the same holds for the third method, which follows.

The third method is more elegant because it uses the theory of proportions only for dividing one of the sides of the triangle, let it be AB, in the ratio of the three segments D, E, G:

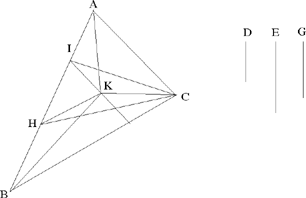
Fig. 7

The three triangles ACI, ICH and HBC have areas in the required ratio.

Through I we draw IK parallel to AC and through H we draw HK parallel to BC; then the area of the triangle AKC is equal to the area of the triangle AIC, and in the same way the area of the triangle BKC is equal to the area of the triangle BHC. The areas of the triangles AKC, AKB and BKC are now in the ratios of the segments D, E, G.

Al-Sijzī thus provides three methods – and he is at pains to point out that they are three among many – for constructing an object that has a given property.

3.4. Analysis and variation of lemmas

In the first part of the treatise, al-Sijzī recommended, as a useful rule in analysis and synthesis, that one should look back to the lemmas of the lemma that allowed the proposition to be proved. This rule is in turn based on the idea that the lemmas can be varied, at the least by working back up the chain of lemmas that are necessary for establishing the proposition. Here we are obviously concerned with an indirect approach, that is intended to increase the number of routes for making discoveries. Here al-Sijzī gives an example that illustrates this rule, Proposition III.20 of the Elements:

In a circle the angle at the centre is double of the angle at the circumference, when the angles have the same circumference as base.

Euclid had proved this proposition from a lemma that required two other preliminary lemmas, that is I.32 (the exterior angle of a triangle), itself based on I.29 and I.31. Al-Sijzī proves the proposition directly from these last lemmas (see text).

3.5. Analysis and variation of constructions carried out using the same figure

In the first part of the treatise, al-Sijzī recommends that, as a preliminary approach, one should try to recognise the element which is common to the propositions that will be used in carrying out the analysis and synthesis. He also advises us to grasp what it is that distinguishes these propositions one from another. An investigation that is the more necessary because these ‘contribute to one another’ (p. 607). Here al-Sijzī illustrates this phenomenon by means of an example, from which he develops a supplementary procedure to make the analysis more powerful: We use the same figure to arrive at different constructions. That is, we fix the figure and we vary the constructions carried out with it. Let us return to al-Sijzī’s approach, whose text has been heavily corrupted by the copyist of the manuscript.

Al-Sijzī starts with several propositions which he does not prove on division in extreme and mean ratio, which ‘contribute to one another’. Al-Sijzī notes that they have in common the number five, it being given that ‘the construction of the regular pentagon in fact involves the division of a straight line in mean and extreme ratio’.²⁰ Let us return to al-Sijzī’s exposition.

Proposition 1: We know from Euclid’s Elements that the construction of the regular pentagon starts with making a division in extreme and mean ratio. Thus, Book XIII of the Elements opens with some propositions on this division, on which al-Sijzī comments²¹ in Euclidean style.

Using trigonometry, we find the side of the regular decagon inscribed in a circle of radius r:

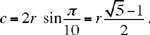
For the side of the regular pentagon we have

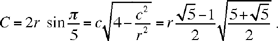
Proposition 2: The sum 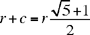is divided in extreme and mean ratio by r and c: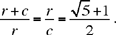

Proposition 3: The ratio of D, the diagonal of the regular pentagon, to its side C is again equal to 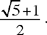In other words, the diagonal PN is divided in extreme and mean ratio at the point Q such that PQ = PM = C.

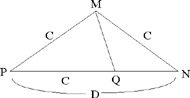
Fig. 8

The isosceles triangles PMN and MQN are similar, so

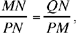
or

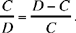
Proposition 4: If a straight line of length 2a is divided in extreme and mean ratio, the greater part is a(√5−1). So if we add to it a, half the whole straight line, the sum is a√5 and its square is five times the square of half the whole straight line.

Proposition 5: If we divide a straight line into two parts in this ratio, and if to the greater part we add twice the smaller part, then the square of the whole straight line is five times the square of the first part.²²

Let a be the greater part; the smaller part accordingly has the value 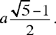Twice this added to a gives a√5, whose square is five times the square of a.

Proposition 6: Let us continue to consider a straight line divided in extreme and mean ratio, whose greater part is 2a; and the smaller part is then a(√5 − 1). If to this part we add a, half the greater part, we obtain a√5, whose square is five times that of half the greater part.

Proposition 7: Propositions 4 to 6 show how, starting from a division in extreme and mean ratio, we can construct two segments such that the square of one is five times the square of the other. Now, we carry out the inverse procedure, starting from a square divided into five equal squares and proceeding so as to obtain a division in extreme and mean ratio.

For example, if we are given a and a√5, the sides of two squares, their sum a(1+√5)(‘composition’), when divided by two, is in the ratio 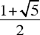with the first side a; in other words this side a divides half the sum in extreme and mean ratio.

In the same way, the difference a(√5 − 1) (‘separation’), when divided by two, is in the ratio 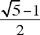with the first side a; in other words, half the difference divides this side in extreme and mean ratio.

Here we propose a construction of the division in extreme and mean ratio that has several stages (‘propositions that participate in one another’). In the first stage, we construct two segments such that the square of one is equal to three times the square of the other; in the second stage, we use this construction to obtain the division in extreme and mean ratio. The two constructions are done with the same figure.

Example: In this example, we consider a triangle AEB, right-angled at E, and we carry over the smallest side EB to be EG on the larger side EA.

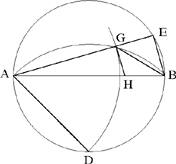
Fig. 9: 2AD² = AB²; 3AE² = (AG + AE)²

We have

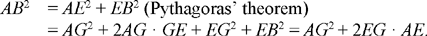
As the first stage, we take AG such that 2AG² = AB²; so we have

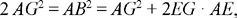
hence

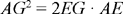
and

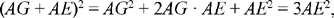
as we wished for the first part.

The construction of G is carried out stating from AB as follows: we find AD such that 2AD² = AB2 by dividing the semicircle ADB of diameter AB into two equal arcs. We must have AG = AD and angle 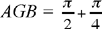(exterior angle of the right-angled isosceles triangle BEG); accordingly Glies at the intersection of the circle with centre A and radius AD and the arc subtending the angle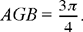

We then extend AG to E so as to make angle AEB a right angle; so this point is the intersection of the extension of AG and the circle of diameter AB.

In the second stage, we use the same construction, but this time we suppose that 3AG² = AB² = AG² + 2EG · AE. We then have AG² = EG · EA and the straight line AE is divided in extreme and mean ratio at the point G.

So the method consists of constructing AD such that 3AD² = AB² by using the first part, then constructing G as the point of intersection of the circle with centre A and radius AD and the arc subtending the angle 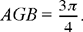We then complete the procedure as in the first stage: we extend AG to E, its point of intersection with the circle of diameter AB. We then have

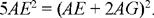
Fig. 10: 3AD² = AB²; 5AE² = (2AG + AE)² (Ae = AE, eB = AG in Fig. 9)

Note: This construction provides a general method of constructing two segments such that the ratio of their squares is of the form 2ⁿ + 1. For n = 2, this ratio is 5 and the construction is equivalent to division in extreme and mean ratio.

Let us suppose that (2^n–1 + 1)AD² = AB². If AG = AD, as in the figure, we have:

so

Thus,

So, to obtain a ratio of squares equal to 2ⁿ + 1, we repeat the construction n times. Each figure is obtained from the previous one:

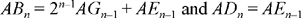
give

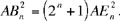
We are always dealing with the same figure, with a different choice for the point D.

That is exactly the idea to which this text is trying to draw attention. The case we are considering has two parts since n = 2; that explains the jump to a later occurrence of the same word which has caused lacunae in the text. For each part, the figure is the same and the argument is identical and this is the sense in which to understand the term ‘participation’.

Al-Sijzī then states that if, by a similarity-transformation, we draw GH parallel to EB, we have divided AB in the required manner, that is in such a way that

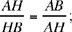
which is an application of Thales’ theorem.

3.6. Variations on a problem from Ptolemy

Al-Sijzī returns to a problem in the Almagest. His investigation is both careful and detailed; he emphasises the difficulties he encountered in carrying out the analysis, providing four proofs, and thus showing that many different methods can be used to solve the problem. In the course of his discussion al-Sijzī demonstrates the part played by auxiliary constructions as well as showing, in each case, the purpose served by their use; but he does not mention, or even hint at, the questions of logic that are raised by there being multiple proofs for the same problem. His principal concern is always the same: to discover the best method of obtaining the required property. This is indeed his motive for providing multiple solutions.

Ptolemy’s proposition²³ shows that if in a given circle we take two unequal arcs AC and AB such that arc AC > arc AB, then

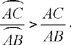
We take K on BA produced such that AK = AC and take G as the point of intersection of KC and a line through A parallel to BC.

Since the arc AC is cut off by the angle AB̂C = KÂG and the arc AB is cut off by the angle AĈB = GÂC, we have

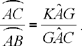
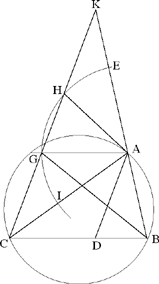
Fig. 11

So we want to show that

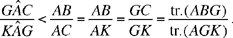
Now the first ratio is equal to the ratio of the sectors GAI and GAE, and we have

sect.(GAI) = sect.(HAE)²⁴ and sect.(GAE) = sect.(AEH) + sect.(HGA).

Moreover,

tr.(AGC) = tr.(KAH) and tr.(KAG) = tr.(KAH) + tr.(HAG);

since

tr.(HAG) < sect.(HAG) and tr.(KAH) > sect.(HAE),

we thus have

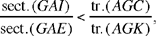
hence

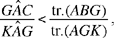
which is what it was required to prove.

Note 1: We have presented the argument using Fig. 11, where the angles satisfy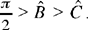

Let us suppose AB̂C is obtuse, with 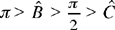(Fig. 12). The symmetry we pointed out in the first case still exists and the reasoning is identical, because all the equations are satisfied.

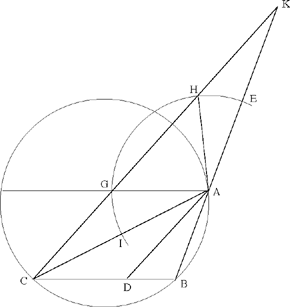
Fig. 12

Note 2: To express it differently, let us make β = AB̂C, γ = AĈB and r the radius of the circle ABC. The arc AC is equal to 2 rβ and the arc AB is equal to 2 rγ; as for the chords, we have: AC = 2r sin β, AB = 2r sin γ. Ptolemy’s inequality is written as

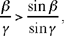
that is

Thus, this inequality indicates that the function 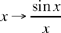decreases over the interval 0 < x < π.

Note 3: In another text by al-Sijzī (see below) we find a solution of this problem using a slightly different auxiliary construction, but employing the same reasoning.

Al-Sijzī continues his discussion of this same problem from Ptolemy by proposing a second method of proving the same inequality. For this, he introduces the line CD, the bisector of the angle ACB,²⁵ which gives him 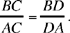If the extension of CD meets the circle circumscribed about the triangle ABC in H, we consider the circle with centre H that passes through D; it meets HA in E and HB in I. Since HA > HD, the point E lies between H and A. If I lay outside HB, the proof would be immediate because

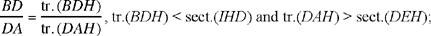
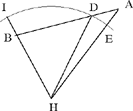
Fig. 13

So we have

thus,

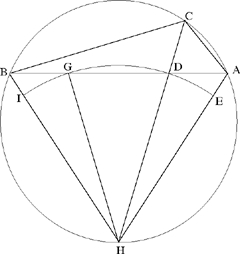
Fig. 14

But Figure 13 is impossible because HB = HA and the point I thus lies between H and B, as the point E lies between H and A. Al-Sijzī then notes that the preceding reasoning is false. But understanding the nature of the error allows us to move forward along the road of discovery and to correct the reasoning. That is probably the point that al-Sijzī wanted to illustrate by this example. This is how he proceeds:

Let G be the point where the circle with centre H and radius HD cuts the side AB. The triangles HDA and HGB are equal and the sectors DHE and GHI are also equal. Now we have

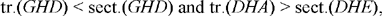
so

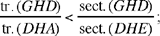
if we add unity to the two sides, that is by composition of the ratios, we obtain

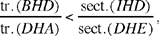
and the proof is completed as above.

We may note that, in another text, al-Sijzī gives the same solution, that is the same apart from some small variants, in the course of the proof. He in fact starts from the same figure with the same lettering and the same assumptions (see below).

Al-Sijzī continues to give more variations on Ptolemy’s problem. This time he wants to take account of a special condition that is sufficient as Ptolemy proposes it, namely that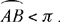

We introduce a point D on the circular arc ACB such that 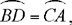and we call the point of intersection of AD with BC the point E. The circle with centre A and radius AE meets the extension of AC in G and the side AB in H.

We have

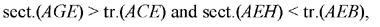
so

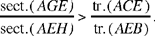
By composition of the ratios, we have

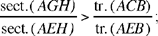
the ratio on the left is equal to

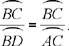
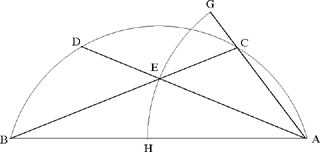
Fig. 15

Further

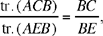
so

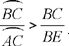
Al-Sijzī concludes by saying that BE = AE > AC; unfortunately that gives

and one cannot draw any conclusion as he has inadvertently done.

He also gives a fourth solution to this problem (see below).

Al-Sijzī continues his variations on Ptolemy’s problem. He still starts with three points A, B, C on a given circle, with arc AC > arc CB; he draws CD ⊥ AB and wishes to show that

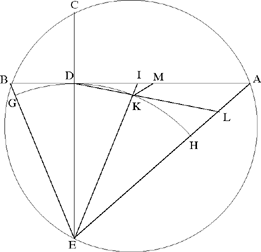
Fig. 16

This time we have a problem of the same kind, even though al-Sijzī does not directly consider the chords of the arcs, but those of the segments associated with them.

We extend CD to the point E on the circle; we take I on BA such that EI = EB. The circle (E, ED) cuts the straight lines EB, EI and EA in G, K and H respectively.

Al-Sijzī then says that

(1)

He does not prove this inequality, but deduces from it that

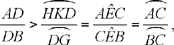
hence

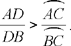
This proof is correct, although it is simply indicative, since al-Sijzī has not proved (1). We can reconstruct the missing proof as follows:

Let us draw DK; it cuts EA in L; through K let us draw a line parallel to EA, which cuts DA in M between I and A. We have

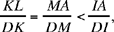
so

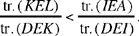
Now

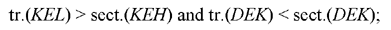
so

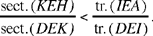
By composition of the ratios, we find

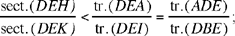
this is what we wanted to prove.

This proof is not only in al-Sijzī’s style but is faithful to the way he proceeds. To employ another style, one he did not know, we may let BÊD = α, DÊA = β and r = ED. The segments BD and DA are measured by r tan α and r tan β respectively; so their ratio is 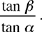The arcs AC and CB, intercepted by the inscribed angles CEA and CEB, are in the ratio 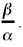The inequality that has been proved means that 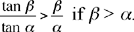In other words, the function 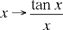increases, for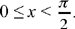

Making this translation might in fact shed light, at least indirectly, on the variations al-Sijzī imposes on Ptolemy’s problem.

Al-Sijzī continues his variations on this problem. This time, instead of considering the ratio of the chords of the given arcs, he looks at the ratio of twice the chords of the given arcs. The discussion is, however, not complete. So let us return to the problem.

Let us put 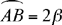and 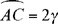with γ > β. If AE, the diameter through A, cuts CB in D, we have

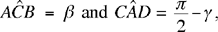
hence

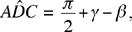
an obtuse angle; the same is true for the angle EDB and in consequence we have EB > ED.

Fig. 17

We draw the circle (E, ED); it cuts EB in H and EC in G.²⁶ The position of G in relation to the straight line CD depends on the lengths of EC and ED. We have the following cases:

1. G lies beyond C, so it is above CD if ED > EC (Fig. 18).

2. G is at C if ED = EC (Fig. 19).

3. G is below C, so it is on EC, if ED < EC (Fig. 20).

Fig. 18

Fig. 19

Fig. 20

In the triangle EDC, the greatest angle is opposite the greatest side:

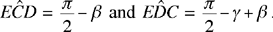
So we have the following conditions:

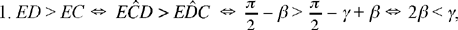
which is possible because γ>β.

2. ED = EC ⇔ = γ = 2β, which is also possible.

3. ED < EC ⇔ γ 2β, which would impose the condition β < γ < 2β; a condition that is necessary for G to be below C, and a condition which is not stated by al-Sijzī. His argument applies in cases 1 and 2. Thus, we have

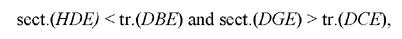
so

The triangles DBE and DCE have equal heights (same vertex and bases on the same straight line), so we have

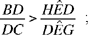
but

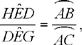
hence

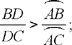
which is what al-Sijzī wished to prove.

However, the argument does not apply in case 3, as we can easily check. Let us proceed in the same style as al-Sijzī does:

The triangle EDB is always greater than the sector EDH, but, in this case of the figure (Fig. 20), we do not know whether the triangle ECD is smaller or greater than the sector EGD. We know only that the triangle EXD is smaller than the sector EXD. But the triangle EXC is greater than the sector EXG; which does not allow us to draw any conclusions. We can, however, establish that the ratio is greater than the ratio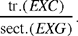

Let us prove this inequality: let us construct a point C₁ on DB such that DC₁ = XC; the triangle EXC is equal to the triangle EDC₁. As EC < EB, since arc EC < arc EB, we have EC₁ = EC < EB, so DC₁ < DB and C₁ lies between D and B.

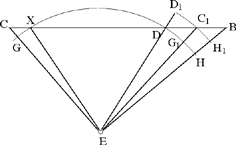
Fig. 21

We draw the circle with centre E and radius EC₁ = EC; it cuts EB in H₁ and ED in D₁. We have

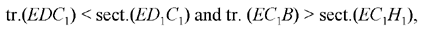
so

by composition of the ratios, we have

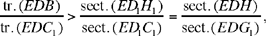
where G₁ is the point of intersection of EC₁ with the circle GXDH.

So we have

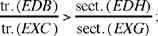
which is what we wished to establish.

Thus,

So finally we have

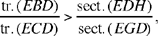
the inequality we wished to prove.

This inequality is, moreover, equivalent to a decrease in the function 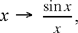as has been explained in the note on page 545.

Al-Sijzī presents one last variation on Ptolemy’s problem, which is stated like this: Let there be two chords AC and BD in a given circle ADBC cutting one another in E; we have

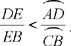
The ideas in the proof are essentially the same as before. We begin with an auxiliary construction, of a circle (B, BA) that cuts the extension of the chord BD in H; the line through B parallel to AC cuts this circle in I and the extension of DA in G. We have

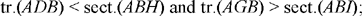
hence

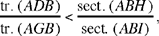
hence

But AB̂G = CÂB; DB̂A intercepts the arc AD and CÂB intercepts the arc BC, so

but

because EA ∥ BG; hence the conclusion.²⁷

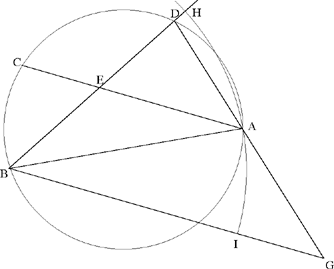
Fig. 22

The preceding argument assumes that BA > BD; this is always true if the arc ADCB≤ π, the points A, D, C, B being in that order. We then have AB > BD and AB < BG; we need to have H lying beyond D and I lying between B and G and the argument then applies (see Figs 22.1 and 22.2).

Fig. 22.1

Fig. 22.2

But for the third case, the arc ADCB < π, we can have: AB < BD, AB = BD or AB > BD.

In fact, let BB₁ be the diameter (2r) and A₁ such that the arc AB₁ is equal to the arc B₁A₁. If a point D describes the arc AB₁ from A towards B₁, the length BD increases from BA to BB₁ = 2r. If D describes the arc B₁A₁, the length BD decreases from 2r to BA₁ = BA. If D describes the arc A₁B, the length BD decreases from BA₁ = BA to 0; hence

So if we take D beyond A₁, we shall have, as in the first two cases,

where H lies beyond D and I lies between G and B; and the argument again applies.

Fig. 22.3

If we take D at the point A₁, we have BD = BA, so D = H; we still have

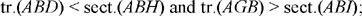
and the argument still applies.

If D is an arbitrary point on the arc AA₁, we have BD > BA; in this case, H lies between B and D. But the position of the point I depends on the positions of D and C. Thus, if D lies between B₁ and A₁, the angle DAB is acute and the circle (B, BA) cuts AD between A and D (Fig. 22.4) and cuts BG in I between B and G.

Fig. 22.4

The segment AD cuts the arc AH and we cannot make a comparison between the area of the triangle ABD and that of the sector ABH. The proposed method can no longer be applied.

If D is at the point B₁, the angle DAB is a right angle, the circle (B, BA) touches AD, the point G lies on AD and the point I again lies between B and G; the argument does not apply either, we have

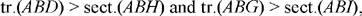
and we thus cannot draw any conclusions (Fig. 22.5).

Fig. 22.5

But if D lies between B₁ and A, the angle DAB is obtuse and the straight line AD cuts the circle (B, BA) again beyond A; in this case, depending on the position of D and that of the point C on the arc BC₀ (arc BC₀ = arc AD and arc BC < arc AD), we can have the point G between B and I, G = I, or I between B and G (Figs 22.6, 22.7 and 22.8 respectively).

In cases 22.6 and 22.7, the point G lies between B and I or G = I; we have

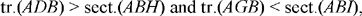
so

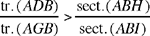
and in consequence

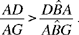
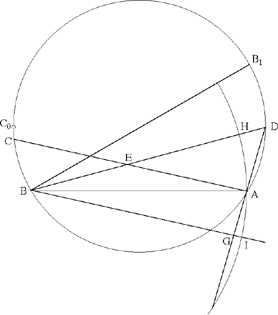
Fig. 22.6

Fig. 22.7

We have BG ∥ AE, hence

and we thus have

which is contrary to the conclusion stated earlier.

Fig. 22.8

In case 22.8, we cannot compare the area of the triangle ABG with that of the sector ABI.

All this discussion shows that, without stating this in so many words in his text, al-Sijzī seems to assume that he has simply accepted the hypothesis that arc ADCB ≤ π, which indeed corresponds with the figure in the text.

As readers will no doubt have noticed, al-Sijzī’s variations on Ptolemy’s problem do not relate only to the proofs, but also to deriving different statements and discovering other properties, such as that of the tangent. Moreover, al-Sijzī makes a point, at least at the beginning of the discussion, of raising all the difficulties that the geometer encounters in the course of examining the problem.

3.7. Variations on the same problem from Ptolemy in other writings by al-Sijzī

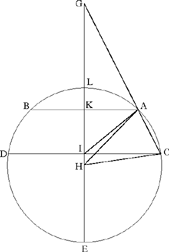
In the manuscripts of al-Sijzī’s writings that have come down to us, we find three additional solutions of this same problem. Two of them differ only very slightly from the two solutions we have given here. The third is simpler, but the argument is based on the same idea. So let us start by looking at this last solution.

1. We wish to prove that if arc CD > arc AB, then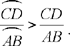

The figure in the text as well as the argument that is presented assume AB ∥ CD. But the result that is established in this case is valid whatever the position of the arcs.²⁸

Let H be the centre of the circle; the perpendicular drawn from H to CD cuts CD and AB in their respective mid points I and K and cuts the arc AB in L, the mid point of the arc AB. The straight line HL cuts AC in G. We have

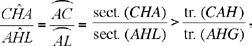
because tr. (CAH) < sect. (CHA) and tr. (AHG) > sect. (AHL).

By composition, we have

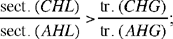
now

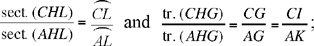
so we have

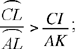
hence

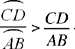
This solution is simpler than those we examined before. The diameter EL is an axis of symmetry for the given arcs and for their chords and the argument is based on the relations

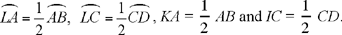
But, as in all the solutions al-Sijzī proposes, the argument rests on the inequality between the ratio of two sectors and the ratio of the two triangles associated with them and having their bases on the same straight line. In every case, it is from this inequality that the conclusion is deduced. It is only the auxiliary constructions that are different.

The passage that supplies this solution forms part of the text Reply of Aḥmad ibn Muḥammad ibn ‘Abd al-Jalīl al-Sijzī to Geometrical Problems Raised by the People of Khurāsān (Jawāb Aḥmad ibn Muḥammad ibn ‘Abd al-Jalīl al-Sijzī ‘an masā’il handasiyya sa’ala ‘anhu Ahl Khurāsān). See the manuscripts Dublin, Chester Beatty Library 3652, fol. 57, and Istanbul, Süleymaniye Library, Reshit 1191, fol. 118. As we have shown,²⁹ this last manuscript is a copy of the one in Dublin and from only that one manuscript. For this text, there is an edition comparable to that of the treatise To Smooth the Paths for Determining Geometrical Propositions. It is this edition that was translated into English in 1996.³⁰

We wish to show that the ratio of the large arc to the small arc of a circle is greater than the ratio of the chord of the large arc to the chord of the small arc, using a method different from that of Ptolemy in his book, the Almagest.

I have solved this problem by a different method and [using] proofs that can be found in the examples that I have given in the book: To Smooth the Paths for Determining Geometrical Propositions. Nevertheless, a proof by a method different from those that we have followed in this book is possible; it is as follows.

Let there be two unequal arcs AB and CD. I say that the ratio of the arc CD, the greater [arc], to the arc AB, the smaller [arc], is greater than the ratio of the chord CD to the chord AB.

Proof. Let the two chords be parallel. We draw from the centre the line HIK perpendicular to the two chords. We extend it on both sides to E and L. We join HC and HA and we extend CA and EL to meet one another in G. The ratio of the angle CHA to the angle AHL is equal to the ratio of the arc CA to the arc AL and is equal to the ratio of the sector CAH to the sector AHL. But the ratio of the sector CAH to the sector AHL is greater than the ratio of the triangle CAH to the triangle AHG. Thus, by composition, the ratio of the sector CHL to the sector AHL is greater than the ratio of the triangle CHG to the triangle AHG. But the ratio of the triangle CHG to the triangle AHG is equal to the ratio of CG to AG and to the ratio of CI to AK. The ratio of the arc CL – respectively³¹ CLD – to the arc AL – respectively ALB – is thus greater than the ratio of the straight line CI – respectively the chord CD – to the straight line AK – respectively the chord AB. Which is what it was required to prove.

2. The two other solutions attributed to al-Sijzī are to be found in a text called Geometrical Glosses from the Book by Aḥmad ibn Muḥammad ibn ‘Abd al-Jalīl al-Sijzī (Ta‘līqāt handasiyya min Kitāb Aḥmad ibn Muḥammad ‘Abd al-Jalīl al-Sijzī), which has come down to us in two manuscripts, one Dublin, Chester Beatty, no. 3045/14, fols 74^r–89^v; and the other Cairo, Dār al-Kutub, no. 699 riyāḍa, 35 pages. The latter is a copy of the former.

The manner in which this book was composed raises an important problem: are we really dealing with a book by al-Sijzī or with a pot pourri made up of parts of his writings, notably from his Anthology of Problems? We discuss this question elsewhere,³² though we regard the matter as settled; here, we give these solutions, which in fact differ from those already given by al-Sijzī in his To Smooth the Paths … only in a slight modification of the auxiliary construction.

Let us start by returning to the first of these two solutions.

Proof of a proposition from the first book of the Almagest, [a proof] that we have established.

The arc AC is greater than the arc AB; I say that the ratio of the chord of the arc AC to the chord of the arc AB is smaller than the ratio of the arc AC to the arc AB.

Proof. We draw AC, AB, BC and we divide the angle CAB into two halves with the straight line AD.

We draw CE parallel to AD and we extend BA to E; we draw AG parallel to BC, with centre A and distance AG we draw the arc IGHK and we join AH. Given that the angle B is greater than the angle ACB, AC will be greater than AB. But the triangle ACE is isosceles and AC is equal to AE, so AE is greater than AB. But the ratio of CG to GE is equal to the ratio of BA to AE, so CG is smaller than GE, and the angle AGE is acute.

But the straight line AH is equal to the straight line AG, so the triangle AEH is equal to the triangle AGC and the ratio of the triangle AGC to the triangle AGE is greater than the ratio of the sector AGI to the sector AGK, because the sector AGH is greater than the triangle AGH of the segment HG. But the ratio of the triangle AGC to the triangle AGE is equal to the ratio of GC to GE, and the ratio of the sector AGI to the sector AGK is equal to the ratio of the angle CAG to the angle GAE; so the ratio of CG to GE is greater than the ratio of the angle CAG to the angle GAE. But the ratio of GC to GE is equal to the ratio of BA to AC, so the ratio of BA to AC is greater than the ratio of the angle CAG to the angle GAE; but the angle CAG is equal to the angle ACD and the angle GAE is equal to the angle ABD, so the ratio of BA to AC is greater than the ratio of the angle BCA to the angle CBA. Now the two angles BCA and CBA intercept the arcs BA and AC, so the ratio of BA to AC is greater than the ratio of the arc BA to the arc AC. If we permute, then the ratio of AC to AB is smaller than the ratio of the arc AC to the arc AB. This is what we wanted to prove (ms. Dublin, Chester Beatty, no. 3045, fol. 81^r-^v).

It is clear that this solution is the same as the one given before, the difference being merely that the hypothesis we make here corresponds to the conclusion in the solution given in the treatise; except that the two letters K and E are exchanged, the proof is the same in both cases. Thus, in the Treatise, we extend BA by a length AK = AC; the triangle KAC is isosceles and we then have KC ∥ AD (AD is the bisector of the angle BAC). Here, we draw through C a line parallel to AD the bisector of the angle BAC; it cuts the extension of BA in E. We have CE ∥ AD and we deduce that EAC is isosceles; hence EA = EC. For both constructions, we draw AG ∥ BC.

We may have a first draft of al-Sijzī’s solution, of perhaps a revised version of it. The question remains open.

3. Return to the third solution.

We have determined it in another manner.

The arc CB is greater than the arc CA. I say that the ratio of the arc CB to the arc CA is greater than the ratio of the chord BC to the chord CA.

Proof. We divide the arc AB into two halves at the <point> H, we draw AB, BH, AH and CH, and with centre H and with distance HD we draw the circle EDGI and we draw HG. HG is thus equal to DH (ms. Dublin, Chester Beatty, no. 3045, fol. 82^r).

The ratio of the arc GD to the arc DE is greater than the ratio of the straight line DG to the straight line DA.³³ By composition, the ratio of the arc ID to the arc DE is greater than the ratio of the straight line DB to the straight line DA. But the ratio of DB to DA is equal to the ratio of CB to CA, and the ratio of the arc ID to the arc DE is equal to the ratio of the arc CB to the arc CA. This is what we wanted to prove.

In this solution, as in the one in the Treatise, we make use of CH, the bisector of the angle ACB defined by the point H the mid point of the arc BA; the straight line CH cuts the chord AB in D. In both solutions – the one in the Treatise and the one given here – we make use of the property of the point D, the foot of the bisector of the angle ACB; we have

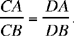
The figure drawn is the same in both cases, with identical lettering. The single slight difference to be found between the two versions is that, in the solution reproduced here, we give the inequality

(1)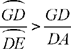

without proof. Now it follows from the inequality

(2)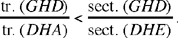

But here we are arguing from (1) by composition, whereas in the Treatise we proceeded from (2) by composition:

(2)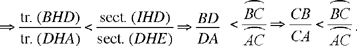

4. Analysis and synthesis: variation of the auxiliary constructions

Without the slightest acknowledgement of making a transition, al-Sijzī then move on to ‘analysis and synthesis’ of two similar problems of the division of a straight line by a point that has a certain geometrical property. Why do we have these problems? And why here and now? In regard to these reasons and the order of his exposition, al-Sijzī himself, at least in the existing manuscript, says not a word. We may note, however, that, for these examples, he takes the trouble to give a formal exposition, that is he carries out an analysis and then a synthesis of the problems. Finally, the problems themselves are of the same kind as several others that his predecessor Ibrāhīm ibn Sinān had considered in order to illustrate different species of analysis and of synthesis. There is thus every indication that here al-Sijzī is modelling his work on the study by Ibn Sinān. Better still, as is shown by the examples that are investigated, this second look is directed at one of the questions that most interested Ibn Sinān in his researches on analysis and synthesis: auxiliary constructions. Let us now turn to the example studied by al-Sijzī.

Problem 1: Al-Sijzī begins with a straight line AB; he wishes to divide AB in D such that

(1)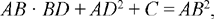

where C is a given arbitrary square.

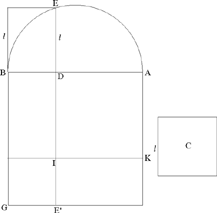
Fig. 23

Let us suppose D is known and satisfies (1). Let us draw BG ⊥ AB, where BG = AB and DI ∥ BG. We have area (DG) = AB · DB. We construct on AD the square AKID. For D to be a solution to the problem, we require area (KE′) = KI · IE′ = AD · DB = C. So it is necessary that l, the side of C, shall be less than or equal to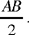

Problem 2: This time al-Sijzī wishes to divide AB in D such that

(2)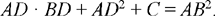

Let us suppose that D is known and satisfies (2). We take BK = AD and we construct the rectangle DK; we have area (DK) = AD · DB. We draw KHI ∥ AD, so we have area (AH) = AD²; there remains area (IG) = C; so we require that IK · KG = C, that is that AB · BD = C.

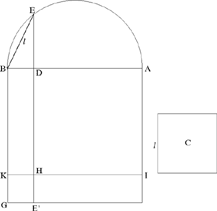
Fig. 24

We draw the semicircle with diameter AB and from the point B we draw the chord BE = l; now we have EB² = l² = AB · BD, a construction that is always possible because l < AB.

If we put AB = a and AD = x, the first problem can be written ax = x² + c and the second one ax + c = a². We may note that al-Sijzī has avoided making this algebraic translation.

The synthesis of these analyses begins with the construction of E on the circle.

5. Two principal methods of the ars inveniendi

We recollect that at the beginning of his treatise al-Sijzī gave a list of methods for facilitating invention in geometry; at least seven of them, according to the author. We showed that there is in fact one principal method, ‘analysis and synthesis’, and several special methods, which will provide the first method with actual means of making discoveries. These special methods all have in common the idea of transformation and of making variations in not only the figures but also the propositions and the procedures used for solution of problems. The set as a whole, including both the principal method and the special ones, suits al-Sijzī’s intellectual style, and also the list he proposes, but with the exception of one method that he mentions: that of ingenious procedures, procedures like those of Hero of Alexandria. Having mentioned this method at the beginning of his treatise, al-Sijzī in fact never refers to it again. Perhaps he had introduced it merely to make the list complete. Perhaps he had simply forgotten about it because it does not fit precisely into the ars inveniendi as he conceives it. It does not seem that this can be so, assuming that our analysis of al-Sijzī’s treatise is correct. Indeed if ‘analysis and synthesis’ is the principal method, and if all the others, its faithful auxiliaries, are there to serve it, the role of the mechanical procedures for discovery, however important it may be, is of a completely different order: it is that of an outside collaborator of a practical kind. It is al-Sijzī himself who suggests an interpretation along these lines.

Near the end of the treatise, the author recapitulates the list of methods that he has just applied, and he indicates two principal methods. This is what he writes:

Since an investigation of the nature of propositions (askhāl, singular shakl) and of their individual properties is always carried out in one of these two ways: either we bring to mind the necessity of their properties by considering a variety of species, [an act of] imagination that draws on sensation or on what is perceived by the senses; or we assume these properties and also the lemmas they make necessary, in succession, by geometrical necessity […].³⁴

Al-Sijzī follows this conclusion with several examples.

So for al-Sijzī the ars inveniendi essentially involves only two methods. All the special methods are grouped around the first method, and the second one is simply ‘analysis and synthesis’. Now it is exactly this distinction on the one hand, and the nature of the first method on the other hand and, finally, this intimate relationship between the two of them, which characterise al-Sijzī’s conception and shows up the novelty of his contribution.

Moreover, we must note that the first of the two methods splits into two, in accordance with the two meanings of the term shakl. This word, which the translators of Greek mathematical writings³⁵ chose to render as διάγραμμα, designates, as does the Greek, indiscriminately both the figure and the proposition. This double meaning is not too troublesome in causing ambiguity when the figure provides a translation of the proposition into graphic terms, in a static way (so to speak); in other words so long as geometry remains essentially a study of figures. But everything becomes more complicated when we begin to transform figures to give variants of the figure, as is already happening in some branches of geometry in the time of al-Sijzī. The double significance then requires an explanation.³⁶ Let us start with the first sense, that of ‘figure’.

In this treatise, al-Sijzī recommends three times that we proceed by varying the figure: when we carry out a point-by-point transformation; when we vary one element of the figure, all the others remain fixed; finally, in the choice of an auxiliary construction. Now several elements are common to these different procedures. The purpose first of all: we are always looking to find, by means of transformation and variation, the invariant properties in the figure associated with the proposition, the properties that are its particular characteristics. Now these are, precisely, the invariant properties that are set out in the figure as a proposition. The second element also relates to purpose: variation and transformation are means to discovery insofar as they lead to these properties that do not change. It is here that the imagination intervenes, as a faculty of the soul capable of pulling out from among the multiplicity offered by the senses, among the variable properties of figures, those properties that do not change, the essences of things. The third common element is concerned with a particular role of the figure, this time as a representation, referred to a number of times by al-Sijzī, that of engaging the imagination, of helping it carry out its task when it is assessing the evidence of the senses. The fourth, no less important, is connected with the figure-proposition duality: there is no bi-univocal relationship. To one and the same proposition there may correspond a variety of figures; similarly to one single figure there may correspond a whole family of propositions. Al-Sijzī chose, moreover, to treat this last case at length. These new relationships between figure and proposition that al-Sijzī, as far as I know, was the first to point out, require that we think about a new area in the ars inveniendi: analysis of figures and of their relations to propositions. Now this is precisely what al-Sijzī seems to have initiated.

As an example of the first method for the ars inveniendi, al-Sijzī does no more than refer back to one he has already considered: the equality, for any triangle, of the sum of its angles, a property grasped by the imagination on the basis of what is common to the senses. He also mentions another similar example.

For the second method, that of analysis and synthesis in geometry, al-Sijzī adds nothing of substance, but he emphasises the role of apprenticeship and of practice in strengthening the faculty for conceiving properties. He gives only several particularly simple examples to illustrate the procedure.

1. Let there be a circle in which two chords AB and CD cut one another at the point H. We wish to know the origin of the necessity of the equality AH · HB = CH · HD. Al-Sijzī begins by drawing CA and DB, and proves that the triangles HCA and HDB are similar; so we have 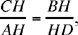hence the result. But to show that the property is an invariant one, he begins again and draws another circle, EG, passing through H; as before we have that triangles CEH and DHG are similar, hence 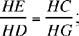hence the result. So the property does not depend on the choice of the chord, but on the similarity of the triangles that are formed, and thus on the fact that the angles inscribed in the circle intercept the same arc.

Fig. 25

2. An arc of a circle is intercepted by an inscribed angle equal to the angle formed by the chord of that angle and the tangent to the circle at one end of that chord. Here again al-Sijzī takes his reader by the hand to show him how to find that the property does not vary.

He draws the circle ABC with diameter AB, and BD the tangent at the point B. It is clear that AB̂BD = AĈB because AĈB intercepts a semicircle; so AĈB = 1 right angle = AB̂D . Al-Sijzī then writes:

we have to look for the variety of the species of that figure, and the necessity of their properties, by an investigation of their nature (p. 620).

Fig. 26

He in fact proceeds by varying the angle B formed by the chord and the tangent, and proves that it is equal to any inscribed angle such as E ˆ XB that also intercepts the arc EACB, ‘visually and geometrically’.

Al-Sijzī concludes his treatise by returning to the didactic intentions he had stated so forcefully at the beginning of it, with an exercise in the way to carry out analysis, written for beginners.

III. HISTORY OF THE TEXTS

3.1. Book by Thābit ibn Qurra for Ibn Wahb on the Means of Arriving at Determining the Construction of Geometrical Problems

Thābit ibn Qurra’s letter to Ibn Wahb appears in the list of his writings drawn up by Abū ‘Alī al-Muḥsin ibn Ibrāhīm al-Ṣābi’, and reproduced by al-Qifṭī, with the title Fī istikhrāj al-masā’il al-handasiyya (On the Determination of Geometrical Problems),³⁷ it has come down to us under three different titles, the first of which is the closest to that given by al-Ṣābi’, and in five manuscripts.³⁸ Thus, we have:

1. Fī al-ta’attī li-istikhrāj ‘amal al-masā’il al-handasiyya (On the Means of Arriving at Determining the Construction of Geometrical Problems). This is the title of the letter in the copy in the hand of the tenthcentury mathematician al-Sijzī. This copy is part of the famous collection no. 2457 in the Bibliothèque nationale in Paris, fols 188^v–191^r, here called B. We have described this collection already.³⁹ The point to remember here is merely that al-Sijzī checked his copy against his model, as he tells us himself in the colophon.

2. Fī kayfa yanbaghī an yuslaka ilā nayl al-maṭlūb min al-ma‘ānī alhandasiyya (How to Conduct Oneself so as to Obtain what one Requires among Geometrical Propositions). The same letter by Ibn Qurra has come down to us under this title in two manuscripts. The first belongs to the collection Aya Sofya 4832, fols 1^v–4^r, in the Süleymaniye Library in Istanbul, here called A; the second is part of the collection 40, fols 155^v–159^v, here called C, of Dār al-Kutub in Cairo. These two manuscripts have also already been described.⁴⁰

3. Fī al-‘illa allatī lahā rattaba Uqlīdis ashkāl kitābihi dhalika altartīb (On the Cause of Euclid’s Ordering of the Propositions in his Book according to this Order). The letter has come down to us, under this title, in two other manuscripts. The first belongs to the collection Aḥmadiyya 16167, fols 86^v–90^v, in the Library of Tunis, here it is called T; the second is part of the famous collection Leiden, Or. 14, fols 380–388, here called L. We have described this collection and even discovered the models for twelve of the twenty-three treatises it comprises,⁴¹ that is the collection in Columbia University Library, Smith, Or. 45. So the only newcomer is the manuscript collection in Tunis.

This collection of 90 folios – size 13 × 21.5 cm – each with 23 lines of about 13 words, in nasta‘līq – was copied before 971/1563, the date when it was bought by one of its owners. The copyist himself has not indicated either the date or the place of his copy. The collection comprises the following treatises:

1. Commentary on Euclid’s Postulates by Ibn al-Haytham (Sharḥ muṣādarāt Uqlīdis), fols 1^v–59^v; folio 60^r is blank.

2. Additions by al-‘Abbās ibn Sa‘īd to Book Five of Euclid (Ziyādāt al-‘Abbās ibn Sa‘īd fī al-maqāla al-khāmisa min Uqlīdis), fols 60^v–61^r.

3. Remarks from the Commentary on Book Ten of the Work of Euclid, Composed by al-Ahwāzī (Kalimāt min sharḥ al-maqāla al-‘āshira min kitāb Uqlīdis), fols 61^v–65^r.

4. Commentary on the Introduction to Book Ten of Euclid by Abū Ja‘far Muḥammad ibn al-Ḥasan al-Khāzin (Tafsīr ṣadr al-maqāla al-‘āshira min Uqlīdis li-Abī Ja‘far Muḥammad ibn al-Ḥasan al-Khāzin), fols 65^v–71^r.

5. Anonymous letter on the Fifth Postulate of Euclid, fols 71^v–73^r.

6. Treatise by al-Fārisī who Makes Additions to al-Abharī’s Edition on the Famous Problem of the Book of Euclid (Maqāla li-al-Fārisī yuḍīfu ‘alā taḥrīr al-Abharī fī al-masā’il al-mashhūra min kitāb Uqlīdis), fols 73^r–75^r.

7. Book by Abū Dāwud Sulaymān ibn ‘Iṣma on Binomials and Apotomes in Book Ten of the Work by Euclid (Kitāb Abī Dāwud Sulaymān ibn ‘Iṣma fī zawāt al-ismayn wa al-munfaṣilāt allatī [ms. alladhī] fī al-maqāla [ms. al-maqālāt] al-‘āshira min kitāb Uqlīdis), fols 76^v–85^v.

8. A fragment, complementing the preceding book, fols 85^v–86^v.

Now a detailed comparison of T with L allows us to show that treatises 3, 4, 6, as well as the letter by Thābit, are respectively the sole models for treatises 19, 18, 20 and 21 of the Leiden collection, Or. 14. This important finding concerning the history of the text permits us to draw conclusions regarding 17 of the 26 treatises that make up L. We have already identified the single model transcribed by the copyist of L for twelve treatises.⁴² Adding in these four extra treatises, we now know the models that were copied for 16 treatises. Further, the model for al-Ṭūsī’s edition of the last three books of Apollonius’ Conics, which is part of this collection, is also known. So we could have set aside the variants of L in establishing the text of Ibn Qurra’s letter; if we have noted them, it is because they provide evidence for what we have just said, namely that T is the sole model for L for this treatise, as for the three others mentioned earlier. T and L have in common three omissions of a sentence and of twenty-three words, while L has eleven omissions of a word that are specific to it.

If we now examine the relationships between the other manuscripts, we may note, among other results:

• The copyist of A had two copies at his disposition. Thus, he writes in the colophon, fol. 4^r:

So manuscript A is copied from two manuscripts A₁ and A₂. However, A is missing a sentence (kānat al-zāwiyatān al-bāqiyatān mutasāwatayn), fol. 2^v. The copyist has indicated with a cross the place where this is missing, but has forgotten to transcribe the missing sentence.

• The copyist of C – the famous Muṣṭafā Ṣidqī – writes in the colophon that he had transcribed the text from a copy in the hand of Avicenna:

We have discussed this relation of a somewhat legendary tale and shown that C and A have a common ancestor. In any case, for Ibn Qurra’s letter alone, they present twelve common omissions of a word, while C has two omissions of a word that are specific to it. As for the sentence omitted in A, Muṣṭafā Ṣidqī could easily have completed it, given his mathematical education.

• Manuscript B in the hand of al-Sijzī contains five omissions of a word that are specific to it.

Examining the variants – additions, errors, etc. – leads us to propose the following stemma:

Ibn Qurra’s text has been edited from manuscript B alone by A.S. Saidan, in an edition we shall call S in the apparatus criticus; it has never been the subject of a translation or commentary.

3.2. To Smooth the Paths for Determining Geometrical Propositions, by al-Sijzī

Al-Sijzī’s treatise has come down to us in a single manuscript which belongs to the collection of Nabī Khān and Obaidur-Rahman Khan of Lahore. This collection includes, among many other treatises by different mathematicians, six writings by al-Sijzī. All the treatises in this collection were copied in the Niẓāmiyya school in Mosul and in the school of Baghdad, between 554 and 557 of the Hegira (1159–62). As for the six texts by al-Sijzī, they were transcribed in Baghdad from the year 556 and in the course of the year 557. The book whose text is translated here appears before two short works by al-Sijzī: a letter to Naẓīf ibn Yumn, copied at the Niẓāmiyya school in Baghdad at the end of the month of Rabī‘ al-ākhir in the year 557 of the Hegira (bi-tārikh salkh shahr Rabī‘ alākhir sanat sab‘ wa-khamsīn wa-khamsimi’at hijriya), that is in mid April 1162; and the other one is on the two means and the trisection of an angle, transcribed in the same city and in the same school, at the beginning of Jumādā al-ūlā in the year five hundred and fifty-seven (bi-tārikh ghurrat Jumādā al-ūlā li-sanat sab‘ wa-khamsīn wa-khamsimi’at), that is at the end of April 1162. So it is very probable that the treatise whose text is translated here was transcribed at about that date, that is the end of 556-beginning of 557, in the Niẓāmiyya school of Baghdad. This text covers folios 2–27 in nasta‘līq script; the figures are drawn carefully and the whole thing is done with care. There are neither additions nor glosses in the margins of the manuscript. The copyist wrote his name at the end of the other texts, but it remains illegible.

The attribution of this treatise to al-Sijzī is not in doubt. The work in fact appears on both the lists of his writings that we possess: the first transcribed by the copyist of the manuscript Chester Beatty 3652, fol. 2^r, no. 34, under the title Fī tashīl al-subul li-istikhrāj al-ashkāl al-handasiyya (To Smooth the Paths for Determining Geometrical Propositions); the second by the copyist of the manuscript from Lahore, fol. 371^v, under the same title. Al-Sijzī himself cites it several times, as for example in his treatise On the Asymptotes to an Equilateral Hyperbola,⁴³ or in his Reply to Geometrical Problems Raised by the People of Khurāsān (Jawāb al-Sijzī ‘an masā’il handasiyya sa’ala ‘anhu Ahl Khurāsān), Chester Beatty 3652, fol. 57^v.

This text was published for the first time by A. S. Saidan in The Works of Ibrāhīm ibn Sinān, Kuwait, 1983, pp. 339–72. Our late friend, no doubt aware of the importance of this work by al-Sijzī, as of that of Thābit ibn Qurra, but in all probability pressed for time, may have wished to draw historians’ attention to these texts by getting them published, albeit in a form that is at best provisional (called S). It is this publication of al-Sijzī’s text that J. P. Hogendijk reproduced,⁴⁴ while, however, adding some corrections, the majority of which are due to comparing A. S. Saidan’s text with the only extant manuscript. This comparison, which was certainly necessary, would have been welcome had it not left unchanged not only most of the mistakes, but also the mutilations that the manuscript had undergone, and if the checking had not itself afforded an opportunity for new errors. The errors unfortunately remain excessively numerous and prevent a true understanding of al-Sijzī’s text. It is this publication (called H) which was translated into English, often in a free manner.⁴⁵

3.3. Letter of al-Sijzī to Ibn Yumn on the Construction of an Acuteangled Triangle

This text was edited from the autograph version by al-Sijzī, composed in the month of Ābān 339 of the era Yazdegerd,⁴⁶ Bibliothèque nationale, Paris, no. 2457, fols 136^v–137^r, called B. We have also used another copy – Lahore, fols 28–30, called L – of this same text, although we knew this was not in any way necessary.

J. P. Hogendijk has published an edition of this text that is comparable with the one he produced of the preceding treatise; in our apparatus criticus it will be called H.

3.4. Two Propositions from the Ancients on the Property of Heights of an Equilateral Triangle: Ps-Archimedes, Aqāṭun, Menelaus

The propositions of the ancients taken up by Ibn al-Haytham have come down to us in two versions, one attributed to Archimedes, translated by Thābit ibn Qurra (ms. Patna, Khuda Bakhsh 2519, fols 142^v–143^r);⁴⁷ the other to a certain Aqāṭun (ms. Istanbul, Süleymaniye, Aya Sofya 4830, fols 91^v–92^r),⁴⁸ as well as in a text by al-Sijzī with the title On the Properties of Perpendiculars Dropped from the Given Point to the Given Equilateral Triangle by the Method of Discussion (mss Dublin, Chester Beatty 3652, fol. 66^v – called B; Istanbul, Reshit 1191, fols 124^v–125r^r– called R).⁴⁹ We have discussed⁵⁰ the probable relations between these three texts, of which we give translations here.

 

________________

¹ R. Rashed and H. Bellosta, Ibrāhīm ibn Sinān. Logique et géométrie au X^e siècle, Leiden, 2000.

² Thābit ibn Qurra addresses this letter to Ibn Wahb; but which one? The family of the Banū Wahb, a family of ministers, secretaries of state and men of letters, had moved in the circles of power in Baghdad for at least a century. Except for the founder, Wahb himself, secretary of the famous Barmecide and a minister of Hārūn al-Rashīd, Ja‘far (d. January 803), all the others, his sons, grandsons and great grandsons, could have been the Ibn Wahb to whom Ibn Qurra refers. Ibn Qurra does nothing to help us: he does not give any date for his letter, nor the first name or title of his correspondent.

A first possible candidate is Sulaymān ibn Wahb (d. 885). Thābit was already in Baghdad and, with his protectors and teachers, the Banū Mūsā, moved in the circles of power. Two other possible candidates are the two sons of Sulaymān: Aḥmad, secretary of state for taxations, celebrated literary expert and poet, the subject of a brief biography by Yāqūt in his Mu‘jam al-Udabā’ (ed. Būlāq, Cairo, n.d., vol. III, pp. 54–63); or ‘Ubayd Allāh, a minister of the Caliph al-Mu‘taḍid for about a decade, who died in 900, and was thus also a contemporary of Thābit ibn Qurra. It is also possible that Thābit is addressing this letter to al-Qāsim, the son of ‘Ubayd Allāh, with whom he shared ministerial responsibilities before himself becoming a minister on his father’s death. It was exactly for this same al-Qāsim that Ibn Qurra wrote his Talkhī.s (summary) of Aristotle’s Metaphysics. This latter essay has the title Treatise by Thābit ibn Qurra on the Summary of what Aristotle Presents in his Book on Metaphysics … written for the Minister Abū al-Ḥusayn al-Qāsim ibn ‘Ubayd Allāh. It is possible that this same al-Qāsim, who was interested in metaphysics, might be the person who was interested in Euclid’s Elements, and above all in the method of discovery. In any case, in the present state of knowledge, this last suggestion seems the best one (see for example D. Sourdel, Le Vizirat abbaside, Institut Français de Damas, Damascus, 1959–60, vol. I, pp. 300–1, pp. 329–57; vol. II, p. 745).

³ Ramus (Pierre de la Ramée) had questioned the order propositions in Euclid’s Elements: ‘Ordo Euclidis displicuit Petro Ramo, quemadmodum ex iis intelligitur, quae in Scholis Mathematicis lib. 6 et sqq., contra Euclidem passim disputat’, quoted in Antoine Arnauld and Pierre Nicole, La Logique ou l’art de penser, contenant, outre les règles communes, plusieurs observations nouvelles, propres à former le jugement, a critical edition with an Introduction by Pierre Clair and François Girbal, coll. Le mouvement des idées au XVIIe siècle, Paris, 1965.

⁴ La Logique ou l’art de penser, reference in the previous note.

⁵ For the editio princeps of the Arabic text together with a French translation, see Les Mathématiques infinitésimales du IX^e au XI^e siècle, vol. IV: Méthodes géométriques, transformations ponctuelles et philosophie des mathématiques, London, 2002.

⁶ R. Rashed and H. Bellosta, Ibrāhīm ibn Sinān. Logique et géométrie au X^e siècle, p. 96.

⁷ Ibid., pp. 21–56.

⁸ Ibn Sinān, Maqāla fī ṭarīq al-taḥlīl wa-al-tarkīb fī al-masā’il al-handasiyya, ms. Paris, Bibliothèque nationale, no. 2457, fols A^v–18^v.

⁹ See R. Rashed and H. Bellosta, Ibrāhīm ibn Sinān. Logique et géométrie au X^e siècle, p. 89.

¹⁰ Kitāb Thābit ibn Qurra ilā Ibn Wahb fī al-ta’attī li-istikhrāj ‘amal al-masā’il al-handasiyya, ms. Paris, Bibliothèque nationale, no. 2457, fols 188^v–191^r; see Les Mathématiques infinitésimales, vol. IV, pp. 742–65, and below, pp. 581–9.

¹¹ R. Rashed, ‘Al-Sijzī et Maïmonide: Commentaire mathématique et philosophique de la proposition 11–14 des Coniques d’Apollonius’, Archives internationales d’histoire des sciences, vol. 37, no. 119, 1987, pp. 263–96. See also P. Crozet, ‘Al-Sijzī et les Éléments d’Euclide: Commentaires et autres démonstrations des propositions’, in A. Hasnawi, A. Elamrani-Jamal and M. Aouad (eds), Perspectives arabes et médiévales sur la tradition scientifique et philosophique grecque, Paris, 1997, pp. 61–77.

¹² Ibid.

¹³ He considers the example of Proposition II.4 of the Conics, which concerns the asymptotes of a rectangular (equilateral) hyperbola.

¹⁴ Les Mathématiques infinitésimales du IX^e au XI^e siècle, vol. I: Fondateurs et commentateurs: Banū Mūsā, Thābit ibn Qurra, Ibn Sinān, al-Khāzin, al-Qūhī, Ibn al-Samḥ, Ibn Hūd, London, 1996, pp. 885 ff.; English trans. Founding Figures and Commentators in Arabic Mathematics, A History of Arabic Sciences and Mathematics, vol. 1, Culture and Civilization in the Middle East, London, 2012.

¹⁵ The term naql, from the verb naqala (to displace), which was already present in the lexicon in the ninth century. Thābit ibn Qurra uses it, first, to mean a displacement to superimpose two figures, and goes on to modify its meaning so that it signifies a displacement of a magnitude in a continuous motion, that is a transformation. See the text by Thābit ibn Qurra with title If we extend two straight lines at two angles less than two right angles, they meet one another (see R. Rashed and C. Houzel, ‘Thābit ibn Qurra et la théorie des parallèles’, in R. Rashed [ed.], Thābit ibn Qurra. Science and Philosophy in Ninth-Century Baghdad, Scientia Graeco-Arabica, vol. 4, Berlin, 2009, pp. 27–73, especially pp. 42–7). Al-Sijzī, who knew this text (since he made a copy of it), in turn modifies the meaning of the term, as in this treatise it is used for a similarity, thus confirming the tendency, already found in Thābit ibn Qurra, who uses the term naql for a geometrical transformation: translation or a similarity and so on.

¹⁶ See p. 596.

¹⁷ R. Rashed, Les Mathématiques infinitésimales du IX^e au XI^e siècle, vol. III: Ibn al-Haytham. Théorie des coniques, constructions géométriques et géométrie pratique, London, 2000; English translation by J. V. Field: Ibn al-Haytham’s Theory of Conics, Geometrical Constructions and Practical Geometry. A History of Arabic Sciences and Mathematics, vol. 3, Culture and Civilization in the Middle East, London/New York, 2013, Chap. III.

¹⁸ A. M. Legendre, ‘Réflexions sur les différentes manières de démontrer la théorie des parallèles ou le théorème sur la somme des trois angles du triangle’, Mémoires de l’Académie des sciences, 12, 1833, pp. 367–410.

¹⁹ The triangles ABH and CBH have a common base BH, so their areas are in the ratio of the heights AA′ and CC′ from A and C. Now 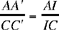in the homothety with centre I. So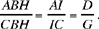

²⁰ See p. 607.

²¹ See apparatus criticus in Les Mathématiques infinitésimales du IXe au XIe siècle, vol. IV, on p. 799, 16.

²² See p. 607.

²³ Ibn al-Haytham takes up this proposition and varies the conditions; see R. Rashed, Les Mathématiques infinitésimales du IXe au XIe siècle, vol. V: Ibn al-Haytham: Astronomie, géométrie sphérique et trigonométrie, London, 2006; English translation by J. V. Field: Ibn al-Haytham. New Spherical Geometry and Astronomy, A History of Arabic Sciences and Mathematics, vol. 4, Culture and Civilization in the Middle East, London/New York, 2014. See also Géométrie et dioptrique, pp. 248 sqq.

²⁴ Triangle KAC is isosceles, so the perpendicular bisector of KC passes through A; it is the axis of symmetry of the triangle KAC and of the circle (A, AG); so KH = GC and arc HE = arc GI and parts KHE and CGI (curvilinear triangles) are equal.

²⁵ Note that the names of the points A and C are reversed in this new proof.

²⁶ If the circle (E, ED) touches the straight line BC, we have CD ⊥ AE, so AD̂C = 1 right angle and 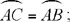which is impossible because

The point G can lie below the straight line CD without the angle ADC being acute (see case 3); but that requires

 

The condition was not considered by al-Sijzī, and the proof that is given does not apply in this case.

²⁷ We may note that the figure drawn in the manuscript, which is not very clear, seems to show a semicircle ACB. The argument is the same for a circle. We may have ACB ≤ π or ACB > π.

²⁸ In fact, let A′B′ be an arc of the same circle such that the arc A′B′ is equal to the arc AB, A′B′ is not parallel to CD; then we have A′B′ = AB. So

 

 

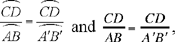
and consequently

 

 

²⁹ See pp. 151–2.

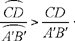
³⁰ Al-Sijzī’s Treatise on Geometrical Problem Solving (Kitāb fī Tashīl al-Subul li-Istikhrāj al-Ashkāl al-Handasiyya), translated and annotated by Jan P. Hogendijk, with the Arabic text and a Persian translation by Mohammad Bagheri, Tehran, 1996, Arabic p. 18; English trans. p. 31. Cf. our edition in Les Mathématiques infinitésimales, vol. IV, pp. 724–5.

³¹ Lit.: I mean.

³² R. Rashed and P. Crozet, Al-Sijzī, OEuvres mathématiques, forthcoming.

³³ We have

 

 

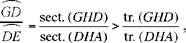
because

sect. (GHD) > tr. (GHD) and sect. (DHE) < tr. (DHA).

But

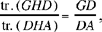
hence

³⁴ See p. 619.

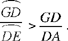
³⁵ Shakl was in fact the term the Arabic translators used to render διάγραμμα, when they met it, or, more frequently still, καταγραφή and θεώρημα. Thus, when Apollonius writes in Conics, I.53, ἐν τῷ μθ´ θεωρήματι, the Arabic translator writes fī shakl 49. Examples of this translation are too numerous to merit further discussion here.

It remains that, in contexts like this, it has been possible for the same term θεώρημα to be rendered by the Arabic ṣūra (form). For example when Apollonius writes τοῦτο γὰρ δέδεικται ἐν τῷ ια´ θεωρήματι (Conics, I.52), the Arabic translator writes wa-qad tabayyana dhālika fī al-ṣūra 11 (this has been shown in the ṣūra 11); or again when he writes ταῦτα γὰρ ἐν τῷ ιβ´ θεωρήματι δέδεικται (Conics, I.54), what we read in the Arabic translation is kamā tabayyana fī al-ṣūra 12 (as was shown in the ṣūra 12). The term ‘theorem’ has thus been rendered indifferently as shakl and as ṣūra. So in regard to terminology the situation is more complex than may at first appear.

We may start by noting that there is some stability in Arabic geometrical vocabulary from about the mid ninth century onwards. This of course does not prevent a certain amount of innovation and a certain amount of adjustment. The terms shakl and ṣūra provide examples of adjustment. The first term, shakl, is stable, and retains its double sense in the geometrical lexicon. As for the term ṣūra, it keeps some links with its primary usage, whereas others are modified to apply to a geometrical drawing. Thus, in mathematical writings, ṣūra carries multiple meanings:

1. The ‘form’ of an object, that is its essence; thus we speak of the form of a ratio, or of a number, and so on.

2. The sense of a state of the proposition itself, for example universal or special.

3. The sense of a case of the figure for a proposition which has several.

4. The sense of a possible form of a geometrical object, for example the form of a triangle: isosceles, right-angled and so on. All these senses apply to propositions or geometrical objects, without any special reference to a figurative representation, that is to a drawing.

5. Finally, there is the sense of ṣūra: form, as an image, and expressing the sense of a graphic representation. Thus we speak of ṣūrat shakl, the form of a figure, that is the drawing of a figure, or the figure as a representation. It seems, but this is conjectural, that after a time writers gave up using the term ṣūra to designate a theorem, but did so while retaining all its other senses. The result is that to the double meaning of shakl there is added the multiplicity of meanings of ṣūra, without any possibility of setting up an opposition between the two terms. The glossaries of the four previous volumes provide a sufficient number of occurrences of these meanings.

³⁶ In this connection, see P. Crozet, ‘À propos des figures dans les manuscrits arabes de géométrie: l’exemple de Siǧzī’, in Y. Ibish (ed.), Editing Islamic Manuscripts on Science, Proceedings of the Fourth Conference of al-Furqān Islamic Heritage Foundation, 29th–30th November 1997, London, 1999, pp. 131–63, esp. pp. 140–3.

³⁷ See Les mathématiques infinitésimales, vol. I, p. 145; al-Qifṭī, pp. 116–17.

³⁸ The multiple titles each of which, as we shall see, expresses one aspect of the letter, have been a cause of confusion for bibliographers. Some have believed we had three different texts by Thābit ibn Qurra and have catalogued them as such. Thus, F. Sezgin in his Geschichte des arabischen Schrifttums includes this same letter as numbers 4, 7 and 22, in the belief that he was dealing with three different treatises, pp. 268–70.

³⁹ See for instance Les Mathématiques infinitésimales, vol. I, pp. 147–8, 680; English trans. pp. 125, 465.

⁴⁰ Ibid., vol. I, pp. 147–9, 679; English trans. pp. 124–9, 464–5.

⁴¹ Ibid., vol. III, pp. 532–4; English trans. pp. 506–8.

⁴² Ibid., vol. III, p. 534.

⁴³ R. Rashed, ‘Al-Sijzī et Maïmonide: Commentaire mathématique et philosophique de la proposition II–14 des Coniques d’Apollonius’, p. 288.

⁴⁴ Al-Sijzī’s Treatise on Geometrical Problem Solving (Kitāb fī Tashīl al-Subul li-Istikhrāj al-Ashkāl al-Handasiyya), translated and annotated by Jan P. Hogendijk.

⁴⁵ See the apparatus criticus in Les Mathématiques infinitésimales, vol. IV, and the review by P. Crozet in Isis, 90.1, 1999, pp. 110–11.

⁴⁶ The month persan of Ābān 339 of the era of Yazdegerd is between 20 October and 18 November 970 in our era. There are five Thursdays in that interval: the 20 and 27 October and the 3, 10 and 17 November. Since ‘day’ can only refer to the 8th, 15th or 23rd day of this month, the date that is indicated can correspond to two days: 27 October or 3 November 970.

⁴⁷ See the description of this manuscript p. 473.

⁴⁸ See p. 454, n. 8.

⁴⁹ See section 3.3.

⁵⁰ See pp. 453–4.