III. ANALYSIS AND SYNTHESIS: EXAMPLES OF THE GEOMETRY OF TRIANGLES
According to the tenth-century biobibliographer al-Nadīm, Archimedes composed two books devoted exclusively to the geometry of triangles: The Book on Triangles and The Book on the Properties of Right-angled Triangles.1 Again according to al-Nadīm, Menelaus too was the author of a Book on Triangles, of which ‘a small part has been translated into Arabic (wa-kharaja minhu ilā al-‘arabī shay’ yasīr)’.2 On the basis of this testimony, it seems that ancient mathematicians had singled out triangles by dedicating specialised texts to them, and that at least two of these were translated into Arabic. Given its association with the illustrious name of Archimedes, there was every chance that the subject would be taken up by his successors, in particular by the mathematicians of the tenth century; but the historical research required to establish the details still remains to be done. For the time being, al-Sijzī provides an example that supplies a partial answer to our questions. He too wrote a book called On Triangles.3
So we would expect that Ibn al-Haytham, who wrote a monograph on the ‘properties of circles’ and a treatise on the ‘properties of conic sections’, would also have written a book about triangles. He did not do so expressly, but he did write two short treatises on the geometry of triangles. One has come down to us under the simple title On a Geometrical Problem and the other under the more explicit title On the Heights of Triangles or On the Properties of the Triangle in Regard to Height. In both of these texts, Ibn al-Haytham’s work follows on from what was done by his predecessors; in the first treatise, his immediate predecessors – Ibn Sahl and al-Sijzī, and in the second one those he calls the ancients. In the former treatise he proceeds by analysis and synthesis, whereas in the second he gives only the synthesis.
1. On a geometrical problem: Ibn Sahl, al-Sijzī and Ibn al-Haytham
In his treatise on analysis and synthesis, Ibn al-Haytham makes use of a series of distinctions that he presents as being valid in all the mathematical disciplines of the quadrivium. The principal distinction is that between theoretical analysis and practical analysis (‘amalī). Theoretical analysis is applicable to propositions and theorems; practical analysis deals with constructions and the determination of an unknown magnitude or number. This distinction, which was already introduced by Thābit ibn Qurra and was taken up by his successors, reappears here. Practical analysis is not in any way to be identified with the ‘problematic’ analysis of Pappus, and this for two related reasons. On the one hand it in fact also includes geometrical constructions as well as the determination of unknown magnitudes and numbers; on the other hand, it is applicable to all the mathematical disciplines and not only to geometry. This practical analysis can in turn be subdivided into several types: when there is a single solution, when there are several solutions, when there may be an infinite number of solutions; when there is no diorism (that is, no discussion), when there is a diorism, and so on. Now, investigating the conditions for passing from one of these types to another is an interesting logical problem and one that is very fertile in yielding mathematical insights; it in fact requires that we return to the conditions for the problem and those for the construction, in order to change them. This change in the conditions from one type to another in turn constitutes a valuable method of invention; Ibn al-Haytham carries this out, as well as the transformation of a problem of the geometry of triangles that had already been considered, successively, by his direct predecessors Ibn Sahl and al-Sijzī.
One of the problems proposed by Ibn Sahl, and for which he provides the synthesis,4 is that of the construction of a triangle such that one of its sides is equal to a given straight line DC = 2c, and the sum of the other two sides is equal to a given straight line AB = 2a. Ibn Sahl imposes a supplementary condition, namely that all the angles of the triangle should be acute.
We know from the outset that it is necessary to have a > c. Ibn Sahl accordingly considers the ellipse with major axis AB = 2a, centre E, foci C and D, where EC = ED = c. Let us put IK = 2b as the minor axis (EK = b).
Any point X on this ellipse gives a triangle with base CD = 2c, and XC + XD = 2a. Thus, the problem has an infinite number of solutions.
The supplementary condition – that the triangle must have only acute angles – leads Ibn Sahl to consider the perpendiculars to the axis AB at C and D and the circle with diameter CD, in order to find the arcs of the ellipse on which to take X so as to ensure the triangle XCD satisfies the three conditions.
By hypothesis a > c and a > b; but we can have b > c, b = c, or b < c, which are the three cases Ibn Sahl investigates. The circle C with diameter CD cuts the straight line IK in K′.
• b > c, K′ lies inside the ellipse.
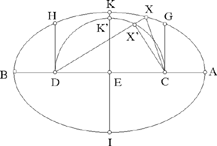
Fig. 2.3.1
For any point X on the arc GKH of the ellipse, X lies outside the circle C, DX̂′C = 1 right angle, so X̂ is acute. We also have that D̂ and Ĉ are acute and XC + XD = 2a = AB, except if X is at G or at H.
• b = c K = K′.
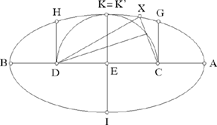
Fig. 2.3.2
Any point X on the arc GKH, except for G, K and H, makes X̂ acute, because X lies outside the circle; Ĉ and D̂ are acute.
• b < c K′ lies outside the ellipse.
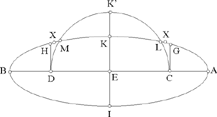
Fig. 2.3.3
The circle cuts the ellipse in L and M. Any point X on the arcs LG and HM, excluding the endpoints, lies outside the circle and makes X̂, Ĉ and D̂ acute.
This is Ibn Sahl’s solution, as given by al-Sijzī. It is clear that the idea of using an ellipse gives a solution immediately. But one can find a construction for such a triangle by means of straightedge and compasses, as al- Sijzī indeed noted. This is precisely what he says in a letter to Naẓīf ibn Yumn,5 to whom he communicates his own construction. But before we examine al-Sijzī’s solution, let us look in more detail at the one by Ibn Sahl.
If a point X provides a solution to the problem, that is if XCD is the triangle constructed with XC + XD = 2a and CD = 2c, which are given lengths, and if we extend CX by a length XM = XD, we have CM = 2a. The point M lies on the circle with centre C and radius 2a. Conversely, to any point M of this circle there corresponds a point X, the point of intersection of the straight line CM and the perpendicular bisector of MD,6 and the triangle CXD that we obtain satisfies the two given conditions.
But Ibn Sahl imposes a supplementary condition: the triangle CXD must have all its angles acute. Let us examine its three angles.
1. The angle DCX. It is acute if the straight half line [CX) lies within the angle FCE (E is the point of intersection of the circle (C, 2a) and the straight half line [CD)). Consequently, the angle DCX is acute if M is any point on the arc FE, apart from its endpoints (to the endpoint F there corresponds the point X’, the point of intersection of CF and the perpendicular bisector of DF).
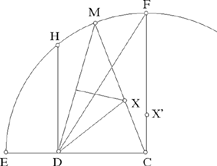
Fig. 2.3.4
2. The angle CDX. The perpendicular to CD at D cuts the circle in H. We shall have CD̂H = 1 right angle; if X is at X1 on the straight line DH, the point M then lies on the arc HE at the point M1 such that M1X1D is an isosceles triangle. In the triangle CM1D we have CD̂M1 = 1 right angle + M̂1, so
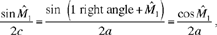
hence
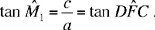
So we have HD̂M1 = M̂1 = DF̂C = FD̂H . The straight line HD bisects the angle FDM1. When M lies on the arc FM1, but not at either of its endpoints F and M1, then both XĈD and XD̂C are acute.
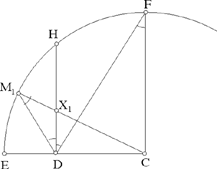
Fig. 2.3.5
3. The angle CX̂D. We have CX̂D = 2 CM̂D (Fig. 2.3.4); so for CX̂D to be acute, we must have CM̂D < 45°. Consequently, the point M must lie outside the arc that subtends 45° constructed on CD. This arc cuts the straight line DH in a point K whose position in regard to the point H depends on the given lengths 2a and 2c.
We have CDK, a right-angled triangle that is isosceles (because DK̂C = 45°), so DK = 2c and CK = 2c√2; CK is a diameter of the circle, on which we find the subtending arc. Moreover, by hypothesis we have CH = 2a and a > c, hence there are three possibilities:
• If c√2 < a, we have CK < CH (Fig. 2.3.6). The subtending arc lies completely inside the circle (C, 2a), so any point on the arc FM1, apart from the endpoints, gives a solution.
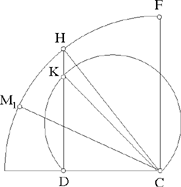
Fig. 2.3.6
• If c√2 = a, we have CK = CH (Fig. 2.3.7). The subtending arc and the circle (C, 2a) touch one another at the point H (K = H), so any point on the arc FM1, apart from the points F, H and M1, gives a solution.
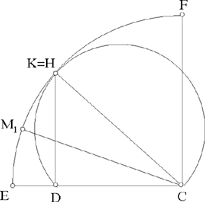
Fig. 2.3.7
• If c√2 > a, we have CK > CH (Fig. 2.3.8). The subtending arc cuts the circle (C, 2a) in two points M2 and M3 symmetrical with respect to the straight line CK, and it cuts the straight line CF in a point K′ such that CK′ = DK = DC = 2c. If a point describes the subtending arc from the point K to the point K′, its distance from the point C decreases from CK = 2c√2 to CK′ = 2c; so at one moment this distance takes the value 2a (because 2c < 2a < 2c√2); so the subtending arc cuts the arc HF of the circle with centre C at the point M2 and cuts the arc HE of the circle at the point M3. So we must investigate the positions of the points M1 and M3 that both lie on the arc HE. The triangles M1DC and M3DC have a common side CD, of length 2c, and the sides M1C and M3C are of equal length 2a. The angles M1DC and M3DC are obtuse; in triangle M3DC, we have
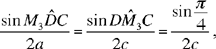
and in triangle M1DC,
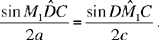
Now, we have seen that DM̂1C = DF̂C (Fig. 2.3.5) and in the present case
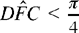 because F lies outside the subtending arc. So we have sin M1D̂C < sin M3D̂C and consequently M1D̂C > M3D̂C (because the angles are obtuse). We then have that M3 lies between M1 and H. So, if c√2 > a, to any point M on one or other of the arcs FM2 or M3M1 (apart from the endpoints) there corresponds a point X that gives a solution to the problem.
because F lies outside the subtending arc. So we have sin M1D̂C < sin M3D̂C and consequently M1D̂C > M3D̂C (because the angles are obtuse). We then have that M3 lies between M1 and H. So, if c√2 > a, to any point M on one or other of the arcs FM2 or M3M1 (apart from the endpoints) there corresponds a point X that gives a solution to the problem.
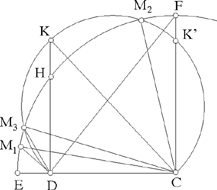
Fig. 2.3.8
Thus, the straightedge and compasses construction is possible and, in all cases for the figure, it leads to an infinity of solutions. The method employed here in the discussion that arises when we have the condition that the triangle should be ‘acute-angled’ leads us to consider the relative positions of a subtending arc and a circle.
However, Ibn Sahl’s method involves the relative positions of a circle and an ellipse, and, in the last case for his figure, the circle cuts the ellipse at the points L and M, for which Ibn Sahl gives no construction. We may also note that the three cases for the figure that are considered here (a > c√2, a = c√2 and a < c√2) correspond to the three cases examined by Ibn Sahl: b > c, b = c and b < c. In fact, given a2 = b2 + c2, if b = c, a2 = 2c2. The point X which lies on the ellipse can be found from the point M which lies on the circle with centre C and radius 2a. To the points F, M2, M3, M1 that come into play when M lies on the circle there correspond, for X, the points X’, X2, X3, X1 that are none other than the points G, L, M, H of the ellipse in the text by Ibn Sahl (Fig. 2.3.3 in this text). In fact, the circle with centre C and radius 2a is the ‘director circle’ of the ellipse; the latter is the locus of the centres of the circles that pass through D and touch the director circle at M.
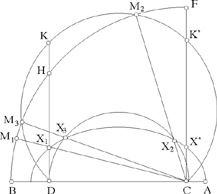
Fig. 2.3.9
So at the request of Naẓīf ibn Yumn, al-Sijzī looks again at Ibn Sahl’s problem. He makes his preference clear: he prefers not to have recourse to the intersection of two conics when the problem can be solved with straightedge and compasses. So he proceeds to construct an acute-angled triangle ABG whose base AB is given in position and in magnitude, and in which the sum of the two other sides is known (let AB = 2c and BG + AG = 2a). Al-Sijzī’s response is synthetic, but we can imagine how his analysis went.
Let ABG be a triangle that provides a solution to the problem; we extend AG by a length GE = GB; so we have AE = 2a, a known length. Moreover, the triangle GBE is isosceles, hence GB̂E = BÊG. So we have BĜA = 2BÊA , so angle BGA being acute corresponds to BÊA < 45°. So the point E lies on the circle with centre A and radius 2a, and outside the arc subtending 45° constructed on AB.
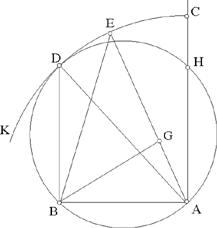
Fig. 2.3.10a
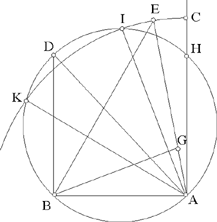
Fig. 2.3.10b
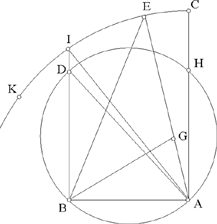
Fig. 2.3.10c
Al-Sijzī does not mention the ellipse with foci A and B and major axis 2a on which the point G lies. But it is clear that the whole problem is connected with constructing this ellipse point by point. Using the subtending arc leads to distinguishing the different cases for the figure, but al-Sijzī does not show that these different cases correspond to the equality or inequality of the lengths a and c√2.
Al-Sijzī’s discussion is incomplete; he does not in fact mention the angles A and B of the triangle ABG (the angles that must be acute) except in the last lines of his letter. He refers to the straight lines from A and B and concludes: ‘so let us take the triangle lying between the straight lines AC and BD which are parallel’. The point G obviously indeed lies between these straight lines, but the point E can move beyond the straight line perpendicular to AB at the point B. If we take E between the two straight lines AC and BD, we have a condition that is sufficient but not necessary.
However, as can be seen from the preceding commentary, using the method presented by al-Sijzī, we can provide a complete discussion which produces the results obtained by Ibn Sahl.
Ibn al-Haytham very probably knew the problem set out by Ibn Sahl, as well as the solutions proposed by him and by al-Sijzī. In any case, Ibn al- Haytham deals with this same problem, while substituting for the condition that the triangle has acute angles the condition that the triangle has a given area, S; which reduces to saying that the height XH (Fig. 2.3.11) measured from the base CD is of magnitude
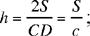 so h is thus a known length.
so h is thus a known length.
Fig. 2.3.11
Let us return to the preceding solution, that of Ibn Sahl; we have
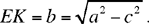 . We know that EK = b is the maximum ordinate for the points of the ellipse. If we now draw a straight line parallel to AB at a distance h from that straight line, we shall have the following cases:
. We know that EK = b is the maximum ordinate for the points of the ellipse. If we now draw a straight line parallel to AB at a distance h from that straight line, we shall have the following cases:
h > EK, the parallel line does not meet the ellipse; no point of the ellipse provides a solution to the problem;
h = EK, the required point X is at K and the triangle is isosceles;
h < EK, the parallel line cuts the ellipse in two points X and X’ which give two triangles that provide a solution to the problem. These triangles are equal.
So the necessary and sufficient condition for X to exist is h ≤ EK; now
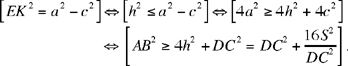
This condition, which is not mentioned by Ibn Sahl or al-Sijzī, is the one that Ibn al-Haytham gives in his diorism.
Ibn al-Haytham seems in fact not to have forgotten al-Sijzī’s recommendations. He returns to the problem using the inscribed circle of the triangle or the circumscribed one. So all the constructions he proposes can be carried out with straightedge and compasses.
Ibn al-Haytham gives five analyses of the transformed problem, one after the other. In the first four, he employs the inscribed circle of the triangle and in the fifth the circumscribed circle.
Let us summarise these analyses.
In the first four, let us call the triangle ABC, the centre of the inscribed circle I, let AB, BC, CA be the sides and their points of contact with the circle E, G and D respectively. Let us put BC = a the known side, AB + AC = l a known length, let S be the area of the triangle, a known area.
Analysis 1: The known lengths allow us to calculate
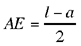 and
and
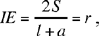 , the radius of the circle; tan
, the radius of the circle; tan
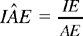 is known and the angle IAE is also known; so CÂB = 2 IÂE is known. We take K on BC such that AK̂C = BÂC; we prove that AK is known and that the triangles ABC and AKC are similar; hence AK · BC = AB · AC, so AB · AC is known. So we have that the sum l and the product p of the two sides are known, so the two sides are known.
is known and the angle IAE is also known; so CÂB = 2 IÂE is known. We take K on BC such that AK̂C = BÂC; we prove that AK is known and that the triangles ABC and AKC are similar; hence AK · BC = AB · AC, so AB · AC is known. So we have that the sum l and the product p of the two sides are known, so the two sides are known.
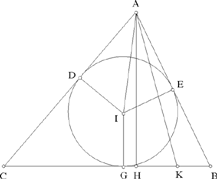
Fig. 2.3.12
Note: Ibn al-Haytham does not carry out the synthesis corresponding to this analysis. We may note that AB and AC are the roots of the equation x2 − lx + p = 0, where Δ = l2 − 4p. These roots are real if l2 ≥ 4p, that is if l2 ≥ a2 + 4h2, where h = AH the perpendicular to BC at H. In fact, we have
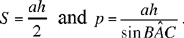
Now
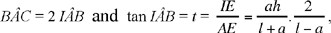
so
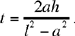
Moreover,
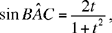
hence
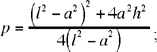
and we have
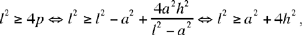
a condition that Ibn al-Haytham gives in the course of the synthesis for the fifth analysis.
Analysis 2: As in the first analysis the angles IAC and BAC are known. If we use the letter K to designate the point of intersection of the height AH and the line drawn through I parallel to BC, we prove that the angle IAK is known
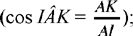 from this we deduce the angles KAE and ABC. Ibn al-Haytham draws his conclusion in two ways:
from this we deduce the angles KAE and ABC. Ibn al-Haytham draws his conclusion in two ways:
• 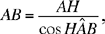 so AB is known and AC = l − AB is also known.
so AB is known and AC = l − AB is also known.
• We know that BÂC = 2 IÂB and A ̂BC; so the triangle ABC is of known shape and the ratio
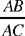 is known. Thus, the lengths AB and AC whose sum and ratio are known are themselves known.
is known. Thus, the lengths AB and AC whose sum and ratio are known are themselves known.
Fig. 2.3.13
Note: As before,
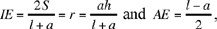 hence
hence
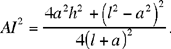
Moreover,
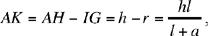
hence
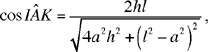
hence
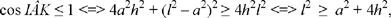
a condition that Ibn al-Haytham gives in the course of the fifth analysis.
Analysis 3: If we extend BA by a length AF = AC, the length BF = l is known and we have CF ∥ AI. We then prove that the triangle BCF is of known shape (that of BAH, in which we know the angles BAH [see Analysis 1] and ABH [see Analysis 2]), so the length CF is known. So the triangle AFC is also of known shape, and the ratio
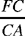 is known. So we know the length CA and from it we deduce AB = l − CB.
is known. So we know the length CA and from it we deduce AB = l − CB.
Note: Here one recognises a construction similar to that of al-Sijzī. The straight line FC is parallel to AH, the bisector of the angle BAC, a known angle, as we have seen in Analysis 1. If we put BÂC = 2α, we have AF̂C = FĈA = CÂH = α. Now
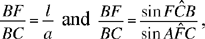
so sin
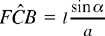 and angle FCB is thus known and we have
and angle FCB is thus known and we have
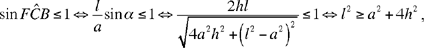
a condition that Ibn al-Haytham gives in the synthesis of the fifth analysis.
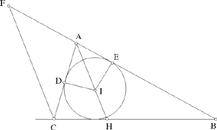
Fig. 2.3.14
Analysis 4: S, the area of the triangle ABC, is given and the angle BAC can be determined as in the first analysis. The product
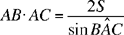 is known. As, by hypothesis, we also know the sum AB + AC, we can find each of the sides, as in the first analysis. In the same way, we can derive the necessary and sufficient condition.
is known. As, by hypothesis, we also know the sum AB + AC, we can find each of the sides, as in the first analysis. In the same way, we can derive the necessary and sufficient condition.
Analysis 5: Ibn al-Haytham considers the circle circumscribed about triangle ABC. The bisector of the angle BAC cuts BC in E and the circle in D. Using the property of E, as the foot of the bisector:
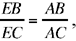 and the fact that the triangles ABD and BDE are similar, we prove that the ratio
and the fact that the triangles ABD and BDE are similar, we prove that the ratio
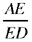 is known, and from it we deduce that the lengths DG (G is the mid point of BC; we have
is known, and from it we deduce that the lengths DG (G is the mid point of BC; we have
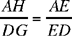 and AH is known), DB, DA, AE and ED are known. Now the power of the point E with respect to the circle gives EA · ED =
EB · EC, so the product EB · EC is known; as we know that
and AH is known), DB, DA, AE and ED are known. Now the power of the point E with respect to the circle gives EA · ED =
EB · EC, so the product EB · EC is known; as we know that
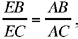 we deduce that the product AB · AC is known; but since, by hypothesis, the sum is also known, each of the straight lines AB and AC is thus known.
we deduce that the product AB · AC is known; but since, by hypothesis, the sum is also known, each of the straight lines AB and AC is thus known.
Fig. 2.3.15
Synthesis of 5: The base given for the construction is AB; the required vertex is the point M. The given lengths are GH and CD such that
(1) GH = MA + MB
(2) Area (AMB) = AB · CD.
So the height from M is MN = 2 CD = DE.
On GH we take a point I such that
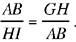 Let K be the mid point of AB and let L be a point on the perpendicular bisector of AB such that
Let K be the mid point of AB and let L be a point on the perpendicular bisector of AB such that
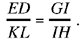 We draw the circumscribed circle of triangle ABL. On the straight half line LA, we take P such that
We draw the circumscribed circle of triangle ABL. On the straight half line LA, we take P such that
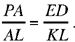 If the line drawn through P parallel to AB cuts the circle at the point M, then the triangle AMB is the triangle we require.
If the line drawn through P parallel to AB cuts the circle at the point M, then the triangle AMB is the triangle we require.
Proof: By hypothesis, we have
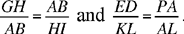
We draw MN perpendicular to AB, and ML, which cuts AB in F; we have
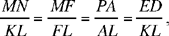
hence MN = ED.
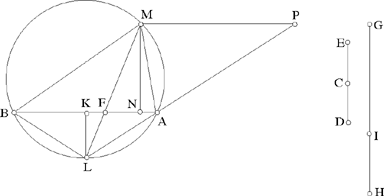
Fig. 2.3.16
So we then have area
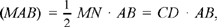 and (2) is satisfied. The point L is the mid point of the arc AB, hence arc BL = arc AL which implies BM̂L = AM̂L = BÂL; so the triangles AML and AFL are similar, and we have
and (2) is satisfied. The point L is the mid point of the arc AB, hence arc BL = arc AL which implies BM̂L = AM̂L = BÂL; so the triangles AML and AFL are similar, and we have
(1) 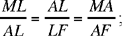
moreover,
(2) 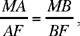
because F is the foot of the bisector of the angle BMA.
From (1) we deduce LA2 = ML · LF, and from (1) and (2) we deduce
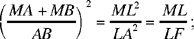
but
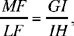
so
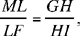
but
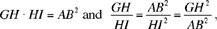
hence
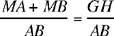
and finally MA + MB = GH.
So if the line parallel to AB cuts the circle in M, the triangle MAB provides a solution to the problem.
But, in this line of reasoning, we assume that the line drawn through P parallel to AB cuts the circle in M, which requires a discussion of the existence of this point M, a discussion to which Ibn al-Haytham turns his mind.
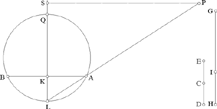
Fig. 2.3.17
Ibn al-Haytham then gives the condition GH2 ≥ AB2 + 4ED2. He first proves that if GH2 < AB2 + 4ED2, the problem is impossible. Next he proves a property which holds for any triangle, a property from which the condition (1) follows. He then returns to the discussion and proves that if GH2 = AB2 + 4ED2, we have ED = MN = KQ; M is at Q and the required triangle is isosceles.
Finally, he proves that if GH2 > AB2 + 4ED2, we have ED < KQ.
The straight line drawn through P parallel to AB cuts the straight line LQ between K and Q; so it cuts the circle in a point M of the arc QA and in a point M′ of the arc QB; the points M and M′ give the triangles MAB and M′AB, equal triangles, which are solutions to the problem. Ibn al-Haytham gives only the point M.
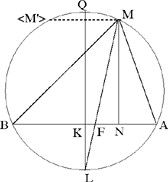
Fig. 2.3.18
Note: In the course of the discussion Ibn al-Haytham notes that any triangle AMB can be inscribed in a circle and proves that if we have GH = MA + MB and ED = MN (MN being the height of the triangle) and if LQ is the diameter perpendicular to the base AB at K, we have
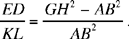
From this equality we can deduce
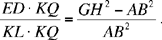
Now
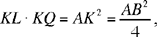
so we have
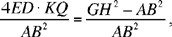
hence
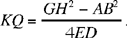
Constructing the point M is possible only if MN ≤ KQ (Euclid, Elements, III.15). Now
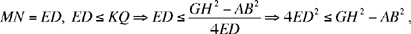
the necessary and sufficient condition.
We may ask ourselves why Ibn al-Haytham did not put the paragraph that begins ‘Indeed, in every case a triangle is inscribed in a circle …’ (p. 483) at the beginning of the discussion, and why he has not proved that, from the equality he has established,
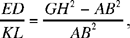 we can deduce the condition GH2 < AB2 + 4ED2 which he gives at the beginning of the discussion without explaining how it has been obtained. Perhaps it is a simple question of editing. Starting, as we have seen, from a problem proposed by Ibn Sahl, who solved it by using the intersection of conic sections, a problem then picked up by al-Sijzī, who looked for a solution by straightedge and compasses, Ibn al-Haytham transforms the problem and thus moves from one kind of analysis to another: from an indeterminate practical analysis to a determinate practical analysis. The obligation he adopts deliberately and almost systematically that, when it is required, he should give a proof of existence, led him to establish the existence of the point M, and then to prove the necessary and sufficient condition for there to be a solution to the problem. Thus, everything seems to point to the passage from one kind of analysis to another being one of the procedures in mathematical invention. Indeed, this research leads Ibn al-Haytham to discover new properties of the triangle in relation to its inscribed circle and its circumscribed circle.
we can deduce the condition GH2 < AB2 + 4ED2 which he gives at the beginning of the discussion without explaining how it has been obtained. Perhaps it is a simple question of editing. Starting, as we have seen, from a problem proposed by Ibn Sahl, who solved it by using the intersection of conic sections, a problem then picked up by al-Sijzī, who looked for a solution by straightedge and compasses, Ibn al-Haytham transforms the problem and thus moves from one kind of analysis to another: from an indeterminate practical analysis to a determinate practical analysis. The obligation he adopts deliberately and almost systematically that, when it is required, he should give a proof of existence, led him to establish the existence of the point M, and then to prove the necessary and sufficient condition for there to be a solution to the problem. Thus, everything seems to point to the passage from one kind of analysis to another being one of the procedures in mathematical invention. Indeed, this research leads Ibn al-Haytham to discover new properties of the triangle in relation to its inscribed circle and its circumscribed circle.
2. Distances from a point of a triangle to its sides
In a second treatise with the title On the Properties of the Triangle in Regard to Height, Ibn al-Haytham proposes to study the sum of the distances from a point on one of the sides of the triangle or lying inside it, to the sides of the same triangle. The treatise is purely synthetic. In the preamble Ibn al-Haytham gives a clear explanation of his intention and its development. He starts by referring to the fact that the ancients had considered this problem for the case where the triangle is equilateral, and he gives the two propositions they had established. In regard to other triangles, no results had been found. Ibn al-Haytham accordingly takes up the problem for isosceles triangles, then for arbitrary triangles. He states that he has found, for one and the other variety ‘a uniform order’ (niẓām muṭṭarid, see below, p. 485), that is a formula sufficiently general to define the character of each class. We shall see that this is indeed so. Nonetheless, despite these interesting results, readers familiar with Ibn al-Haytham’s writings cannot but be disconcerted by this treatise. Ibn al-Haytham has indeed accustomed us to works that break new ground, always innovative and profound; now this text, although not entirely lacking in interest, nevertheless does not rise to such heights. The fact remains that this relatively modest contribution is shaped by the same principle that governed the composition of other, incomparably more important, works: the purpose is to complete what his predecessors had begun and to exploit all the potentialities to be found in their research. And in fact, this problem of the distance from a point of a triangle to its sides presents itself to Ibn al-Haytham as given prestige by the participation of the ‘ancients’ – somewhat like the example of the problem of the regular heptagon.7 But we may ask why Ibn al-Haytham chose the generic term, ‘the ancients’ (almutaqaddimūn), whereas he is not usually sparing in using names when he is dealing with authors as highly esteemed as Archimedes. In short, we may wonder which ancients he is referring to.
A manuscript copied at the beginning of the thirteenth century informs us of the existence of a text attributed to Archimedes, with the title On the Foundations of Geometry (Fī al-uṣūl al-handasiyya), a work translated by Thābit ibn Qurra. The attribution to Archimedes appears in the title, together with the name of the translator, and it is repeated in the colophon.8 This is a treatise that includes nineteen propositions, the first of which is proved twice. Better still, in the title we find not only the name of the mathematician of Syracuse and that of the prestigious translator, but also the name of the person who commissioned the translation: Abū al-Ḥasan ‘Alī ibn Yaḥyā, the friend and protégé of the Caliph al-Mutawakkil and the son of Caliph al-Ma’mūn’s astronomer Yaḥyā ibn Abī Manṣūr. So we are given a set of pieces of information that is perfectly coherent and plausible. Now this is the book in which we meet this problem of the distance from a point of a triangle to its sides in the single case of the equilateral triangle, as it was cited by Ibn al-Haytham as according to the ancients.9 We are only one easy step away from a claim that it is this treatise that Ibn al-Haytham was using. But on the other hand, no tenth-century source, biobibliographical, historical or mathematical, provides evidence that Archimedes wrote such a book, or that Thābit ibn Qurra translated a work with such a title into Arabic.
But yet another fact contributes to confusing a picture that has so far seemed to be clear. Another manuscript, also dating from the beginning of the thirteenth century, a manuscript of a book called Kitāb al-mafrūḍāt (Book of Hypotheses), contains all the propositions of the previous one plus twenty-four supplementary propositions; this time the whole thing is attributed to a certain Aqāṭun. The common propositions – nineteen or twenty depending on whether we count the first as one proposition or as two – are the same despite variations in the editing.10 As for the author, Aqāṭun, not only is he unknown, but there is no proof he ever existed. Furthermore, there is no ancient testimony to confirm that a book with such a title existed or was translated. But such a case is not unique, and other books are translated from Greek without our knowing the translator and without their being cited by early biobibliographers. In this particular case, however, careful examination shows that we in fact have a compilation by a late author, put together from several sources, mainly Greek. This is indeed the conclusion which those who have studied this book seem inclined to draw.11 So, rather than helping us to know ‘the ancients’ better, this book tends to complicate the situation.
But we are presented with two other testimonies, which make the situation even more complicated. The first comes from al-Nadīm, the early biobibliographer. He tells us that Thābit ibn Qurra did indeed translate a treatise with exactly this title, a work in three books. This work is not attributed to Archimedes but to Menelaus.12 Moreover, several other sources inform us of the existence of a work with this title and its translation into Arabic.13 To add to this precise information we have another testimony, from al-Sijzī one of the immediate predecessors of Ibn al-Haytham.
Not only has al-Sijzī had a copy of this book by Menelaus in his hands, but he also informs us about a part of its content that is of interest here: according to al-Sijzī, at the beginning of his book On the Foundations of Geometry (Fī al-uṣūl al-handasiyya) Menelaus considered the problem of the property of equality working from the perpendiculars drawn in the equilateral triangle to its perimeter. Not satisfied by the proof given by Menelaus, al-Sijzī proposes to work through all possible cases – for the equilateral triangle – when the point lies inside or outside the triangle.14 In his account, he presents, with his own proof, the propositions that Ibn al-Haytham attributes to the ‘ancients’.
This rather complicated situation and the small amount of available evidence merely increases the number of possibilities. For example, we might suppose that the Pseudo-Archimedes, the translation of whose work is attributed to Thābit ibn Qurra, formed part of an authentic Menelaus. we might also suppose that the compilation made by Aqāṭun contained part of the work in three books by Menelaus. Obviously, to become plausible, such a conjecture would require us to start by establishing critical editions of all these texts – something that has not yet been done – and to carry out a rigorous study of the history of the text. For the moment, it is enough to know that Ibn al-Haytham had access to the writings attributed to the ancients – Pseudo-Archimedes or genuine Menelaus – which had raised the question in regard to the equilateral triangle. The text by Menelaus had already been studied by al-Sijzī who had generalised the problem by discussing the case of points lying outside the equilateral triangle. Ibn al-Haytham, who probably knew about this work, wanted to go further still by investigating the case of other triangles – isosceles and scalene – but limiting himself to considering points lying inside the triangles, so as to be able to arrive at what we might call a canonical rule. But why did he not, like al-Sijzī, consider points lying outside the triangle? Even if he did not know al-Sijzī’s text, it would have been entirely natural for him to think about such points. Perhaps he wanted to look only at generalising the problem under exactly the conditions found in the ancients, that is only for points lying inside the triangle. We shall see later how easy it is to discuss the case of points that lie outside the triangle.
Thus, having readopted the case investigated by the ancients, Ibn al-Haytham considers the same question for an isosceles triangle, then for a scalene triangle. In this last case, he seems to stop at the investigation of the distances from an arbitrary point on one side of the triangle to the two other sides. However, Ibn al-Haytham’s treatise ends with the case of an arbitrary point that lies inside the scalene triangle. This final proposition contains an error that is, to say the least, surprising: not that Ibn al-Haytham never makes a mistake – that, obviously, happens to him as it does to everyone – but this type of error is one he never commits. The only reasonable suggestion is that a reader took it upon himself to complete Ibn al-Haytham’s treatise by adding a proposition, when the eminent mathematician intended to go no further. The single surviving manuscript of this text does not provide a basis for any textual argument that might put such a conjecture to the test. So all we have to go on is our knowledge of Ibn al-Haytham’s style and his mathematical works.
Ibn al-Haytham begins by setting out the two propositions established by the ancients with the proofs they provided, which he will use as lemmas:
a) Let there be an equilateral triangle ABC, and an arbitrary point D on one of the sides – for example AB –, then the sum of the distances DE and DG to the two sides BC and AC is constant and equal to the height of the triangle.
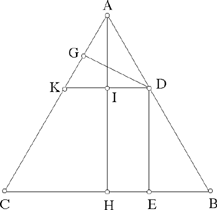
Fig. 2.3.19
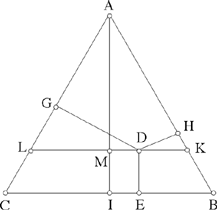
Fig. 2.3.20
b) The sum of the distances from an arbitrary point D inside an equilateral triangle ABC to the sides AB, BC, AC is constant and equal to the height of the triangle.
According to Ibn al-Haytham, these results were, so far, the only ones known. So the great question is to know how to extend them, with the necessary rigour, to the case of an isosceles triangle, then to an arbitrary one. So it is a matter of finding a similar property, even if it does not involve a constant as in the case of the equilateral triangle; which in fact means finding an expression for the sum of the distances in terms of a parameter. Ibn al-Haytham will first establish that the sum of the distances from a point D on one of the sides of an isosceles triangle, or inside it, to the sides of the triangle is constant for any point lying on a line parallel to the base of the triangle; the sum depends on the distance x from the parallel line to the base of the triangle. Then, as we shall see later, he looks at the scalene triangle.
Ibn al-Haytham begins by establishing two lemmas:
Proposition 1.—In any triangle, the heights are inversely proportional to the sides on which they stand.
Proposition 2.—Let ABC be a scalene triangle with a right angle at A; we draw the height AD, we take a point E on BC such that CD = DE and we draw AG, the bisector of the angle EAB; then GD = AD.
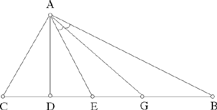
Fig. 2.3.21
After these lemmas, Ibn al-Haytham proves six propositions on the distances. The first four propositions relate to an isosceles triangle.
Proposition 3.—For any isosceles triangle ABC with vertex A, the sum of the distances from an arbitrary point D, taken on BC, to the sides AB and AC, is equal to the height drawn from the endpoints of the base.
For this proposition there are three cases for the figure depending on whether angle A is acute, a right angle or obtuse (see figures of the text, p. 489). Here we shall consider only one of the cases for the figure, to make the underlying ideas clear; the reasoning is identical in all the cases.
Let us put BC = a, AC = b, AB = c, AH = hA, CH = hC, DC = u, 0 < u < a. We have
DE = (a – u) sin B̂, DG = u sin Ĉ = u sin B̂,
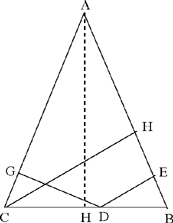
Fig. 2.3.22
hence
S = DG + DE = a sin B̂ = CH.
We can write
(1) 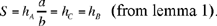
In the previous proposition Ibn al-Haytham considered an arbitrary point on the base of the triangle, in the following proposition he considers an arbitrary point on one of the equal sides of the isosceles triangle.
Proposition 4.— Let ABC be an isosceles triangle, D an arbitrary point on AB; we draw DG ⊥ BC and DH ⊥ AC. Let AE be the height from A, on which we define the two points I and L such that
(1)
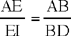 and (2)
and (2)
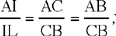
we then have
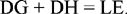
For this proposition there are again three cases for the figure; let us take one of them to make the underlying ideas clear.
The position of D on AB can be described by DG = x, DG = IE, so AI = hA – x. Now
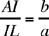
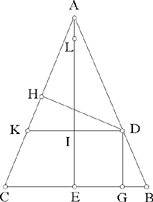
Fig. 2.3.23
implies
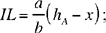
but
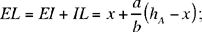
now
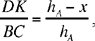
hence
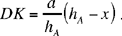
But
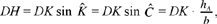
so
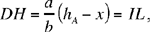
and
(2) 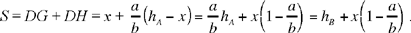
We may note that, if a = b, the triangle is equilateral and we then find DG + DH = hA, the result (a) obtained by Ibn al-Haytham’s predecessors.
In the following proposition, Ibn al-Haytham considers an arbitrary point inside the isosceles triangle and investigates the sum of its distances from the three sides; he proves that for any point on a line parallel to the base, the sum of the distances can be expressed in terms of the distance of the parallel from the base of the triangle.
For this proposition also there are three cases for the figure (see text, p. 490); let us take one of them to make the underlying ideas clear.
Proposition 5.—Let there be an isosceles triangle ABC; through an arbitrary point D inside the isosceles triangle we draw DE ⊥ AB, DG ⊥ AC, DH ⊥ BC. Let AK be the height of ABC. The line through D parallel to BC cuts AB in M, AK in I and AC in L. Let N be a point on the straight line AK such that
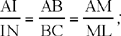 we prove that DE + DG + DH = NK.
we prove that DE + DG + DH = NK.
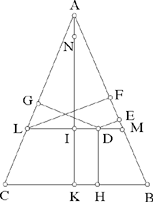
Fig. 2.3.24
We can see at once that the length KN depends on the position of the straight line LM but not on the position of D on this straight line. So let us work out the length of this segment KN.
Let us put DH = x and let us use the same lettering as before. We have AK = h A and IK = DH = x; hence AI = hA – x. But
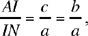
hence
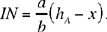
Now
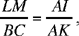
hence
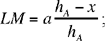
moreover,
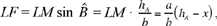
so
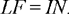
Now DE + DG = LF, from Proposition 3; so
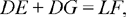
and
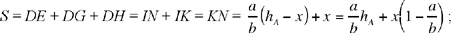
and by lemma 1 we have
(3) 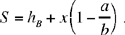
We may note that
• if a = b in (3), triangle ABC is equilateral and we obtain the result (a) obtained by Ibn al-Haytham’s predecessors: S = h.
• if x = 0, D lies on BC, the base of the isosceles triangle, and we have
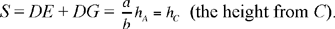
• if x ≠ 0, D lies on one of the two sides or on a straight line parallel to the base, and we have the relation (3).
Proposition 6. — This proposition is a corollary to Proposition 5. We consider BE the bisector of the angle B; we have
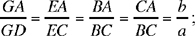
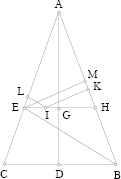
Fig. 2.3.25
If we put GD = x, we have
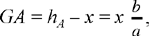 hence
hence
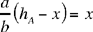
and from formula (3) we have
(4) 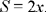
In Propositions 3, 4, 5, 6 Ibn al-Haytham derived a formula for finding the sum of the distances from a point on the equal sides of an isosceles triangle or inside it. He has proved that this sum depends on a parameter. It is constant only for the equilateral triangle and in the obvious case where the parameter is zero in the isosceles triangle, when the point lies on its base.
In the following proposition, Ibn al-Haytham deals with another property of the isosceles triangle. Starting from the height CE measured from the side AB, he proves that there are three magnitudes that are in continuous proportion.
Proposition 7. — Let ABC be an acute-angled isosceles triangle with AB = AC; we draw the heights AD and CE; then AB – CE, CE – EB and 2EB are in continuous proportion.
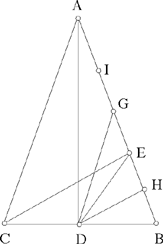
Fig. 2.3.26
Then, next, Ibn al-Haytham deals with an arbitrary triangle. He knows perfectly well that formula (3) does not apply in a more general case. He establishes in what cases this formula still holds, that is when the point is taken on one of the sides.
Proposition 8. — The sum of the distances from a point on a side of the scalene triangle to the two other sides is given by
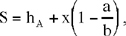
where x = DE, the distance from D to the side AC.
In the proof, the height used this time is the height from B.
Let us put BH = hB; we then have KB = hB – x.
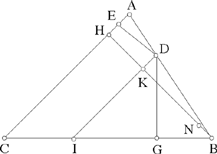
Fig. 2.3.27
Let us put
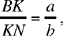
hence
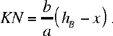
Moreover,
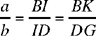 (by Proposition 1),
(by Proposition 1),
so KN = DG; and it follows that
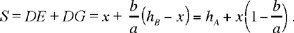
If we consider the height from A (as in Propositions 4 and 5), we then take DG as an unknown line parallel to that height (we interchange the roles of BC and AC as well as the letters a and b), and we have
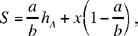 where x = DG
where x = DG
hence
(5)
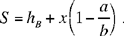
Following this proposition, there is a ninth proposition in which an effort is made to establish that this property holds for an arbitrary point. Let us first examine the content of this proposition before raising the question of its authenticity.
Let us start by presenting it as it appears in the manuscript.
Proposition 9. — Through a point D inside the scalene triangle ABC we draw DE ⊥ AB, DG ⊥ AC, DH ⊥ BC, LM ∥ BC which cuts the height AK in I. We take N on AI such that
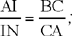 we prove that
we prove that
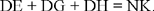
It is true – apart from one correction:
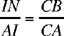 instead of
instead of
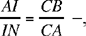 that
that
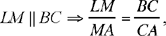
so
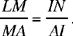
Even with this correction, the remainder of the proof is false.
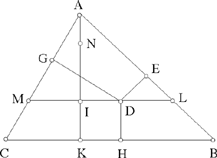
Fig. 2.3.28
In the statement of Proposition 9, the point I is defined by the equality
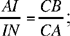 then we have
then we have
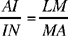 in the triangle ALM with height AI. In Proposition 8 on which Proposition 9 depends in the mind of the editor, the reasoning brings in the scalene triangle BDI with height BK, and the point N on BK defined by
in the triangle ALM with height AI. In Proposition 8 on which Proposition 9 depends in the mind of the editor, the reasoning brings in the scalene triangle BDI with height BK, and the point N on BK defined by
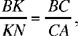 and we have
and we have
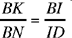 (see Fig. 2.3.26). But in Proposition 9 the height AI goes to LM and in Proposition 8 the height BK goes to ID. Further, in 8 the point D is a vertex of the triangle IBD and in 9 the point D is an arbitrary point of LM, the base of the triangle ALM. One cannot refer back to 8 to prove 9, though this is indeed what is done by the editor of the text.
(see Fig. 2.3.26). But in Proposition 9 the height AI goes to LM and in Proposition 8 the height BK goes to ID. Further, in 8 the point D is a vertex of the triangle IBD and in 9 the point D is an arbitrary point of LM, the base of the triangle ALM. One cannot refer back to 8 to prove 9, though this is indeed what is done by the editor of the text.
If we correct the text and put
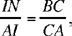 we return to the condition imposed in Proposition 5 in the case of an isosceles triangle ABC. Further, the figures for Propositions 5 and 9 are constructed in the same way, with the same lettering, and in 9 the expression ‘as it was proved earlier’ is undoubtedly a reference to Proposition 5. But the result DE + DG = IN is proved in 5 starting from the conclusion of Proposition 3 in which use is made of the similar triangles DLG and DME (DLE and DMG respectively in 9). The fact that these triangles are similar derives from the equality B̂ = Ĉ that implies L̂ = M̂; now in 9, B̂ ≠ Ĉ, so in Proposition 9 one cannot have DE + DG = IN. Let us find what this sum is.
we return to the condition imposed in Proposition 5 in the case of an isosceles triangle ABC. Further, the figures for Propositions 5 and 9 are constructed in the same way, with the same lettering, and in 9 the expression ‘as it was proved earlier’ is undoubtedly a reference to Proposition 5. But the result DE + DG = IN is proved in 5 starting from the conclusion of Proposition 3 in which use is made of the similar triangles DLG and DME (DLE and DMG respectively in 9). The fact that these triangles are similar derives from the equality B̂ = Ĉ that implies L̂ = M̂; now in 9, B̂ ≠ Ĉ, so in Proposition 9 one cannot have DE + DG = IN. Let us find what this sum is.
We have
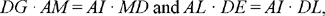
hence
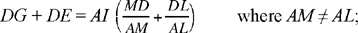
so this sum depends on the position of D on ML.
Now if we define N by
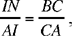 we have
we have
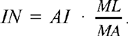 So, in Proposition 9, for a scalene triangle we necessarily have DE + DG ≠ IN and DE + DG + DH ≠ KN. It is not exactly controversial to say that this type of error is not the kind that Ibn al-Haytham might have committed. So it is likely that some editor thought he could complete Ibn al-Haytham’s text in this way.
So, in Proposition 9, for a scalene triangle we necessarily have DE + DG ≠ IN and DE + DG + DH ≠ KN. It is not exactly controversial to say that this type of error is not the kind that Ibn al-Haytham might have committed. So it is likely that some editor thought he could complete Ibn al-Haytham’s text in this way.
If this is so, we need to find a plausible explanation why Ibn al-Haytham did not present a proposition on the sum of the distances to the sides from a point inside a scalene triangle. Perhaps it is because this time the formula does not involve only a single parameter but two at a time, which makes it considerably less interesting. To illustrate this let us find the sum DE + DG in terms of what is given and the parameters that determine the position of D.
As before, let us put BC = a, AB = c, AC = b, AK = hA, DH = x, DL = y (see previous figure). We have
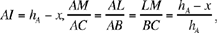
hence
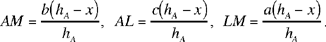
But
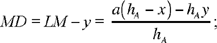
we have
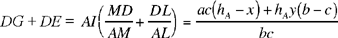
and
(6)
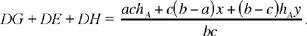
Thus, the sum depends on the three sides of the triangle, on a height and on two parameters.
Notes:
1. If D lies on AB as in 8, we have y = 0 and DE = 0, and we return to (5) starting from (6). In fact, (6) can be rewritten
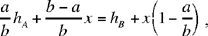
a result that depends on a single parameter.
2. If the triangle is isosceles, we have b = c and we obtain (3) starting from (6), a result that depends on a single parameter.
3. If in (6) we take the parameter x as given, which is the same as taking LM as given, the sum DG + DE + DH depends on the parameter y, that is it depends on the position of D on LM; so it will not be a sum that is constant, and it could not be represented by a segment such as the segment KN that appears in the text.
Perhaps these difficulties encountered in trying to provide a usable generalisation of a formula that describes the sum of the distances, to include the case of a point inside a scalene triangle, prevented Ibn al-Haytham from providing a proposition, which as presented here seems to be the work of an editor who was much less expert than Ibn al-Haytham; unless, perhaps, we should consider the possibility that we are dealing with a rather naïve investigation dating from his youth. Only further manuscript copies, from a manuscript tradition different from that of the copy we have, would allow us to return to this question.
4. There is, however, a linear combination of the three distances DE, DG and DH that remains constant, that is independent of the position of D, an arbitrary point inside the triangle or on one of its sides: this is c · DE + b · DG + a · DH which is always equal to the area of the triangle ABC. If D lies outside the triangle, we need to attach a suitable sign to each of the terms in the preceding sum in order to make it remain equal to the area of ABC.
Finally, let us turn to the question of the distances from exterior points to an equilateral triangle that was examined by al-Sijzī15 but was not considered by Ibn al-Haytham. The part of the plane outside the equilateral triangle ABC can be divided into six parts obtained by extending its sides. We have the three straight lines XBAX′, YCAY′ and ZCBZ′. With the vertex A we associate the region IA, or (XBCY), lying beyond BC; and the region IIA, enclosed by the angle X′AY′. In the same way to the point B there correspond the regions IB and IIB, and to the point C the regions IC and IIC.
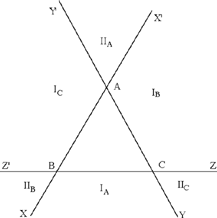
Fig. 2.3.29
Triangle ABC is equilateral, each of its sides is equal to the length a and the heights are each equal to
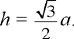 So it is sufficient to investigate the sum of the distances for any point situated in IA or IIA.
So it is sufficient to investigate the sum of the distances for any point situated in IA or IIA.
1. First let M be a point in IA, that is in the region (XBCY) and let the three distances be ME, MK, MI. Let AH be the height from A (AH = h); the line drawn through M parallel to BC cuts AX in B1, AY in C1 and AH in H1. Let us put ME = x, a parameter that determines the position of the straight line B1C1; we have AH1 = h + x. Moreover,
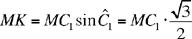
and
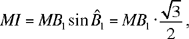
so
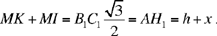
In fact, triangle AB1C1 is equilateral with height AH1 and M is a point on its base; we know from Lemma (b) (p. 457) that MK + MI = AH1.
We have that the sum
(1)
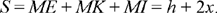
This sum is the same for any point M of the segment B1C1, including the endpoints. If x = 0, M is at E on BC and we have MK + MI = h, a result proved earlier.
So it follows that for any point M in the region XBCY, including the edges, the required sum depends on a parameter that is the distance from M to the straight line BC.
2. Now let there be a point N lying within the angle X′AY′, that is in the region IIA and NE ⊥ BC, NK′ ⊥ AC, NI′ ⊥ AB. The line drawn through N parallel to BC cuts AX′ in B′, AY′ in C′ and AH in H′. Let us put NE = x > h; we have AH′ = x – h. Moreover, we have
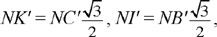 so
so
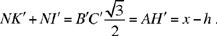
In fact, triangle AB′C′ is equilateral with height AH′ and N is a point on its base, so NK′ + NI′ = AH′ = x – h, from the lemma mentioned earlier, and
(2) 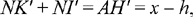
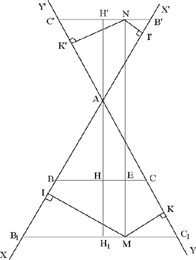
Fig. 2.3.30
This sum is the same for any point N of the segment B′C′. If the point N is at A, we have x = h, NK′ = 0, NI′ = 0 and the sum is equal to AH = h.
It is obvious that the same method can be applied for the points in the regions IB and IIB or IC and IIC and leads to the same result.
So the sum we are examining can be expressed in terms of h, the height of the equilateral triangle, and a single parameter x that is the distance from the point we are considering to a side of the triangle, that is the distance to BC if M is in one of the regions IA or IIA, the distance to AC if M is in one of the regions IB or IIB, and the distance to AB if M is in one of the regions IC or IIC. So we have two different results for the sum S.
• M in IA, IB, IC, we have S = h + 2x
• M in IIA, IIB, IIC, we have S = 2x – h.
It is clear that nothing in the above procedure could be unknown to Ibn al-Haytham, nor inaccessible to him. If he did not wish to consider these cases, perhaps it is, as we have said, in order to remain within the framework of the hypotheses of the ancients: considering only interior points. Al-Sijzī, on the other hand, had thought about these exterior points. Ibn al-Haytham’s predecessor, al-Sijzī, considered the cases of a point at the vertex of an equilateral triangle, on one of its sides or inside it; in all cases, we have S = h, a result established by the ancients and, according to him, by Menelaus. Next he considered the points in the region IA investigating various positions for the point and he determined S1, the sum of the distances to the two sides AB and AC of the triangle. In fact, if x is the distance from the point to the base BC, we have in all cases that
S1 = AD + x = h + x.
And consequently
S = h + 2x.
However, al-Sijzī does not examine the case where the point is in the region II and he does not complete the generalisation he began. Perhaps he was interested only in the relation between the three perpendiculars D1, D2 and D3 from the point D. In the case he considers, we have D1 + D2 = D3 + h. But he would then have been able to deduce from this that D1 + D2 – D3 is constant in the case concerned, which he did not do.
In conclusion, it is clear that the chief concern in these investigations carried out by al-Sijzī, and above all in those by Ibn al-Haytham, is the search for a quantity that remains constant. But the weight of the tradition stemming from the ancients led them to consider only the sum of the distances from a point to the sides of a triangle instead of, in a more algebraic way, thinking about a suitable linear combination of the distances.
3. History of the texts
3.1. On a Geometrical Problem
Ibn al-Haytham’s first treatise, On a Geometrical Problem (Fī mas’ala handasiyya), appears in two old lists of his writings: we find it mentioned by al-Qifṭī and by Ibn Abī Uṣaybi‘a.16 The treatise itself has come down to us in two manuscripts. It in fact forms part of two particularly important manuscript collections, each of which includes several treatises by Ibn al-Haytham. The first is the collection in the Oriental Institute in St Petersburg, whose former number is B 1030 and its present one 89. This collection contains twelve treatises, eleven by Ibn al-Haytham and the twelfth by al-‘Alā’ ibn Sahl. The treatise that is of interest to us here is the eighth. This collection is one we have come across several times;17 it was copied about 750/1349 – the date when it was revised by comparing it with its original. It is all in the same hand, in nasta‘līq script. The treatise on a geometrical problem, which covers folios 102r–110v, has neither additions nor glosses. The only addition (fol. 107v) has been made in the hand of the copyist – in the course of making the copy or during its revision against the original – so as to remedy the omission of a term in a proposition. The figures are drawn by the copyist. The only peculiarity in the copy is the repetition of the text of a page, but not of the figure that accompanies it. The copyist noticed this error, and at the top of the page wrote the word mukarrara (repeated). Here this collection is referred to as L.
The second collection is found in the Bodleian Library, Oxford, Seld. A 32. It too contains eight treatises by Ibn al-Haytham, the one that interests us here being the fifth (fols 115v–120r). We have already come across this collection.18 It is written in naskhī. The copyist does not give either the place or the date; he has drawn the figures and compared his copy with its original, as is indicated by additions in the margin in the same hand. We may note, however, that there are some glosses in a different hand (fol. 117r). Here this collection is referred to as O.
These two manuscripts are fully independent. Thus, three words that are missing in L are present in O, while, in relation to L, O is missing six words and a sentence. If such confirmation were needed, other peculiarities, grammatical errors, errors in letters, and so on, further confirm that the two are independent.
As far as we know, this treatise was edited and translated for the first time in our French edition of 2002 and appears here in English for the first time.19 Nor do we know of any serious and comprehensive study of its content.
3.2. On the Properties of the Triangle
The second treatise On the Properties of the Triangle in Regard to Height (Fī khawāṣṣ al-muthallath min jihat al-‘amūd), which is also mentioned by al-Qifṭī and by Ibn Abī Uṣaybi‘a,20 has come down to us in a single manuscript that forms part of the collection 2519 of the Library of Khuda Bakhsh (Patna, India). This important collection, which we have already mentioned,21 consists of 42 treatises on mathematics (Archimedes, al-Qūhī, Ibn ‘Irāq, al-Nayrīzī and others); it has 327 folios (32 lines per page, dimensions 24 × 15 cm, and 20 × 12.5 cm for the text) and it was copied in 631–632 of the Hegira, that is in 1234–1235 AD, at Mosul, in naskhī. The text by Ibn al-Haytham was transcribed in 1235 and occupies folios 189r–191r; it has neither additions nor marginal annotations. Here it is referred to as H.
An edition of this text, but a not a critical one, was printed in Hyderabad in 1948; we have referred to it as Kh.
This treatise was edited and translated for the first time in our French edition of 200222 and appears here in English for the first time. The inadequate Hyderabad edition was translated into English by F. A. Shamsi, with a commentary, under the title Properties of Triangles in Respect of Perpendiculars, in Hakim Mohammed Said (ed.), Ibn al-Haytham, Proceeding of the Celebrations of 1000th Anniversary, Karachi, n.d., pp. 228–46.
____________________
1 Al-Nadīm, Kitāb al-fihrist, ed. R. Tajaddud, Teheran, 1971, p. 326.
2 Ibid., p. 327.
3 Al-Sijzī refers several times to this book. For instance, in his Anthology of Problems (ms. Dublin, Chester Beatty 3652), he refers ‘to our book on triangles’ (Problem 9, Proposition 20), and similarly in Problem 45, Proposition 72; Problem 50, Proposition 80; Problem 53, Proposition 86. See R. Rashed and P. Crozet, Al-Sijzī: Œuvres mathématiques, forthcoming.
4 See R. Rashed, Géométrie et dioptrique au Xe siècle. Ibn Sahl, al-Qūhī, Ibn al- Haytham, Paris, 1993; English version: Geometry and Dioptrics in Classical Islam, London, 2005; and ‘Ibn Sahl et al-Qūhī: Les projections. Addenda & corrigenda’, Arabic Sciences and Philosophy, vol. 10.1, 2000, pp. 79–100.
6 This is the method used in the point by point construction of the ellipse with foci C and D and major axis 2a.
7See Les Mathématiques infinitésimales du IXe au XIe siècle, vol. III: Ibn al-Haytham. Théorie des coniques, constructions géométriques et géométrie pratique, London, 2000, Chap. III; English translation by J. V. Field: Ibn al-Haytham’s Theory of Conics, Geometrical Constructions and Practical Geometry, A History of Arabic Sciences and Mathematics, vol. 3, Culture and Civilization in the Middle East, London, 2013.
8See mss Istanbul, Aya Sofya 4830/5 and Khuda Bakhsh 2519/28 (=2468/28) and below, Appendix, Text 4. This book has been published, but not in a critical edition: Rasā’il Ibn Qurra, Osmania Oriental Publications Bureau, Hyderabad, 1947. H. Hermelink has noted that under the title in the manuscript 4830, fols 91v–92r (Kitāb al-mafrūḍāt li-Aqāṭun) there is a fragment of the text on the foundations of geometry attributed to Archimedes and translated by Thabit ibn Qurra. Further, he discusses Van Schooten’s possible knowledge of this text via Golius (H. Hermelink, ‘Zur Geschichte des Satzes von der Lotsumme im Dreieck’, Sudhoffs Archiv für Geschichte der Medizin und der Naturwissenschaften, Band 48, 1964, pp. 240–7).
9See p. 485 and Appendix, Text 4: Two Propositions of the Ancients.
10See Appendix, Text 4: Two Propositions of the Ancients.
11Y. Dold-Samplonius, Book of Assumptions by Aqāṭun, Thèse de doctorat, Université d’Amsterdam, 1977.
12Al-Nadīm, Kitāb al-fihrist, ed. R. Tajaddud, Teheran, 1971, p. 327: Kitāb fī uṣūl al-handasa ‘amilahu Ibn Qurra (thalātha maqālāt).
13Al-Bīrūnī, Risāla fī istikhrāj al-awtār fī al-dā’ira, Hyderabad, 1948, p. 49; ed. A.S. Demerdash, Le Caire, 1965, p. 90.
14See Appendix, Text 4: On the Properties of the Perpendiculars, p. 630.
15Qawl Aḥmad ibn Muḥammad ‘Abd al-Jalīl al-Sijzī fī khawāṣṣ al-a‘mida al-wāqi‘a min al-nuqṭa al-mu‘ṭā ilā al-muthallath al-mutasāwī al-aḍlā‘ al-mu‘ṭā bi-ṭarīq al-taḥdīd, mss Dublin, Chester Beatty 3652, fols 66r–67r; Istanbul, Reshit 1191, fols 124v–125v. See J. P. Hogendijk, ‘Traces of the lost geometrical elements of Menelaus in two texts of al-Sijzī’, Zeitschrift für Geschichte der arabisch-islamischen Wissenschaften, Band 13, 1999–2000, pp. 129–64, p. 142 sqq; and P. Crozet, ‘Geometria: La tradizione euclidea rivisitata’, in R. Rashed (ed.), Storia della scienza, vol. III: La civiltà islamica, Rome, 2002, pp. 326–41.
16See Les Mathématiques infinitésimales, vol. II, pp. 526–27.
17Ibid., vol. II, pp. 24, 26, 27.
18Les Mathématiques infinitésimales du IXe au XIe siècle, vol. III: Ibn al-Haytham. Théorie des coniques, constructions géométriques et géométrie pratique, London, 2000, p. 535. English translation: Ibn al-Haytham’s Theory of Conics, Geometrical Constructions and Practical Geometry. A History of Arabic Sciences and Mathematics, vol. 3, Culture and Civilization in the Middle East, London, 2013.
19Les Mathématiques infinitésimales du IXe au XIe siècle, vol. IV: Méthodes géométriques, transformations ponctuelles et philosophie des mathématiques, London, 2002, pp. 619–33.
20Ibid., vol. II, pp. 522–3.
21Les Mathématiques infinitésimales du IXe au XIe siècle, vol. I: Fondateurs et commentateurs: Banū Mūsā, Thābit ibn Qurra, Ibn Sinān, al-Khāzin, al-Qūhī, Ibn al-Samḥ, Ibn Hūd, London, 1996, p. 680; English trans. Founding Figures and Commentators in Arabic Mathematics, A History of Arabic Sciences and Mathematics, vol. 1, Culture and Civilization in the Middle East, London, 2012.
22Les Mathématiques infinitésimales, vol. IV, pp. 635–53.