
|
There is no doubt that in the beginning the origin was one: the origin of all numbers is one and not two. Then it is evident that in the beginning matter was one, and that one matter appeared in different aspects in each element. Thus various forms were produced, and these various aspects as they were produced became permanent, and each element was specialized. Then these elements became composed, and organized and combined in infinite forms; or rather from the composition and combination of these elements innumerable beings appeared.
—Abdu’l-Baha, 19th century |
“Mr. Plex, I think I’m in love.”
There is a sudden crackling sound as Mr. Plex ambles over to you and his right foreleg crushes a half-eaten bag of tortilla chips he had brought back from the future. “Theano?”
“Right.” You pause. “Let’s take our minds off this.”
“More Pythagorean mysticism?” Mr. Plex says eagerly.
You nod and walk over to a nearby wall of the backroom hideout. “As you know, Pythagoras’ famous theorem is that in a right-angled triangle the sum of the squares of the shorter sides, a and b, is equal to the square of the hypotenuse c, that is (c2 = a2 + b2).”
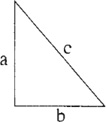
Mr. Plex nods.
“Mr. Plex, more proofs have been published of Pythagoras’ theorem than of any other proposition in mathematics! There’ve been several hundred proofs.”
“Sir, are Pythagorean triangles ones where a, b, and c are integers, like 3-4-5 and 5-12-13?”
“Correct, but Pythagoras’ favorite, 3-4-5, has a number of properties not shared by other Pythagorean triangles, apart from its multiples such as 6-8-10.”
“I know. It’s the only Pythagorean triangle whose three sides are consecutive numbers.”
“Very astute, Mr. Plex. It’s also—”
Mr. Plex, beaming from your compliment, lifts his foreleg to silence you. “Sir, it’s the only triangle of any shape with integer sides, the sum of whose sides (12) is equal to double Gnomons, its area (6).” and Oblong
You continue, slightly annoyed by Mr. Plex’s interruption. “It’s truly an amazing triangle. But here’s something that may make you think twice about 666, the Number of the Beast in the Book of Revelation.”
“Go on, sir.”
“There exists only one Pythagorean triangle except for the 3-4-5 triangle whose area is expressed by a single digit. It’s the triangle 693-1924-2045. Its area is …” You pause to heighten the suspense. “666,666.”
“Mon Dieu!” Mr. Plex screams like a raving lunatic. “It cannot be.” His abdomen pulsates and his eyes quiver.
Again, for a moment, you think you hear the chanting of monks. It must be the wind.
You calmly reach for a notebook computer hidden beneath some paper napkins and soda cans. “Let me show you a magic set of formulas that will allow you to search for Pythagorean triangles. They’ve been known since the time of Diophantus and the early Greeks”:
|
One Leg of Triangle: |
X = m2– n2 |
|
Second Leg of Triangle: |
Y = 2mn |
|
Hypotenuse of Triangle: |
Z = m2 + n2 |
“Sir, how do you use the formulas?”
“Just select any integers m and n and you should get a useful result.”
“Fascinating, sir. Let me write a program to search for Pythagorean triplets.”
Mr. Plex furiously types on the notebook computer and hands you a computer print-out:
X |
Y |
Z |
4 |
3 |
5 |
6 |
8 |
10 |
8 |
15 |
17 |
10 |
24 |
26 |
“Mr. Plex. Here are some mind-boggling facts about Pythagorean triangles. In everytriplet of integers for the sides ofthe triangles, one of them is alwaysdivisible by 3 and one by 5. Theproduct of the two legs is alwaysdivisible by 12, and the product ofall three sides is always divisible by 60.” You pause. “Here’s a starshowing Pythagorean triangles eachhaving one side equal to 120.
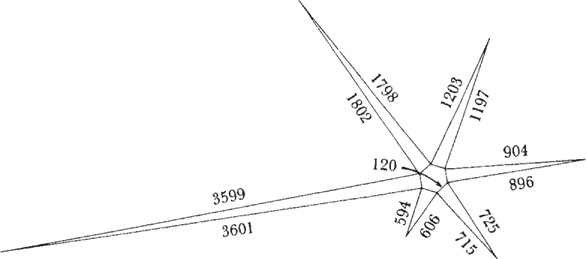
“Finally, Mr. Plex, can you find any triangles, like 3-4-5, that have consecutive leg lengths?”
Mr. Plex seems breathless with your endless barrage of facts. “Do any other triangles like that exist?”
The view-screen, still hanging on the wall although slightly askew, flickers to life.
You walk over to the view-screen and tap it. “Mr. Plex, our new electronic fly must have reached its destination.”
On the screen is Pythagoras talking to Heraclitus near a pool of water. The sky is reflected in the water; the clouds are bathing in its dark depths and trembling with the quivering eddies.
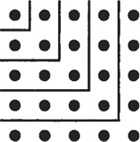
Pythagoras is drawing in the sand. He turns to Heraclitus. “If we start with one dot, we can continue to make squares by adding L-shaped arrangements of dots called gnomons.” He pronounces it “nuh-muhns.”
Pythagoras rests for a while, and you turn toward Mr. Plex. “The gnomon originally was simply a stick and its accompanying shadow when placed in the sun. Oenopides of Chios called a perpendicular a straight line drawn ‘gnomon-wise’ (καταγνoμoνα). Theognis used the term gnomon to describe a carpenter’s square. ThePythagoreans consider the odd numbers good because gnomons always form squares around odd numbers. Even numbers are evil because the sides of their gnomons are rectangular, not square.”
Mr. Plex nods and turns his attention to the view-screen where Heraclitus is talking.
“Pythagoras, how many dots are in each gnomon?”
“1, 3, 5, 7 … the odd numbers.” He pauses. “If we generalize gnomons, all the polygonal numbers, like triangular and square numbers, are formed by adding different shaped gnomons successively to one. One is the first polygonal number of any form.” Pythagoras draws in the sand. “Here is how we can construct pentagonal and hexagonal numbers by adding successive gnomons.
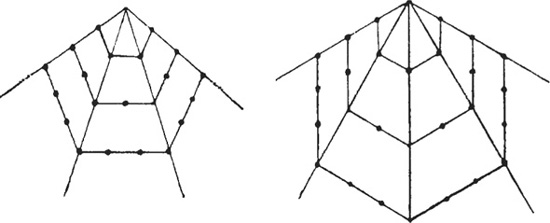
“In the case of the pentagon, the gnomons are 4, 7, 10 … with the common difference 3, and in the case of the hexagon we have 5, 9, 13 … with the common difference 4.”
Heraclitus scratches his head. “Pythagoras, in general, the successive gnomonic numbers for any polygonal number, say of n sides, have n – 2 for their common difference.”
Pythagoras nods. “Now let me tell you about the wonderful oblong numbers. They’re formed by adding successive even numbers, and they’re called oblong because they can be represented by oblong blocks of dots.
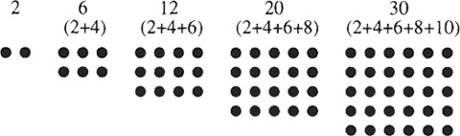
Pythagoras looks up to the heavens and says, “Let us pray for a moment.” After a minute of silence, he says, “Just as the sum of any consecutive numbers (1, 2, 3, …) is a triangular number, the sum of any consecutive even numbers is an oblong number with sides differing by 1. You can see this if you place successive gnomons in oblong numbers.”
Heraclitus nods. “I notice that oblong numbers are exactly double the corresponding triangular numbers represented by two triangles side by side. Pythagoras, I think that any oblong number is the sum of two equal triangular numbers.”
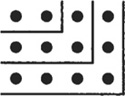
“Heraclitus, who’s the teacher around here?”
“Sorry, Oh Great One.”
Pythagoras looks up at some storm clouds. Already there is a faint drizzle. “Let us pray,” he says.

While Pythagoras and Heraclitus are deep in prayer, you start discussing oblong numbers with Mr. Plex.
“Mr. Plex, these oblong numbers behave in some surprising ways. If you want to make a large oblong number, pick a large number, square it, and add it to itself. For example, 1002 + 100 would make an oblong number.”
Mr. Plex is gazing at a nearby statue. Why is he ignoring you?
“Mr. Plex?”
“Sir, look here.”
Your heart suddenly skips a beat. “What in the world?”
You go closer.
The statue of Aphrodite has changed in a subtle way. Most notably, she has six fingers on her right hand.
“Sir, was it like that before?”
“I don’t think so.”
“What could it mean?”
“We may be doing something here in ancient Greece, in this backroom of the temple, that is tearing the fabric of time.” You gently touch Aphrodite’s cold, marble hand. “Maybe our presence in the past is spawning a parallel universe subtly different from our own.” You pause. “We’ve done something to alter the course of history, and maybe we’re splitting off from our future universe.”
You feel as if you are about to swoon as the rain upon Pythagoras faintly falls through the universe, upon all the living and the dead.
THE MATHEMATICS AND HISTORY BEHIND THE SCIENCE FICTION
The Praying Triangles
Pythagorean triangles with integral sides have been the subject of a huge amount of mathematical inquiry. For example, Albert Beiler, author of Recreations in the Theory of Numbers, has been interested in Pythagorean triangles with large consecutive leg values. These triangles are as rare as diamonds for small legs. Triangle 3-4-5 is the first of these exotic gems. The next such one is 21-20-29. The tenth such triangle is quite large: 27304197-27304196-38613965.
A few years ago I wrote a short story about these kinds of triangles. Before God created the Universe—eons before the Book of Genesis—He created mathematics. Since He is omnipotent, He created two classes of mathematical shapes: those that exist, and those that don’t exist. In this latter group are such objects as planar triangles whose three angles’ sum equals less than 180 degrees and Pythagorean triangles with two identical leg lengths. After a few centuries, these Pythagorean triangles prayed to God to make them exist so that they could have an effect on the real world. In God’s infinite kindness He started to transform them in order to give them the legitimacy of existence for which they craved. However, due to distractions caused by a band of rowdy ellipses, God created Pythagorean triangles whose leg lengths differ by a mere one and forgot about the equal-legged triangles. To this day Pythagorean triangles with legs differing by one pray that their equal-legged brethren be transformed into “things that exist,” but the fabric of the Universe has gelled, and God has since moved on to more weighty problems.
You can compute the Praying-Triangle leg lengths using the BASIC program listing in the Appendix. The recipe is as follows. Start with “1” and multiply by a constant D = (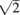 + 1)2 = 5.828427125.… Truncate the result to an integer value and multiply again by D. Continue this process for as long as you like creating a list of integers: 1, 5, 29.… To produce the leg length values for Praying Triangles, pick one of these integers, square it, divide by 2, and then take the square root. The two leg lengths are produced by rounding up and rounding down the result.
+ 1)2 = 5.828427125.… Truncate the result to an integer value and multiply again by D. Continue this process for as long as you like creating a list of integers: 1, 5, 29.… To produce the leg length values for Praying Triangles, pick one of these integers, square it, divide by 2, and then take the square root. The two leg lengths are produced by rounding up and rounding down the result.
Divine Triangles
In 1643, French mathematician Pierre de Fermât wrote a letter to his colleague Marin Mersenne asking for a Pythagorean triangle the sum of whose legs and whose hypotenuse were squares. In other words, if the sides are labeled X, Y, and Z, this requires
X + Y= a2
Z = b2
X2 + Y2 = Z2 = b4
It is difficult to believe that the smallest three numbers satisfying these conditions are: X = 4565486027761, Y = 1061652293520, and Z = 4687298610289. I’ve called triangles of this rare type divine triangles because only a god could imagine a second solution to this problem. Why? It turns out that the second triangle would be so large that if its numbers were represented as feet, the triangle’s legs would project from Earth to beyond the Sun!
If Pythagoras was told that a race of beings could compute the values for the sides of the second divine triangle, surely he would believe such beings were gods. Yet today we can compute such a triangle. We have become Pythagoras’ gods. We have become gods through computers and mathematics.
Bricks Beyond Imagination
You and Mr. Plex discussed the interesting problem of finding Pythagorean triangles with integer values for the sides. A related, but fiendishly more difficult, task involves searching for solutions to the “integer brick problem.” Here one must find the dimensions of a three-dimensional brick such that the distance between any two vertices is an integer. In other words, you must find integer values for a, b, and c (which represent the lengths of the brick’s edges) that produce integer values for the various diagonals of each side: d, e, and f. In addition, the three-dimensional diagonal g spanning the brick must also be an integer. This means that the following equations must have an integer solution:
a2 + b2 = d2
a2 + c2 = e2
b2 + c2 = f2
a2 + b2 + b2 + c2 = g2
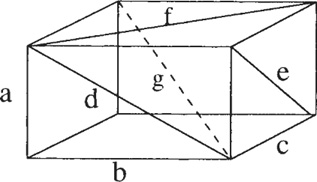
The Holy Grail
No solution has been found. However, mathematicians haven’t been able to prove that no solution exists. Many solutions have been found with only one non-integer side.
FACT FILE: 666
Anonymous Interneter: “What!? Does that mean if I buy 6 things on June 6, or look through a six-pane window from six feet away at six o’clock, I’m worshiping the devil?!” A response: “Quite simply, yes!”
As discussed in this chapter, the number 666,666 has mathematical significance for the study of Pythagorean triangles. Here are some other (non-mathematical) 666 anecdotes.
• |
On July 10, 1991, Procter & Gamble announced that it was redesigning its moon and stars company logo. The company said it eliminated the curly hairs in the man in the moon’s beard because it looked to some like 6s. The Fall 1991 issue of the Skeptical Inquirer notes that “the number 666 is linked to Satan in the Book of Revelation, and this helped fuel the false rumors fostered by fundamentalists.” A federal judge in Topeka, Kansas, has approved settlements in the last of a dozen lawsuits filed by Procter & Gamble Co. to halt rumors associating the company with Satanism. |
• |
President Ronald Reagan altered his California address to avoid the number 666. His name becomes 666 if you count the letters in his name. |
• |
Why is it that when you add up the Roman numerals I = 1, V = 5, X = 10, L = 50, C = 100, and D = 500, you get 1 + 5 + 10 + 50 + 100 + 500 = 666? |
• |
On May 1, 1991, the British vehicle licensing office stopped issuing license plates bearing the numbers “666.” The Winter 1992 issue of the Skeptical Inquirer reports two reasons given for the decision: cars with 666 plates were involved in too many accidents, and there were “complaints from the public.” |
• |
Pope Innocent IV, whose Latin name corresponds to 666, was branded an anti-Christ by his opponents. |
SIX-SIDED PRISONS AND MAGIC SQUARES
The Pythagoreans associate six with marriage and health because six is the product of the first even and first odd numbers, which are female and male, respectively.
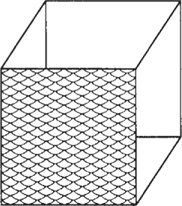
The number six also plays an important role in Islamic tradition. Islamic mystics consider our world a cubic cage, a six-sided prison. Humans struggle in vain to escape the bondage of the senses and physical world. Persian poets refer to such imprisonment as “six-door,” or shishdara—the hopeless position of a gambler playing a form of backgammon. In this game, players use a six-sided die to move pieces. If an opposing player has locked (occupied) all six locations to which your playing piece could potentially have moved, then you are “shish-dar,” or six-out, since your piece cannot move.
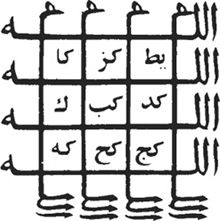
An Islamic magic square that expresses the number 66 in every direction. The grid is formed by the letters in the word Allah.
In Islam, the number 66 corresponds to the numerical value of the word Allah. Shown at left is an Islamic magic square that expresses the number 66 in every direction when the letters are converted to numbers. The square’s grid is formed by the letters in the word Allah. Magic squares such as this were quite common in the Islamic tradition, but did not seem to have reached the West until the 15th century. From a historical perspective, my favorite Western magic square is Albrecht Dürer’s which is drawn in the upper right hand column of his etching Melencolia I (see p. 77). The variety of small details in the etching have confounded scholars for centuries. Scholars believe that the etching shows the insufficiency of human knowledge in attaining heavenly wisdom, or in penetrating the secrets of nature.
16 |
3 |
2 |
13 |
5 |
10 |
11 |
8 |
9 |
6 |
7 |
12 |
9 |
6 |
7 |
12 |
4 |
15 |
14 |
1 |
Dürer’s 4×4 magic square, shown below, contains the first 16 numbers and has some fascinating properties. The two central numbers in the bottom row read 1514, the year Dürer made the etching. Also, in the vertical, horizontal, and two diagonal directions, the numbers sum to 34. In addition, 34 is the sum of the numbers of the corner squares (16 + 13 + 4 + 1) and of the small central square (10 + 11 + 6 + 7). The sum of the remaining numbers is 68 = 2 × 34. Was Dürer trying to tell us something profound about the number 34?
Mark Collins, a colleague from Madison, Wisconsin, with an interest in both number theory and Dürer’s works, has studied the Dürer square and finds some astonishing features when converting the numbers to hexadecimal binary code. (In the binary representation, numbers are written in a positional number system that uses only two digits: 0 and l.1) Since the first 16 numbers of this kind start with the number 0 and end with 15, he subtracts 1 from each entry in the magic square. Below is the result:
15 |
2 |
1 |
12 |
1111 |
0010 |
0001 |
1100 |
4 |
9 |
10 |
7 |
0100 |
1001 |
1010 |
0111 |
8 |
5 |
6 |
11 |
1000 |
0101 |
0110 |
1011 |
3 |
14 |
13 |
0 |
0011 |
1110 |
1101 |
0000 |

Melencolia I, by Albrecht Dürer (1514). This figure is usually considered the most complex of Dürer’s works, the various symbolic nuances confounding scholars for centuries. Why do you think he placed a magic square in the upper right? Scholars believe that the etching shows the insufficiency of human knowledge in attaining heavenly wisdom, or in penetrating the secrets of nature.

A detail from the engraving Melencolia 1.
Remarkably, if the binary representation for the magic square is rotated 45 degrees clockwise about its center so that the “15” is up and the “0” down, the resultant pattern has a vertical mirror plane down its center:

For example, in row two, 0100 is the mirror of 0010. (I very much doubt that Dürer could have known about this symmetry.)
If we rotate the square counterclockwise so that the “12” is at the top and the “3” at Gnomons, the bottom, we get a pattern that has a peculiar left-right inverse when drawing an imaginary vertical mirror down the center of the pattern.

For example, in the second row, 0001 and 0111 are mirror inverses of each other.
Finally, Mark Collins has discovered the presence of mysterious intertwined hexagrams when the even and odd numbers are connected (see below).
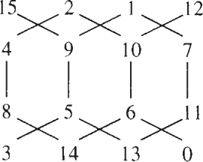
I would be interested in hearing from those of you who find additionalmeaning in Dürer’s magic square. Mark Collins and I are unaware of other magic squares having the symmetrical properties when converted to binary numbers. Mark has also done numerous experiments converting these numbers to colors, and comments:
“I believe this magic square is an archetype as rich in meaning and mysticism as the I-Ching. I believe it is a mathematical and visual representation of nature’s origami—a photon of light.”
Mark suggests you should create other mitosis-like diagrams by connecting 0 to 1 to 2 to 3. Then lift up your hand. Connect 4 to 5 to 6 to 7. Connect 8 to 9 to 10 to 11. Connect 12 to 13 to 14 to 15.
In concluding this section, I present a rather bizarre six-by-six magic square invented by the mysterious A. W. Johnson. All of its entries are prime numbers, and each row, column, diagonal, and broken diagonal sum to 666, the Number of the Beast. (By “broken diagonal,” I mean the diagonal produced by wrapping from one side of the square to the other; for example, 131, 83, 199, 113, 13, 127 forms a broken diagonal).
The Apocalyptic Magic Square |
|
3 |
107 |
5 |
131 |
109 |
311 |
|
|
7 |
331 |
193 |
11 |
83 |
41 |
|
|
103 |
53 |
71 |
89 |
151 |
199 |
|
|
113 |
61 |
97 |
197 |
167 |
31 |
|
|
367 |
13 |
173 |
59 |
17 |
37 |
|
|
73 |
101 |
127 |
179 |
139 |
47 |
|
The Seven Sleepers
The Pythagoreans call “7” a crisis, and consider all days of the month that could be divided by seven as critical days. The number seven is also important in Islamic tradition. For example, the Koran states that God created Heaven and Earth in seven layers.2 In addition, the seven Sleepers known from early Christian history also appear in the Koran (18:21). The names of the seven religious youths along with their dog are often presented in ornate Arabic calligraphic designs.
According to Christian legend, seven Christian boys of Ephesus hid themselves in acave on Mount Coelian during the Decian persecution (A.D. 250). Eventually their hidingplace was discovered, and its entrance blocked. The seven unfortunate youths fell asleep inmutual embrace. Then, about 200 years later, a herdsman rediscovered the cave and awoke the boys. One of the boys went to the market to buy food and was surprised to hear the name of Christ openly spoken. After the townspeople and the local emperor confirmed the presence of the boys in the cave, strengthening their faith in God and in the possibility of resurrection of dead, the boys fell asleep again.
In another 9th century version of the legend, certain undecayed corpses of monks were found in a cave and thought to be the sleepers of Ephesus.
In the Koran (18:18), the seven Sleepers also have a dog with them in the cave:

An amulet from Turkey showing the names of the seven sleepers surrounding their special dog.
Thou wouldst have deemed them awake, whilst they were asleep, and we turned them on their right and on their left sides. Their dog stretched forth his two fore-legs on the threshold. If thou hadst come up on to them, thou wouldst have certainly turned back from them in flight, and wouldst certainly have been filled with terror of them.
There is an incredibly large number of occurrences of seven in all religions. Here are just a few examples:
• |
Old Testament: Lamech, father of Noah and son of the famous long-lived Methuselah, is born seven generations after Adam. Lamech lives for 777 years. (Did you think that 666 was the only important triplet for Christians?) Lamech should be avenged 77-fold (Genesis 4:24). Zechariah, a major biblical prophet, speaks of the seven eyes of the Lord. (Zechariah was concerned with the cosmic work of God, including the final judgment, restoration of Israel, and the coming of the messianic age.) |
• |
Sufism: The idea of seven divine eyes occurs in Sufisim in connection with seven important saints who are the eyes of God. God is praised by creatures with 70,000 heads, each of which has 70,000 faces. There are seven points in the body upon which mystics concentrate their spiritual power. |
• |
Later Judaism: Seven is important for Kabalists (see Chapter 19). In fact, Trachtenberg in his Jewish Magic and Superstition mentions the following cure for tertian (malarial) fever: |
Take seven pickles from seven palmtrees, seven chips from seven beams, seven nails from seven bridges, seven ashes from seven ovens, seven scoops of earth from seven door sockets, seven pieces of pitch from seven ships, seven handfuls of cumin, and seven hairs from the beard of an old dog, and tie them to the neck-hole of the shirt with a white twisted cord.
• |
Christianity: The seven last words of Christ on the Cross. In the Book of Revelation, seven seals are opened, and there are seven trumpets blown to usher in the Day of Judgment. Also: seven sacraments, seven gifts of the Holy spirit, seven deadly sins, seven layers of purgatory. |
• |
Islam: The holy phrase: la ilaha ilia Allah Muhammad rasul Allah has seven Gnomons, words (“There is no deity save God, Muhammad is the messenger of God.”) Pilgrims must circle Kaaba in Mecca (Chapter 21) seven times. |
• |
Ancient Greece: Swans circle seven times before Leto gives birth to Apollo. Apollo stays with the Hyperboreans for seven months. |
• |
Mithras: In the ancient Iraninan religion of Mithras, the souls rise through seven planetary spheres into the divine presence. |
• |
Vedas: In India, Agni, the god of fire, has seven wives, mothers, or sisters as well as seven flames, beams, or tongues. The sun god owns seven horses. |
Practicality of Number Theory
What could be more beautiful than a deep, satisfying relation between whole numbers. How high they rank, in the realms of pure thought and aesthetics, above their lesser brethren: the real and complex numbers …
—Manfred Schroeder, Number Theory in Science and Communication, 1984
In this chapter, like others, we’ve discussed integer patterns both in geometry and mysticism. Is there anything special about integers in the fabric of the universe? Or do other kinds of numbers contribute equally to the loom upon which God weaves? Leopold Kronecker (1823–1891), a German algebraist and number theorist, once said, “The primary source of all mathematics are the integers.” Since the time of Pythagoras, the role of integer ratios in musical scales has been widely appreciated. More importantly, integers have been crucial in the evolution of humanity’s scientific understanding. For example, in the 18th century, French chemist Antoine Lavoisier discovered that chemical compounds are composed of fixed proportions of elements corresponding to the ratio of small integers. This was very strong evidence for the existence of atoms. In 1925, certain integer relations between the wavelengths of spectral lines emitted by excited atoms gave early clues to the structure of atoms. The near-integer ratios of atomic weights was evidence that the atomic nucleus is made up of an integer number of similar nucleons (protons and neutrons). The deviations from integer ratios led to the discovery of elemental isotopes (variants with nearly identical chemical behavior but with different radioactive properties). Small divergences in the atomic weight of pure isotopes from exact integers confirmed Einstein’s famous equation E = mc2 and also the possibility of atomic bombs. Integers are everywhere in atomic physics. Integer relations are fundamental strands in the mathematical weave—or as German mathematician Carl Friedrich Gauss said, “Mathematics is the queen of sciences—and number theory is the queen of mathematics.”








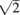 + 1)2 = 5.828427125.… Truncate the result to an integer value and multiply again by D. Continue this process for as long as you like creating a list of integers: 1, 5, 29.… To produce the leg length values for Praying Triangles, pick one of these integers, square it, divide by 2, and then take the square root. The two leg lengths are produced by rounding up and rounding down the result.
+ 1)2 = 5.828427125.… Truncate the result to an integer value and multiply again by D. Continue this process for as long as you like creating a list of integers: 1, 5, 29.… To produce the leg length values for Praying Triangles, pick one of these integers, square it, divide by 2, and then take the square root. The two leg lengths are produced by rounding up and rounding down the result.







