4. Euclide e la comunità alessandrina

Indicazioni per la costruzione di un icosaedro regolare, esercitazione in base al XIII libro degli Elementi di Euclide, ostrakon da Elefantina (Egitto), III sec. a.C., Berlino, Bode-Museum
4.1 Oggetti della matematica e geometria dei teoremi
Nel IV secolo a.C. la matematica non ha ancora definito in maniera univoca la sua fisionomia, ma si trova in una situazione per così dire fluida che si risolve, infine, nel prevalere della geometria dei teoremi, ossia della geometria ordinata secondo il modo assiomatico: assunte alcune proposizioni come punti di partenza, tutte le altre ne derivano secondo un ordine univoco e rigoroso.
Si è soliti mettere in relazione questo esito con la concezione della matematica elaborata da Aristotele che la colloca accanto alla filosofia prima e alla fisica: è il gruppo delle tre scienze teoretiche, contemplative, volte alla conoscenza della realtà per il solo amore di conoscere; esse saranno dunque pure, libere da interessi di natura pratica e utilitaristica. La matematica ha come oggetto l’essere, considerato sotto l’aspetto della quantità e dispone per la sua indagine di principi propri a partire dai quali svolge le sue dimostrazioni. Anzi, il suo grado di astrazione permette di cogliere con estrema chiarezza lo svolgersi dell’argomentazione; per questo, Aristotele ne fa il modello della scienza deduttiva.
ESERCIZIO
E16: La scienza
È difficile comunque valutare con precisione quanto la posizione di Aristotele abbia davvero influito sull’affermazione assiomatica della geometria o, viceversa, quanto questa abbia contribuito a delineare un modello del sapere in cui ogni singola scienza vede riconosciuta la propria autonomia. Di sicuro la geometria assiomatica risponde a quelli che ancora oggi sono criteri “interni” con cui giudichiamo la matematica: bellezza, semplicità, coerenza, ordine.
4.2 Euclide e gli Elementi
Su Euclide non abbiamo notizie precise: non conosciamo il suo luogo di nascita e neppure le date esatte della sua vita. In base a quanto riportato dal filosofo neoplatonico Proclo (412-485), si ritiene che egli abbia composto il suo trattato, intitolato Elementi, intorno al 300 a.C.; dunque proprio all’inizio dell’età ellenistica, negli anni in cui viene a delinearsi un quadro politico e sociale profondamente nuovo rispetto al precedente. Anche nell’ambito della cultura si verifica una modificazione profonda, che viene solitamente riassunta nell’immagine del divorzio fra la filosofia e le scienze. Queste vengono a organizzarsi secondo un modello e un ambito di ricerca autonomi e trovano la loro sede esemplare nel Museo, la grande istituzione voluta ad Alessandria dal re Tolomeo I. Proprio ad Alessandria Euclide insegna e svolge le sue ricerche.
Gli Elementi non si presentano come un’opera originale, ma come una sorta di collezione nella quale confluiscono ricerche precedenti, alle quali Euclide ha dato veste compiuta: a Euclide, sempre secondo Proclo, si deve l’ordinamento in forma sistematica di altri risultati, come ad esempio quelli raggiunti dal matematico Eudosso di Cnido. Inoltre egli ha fornito dimostrazioni inconfutabili a questioni che i suoi predecessori avevano trattato in maniera poco rigorosa.
| I cinque postulati di Euclide | |
|---|---|
|
Negli Elementi Euclide enuncia cinque postulati: |
|
|
1. |
Tra due punti qualsiasi è possibile tracciare una e una sola retta. |
|
2. |
Si può prolungare una retta oltre i due punti indefinitamente. |
|
3. |
Dato un punto e una lunghezza, è possibile descrivere un cerchio. |
|
4. |
Tutti gli angoli retti sono uguali. |
|
5. |
Se una retta taglia altre due rette determinando dallo stesso lato angoli interni la cui somma è minore di quella di due angoli retti, prolungando indefinitamente le due rette, esse si incontreranno dalla parte dove la somma dei due angoli è minore di due angoli retti. |
I libri degli Elementi
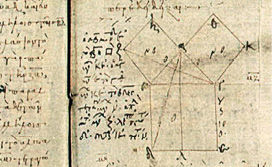
Il teorema di Pitagora nel libro I degli Elementi, ms. Vat. gr. 190, vol. 1, ff 38v-39r, IX sec., Città del Vaticano, Biblioteca Apostolica Vaticana
Gli Elementi si articolano in 13 libri. Il libro I inizia con l’enunciazione dei principi fondamentali di tutta la geometria; prosegue poi con i teoremi elementari sui triangoli, sulle rette parallele e su quella che, per noi, costituisce l’equivalenza dei poligoni, per concludersi con il teorema di Pitagora. Il libro II tratta la quadratura di un poligono qualunque, ossia quella che noi definiamo “algebra geometrica”. Il libro III è incentrato sulle proprietà del cerchio, mentre il IV verte sulle figure inscritte in un cerchio e ad esso circoscritte (e, secondo uno scolio al testo, risalirebbe ai pitagorici). Nel complesso, quindi, si può dire che i primi quattro libri trattino della geometria piana, come doveva essere già nota ai matematici del VI e V secolo a.C. Questa, il cui nucleo originario risale ai risultati ottenuti da Eudosso, viene esposta nel libro V in relazione non alla geometria, ma alle grandezze in generale. Le applicazioni della teoria delle proporzioni alla geometria sono trattate invece nel libro VI. I libri VII, VIII, IX sono dedicati all’aritmetica e trattano le proprietà dei numeri interi e i rapporti di numeri interi, senza fare ricorso a esempi numerici, ma attraverso segmenti e rettangoli. Il libro X, il più esteso e complesso, riprende gli studi del matematico Teeteto sui numeri irrazionali. I libri XI, XII e XIII sono dedicati alla trattazione della geometria solida attraverso il metodo di esaustione per il calcolo delle aree di figure geometriche piane.
Rielaborazione della tradizione
Il processo di riscrittura dei contenuti della tradizione, in realtà, non si esaurisce in una loro semplice trascrizione, ma comporta una profonda rielaborazione da parte di Euclide. Non si tratta tanto di rivedere e approfondire singoli aspetti delle ricerche compiute dai predecessori, e nemmeno di partire da quei risultati disponibili per aprire nuove vie – come pure è il caso del celebre quinto postulato che dà sistemazione rigorosa alla teoria delle parallele. Il contributo decisivo del matematico greco sta nel progetto stesso di riunire ambiti, che prima erano trattati in modo non articolato, in un corpo sistematico, nel quale le proposizioni si susseguono secondo una rigorosa e coerente struttura logica. Negli Elementi siamo in presenza di una connessione totale governata da un ordine univoco di antecedenza e conseguenza a partire da proposizioni che sono gli elementi di tutte le altre.
4.3 I principi della geometria
Nel libro I sono enunciati i principi fondamentali dell’intero edificio della geometria: termini, postulati, nozioni comuni. Euclide non ne spiega il significato, e qualche secolo più tardi Proclo, per chiarirlo, li pone in relazione con le nozioni di definizione, ipotesi e assioma elaborate da Aristotele. Euclide elabora una divisione in ipotesi, postulati e assiomi. Si ha un’ipotesi quando una proposizione non è evidente per se stessa a chi apprende, ma viene comunque da questi concessa a chi l’assume; e si ha un postulato quando si assume una proposizione che non è conosciuta né ammessa da chi apprende. Si ha un assioma quando una proposizione risulta insieme nota a chi apprende e credibile per se stessa.Tuttavia tra questa tripartizione e le distinzioni aristoteliche non è possibile stabilire una corrispondenza esatta. Le nozioni comuni di Euclide non hanno tutte lo stesso grado di generalità e non è detto che egli le considerasse davvero dotate di maggior evidenza e necessità rispetto ai postulati. Una certa analogia si può riscontrare fra i termini e la concezione aristotelica di definizione, come nel caso di quella di “uomo” prodotta da genere (“animale”) e differenza (“razionale mortale”): tuttavia alcuni termini euclidei più che definizioni costituiscono dei veri e propri postulati o addirittura dei teoremi. Ancora più problematico appare il riferimento alle ipotesi. In Euclide, infatti, la nozione di ipotesi non compare.
Proprietà degli oggetti matematici

Euclide, Elementi di geometria, II libro, Proposizione 5, papiro da Ossirinco, 75-125 ca., Filadelfia, University of Pennsylvania Museum of Archaeology and Anthropology
Per Euclide gli oggetti matematici esistono indipendentemente dalla loro costruzione. Che esistano di per sé, come forme ideali e trascendenti, come vuole Platone, oppure che siano immanenti alla materia, cioè realtà immobili ma non separate, come sostiene Aristotele, tali oggetti sono studiati dal matematico che ne scopre le proprietà. In questa prospettiva, i postulati di Euclide permettono di studiare le figure geometriche, stabilendo tra essi un confronto e un legame mediante costruzioni argomentative. Così, per esempio, nel primo postulato si tratta di collegare mediante un segmento di retta due punti qualunque; nel terzo entrano in gioco considerazioni di uguaglianza e disuguaglianza attraverso la figura circolare, la quale permette di riconoscere che due segmenti sono uguali in quanto raggi dello stesso cerchio. Segmenti e cerchi, riga e compasso sono per Euclide strumenti privilegiati, come già lo erano nella tradizione precedente: essi sono i soli a poter entrare nel campo della geometria, senza scalfirne il carattere di pura scienza speculativa.
Non solo una funzione didattica
Esiste un rapporto profondo fra l’organizzazione assiomatica della geometria e la definitiva affermazione della scrittura che prende la forma del trattato. Questa nuova struttura offre infatti una serie di “vantaggi logici”: costituire una terminologia, stabilire schemi di argomentazione fissi e ripetibili, esercitare un controllo ripetuto sui procedimenti e i risultati, favorire l’incremento della conoscenza. Il che ha portato ad attribuire agli Elementi una mera funzione didattica. Sicuramente nel tempo gli Elementi hanno svolto un importante ruolo educativo, e in una certa misura continuano a svolgerlo, ma il loro significato va ben oltre. Anzi, come risponde Euclide stesso al re Tolomeo, che gli chiede se esista una via più breve della sua per imparare questa disciplina, “in geometria non esistono vie regie”. Il trattato, piuttosto, va inteso come testo di riferimento intorno al quale si costituisce una comunità scientifica di matematici, che condividono problemi e metodi per affrontarli.
AMBIENTE CULTURALE
Alessandria: il museo e la biblioteca
Alessandria: gli spazi della scienza
La transizione dall’età classica all’ellenismo è accompagnata da importanti cambiamenti in campo culturale e scientifico. Approssimandosi la fine del IV secolo a.C., nuove capitali della cultura sorgono nei regni ellenistici: Antiochia, Pergamo, Alessandria d’Egitto vanno ad affiancare Atene, Siracusa, Samo, Rodi e tutti quei centri che da tempo avevano visto fiorire forme di sapere non solo letterario e filosofico, ma anche tecnico. Se Atene continua a essere il centro principale per l’attività filosofica, sulla sponda opposta del Mediterraneo, ad Alessandria, va organizzandosi una nuova sistemazione del sapere, propensa a riconoscere autonomia a una serie di discipline scientifiche.
All’inizio del III secolo a.C., probabilmente seguendo i suggerimenti di Demetrio Falereo, esiliato da Atene e rifugiatosi ad Alessandria, vengono creati i presupposti per dotare il palazzo reale della città egizia di due punti di riferimento culturali, la Biblioteca e il Museo, destinati a restare nell’immaginario collettivo come il momento più alto mai raggiunto nel mondo antico dall’organizzazione del sapere. Edificato nel palazzo reale, il Museo, in particolare, diviene il punto di incontro per studiosi, provenienti da ogni dove, che soggiornano ad Alessandria. Istituzioni culturali simili sorgono poi anche negli altri regni ellenistici.
LETTURE
I regni ellenistici: Tolemei, Seleucidi, Attalidi
LETTURE
I diadochi
Il Museo e la BibliotecaIl Museo faceva parte del palazzo reale e comprendeva una passeggiata, uno spazio dove venivano consumati i pasti in comune, un’esedra munita di sedili, un ampio parco con specie animali e vegetali. Collegata al Museo e all’interno del palazzo reale era la Biblioteca: se sono attendibili i dati che riferisce Aulo Gellio, i volumi all’epoca dei Tolomei avrebbero raggiunto il numero di 700mila. Si tratta di rotoli nei quali, in greco, è scritto tutto lo scibile esistente o presunto tale. A tal proposito è interessante un’informazione in Galeno, secondo il quale il re Tolomeo II Filadelfo aveva dato ordine di copiare il contenuto dei testi che si trovavano a bordo delle navi che entravano nel porto di Alessandria. Un passo di Ateneo di Naucrati relativo alla grande nave Syrakousia costruita da Archimede a Siracusa e diretta proprio ad Alessandria descrive, tra le varie meraviglie a bordo, anche una biblioteca. L’innovativa idea è dunque quella di racchiudere in un’immensa biblioteca tutto lo scibile umano, raccogliendo i testi scritti da tutti i popoli. Per questo i Tolomei chiamano a sé numerosi traduttori e i più grandi storici, filosofi, astronomi e matematici del tempo, mettendo loro a disposizione oltre mille scribi. Sono questi traduttori i personaggi che per primi hanno goduto dello straordinario scenario della Biblioteca ricchissima di testi, che per secoli scatenerà le fantasiose ricostruzioni dei posteri. L’idea della biblioteca universale scaturisce da un progetto che ha varie radici: da una parte la diretta continuazione, in campo culturale, del piano politico di Alessandro che voleva “varcare i confini del mondo” e che, fermatosi a Ninive, aveva voluto una biblioteca imponente per la quale aveva fatto preparare traduzioni dei testi dei Caldei; dall’altra la convinzione che, per dominare il mondo, occorra comprendere il pensiero e il linguaggio degli altri popoli, ovvero conoscerne i testi.

Lucerna con veduta schematica della necropoli reale presso il porto di Alessandria, Alessandria d’Egitto, Museo Greco Romano
Nonostante i dubbi espressi da molti studiosi, è plausibile che la Biblioteca di Alessandria contenesse anche testi scientifici: lo confermerebbe la presenza di molti illustri “scienziati” nelle istituzioni alessandrine nell’arco di cinque secoli di vita.
La ricerca dei volumi è facilitata dall’accurato sistema di classificazione in base al quale i bibliotecari danno un titolo e un autore a tutti i testi conservati nella Biblioteca, rendendo le opere immediatamente accessibili. Leggere, commentare e dibattere divengono così le parole chiave degli studiosi che frequentano le istituzioni di cultura alessandrine. Grazie al finanziamento dei sovrani, inoltre, essi godono di una nuova condizione di privilegio, che sarebbe stata per lungo tempo irripetibile.
L’esistenza della Biblioteca è la causa prima della fondazione del Museo. Nei suoi spazi gli astronomi devono avere a disposizione un osservatorio con i relativi strumenti, e lo stesso doveva accadere per gli studiosi di meccanica, in specie quelli che, come Ctesibio, Filone di Bisanzio ed Erone, erano interessati alla pneumatica: disciplina sorta in relazione ai dibattiti sull’esistenza o meno del vuoto, la pneumatica ha bisogno, per essere studiata, di tutta una serie di apparati che devono essere progettati, costruiti e messi in funzione in appositi spazi, veri e propri laboratori dove si osservano gli effetti meravigliosi della contiguità degli elementi.
Nel Museo, infine, i medici devono mettere a frutto le osservazioni derivanti dal permesso di sezionare i cadaveri e, talvolta, anche i prigionieri condannati a morte nelle carceri cittadine: nel proemio al De medicina, infatti, Celso afferma che i medici Erofilo ed Erasistrato hanno potuto effettuare vivisezioni sui carcerati messi a disposizione dai Tolomei. Criticata violentemente dai medici successivi per la sua inutilità, questa pratica viene abbandonata e forse praticata solo sugli animali. Attorno a questi spazi va dunque costituendosi un modo di fare ricerca assolutamente nuovo basato anche sull’idea di cooperare, come dimostrano le lettere premesse da Archimede, Apollonio e Diocle ai loro trattati.
LETTURE
La “medicina delle donne”
LETTURE
La meccanica: origini tecniche e sviluppo teorico. Le enciclopedie meccaniche alessandrine
Gli altri centri del sapere ellenisticoLe poche informazioni a nostra disposizione non consentono di conoscere con precisione il contenuto delle biblioteche fondate in altri centri all’interno dei regni di età ellenistica. Per volere di Antigono Gonata ne viene istituita una a Pella, in Macedonia, il cui contenuto sarà poi portato a Roma da Emilio Paolo nel 168 a.C., successivamente alla vittoria sui Macedoni. Circa 100 anni più tardi Lucullo trasferirà a Roma la biblioteca di Mitridate, re del Ponto. È possibile che la principale tra queste altre biblioteche fosse, comunque, la biblioteca reale di Pergamo.
L’autonomia delle scienze: il divorzio dalla filosofia
Abbandonato il legame con la pólis, si pongono adesso i presupposti per la separazione delle scienze dalla filosofia e dalla sua pretesa di universalità. In realtà già Aristotele e la sua scuola avevano sostenuto la tesi dell’autonomia delle scienze, che avrebbero semmai potuto essere raggruppate come in una grande enciclopedia del sapere a beneficio dell’umanità. È questo l’atteggiamento che ha guidato l’attività di Aristotele e dei suoi allievi, che hanno raccolto numerosi dati scientifici riordinandoli prima di esporli nei testi della scuola aristotelica. Non a caso, la creazione del Museo alessandrino finisce col privare il Liceo ateniese della ricerca scientifica, che Stratone sposta ad Alessandria. Favoriti dalla protezione dei sovrani, gli studiosi alessandrini vanno sviluppando discipline specialistiche i cui contenuti hanno ormai scisso ogni legame con la religione tradizionale. Naturalmente non bisogna immaginarsi di trovare contenuti corrispondenti alle attuali denominazioni delle nostre discipline attuali: la divisione tra le discipline è molto diversa e, tra l’altro, molto più fluida.
La Biblioteca sarà distrutta parzialmente più volte. La leggenda della sua apocalittica fine al tempo della guerra alessandrina (48-47 a.C.) a opera di Giulio Cesare è smentita, se non altro, dal fatto che Strabone vi soggiorna e lavora, poi, durante un suo viaggio in Egitto, compiuto tra il 25 e il 20 a.C. La distruzione della Biblioteca avviene, in realtà, al tempo del conflitto tra Aureliano e Zenobia di Palmira nel 270-275, quando vi sono durissimi scontri nelle strade di Alessandria. È allora che, come dice lo storico Ammiano Marcellino, “Alessandria perse il quartiere chiamato Bruchion, sede per lunghissimo tempo di studiosi dal nome prestigioso”. Dobbiamo quindi assegnare alla Biblioteca e al Museo tre secoli di vita successivamente alle vicende belliche del 48-47 a.C., a conferma del fatto che le istituzioni culturali alessandrine furono ancora capaci di svolgere un ruolo primario in età imperiale romana.