5. L’astronomia ellenistica

Atlante inginocchiato sotto il peso del globo (Atlante Farnese), dettaglio. La statua, certamente derivata da un originale di età ellenistica di cui sono note varie repliche, contiene una delle più complete rappresentazioni della sfera celeste giunte sino a noi, Napoli, Museo Archeologico Nazionale
5.1 Nuovi modelli geometrici per la spiegazione dei fenomeni celesti
L’astronomia ellenistica appare caratterizzata dalla ricerca di modelli geometrici alternativi a quelli delle sfere omocentriche, i quali prevedono un solo centro di rotazione in cui si trova la Terra immobile. I modelli astronomici elaborati nel IV secolo a.C. da Eudosso di Cnido, perfezionati da Callippo di Cizico e adottati da Aristotele per descrivere il funzionamento del cosmo, infatti, presentano alcuni limiti nella spiegazione dei fenomeni celesti e appaiono poco pratici per calcolare le posizioni planetarie. Le varie proposte elaborate dagli astronomi ellenistici delineano le due strade maestre dell’astronomia occidentale: i modelli epiciclici, che porteranno al trionfo l’ipotesi geocentrica del cosmo, e i modelli eliocentrici, che torneranno invece in auge dalla prima metà del XVI secolo.
LETTURE
I confini del mondo: geografi ellenistici e tardoantichi
Limiti dei modelli omocentrici
I modelli omocentrici nascono dall’osservazione dei fenomeni celesti (uno studio del corso dei pianeti protrattosi per più anni) e si servono di una serie di parametri numerici e di un solo tipo di figura geometrica solida, la sfera, in grado di rappresentare sufficientemente bene una parte della realtà. Una volta definiti, questi modelli ambiscono a rendere conto sia dei fenomeni già osservati sia di quelli ancora da osservare, come per esempio le posizioni future dei pianeti. I modelli a sfere omocentriche presentano tuttavia due limiti piuttosto evidenti.

Diagramma del moto retrogrado di un pianeta.
Lo schema rappresenta ciò che si vede tracciando la proiezione del moto di un pianeta, giorno dopo giorno, fra le costellazioni dello Zodiaco. Le frecce rivolte a sinistra indicano il moto diretto; le frecce a destra, il moto retrogrado. B e C sono rispettivamente il primo e il secondo punto stazionario.
Il primo limite riguarda la particolare curva che ciascun pianeta dotato di moto retrogrado – come per esempio Mercurio, Venere, Marte, Giove e Saturno – esegue sullo sfondo dello Zodiaco. Questa curva (che oggi sappiamo prodotta dai moti relativi del pianeta e della Terra intorno al Sole) assume la foma di un cappio rivolta verso l’alto o verso il basso, oppure si presenta come una “S”. Cappi e “S” appaiono talora molto ampi, sia in longitudine, cioè parallelamente all’eclittica (la traiettoria apparente – una circonferenza – che il sole descrive in un anno sullo sfondo delle costellazioni dello zodiaco) sia in latitudine, cioè perpendicolarmente all’eclittica. Forma e ampiezza della curva volta per volta eseguita dipendono dal pianeta considerato e dalla costellazione zodiacale dove esso appare con moto retrogrado.
Nei modelli planetari omocentrici, sempre costruiti da quattro o da cinque sfere concentriche che si muovono uniformemente l’una dentro l’altra, la curva del moto retrogrado di ciascun pianeta è sempre uguale a se stessa. I modelli elaborati da Eudosso e dai suoi successori offrono cioè una prima approssimazione delle apparenze. Essi spiegano qualitativamente il moto retrogrado, ma la curva che ne deriva assomiglia solo vagamente a quella che si osserva in cielo.
Un secondo limite dei modelli omocentrici riguarda la luminosità apparente di ciascun pianeta dotato di moto retrogrado. In particolare Marte, Giove e Saturno presentano variazioni di luminosità non trascurabili. Quando uno di questi tre pianeti si muove di moto diretto (cioè da ovest verso est rispetto alle stelle, cosa che avviene subito dopo la congiunzione con il Sole) presenta una bassa luminosità. Questa aumenta man mano che il pianeta si avvicina all’opposizione con il Sole. Il massimo di luminosità si verifica al centro della curva di moto retrogrado, quando il pianeta assume la massima velocità da est verso ovest rispetto alle stelle. Ripreso il moto diretto, la luminosità del pianeta torna ad attenuarsi. Il fenomeno può essere spiegato in due modi, entrambi in contraddizione con i modelli omocentrici. Uno consiste nel supporre, in contrasto con quanto pensava Aristotele sull’immutabilità dei cieli, che il pianeta modifichi la propria luminosità; l’altro consiste nel supporre che la distanza del pianeta dalla Terra aumenti e diminuisca periodicamente. Ma anche questa seconda spiegazione è in contraddizione con la struttura del cosmo aristotelico. In ciascun modello omocentrico, infatti, il pianeta si trova incastonato sull’equatore della sfera più interna (la quarta per Saturno e Giove, la quinta per Marte, Venere e Mercurio). La distanza del pianeta dalla Terra è, quindi, per definizione, invariabile ed è sempre pari al raggio della sfera che lo contiene. Non è perciò possibile far dipendere una variazione di luminosità da una variazione di distanza.
Modelli alternativi: il sistema geo-eliocentrico di Eraclide Pontico
I limiti di una teoria scientifica portano talora a introdurre alcuni elementi in grado di perfezionarla. Ne consegue di solito la revisione e la sostituzione di alcuni aspetti o, a lungo andare, la completa dismissione della teoria. Nel caso dei modelli a sfere omocentriche, l’elaborazione delle ipotesi alternative ha inizio già a partire dal III secolo a.C. per opera di alcuni matematici attivi nell’area mediterranea soggetta all’influenza culturale greca. Le nuove teorie rientrano tutte nell’ambito del principio di circolarità e uniformità dei moti planetari enunciato da Platone. Alcune di esse si aprono però a radicali cambiamenti di prospettiva, ipotizzando non soltanto la rotazione della Terra sul proprio asse, ma anche la rivoluzione della Terra intorno al Sole.
Un filosofo attivo ad Atene e che influenza i matematici ellenistici è Eraclide Pontico. Dopo aver studiato il pensiero platonico, pitagorico e aristotelico, egli formula la propria concezione di un universo infinito nel quale ogni pianeta è un corpo di natura terrestre circondato da un’atmosfera. Tutte le opere di Eraclide sono andate presto perdute. Quanto di esse si dice nei lavori degli autori posteriori permette tuttavia di ricavare indicazioni essenziali su due importanti idee astronomiche. La prima idea consiste nello spiegare il moto diurno delle stelle fisse da est verso ovest mediante la rotazione della Terra in verso opposto intorno al proprio asse. In altri termini, non la Terra, ma le stelle sono perfettamente immobili e il loro moto diurno, soltanto apparente, è prodotto dal continuo mutare di posizione dell’osservatore. Eraclide delinea in più un sistema cosmologico “misto”, che prevede due centri principali e distinti di rotazione: la Terra e il Sole. Al primo centro competono la rotazione della Terra sul proprio asse e le lente rivoluzioni da ovest verso est della Luna, del Sole, di Marte, Giove e Saturno. Al secondo centro di rotazione competono invece le rivoluzioni di Mercurio e di Venere, con velocità crescente al diminuire della distanza dal Sole.
5.2 Aristarco di Samo e la prima formulazione del sistema eliocentrico
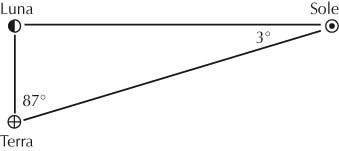
Schema del metodo di Aristarco per determinare la distanza Terra-Sole
L’idea di Eraclide viene ripresa da Aristarco di Samo (310 ca.-250 a.C.) allo scopo di spiegare tutti i fenomeni celesti, cioè sia i moti retrogradi sia le variazioni di luminosità e di distanza dei pianeti, all’interno di un sistema di sfere concentriche che ruotano in modo uniforme. La spiegazione trovata da Aristarco comporta però una ridefinizione generale dell’architettura del cosmo. Di Aristarco si è conservato soltanto un breve lavoro, Sulle dimensioni e la distanza del Sole e della Luna, nel quale vengono stimate, sulla base di osservazioni, le principali grandezze cosmologiche. Aristarco determina il rapporto fra i diametri della Terra e della Luna in base a quante volte il disco lunare entra nell’ombra proiettata dalla Terra durante una eclisse. Il risultato del confronto è che la Terra ha un diametro pari a circa tre volte quello della Luna. Quanto al rapporto fra le distanze Terra-Luna e Terra-Sole, Aristarco procede stimando l’angolo che separa il Sole dalla Luna quando il disco lunare appare illuminato a metà (primo o ultimo quarto). Secondo Aristarco questo angolo è un po’ più piccolo dell’angolo retto. Le sue misure lo portano a concludere che il Sole è relativamente vicino alla Terra, distandone appena fra le 18 e le 20 volte più della Luna.
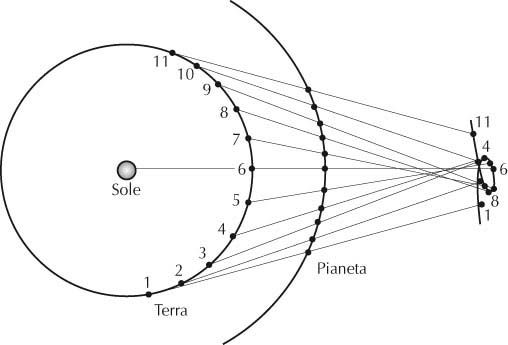
Il moto retrogrado di un pianeta esterno all'orbita della Terra spiegato dal punto di vista eliocentrico. Lo schema spiega il moto retrogrado di un pianeta come fenomeno apparente. I numeri rappresentano posizioni successive della Terra e del pianeta lungo le proprie orbite eliocentriche, nonché del punto dove il pianeta appare proitettato nel cielo.
Si deve però ad Archimede di Siracusa l’informazione sulla più rivoluzionaria idea di Aristarco, vale a dire la prima formulazione dell’ipotesi eliocentrica: “Aristarco di Samo”, scrive Archimede nell’Arenario, “espose per iscritto alcune ipotesi, secondo le quali si ricava che il cosmo è più volte maggiore di quello suddetto. Egli suppone infatti che le stelle fisse e il Sole rimangano immobili, e che la Terra giri, seguendo la circonferenza di un cerchio, intorno al Sole, che sta nel mezzo dell’orbita; e che la sfera delle stelle fisse, intorno allo stesso centro del Sole, abbia tale grandezza che il cerchio lungo il quale suppone che giri la Terra, abbia rispetto alla distanza delle fisse la stessa proporzione che il centro della sfera ha rispetto alla superficie”, il che ci dice che se tutti i pianeti, inclusa la Terra, girano intorno al Sole, le loro posizioni e distanze reciproche cambiano ciclicamente nel tempo.
Nell’architettura del cosmo di Aristarco, le retrogradazioni, le variazioni di luminosità e le circostanze in cui tali fenomeni avvengono, sono considerati fatti necessari conseguenti ai moti relativi della Terra e dei pianeti intorno al Sole. Per esempio, circa ogni due anni la Terra passa accanto a Marte e lo sorpassa. Durante il sorpasso Marte sembra rimanere indietro sullo sfondo delle costellazioni zodiacali (moto retrogrado). Poiché, durante il sorpasso, la Terra tocca il punto di minima distanza dal pianeta, Marte appare massimamente luminoso proprio in coincidenza del massimo di velocità retrograda. E ancora, durante il sorpasso, la Terra viene a trovarsi esattamente fra Marte e il Sole, cosicché questi due astri appaiono in punti opposti dello Zodiaco (opposizione).
Ostacoli all’ipotesi eliocentrica
Se l’idea eliocentrica spiega così bene i fenomeni, perché non viene subito presa in considerazione dai contemporanei di Aristarco? Perché essa si perde quasi subito per essere recuperata solo nell’Europa del Cinquecento? Tre sono i principali ostacoli filosofici che la teoria si trova ad affrontare.
Il primo ostacolo riguarda la necessità, evidenziata da Archimede, di ingrandire eccessivamente la sfera delle stelle fisse. Nel sistema geocentrico le stelle si trovano relativamente vicine alla Terra. Per il più grande astronomo e matematico dell’antichità, Claudio Tolomeo (II sec. d.C.), basta infatti supporre che la Terra sia come un punto rispetto alla sfera delle stelle. Se così non fosse, l’arco di separazione tra due stelle sarebbe minore quando esse sorgono (o tramontano) all’orizzonte rispetto a quando esse sono alte nel cielo, poiché nel secondo caso esse si troverebbero sensibilmente più vicine all’osservatore. Nel sistema di Aristarco è invece l’orbita della Terra a dover essere come un punto rispetto alla sfera delle stelle. Se così non fosse, l’arco di separazione tra due stelle sarebbe minore quando le stelle appaiono aldilà del Sole rispetto a quando la Terra, compiuta metà della sua orbita vi passa davanti. A conti fatti, come afferma Archimede, nel cosmo eliocentrico di Aristarco la sfera delle stelle avrebbe un raggio almeno mille volte più grande che nel tradizionale cosmo geocentrico. Un simile aumento di dimensioni inquieta i filosofi, imbarazzati dal dover trovare un significato a un così grande spazio prevalentemente “vuoto”.
Un secondo ostacolo riguarda invece l’impossibilità di spiegare perché, nonostante la Terra ruoti intorno al Sole e sul proprio asse con velocità vertiginose, le cose sulla sua superficie si comportino come se fosse immobile. Per la fisica aristotelica, un corpo non soggetto al moto naturale secondo la verticale, proprio della regione terrestre, deve subire l’azione di una forza motrice. Se la Terra si muovesse, tutti gli oggetti non mantenuti nella direzione del moto da qualcosa in grado di esercitare su di essi una qualche forza, dovrebbero mostrare uno stesso comportamento. Per esempio le nuvole non potrebbero mai dirigersi verso est, poiché il moto della Terra in quella stessa direzione le sorpasserebbe. Le nuvole, e con loro qualsiasi oggetto che voli o sia gettato in aria, rimarrebbero sistematicamente indietro e sembrerebbero sfrecciare verso ovest. Il che ci dice che, per risultare convincente, la concezione di Aristarco comporta l’elaborazione di una nuova fisica del moto da sostituire alla fisica aristotelica.
Un terzo ostacolo è infine costituito dalla rottura di simmetria insita nel nuovo sistema cosmologico. Diversamente dal sistema geocentrico, nel quale tutti gli astri ruotano intorno alla Terra, nel sistema di Aristarco tutti i pianeti, inclusa la Terra, orbitano intorno al Sole, tranne la Luna, che gira intorno alla Terra. Si tratta di un’eccezione non banale, dato che le considerazioni di simmetria e di bellezza di una teoria scientifica affascinano da sempre la mente umana.
5.3 La teoria degli epicicli
Tra il III e il II secolo a.C. si assiste anche al profilarsi dell’elaborazione di altri modelli planetari alternativi alle sfere omocentriche. I nuovi modelli si dimostrano in grado di rendere conto dei fenomeni osservati con straordinaria precisione, senza tuttavia dover rinunciare alla centralità e alla immobilità della Terra. Il merito di questa impresa spetta a due grandi matematici, Apollonio di Perga (III secolo a.C.) e Ipparco di Nicea (II secolo a.C.), entrambi legati alla comunità scientifica alessandrina.
Purtroppo, l’unica opera di Apollonio parzialmente sopravvissuta riguarda lo studio delle particolari curve che si ottengono tagliando un cono circolare retto con un piano – ellisse, parabola e iperbole – e che perciò sono dette “sezioni coniche”. Tutto quanto si conosce sulle scoperte astronomiche di Apollonio si deve, invece, ad alcuni passi della Mathematiké sýntaxis (Composizione matematica) di Claudio Tolomeo, meglio nota come Almagesto.
Spiegazione del moto retrogrado di un pianeta
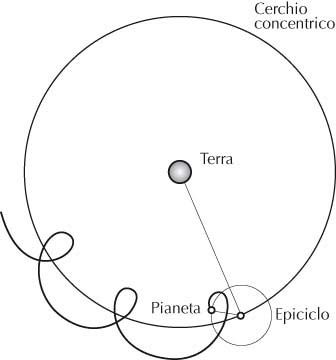
Schema di un modello a epiciclo-concentrico
Da quest’opera apprendiamo che secondo Apollonio è possibile spiegare il moto retrogrado di un pianeta grazie alla sovrapposizione di due circonferenze. Una prima circonferenza concentrica alla Terra, e per questo motivo denominata “concentrico”, porta sopra di sé una seconda circonferenza più piccola, detta “epiciclo” (cioè “cerchio di sopra”), sulla quale si trova il pianeta. Quest’ultimo scorre di moto uniforme lungo l’epiciclo da ovest verso est, mentre il centro dell’epiciclo scorre a sua volta di moto uniforme lungo il concentrico, sempre da ovest verso est. Così, le posizioni di Saturno, Giove, Marte, Venere e Mercurio lungo lo Zodiaco possono riprodursi assegnando valori opportuni alle velocità di rotazione e al rapporto fra i raggi delle due circonferenze.
I modelli planetari “a epiciclo-concentrici”
In questi modelli planetari, definiti “a epiciclo-concentrico”, il centro dell’epiciclo compie una rivoluzione con il periodo zodiacale del pianeta. Tale periodo, dato dal tempo che un pianeta impiega per compiere un giro completo dello Zodiaco, corrisponde a un anno per Mercurio e Venere, a circa due anni per Marte e poco più di un anno per Giove e Saturno. Nel corso della propria rivoluzione geocentrica, ogni pianeta tocca un punto di massima distanza dalla Terra. Ciò accade quando esso è in congiunzione con il Sole e, in questa situazione, il pianeta appare assai poco luminoso. Inoltre, poiché il moto del pianeta e il moto dell’epiciclo hanno la stessa direzione, il pianeta appare spostarsi da ovest verso est con la massima velocità. Poi, progressivamente, il pianeta si allontana dal Sole e passa dal punto di massima distanza a quello di minima distanza dalla Terra, il che accade esattamente in opposizione al Sole. In questa situazione, al contrario di quella precedente, il pianeta appare estremamente luminoso e il moto del pianeta lungo l’epiciclo e il moto dell’epiciclo sul concentrico seguono direzioni opposte. Poiché il moto del pianeta è superiore a quello dell’epiciclo, il pianeta appare retrogradare per alcuni giorni.
5.4 Ipparco di Nicea e la precessione degli equinozi
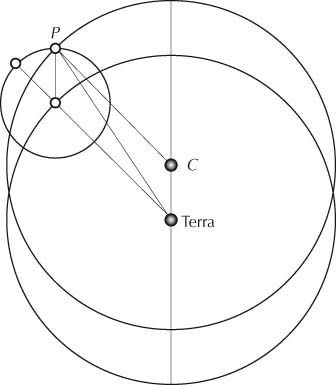
Schema di comparazione di un epiciclo-concentrico particolare e di un eccentrico fisso. Lo schema rappresenta una identità geometrica fra a) la combinazione di una circonferenza concetrica (cerchio grande centrato sulla Terra) e di un epiciclo (cerchio piccolo che si muove sul cerchio grande con raggio che rimane sempre parallelo a se stesso) e b) un cerchio eccentrico con centro C spostato rispetto al centro del concentrico di una quantità uguale al raggio dell’epiciclo.
Resta comunque un problema. Il Sole e la Luna, che percorrono lo Zodiaco a velocità variabile, ma senza mai essere retrogradi, costituiscono casi particolari che non si possono descrivere con un modello a epiciclo-concentrico ordinario. Sempre secondo la testimonianza di Claudio Tolomeo, il primo autorevole interprete del moto di questi due astri è un altro illustre matematico, Ipparco di Nicea.
Questi ipotizza che sia il Sole che la Luna si muovano intorno alla Terra immobile lungo circonferenze eccentriche (ossia il cui centro non è fissato nel medesimo punto). In questo modo, per esempio, quando il Sole percorre la metà dell’eccentrico più vicino alla Terra (in autunno e in inverno), esso appare muoversi più velocemente lungo lo Zodiaco. Quando invece il Sole percorre la metà dell’eccentrico più lontana dalla terra (in primavera e in estate), esso appare muoversi più lentamente lungo lo Zodiaco.
L’unica opera che di Ipparco ancora ci rimane, il Commentario ai fenomeni di Arato ed Eudosso, espone i tempi del sorgere, culminare e tramontare delle stelle. Da Tolomeo sappiamo che la precisione non eccelsa delle osservazioni basta comunque a Ipparco per scoprire, mediante il confronto con le coordinate di alcune stelle registrate in Mesopotamia alcuni secoli prima, un nuovo fenomeno celeste. Con il trascorrere del tempo la longitudine delle stelle sull’eclittica aumenta in modo progressivo. È come se la sfera delle stelle non ruotasse soltanto da est verso ovest in un giorno intorno ai poli dell’equatore celeste, ma anche di un grado ogni cento anni da ovest verso est e intorno ai poli dell’eclittica. In questo fenomeno, noto come “precessione degli equinozi”, i punti di intersezione dell’eclittica con l’equatore celeste (chiamati equinozi), sembrano spostarsi verso ovest.

Helios sul suo carro: metopa del tempio di Atena a Troia, III sec. a.C., Berlino, Staatliche Museen
Ipparco e lo studio del Sole e della Luna
Il genio di Ipparco è riconosciuto dal grande astronomo Claudio Tolomeo soprattutto nello studio dei moti del Sole e della Luna. Riguardo al Sole, misurazioni ripetute degli istanti degli equinozi e dei solstizi inducono Ipparco ad accertare che le stagioni non hanno tutte uguale durata. Il periodo autunno-inverno è di alcuni giorni più breve del periodo primavera-estate. Per rendere conto di questa differenza, Ipparco ricorre a due ipotesi basate su un sistema particolare a epiciclo-concentrico, e su uno a eccentrico fisso. Nel primo caso, il Sole si muove su un piccolo epiciclo che scorre lungo un concentrico. Tuttavia, diversamente dai pianeti, il Sole compie uniformemente un giro sull’epiciclo da est verso ovest nel medesimo tempo in cui il centro dell’epiciclo compie uniformemente un giro da ovest verso est lungo il concentrico. La composizione dei due movimenti dà come risultato un ulteriore movimento uniforme, che corrisponde di fatto al modello dell’eccentrico fisso. In questo secondo caso, scelta opportunamente la direzione e l’ammontare della distanza fra il centro della Terra e il centro dell’eccentrico, è possibile rappresentare con buona approssimazione l’anomalia data dal moto in apparenza ineguale del Sole. Allo stesso modo è possibile spiegare le lievi variazioni del diametro apparente del Sole, più grande in inverno e più piccolo in estate.
Il caso della Luna, che presenta anch’essa un’anomalia zodiacale, è risolto da Ipparco in maniera analoga ricorrendo ai modelli geometrici a epiciclo-concentrico e a eccentrico fisso. Tuttavia, il moto lunare è molto più complicato di quello solare e a Ipparco si devono tre importanti scoperte in merito. La prima consiste nella constatazione che l’orbita della Luna non è complanare all’eclittica, ma inclinata di un angolo pari a circa 5 gradi. La seconda riguarda una ulteriore particolarità del piano dell’orbita lunare. La linea che congiunge i due punti in cui l’orbita della Luna interseca l’eclittica (la “linea dei nodi”), non mantiene sempre la stessa orientazione rispetto alle stelle dello Zodiaco, ma appare ruotare in modo retrogrado (da est verso ovest), compiendo un giro completo in quasi 19 anni. Infine, l’apogeo dell’orbita lunare non è fisso, ma si muove progressivamente da ovest verso est rispetto alle stelle fisse compiendo un giro dello Zodiaco in circa nove anni. Per tenere in debito conto questi fenomeni peculiari della Luna, Ipparco scarta in questo caso il modello a eccentrico semplice in favore del modello a epiciclo-concentrico. Il piano in cui colloca le due circonferenze componenti non è più coincidente con l’eclittica, come nel caso del Sole, ma inclinato di 5 gradi su di essa. Inoltre, il piano del modello ruota regressivamente in 19 anni, in modo da spiegare la precessione dei nodi lunari. Quanto al moto progressivo dell’apogeo, Ipparco introduce una lieve differenza fra il periodo di rotazione uniforme della Luna da est verso ovest sull’epiciclo e il periodo di rotazione uniforme dell’epiciclo da ovest verso est lungo l’eccentrico. Se il primo periodo è leggermente più lungo del secondo, la Luna arriverà di volta in volta leggermente in ritardo all’apogeo, spiegandone così il progressivo avanzamento.
VIDEO
Cosmologie antiche
5.5 Un nuovo sistema del cosmo
I modelli geometrici di Apollonio e di Ipparco iniziano a delineare un sistema del cosmo che nell’essenza geocentrica è analogo a quello di Eudosso, Callippo e Aristotele, ma ne differisce enormemente nei dettagli. Non solo i nuovi modelli spiegano molto meglio le apparenze dei fenomeni celesti da entrambi i punti di vista qualitativo e quantitativo; essi hanno potenzialità di calcolo inimmaginabili rispetto ai modelli a sfere concentriche e sono trasformabili in dispositivi meccanici (planetari). Nell’astronomia omocentrica, calcolare la posizione di un pianeta lungo lo Zodiaco richiede la soluzione di un complicato problema di trigonometria sferica che ha per oggetto alcune sfere mutuamente inclinate e ruotate. Nell’astronomia degli epicicli, calcolare la posizione di un pianeta richiede invece la soluzione di un più semplice problema di trigonometria piana che ha per oggetto due circonferenze mutuamente ruotate. I vantaggi pratici sono notevoli e indirizzano gli astronomi antichi verso la ricerca di una precisione di calcolo e di previsione dei fenomeni celesti sempre maggiore che avrà il suo culmine, nel II secolo d.C., in Tolomeo.
LETTURE
Le teorie meteorologiche