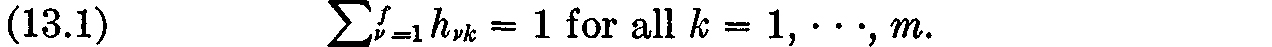
The Neoclassical or Walrasian Equilibrium—Introduction
Our discussion of cycle theory and our preliminary discussion of Keynesian equilibrium has now given us sufficient perspective so that we may profitably return to price theory, taking up the study of general “neoclassical” or “Walrasian” price equilibrium of an economy. The history of this topic, as well as an interpretation of its significance, is given by Karlin.
The main advances to date in the study of equilibrium models are associated with the names of Walras, Wald, McKenzie and Arrow and Debreu. To Walras we owe the first sophisticated formulation of the equilibrium phenomenon. Wald later carried out a comprehensive mathematical analysis of Walras’s equations and established the existence and uniqueness of solutions to these equations under a wide variety of conditions. Finally, McKenzie, and Arrow and Debreu independently formulated general models of equilibrium and proved the existence of a competitive equilibrium. None of the three models (Walras-Wald, McKenzie, Arrow-Debreu) subsumes any of the others as a special case; rather, all three should be viewed as variant descriptions of equilibrium in a competitive economy. Alternative analyses of the same models or other versions of equilibrium have been proposed independently by Gale, McKenzie and Uzawa.
It will soon be seen that we regard this theory somewhat critically.
Our model will be like that of Arrow and Debreu, but with linear Leontief-like features as introduced in the first four lectures, differing only in an expanded treatment of consumer preference. Thus the equilibrium price theory will be strictly comparable to the price theory developed in the first four lectures: we will be able to see explicitly how much or how little is added to the conclusions we are able to draw, by the introduction of consumer preferences.
The elements of the model are to be as follows. In the first place, we will have a number of competing firms, each of which seeks to maximize its own profits; secondly, we will have a number of consumption units (families) each of which places a subjective “utility” upon each “bill of goods” that their labor and their dividends from ownership of industry will purchase. Each consumption unit then seeks to maximize this subjective utility, measured by an individual “utility function.” A careful formulation of the law of supply and demand will then allow us to find the conditions under which there exist prices at which all of these maxima are simultaneously realized; continuing, we shall investigate the further properties of such a “competitive equilibrium.”
1.The Model Explicitly Defined
Our model of the whole economy will consist first of a number m of “firms” or “investment syndicates” each of which is capable of producing (i.e., has the ability and the freedom to produce) any, several, or all of the n commodities C1, · · ·, Cn of the economy. Labor will first be considered (inessentially) as being homogeneous and regarded as commodity C0; consequently we will generalize the model to include various distinct labor sectors. The kth firm in the first instance is described by a set of numbers πij(k) which represent the amount of Cj required by firm k for the production of one unit of Ci. We shall take these numbers as being the same for all firms, however, and write πij for each of them. Thus we assume that no firm can have a clear technological advantage over another firm. We measure the wealth of each firm by assuming that firm k has an initial ownership inventory of qi(k) units of commodity Ci, (i = 1, · · ·, n) and that this inventory is economically liquid, i.e., could be freely sold or traded for equal value (under prices yet to be determined). In this model, then, the only distinction between different firms is their total capitalization as reflected in their ownership inventories. In the same way we assume a fixed capital matrix with elements ϕij, taking ϕoi = ϕio = 0 for all i.
The model consists next of a number f of consumption units, or families. The vth family’s fractional title to the ownership of the kth firm is hvk, where
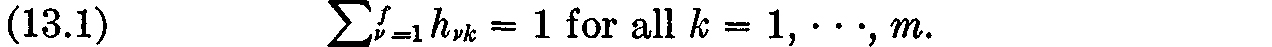
The vth family’s satisfaction as derived from consumption of commodities C1, · · ·, Cn, as well as the negative consumption of commodity Co (the amount of labor which is supplied by the consumption unit) is described by a utility function:
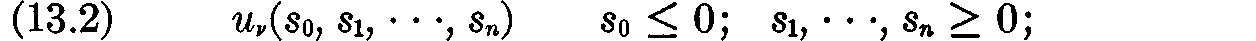
this is subjective value placed by the vth family on the “bill of goods” or “commodity bundle” or “labor-consumption plan” consisting of (consumption of) commodities of the various kinds in amounts s1 · · ·, sn and (expenditure of) labor in the amount –s0. It clearly would not be realistic to assume linearity here, for ten cars cannot have ten times the subjective value of one for most families. Fortunately, it is not necessary to delve deeply into the form of the utility functions.
It is canonical to remark here that these utility functions play a role in the determination of equilibrium only through being maximized; thus each of these functions may be indifferently replaced by any monotone-increasing function of itself. Putting this differently, it is not the functions uv themselves, but only the “indifference surfaces” uv = constant that are strictly necessary for the model. Another perfectly equivalent way of putting this same circumstance is to state that what we require is a linear ordering of bills of goods, some being rated as preferable to others. The utility function is then a mere shorthand for expressing these somewhat more subtle facts.
We assume about our utility functions that for each x(1) and ν there exists an x(2) for which
Since the signs of the parameters s0 have been taken as negative, this says that, given any family and any bill of goods, either a decrease in the amount of labor expended, or an increase in the amount of some commodity, consumed, or both, will always be considered desirable. Our assumption says in consequence that there is no “saturation point,” i.e., given any commodity bundle x(1), there is always another commodity bundle x(2) which the vth family will regard as strictly preferable.
A rather opposite fact was emphasized in the preceding Keynesian discussions; that consumption did not always rise to meet income, but that in certain circumstances inventories of producer goods or trade inventories would be purchased if the possibility of using these producer goods or trade inventories profitably was real. Thus, in making the assumption expressed by (13.3), which is a mathematical form of the oft-repeated economic dictum “appetite is boundless,” we implicitly assume away all Keynesian difficulties. We shall see that without the assumption expressed by (13.3), our model does not necessarily admit any equilibrium; if we admit accumulation of producer inventories as an auxiliary term in the consumer utility functions, then our whole notion of “equilibrium” comes into question, since our equilibrium corresponds to a continual (and continually unobstructed) growth of the wealth of firms. It follows that notions derived from the Walrasian equilibrium cannot legitimately be used to criticize the Keynesian analysis; to bring these two approaches to a direct confrontation, a common model generalizing them both is required. Holding all these difficulties in abeyance for the moment, we shall continue to investigate price equilibrium in the neoclassical model as we have it.
We shall introduce a few more assumptions as the discussion proceeds, but the model defined in the last few paragraphs is basically the model we shall analyze.
We now wish to study the following question. With each of the firms attempting to maximize its own profits, and with each of the consumption units attempting to maximize its individual utility functions, is there a price vector (i.e., a set of prices p0, p1, · · ·, pn) which leads to a production and exchange equilibrium? The answer is yes, as we shall see. In obtaining this positive answer, we shall also explore the properties of the “equilibrium price vector”; this exploration will put us in a position to criticize the theory under examination.
2.Price Equilibrium
We must now give the rather lengthy definition of “price equilibrium,” thereby giving, in the sense of Walras, a complete and general definition of the more fragmentary concept ordinarily called the “law of supply and demand.”
By a “price equilibrium,” we shall mean a set of prices p0, · · ·, pn, a set of production figures a1(k), · · ·, an(k), and a set of consumption figures s0(v), · · · sn(v), which satisfy the following four conditions.
Condition (a). The prices are nonnegative, i.e.,
and at least one price is not zero.
The significance of this condition is evident.
Condition (b). For each firm k = 1, · · ·, m the number (profit)
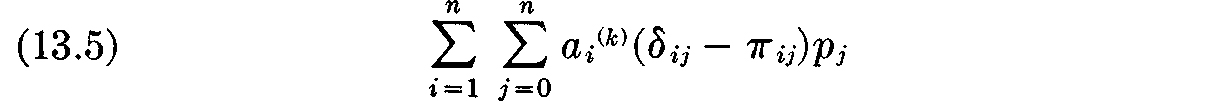
is a maximum over all sets ãi which satisfy
This condition states that, whatever the equilibrium prices of the various commodities (including labor) may be, each firm will choose to manufacture a list of products (in amounts a1(k), · · ·, an(k)) for which the profit is greater than (or at least not less than) the profit obtainable by production of any other list of products which could be produced, subject to the budgetary condition (13.6). The left-hand side of (13.6) is the amount of capital which must be laid out to assemble the elements necessary for production of commodities in the amounts 
ij, while the right-hand side is the value of the total assets of the firm. We are therefore neglecting the possibility of borrowing, but since the amount of money a firm can borrow is approximately proportional to its total assets, this should not introduce overwhelming errors.
Condition (c). For each consumer unit ν = 1, · · ·,f, the number
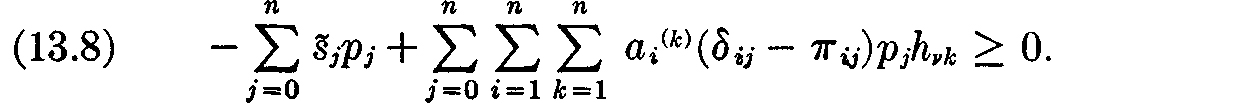
This condition states that, whatever the equilibrium prices may be, each consumption unit will choose to consume that list of commodities whose subjective value is the greatest among all lists of commodities which could be consumed subject to the budgetary condition (13.8). The first term in (13.8) is the excess of expenditure over wages, while the second term is dividend income. Borrowing is therefore ruled out again.
Condition (d). Everything that is consumed must be produced, i.e.,
We assume in addition that if there is an excess at equilibrium of production over consumption for some commodity Ci, then at equilibrium the price of this commodity must drop to zero, so that equality holds in (13.9) whenever pi > 0.
Conditions (a) through (d) are then the conditions to be satisfied by the p, the a, and the s, for a Walrasian price equilibrium to subsist.
We intend in what follows to prove the existence of a price equilibrium. However, let us, for the moment, assume the existence of such a price equilibrium, and develop its properties. To establish the consequences of condition (b), we shall use the following lemma.
LEMMA. Let it be required to find that solution x1 · · ·, xm of the inequalities
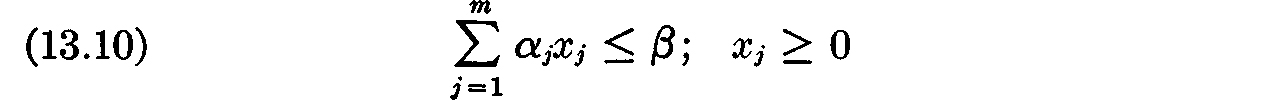
(where α1, · · · αj, are nonnegative constants not all zero) for which
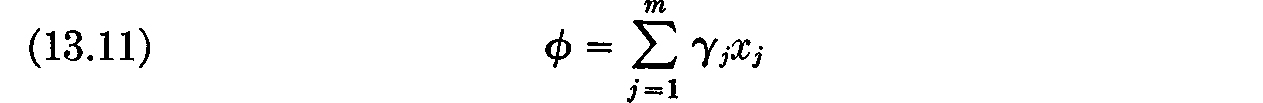
(where γ1 · · ·, γj are nonnegative constants) is a maximum. Let S be the set of indices s for which
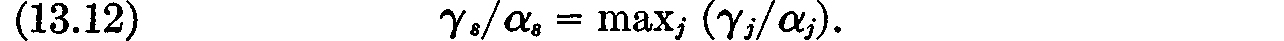
Then the most general solution of our maximum problem is at the same time the most general vector x for which xj = 0 if j ∉ S and for which 
is satisfied as an equality.
This principle is useful in various branches of mathematics, particularly in statistics, where it is known as the fundamental lemma of Neyman and Pearson. We shall give a heuristic rather than a formal proof; the former is at once more convincing and more transparent than the latter.
Suppose that various types of sand from various sacks are available for purchase at various fixed amounts per pound and that, subject to the requirement that one not exceed a given budget (condition (13.10)) one wishes to acquire as much sand as possible (maximize (13.11)). How to proceed? Evidently the answer is to buy sand only from those sacks which are cheapest per pound of sand; it is, however, a matter of complete indifference from which of these sacks one purchases sand. But this is the conclusion which we have expressed more formally in our lemma. Q.E.D.
This lemma shows that condition (b) requires that each firm produce only those commodities Ci for which
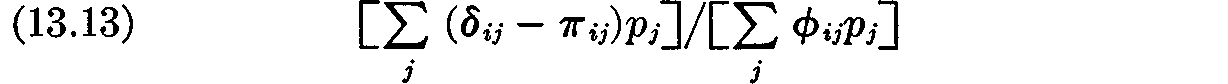
is a maximum over i. Let this maximum be p. Then we have
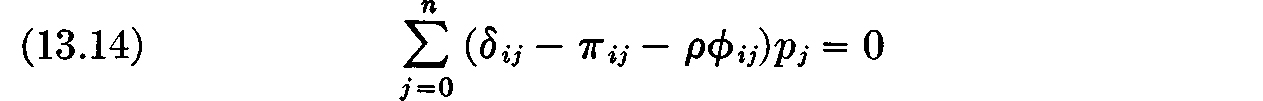
for each commodity Ci which is produced in nonzero quantities. We have encountered this equation before–it tells us that all commodities produced are produced at the same profit per unit investment, i.e., the same rate of profit. Thus, in the present model we recover in a more formal way the fundamental principle for equilibrium which we derived heuristically in our earlier discussion of prices: the rate of profit on each commodity produced is the same for all firms. Further, since only those commodities for which the rate of profit is maximum will be produced, we can conclude that the rate of profit is the same for all commodities which are produced in positive amounts. Unless all firms are to refrain from producing nonzero amounts of any commodity, ρ must of course be nonnegative. If ρ = 0, so that no profit is obtained in any case, then expression (13.5) has the “maximum” zero identically for all activity levels satisfying the inequality (13.6). However, if ρ > 0 then the preceding lemma shows that the expression (13.5) only attains its maximum if the inequality (13.6) degenerates into an equality; i.e., if ρ > 0 condition (b) implies that
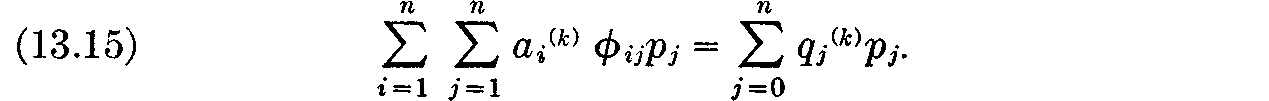
That is, if equilibrium occurs at a positive rate of profit, each firm will insist upon utilizing all its capital.
If the elements πij (not including the zero row) form a connected matrix, we find that we have returned to the price theory of the first four lectures. Making reference to the results established there, we find that (13.11) alone determines the price ratios as a function of p.
Thus the only possible effect that the consumer utility functions can have upon prices is through the determination of the rate of profit. We emphasize: as far as equilibrium price theory in our model goes, the generalization of our model (as compared to the simpler model discussed in the first four lectures) to include consumer preferences can at best only determine the rate of profit; we shall find even this much cannot be very securely attained.