No investment guide is complete without a discussion of certain ancillary topics. Now that you’ve mastered the basics of asset-class behavior and portfolio construction, we’ll tie things together with a treatment of the following areas: value investing and the three-factor model, “new era” investing, hedging, dynamic asset allocation, and behavioral finance.
Is it possible to beat the market in the long run? I hope by now that I have convinced you otherwise. A better question can be asked: Are there market segments and subsegments that outperform or underperform relative to their risk? Examples of this have already been presented; the long-term return of precious metals and other “hard assets” (collectibles, precious stones) is trifling compared to their very high risk. More subtly, the risk of owning long-term bonds is much higher than that of short-term bonds, yet their returns are the same. Are there any characteristics of stocks that predict higher or lower expected return? We are already aware of one: company size. As we have seen, small stocks outperform large stocks in the long run. Unfortunately this comes at the cost of higher risk.
Stocks outperform almost all other assets in the long run because you are buying a piece of our almost constantly growing economy. Think of all the technological advances of the twentieth century and the wealth they have created: air transport, radio, television, automobiles, consumer electronics, and computers. You benefit financially from these wonders by owning stock, not T-bills or corporate bonds. So far, so good. Unfortunately, investors then make a fatal extrapolation: that the most profitable stocks to own must be those of the most rapidly growing companies with the hottest products. These are known as “growth companies.”
A key investment concept is that of “valuation,” i.e., how to tell when an individual stock or stock market is expensive or cheap. (It is a much simpler matter to talk about the valuation of the stock market as a whole or of an individual market sector.)
There are three commonly used measures of individual stock or of aggregate stock market value: price/earnings (P/E) ratio, price/book (P/B) ratio, and dividend yield. Ultimately, you are buying a stock in order to own a piece of its earnings. P/E describes how much you are paying for those earnings. Say XYZ Multimedia, Inc. earns $5 per share and sells for $100 per share. It has a P/E ratio (also called the multiple) of 20; you are paying $20 for each $1 of earnings. A company selling at a P/E of 30 is said to be expensive, and one selling at a P/E of 10 is said to be cheap. Unfortunately, company earnings are not particularly stable. Quite frequently the earnings of even the largest and most stable companies disappear entirely, and on rare occasions net corporate profits disappear for the entire U.S. stock market. (This happened for a prolonged period during the Great Depression and for a brief period during the early 1980s; the losses sustained by many large U.S. corporations exceeded the profits of the rest, resulting in a net loss for U.S. industry as a whole.) Further, it is easy for corporate accountants to “fiddle” with reported earnings to the point where they are meaningless. For this reason, P/E has only limited value. Ben Graham made the astute observation that corporate earnings provide useful information only when averaged over several years.
All companies have a book value; this can be thought of as the net value of a company’s total assets, although the accounting reality of this number is much more complex. It is a rough number. The book value of an airline is easily understood; it is primarily the value of its planes, buildings, and office equipment, minus its liabilities. Let’s assume ABC Airlines owns assets valued at $2 billion and liabilities of $1 billion, resulting in net assets of $1 billion; let’s further assume that the value of all of its outstanding stock is $2 billion. Its P/B ratio is 2; it is selling for twice its book value. A stock with a P/B of less than 1 is said to be cheap; one with a P/B of more than 5 is said to be expensive, at least relative to its book value. The book value of a stock is very stable; corporate accountants usually have no need to fudge this number.
Finally, there is dividend yield. This is easy to understand—it is simply the amount of dividend remitted to the shareholders divided by the price of the stock. If XYZ Multimedia, Inc. sells for $100 per share, earns $5 per share and remits $3 of this to the shareholders, then the dividend yield is 3%. It is possible for a company to pay more in dividends than its earnings, but it obviously cannot do this indefinitely. Small or rapidly growing companies frequently pay no dividends at all; they need to retain all of their profits in order to grow. Until very recently, large, slowly growing companies often paid dividends in excess of 5%.
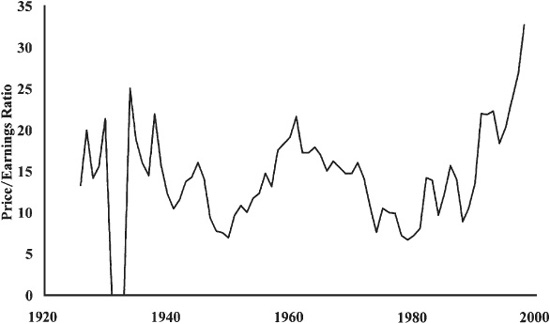
We are now capable of telling how expensive the tomatoes are. First, it is useful to examine the P/E, P/B, and dividend yield of the entire U.S. stock market. Figure 7-1 plots the P/E of the market over the past 73 years. We see that this number usually varies between about 7 and 20 and averages about 14; in fact, the number can be much larger than this if earnings are near zero because the denominator is so small. When the market P/E is about 7, it is definitely cheap; when it is greater than 20, it is expensive.
Figure 7-1. Price/earnings ratio, 1926–1998.
Figure 7-2 plots the P/B of the market. Until recently it had varied between about 1 (cheap) and 3 (expensive); it averages about 1.6. Recently it has ballooned to about 8. Because of the recent data, some have questioned the validity of this measure of expensiveness.
Figure 7-2. Price/book ratio, 1926–1998.
Figure 7-3 plots dividend yield. Historically it has varied between 2.5% (expensive) and 7% (cheap); it averages about 4.5%. The higher the yield, the cheaper the price; the lower the yield, the higher the price. Again, currently stocks yield a historically low 1.3%, and many question its usefulness as well.
Figure 7-3. Stock dividend yield, 1926–1998.
Solid data on the ranges of P/E, P/B, and dividend yield are available only for the largest U.S. stocks. For smaller U.S. stocks, the data are more fragmentary, but the ranges of P/E and P/B are similar; dividend yields are considerably smaller. Valuation of foreign stocks is highly problematic because of the differences in accounting standards among nations; nonetheless, the ranges of P/B of most of the EAFE nations seem similar to that of the United States.
We shall see that long-term returns are usually higher when valuations are cheap and lower when they are expensive. Whether this is of any practical use is open to question.
At any one time, some individual stocks are cheaper than others. Is it useful to purchase cheap stocks in preference to expensive ones? There is a very large volume of data that answers this question resoundingly in the affirmative.
The first study of buying cheap stock used a “Dow P/E strategy,” similar to the recent, more popular Dow dividend strategy described next. In 1964 Paul Miller, head of research at Drexel & Co., examined buying the 10 lowest P/E stocks of the Dow 30. He published a memorandum in which he summarized the results of this technique for the 28 years from July 1936 to June 1964 (Table 7-1).
TABLE 7-1. Value-Stock Performance, 1936–1964
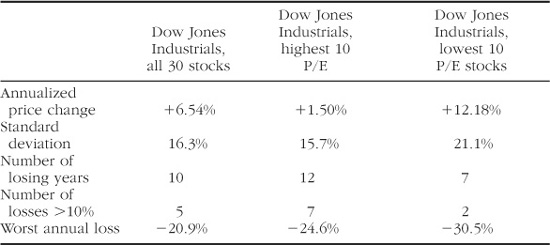
Mr. Miller’s data was collected in a slightly unusual manner. First, he used July to June fiscal years. Second, the return statistic used was price change only; this does not take reinvested dividends into account. Adding in reinvested dividends would result in actual returns of about 5% higher. These data are clear-cut: The lowest P/E stocks (the ones that everybody hates) greatly outperformed the market, and the highest P/E stocks (the ones that everybody loves) greatly underperformed the market. Does this extra return come at higher risk? This hypothesis is supported by the standard deviation and “worst annual loss” data, which are greater for the low P/E stocks than for the high P/E stocks and the whole Dow Jones 30. The higher SD of the low-P/E stocks is mostly due to the very large gains registered by them in several years. The low-P/E stocks are actually the least risky when looked at from the perspective of the total number of losing years or of losses greater than 10%.
Investors are increasingly seeking higher returns with value stocks, but let’s take a step back and see what this means in actual practice. Perhaps the most currently popular method is the so-called Dow dividend strategy, which buys the five highest-yielding Dow stocks. I’ve listed the five highest-yielding and lowest-yielding stocks at the time of this writing:
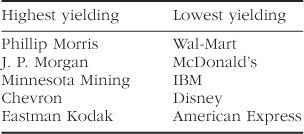
Most readers will recognize the high-yielding (cheap) group as “terrible” companies, and the low-yielding (expensive) as “good” companies.
Probably the most impressive work in this area was done by Professors Fama and French, published in the Journal of Finance in June 1992. They exhaustively studied stock returns from July 1963 through December 1990 and found that all of the variation in return among stocks could be explained by just two factors: company size (no surprise here) and P/B. They divided their stock database into 10 groups ranging from the lowest P/B (cheapest) to the highest P/B (most expensive). The cheapest one-tenth of the market returned 19.6% annually, and the most expensive tenth, 7.7% annually. The smallest cheapest stocks returned 23% annually. They also found P/E useful, but not nearly as useful as P/B. After taking P/B into consideration, P/E had no predictive value.
Are Ben Graham, Fama, French, and a legion of others all telling us that we shall profit by buying bad companies? Yes. Bad companies are cheap; it is quite possible that management will turn the company around and make them back into “good” companies. Further, even if a bad company’s performance worsens, it will not surprise the investment world; the price will probably not drop all that much. On the other hand, good companies are expensive; they are expected to grow to the sky. When, as inevitably happens, they stop growing to the sky, they are taken out and shot by the market. David Dreman has beautifully documented this phenomenon. The largest movements in a company’s price usually occur when its earnings either greatly exceed or fall short of analysts’ expectations. (Note that in the short term it matters little to the price of a stock whether its earnings are high, low, or negative. What really matters is whether they are higher or lower than the “Street” anticipates; better to have a loss for the quarter which is less than the Street expects than to have great earnings which are less than the Street expects.) Dreman has observed that “value” stocks tend to fall much less in price than “growth” stocks when earnings disappoint. Conversely, “value” stocks tend to rise more in price than “growth” stocks when earnings exceed expectations. To repeat:
Good companies are generally bad stocks, and bad companies are generally good stocks.
This concept is very hard for both small investors and professionals to grasp, and probably underlies the poor performance of most professional money managers. No matter how many finance journals they read, they cannot bring themselves to buy bad companies.
Probably the most vivid example of the good company–bad stock paradigm was provided by the popular 1982 book In Search of Excellence, by management guru Tom Peters. He identified numerous “excellent” companies using several objective criteria. Several years later, Michelle Clayman, a finance academic from Oklahoma State University, examined the stock market performance of these companies and compared it with a matched group of “unexcellent” companies using the same criteria. For the five-year period following the book’s publication, the unexcellent companies outperformed the excellent companies by an amazing 11% per year. As you might expect, the unexcellent companies were considerably cheaper than the excellent companies by P/E, P/B, and dividend criteria. People naturally assume that good companies are good stocks, when the opposite is true most of the time. Psychologists refer to this sort of syllogistic error as “representativeness.”
It has long puzzled academic efficient-market theorists that these popular strategies (low P/E, low P/B, high dividend) have worked so well for so long. They are so well-known that enough people should use them so that their advantage should vanish. The reason why these strategies still work, decades after they were described is simple: Cheap companies are dogs, and most people cannot bring themselves to buy them. Ben Graham wrote Security Analysis 50 years ago, which is basically a primer on how to identify cheap, safe stocks. Ben Graham’s disciples are among the most successful money managers in the United States. One of them, Warren Buffett, is one of the wealthiest men in the world. By all rights, Graham’s method should have long since stopped working, but it continues to work. Everybody wants to own Amazon.com, Microsoft, Intel, and AOL. No one wants to buy Woolworth’s.
Looking for cheap stocks is called value investing. The opposite of this is growth investing, looking for companies with rapidly growing earnings. Although there certainly are some very successful growth-stock investors, they have been swimming upstream. You are more likely to swim faster if you head downstream.
Efficient-market theorists are fond of pointing out that there is no pattern to stock or market prices. (As we have already seen, this is not strictly true.) Growth-stock investors believe that they can pick those companies which will have persistent earnings growth and thus reap the benefits of their ever-increasing earnings stream. Unfortunately, established growth companies are very expensive, often selling at P/Es two or three times that of the market as a whole. A company growing 5% faster than the rest of the market and selling at a P/E twice the market’s will have to continue growing for another 14 years at that rate before the shareholder is fairly compensated. As we’ve already seen, stock price movements are essentially an unpredictable “random walk.” Interestingly, it turns out that earnings growth also exhibits random-walk behavior; a company with good earnings growth this year is quite likely to have poor earnings growth next year (and vice versa). In other words, this year’s growth stock is quite likely to become next year’s value stock, at great cost to its shareholders. Contrariwise, a value stock with poor earnings growth will frequently surprise the market with strong earnings growth, with an agreeable change in P/E and price. This typically happens to only a few stocks in a value portfolio in a given year, but the effects on total portfolio performance are still dramatic.
Perhaps the most lucid explanation of the value effect can be found in Robert A. Haugen’s The New Finance: The Case Against Efficient Markets. Professor Haugen points out that in mid-1993 the 20% of stocks with the highest P/E (growth stocks) had an average P/E of 42.4. This resulted in an earnings yield of 2.36%. (The earnings yield is simply the inverse of the P/E—it’s the amount of earnings you’re buying for each dollar of stock.) The lowest 20% (value stocks) had a P/E of 11.93, or an earnings yield of 8.38%. In other words, when you bought the glamorous growth stocks in mid-1993, you were getting $2.36 in earnings for each $100 invested; when you bought the doggy value stocks, you were getting $8.38. If you are to come out ahead with growth stocks in the long term, their earnings will obviously have to grow over three times larger than the value stocks. Haugen then followed the earnings growth of the growth and value cohorts. While the growth stocks, as expected, experienced higher earnings growth, this advantage decayed over time, and their dollar earnings never surpassed those of the value group. In fact, they never even got close; Haugen estimates that each dollar invested in growth stocks leaves you with less than half of the long-term earnings obtainable from value stocks. Again, as Ben Graham said, in the short term the markets are a voting machine, but in the long run they are a weighing machine. And what they are weighing is earnings.
In a paper published in the Journal of Finance in December 1994, Josef Lakonishok and colleagues confirmed earlier work demonstrating the superiority of low P/B and low P/E stocks. They also found that sales growth affected future returns; the most rapidly growing companies had the lowest returns. Although Fama and French and Lakonishok and colleagues all agree that low P/B and P/E stocks outperform growth stocks, they disagree as to why. Fama and French are devout “efficient marketeers,” and believe that the higher return of value stocks must be due to some sort of associated increased risk. They’ve had a difficult time explaining to the investment community the precise nature of this risk, but it goes something like this: Value stocks are sick companies. They have weak profitability, earnings growth, and balance sheets. An economic downturn or even a slight breeze may bankrupt them. Because of this increased risk, they must offer higher returns. After all, if both Kmart and Wal-Mart offered the same future return, who would want to own Kmart? Ergo, value stocks are by definition not a free lunch.
On the other hand, Lakonishok and colleagues maintain that the higher returns of value stocks come without higher risk, and then present convincing evidence that the risk of value stocks is lower than that of growth stocks. In other words, there is a free lunch. Wilshire Associates publishes data of the returns of growth and value stock groupings of various company sizes from 1978 (one of the many goodies available in the Morningstar database). For each company size, the value portfolio returns several points more annualized performance than the same company-size growth portfolio, with a considerably lower standard deviation. In fact, it appears that value stocks seem to outpace growth stocks precisely because they are less risky. During bull markets growth beats value, but during bear markets value stocks lose much less than growth stocks. At the end of the day, the returns on value stocks may be superior to growth stocks simply because of their more benign bear-market performance.
The alternative hypothesis, as we’ve already mentioned, is that there is no excess return without increased risk exposure. This theory is advanced by Fama and French in the form of their three-factor model. This simple, yet powerful construct is extraordinarily useful in understanding long-term returns in markets around the globe. Simply put, any stock asset class earns four different returns:
![]() The risk-free rate, that is, the time value of money. Usually set at the short-term T-bill rate.
The risk-free rate, that is, the time value of money. Usually set at the short-term T-bill rate.
![]() The market-risk premium. That additional return earned by exposing yourself to the stock market.
The market-risk premium. That additional return earned by exposing yourself to the stock market.
![]() The size premium. The additional return earned by owning small-company stocks.
The size premium. The additional return earned by owning small-company stocks.
![]() The value premium. The additional return earned by owning value stocks.
The value premium. The additional return earned by owning value stocks.
Everyone earns the risk-free rate. So in the Fama-French universe, the only important decision you have to make is how much exposure you want to the other three factors. If you’re a complete coward, you have zero exposure to all three and own only T-bills. And if you’re a highly risk-tolerant individual, you have maximal exposure to all three and own only small value stocks.
Let’s look at each risk factor individually. In Figure 7-4, I’ve plotted the trailing five-year annualized “market premium” (the return of the CRSP 1-10 Index—roughly the Wilshire 5000—minus the T-bill return) for the past 36 years. Notice that while it has been persistently positive for the past two decades, things were a good deal rockier in the 1960s and 1970s. Over the entire period, the premium was 5.65% annualized. It certainly wasn’t a sure thing, being positive in only 78% of the rolling five-year periods.
Figure 7-4. Five-year annualized market premium.
Is it possible to bear more risk and thus earn still higher premiums? Yes. You can decide to invest in smaller companies, which are more likely to suddenly disappear than large ones. For the past 36 years, the “size premium” (defined as the return of the smallest half of companies on the NYSE minus the largest half) has been 1.71%. I’ve plotted it in Figure 7-5. Its rolling five-year return has been positive only 53% of the time.
Figure 7-5. Five-year annualized size premium.
Last, there is the third, and much more controversial, premium, which I’ve plotted in Figure 7-6. According to Fama and French, if you are a real risk junkie and want to increase your premium payments even further, you can invest in value companies. These are the sickest puppies in the litter. Think Harvester, Kmart, Nissan. They are identified by their low valuations, such as price/book ratio. The 36-year premium for investing here (defined as the return of the stocks with the lowest P/B ratios minus the return of the stocks with the highest P/Bs) has been 3.77% annualized. Somewhat surprisingly, as you can see in the plot, this premium has been fairly consistent, being positive 87% of the time. In fact, the reliability of the value premium has caused some to question whether this is not really a free lunch, as opposed to a real “risk story.”
Figure 7-6. Five-year annualized value premium.
These three risk premiums—market, size, and value—have been researched extensively by Fama and French. They, and others, have shown the existence of all three in the U.S. market over a very long time period, as well as in many other countries. Are there other premiums? Probably. There is likely a premium for investing in momentum stocks. The nature of the risk associated with momentum—if any—has yet to be determined.
The three-factor model has another use, which we’ve previously encountered, and that is the evaluation of money managers. Through the use of sophisticated statistical techniques, it is possible to attribute just how much of a manager’s returns can be accounted for by each of the risk factors, and how much, if any, is due to skill. For example, if a manager does particularly well in a given period, it may be because he or she was skillful (or lucky). However, it may also be because the manager was exposed to a market factor that had high returns. As you might already suspect, it turns out that most of the performance of top-ranked managers is due to their factor exposure and that few, if any, of these top-ranked managers actually demonstrate anything which looks like skill in a statistical sense.
Ultimately, the rewards of the capital marketplace go to those who can most intelligently balance the three risk factors, as well as the risks of their employment. A small example: Employees of cyclical, “value” companies should be particularly wary of value portfolios, as in the event of a severe recession both their job prospects and portfolios will suffer disproportionately. Workers who tend to keep their jobs in hard times, like letter carriers and repo men, are in a better position to own value stocks.
The investment climate of the past five years has been so vastly different from that of the prior decades that a discussion of our so-called new era is warranted. As this book is being written, stocks are selling at valuations far higher than ever before seen. Dividend yields of large stocks, which typically range between 3% and 7%, are now 1.3%. P/B ratios, which typically run between 1 and 3, are now 8. And stocks now sell at about 30 times earnings, compared to the historical norm of between 10 and 20. Arguments as to how the old standards don’t matter any more, and that we are in a “new era” attempt to rationalize current prices.
So, has the investment paradigm permanently changed? Are the old road markers now useless? Investment paradigms do sometimes shift: In 1958, for the first time in history, stock yields fell below bond yields, and disaster was predicted. None occurred (except for bonds!), and stock yields never again rose above bond yields.
And yet, it is difficult to argue against mathematics and the laws of gravity. In 1958 it could still be pointed out that stock dividends grew over time, whereas bond dividends, being fixed, did not. So it is not unreasonable that bond yields should be higher than stock yields.
But there is no getting around the fact that in the long run equity returns are closely approximated by the sum of the dividend rate, now 1.3%, and the earnings growth rate, historically about 5%. Add these together today and you get an expected stock return of 6.3%. So, in order to justify current valuations one has to postulate that earnings and dividends will begin to rise faster than they have in the past.
No such thing seems to be happening. Go back to Figure 2-11, which plots Dow earnings over the past 80 years. The top surface of the plot is the place to focus. From time to time, recessions and depressions produce sharp downward deviations in earnings, but the upper surface of the plot represents the “full capacity” of corporate earnings. Do you see an accelerating trend the past decade or two? If you do, Mulder and Scully are right outside, and they have some little green men they’d like you to meet.
One often hears the argument that with the accelerating pace of technological change, U.S. companies are on the verge of dramatically increased profitability. A bit of historical perspective is useful. The period from 1830 to 1860 saw the arrival of the two most dramatically transformative inventions in the history of mankind—the steam engine and the telegraph. Within a few short decades, the speed of cross-country transportation increased by almost an order of magnitude. Cheap and reliable power became available to manufacturers for the first time in history. Long-distance communication became almost instantaneous. Of course, the past 30 years have also seen wondrous technological innovation. However, consider that today really important news gets from New York to San Francisco only slightly faster than in Grover Cleveland’s time and, more likely than not, it takes you and me longer to travel cross town or cross country today than it did 30 years ago. Oh yes, the return of U.S. equity from 1830 to 1860 was 4.2%.
In fact, we’ve heard the new-era argument before—first in 1926–1929, then in the late 1960s. On both occasions, the conventional wisdom was that the old methods of stock valuation had become obsolete and that it was acceptable to pay 50 or 100 times earnings for companies poised on the cutting edge of technological progress. I cannot recommend highly enough Ben Graham’s description of the new-era stock market of the 1920s in the recently reprinted 1934 edition of Security Analysis. One does not have to change very many words to get a vivid description of today’s market frenzy surrounding technology and Internet-related earnings. Just change “100 times earnings” to “100 times sales” and you’re there.
Finally, it’s worth reflecting on the recent returns of some selected asset classes. For the 10-year period from 1989 to 1998, the return of the Barra Large Cap Growth Index was an astonishing 21.35% annualized; the large-cap value index 16.67%; for 9–10 decile small-cap stocks, 13.2%; and the EAFE index, of foreign stocks 5.54%. The experience of the past decade has convinced many that large-cap stocks have higher returns than small-cap stocks, that growth outperforms value, and that domestic outperforms foreign. As we’ve seen from more complete historical data, it is likely that none of these assumptions is true.
For those tempted to invest all their money in McDonald’s, Coke, Microsoft, and Intel, I’ve calculated the growth of $1 invested from July 1927 to March 1998 for the most extreme quintiles of small value, small growth, large value, and large growth in Figure 7-7. The annualized returns were 17.47% for small value, 2.18% for small growth, 13.99% for large value, and 10.04% for large growth. One always has to be cautious interpreting historical data. First, they do not include the trading expenses detailed earlier in Chapter 6. Second, the pre-1960s data is extremely sketchy in places.
Figure 7-7. Value of $1 invested July 1927. (Source: Kenneth French)
That said, the message is clear: Over the long term value beats growth, and small value may very well beat everything else. The miserable returns for small growth stocks will hopefully come as a wake-up call to those of you considering investing in small technology companies. Recent returns in this area have not been quite that bad, with the real damage being sustained in the pre-1960 era. But clearly, this is an area to be wary of.
In fact, the poor returns of small growth stocks are something of a mystery, as they are even lower than academic theory would predict. My own theory is that there is a “lottery ticket” premium being charged these investors. Just as people purchase lottery tickets, which have a return of about −50%, on the off chance that they may win the grand prize, so too do investors invest in small, rapidly growing companies on the slim chance that they are getting in on the ground floor of the next Microsoft. In other words, this asset class makes up in entertainment value what it lacks in return.
The new era has recently gotten a persuasive boost from the bestseller list. Writing in the op-ed section of The Wall Street Journal, the Atlantic Monthly, and more recently their book, Dow 36,000, journalist James Glassman and economist Kevin Hassett (hereafter referred to as GH) contend that the market, far from being historically overvalued, is actually ridiculously undervalued. Nervous at Dow 11,000? Get over it. This fearless duo sees fair value at about 36,000.
Their chosen vehicle is the venerable discounted dividend model (DDM), which we have already encountered in Chapter 2. Formulated in 1938 by John Burr Williams, it rests on a deceptively simple premise: Since all companies eventually go bankrupt, the value of a stock, a bond, or an entire market is simply the value of all its future dividends discounted to the present. (In GH-speak, this is referred to as the “perfectly reasonable price,” or PRP.) Since a dollar of future dividends is worth less than a dollar today, its value must be reduced, or discounted, to reflect the fact that you will not receive it immediately. This amount of reduction is called the discount rate (DR). And as we shall soon see, fiddling even a little bit with the DR opens the door to all kinds of mischief.
If this model looks complicated, it is. For each future year you take the present dividend, multiply it by (1 + g)n, where g is the rate of dividend increase and n is the number of years in the future, and then divide by (1 + DR)n. Plus, you have to compute this for an infinite number of years. It can get worse, with two- and three-stage models with varying growth rates over time. But don’t sweat the math, because with a constant growth rate the whole infinite sequence simplifies to:
PRP = (div)/(DR − g)
where
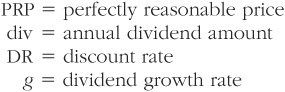
If the Dow throws off about $150 per year in dividends, and if you optimistically assume (as GH do) that dividends are growing at 6% per year, then the only other number left to toss into the above equation is that pesky DR. And amazingly, throughout much of the book GH maintain that the appropriate DR is the Treasury bond rate, which at the time was 5.5%. Because the growth rate is greater than the DR, an infinite value for the market results (because in this case the discounted dividend rises each and every year, ad infinitum), which even they find hard to swallow. (What the authors missed is that their 6% dividend growth rate covered a period when inflation was around 4%–5%, while the recent 5.5% rate for Treasury bonds presumably reflects a considerably lower future inflation rate.) So lower the dividend growth to 5.1%, keep the DR at 5.5%, and abracadabra, the above equation yields Dow 37,500:
PRP = 150/(.055 − .051) = 150/.004 = 37,500
Per finance convention, the numbers in the denominator are expressed as decimals, where .055 refers to the DR of 5.5%, and .051 to the dividend growth rate of 5.1%. Notice how tiny the denominator of .004 is relative to the input numbers. Move both of the numbers in the denominator the wrong way by just 1% (.01) and you have a Dow PRP of 6250. And if that displeases you, make your estimates just a hair more optimistic, and you get a Dow PRP of infinity. In other words, using the GH model, you can make the PRP of the Dow whatever you want it to be by moving the discount rate and growth rate a smidgen in either direction.
The Glassman-Hassett model is akin to balancing an elephant on a fence post: One small wobble in the post and several thousand pounds will lurch in an unexpected direction. This is evidenced by Figure 7-8, which shows the Dow’s value using the Glassman-Hassett growth assumptions over a range of discount rates.
Figure 7-8. 1999 dividends = $150, growth = 5.1%.
To reiterate, the value of the DR is critical. For example, if the actual DR is 8% instead of 5.5%, then fair value for the Dow falls to 5172. Oops. The same thing happens if the dividend growth estimate is off. As already mentioned, the 6% dividend growth of the past two decades included over 4% of inflation. In other words, real growth was less than 2%. So the dividend growth rate going forward may be quite a bit lower than it has been in the past. Decreasing dividend growth by 2.5% has the same effect as increasing the DR by the same amount—Dow 5172.
So what determines the appropriate DR? It is very simply two things: the cost of money (or the risk-free rate) plus an additional amount to compensate for risk.
Think of the DR as the interest rate a reasonable lender would charge a given loan applicant. The world’s safest borrower is the U.S. Treasury. If Uncle Sam comes my way and wants a long-term loan, I’ll charge him just 6%. At that DR the DDM predicts that a perpetual $1 annual loan repayment, or coupon, is worth a $16.67 loan.
Next through the door is General Motors. Still pretty safe, but not as riskless as Uncle Sam. I’ll charge them 7.5%. At that DR a perpetual $1 repayment/coupon is worth a $13.33 loan.
Finally, in struts Trump Casinos. Phew! For the risk of lending these clowns my money I’ll have to charge 12.5%, which means that The Donald’s perpetual $1 repayment/coupon is worth only an $8 loan.
So the DR we apply to the market’s dividend stream hinges on just how risky we think the market is. And here things get really sticky. Relying on long-term data, GH observe that the stock market is actually less risky than the long Treasury bond. For example, since 1926 the worst 30-year annualized return for common stocks was 8.47% versus only 1.53% for Treasuries.
Of course, a very different picture emerges when one looks at shorter periods. For example, the worst one-year returns are −43.35% for stocks and −7.78% for bonds. And at a gut level, no matter how much of a long-term investor you think you are, the market still probably got your attention on October 19, 1987.
So the GH-Dow controversy depends on whether you think that investors experience risk as a short-term or a long-term phenomenon. What the authors are saying is that U.S. investors have abruptly lengthened their risk time horizon:
Seventy years ago few investors understood that excessive trading undermines profits, that stock-price fluctuations tend to cancel themselves out over time, making stocks less risky than they might appear at first glance, and that it is extremely difficult to outperform the market averages. Americans have learned to buy and hold.
One wonders what planet GH inhabit. Are they unaware that trading volume has been steadily increasing for decades, not decreasing? That average domestic mutual fund turnover has increased from 30% to over 90% in the past 25 years? That a recent survey of over 66,000 accounts at a large West Coast discount brokerage showed an average annual portfolio turnover of 75%? That only 7% of mutual fund investments are indexed? That the historically modest market declines of 1987, 1990, and 1997, far from resulting in inflows from legions of long-termers buying cheap, produced dramatic mutual fund outflows? Most authoritatively of all, in an elegant study published in the Quarterly Journal of Economics in 1993 Shlomo Benzarti and Richard Thaler calculated that the risk horizon of the average investor was just one year.
The easiest way of thinking about the interplay of short- and long-term risk is to imagine a new kind of 30-year Treasury bond, similar to the conventional bond, except that the government stands ready at all times to redeem it at par (face value). Clearly, the redeemable bond would carry a considerably higher price and lower yield because it is immunized against the shock of a short-term increase in rates. And yet on the GH planet, where investors only care about long-term return, it would be priced identically to the conventional 30-year bond, since both have the same return to maturity.
Even conceding GH’s point that investors are increasingly focused on stocks for the long run and will manage to push the Dow up past 36,000, one has to ask just how free of risk stocks would be at that point. The authors ignore a rather inconvenient fact: that recent market history has dramatic effects on DR. In 1928, just as today, everybody was a “long-term investor,” and the DR for stocks was quite low (although probably not as low as it is today). Five years later, with the attrition rate of buy-and-holders approaching 100%, the DR was dramatically higher. And at Dow 36,000, it wouldn’t take much of a change in the DR in order for the risk-free world of stocks to come to an abrupt end. If investors decided that they demanded even a measly 1% risk premium, the Dow would decline by about two-thirds. The irony being that to the extent GH are right about a near-term “correction” of stock prices past 36,000, the risks of subsequent stock ownership increase dramatically.
Ignoring the crash scenario still does not make the GH planet look very appetizing. For the DR has another, even more profound significance. Namely, that the DR of an asset is the same as its expected return. If the true discount rate is 5.5% and the Dow is correctly priced at 36,000, then the future return of stocks is also 5.5%. Assuming inflation averages 2.5% over the next 30 years, that’s a real return of just 3%. Why would any rational investor invest in stocks priced to a 3% real return with Treasury Inflation Protected Securities (TIPS) priced to produce a guaranteed 4% real return?
There are other, more fundamental problems with Dow 36,000. For starters, consider the significance of a 5.5% long-term stock return. The “cost of capital” for corporations is necessarily the same as this long-term return. At a dirt-cheap capital cost of 5.5%, corporations are not going to be particularly careful about how they spend it. The free-spending behavior of the dot-coms, whose capital comes even cheaper, is not encouraging. (Or, on a grander scale, just how careful is Uncle Sam with his 5.5% capital?)
That said, on rare occasions investment paradigms do dramatically and permanently shift. We’ve already mentioned what happened in 1958, when for the first time stock yields fell below bond yields. At the time there was an almost universal outcry from financial pundits that this was an unnatural state of affairs and that stock prices were destined to fall, once again raising their yields, so as to restore the old order. And yet the stock market never looked back; prices continued to rise, and stock yields fell even farther below bond yields. (New paradigms can also be painful. The year 1958 also brought the start of a bear market in bonds much worse than anything seen since the time of Alexander Hamilton.) Today, stocks yield a full 4%–5% less than bonds. So I would not dismiss Dow 36,000 out of hand. But some skepticism is in order. (Even the authors themselves admit that they could be wrong, and thus hold about 20% of their assets in bonds.)
The holder of a foreign stock or bond is subject not only to the intrinsic risks of that security but also to the additional risk of currency fluctuation. For example, a bond denominated in U.K. pounds will rise or fall in value along with the value of that currency relative to the dollar. This currency risk can be eliminated (hedged) by selling forward a pound contract in the futures market at nominal cost. In the real world, you must first buy something before you sell it. But in finance, you can often sell something first before buying it back later; this is called selling forward (and is similar to “shorting” a stock). A currency contract that is sold forward increases in value as that currency falls, and vice versa. The resultant hedged bond generally has considerably lower risk than the unhedged bond, since the currency value change in the bond is exactly counterbalanced by the opposite change in value of the futures contract.
However, the situation with foreign stocks is much more complicated. Consider the 20 years ending October 1999. The annualized standard deviation for hedged European stocks (Morgan Stanley Capital Index-Europe) was 14.92% for the period. (The hedged index is the return that a European investor would see in the native currency. It is also called the local return.) The past decades have been an extremely turbulent time in the foreign exchange markets, with the monthly returns of the European currencies themselves experiencing an annualized SD of 10.44%. However, because this currency return is uncorrelated with the stock return, the SD of the dollar-denominated European market was just 16.25%—only slightly higher than that of the hedged (local currency) index. It is in fact not difficult to find short periods where hedging actually increased the risk of a European stock portfolio.
By now, of course, you are sophisticated enough to know that just because unhedged foreign stocks are slightly more risky than the hedged variety, this does not imply adverse portfolio behavior. In order to examine this problem, I looked at the behavior of three assets for the November 1979 to October 1999 period: the broad U.S. market (represented by the CRSP 1-10 Index) and the hedged and unhedged MSCI-Europe. One problem becomes immediately apparent—the returns for the three assets are somewhat different. The hedged European index yielded a 13.43% return, with the currency return boosting the unhedged portfolio’s return to 15.18%. And, as we saw in Chapter 4, during the 1980s and 1990s the domestic U.S. return was much higher—in this case 17.21%. During this period, then, hedging and foreign exposure were both highly detrimental, and the best portfolio was almost exclusively domestic.
To correct these biases I adjusted the unhedged European and domestic portfolio returns down to the 13.43% level of the hedged European portfolio, and looked at the return-versus-risk characteristics of the various U.S. and European mixes in Figure 7-9. As can be seen, the hedged portfolios (the loop on the left) have both lower return and lower risk than the unhedged portfolios (the loop on the right). In any case, note the very narrow vertical returns scale—we are talking about less than a dozen basis points difference. So all things being equal, hedging European stocks is a wash. But, of course, in the real world things are never equal. It is quite likely that currency exposure may turn out to be either highly beneficial or detrimental in the coming years. And we can’t predict which in advance.
Figure 7-9. Hedging effect, U.S. and Europe, November 1979 to October 1999.
Fortunately, the advantages of hedging (lower individual asset risk, positive hedging return) and disadvantages (higher correlation with the rest of the portfolio) largely offset each other; in the very long run there is not that much difference in risk and return characteristics of hedged-versus-unhedged portfolios. Over shorter periods, however, the differences can be considerable. For example, during the rapid depreciation of the dollar that occurred in 1984–1986 and 1994–1995, unhedged portfolios greatly outperformed hedged portfolios. The opposite occurred when the currency cycle unwound in 1998–1999.
For those few people who are planning to spend their retirement in Europe or Japan, their eventual risk may be lessened by not hedging. In other words, since their liabilities will be in foreign currency, the chance of having sufficient funds to meet their needs is increased by not hedging.
Math Details: The Hedging Hall of Mirrors
To complicate things even more, the cost of hedging needs to be considered as well. At the institutional level of mutual funds, the fees, commissions, and opportunity costs associated with hedging are minimal, perhaps no more than a few dozen basis points. The real cost of hedging has to do with the nature of forward currency contracts. As this is being written, the spot and six-month forward contracts for the pound, yen, and deutsche mark are as follows:
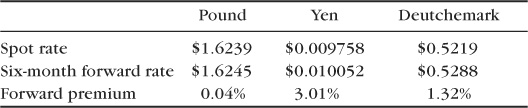
When you purchase a hedge, you “sell short” the forward rate and buy it back at a later date. If you sell short the six-month forward contract and wait until just before it expires six months later to buy it back, you will be buying the currency (or “covering the short position”) at the spot rate. If the spot and forward rates do not change in the interim, you will earn a profit equal to the forward premium, which is the difference between the spot and forward rates. This is negligible in the case of the pound, 3.01% for the yen, and 1.32% for the deutsche mark. In effect, you are being paid to hedge these currencies. (This is because at the present time interest rates are lower in each of these countries by an amount equal to the forward premium rate. If you wished to hedge an unstable currency with high interest rates, such as the ruble, the forward premium would be highly negative, with a very high hedging expense.)
And, if you own stocks or bonds exactly equal to your hedging amount, you will earn the forward premium no matter what happens to the exchange rate, as long as the forward premium stays intact.
You would think that the forward rate would be predictive of the future exchange rate. It isn’t. For example, the reason that the yen forward premium is so high (3% over six months, or 6% per year) is that Japanese interest rates are so low. What the forward premium seems to be saying to the U.S. holder of a Japanese five-year bond (currently yielding only 1%) is: “Don’t worry about the low yield, you’ll make up the difference with a 6% annual currency appreciation.” In fact, however, exchange rate history suggests that on average this doesn’t happen. Over the past several decades, global bond managers have made excess returns purchasing unhedged high-yielding bonds of developed nations with negative forward spreads, reaping advantage when the underlying currency fails to depreciate as much as forecast by the forward spread. This market inefficiency is probably the result of the fact that governments are major players in the currency game; governments are different from individual and institutional investors in that their primary goal is not profit, but rather currency defense.
Lastly, hedging cost needs to be considered when evaluating historical data. As pointed out by Jeremy Siegel in Stocks for the Long Run, in 1910 the pound was worth $4.80. It has since fallen to one-third that value. One might think that hedging the currency would have increased one’s return from British stocks. Wrong. Since for almost all of that period British interest rates were higher than those in the United States, the hedging costs were considerable; you’d have been much better off not hedging.
The question of how much currency hedging is best is one of the thorniest questions faced by investors; neither mean-variance analysis nor spreadsheet analysis provides any clear-cut answers. As a practical matter this decision has already been made for you. All of the foreign stock index funds recommended in Chapter 8 are unhedged, and the only low-cost foreign bond funds are hedged. And, as we’ve already seen, this is not a bad state of affairs.
More importantly, be aware that the degree of hedging strongly affects the short-term performance of foreign stock and bond mutual funds; do not be too upset if one or more of your funds has a bad year simply because they were completely hedged with a falling dollar, or vice versa. As long as your funds stick to their hedging policies, you will be rewarded when the currency pendulum swings the other way, which it almost always does.
Dynamic asset allocation refers to the possibility of varying your policy allocation because of changing market conditions. After spending much of this book convincing you of the virtue of fixed allocations, why am I relaxing this valuable discipline so late in the game? Isn’t changing the policy allocation tantamount to market timing, a demonstrably profitless activity?
Before proceeding further, let me be clear: Adherence to a fixed policy allocation with its required periodic rebalancing is hard enough. It takes years to become comfortable with this strategy; many lose their nerve and never see the thing through. You cannot pilot a modern jet fighter before mastering the trainer; likewise, you should not attempt dynamic asset allocation before mastering fixed asset allocation.
In the 1995 version of this book, I provided an example of how changing the stock and bond allocation in the opposite direction of P/B produced a slight improvement in risk-adjusted return. Alas, this is no longer true, as a P/B sensitive investor would have completely exited the stock market by last year. However, for what it’s worth, Figure 7-10 is a graph of P/B versus five-year forward average return. Although there is some scatter, there is obviously a strong tendency for returns to be high with low starting P/Bs, and low with high P/Bs. The most remarkable aspect of this plot is that the lower boundary of the data points forms quite a straight line; this represents the minimum return which can be expected for a given P/B. At a P/B of 1.5, an average five-year return of about 2% seems guaranteed; at a P/B of 1.25, 7.5%; and at 1.0, a return of 13% seems assured. Is this a useful relationship? That’s anybody’s guess. However, Figure 7-10 is a good reminder that when stocks get more expensive, their future returns are likely to decline, and that when stocks are very cheap, future returns are likely to be more generous.
Figure 7-10. Five-year forward stock returns versus P/B 1926–1993.
However, it is still not a bad idea to occasionally change your allocation slightly in the opposite direction from valuation. If two years ago you thought that a 6% exposure to emerging markets was appropriate, perhaps with the recent carnage in this area 7% or 8% might not be inappropriate. If three years ago you were holding 40% S&P 500, perhaps 35% might not be a bad idea in the current bubbly environment. Think of it this way—when you rebalance your portfolio in order to maintain your target allocation, you purchase more of an asset that has declined in price, and thus gotten cheaper. When you actually increase the target portfolio weighting of an asset when its price declines and it gets cheaper, you are simply rebalancing in a more vigorous form—you are “overbalancing.” A simpler way of overbalancing is to increase your target allocation ever so slightly—perhaps by 0.1% for every percent that the asset falls in value, and vice versa.
Dynamic asset allocation gets a bad rap because most investors change their allocations around in response to changes in economic or political conditions. As we have discussed, this is a poor approach. In the author’s opinion, changes in allocation that are purely market-valuation driven are quite likely to increase return. Rebalancing requires nerve and discipline; overbalancing requires even more of both of these scarce commodities. Very few investors, small or institutional, can carry it off.
The overarching premise of this book is that rational investors, faced with the facts of modern investing, will make certain logical decisions and choices. There’s only one problem. Human beings are not rational. The past few decades have seen an explosion in the field of behavioral finance—the study of the logical inconsistencies and foibles that plague investors. Three human behavioral phenomena are worth discussing: overconfidence, recency (which we have already mentioned), and risk aversion myopia.
For those of you with a congenital dislike of public radio, for nearly two decades show host, writer, and (dare I say it) singer Garrison Keillor has produced A Prairie Home Companion, set in the mythical town of Lake Wobegon, Minnesota. (A small confession: I listened to the show for over two years before nagging doubts sent me to my Rand McNally.) Mr. Keillor is heard to intone at the beginning and end of each show that in Lake Wobegon, “all the women are strong, all the men are good-looking, and all the children are above average.”
Well, on Wall Street everyone’s above average too. In a piece on investor preconceptions in the September 14, 1998, “Abreast of the Market” series in The Wall Street Journal, writer Greg Ip examined the revision in investor attitudes with the market decline in the summer of 1998. He tabulated the change in investors’ return expectations as follows:

The first thing that leaps out of this table is that the average investor thinks that he or she will best the market by about two percent. While it is possible that many investors may in fact beat the market by a few percent, it is of course mathematically impossible for the average investor to do so. In fact, as we’ve already discussed, the average investor must of necessity obtain the market return, minus expenses and transaction costs. Even the most casual observer of human nature should not be surprised by this paradox—folks tend to be overconfident
Overconfidence likely has some survival advantage in a state of nature, but not in the world of finance. Consider the following:
![]() In one study, 82% of U.S. drivers considered themselves in the top 30% of their group in terms of safety. (In Sweden, not unsurprisingly, the percentage is much lower.)
In one study, 82% of U.S. drivers considered themselves in the top 30% of their group in terms of safety. (In Sweden, not unsurprisingly, the percentage is much lower.)
![]() In another study 81% of new business owners thought they had a good chance of succeeding, but that only 39% of their peers did.
In another study 81% of new business owners thought they had a good chance of succeeding, but that only 39% of their peers did.
![]() Several housewives from Beardstown form an investment club, incorrectly calculate their portfolio returns, and then write a bestseller describing the reasons for their “success.”
Several housewives from Beardstown form an investment club, incorrectly calculate their portfolio returns, and then write a bestseller describing the reasons for their “success.”
The factors associated with overconfidence are intriguing. The more complex the task, the more inappropriately overconfident we are. Calibration (receipt of results) of one’s efforts is also a factor. The longer the feedback loop between our actions and their calibration, the greater our overconfidence. For example, meteorologists, bridge players, and emergency room physicians are generally quite well calibrated. Most investors are not.
The second surprising piece of data from the above table of return expectations was that in September 1998, after prices had fallen by a considerable amount, investors’ estimates of stock returns were lower than they were in June. This is highly irrational. Consider the following question: On January 1, you buy a gold coin for $300. In the ensuing month the price of gold falls, and your friend then buys an identical coin for $250. Ten years later, you both sell your coins at the same time. Who has earned the higher return?
Very few investors would not chose the correct answer—your friend, having bought his coin for $50 less, will make $50 more (or at worst, lose $50 less) than you. Viewed in this context, it is astonishing that any rational investor would impute lower expected returns from falling stock prices. The reason for this is what behavioral scientists call recency—we tend to overweight more recent data and underweight older data, even if it is more comprehensive. Had any conversations lately with someone with less than five years’ investing experience and tried to convince him that he cannot expect 20% equity returns over the long term? Blame recency. Make the recent data spectacular and/or unpleasant, and it will completely blot out the more important, if abstract, longer-term data.
All very interesting, you say, but of what use are such metaphysics? First and foremost, it explains why most investors are “convex” traders. This is a term coined by academicians William Sharpe and Andre Perold to describe “portfolio insurance” strategies in which equities are bought as prices rise and sold as they fall. A “concave” strategy represents the opposite—buying as prices fall and selling as they rise. Although some may find one or the other strategy more appealing, Sharpe and Perold make a more profound point: In a world populated by concave traders, it is advantageous to be a convex trader, and vice versa. Financial history in fact suggests that because of recency the overwhelming majority of equity investors are convex—when prices rise, investors’ estimates of returns irrationally rise, and they buy more. If indeed most investors exhibit such convex behavior, then the rational investor is concave. (Bond investors, on the other hand, appear to be less subject to recency, and thus a bit less convex, probably because falling bond prices make the most overt feature of a bond, its current yield, more immediately attractive to the investing public.)
Human beings experience risk in the short-term. This is as it should be, of course. In the state of nature, our ancestors’ ability to focus on the risks of the moment had much greater survival value than a long-term strategic analytic ability. Unfortunately, a visceral obsession with the here and now is of rather less value in modern society, particularly in the world of investing.
Overemphasis on the possibility of short-term loss is referred to as risk aversion myopia. In Chapter 2, after looking at the long-term superiority of stocks over bonds, you might have found yourself asking the question, “Why doesn’t everybody buy stocks?” Clearly, in the long term, bonds are actually more risky than stocks; there is no period of more than 30 years in which stocks did not outperform bonds. In fact, many academicians refer to this as “the equity risk-premium puzzle”—why stocks have been allowed to remain so cheap that their returns so greatly and consistently exceed that of other assets. The answer is that our primordial instincts, a useless relic of millions of years of evolutionary history, cause us to feel more pain when we suddenly lose 30% of our liquid net worth than the more damaging possibility of failing to meet our long-term financial goals. How bad is the problem? I’ve already mentioned the immensely clever article by Shlomo Benzarti and Richard Thaler (one of behavioral finance’s brightest stars) which examined the interaction of the risk premium and investor preference. They estimated that the risk horizon of the average investor, was about one year. Myopic indeed.
Socrates told us that the unexamined life is not worth living. For the modern investor, failure of self-examination can be as damaging to the pocketbook as to the soul.
1. Bad companies are usually good stocks, good companies are usually bad stocks. Value investing probably has the highest long-term returns.
2. Currency hedging has important effects on short-term portfolio behavior, but little in the way of long-term impact.
3. It is permissible to change your allocation slightly from time to time, as long as you do so in a direction opposite from valuation changes.