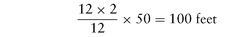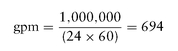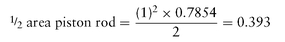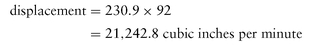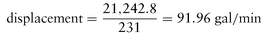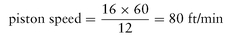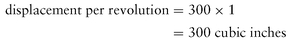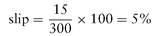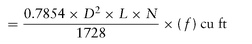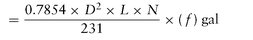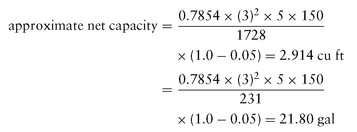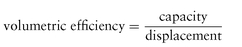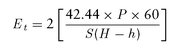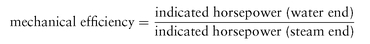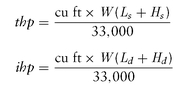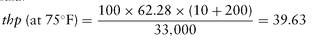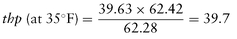Chapter 5
Reciprocating Pumps
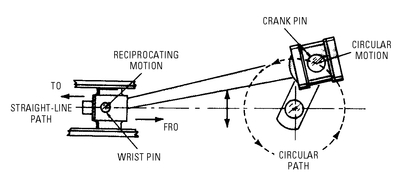
A reciprocating pump is described as a pump having a to-and-fro motion. Its motion is backward and forward or upward and downward—as distinguished from the circular motion of centrifugal and rotary pumps. A piston or plunger differentiates the reciprocating pump from a centrifugal or rotary pump. In a reciprocating pump, the reciprocating motion of the wrist pin is converted to a circular motion by means of a connecting link or connecting rod (see
Figure 5-1). Following are three moving elements necessary for operation of a reciprocating pump:
• Piston or plunger
• Inlet or admission valve
• Outlet or discharge valve
Figure 5-1 The basic difference between reciprocating motion (left) and circular motion (right).
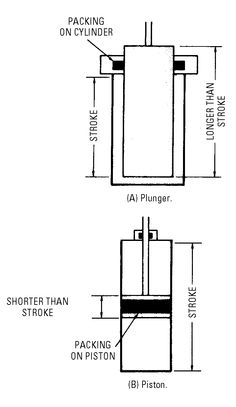
The piston or plunger works within a watertight cylinder. The basic difference between a piston and a plunger should be noted (see
Figure 5-2). A piston is shorter than the stroke of the cylinder; the plunger is longer than the stroke. Another distinguishing feature is that the packing is inlaid on the rim of the piston for a tight seal. When a plunger is used, the packing is moved in a stuffing box located at the end of the cylinder to provide a tight seal.
Principles of Operation
In general (and with respect to the way that the water is handled), reciprocating pumps may be classified as lift pumps or force pumps, which in turn, are either single-acting or double-acting pumps.
Figure 5-2 Basic differences between a piston and a plunger.
Lift Pumps
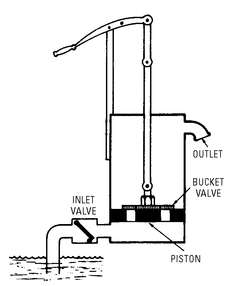
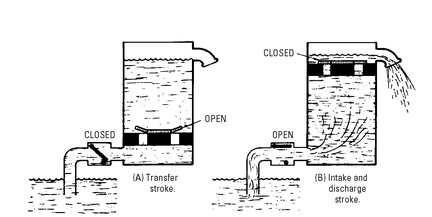
A lift pump is a single-acting pump; it consists of an open cylinder and a discharge or bucket-type valve (see
Figure 5-3). An open cylinder and a discharge or bucket-type valve in combination are the basic parts of the lift pump—it
lifts the water, rather than forces it. In the lift pump, the bucket valve is built into the piston and moves upward and downward with the piston.
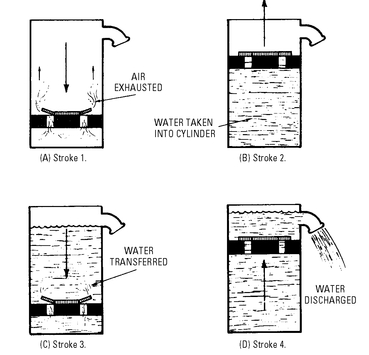
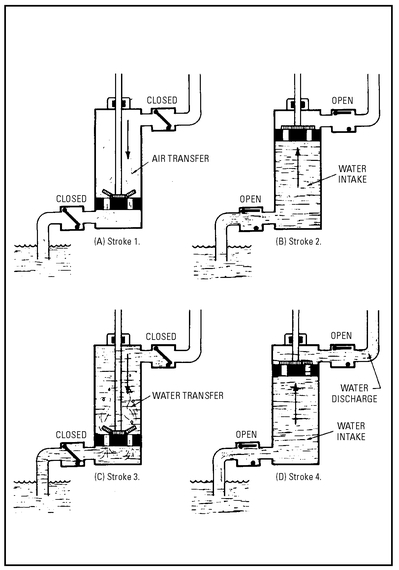
A four-stroke cycle is necessary to start the lift pump in operation (see
Figure 5-4). The strokes are as follows:
• Air exhaust—The piston descends to the bottom of the cylinder, forcing out the air.
•
Water inlet—On this upward stroke, a vacuum is created. Atmospheric pressure causes the water to flow into the cylinder.
Figure 5-3 Basic construction of a single-acting lift pump.
• Water transfer—During this downward stroke, the water flows through the bucket valve (that is, it is transferred to the upper side of the piston).
• Water discharge—As the piston rises, the water is discharged (that is, it runs from the pump).
After the pump has been primed and is in operation, the working cycle is completed in two strokes of the piston—a downward stroke and an upward stroke (see
Figure 5-5). The downward stroke of the piston is called the
transfer stroke, and the upward stroke is called the
intake and discharge stroke, because water enters the cylinder as the preceding charge of water is being discharged.
Force Pumps
The force pump is actually an extension of a lift pump, in that it both lifts and forces the water against an external pressure. The basic operating principle of the force pump is that it forces water above the atmospheric pressure range, as distinguished from the lift pump, which elevates the water to flow from a spout.
Single-Action
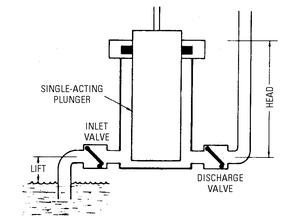
In a force pump, the water is forced out of the cylinder by means of a piston or plunger working against a pressure that corresponds to the head or elevation above the inlet valve to which the water is pumped. In its simplest form, the force pump consists of an inlet valve, a discharge valve, and a single-acting plunger (see
Figure 5-6).
Figure 5-4 Four-stroke starting cycle for a single-acting lift pump.
Figure 5-5 Two-stroke working cycle (after priming) for a single-acting lift pump.
Figure 5-6 Basic construction of a single-acting plunger-type force pump.
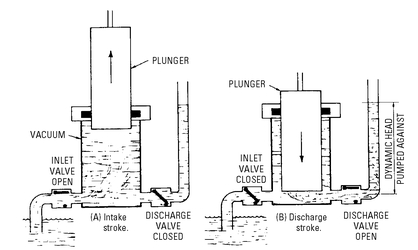
In a single-acting force pump, the working cycle is completed in two strokes—an upward (intake) stroke and a downward (discharge) stroke (see
Figure 5-7). During the upward stroke, the vacuum that is created enables atmospheric pressure to force the water into the cylinder. During this stroke the inlet valve is open and the discharge valve is closed. During the downward stroke, the plunger displaces (forces open) the discharge valve, and the water flows out of the cylinder against the pressure resulting from the dynamic head.
Figure 5-7 Two-stroke working cycle of a single-acting plunger-type force pump.
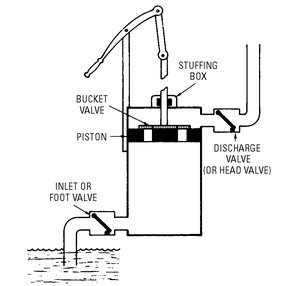
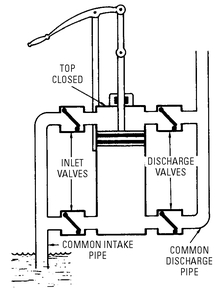
Another type of force pump uses inlet valves, bucket valves, and discharge valves (see
Figure 5-8). The piston works in a closed cylinder (note the stuffing box for the piston rod). The water flows progressively through the inlet or foot valve, the bucket valve, and the discharge valve.
Figure 5-8 Basic construction of a single-acting force pump with bucket-type valve in piston.
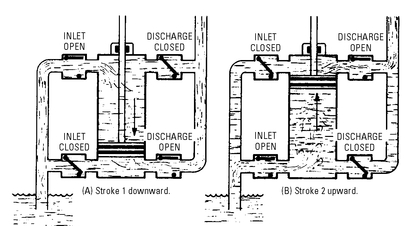
In starting the pump (see
Figure 5-9), the air in the cylinder (assuming the system to be full of air) is transferred from the lower side of the piston to the upper side on the downward (first) stroke. On the upward (second) stroke, the vacuum that is created enables the atmospheric pressure to force the water into the cylinder. On the next downward (third) stroke, the water is transferred to the upper side of the piston, and is discharged on the upward (fourth) stroke through the discharge valve.
When the system is cleared of air and in operation, the working cycle is completed in two strokes of the piston—a downward (transfer) stroke and an upward (discharge) stroke. On the downward stroke, the water is transferred through the bucket valve. On the upward stroke, the water above the piston is discharged, and the water is admitted to the lower side of the piston.
Table 5-1 shows the positions of the valves during the working cycle.
Figure 5-9 Four-stroke starting cycle of a single-acting force pump with a bucket-type valve in the piston.
Table 5-1 Valve Positions in a Single-Acting Force Pump
Double-Acting Force Pumps (Piston-Type)
In a double-acting piston-type force pump, the piston discharges water on one side of the piston while drawing water into the cylinder on the other side—without a transfer stroke. Thus, water is discharged on every stroke, rather than on every other stroke as in the single-acting pumps. Therefore, the capacity of a single-acting pump can be doubled in a double-acting pump having an identical cylinder displacement.
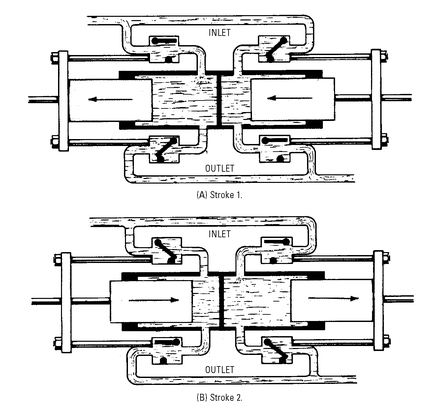
Figure 5-10 shows the basic construction of a double-acting piston-type force pump, and
Figure 5-11 shows the two-stroke working cycle. The valve positions for the two strokes in the working cycle should be noted. The diagonally-opposite inlet and discharge valves work in unison (that is, they are either open or closed at a given time).
Figure 5-10 Basic construction of a double-acting piston-type force pump with two sets of inlet and discharge valves.
Figure 5-11 Two-stroke working cycle of a double-acting piston-type force pump.
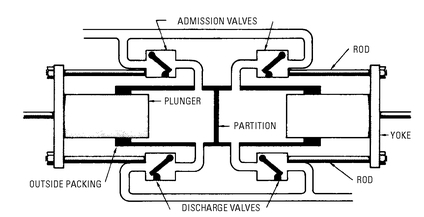
Double-Acting Force Pump (Plunger-Type)
The operation of this pump is identical to the operation of the piston-type double-acting force pump, except for the replacement of the piston with a plunger. These pumps are of two different types with respect to the location of the packing:
• Inside packed
• Outside packed
Figure 5-12 shows the basic construction of a pump with inside packing.
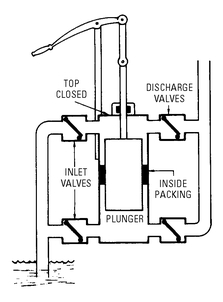
In the pump with inside packing (see
Figure 5-12), the long cylinder is virtually divided into two separate chambers by the packing.
Figure 5-13 shows the basic two-stroke working cycle of this pump. In its upward and downward movements, the plunger alternately displaces water in the two chambers. A disadvantage of this type of pump is that it is necessary to remove the cylinder head to adjust or to renew the packing. Leakage through the packing cannot be determined while the pump is in operation.
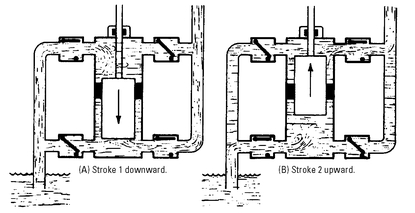
These disadvantages are overcome in the plunger-type pump with outside packing (see
Figure 5-14). This design requires two plungers that are connected rigidly by yokes and rods. The packing is on the outside. It is serviced easily and its condition can be checked easily.
Figure 5-12 Basic construction of a double-acting plunger-type force pump with inside packing.
Figure 5-13 The two-stroke working cycle of a double-acting plunger-type pump with inside packing.
Figure 5-14 Basic construction of double-acting plunger-type force pump with outside packing.
Figure 5-15 shows the two-stroke working cycle of the outside-packed plunger-type pump. Note that the plungers move in unison. Water is discharged at one end, while the opposite plunger is receding to fill the other end. A disadvantage of the outside-packed pump is that its construction is more complicated, and, therefore, more expensive than the inside-packed pump.
Self-Priming or Siphon Pumps
Since there is a considerable clearance or enclosed space between the inlet and discharge valves (which becomes filled with air), most pumps require priming. Priming is necessary because the piston or plunger attempts to remove the air, creating a vacuum. Then, atmospheric pressure can force the water into the pump chamber.
Priming is an operation in which the pump chamber is filled with water to increase the vacuum. Thus, water is drawn in from the source. Unless the pump is provided with a vent and inlet opening, it may be necessary to remove a pump part to get water into the cylinder.
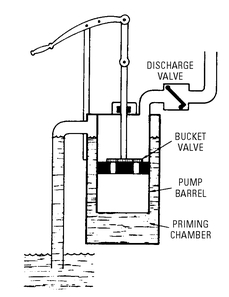
Figure 5-16 shows the basic construction of a self-priming or siphon pump. The pump casting consists of a pump barrel and a concentric outer chamber—the lower end of the barrel opening into the outer chamber. As shown in
Figure 5-16, the piston contains a bucket-type valve with a discharge valve at the top. The inlet is also at the top, so that the water is trapped in the outer chamber.
Figure 5-15 Two-stroke working cycle of a double-acting plunger-type pump with outside packing.
Figure 5-17 shows the two-stroke working cycle of the self-priming pump. Initially, the outer chamber is filled with water. On the downward stroke, water is transferred through the bucket-type valve in the piston. This does not change the water level in the outer barrel. On the upward or discharge stroke, water is drawn into the barrel, which causes the water level in the outer chamber to recede to a low point. This, in turn, creates a vacuum in the outer chamber, which causes the water to flow in from the source and fill the outer chamber.
Construction
In industrial hydraulic applications, the reciprocating piston pumps are usually of a large capacity. These pumps are often used to supply fluid to a central hydraulic system. Water, soluble oil in water, hydraulic oil, and fire-resistant hydraulic fluid are some of the fluids that are handled by this type of pump.
Figure 5-16 Basic construction of a siphon (self-priming) pump.
Figure 5-17 Two-stroke working cycle of a siphon (self-priming) pump.
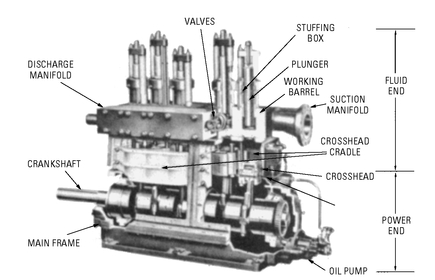
Reciprocating pumps are designed with three, five, seven, or nine plungers. In the pump shown in
Figure 5-18, the
fluid end of the pump is mounted at the top of the
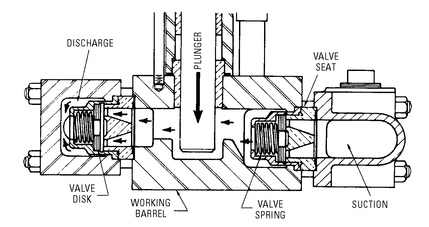
power end of the pump. This permits removal or replacement of valves without removing them from the pump entirely. In the direct-flow design (see
Figure 5-19), the liquid is passed from the suction end to the discharge end in a straight horizontal line through the valves and working barrel. The suction valve closes as the plunger moves downward, and the liquid is forced through the discharge valves, which open against light spring pressure. When the plunger moves upward, the discharge valves close and liquid is drawn inward through the suction valves, which open against similar spring pressure. Both valves are aided and sealed by the fluid pressure on closing.
Figure 5-18 The internal parts of a reciprocating piston pump.
The plunger-type pumps are widely used in industry to accomplish medium- to high-pressure chemical feeding. For example, a plunger-type pump can be used to meter chemicals and general industrial fluids, ranging from 0.2 to 1200 gallons per hour in pressures up to 1600 psi. This pump is available in either simplex or duplex design, with an optional stroke-adjustment-in-motion attachment. All the common water-treatment chemicals and liquids (such as acids, caustics, solvents, and many other industrial processing liquids) can be handled by this pump. The pump is readily adapted to applications requiring continuous, intermittent, or flow-responsive feeding.
Figure 5-19 Direct-flow principle in the reciprocating piston pump.
(Courtesy The Aldrich Pump Company, Standard Pump Div.)
Calculations
The numerous calculations, data, and tables relative to the various types of pumps can be useful to both operators and installation personnel. The calculations are diversified, and are intended to cover situations commonly encountered.
Lift
Theoretical lift and actual lift are quite different. A number of factors cause the actual lift of a pump to be considerably less than its theoretical lift. Numerous installation failures have resulted from calculating the actual lift incorrectly.
Theoretical Lift
Although Torricelli demonstrated by experiment that atmospheric pressure of 14.7 pounds per square foot will support a 33.83-foot column of water at its maximum density, a pump cannot perform this feat. A barometer reading of 30 inches of mercury corresponds to the atmospheric pressure reading of 14.74 psi. Since a column of water approximately 2.31 feet high exerts a pressure of 1 psi, the corresponding theoretical lift is:
theoretical lift = 2.31 × 14.74 = 34.049 feet
Actual Lift
In practice, the actual lift of a pump is limited by the following factors:
• Water temperature
• Air pressure decreasing at higher elevations
• Frictional resistance through pipes, fittings, and passages
• Leakage
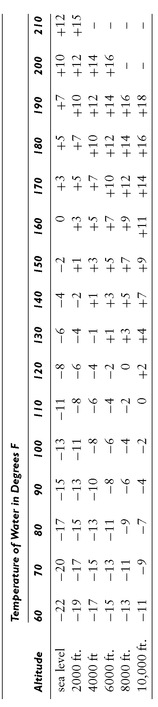
Table 5-2 shows the practical or permissible lifts for the various temperatures and elevations. Values that are preceded by a minus (−) sign indicate
lift, and values preceded by a plus (+) sign indicate
head. The table applies only for water, not for any other liquids that may be pumped. The actual lift depends on the specific gravity of the liquid being pumped. The thicker liquids (such as tar and molasses) should be moved toward the pump by means of gravity. Then, the inlet head is often called
negative lift.
The inlet pipe is often called the suction pipe. To minimize frictional resistance, avoid elbows, or a number of closely spaced elbows; the inlet pipe should be proportioned for a flow rate of 250 feet per minute, for example. The following examples may be used to determine the nominal pipe size.
Problem
Calculate the diameter of the inlet pipe (at 250 feet per minute) required for a double-acting duplex pump with 10-inch cylinders by 12-inch stroke, operating at 50 rpm.
Solution
Since each pump makes two discharge strokes per revolution, the piston in each pump travels:
At 100 feet per minute per pump, the total distance traveled by the two pistons, or total piston speed, is 200 feet per minute (2 × 100). The area of the two pistons is:
area = 2 × 102 × 0.7854 = 157.1 sq. in.
Table 5-2 Practical Lifts at Various Temperatures and Altitudes
Therefore, the area of the inlet pipe is as much smaller than the cylinder area, as 200 is to 250, that is:
Problem
What diameter is required for the inlet pipe for a 1,000,000-gallon (per 24 hours) capacity pump for a flow through the pipe of 250 feet per minute?
Solution
For 1,000,000 gallons per 24-hour period, the gallons per minute (gpm) rating is as follows:
Since 1 gallon of water has a volume of 231 cubic inches, the volume of flow per minute is 160,314 cubic inches (694 × 231). For a flow of 250 feet per minute, the area of the inlet pipe must be as follows:
Therefore, the next larger nominal pipe size (9 inches) is required. This is especially important for the inlet side, because increased flow with a smaller pipe adds to the frictional resistance of the pipe. Many pump manufacturers make the outlet opening one nominal pipe size smaller than the inlet opening. Nominal pipe size is smaller than the inlet opening.
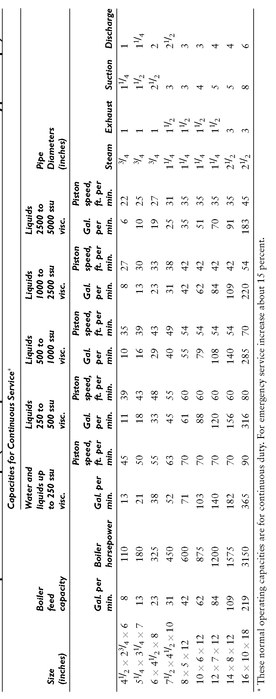
Table 5-3 shows nominal pipe sizes for the water end and the steam end.
Table 5-3 Pipe Sizes for Pumps (for Simplex Boiler Feed and General Service Piston-type Pumps)
Size of Discharge Pipe
The nominal size of the discharge pipe is usually smaller than the nominal size of the inlet pipe. The required size of the discharge line is dependent on its length, number of elbows in the line, and other conditions that tend to resist the flow of water. In most calculations, a flow of 400 feet per minute can be used for building installations or tank service.
Head
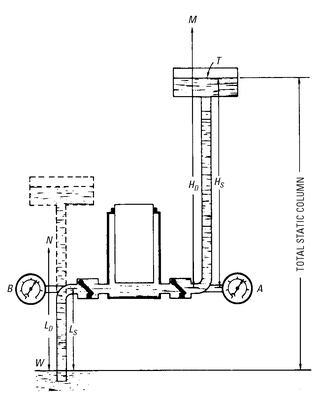
As shown in
Figure 5-20, the static head (
Hs) or dynamic head (
Hd) may be determined by means of a test gage
A placed on the discharge side of a pump. If the pump is at rest, the gage reading can be used to determine the static head
Hs. If the pump is in operation, the dynamic head
Hd can be determined.
Figure 5-20 Gage method of obtaining static and dynamic head, static and dynamic lift, and static and total dynamic column.
Problem
When the gage A indicates 35 pounds, what is the static head Hs with the pump at rest?
Solution
Since a column of water 2.31 feet in height exerts a pressure of 1 psi, the corresponding head
Hs for a gage reading of 35 pounds is as follows:
Hs = 2.31 × 35 = 80.9 feet
If the pump were in motion, the gage A would indicate a higher reading because of frictional resistance to flow in the pipe, thus indicating the dynamic head Hd.
As indicated in
Figure 5-20, the head is not the total load on the pump, because lift must also be considered. The pump must raise the water from the level
W in the well to the level
T in the tank; this is referred to as
total static column (
Cs) or:
Also, the total dynamic column (
Cd) is equal to:
The static lift (
Ls) and the dynamic lift (
Ld) can be determined by means of the vacuum gage
B (see
Figure 5-20); the gage reading can be converted to the elevation in feet as shown in the following problem.
Example
What is the dynamic lift Ld if the vacuum gage B reads 18 inches?
lift (in feet) = vacuum reading × 0.49116 × 2.31
In the equation, 0.49116 psi corresponds to 1 inch of mercury, and a 2.31-foot column of water exerts a pressure of 1 psi. Substituting the vacuum gage
B reading into the equation:
lift, in feet = 18 × 0.49116 × 2.31 = 20.4 feet (approximately)
To calculate the total column when the water flows toward the pump (from point
N in
Figure 5-20), the inlet head should be subtracted from the discharge head. Therefore, the total column is (
H −
Ln), in which the symbol
n represents the negative lift. In direct-acting pumps, the allowance for velocity head is negligible if the velocities are low.
Displacement
The volume of fluid that is displaced by the piston or plunger in a single stroke is called displacement in a reciprocating pump. Displacement is expressed as cubic inches per stroke, cubic inches per minute, and gallons per minute. Displacement is more commonly stated in terms of cubic inches per stroke. To determine piston displacement, in cubic inches per stroke, multiply the effective area of the piston or plunger by the length of the stroke.
Problem
Calculate the displacement, in cubic inches per stroke, in a double-acting simplex reciprocating pump with a water cylinder that is 5 inches by 12 inches, with a 1-inch piston rod.
Solution
The effective piston area is:
piston area = (5)2 × 0.7854 = 19.635 sq. in.
total effective area of piston = 19.242 sq. in.
(the rod reduces displacement on only one side of piston; therefore, one-half the rod area is an average)
To determine the displacement, in cubic inches per minute, multiply the cylinder displacement per stroke by the number of discharging strokes per minute. Thus, in the preceding problem, each stroke is a discharging stroke, because the pump is a double-acting pump. Therefore, if the pump is operating at 92 strokes per minute:
To determine the displacement, in gallons per minute, divide the displacement per minute by 231 (volume of 1 gallon of water). Therefore, displacement is:
Piston Speed
The total distance (in feet) traveled by a piston (or plunger) in 1 minute is referred to as the piston speed.
Example
If a piston having a 16-inch stroke operates at 60 strokes per minute, its piston speed is:
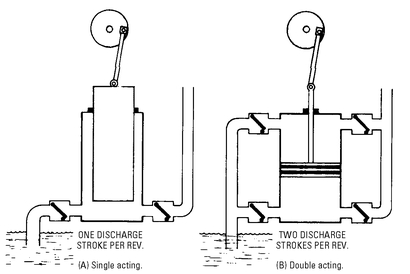
In calculating displacement, piston speed can be used as a factor. Depending on the type of pump, a coefficient stated in terms of the “number of discharging strokes per revolution” must be used. For example, in the simplex
single-acting pump (see
Figure 5-21), only
one discharging stroke per revolution occurs, and in the
double-acting pump,
two discharging strokes per revolution occur.
Figure 5-21 Discharge strokes per revolution as a factor in determining piston speed for calculating displacement in a simplex single-acting pump (left) and double-acting pump (right).
Since piston speed is based on both the upward (charging) stroke and the downward (discharging) stroke, and since only one discharging stroke occurs per two-stroke revolution in a single-acting pump, the coefficient is one-half (0.5). That is, the piston speed must be multiplied by ½, or 0.5, as in the following problem.
Problem
What is the displacement per revolution in a single-acting pump with a 300-cubic inch displacement, operating at 100 rpm?
Solution
Since, in a single-acting pump, only one discharging stroke per revolution occurs, the displacement per revolution is:
Since two discharging strokes per revolution occur in a double-acting pump, the coefficient is one-half (0.5)—that is, if the piston in the preceding problem were a
double-acting pump, the displacement per revolution would be:
Since the displacement per revolution is equal to the displacement times coefficient (displacement × coefficient), the various combinations can be tabulated as follows:
| Single-Acting | Double-Acting |
|---|
| Simplex | 0.5 | 1.0 |
| Duplex | 1.0 | 2.0 |
| Triplex | 1.5 | 3.0 |
Therefore, a triplex single-acting pump with a displacement of 300 cubic inches per cylinder has a displacement per revolution of 450 cubic inches (300 × 1.5), and a duplex double-acting pump with the displacement per cylinder has a displacement per revolution of 600 cubic inches (300 × 2.0).
Slip
In the foregoing problems, the displacements mentioned were theoretical displacements. In actual operating conditions, a pump cannot discharge a volume of water that is equal to its theoretical displacement because of slip through the valves and leakage. The slip is generally expressed as a percentage of the displacement. It is that amount by which the volume of water delivered per stroke falls short of the pump’s displacement.
Problem
What is the slip (in percentage of the displacement) in a pump with a displacement of 300 cubic inches per stroke, but which discharges only 285 cubic inches of water per stroke?
Solution
The slip is 15 cubic inches (300 − 285); Therefore:
That means the percentage is determined by:
• The percentage of slip. It varies from 2 to 10 percent.
• The type of pump. It is piston or plunger.
• The condition of the pump.
• The pressure that the pump is working against.
In actual practice, a slip of 2 percent is a common value for a plunger-type pump. For light-service piston pumps, the slip is approximately 5 percent. A slip of 10 percent is common for pressuretype piston pumps. Another factor that may reduce the output of a high-speed reciprocating pump occurs when the speed is too high for the water to flow through the inlet valves fast enough to completely fill the cylinder.
In pumps with bucket valves, operating on low lift where the column of water has sufficient dynamic inertia to continue in motion during a portion (or all) of the return stroke, the discharge volume may be greater than the displacement. This condition is referred to as negative slip.
Capacity
The capacity of a pump is the actual volume of water or fluid delivered. It is usually stated in terms of gallons per stroke or gallons per minute when discharging at a given speed.
Problem
A single-acting pump with a displacement of 300 cubic inches is operating at 100 strokes per minute. What is its capacity in gallons per minute with a 5 percent slip?
Solution
For a single-acting pump, there are 50 discharging strokes per minute (100 ÷ 2). Hence:
To calculate the capacity of a pump,
multiply the area of the piston (in square inches) by the length of the stroke (in inches) and by the number of delivery strokes per minute.
Divide the product by 1728 (to obtain theoretical capacity in cubic feet) or by 231 (to obtain theoretical capacity in gallons).
Multiply the result by the efficiency factor for the pump to obtain the approximate net capacity. Expressed as a formula:
or
in which the following is true
D is diameter of piston or plunger (in inches)
L is length of stroke (in inches)
N is number of delivery strokes per minute
f is slip, in percentage of displacement
1728 cubic inches in 1 cubic foot
231 cubic inches in 1 U.S. gallon
Problem
Calculate the approximate net capacity of a 3-inch diameter × 5-inch piston stroke double-acting pump, operating at 75 rpm, assuming a 5 percent slip.
Solution
Efficiency
In general, efficiency is the ratio of the useful work performed by a prime mover to the energy expended in producing it. In regard to pumps, there are several types of efficiency (such as hydraulic, volumetric, thermal, mechanical, and overall efficiency).
Hydraulic Efficiency
Hydraulic efficiency is the ratio of the total column (dynamic head + dynamic lift) pumped against, to the total column, plus hydraulic losses, including all losses (such as velocity head) from the source of supply through the water-end cylinders to the point of attachment of the discharge gage.
Volumetric Efficiency
The ratio of the capacity to the displacement, as:
Thermal Efficiency
The ratio of the heat utilized by the pump in doing useful work to the heat supplied. The formula is:
in which the following is true:
P is horsepower
S is steam consumed (in pounds per hour)
H is total heat in 1 pound of steam at initial pressure h is total heat in 1 pound of water supplied
42.44 is heat equivalent of 1 horsepower (in Btu per minute)
Mechanical Efficiency
The ratio of the indicated horsepower of the water end to the indicated horsepower of the steam end:
This factor can be determined only by actual testing. A manufacturer states that the mechanical efficiency of direct-acting pumps varies with the size and type of pump from 50 to 90 percent (see
Table 5-4).
| Stroke of Pump (Inches) | Piston-Type (percent) | Outside-Packed Plunger-Type (percent) |
|---|
| 3 | 55 | 50 |
| 5 | 60 | 56 |
| 6 | 65 | 61 |
| 7 | 68 | 64 |
| 8 | 72 | 68 |
| 10 | 76 | 72 |
| 12 | 78 | 75 |
| 16 | 80 | 77 |
| 20 | 83 | 80 |
| 24 | 85 | 82 |
Horsepower at Water End of Pump
The horsepower required for a given pump capacity can be calculated by the following formulas:
in which the following is true:
thp is theoretical horsepower
ihp is indicated horsepower
W is weight of one cubic foot of water (in pounds)
Ls is static lift (in feet)
Hs is static head (in feet)
Hd is dynamic head (in feet)
Problem
What theoretical horsepower (thp) is required to raise 100 cubic feet of water to 200 feet? The lift is 10 feet and the water temperature is 75°F.
Solution
At 75°F, 1 cubic foot of water weighs 62.28 pounds. Substituting in the formula:
At 35°F (cold weather), the weight of 1 cubic foot of water increases to 62.42. The horsepower increases in proportion to the ratio of the two weights, as follows:
In comparing the preceding equations, it may be noted that temperature causes only a slight difference in the results. Thus, the temperature factor can be disregarded for most calculations, and the common weight value of 62.4 pounds per cubic foot of water can be used.
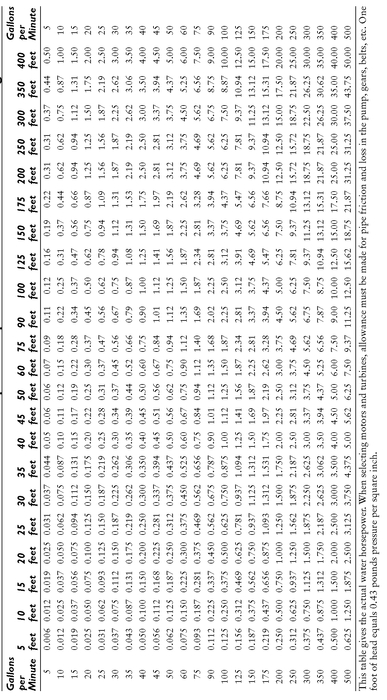
Table 5-5 shows the theoretical horsepower required to raise water to various heights.
Water Supply Pumps
Careful consideration must be given to the selection of pumps for water supply purposes, for each pump, application will differ, not only in capacity requirements, but also in the pressure against which the pump will have to operate. For example, a ½-inch hose with nozzle is to be used for sprinkling water, will be consumed at the rate of 200 gallons per hour. To permit use of water for other purposes at the same time, it is necessary to have a pump capacity in excess of 200 gallons per hour. Where ½-inch hose with nozzle is to be used, it is necessary to have a pump with a capacity of at least 220 gallons per hour. In determining the desired pump capacity, even for ordinary requirements, it is advisable to select a size large enough so that the pump will not run more than a few hours per day.
Typical Water-Supply Pumps
Automatic and semiautomatic pump installations for water supply purposes generally employ the following four types of pumps (all conforming to the same general principles):
• Reciprocating or plunger
• Rotary
• Centrifugal
• Jet or ejector
The ejector pump gets its name from the introduction of a jet stream attached to the centrifugal or reciprocating type of pump.
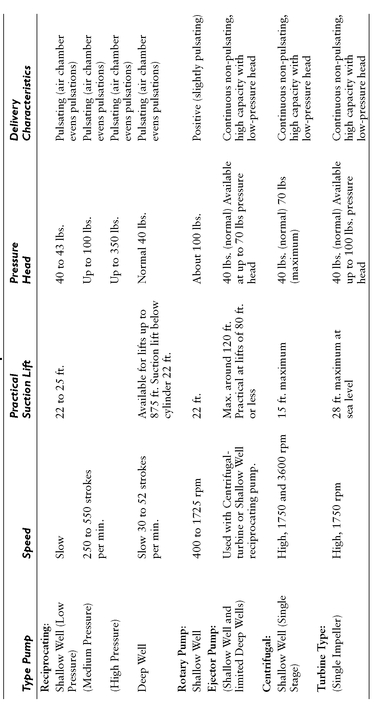
Table 5-6 provides a brief tabulation of the characteristics of the various types of pumps. For convenience, the pumps are classified according to speed, suction lift, and practical pressure head.
Reciprocating pumps will deliver water in quantities proportional to the number of strokes and the length and size of the cylinder. They are adapted to a wide range of speeds, and to practically any depth of well. Since reciprocating pumps are positive in operation, they should be fitted with automatic relief valves to prevent rupture of pipes or other damage should power be applied against abnormal pressure.
Table 5-5 Table of Theoretical Horsepower Required to Elevate Water to Various Helghts
Centrifugal pumps are somewhat critical as far as speed is concerned. They should be used only where power can be applied at a reasonably constant speed. The vertical type centrifugal pump is used in deep wells. They are usually driven through shafting by vertical motors mounted at the top of the well.
Turbine pumps (as used in domestic water systems) are self-priming. Their smooth operation makes them suitable for applications where noise and vibrations must be kept to a minimum.
Ejector pumps operate quietly, and neither the deep well nor the shallow well type need be mounted over the well.
Summary
A reciprocating pump has a to-and-fro motion. Its motion is backward and forward (or upward and downward) as distinguished from the circular motion of centrifugal and rotary pumps. A piston or plunger differentiates the reciprocating pump from a centrifugal or rotary pump. In the reciprocating pump, the reciprocating motion of the wrist pin is converted to circular motion by means of a connecting link or connecting rod.
A lift pump is a single-acting pump. It consists of an open cylinder and a discharge or bucket-type valve. It lifts the water, rather than forces it. A force pump is a single-acting or a double-acting pump.
After the lift pump has been primed, its working cycle is completed in two strokes of the piston: a downward or transfer stroke, and the upward stroke (which is an intake and discharge stroke, because water enters the cylinder as the preceding charge of water is being discharged).
The force pump is actually an extension of the lift pump. It lifts and forces the water against an external pressure. The basic operating principle of the force pump is that it forces water above the level attained by the atmospheric pressure range, as distinguished from the lift pump, which elevates the water to flow from a spout.
In a single-acting force pump, the water is forced from the cylinder by means of a piston or plunger working against a pressure that corresponds to the head or elevation above the inlet valve to which the water is pumped. The working cycle is completed in two strokes: an upward (intake) stroke and a downward (discharge) stroke. During the intake stroke, the vacuum that is created enables atmospheric pressure to force the water into the cylinder. During the discharge stroke, the plunger displaces (forces open) the discharge valve, and the water flows from the cylinder against the pressure resulting from the dynamic head.
In a double-acting force pump, the piston discharges water from one side of the piston while drawing water into the cylinder on the other side—without a transfer stroke. Thus, water is discharged on each stroke, rather than on alternate strokes, as in the single-acting pumps. Therefore, the capacity of a double-acting pump can be twice that of a single-acting pump having an identical cylinder displacement.
Reciprocating piston pumps having a large capacity are used in many industrial applications. They are designed with three, five, seven, or nine plungers. The plunger-type pumps are widely used in industry to accomplish medium- to high-pressure chemical feeding. These pumps are readily adapted to applications requiring continuous, intermittent, or flow-responsive feeding.
Theoretical lift and actual lift are quite different. Actual lift is a lesser value than theoretical lift; it is limited by factors, such as water temperature, decreased air pressure at higher elevations, frictional resistance (through pipes, fittings, and passages), and leakage.
The nominal size of the discharge pipe is usually smaller than that of the inlet pipe. The required size of the discharge line is dependent on its length, number of elbows in the line, and other conditions that tend to resist the flow of water.
The total load on a pump is not equal to the head alone. The lift must also be considered. The pump must raise the water from the surface level in the wall to the surface level in the tank. This is termed total static column. The formula for total static column is:
When all resistances to flow are considered, the total load becomes total dynamic column, and the formula is:
The volume of fluid that is displaced by a piston or plunger in a single stroke is called displacement. Displacement is expressed in cubic inches per stroke, cubic inches per minute, or gallons per minute. To determine piston displacement in cubic inches per stroke, multiply the effective area of the piston or plunger by the length of the stroke.
The total distance, in feet, traveled by a piston (or plunger) in 1 minute is referred to as the piston speed. This is a factor in calculating displacement. In a simplex single-acting pump, only one stroke per revolution occurs. In the double-acting pump, two discharging strokes per revolution occur.
In a pump, slip is generally expressed as a percentage of displacement. Pumps may fall short of the water previously designed to handle. The amount or the volume of water (delivered per stroke) that falls short of the pump’s displacement that is being used in the problem. The percentage of slip varies from 2 to 10 percent. It depends on the type of pump (piston or plunger). The condition of the pump also figures into the slip variation. So does the pressure against which the pump is working. When the discharge volume is greater than the displacement, the condition is called negative slip.
The capacity of a pump is the actual volume of water or fluid delivered. It is usually stated in terms of gallons per stroke or gallons per minute when discharging at a given speed. To calculate capacity, multiply the area of the piston (square inches) by the length of the stroke (inches) and by the number of delivery strokes per minute. Divide the product by 1728 (to obtain theoretical capacity, in cubic feet) or by 231 (to obtain theoretical capacity, in gallons).
Efficiency is the ratio of the useful work performed by a prime mover to the energy expended in producing it. There are several types of efficiency in regard to pumps (such as hydraulic, volumetric, thermal, mechanical, and overall efficiency).
Review Questions
1. How does a reciprocating pump differ from a centrifugal or rotary pump?
2. How does the basic operation of a lift pump differ from that of a force pump?
3. What is the chief difference in the working cycles of the single-acting force pump and the double-acting force pump?
4. Compare the capacities of single-acting and double-acting force pumps having identical cylinder displacements.
5. What are the disadvantages of the inside-packed double-acting plunger-type force pump?
6. Describe the working cycle of the self-priming reciprocating pump.
7. What types of industrial applications use reciprocating piston pumps?
8. Compare theoretical lift and actual lift.
9. Why is the nominal size of the discharge pipe usually smaller than the nominal size of the intake line?
10. Why is the total load on a pump not equal to just the head alone?
11. What is meant by displacement, and how is it expressed?
12. What is meant by slip, and how is it expressed?
13. How is capacity of a pump calculated?
14. What are three moving elements necessary for operation of a reciprocating pump?
15. What is the difference between a piston and a plunger?
16. List the four strokes of a single-acting lift pump.
17. List the four strokes of a single-acting force pump with a bucket-type valve in the piston.
18. How many plungers can reciprocating pumps have?
19. What is the lift at sea level of water at 120°F?
20. What is the term used to indicate the volume of fluid that is displaced by the piston or plunger in a single stroke in a reciprocating pump?
21. Define hydraulic efficiency.
22. Define volumetric efficiency.
23. Define thermal efficiency.
24. Define mechanical efficiency.
25. How much horsepower would it take to lift 40 gallons of water to a height of 10 feet?