Symmetric encryption is at the foundation of all modern secure communications. It is what we use to “scramble” messages so that people can only decrypt them if they have access to the same key used to encrypt them. That’s what “symmetric” means in this case: one key is used on both ends of the communication channel, to both encrypt and decrypt messages.
Let’s Scramble!
Unsurprisingly, the villains1 of East Antarctica are at it again, causing all kinds of trouble for their neighbors. This time, Alice and Bob are spying on the enemy troops to the west, doing reconnaissance on the size of their snowballs and the accuracy of their throws.
In earlier missions, Alice and Bob used the Caesar cipher from Chapter 1 to protect their messages. As you discovered, this cipher is easy to crack. As a result, the East Antarctica Truth-Spying Agency (EATSA) has equipped them with modern cryptography that uses a key to encode and decode secret messages. This new technology belongs to a class of encryption algorithms called symmetric ciphers , because both the encryption and decryption processes use the same shared key. The specific algorithm they are using in this post-et-tu-Brute world is the Advanced Encryption Standard (AES).2
Alice and Bob don’t have a lot of information about the proper care and handling of AES. They have just enough documentation to get encryption and decryption working.
“Wait... really?” Bob asks. “That’s it?”
Alice is right: that’s all it takes! An AES key is just random bits: 128 of them (16 bytes’ worth) in this example. This will allow us to use AES-128.
With the random key created, how do we then encrypt and decrypt messages? Earlier, we used the Python cryptography module to create hashes. It does many other things as well. Let’s see how Bob—encouraged by the ease of creating keys—uses it now to encrypt messages with AES.
Bob takes the documentation from Alice and looks at the next section, noting that there are many different modes of AES computation. Having to choose between them sounds a bit overwhelming, so Bob picks the one that looks easiest to use.
“Let’s use ECB mode, Alice,” he says, looking up from the docs.
“ECB mode? What is that?”
“I don’t really know, but this is the Advanced Encryption Standard. It should all work fine, right?”
Warning: ECB: Not for You
We’re going to find out later that ECB mode is terrible and should never be used. But we’ll just follow along for now.
AES ECB Code
“That’s not so bad,” Alice says. “What happens now?”
“Apparently, both the encryptor and decryptor have an update method. That’s pretty much it. The encryptor’s update returns the ciphertext.”
Exercise 3.1. A Secret Message
Without looking at additional documentation, try to figure out how the aesEncryptor.update() and aesDecryptor.update() methods work. Hint: You are going to get some unexpected behavior, so try lots of inputs. Consider starting with b"a secret message" and then decrypting the result.
Alice and Bob start trying to figure out the update method . Perhaps inspired by the previous chapter on hashing, where they hashed their names, they try encrypting their names in an interactive Python shell. Alice goes first.
“I didn’t get any ciphertext,” Alice grumbles. “What did I do wrong?”
“Wait!” Alice stops him. “You got something!”
“Weird!” Bob exclaims. “I didn’t do anything different. What happened?”
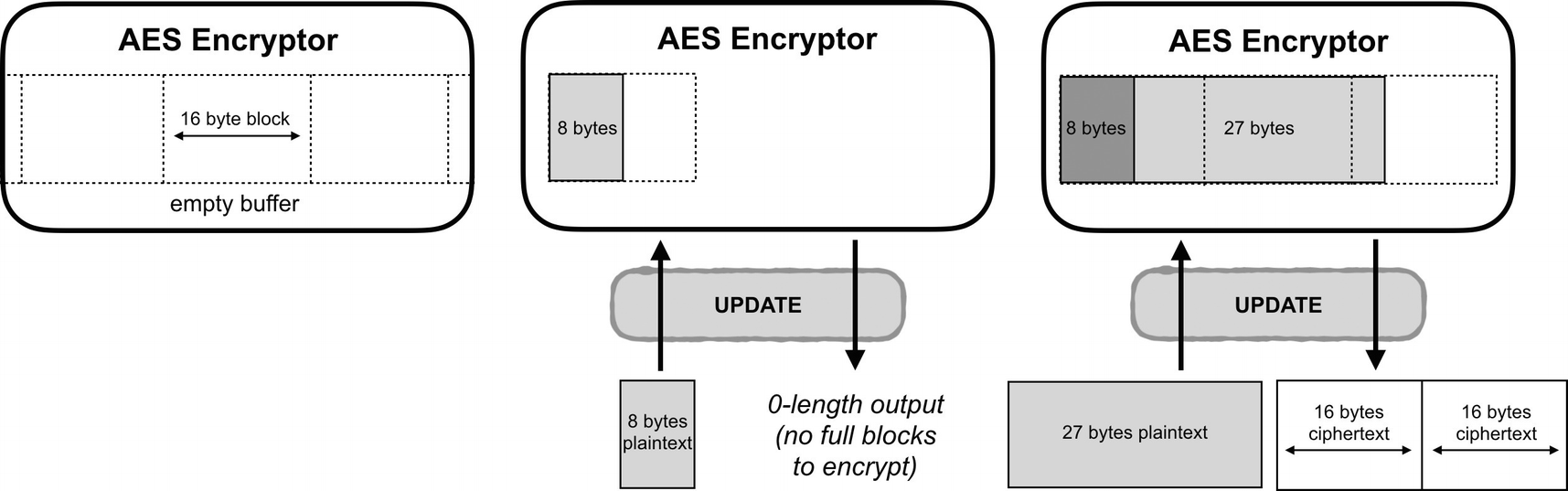
Two calls to the update method . The first 8 bytes return nothing because there isn’t a full block of data to encrypt yet.
Exercise 3.2. Updated Technology
Upgrade the Caesar cipher application from Chapter 1 to use AES. Instead of specifying a shift value, figure out how to get keys in and out of the program. You will also have to deal with the 16-byte message size issue. Good luck!
What Is Encryption, Really?
For those who have heard of cryptography, encryption is probably what they have heard about most. Web sites and online services will often mention encryption to reassure you that your information is “secure.” They will typically include phrases like “All data transmitted over the Internet is protected by 128-bit encryption, preventing theft.”
Don’t you feel better already?
- 1.
Confidentiality
- 2.
Integrity
- 3.
Authentication
The encryption we explore in this chapter is all about confidentiality. Confidentiality means that only folks with the right key are able to read the data. We use encryption to protect messages so that outsiders cannot read them.
Equally important is integrity. Integrity means that the data cannot be changed without you noticing. It is critical to understand that just because something cannot be read does not mean it cannot be usefully altered. To drive that point home, we are going to do exactly that sort of mischief in this chapter.
Finally, authentication relates to knowing the identity of the party with whom you are communicating. Authentication typically includes some mechanism to establish identity and presence,3 as well as the ability to tie communication to the established identity.
Hopefully it is obvious that all three of these properties are essential in many forms of communication. Confidentiality will do Alice and Bob little good if Eve can change what the messages actually say without them knowing: Eve doesn’t need to read the messages to cause real problems. Likewise, Alice and Bob will have little success in their covert communications if they aren’t sure they have the right person on the other end of the channel.
Keep these ideas in mind as you go through this chapter! Our focus on confidentiality is useful for presentation and it is indeed a critical component of security, but it is not enough. Spending some time with confidentiality by itself will help us to demonstrate how inadequate it is without its friends.
AES: A Symmetric Block Cipher
As mentioned before, the idea behind symmetric encryption is that the same key is used for both encryption and decryption. In the real world, almost all keys to physical locks can be thought of as “symmetric”: the same key that locks your door also unlocks it. There are other extremely important approaches to encryption that use distinct keys for each operation, but we’ll get to those in later chapters.
Symmetric key encryption algorithms are often divided into two subtypes: block ciphers and stream ciphers . A block cipher gets its name from the fact that it works on blocks of data: you have to give it a certain amount of data before it can do anything, and larger data must be broken down into block-sized chunks (also, every block must be full). Stream ciphers, on the other hand, can encrypt data one byte at a time.
AES is fundamentally a symmetric key, block cipher algorithm. It is not the only one by any stretch, but it is the only one that we will pay any attention to here. It is used in many common Internet protocols and operating system services, including TLS (used by HTTPS), IPSec, and file-level or full-disk encryption. Given its ubiquity, it is arguably the most important cipher to know how to use properly. More importantly, the principles of correct use of AES transfer easily to correct use of other ciphers.
Finally, even though AES is essentially a block cipher, it (like many other block ciphers) can be used in a way that makes it behave like a stream cipher, so we don’t lose any teaching opportunities by excluding native stream ciphers from the discussion. In the past, RC4 was a commonly used stream cipher, but it has been found vulnerable to various attacks and is being replaced by stream modes of AES.
Also, as Bob says, “It’s advanced!” That ought to be enough for anyone, right?
Exercise 3.3. History Lesson
Do some research online about DES and 3DES. What is the block size for DES? What is its key size? How does 3DES strengthen DES?
Exercise 3.4. Other Ciphers
Do a little research about RC4 and Twofish. Where are they used? What kinds of problems does RC4 have? What are some of Twofish’s advantages over AES?
Since AES is a pretty good place to start, let’s dig in with a little bit of background. We know it’s a symmetric key block cipher. Given what we saw of Alice’s and Bob’s attempts to use it, can you guess the block size?
If you were thinking “16 bytes!” (128 bits), you get a gold star. Tell all your friends!4
- 1.
Electronic code book (ECB) (WARNING! DANGEROUS!)
- 2.
Cipher block chaining (CBC)
- 3.
Counter mode (CTR)
These are not the only modes of operation for AES [11, Chap. 7]. In fact, while CBC and CTR are still used, a newer mode called GCM is now recommended to replace them in many circumstances, and we will examine GCM in detail later in this book. These three modes are, however, very instructive, and together they cover the most important concepts. They will provide a solid foundation on which to build greater understanding of block ciphers in general and AES in particular.
ECB Is Not for Me
Be warned, relying on ECB mode for security is irresponsibly dangerous and it should never be used. Think of it as being good for testing and educational purposes only. Please, don’t ever use it in your applications or projects! Seriously. You have been warned. Don’t make us come over there.
By the way, do you see a pattern developing here? Sometimes the best approaches for explaining a thing are not at all suitable for using it in practice. This seems to apply particularly well to cryptography, which is one reason that we urge people to always use a well established library instead of building their own. The basic principles are simple, but without all of the complex trappings that come with mature libraries and a solid understanding of how to use them, those principles alone will give you very poor security, not just “slightly imperfect” security. There is rarely much in the way of middle ground; once the safe is cracked, it doesn’t matter how thick its walls are. Cryptographic concepts are often simple, but safe and correct implementation is usually complex.
With all of those warnings out of the way (not really, there will be more), what is ECB? In a way, ECB is “raw” AES: it treats every 16-byte block of data independently, encrypting each one in exactly the same way using the provided key. As we will see with counter mode and cipher block chaining mode, there are a lot of interesting ways to use that approach as a building block for a more advanced (and secure) cipher, but it’s really not a good way to go about encryption by itself.
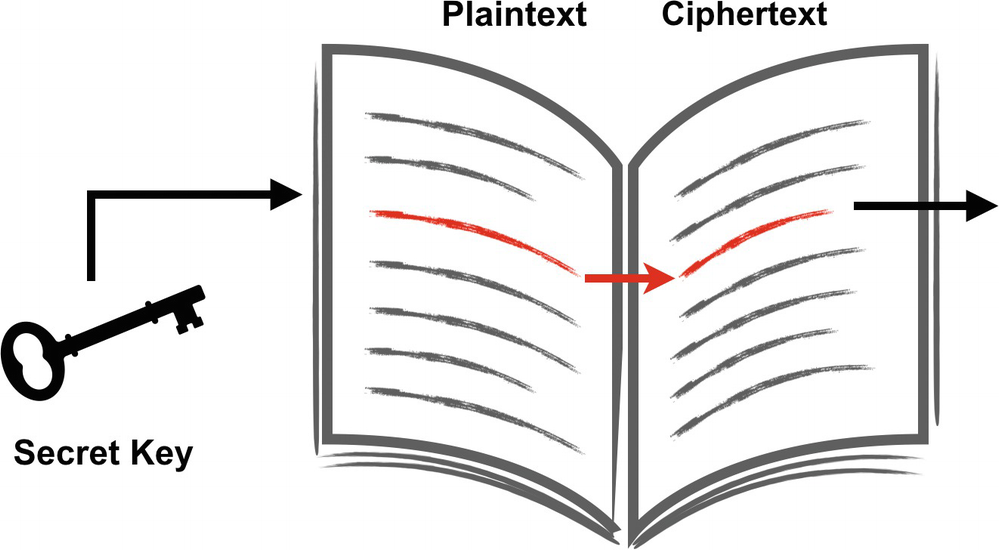
ECB mode is analogous to having a big dictionary of plaintext to ciphertext. Every 16 bytes of plaintext has a corresponding 16-byte output.
As we will see, the properties of determinism and independence are useful but not sufficient properties for message security. ECB mode is useful because it can be used for testing, for example, to make sure that the AES algorithm is behaving as expected. Some systems will pick a special key, say, all zeros, as a “test key.” As part of a self-test, the system will run AES in ECB mode with the test key to see if it encrypts as expected. You will sometimes see tests of this kind called “KATs” (known answer tests) .
AES ECB KATs
Assuming that your processor is working correctly, you should see a 4/4 passing score.
Exercise 3.5. All NIST KATs
Write a program that will read one of these NIST KAT “rsp” files, and parse out the encryption and decryption KATs. Test and validate your AES library on all vectors on a couple of ECB test files.
This all seems very reasonable. So, what’s wrong with ECB? Unless you’ve been completely asleep, you’ve noticed our dire warnings about it. Why? In a nutshell, because of its independence properties.
Let’s return to Alice, Bob, and their nemesis Eve down in Antarctica. Alice and Bob are on a covert mission within the West Antarctica borders. They will send secret messages to each other over radio channels that Eve can monitor. Before they leave, they generate a shared key for encrypting and decrypting their messages, and they keep that key safe during their travels.
AES ECB Padding
Listing 3-3 shows a straightforward but perhaps not optimal padding. We’ll use more standard approaches in the next section. It is, however, good enough for now. When Bob decodes his message, it will simply have a few extra “E” characters at the end.
Exercise 3.6. Sending Bob a Message
Using either a modification of the preceding program or your AES encryptor from the beginning of the chapter, create a couple of meetup messages from Alice to Bob. Also create a few from Bob to Alice. Make sure that you can correctly encrypt and decrypt the messages.
With their new cryptographic technology at the ready, Alice and Bob begin surveillance in West Antarctica. They meet occasionally to share information and coordinate their activities.
Meanwhile, Eve and her counter-intelligence colleagues learn of the infiltration and soon begin to identify the coded messages. Take a look at several messages from Alice to Bob from Eve’s perspective, where all she can see is the ciphertext. Do you notice anything?
Message 1, Block 1 | a3a2390c0f2afb700959b3221a95319a |
Message 2, Block 1 | a3a2390c0f2afb700959b3221a95319a |
Message 1, Block 2 | 0fd11a5dcfa115ba89630f93e09312b0 |
Message 2, Block 2 | 0fd11a5dcfa115ba89630f93e09312b0 |
Message 1, Block 3 | 87597bf7f98759410ae3e9a285912ee6 |
Message 2, Block 3 | 87597bf7f98759410ae3e9a285912ee6 |
Message 1, Block 4 | 8430e159229e4bf5c7b39fe1fb72cfab |
Message 2, Block 4 | 8430e159229e4bf5c7b39fe1fb72cfab |
Message 1, Block 5 | a5c7412fda6ac67fe63093168f474913 |
Message 2, Block 5 | c9b3ccefda71f286895b309d85245421 |
Message 1, Block 6 | dbd386db053613be242c6059539f93da |
Message 2, Block 6 | 699f1cd5adbeb94b80980a0860ead320 |
Message 1, Block 7 | 800d3ece3b12931be974f36ef5da4342 |
Message 2, Block 7 | a8ff0ed2ca9b80908757f8c3ecbc9b0d |
How many of the 16-byte blocks are identical? Why?
Remember that AES in its raw mode is like a code book. For every input and key, there is exactly one output, independent of any other inputs. Thus, because much of the message header is shared between messages, much of the output is also the same.
Eve and her colleagues notice the repeating elements of the messages they see day after day and soon start to figure out what they mean. How do they do this? They might make a good start by guessing. If you saw the same message being sent repeatedly, you could start to guess at some of its contents.
Another way to make progress might be to utilize a deserter or mole within the enemy organization. They could conceivably get Eve a copy of the form or a discarded decoded message. All told, there are many ways for an adversary to learn about the structure and organization of an encrypted message, and you should never assume otherwise. A common error made by those trying to protect information is to assume that the enemy cannot know some detail about how the system works.
Instead, always live by Kerckhoff’s principle. This nineteenth-century (long before modern computers) cryptographer taught that a cryptographic system must be secure even if everything is known about it, except the key. That means we should find a way for our messages to be secure if the enemy knows just about everything about our system and merely lacks access to the key.
We made this silly example with an overly bureaucratic form, but even in real messages, there is often a significant amount of predictable structure. Consider HTML, XML, or email messages. Those often have huge amounts of predictably positioned, identical data. It would be a terrible thing for an eavesdropper to start learning what’s in a message just because it shares protocol headers with every other message.
Even worse, imagine if Eve’s team can figure out a way to do what is called a “chosen plaintext” attack. In this attack, they figure out a way to get Alice or Bob to encrypt something on their behalf. Imagine, for example, that they figure out that Alice always calls a meeting with Bob after the Prime Minister of Western Antarctica gives a public speech. Once they know this, they can use political speeches to trigger a message where much of the content is known. Or maybe they manage to slip Bob some false information to send to Alice, encrypted. Once they can control some or all of the plaintext, they can look at the encryption and begin to create their own code book.
Eve can also easily create new messages by putting together bits and pieces of old messages. If Eve knows that the first blocks of a ciphertext are the header with a current date, she can take an old message body that directs Bob to an old meeting site and attach it to the new header. Then Bob ends up in the wrong place at the wrong time.
Exercise 3.7. Sending Bob a Fake Message
Take two different ciphertexts from Alice to Bob with different meeting instructions on different dates. Splice the ciphertext from the body of the first message into the body of the second message. That is, start by replacing the last block of the newer message with the last block (or blocks if it was longer) of the previous message. Does the message decrypt? Did you change where Bob goes to meet Alice?
All of this may still seem just a bit hypothetical. Perhaps ECB mode isn’t really all that bad. Perhaps it is only bad in extreme situations or something like that. Just in case there is a shadow of a doubt remaining, let’s do one more test (a pretty fun one) to convince ourselves that ECB mode should never, ever be used for real message confidentiality.
AES Exercise Example

An image with the text “TOP SECRET.” Encrypting it should make it unreadable, right?
Take your newly created file and run it through your encryption program, saving the output to something like encrypted_image.bmp. When finished, open the encrypted file in an image viewer. What do you see?

This image was encrypted using ECB mode. This message is not very confidential.
What happened here? Why is the text of the image still so readable?
AES is a block cipher that operates on 16 bytes at a time. In this image, many 16-byte chunks are the same. A chunk of black pixels is encoded with the same bits everywhere. Every time there’s a 16-byte block of all black or all white, they encode to the same encrypted output. The structure of the image is thus still visible even once the individual 16-byte chunks are encrypted.
Really. Never use ECB. Leave that kind of thing to the “professionals” of the East Antarctica Truth-Spying Agency.
Wanted: Spontaneous Independence
Encrypt the same message differently each time.
Eliminate predictable patterns between blocks.
To solve the first problem, we use a simple but effective trick to ensure that we never send the same plaintext twice, which means that we also never send the same ciphertext twice! We do this with an “initialization vector,” or IV.
An IV is typically a random string that is used as a third input—in addition to the key and plaintext—into the encryption algorithm. Exactly how it is used depends on the mode, but the idea is to prevent a given plaintext from encrypting to a repeatable ciphertext. Unlike the key, the IV is public. That is, one assumes that an attacker knows, or can obtain, the value of the IV. The presence of an IV doesn’t help to keep things secret so much as it helps to keep them from being repeated, avoiding exposure of common patterns.
As for the second problem, that of being able to eliminate patterns between blocks, we will solve it by introducing new ways to encrypt the message as a whole, rather than treating each block as an individual, independent mini-message like ECB mode does.
The details of each solution are specific to the mode being used, but the principles generalize well.
Not That Blockchain
Recall from Chapter 2 that good hash algorithms are expected to have the avalanche property. That is, a single change in one input bit will cause approximately half of the output bits to change. Block ciphers should have a similar property, and thankfully, AES does. In ECB mode, however, the avalanche’s impact is limited to the block size: if the plaintext is ten blocks long, a change in the very first bit will only change the output bits of the very first block. The remaining nine blocks will remain unchanged.
What if a change in the ciphertext of one block could affect all subsequent blocks? Well, it can, and it is quite easy to accomplish. When encrypting, for example, one can XOR the encrypted output of a block with the unencrypted input of the next block. To reverse this while decrypting, the ciphertext is decrypted and then the XOR operation is again applied to the previous ciphertext block to obtain the plaintext. This is called cipher block chaining (CBC) mode .
Input 1 | Input 2 | Output |
|---|---|---|
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Truth tables are useful, showing precisely how functions like XOR behave for all combinations of inputs, but you actually don’t need to think about XOR at this level. What is important is that XOR has an amazing inversion property: the XOR operation is its own inverse! That is, if you start with some binary number A and XOR it with B, you can recover A by XORing the output with B again. Mathematically, it looks like this: (A ⊕ B) ⊕ B = A.
Why does this work? If you look at “Input 1” as a control bit, when it is 0, what comes out is simply “Input 2.” When “Input 1” is 1, on the other hand, what comes out is the inverse of “Input 2.” If you take the outputs and apply XOR with “Input 1” again, it leaves the previously unchanged things unchanged (XOR with 0 again) while flipping the inverted things back to the way they were (XOR with 1 again).

You can see here how applying ⊕10110001 twice to 11011011 causes it to reappear.
Exercise 3.8. XOR Exercise
Because we will use XOR so much, it’s a good idea to get comfortable with XOR operations. In a Python interpreter, XOR a few numbers together. Python supports XOR directly using ^ as the operator. So, for example, 5^9 results in 12. What do you get when you try 12^9? What do you get when you try 12^5? Try this out with several different numbers.
Exercise 3.9. The Mask of XOR-O?
Although this exercise will be even more important in counter mode, it’s useful to understand how XOR can be used to mask data. Create 16 bytes of plaintext (a 16-character message) and 16 bytes of random data (e.g., using os.urandom(16)). XOR these two messages together. There’s no built-in operation for XORing a series of bytes, so you’ll have to XOR each byte individually using, for example, a loop. When you are done, take a look at the output. How “readable” is it? Now, XOR this output with the same random bytes again. What does the output look like now?
![$$ {P}^{\prime}\left[n\right]=P\left[n\right]\oplus C\left[n-1\right], $$](../images/472260_1_En_3_Chapter/472260_1_En_3_Chapter_TeX_Equb.png)
From there we can apply AES encryption to P′[n], which is the length of an AES block, to get C[n]. When decrypting, then, we don’t get the plaintext, we get the “munged, pre-encryption plaintext” P′[n]. To get the actual plaintext, we need to reverse the preceding process, which we can do by running it through XOR with the previous encrypted block (recalling that XOR is its own inverse). You can see why this works by performing some basic algebraic manipulations:
![$$ {\displaystyle \begin{array}{l}\kern7.75em {P}^{\prime}\left[n\right]=P\left[n\right]\oplus C\left[n-1\right]\\ {}\kern3.875em {P}^{\prime}\left[n\right]\oplus P\left[n\right]=P\left[n\right]\oplus P\left[n\right]\oplus C\left[n-1\right]\\ {}\kern3.875em {P}^{\prime}\left[n\right]\oplus P\left[n\right]=C\left[n-1\right]\\ {}{P}^{\prime}\left[n\right]\oplus {P}^{\prime}\left[n\right]\oplus P\left[n\right]={P}^{\prime}\left[n\right]\oplus C\left[n-1\right]\\ {}\kern7.875em P\left[n\right]={P}^{\prime}\left[n\right]\oplus C\left[n-1\right].\end{array}} $$](../images/472260_1_En_3_Chapter/472260_1_En_3_Chapter_TeX_IEq1.png)
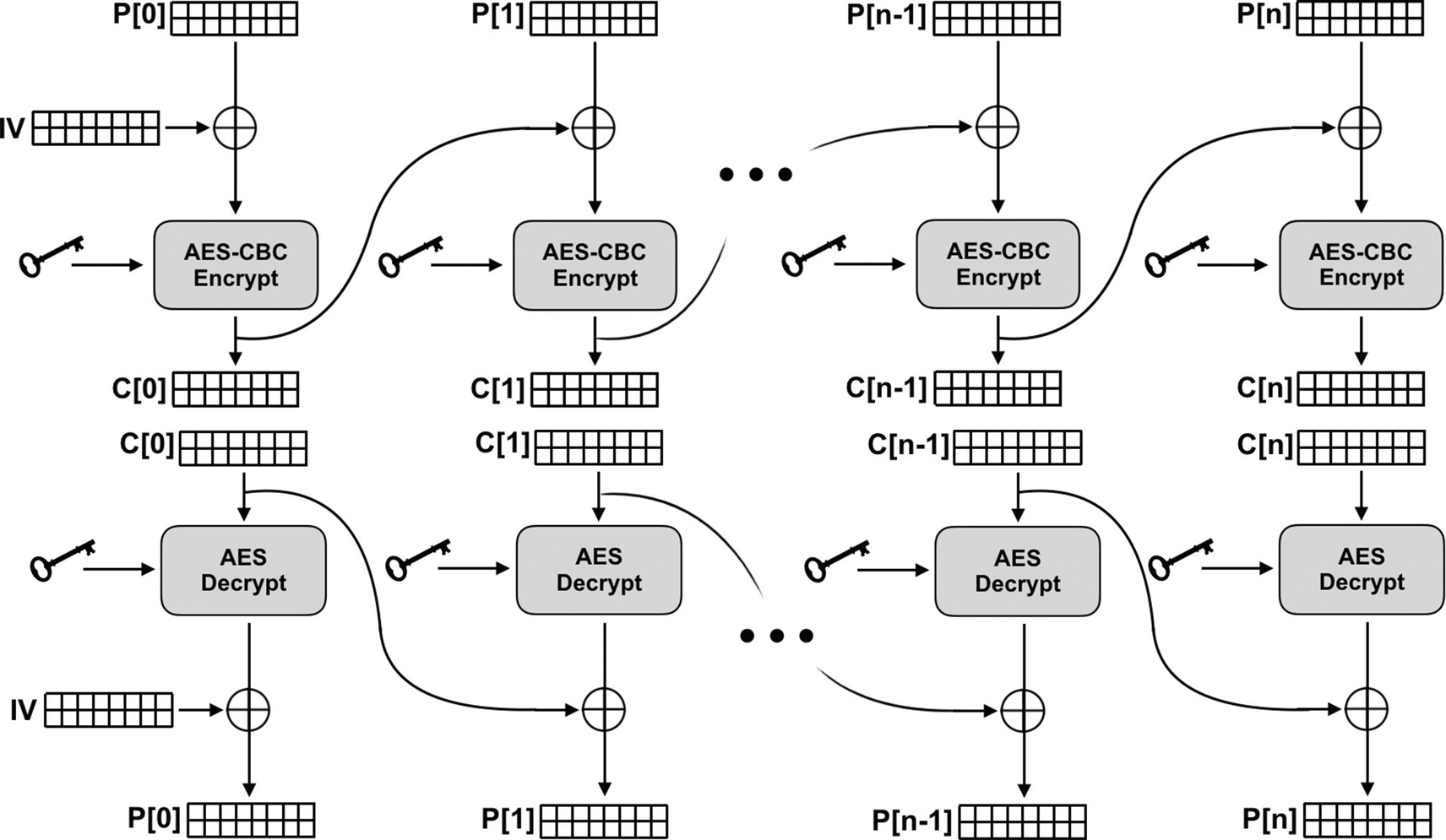
Visual depictions of CBC encryption and decryption. Note that in encryption, the first block of plaintext is XORed with the IV before AES, while in decryption, the ciphertext goes through AES first and is then XORed with the IV to correctly reverse the encryption process.
In CBC mode, changes to any input block thus affect the output block for all subsequent blocks. This doesn’t produce a complete or perfect avalanche property because it does not affect any preceding blocks, but even having the avalanche effect moving forward prevents exposing the kinds of patterns that we observe in ECB mode.
Configuration of CBC mode is mostly familiar: we generate a key and then take the extra step of generating an initialization vector (IV) . Because the IV is XORed with the first block, AES-CBC IVs8 are always 128 bits long (16 bytes), even if the key size is larger (typically 196 or 256 bits). In the following example, the key is 256 bits and the IV is 128 bits, as it must be (Listing 3-5).
AES-CBC
Notice that in this example, algorithms.AES takes the key as the parameter while modes.CBC takes the IV; AES always needs a key, but the use of an IV is dependent on the mode.
Proper Padding
While we are in the business of improving things, let’s introduce a better padding mechanism. The cryptography module provides two schemes, one following what is known as the PKCS7 specification and the other following ANSI X.923. PKCS7 appends n bytes, with each padding byte holding the value n: if 3 bytes of padding are needed, it appends \x03\x03\x03. Similarly, if 2 bytes of padding are needed, it appends \x02\x02.
ANSI X.923 is slightly different. All appended bytes are 0, except for the last byte, which is the length of the total padding. In this example, 3 bytes of padding is \x00\x00\x03, and two bytes of padding is \x00\x02.
The cryptography module provides a padding context that is analogous to the AES cipher context. In the next code listing, padder and unpadder objects are created for adding and removing padding. Note that these objects also use update and finalize, since no padding is created from calling the update() method . It does, however, return full blocks, storing the rest of the bytes for either the next call to update() or the finalize() operation . When finalize() is called, all remaining bytes are returned along with enough bytes of padding to make a full block size.
AES-CBC Padding
Why did it not produce the original messages exactly as specified?
There is technically nothing incorrect with this code, but there is definitely a mismatch between the apparent intention of the code and the actual output. This code suggests that the author intended to encrypt each one of the three strings as an independent message. In other words, the probable intention of the code was to encrypt three distinct messages and get back three equivalent messages upon decryption.
That is not what we got. Listing 3-6 is reporting five outputs and two of them are empty.
Let’s talk about the update() and finalize() API one more time. Because of how these methods behave for certain modes (e.g., ECB mode), it can be tempting to think about update() as a stand-alone encryptor wherein a plaintext block is provided as input and a ciphertext block is provided as output.
In reality, the API is designed such that the number of calls to update() is irrelevant. That is, what is being encrypted is not the input to \lstinline{update()}, but \emph{the concatenation of every input} to some number of \lstinline{update()} calls, and, of course, output (if any) from a finalize() call at the end.
Thus, the program in Listing 3-6 is not encrypting three inputs and producing five outputs, it is processing a single continuous output and producing a single continuous output.
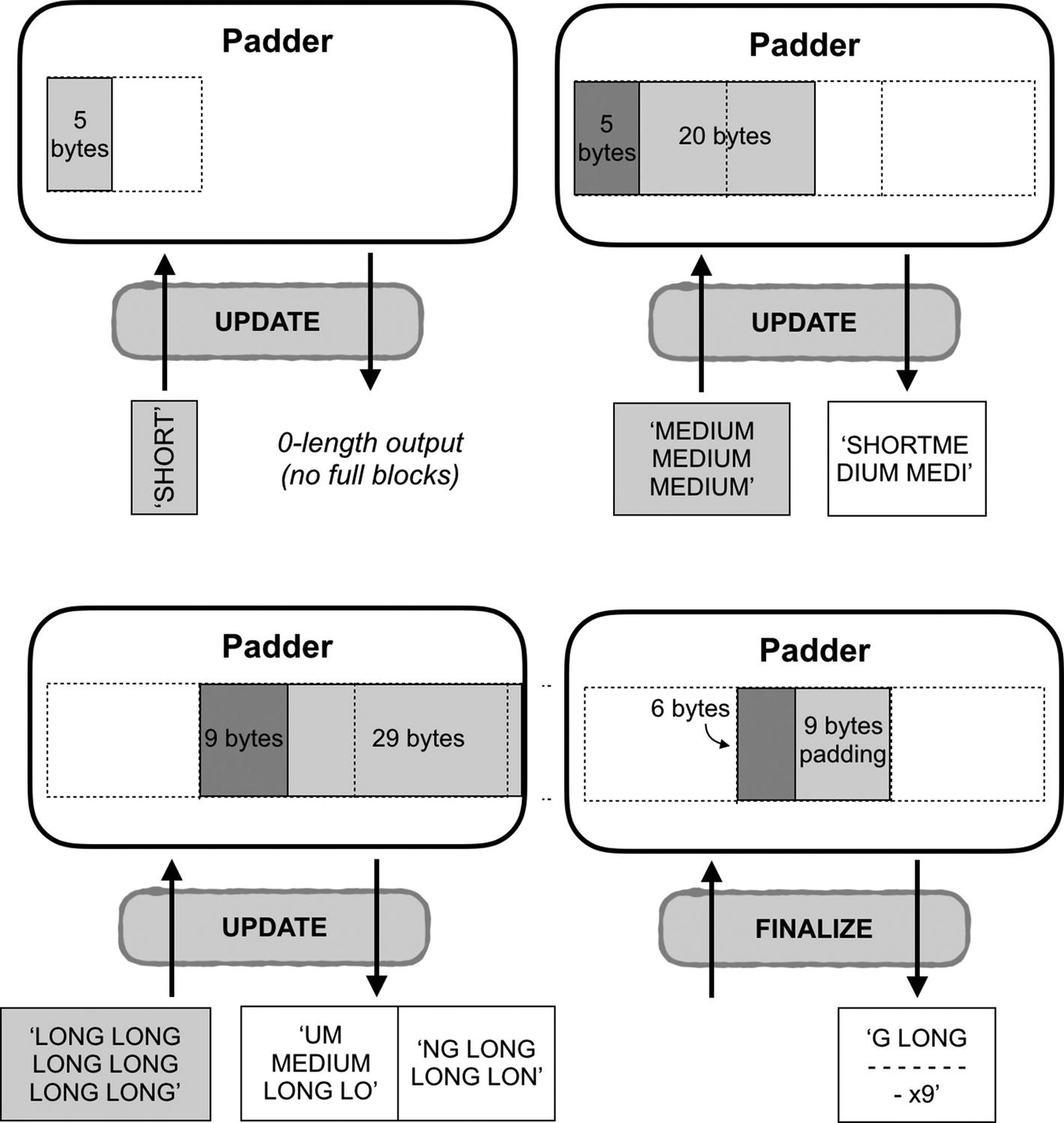
PKCS7 padding does not add any padding until the finalize operation
Unpadding can be even more jarring. Unlike the padding operations, you can submit a full block to the unpadder and still get nothing back. This is because the unpadder has to reserve the last block received in update() calls in case it is the last block. Because unpadding requires examining the last block, the unpadder has to be sure it has received all the blocks to know that it has the last one.
Walking through Listing 3-6 one more time illustrates how the effects of these operations are compounded when the padder and encryptor are used together. On the first pass through the loop for encrypting the messages, the input is SHORT. Five characters is less than of a block. The padder’s update() method does not add any padding, so the padder buffers these five characters and the update() method returns an empty byte string. When this gets passed to the encryptor, there is obviously not a full block so the encryptor’s update method also returns an empty byte string. This gets appended to the list of ciphertexts.
On our second pass through the loop, the input is MEDIUM MEDIUM MEDIUM. These 20 characters are passed into the padder’s internal buffer and are added to the 5 that were there before. The UPDATE method now returns the first 16 of those 25 bytes (a full block), leaving the remaining 9 bytes in the internal buffer. The 16 bytes from the padder are encrypted and stored in the list of ciphertexts.
In the final pass, the LONG LONG LONG LONG LONG LONG input is added to the padder’s internal buffer. These 29 bytes are added to the current 9 bytes in the buffer for a total of 38 bytes. The padder returns the 2 full blocks (of 16 bytes each) leaving the last 6 bytes in its buffer. The two blocks are encrypted, and the two-block output is stored in the list of ciphertexts.
Once the loop exits, the padder’s finalize method is called. It takes the last bytes of input, appends the necessary padding, and passes it to the encryption operation. The ciphertext is appended to the list and encryption is over. There are now four ciphertext messages to decrypt. Reversing the process, the first message is, you may recall, the empty buffer. It just passes straight through everything and comes out as an empty message.
But the next recovered text is also empty. That’s because the first full block to the unpadder is reserved for the reasons we explained. It produces an empty output fed into the AES decryptor’s update() method . This generates our second empty output.
The remaining three are more straightforward.
Now that the walk-through is finished, did you notice that we were still using the incorrect terminology? We referred to individual outputs from update() methods as individual ciphertexts rather than a snippet of the ciphertext. Similarly, we called the output of the decryptor update methods recovered texts rather than part of a single recovered message.
This was intentional. The crucial principle is that semantics matter. How we think about our code can be different from how it operates, and this can result in unexpected, and often insecure, results. When you use a library (always better than creating your own!), you must understand the API’s approach and design. It is critical that you think the way the API is designed to be used.
For the cryptography library, always think about everything submitted to a sequence of encryption update() calls and one finalize() call as a single input. Similarly, think about everything that is recovered from a series of decryption update() calls and one finalize() call as a single output.
And what is going on with the decryption? How did we get five outputs instead of four? The first ciphertext in the list was just the empty string so it makes sense that the first “recovered” plaintext was empty. But why was the second one empty too?
Broken AES-CBC Manager
Run the code and observe the output. Did you get each message individually this time? Good! You probably like this version a lot better!
The API might be more semantically aligned, this time, but the implementation is very broken and incredibly dangerous. Before we tell you what is wrong with it, can you try and see it yourself? Are there any security principles we’ve talked about in this chapter that we are violating? If it isn’t obvious, read on!
A Key to Hygienic IVs
The problem with Listing 3-7 is that it is reusing the same key and IV for different messages. Take a look at the constructor where the key and IV are created. Using that single key/IV pair, the offending code re-creates encryptor and decryptor objects in every call to encrypt_message and decrypt_message. Remember, the IV is supposed to be different each time you encrypt, preventing the same data from being encrypted to the same ciphertext! This is not optional.
Once again, it is important to understand how an API is built and the security parameters associated with it. Go back and look at Figure 3-5. Remember that in CBC encryption, the algorithm combines the first plaintext block with the IV using the XOR operation before the AES operation is applied. Each subsequent plaintext block is combined with the previous ciphertext block using XOR before AES encryption. With the Python API, each call to update() adds blocks to this chain, leaving data less than a full block in an internal buffer for subsequent calls. The finalize() method does not actually do any more encrypting, but will raise an error if there is incomplete data still waiting to be encrypted.
Calling the update() method over and over is not reusing a key and IV because we are appending to the end of the CBC chain. On the other hand, if you create new encryptor and decryptor objects, as we did in Listing 3-7, you are re-creating the chain from the beginning. If you reuse a key and IV here, you will with the same key and IV! This results in exactly the same output for the same input every time!
Accordingly, when using the API of Python’s cryptography module , never give the same key and IV pair to an encryptor more than once (obviously, you give the same key and IV to the corresponding decryptor). In fact, it’s probably best to never reuse the same key again, period.
AES-CBC Manager
Listing 3-8 does not reuse key/IV pairs, but you have probably noticed that we are no longer treating the individual messages as individual messages. Now that we’re back to the update() finalize() pattern, we have to treat all the data passed to a single context as a single input. If we want each message treated separately, with a sequence of update() calls and finalize() call per input. Alternatively, we can submit all three messages as a single input from the perspective of the encryption and decryption and have an independent mechanism for splitting the single decryption output into messages.
In summary, it is important to carefully understand any cryptography APIs that you use, how they work, and what their requirements (especially security requirements) are. It is also important to understand how easy it can be to create an API that looks like it does the right thing but is actually leaving you vulnerable.
Remember, YANAC (You Are Not A Cryptographer... yet!). Don’t roll your own crypto like we are doing in these educational examples.
So why does the cryptography module use the update/finalize pattern? Quite often, data needs to be processed in chunks in many practical cryptographic operations. Suppose that you are transmitting data over the network. Do you really want to wait until you have the entire content before you can encrypt it? Even if you were encrypting a local file on the hard drive, it might be impractically large for all-at-once encryption. The update() method allows you to feed data to an encryption engine as it becomes available.
The finalize() operation is useful for enforcing requirements such as the CBC operation did not leave an incomplete block unencrypted and that the session is over.
Of course, there’s nothing wrong with a per-message API so long as a key and IV aren’t reused. We will look at strategies for this later.
Exercise 3.10. Deterministic Output
Run the same inputs through AES-CBC using the same key and IV. You can use Listing 3-7 as a starting point. Change the inputs to be the same each time and print out the corresponding ciphertexts. What do you notice?
Exercise 3.11. Encrypting An Image
Encrypt the image that you encrypted with ECB mode earlier. What does the encrypted image look like now? Don’t forget to leave the first 54 bytes untouched!
Exercise 3.12. Hand-Crafted CBC
ECB mode is just raw AES. You can create your own CBC mode using ECB as the building block.10 For this exercise, see if you can build a CBC encryption and decryption operation that is compatible with the cryptography library. For encryption, remember to take the output of each block and XOR it with the plaintext of the next block before encryption. Reverse the process for decryption.
Cross the Streams
Counter mode has a number of advantages to CBC mode and, in our opinion, is significantly easier to understand than CBC mode. Also, while CTR is the traditional abbreviation, “CM” is a really nice set of initials.
Although simple, the concept behind this mode can be a little counter-intuitive at first (yup). In CTR mode, you actually never use AES for encryption or decryption of the data. Instead, this mode generates a key stream that is the same length as the plaintext and then uses XOR to combine them together.
Recall from earlier exercises in this chapter that XOR can be used to “mask” plaintext data by combining it with random data. The previous exercise masked 16 bytes of plaintext with 16 bytes of random data. This is a real form of encryption called a “one-time pad” (OTP) [11, Chap. 6]. It works great but requires that the key is the same size as the plaintext. We don’t have the space here to explore the OTP further; the important concept is that using XOR to combine plaintext and random data is a great way to create ciphertext.
AES-CTR mimics this aspect of OTP. But instead of requiring the key to be the same size as the plaintext (a real pain when encrypting a 1TB file), it uses AES and a counter to generate a key stream of almost arbitrary length from an AES key as small as 128 bits.
To do this, CTR mode uses AES to encrypt a 16-byte counter, which generates 16 bytes of key stream. To get 16 more bytes of key stream, the mode increases the counter by one and encrypts the updated 16 bytes. By continually increasing the counter and encrypting the result, CTR mode can produce an almost arbitrary amount of key stream material.11 Once a sufficient amount of key material is generated, the XOR operation is used to combine them together to produce the ciphertext.
Although the counter is changing by a small amount each time (often just changing by a single bit!), AES has good per-block avalanche properties. Thus, each output block appears completely different from the last, and the stream as a whole appears to be random data.
Note: Random Thoughts
Randomness is actually a huge deal in cryptography. Many otherwise acceptable algorithms have been compromised in practice if they did not have sufficient sources of randomness for keys, among other things. The OTP algorithm we briefly mentioned requires a key that is the same size as the plaintext (no matter how large) and that the entire key be truly random data. AES-CTR mode only requires that the AES key be truly random. The key stream produced by AES-CTR looks random, but is actually pseudo-random. This means that if you know the AES key, you know the whole key stream no matter how random it appears to be.
Ensuring that you have a sufficiently random source of data is beyond the scope of this book. For our purposes, we will assume that os.urandom() can return acceptably random data for our needs. In production cryptography environments, you would need to analyze this far more carefully.
Randomness is so important that we will mention it more than once. In fact, we will return to it near the end of this very chapter.
![$$ C\left[n\right]=P\left[n\right]\oplus {n}_k. $$](../images/472260_1_En_3_Chapter/472260_1_En_3_Chapter_TeX_Equc.png)
![$$ C\left[n\right]=P\left[n\right]\oplus {\left( IV+n\right)}_k. $$](../images/472260_1_En_3_Chapter/472260_1_En_3_Chapter_TeX_Equd.png)
XOR is a really versatile mathematical operation. You can think of it as “controlled bit-flipping”: to compute A ⊕ B, you march down their bits in tandem; when you encounter a 1 in B, you invert the corresponding bit in A, and when you encounter a 0 in B, you leave that bit in A alone. Thinking of it that way, it’s easy to see how doing that twice simply restores A to what it was before.
![$$ P\left[n\right]=C\left[n\right]\oplus {\left( IV+n\right)}_k. $$](../images/472260_1_En_3_Chapter/472260_1_En_3_Chapter_TeX_Eque.png)
Of course, nothing happens if you merely XOR with 0 (since A ⊕ 0 = A, which is where the inverse property comes from), so the keys in the stream need to be composed of random-looking bits, but that is exactly the type of key stream that AES produces.
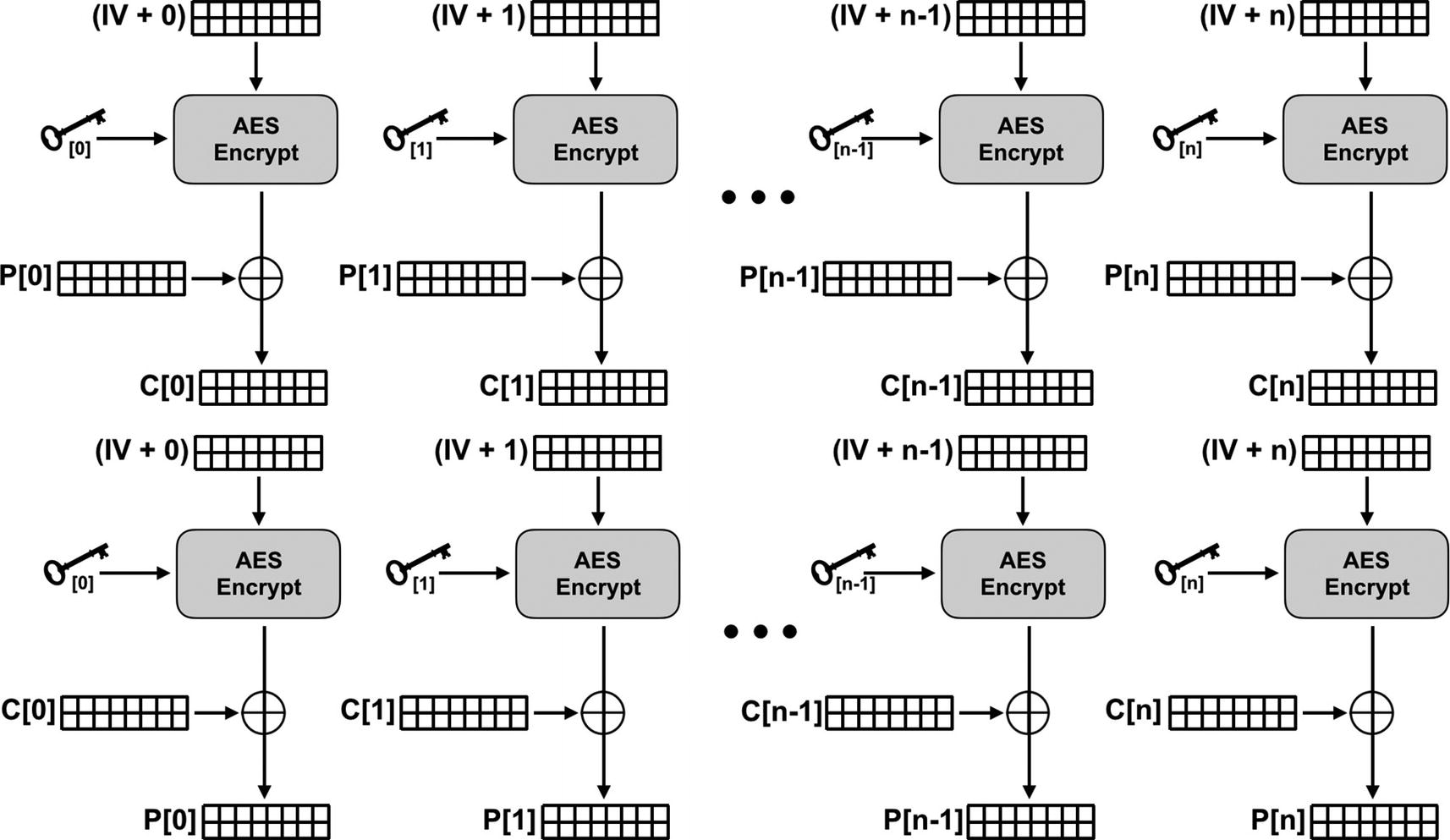
Visual depictions of CTR encryption and decryption. Note that encryption and decryption are the same process!
Happily, stream ciphers do not require padding! It is quite simple to only XOR a partial block, discarding the later parts of the key that aren’t needed.
In general, this approach is much simpler. Padding goes away and blocks can again be encrypted independent of one another.
Let’s see it in action in the cryptography module (Listing 3-9).
AES-CTR
Because no padding is needed, the finalize methods are actually unnecessary except for “closing” the object. They are kept for symmetry and pedagogy.
How do you choose between CTR and CBC modes? In almost all circumstances, counter mode (CTR) is recommended.12 Not only is it easier, but in some circumstances it is also more secure. As if that wasn’t enough, counter mode is also easier to parallelize because keys in the key stream are computed from their index, not from a preceding computation.
Why even talk about CBC, then? At the very least it is still in wide use, so you will benefit from understanding it when you encounter it in the wild.
We will introduce other modes later in the book that build on counter mode to make something even better. For now, it is enough to understand the basic characteristics of CBC and CTR modes and how each one works to build a better algorithm from an underlying block cipher.
Exercise 3.13. Write a Simple Counter Mode
As you did with CBC, create counter mode encryption from ECB mode. This should be even easier than it was with CBC. Generate the key stream by taking the IV block and encrypting it, then increasing the value of the IV block by one to generate the next block of key stream material. When finished, XOR the key stream with the plaintext. Decrypt in the same manner.
Exercise 3.14. Parallel Counter Mode
Extend your counter mode implementation to use a thread pool to generate the key stream in parallel. Remember that to generate a block of key stream, all that is required is the starting IV and which block of key stream is being generated (e.g., 0 for the first 16-byte block, 1 for the second 16-byte block, etc.). Start by creating a function that can generate any particular block of key stream, perhaps something like keystream(IV, i). Next, parallelize the generation of a key stream up to n by dividing the counter sequence among independent processes any way you please, and have them all work on generating their key stream blocks independently.
Key and IV Management
As you have seen, having a library such as cryptography makes all kinds of encryption convenient and simple to use. Unfortunately, this simplicity can be deceptive and lead to mistakes; there are many ways to get it wrong. We have already touched briefly on one of them: reuse of keys or IVs.
That kind of mistake falls under the broader category of “Key and IV Management,” and doing it incorrectly is a common source of problems.
Important
You must never reuse key and IV pairs. Doing so seriously compromises security and disappoints cryptography book authors. Just don’t do it. Always use a new key/IV pair when encrypting anything.
Why don’t you want to reuse a key and IV pair? For CBC, we already mentioned one of the potential problems: if you reuse a key and IV pair, you will get predictable output for predictable headers. Parts of your messages that you might be inclined not to think about at all, because they are boilerplate or contain hidden structure, will become a liability; adversaries can use predictable ciphertext to learn about your keys.
Think about an HTML page, for example. The first characters are often the same across multiple pages (e.g., "<!DOCTYPE html>\n"). If the first 16 bytes (an AES block) of HTML pages are the same and you encrypt them under the same key/IV pair, the ciphertext will be the same for each one. You have just leaked data to your enemy, and they can start to analyze your encrypted data for patterns.
If your web site has a large amount of static content or dynamic results that are identically generated, each encrypted page becomes uniquely identifiable. The enemy may not know what each page says, but they can determine the frequency of use and track which parties receive the same pages.
Reusing a key and IV in CBC mode is bad.
Reusing a key and IV in counter mode, on the other hand, is much worse. Because counter mode is a stream cipher, the plaintext is simply XORed with the key stream. If you happen to know the plaintext, you can recover the key: K ⊕ P ⊕ P = K!
“So what?” you might be thinking. “Who cares if they can get the key stream? If they already know the plaintext, why do we care?”
The problem is, under many circumstances an attacker might know some or all of the contents of one of your plaintext messages. If other messages are encrypted with the same key stream, the attacker can recover those messages too!
Bad, bad, bad.
Let’s explore this idea a little further. Suppose that you buy something for $100.00 with a credit card at a store. Let’s assume a simplified version of the world where the card reader sends a message to your bank to authorize the purchase protected by only AES-CTR encryption.
AES-CTR for a Store
For simplicity, the purchase message was included in the preceding code. Feel free to change it to accept a file or command-line flags that set the buyer’s name, purchase price, and so forth. You probably ought to also write the encrypted message to a file.
Back to our scenario, if you are trying to crack this system, you can spend $100.00 at this store, then tap the line and intercept the purchase message transmitted to the bank. If you do this, how much of the plaintext message do you know? You know all of it! You know who made the purchase, you know the amount of the purchase, you know the date, and you know your own credit card number.
That means that you can recreate the plaintext message, XOR it with the ciphertext, and recover keystream material. Because the merchant is reusing the same key and IV for the next customer, you can trivially decrypt the message and read the contents. Oops. We feel a news story about a data breach coming on.
Exercise 3.15. Riding The Keystream
Put into practice this keystream-stealing attack. That is, encrypt two different purchase messages using the same key and IV. “Intercept” one of the two messages and XOR the ciphertext contents with the known plaintext. This will give you a keystream. Next, XOR the keystream with the other message to recover that message’s plaintext. The message sizes may be a little different, but if you’re short some keystream bytes, recover what you can.

What do you get out of having the XOR of the two plaintext messages? Is that readable? It depends. Because plaintext messages often have structure, private data is often extractable or guessable. Take these made-up purchase messages from our example. If you XORed two such messages together, what could you learn?
First of all, any parts that overlap exactly simply reduce to 0. Instantly, you know where the messages are the same and where they diverge. If the attacker were lucky enough that two messages had the same length of name for the buyer, the amount fields would line up as well. This field yields a lot of information when the two are XORed together because there are so few legal characters for this field (“0”–“9” and “.”). The XOR of the ASCII characters for the digits leaves open only a few possibilities.
For example, there are only two pairs of digits for which the XOR of their ASCII values is 15. These are “7” and “8” (ASCII values 55 and 56) and “6” and “9” (ASCII values 54 and 57). So, if we know that we have the XOR of two purchase amount field digits and the XOR value is 15, then the two messages each have one of these two pairs of numbers. That’s only four possibilities, which will not be very difficult for an attacker to figure out under most circumstances.
You might be surprised how often this vulnerability can show up if you’re not careful. One simple example is full-duplex messages. If you have two parties that want to send encrypted messages to each other, they must not use the same key and IV to encrypt each side of the connection. Each side’s encryption must be independent of the other. If you think about how CBC and CTR mode work, this will be pretty obvious. If you are going to write messages in both directions, each side needs a separate read key and write key.13 The read key of the first party will be the write key of the second and vice versa. This way, different messages will not be written under the same key and IV pair.
Exercise 3.16. Sifting Through XOR
XOR together some plaintext messages and look around for patterns and readable data. There’s no need to use any encryption for this, just take some regular, human-readable messages and XOR the bytes. Try human-readable strings, XML, JSON, and other formats. You may not find a lot that is instantly decipherable, but it’s a fun exercise.
Exploiting Malleability
Some aspects of cryptography are unintuitive at first. For example, an enemy can fail to read a confidential message while still being able to change it in meaningful, deceptive ways. In this section, we will experiment with altering encrypted messages while not being able to read them.
Counter mode is a really good encryption mode for all of the reasons described earlier. At the risk of being too repetitive, however, it only guarantees confidentiality. In fact, because it is a stream cipher, it is trivial to change a small part of the message without changing the rest of it. In counter mode, for example, if an attacker modifies one byte of the ciphertext, it only affects the corresponding byte of plaintext. While that one byte of plaintext will not decrypt correctly, the remaining bytes will remain intact.
Cipher block chaining mode is different because a change to a single byte of ciphertext will affect all subsequent blocks.
Exercise 3.17. Visualizing Ciphertext Changes
To better understand the difference between counter mode and cipher block chaining mode, go back to the image encryption utility you wrote previously. Modify it to first encrypt and then decrypt the image, using either AES-CBC or AES-CTR as the mode. After decryption, the original image should be completely restored.
Now introduce an error into the ciphertext and decrypt the modified bytes. Try, for example, picking the byte right in the middle of the encrypted image data and setting it to 0. After corrupting the data, call the decryption function and view the restored image. How much of a difference did the edit make with CTR? How much of a difference did the edit make with CBC?
HINT: If you can’t see anything, try an all-white image. If you still can’t see it, change 50 bytes or so to figure out where the changes are happening. Once you find where the changes are happening, go back to changing a single byte to view the differences between CTR and CBC. Can you explain what’s happening?
To illustrate this concept of malleability, we are going to let our attacker know some of the plaintext of an encrypted message. This knowledge is going to allow them to change the message en route. What’s different this time around is that this vulnerability is not dependent on a reused keystream.
If an attacker knows the plaintext behind a keystream-enciphered message, it is easy to extract the keystream from the ciphertext. If the keystream is reused, the attacker can decrypt all messages that used it. Even if it is not reused, the attacker can alter a message with known plaintext.
Let’s revisit our encrypted purchase messages. Suppose that Acme’s competitor, Evil LLC, wants to redirect this payment to themselves. They have a tap on the network connection coming out of Acme’s store and can intercept and modify the message. When an encrypted form of this message comes along, even though they don’t have the key and cannot decrypt it, they can strip out the original message parts that are known and replace them with their own chosen parts.
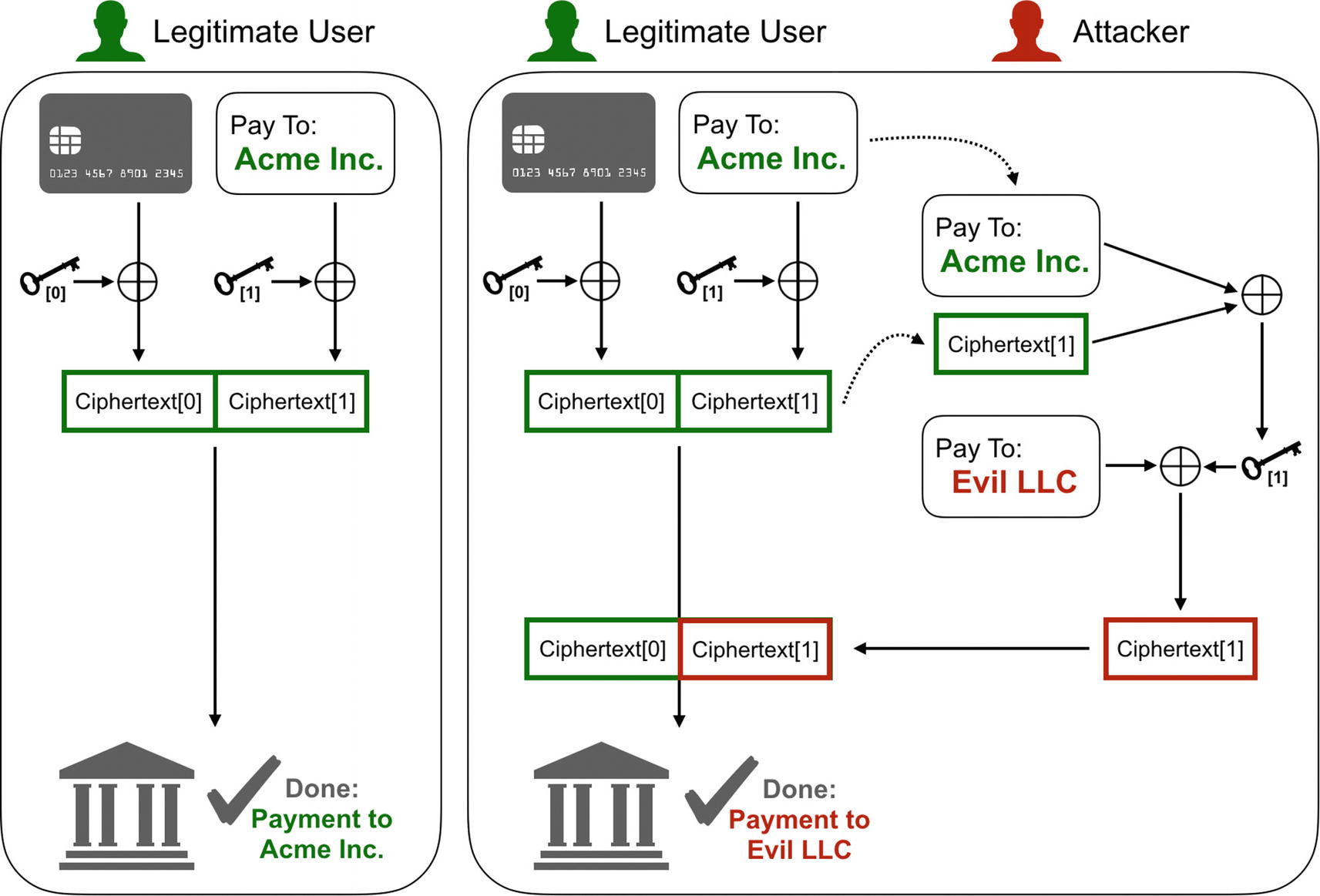
If an attacker knows the plaintext in CTR mode ciphertext, she can extract the keystream to encrypt her own evil message!
Exercise 3.18. Embracing Evil
You work for (or own!) Evil LLC. Time to steal some payments from Acme. Start with one of the encrypted payment messages you created in the earlier exercises. Calculate the size of the header up through the identification of the merchant and extract that many bytes of the encrypted data. XOR the plaintext header with the ciphertext header to get the keystream. Once you have this, XOR the extracted keystream with a header identifying Evil LLC as the merchant. This is the “evil” ciphertext. Copy it over the bytes of the encrypted file to create a new payment message identifying your company as the recipient. Prove that it works by decrypting the modified file.
The key lesson here is that encryption is insufficient to protect data by itself. In subsequent chapters, we will use message authentication codes, authenticated encryption, and digital signatures to ensure that data cannot be altered without disrupting communications.
Gaze into the Padding
While CBC mode is less susceptible to alteration than counter mode, it is by no means perfect in that regard. In fact, it is CBC’s malleability that made one of the early versions of SSL vulnerable. Remember that CBC mode is a block-based mode and requires padding. An interesting error in the padding specification and the malleability of AES-CBC enabled attackers to execute a “padding oracle attack” and decrypt confidential data.
Let’s create that attack right now. It’s extremely interesting and educational.
SSLv3 Padding
Let’s talk about what we have so far (Listing 3-11). The padding bytes in this scheme are completely ignored except for the last byte. It doesn’t matter what the bytes are, so long as the last byte is correct. Padding goes at the end of a message, right? Guess which part of a CBC message is the most malleable.
The reason that the last part of the CBC message is more malleable is that it has no impact on any subsequent blocks. It can be changed without messing up anything else. Recall that CBC decryption starts out the same for every single block no matter where it is. The ciphertext block is decrypted by AES with the key. It’s only after decryption that it is XORed with the ciphertext from the previous block.
This means that you could substitute any block from the CBC chain at the very end of the chain. It will get decrypted at the end just like it would in the middle or the beginning. After decryption, it is XORed with the ciphertext from the previous block.
How is this helpful? Well, suppose that we are fortunate enough to have the original plaintext message be a multiple of 16 bytes long, the AES block length. Because we’re using a padding scheme that always uses padding, there will be a full block of padding at the end. Since we don’t care what bytes are in the padding except for the last one, we can correctly recover the entire message, even if we replace the last block, so long as the very last byte decodes to 15 (the padding length when there is a full block of padding).
Explained another way, when there is a full block of padding at the end, 15 of the 16 bytes are completely ignored. It doesn’t matter what they are. If we’re going to try to “fool” the decryption, this is a great place to do it, because we only have to get one byte correct!
This small change, only caring about the value of the last byte, changes everything! It reduces brute-force guessing to something reasonable. Normally, if you wanted to “guess” a correct AES block, you would have to try all possible combinations of all 16 bytes. You might recall from previous discussion that this works out to a very big number and it is impossible to try every combination for all practical purposes.
But now that we only care about the last byte, we only need to correctly guess one byte of data. To repeat, so long as the last byte decrypts to 15, our padding will be “correct.” One byte of data has 256 possible values, so if our last byte is randomly selected, then 1 out of 256 times it will correctly decrypt to 15!
You might protest that the data isn’t random. We are trying to decrypt a specific byte. Very true! But remember that in CBC we XOR the real plaintext with the ciphertext of the previous block! The ciphertext, at least for our purposes here, behaves like random data. For any given key/IV pair, the last byte of ciphertext that will be XORed with our plaintext byte has an equal chance of being any of the 256 possible 1-byte values. If we are lucky, the “random” byte of ciphertext XORed with our plaintext byte will be 15!
If the padding is accepted and decrypts to 15, we can use our knowledge of the previous ciphertext block to get the true plaintext byte.
Actually, recovering the plaintext byte is a little trick and requires that we think through CBC decryption carefully. Remember that the last block of plaintext (e.g., the true padding in the original message) was XORed with the ciphertext from the second-to-last block. This intermediate data was encrypted by the AES algorithm. So, working backward, if we overwrite the final ciphertext block, the CBC operation will first run this block through the AES decryption operation to produce an intermediate value that is then XORed with the preceding ciphertext. If this is difficult to follow, refer back to Figure 3-5.
If the padding is accepted (e.g., the last byte is 15), we know that the last byte of the intermediate value decrypted by AES is the XOR of 15 and the last byte of the previous ciphertext block. We, of course, have the ciphertext. Now, even without the AES key, we can simply compute the intermediate byte directly (e.g., by taking the XOR of 15 and the last byte of the second-to-last ciphertext block).
But the intermediate value isn’t the plaintext byte. Remember, we are decrypting an earlier ciphertext block. That ciphertext block is the AES encryption of the real plaintext XORed with the actual preceding ciphertext (or the IV if it’s the first plaintext block). So, when we recover the intermediate last byte, we still have to remove that mixed-in data with an appropriate XOR.
SSLv3 Padding Oracle
This might seem a little weird: we have the key and are using it to create the oracle. Just remember: we’re simulating a vulnerable remote server, which would have its own key. The attack we write below will proceed without knowledge of the key used here.
Lucky SSLv3 Padding Byte
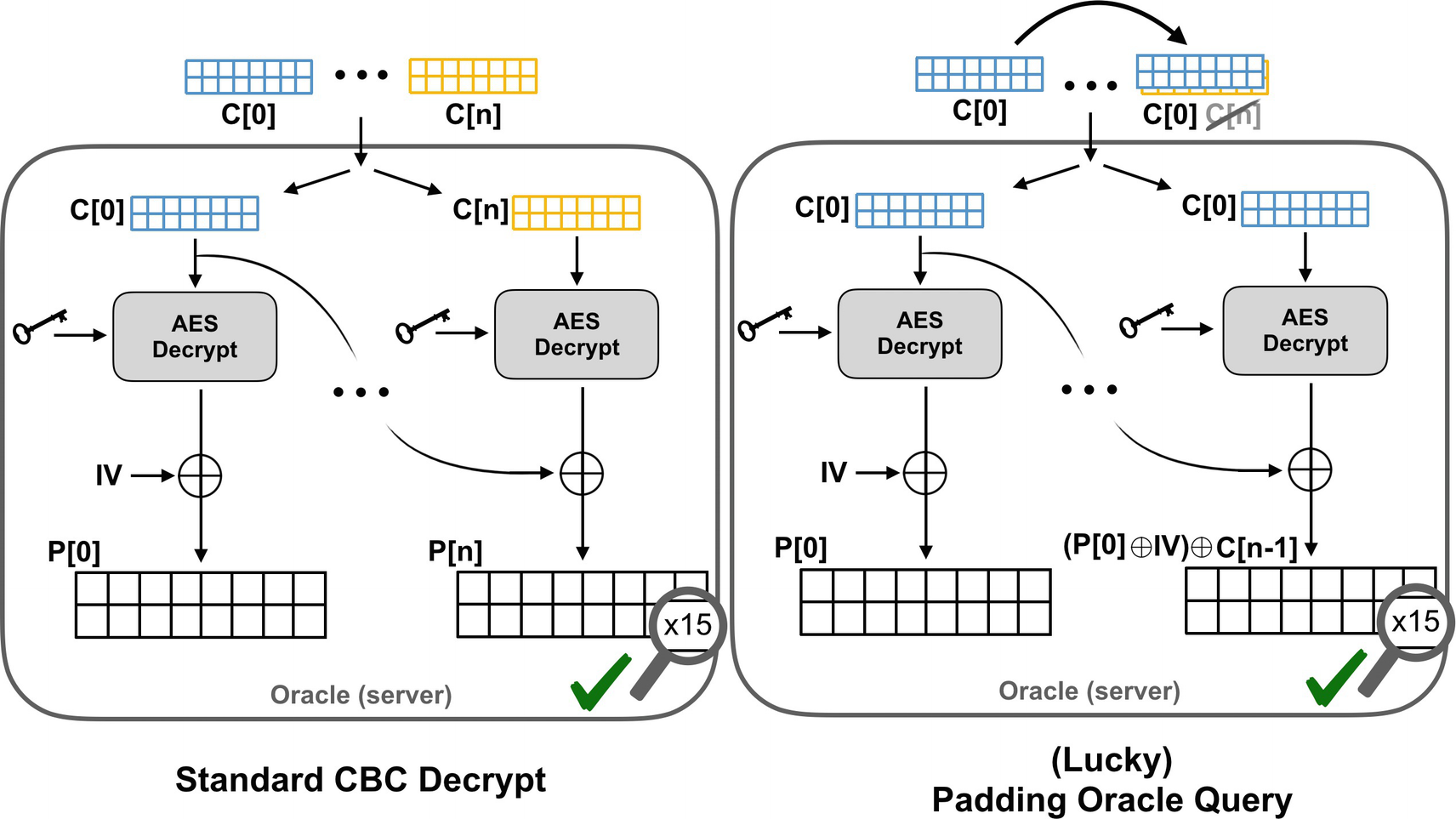
If the first 15 bytes of the padding block are ignored, we can substitute in the second to last block and see if the oracle tells us the padding is correct. If so, we can figure out the last byte in the previous block.
Is that really all that useful? In the first place, we have to be lucky enough to have a full block of padding. In the second place, we only have a 1-in-256 chance of decoding a single byte. That doesn’t seem terribly helpful.
Or does it?
Again, cryptography can be very counter-intuitive. Computers don’t behave like we would expect them to, and that’s where we get into trouble.
While SSLV3 was busy protecting web traffic, it turned out there were a number of ways that a malicious advertisement could generate traffic to an SSL-encrypted web site. But because that advertisement was generating the traffic, its authors could control how long the encrypted message was. Thus, if the attacker was trying to decrypt an encrypted cookie, triggering a GET request of various lengths could control how long the overall message was.
Getting the full block of padding in this case really isn’t very difficult as the malicious requester could put arbitrary data in the GET request.
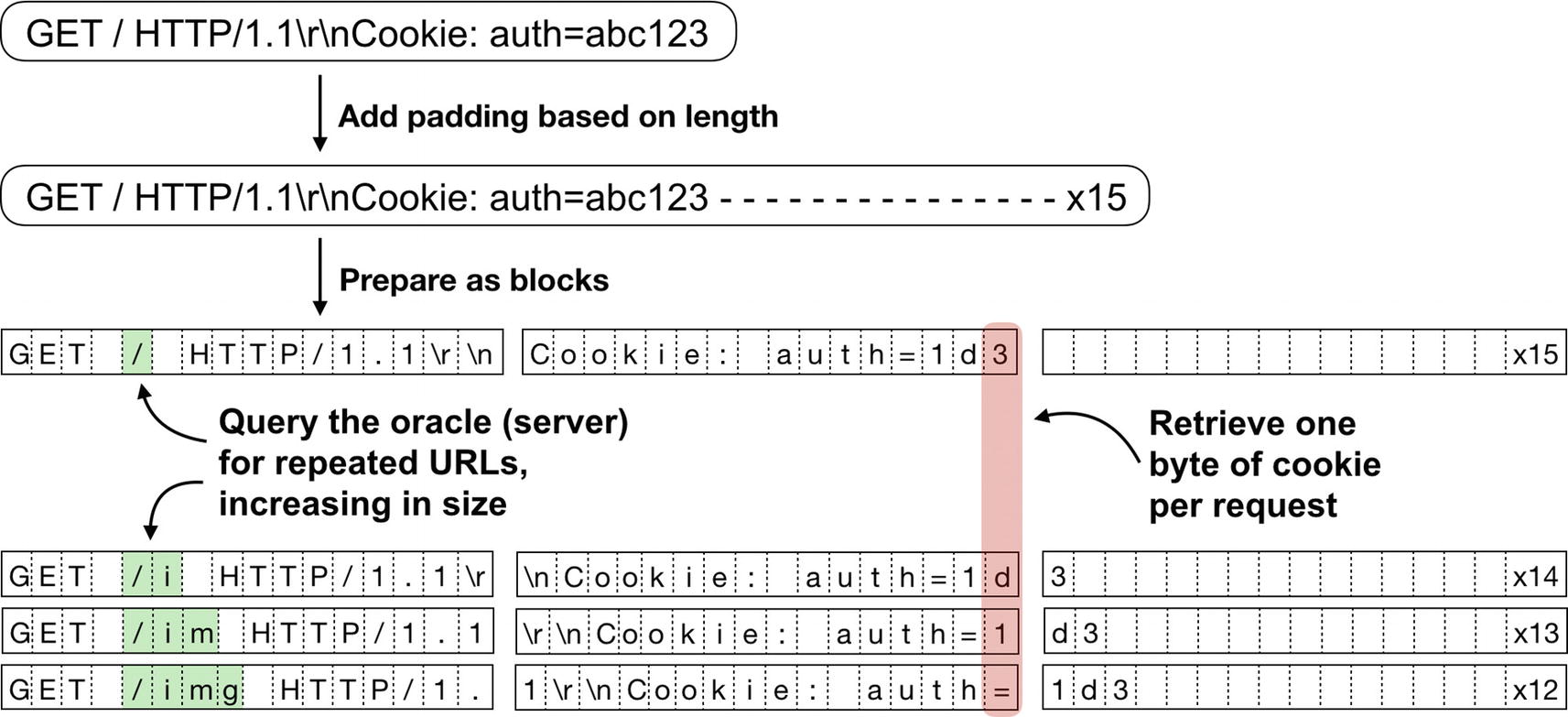
In order to decrypt a byte that matters, an attacker controls the GET request size so that the cookie is in the right spot. This requires the ability to insert arbitrary requests such as an advertiser within a TLS-secured context.
It’s still just one byte, right? As illustrated in Figure 3-10, the attacker can control the length of the message. Once one byte is decoded, it’s pretty straightforward to increase the message length by 1 by inserting a byte earlier in the message, pushing the new byte into the last slot of the arbitrary block. Another 256 tries and that second byte will be decoded too! Wash, rinse, and repeat!
Exercise 3.19. Resistance is Futile
Finish the code for the padding oracle attack. We’ve given you the major pieces, but it will still take some work to put everything together. We will do a few things to try and simplify as much as possible. First, pick a message that is exactly a multiple of 16 bytes in length (the AES block size) and create a fixed padding to append. The fixed padding can be any 16 bytes as long as the last byte is 15 (that’s the whole point of the exercise, right?). Encrypt this message and pass it to the oracle to make sure that code is working.
Next, test recovering the last byte of the first block of the message. In a loop, create a new key and IV pair (and a new oracle with these values), encrypt the message, and call the lucky_get_one_byte() function, setting block number to 0. Repeat the loop until this function succeeds and verify that the recovered byte is correct. Note that, in Python, an individual byte isn’t treated as a byte type but is converted to an integer.
The last step in order to decode the entire message is to be able to make any byte the last byte of a block. Again, for simplicity, keep the message being encrypted a perfect multiple of 16. To push any byte to the end of a block, add some extra bytes at the beginning and cut off an equal number at the end. You can now recover the entire message one byte at a time!
Exercise 3.20. Statistics Are Also Futile
Instrument your padding oracle attack in the previous exercise to calculate how many guesses it took to fully decrypt the entire message and calculate an average number of tries per byte. In theory, it should work out to about 256 tries per byte. But you’re probably working with such small numbers that it will vary widely. In our tests on a 96-byte message, our averages varied between about 220 guesses per byte and 290 guesses per byte.
Once again, encryption is about confidentiality, and confidentiality is simply not enough to solve all security problems. In subsequent chapters we will learn how to combine confidentiality and integrity to solve a larger class of problems.
Weak Keys, Bad Management
To conclude this chapter, let’s briefly discuss keys. Hopefully, it has already become very clear to you how important keys are.
In almost all cryptographic systems, key management is the hardest part. It can be difficult to generate good keys, to share keys, and to manage keys afterward (e.g., keeping them secret, updating them, or revoking them). For now, we’ll focus on key generation.
This code will produce the same “random” numbers on every run of the program. This can sometimes be useful for testing, but you must not leave it in production code!
Although Python’s default seeding is no longer quite so predictable, it is not suitable for generating secrets like passwords. Instead, always pull from os.urandom() or, if using Python 3.6 or later, secrets.SystemRandom(). Under most circumstances, this is enough randomness. If you need something stronger, you might need to use different hardware and should consult an expert cryptographer.
In some deployments, a key is not pulled from random numbers. Instead, it is derived from a password. If you are going to derive a key from a password, the password needs to be very secure! In the previous chapter, you learned about brute-force attacks and all of those lessons apply here.
Let’s get a feel for the difference in difficulty of guessing a key in these scenarios. How long would it take to try every possible 128-bit (random) key? How many tries is that?
There are 2128 different 128-bit keys. That’s this many different keys:
340,282,366,920,938,463,463,374,607,431,768,211,456.
If your key is derived from a five-digit pin number, though, you have reduced it to 99,999! It’s true that very few passwords will be as hard to brute force as a truly random 128-bit key. After all, you’d need to have a password composed of about 20 random characters to require the same kind of brute-force effort as a 128-bit key. But still, 99,999 is just begging a computer to accept your challenge. You can do better than that!
As a reminder, there are proven algorithms for deriving a key from a password. Make sure you use a good one. In the previous chapter, we used scrypt. There are others that some people feel are even better (such as bcrypt or Argon2). What makes a good derivation function? One characteristic is how long it takes. If someone picks a weak password (e.g., “puppy1”), it won’t take the attacker long to figure it out. It might be possible, however, to make it take too long if the derivation function is slow.
In short, don’t bother using a good cipher with a bad key. Make sure that your keys are securely generated and adequately resistant to abuse by a determined adversary.
Exercise 3.21. Predicting Time-Based Randomness
Write an AES encryption program (or modify one of the others you’ve written for this chapter) that uses the Python random number generator to generate keys. Use the seed method to explicitly configure the generator based on the current time using time.time() rounded to the nearest second. Then use this generator to create a key and encrypt some data. Write a separate program that takes the encrypted data as input and tries to guess the key. It should take a minimum time and a maximum time as a range and try iterating between these two points as seed values for random.
Other Encryption Algorithms
In this chapter, we have focused exclusively on AES encryption. There are good reasons for this. AES is the most popular symmetric cipher currently in use. It’s used in network communications as well as storing data on disk. And as we will see in Chapter 7, it is the basis for several advanced AEAD (authenticated encryption with associated data).
Camellia
ChaCha20
TripleDES
CAST5
SEED
Even though we are always encouraging you to use a well-tested, well-respected third-party library, be aware that libraries often include support for less desirable algorithms for legacy support. In this list of algorithms supported by cryptography, a few ciphers are already known to be insecure and are being phased out. For example, while DES is not included in the cryptography library’s ciphers (GOOD! DES is VERY BAD!), the module does include 3DES (TripleDES). While 3DES is not as broken as DES, it should be retired ASAP. CAST5 fits in this same category.
Another cipher supported by cryptography is Blowfish. This algorithm is also not recommended for use, and its stronger successor, Twofish, is not available in the current cryptography implementation.
finalize()
This chapter covered a lot of material, and we barely scratched the surface. Perhaps the most important principle that you can take away from this chapter is that cryptography is usually far more complicated than perhaps it first seems. The different modes of operation we reviewed have different strengths and weaknesses, some of which we explored by example. We found that even how we approach the APIs to cryptographic operations can have a significant impact on security.
Hopefully, this lesson reinforced the YANAC principle (You Are Not A Cryptographer... yet!). Please remember that these exercises are introductory and educational. Please do not go copying this code into production and don’t use the introductory knowledge you have gained to write security-critical operations. Do you really want to risk people’s personal information, financial information, or other sensitive data on your newly developed skills?
At the same time, after just one chapter on encryption, you have a broader view of what that word even means. The next time you hear “protected by AES 128-bit encryption,” you might wonder whether they’re using CTR, CBC, or (heaven forbid!) ECB mode. You might also wonder if they are using their encryption correctly because you already have experienced some of the ways (often unexpected) that symmetric encryption can be broken.
Yes, you’ve taken your first steps into a cryptography world. Are you ready to take a few more? Then let’s talk about asymmetric encryption!