Asymmetric Encryption: Public/Private Keys

Asymmetric encryption is one of the most important advances in cryptographic security ever made. It underpins all of the security on the Web, in your Wi-Fi connections, and in secure email and other communication of all kinds. It is ubiquitous, but it is also subtle and easy to implement or use incorrectly, and a lack of correctness means a sometimes drastic reduction in security.

Perhaps you’ve heard of “public keys,” “public key infrastructure,” and/or “public key encryption.” There are actually multiple operations within asymmetric cryptography and a number of different algorithms. Within this chapter, we are going to focus exclusively on asymmetric encryption and specifically using an algorithm known as RSA. We are going to leave other asymmetric operations, such as signatures and key exchange, for later chapters.

RSA encryption is, in fact, almost completely obsolete. Why study it? Because RSA is one of the classic asymmetric algorithms and does a good job, in our opinion anyway, of introducing some core concepts that will be helpful when learning about more modern approaches.

A Tale of Two Keys

The East Antarctica Truth-Spying Agency (EATSA) has a new mission for Alice and Bob. Bob is to remain behind in East Antarctica (EA) as Alice’s handler and Alice is to get an undercover position in the West Antarctica Government Greasy Spoon (WAGGS). Alice will report back to Bob what the West Antarctica (WA) politicians are eating. EATSA plans to blackmail these politicians over how much hot food they are eating, while their constituents are stuck eating frozen dinners.

EATSA, however, is concerned about compromised communications. If Alice is captured with a symmetric key, the West Antarctica Central Knights Office (WACKO) will be able to use it to decrypt any messages they have intercepted from her to EATSA. That would ruin the entire plan!

EATSA decides to implement a new technology they’ve been hearing about: asymmetric encryption. Their collective minds are blown when they find out that there are encryption schemes with two keys: what is encrypted with one key can only be decrypted by the other!

Using this new technology, Bob can send Alice into the field with just one of the two keys (the “public” key). Alice will be able to encrypt messages back to Bob that not even she can decrypt! Only Bob, safe within EA territory and in possession of the corresponding “private” key, can decrypt the messages. That sounds perfect—if her key is compromised, it will at least not allow her captors to decrypt what she has written, which is strictly better than before.¹ What could go wrong?

To finish cooking up this scheme, EATSA chooses to use RSA encryption, an asymmetric algorithm that uses very large integers as both keys and messages, and the “modular exponentiation” as the primary mathematical operator for encryption and decryption. The algorithm is simple to understand and, with modern programming languages, relatively easy to implement. It looks in all ways to be the perfect recipe for culinary subterfuge.

Getting Keyed Up

Generating keys in RSA is a little bit tricky, as it requires finding two very large integers with a high likelihood of being co-prime. That looked like a lot of math to the agents of EATSA, so they opted to just use existing libraries to do that part. Listing 4-1 shows the package they pulled into Python 3 and the code they wrote that makes use of it.

1 from cryptography.hazmat.backends import default_backend

2 from cryptography.hazmat.primitives.asymmetric import rsa

3 from cryptography.hazmat.primitives import serialization

5 # Generate a private key.

6 private_key = rsa.generate_private_key(

7 public_exponent=65537,

8 key_size=2048,

9 backend=default_backend()

10 )

12 # Extract the public key from the private key.

13 public_key = private_key.public_key()

15 # Convert the private key into bytes. We won't encrypt it this time.

16 private_key_bytes = private_key.private_bytes(

17 encoding=serialization.Encoding.PEM,

18 format=serialization.PrivateFormat.TraditionalOpenSSL,

19 encryption_algorithm=serialization.NoEncryption()

20 )

22 # Convert the public key into bytes.

23 public_key_bytes = public_key.public_bytes(

24 encoding=serialization.Encoding.PEM,

25 format=serialization.PublicFormat.SubjectPublicKeyInfo

26 )

28 # Convert the private key bytes back to a key.

29 # Because there is no encryption of the key, there is no password.

30 private_key = serialization.load_pem_private_key(

31 private_key_bytes,

32 backend=default_backend(),

33 password=None)

35 public_key = serialization.load_pem_public_key(

36 public_key_bytes,

37 backend=default_backend())

Listing 4-1

RSA Key Generation

That’s not too bad, once you know how it’s used. This pattern is the same for any private/public key generation, so even though there are a few constants in there with long names, it definitely seemed like the library was making this easier for EATSA.

See how everything hinges on the private key in RSA? The public key is derived from it. While either key can be used to encrypt (and the other can be used to decrypt), the private key is special because of this property. RSA keys are not only asymmetric because one encrypts and the other decrypts, they are also asymmetric because you can derive an RSA public key from the private key, but not the other way around.

The private_bytes and public_bytes methods convert large integer keys into bytes that are in a standard network- and disk-ready encoding called a PEM. The corresponding serialization “load” methods can be used to decode these after reading those bytes from disk so that they look like keys again to the encryption and decryption algorithms.

It is possible (and a very good idea) to encrypt the private key itself, but we opted not to do that here, which is why no password is used.

RSA Done Wrong: Part One

Alice and Bob are going to help us learn about RSA largely by exploring all the ways to use RSA incorrectly.

The actual encryption and decryption parts looked pretty simple to EATSA, and every library they looked at seemed to have a lot of unnecessary extra stuff making it harder to understand and even (gasp) slowing it down. Not having been taught the YANAC principle, they decided to implement encryption and decryption on their own. Rather than using the third-party library as written, they opted to omit padding. This results in a very “raw” or basic form of RSA that will be useful to us in learning about internals even though the results will be very broken.

Warning: Do Not Roll Your Own Encryption

Once again, implementing your own RSA encryption/decryption, rather than using a library, is not a good idea at all. Using RSA without padding is especially unsafe and insecure for numerous reasons, just a few of which we’ll explore in this section. Although we will be writing our own RSA functions here for educational purposes, do not under any circumstances use this code for real communication.

Here is the math for encryption, where c is the ciphertext, m is the message, and the remaining parameters form the public and private keys, to be explained later:

$c\equiv {m}^e\kern1em \left(\operatorname{mod}\ n\right)$

(4.1)

Similarly, here it is for decryption:

$m\equiv {c}^d\kern1em \left(\operatorname{mod}\ n\right)$

(4.2)

That doesn’t seem too bad, right? Modular exponentiation is a pretty standard operation in large integer math libraries,² so there really isn’t much to this.

If you’re new to this, don’t be thrown off by ≡. For simplicity, you can usually just think about it as an equal sign.

The operations in (4.1) and (4.2) can be written concisely in Python using gmpy2 , a large number math library. The powmod function performs the necessary modular exponentiation operation, as shown in Listing 4-2.

1 #### DANGER ####

2 # The following RSA encryption and decryption is

3 # completely unsafe and terribly broken. DO NOT USE

4 # for anything other than the practice exercise

5 ################

6 def simple_rsa_encrypt(m, publickey):

7 # Public_numbers returns a data structure with the 'e' and 'n' parameters.

8 numbers = publickey.public_numbers()

10 # Encryption is(m^e) % n.

11 return gmpy2.powmod(m, numbers.e, numbers.n)

13 def simple_rsa_decrypt(c, privatekey):

14 # Private_numbers returns a data structure with the 'd' and 'n' parameters.

15 numbers = privatekey.private_numbers()

17 # Decryption is(c^d) % n.

18 return gmpy2.powmod(c, numbers.d, numbers.public_numbers.n)

19 #### DANGER ####

Listing 4-2

GMPY2

As mentioned before, and perhaps more obvious now, RSA operates on integers, not message bytes. How do we convert messages into integers? Python makes this convenient because its int type has to_bytes and from_bytes methods. Let’s make them a little nicer to use in Listing 4-3.

1 def int_to_bytes(i):

2 # i might be a gmpy2 big integer; convert back to a Python int

3 i = int(i)

4 return i.to_bytes((i.bit_length()+7)//8, byteorder="big")

6 def bytes_to_int(b):

7 return int.from_bytes(b, byteorder="big")

Listing 4-3

Integer/Byte Conversion

Important

Because RSA works on integers, not bytes, the default implementation loses leading zeros. As far as integers are concerned, 01 and 1 are the same number. If your byte sequence begins with any number of zeros, they will not survive encryption/decryption. For our example, we are sending text, so it won’t ever be a problem. For binary data transmissions, however, it could be. This problem will be solved with padding.

EATSA now has all of the necessary pieces to create a simple RSA encryption/decryption application. Before looking at their code in Listing 4-4, try creating your own version.

1 # FOR TRAINING USE ONLY! DO NOT USE THIS FOR REAL CRYPTOGRAPHY

3 import gmpy2, os, binascii

4 from cryptography.hazmat.backends import default_backend

5 from cryptography.hazmat.primitives.asymmetric import rsa

6 from cryptography.hazmat.primitives import serialization

8 #### DANGER ####

9 # The following RSA encryption and decryption is

10 # completely unsafe and terribly broken. DO NOT USE

11 # for anything other than the practice exercise

12 ################

13 def simple_rsa_encrypt(m, publickey):

14 numbers = publickey.public_numbers()

15 return gmpy2.powmod(m, numbers.e, numbers.n)

17 def simple_rsa_decrypt(c, privatekey):

18 numbers = privatekey.private_numbers()

19 return gmpy2.powmod(c, numbers.d, numbers.public_numbers.n)

20 #### DANGER ####

22 def int_to_bytes(i):

23 # i might be a gmpy2 big integer; convert back to a Python int

24 i = int(i)

25 return i.to_bytes((i.bit_length()+7)//8, byteorder="big")

27 def bytes_to_int(b):

28 return int.from_bytes(b, byteorder="big")

30 def main():

31 public_key_file = None

32 private_key_file = None

33 public_key = None

34 private_key = None

35 while True:

36 print("Simple RSA Crypto")

37 print("--------------------")

38 print("\tprviate key file: {}".format(private_key_file))

39 print("\tpublic key file: {}".format(public_key_file))

40 print("\t1. Encrypt Message.")

41 print("\t2. Decrypt Message.")

42 print("\t3. Load public key file.")

43 print("\t4. Load private key file.")

44 print("\t5. Create and load new public and private key files.")

45 print("\t6. Quit.\n")

46 choice = input(" >> ")

47 if choice == '1':

48 if not public_key:

49 print("\nNo public key loaded\n")

50 else:

51 message = input("\nPlaintext: ").encode()

52 message_as_int = bytes_to_int(message)

53 cipher_as_int = simple_rsa_encrypt(message_as_int, public_key)

54 cipher = int_to_bytes(cipher_as_int)

55 print("\nCiphertext (hexlified): {}\n".format(binascii.hexlify(cipher)))

56 elif choice == '2':

57 if not private_key:

58 print("\nNo private key loaded\n")

59 else:

60 cipher_hex = input("\nCiphertext (hexlified): ").encode()

61 cipher = binascii.unhexlify(cipher_hex)

62 cipher_as_int = bytes_to_int(cipher)

63 message_as_int = simple_rsa_decrypt(cipher_as_int, private_key)

64 message = int_to_bytes(message_as_int)

65 print("\nPlaintext: {}\n".format(message))

66 elif choice == '3':

67 public_key_file_temp = input("\nEnter public key file: ")

68 if not os.path.exists(public_key_file_temp):

69 print("File {} does not exist.")

70 else:

71 with open(public_key_file_temp, "rb") as public_key_file_object:

72 public_key = serialization.load_pem_public_key(

73 public_key_file_object.read(),

74 backend=default_backend())

75 public_key_file = public_key_file_temp

76 print("\nPublic Key file loaded.\n")

78 # unload private key if any

79 private_key_file = None

80 private_key = None

81 elif choice == '4':

82 private_key_file_temp = input("\nEnter private key file: ")

83 if not os.path.exists(private_key_file_temp):

84 print("File {} does not exist.")

85 else:

86 with open(private_key_file_temp, "rb") as private_key_file_object:

87 private_key = serialization.load_pem_private_key(

88 private_key_file_object.read(),

89 backend = default_backend(),

90 password = None)

91 private_key_file = private_key_file_temp

92 print("\nPrivate Key file loaded.\n")

94 # load public key for private key

95 # (unload previous public key if any)

96 public_key = private_key.public_key()

97 public_key_file = None

98 elif choice == '5':

99 private_key_file_temp = input("\nEnter a file name for new private key: ")

100 public_key_file_temp = input("\nEnter a file name for a new public key: ")

101 if os.path.exists(private_key_file_temp) or os.path.exists(public_key_file_temp):

102 print("File already exists.")

103 else:

104 with open(private_key_file_temp, "wb+") as private_key_file_obj:

105 with open(public_key_file_temp, "wb+") as public_key_file_obj:

106

107 private_key = rsa.generate_private_key(

108 public_exponent =65537,

109 key_size =2048,

110 backend = default_backend()

111 )

112 public_key = private_key.public_key()

113

114 private_key_bytes = private_key.private_bytes(

115 encoding=serialization.Encoding.PEM,

116 format=serialization.PrivateFormat.TraditionalOpenSSL,

117 encryption_algorithm=serialization.NoEncryption()

118 )

119 private_key_file_obj.write(private_key_bytes)

120 public_key_bytes = public_key.public_bytes(

121 encoding=serialization.Encoding.PEM,

122 format=serialization.PublicFormat.SubjectPublicKeyInfo

123 )

124 public_key_file_obj.write(public_key_bytes)

125

126 public_key_file = None

127 private_key_file = private_key_file_temp

128 elif choice == '6':

129 print("\n\nTerminating. This program will self destruct in 5 seconds.\n")

130 break

131 else:

132 print("\n\nUnknown option {}.\n".format(choice))

133

134 if __name__ == '__main__':

135 main()

Listing 4-4

RSA Done Simply

Take a few minutes to try this exercise on your own before we walk through it together. Note, by the way, that because a public key can be derived from a private key, loading the private key also loads the public key.

When you are ready, continue reading! You may want to refer back to Listing 4-4 from time to time. Many of our subsequent listings will reuse these imports and function definitions. To save space, we will generally not reprint them so this listing is also useful as a template.

Exercise 4.1. Simple RSA Encryption

Using the preceding application, set up communication from Alice to Bob and then send a few encrypted messages from Alice to Bob for decryption.

Stuffing the Outbox

Once EATSA has built the RSA encryption application, they hand it off to Alice and Bob and order them to begin the mission. Alice will infiltrate WAGGS and send updates to Bob. What do Alice and Bob need to do first?

What’s amazing about public/private key pairs is that they don’t have to agree on much of anything before they split up in order for Alice to send secure messages to Bob!³ As long as Alice knows where to look, Bob can publish a public key to her anywhere. He could send it in a newspaper, recite it to her over the phone, or publicize it on a Goodyear blimp flying around West Antarctica. The key is public. It does not matter if the West Antarctica Counter Intelligence sees it: they won’t be able to decrypt Alice’s messages.

Right?

Alice departs from EATSA headquarters, crosses the border, and makes her way to West Antarctica City where she infiltrates WAGGS. While she’s thus engaged in her covert culinary caper, Bob generates a public/private key pair. He hangs onto the private key and publishes the public key for Alice to see.

Let’s follow along. Start up an instance of the application that represents Bob’s version and select option 5, which generates new paired keys and saves them to disk. Once that’s done, you will have two files you can inspect in an editor.

Take a look at the public key file (you chose the name for it when prompted). Its contents should look something like this:

-----BEGIN PUBLIC KEY-----

MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEAuGFr+NV3cMu2pdl+i52J

XkYwwSHgZvA0FyIPsZ/rp6Ts5iBTkpymt7cf+cQCQro4FSw+udVt4A8wvZcppnBZ

h+17ZZ6ZZfj0LCr/3sJw8QfZwuaX5TZxFbJDxWWwsR4jLHsiGsPNf7nzExn7yCSQ

sXLNqc+mLKP3Ud9ta14bTQ59dZIKKDHVGlQ1iLlhjcE1dhOAjWlsdCVfE+L/bSQk

Ld9dWKCM57y5tiMsoqnVjl28XcsSuiOd4QPGITprsX0jb7/p/rzXc9OQHHGyAQzs

WTAbZNaQxf9AY1AhE4wgMVwhnrxJA2g+DpY1yXUapOIH/hpD0sMH56IGcMx9oV/y

SwIDAQAB

-----END PUBLIC KEY-----

That’s a PEM-formatted public key. Congratulations! Bob can take this key and publish it to a West Antarctica newspaper in the classifieds.

Meanwhile, Alice has been carefully observing what the West Antarctica politicians like to eat. How un-Antarctican! she thinks to herself as she watches them eat hot dogs and hot chocolate. Then, glancing back to the newspaper in her hands, she finds the classified ad she’s been looking for! The public key has arrived! She copies it down carefully into a file and now has the ability to encrypt messages for Bob’s eyes only.

Following along, let’s copy the public key we just generated into a new file. This represents the file that Alice creates after copying the text out of the classified ads. Now launch a new instance of the application that represents Alice’s copy of the program. Choose option 3 to load her public key.

Alice needs to send a message back to Bob. That’s option 1 in our program. Run it, select option 1, and enter the text “hot dogs” into the plaintext field. Out pops the encrypted message.⁴ If you used the preceding public key, you would get the following output:

Plaintext: hot dogs

Ciphertext (hexlified): b'56d5586cab1764fae575bc5815115f1c5d759

daddccbd6c9cb4a077026e2616dfca756ffa7733538e66997f06ebbbb853028

3926383a6bb80b7145990a29236d042048eed8eb7607bd35fcafe3dadd5d60a

1f8694192bddedac5728061234ffbb7a407155844a7e79b3dbc9704df0de818

d24acad32ccd6d2afe2d0734199c76e5c5c770fa8c3c208eceae00554aa2f29

9a8510121d388d85f35fa49c08f3e9d7540f22fe5eb4ea15da5f387dbdd0e00

6710aa9031b885094773ef3329cde91dbede53ed77b96483d34daa4fedbf5bc

d95e95b6b482a7decbf47fe2df0e309d706ab9c73ce73a2bdef33b786dd12e9

8a9ce34bbc1847f36e13ae9eea4007b616'

Let’s do it again, but this time for “hot chocolate.” If you do so using the preceding public key we showed you, you would get this output (but go ahead and use your own generated public key):

Plaintext: hot chocolate

Ciphertext (hexlified): b'4d1e544e71c4cb15636ef4b0d629294538a05

979db762952cc5f0fc494f71535dff326dbb8543d0f2ace51a2279f65c2a76b

2a5ca5a3ee151e65e516afcb1d4da9ca9871dc7ce1dd4361a3b49def05c5089

99f5fab81b869b251ba8694fb171ab56ca1cde7cef0ac3934da4c28f7bfbb65

b03afa9cff30db974f0bd4fb8dee7fac75c99cd4def94ca8de83d46fffa092a

90642c9cfbfbf07c371f5aa3a62dc997d20e9959fcbec7dd0b434709b679619

ea195008a9a12eaa7462ffdbe8e6f765dd86b21f0f1d9b8b2b523ca7f11785e

fc6da84ec717bd1f0e2191e5a3bef74e489b5e396c49bd8f222ccd89984dbec

8b5e4cbb23ba739637d3307bca4e9f57e7'

Again, Alice cannot decrypt these messages, even though she encrypted them herself: she doesn’t have the private key. At least, that’s what the theory tells them.

Confident in her edible espionage, she takes these messages and sends them to Bob via an insecure carrier penguin [15]. Bob receives the message and reloads his application. First, he loads the private key file using option 4 and then chooses option 2 to attempt a decryption. Sure enough, when he copies in the message for Alice, it decrypts correctly:

Ciphertext (hexlified): 56 d5586cab1764fae575bc5815115f1c5d759da

ddccbd6c9cb4a077026e2616dfca756ffa7733538e66997f06ebbbb85302839

26383a6bb80b7145990a29236d042048eed8eb760735fcafe3dadd5d60a1f86

94192bddedac5728061234ffbb7a407155844a7e79b3dbc9704df0de818d24a

cad32ccd6d2afe2d0734199c76e5c5c770fa8c3c208eceae00554aa2f299a85

10121d388d85f35fa49c08f3e9d7540f22fe5eb4ea15da5f387dbdd0e006710

aa9031b885094773ef3329cde91dbede53ed77b96483d34daa4fedbf5bcd95e

95b6b482a7decbf47fe2df0e309d706ab9c73ce73a2bdef33b786dd12e98a9c

e34bbc1847f36e13ae9eea4007b616

Plaintext: b'hot dogs'

“Hot dogs!” Bob exclaims. “Disgraceful!”

Ciphertext (hexlified): 4d1e544e71c4cb15636ef4b0d629294538a05979

db762952cc5f0fc494f71535dff326dbb8543d0f2ace51a2279f65c2a76b2a5c

a5a3ee151e65e516afcb1d4da9ca9871dc7ce1dd4361a3b49def05c508999f5f

ab81b869b251ba8694fb171ab56ca1cde7cef0ac3934da4c28f7bfbb65b03afa

9cff30db974f0bd4fb8dee7fac75c99cd4def94ca8de83d46fffa092a90642c9

cfbfbf07c371f5aa3a62dc997d20e9959fcbec7dd0b434709b679619ea195008

a9a12eaa7462ffdbe8e6f765dd86b21f0f1d9b8b2b523ca7f11785efc6da84ec

717bd1f0e2191e5a3bef74e489b5e396c49bd8f222ccd89984dbec8b5e4cbb23

ba739637d3307bca4e9f57e7

Plaintext: b'hot chocolate'

Bob’s eyes narrow. “Hot chocolate?! Have they no shame?!”

So far, so good! Alice’s messages got to Bob. They were intercepted by agent Eve of WACKO, but she shouldn’t be able to read them, even though she also has the public key. If Alice can’t read her own messages, why should Eve be able to?

What Alice and Bob don’t know is that Eve is about to wreak all kinds of havoc. In the rest of this chapter, we’ll be walking through some of the ways that RSA can be compromised and how to do it right. But first, exercises!

Exercise 4.2. Who Goes There? Bob? Is That You?

Assume the role of Eve and imagine that you know everything about Alice’s and Bob’s operation except the private key. That is, suppose you know about the classified ads, the carrier penguins, and even the encryption program.⁵ Their scheme is strengthened by using asymmetric encryption, but is still vulnerable to an MITM (man-in-the-middle) attack. How can Eve position herself such that she can trick Alice into sending messages that Eve can decrypt, and Bob into receiving only false messages from Eve instead of Alice?

Exercise 4.3. What’s The Answer To Life, The Universe, And Everything?

We have already talked about chosen plaintext attacks in the previous chapter. The same attack can be used here. Again assume the role of Eve, the WACKO agent. You’ve intercepted Bob’s public key in the newspaper, and you have access to the RSA encryption program. If you suspect you know what Alice is sending in her encrypted messages, explain or demonstrate how you would verify your guesses.

What Makes Asymmetric Encryption Different?

As you learned already in this section, RSA is an example of asymmetric encryption. If you haven’t heard of asymmetric encryption before now, hopefully the exercises you just walked through have exposed you to the key concepts. Now let’s make a few things explicit.

In symmetric encryption, there is a single, shared key that works to both encrypt and decrypt the message. This means that anyone with the power to create an encrypted message has the same ability to decrypt the same message. It is impossible to give somebody the power to decrypt a symmetrically encrypted message without also giving them the ability to encrypt the same kind of messages and vice versa.

In asymmetric cryptography, there is always a private key that must never be disclosed and a public key that can be disclosed widely. Exactly what can be done with the key pair depends on the algorithm. In this chapter we have been focusing on RSA encryption. We’ll review RSA’s operations in this section as a concrete example but keep in mind that they may not apply to other asymmetric algorithms and operations.

Specifically, RSA supports an asymmetric encryption scheme in which you can use one key to encrypt the message and a different key to decrypt a message. Typically, either key can act in either role: a private key can encrypt messages that can be decrypted by the public key and vice versa. With RSA, of course, one key is clearly the private key because the public key can be derived from the private key, but not the other way around. It is impossible to have an RSA private key and not also have the matching public key. Thus, one key is unambiguously designated as “private” and the other is “public.”

The possessor of a properly protected RSA private key and an adequately robust protocol can use asymmetric encryption for two purposes:

1.
Cryptographic dropbox : Anyone with the public key can encrypt a message and send it to the owner of the private key. Only someone with the private key can decrypt the message.
2.
Signatures : Anyone with the public key can decrypt a message encrypted by the private key. This obviously is not helpful for confidentiality (anyone can decrypt the message) but it helps to prove the identity of the sender, or at least that the sender is in possession of the private key; they wouldn’t be able to encrypt a public-key-decryptable message otherwise. This is an example of a cryptographic signatures, which we will talk about later.

Note: RSA Encrypts Small Things

The cryptographic dropbox operation we are learning about right now is almost never used to send complete messages in this way. The most common way RSA encryption was used (again, it is being phased out) was to encrypt a symmetric key for transport from one party to another. This is another concept we’ll save for a later chapter.

What is really fantastic about the asymmetric nature of RSA encryption is that the two parties do not need to have met each other to begin exchanging messages. In our example, Alice and Bob did not need to create any shared keys together. Alice did not even need to meet or know Bob. So long as Alice had Bob’s public key, she can encrypt messages that only Bob can read.

Unfortunately, the ability to encrypt something for only one person is not the only important thing in real life. As demonstrated in the exercises, the advantage of asymmetric encryption is also its weakness. The ability to communicate without any previous interactions also means that, absent additional information, there is no way to know that you are communicating with the right person.

If you worked through the earlier exercises, you will have also learned that it is quite simple for WACKO to both read and alter the communications between Alice and Bob by deceiving both parties by intercepting messages and keys.

1.
They can deceive Alice by intercepting and modifying the public key published in the newspaper. By inserting their own public key—which Alice now wrongly assumes is Bob’s—they can read all messages sent by Alice intended for Bob. Alice, without additional information, cannot know that the public key has been compromised.
2.
They can then deceive Bob by preventing Alice’s incorrectly encrypted messages from reaching him and sending him false messages encrypted under the correct public key, which they intercepted. Bob, without additional information, has no way of knowing who is sending the messages.

This is a critical difference between symmetric keys and asymmetric keys. In fact, some cryptographers distinguish between a “secret” symmetric key and a “private” asymmetric key. Two people can share a secret, but only one person knows their own private key. What this means in practice is that a symmetric key, provided that it remains secret to both parties, can be used to establish that you are talking to the right person (i.e., the person you created the shared secret key with) while asymmetric keys cannot.⁶

Let’s sidestep that problem for now and save it for later, since there is indeed a solution to it that is discussed in the context of certificates.

Pass the Padding

Recall from earlier that the EATSA chose to implement RSA without any padding. They really shouldn’t have done that; it’s a pretty serious mistake. In fact, it’s so serious that the cryptography module does not even allow you to encrypt with RSA without padding!

What, then, is padding, and why is padding such a big deal?

The best way to explain this is to demonstrate how to read messages encrypted with the public key even if you don’t have the private key, so long as those messages are not padded. Another great exercise is to search the Internet for RSA padding attacks. There are many problems with using unpadded plaintext.

Deterministic Outputs

Let’s start with the most basic problem. RSA by itself is a deterministic algorithm. That means that, given the same key and message, you will always get the same ciphertext, byte for byte. Recall that we had the same problem with symmetric key ciphers like AES. It was essential to use the initialization vector (IV) to prevent deterministic outputs. Do you remember why deterministic outputs are so bad?

The problem with deterministic outputs is that they enable passive eavesdroppers, such as Eve, to do some cryptographic reverse engineering. Because the encryption is deterministic, if Eve knows that m encrypts to c then any time Eve sees c she knows what the plaintext is.

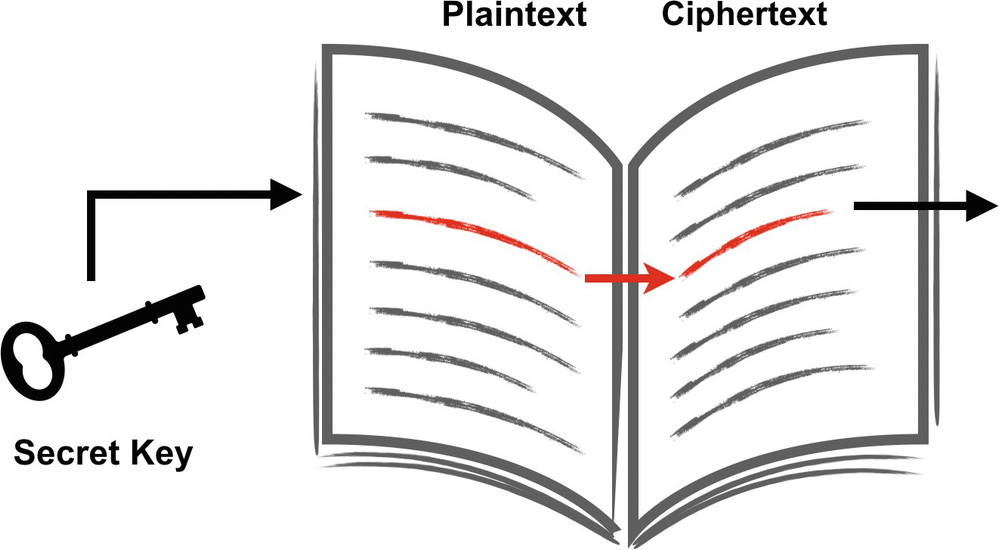
../images/472260_1_En_4_Chapter/472260_1_En_4_Fig1_HTML.png — Figure 4-1
If RSA’s outputs are deterministic, an adversary that discovers the mapping between a plaintext and the corresponding ciphertext can record it into a lookup table for later use. Does this figure look familiar?

Eve has both the public key and the algorithm (you can never assume that a cryptographic algorithm is secret). She can encrypt any number of potential messages and store a lookup table of pre-encrypted values. Does Figure 4-1 look familiar? We showed this same image in Chapter 3 to talk about ECB mode for symmetric ciphers and the problems with it.

But a deterministic asymmetric encryption would be worse. Unlike symmetric encryption we have to assume that the adversary has the (public) key. In our hypothetical Antarctican conflict, Eve could discover, or simply guess, that Alice is sending messages based on her surveillance of the cafeteria. If she tries encrypting a few hundred words by making a list of things found within the room (e.g., the names of the politicians eating in the cafeteria, topics of conversation, and the food being eaten), as soon as she encrypted “hot dogs” or “hot chocolate,” the encrypted values would match up perfectly with what is intercepted in the message back to Bob. For short messages such as these, especially if EA Intelligence always writes words in lowercase, there are less than 300 million messages to try that are 8 characters long. It’s not too much trouble to create a table of that many messages to their ciphertext. Using this lookup table, Eve could identify “hot dogs” relatively quickly.

Even if Eve cannot guess the message, there is still all kinds of analysis that can be done. Suppose that Alice continues to send the same message day after day. While Eve may not be able to decrypt the message, she would still be able to confidently state that it was the same message. We have considered numerous examples wherein this kind of “information leak” is exploited in previous chapters.

Exercise 4.4. Brute-Force RSA

Write a program that uses brute force to decrypt an RSA-encrypted word that is all lowercase (no spaces) and less than four characters. The program should take a public key and the RSA-encrypted ciphertext as the inputs. Use the RSA encryption program to generate a few words of four or fewer letters and break these codes with your brute-force program.

Exercise 4.5. Waiting Is The Hardest Part

Modify the brute-force program to try all possible words of five or fewer letters. Measure the time it takes (worst cast) to brute force a four-letter word vs. a five-letter word. About how many times longer does it take and why? How long would it take to try all possible six-letter words?

Exercise 4.6. Dictionary Attacks

It should be pretty clear that it will take longer than your probable attention span to try all possible lowercase ASCII words of length much greater than four or five. But we already saw this same problem in previous chapters. Let’s try the same solutions. Modify your brute-force program to take a dictionary as input for trying arbitrary English words.

Chosen Ciphertext Attack

RSA without padding is also vulnerable to something called a “chosen ciphertext attack.”⁷ This type of attack works when you can get the victim to decrypt some ciphertexts of your choosing on your behalf. That may sound counter-intuitive. Why would anyone decrypt anything for you? For example, why would Bob decrypt anything for Eve?

Remember that a lot of computer security is all about psychology, trickery, and human thinking [1, Chap. 2]. What is Bob looking for? Bob is assuming that he is decrypting human-readable messages from Alice. What if he got a message that was not human readable? Suppose, for example, that upon decrypting a message (supposedly from Alice) he got the following output:

b'\xe8\xca\xe6\xe8'

It’s entirely possible that this is just assumed to be due to a transmission error. Those things happen in real life all the time. It could be bit error, or a carrier penguin might have smudged the ink. Bob probably sees a lot of messages that do not decrypt correctly.

What does Bob do? If he does not have very good security controls in place, he might just throw it away. But if Alice can infiltrate the enemy, it can work the other way as well. Which do you think is easier for Eve to get into her hands? Top-secret messages that are being sent up the chain of command for analysis, or “incorrect” messages that get thrown away in the trash? If Eve has a covert agent of her own on the janitorial staff, it might be very possible to get discarded paper or inadequately destroyed data.

Let’s assume this scenario then: Eve can send arbitrary ciphertext to Bob. For our purposes, Eve cannot see any of the human-readable messages but can recover the supposedly erroneous messages discarded by Bob because they seem to make no sense.

Unfortunately for Alice and Bob, Eve can use this trick to decrypt almost any message Alice sends back to her home base. The mathematics behind this trick are really cool and are used in multiple examples throughout the chapter. So let’s pause a minute to talk about homomorphisms in encryption.

The basic concept of an encryption homomorphism is that if you perform some kind of computation on the ciphertext, the result is reflected in the plaintext. Not all crypto systems have homomorphic properties, but RSA does to some extent. In RSA we will see that there are ways to do multiplication on the ciphertext that results in multiplications on the plaintext. There are other special homomorphic encryption technologies that exist and are being developed right now that enable third parties to provide services on data without being able to read it. You may have heard of some of these; if not, try searching for “homomorphic encryption” online. It’s pretty interesting stuff.

While RSA is not a homomorphic encryption scheme, this multiplication property is very interesting (and also powers a number of vulnerabilities). Do you remember from algebra class that (a^c)(b^c) = (ab^c)? The same is true for modular exponentiation as shown in the following equation:

${\left({m}_1\right)}^e{\left({m}_2\right)}^e\ \left(\operatorname{mod}\ n\right)={\left({m}_1{m}_2\right)}^e\ \left(\operatorname{mod}\ n\right)$

(4.3)

Does any part of this equation look familiar? Take a look back at (4.1). Do you see it now?

Any time we encrypt a value (m) in RSA, we end up with m^e mod n. On the left-hand side of the (4.3), we have two encryptions, one of m₁ and one of m₂, both using the same public exponent e and both modulo the same modulus n.

On the right-hand side, we have a single encryption of the value m₁ times m₂. What this equation tells us is that if you take each of these individually encrypted values and multiply them together (mod n), you get the encrypted result of the multiplication!

Restated another way, the product of two ciphertexts (encrypted under the same public key) decrypts to the product of the two plaintexts. Try to do the following exercise on your own before we walk through it.

Exercise 4.7. Homomorphic Property Of Unpadded RSA

Use (4.3) to multiply two RSA-encrypted numbers together and decrypt the result to verify the equation.

The code for this exercise is very simple, so definitely try it yourself first. When you’re ready, our solution is in Listing 4-5.

1 # FOR TRAINING USE ONLY! DO NOT USE THIS FOR REAL CRYPTOGRAPHY

3 import gmpy2, sys, binascii, string, time

4 from cryptography.hazmat.backends import default_backend

5 from cryptography.hazmat.primitives import serialization

6 from cryptography.hazmat.primitives.asymmetric import rsa

8 #### DANGER ####

9 # The following RSA encryption and decryption is

10 # completely unsafe and terribly broken. DO NOT USE

11 # for anything other than the practice exercise

12 ################

13 def simple_rsa_encrypt(m, publickey):

14 numbers = publickey.public_numbers()

15 return gmpy2.powmod(m, numbers.e, numbers.n)

17 def simple_rsa_decrypt(c, privatekey):

18 numbers = privatekey.private_numbers()

19 return gmpy2.powmod(c, numbers.d, numbers.public_numbers.n)

21 private_key = rsa.generate_private_key(

22 public_exponent=65537,

23 key_size=2048,

24 backend=default_backend()

25 )

26 public_key = private_key.public_key()

28 n = public_key.public_numbers().n

29 a = 5

30 b = 10

32 encrypted_a = simple_rsa_encrypt(a, public_key)

33 encrypted_b = simple_rsa_encrypt(b, public_key)

35 encrypted_product = (encrypted_a * encrypted_b) % n

37 product = simple_rsa_decrypt(encrypted_product, private_key)

38 print("{} x {} = {}".format(a,b, product))

Listing 4-5

Solution

If this kind of math doesn’t make a lot of sense, don’t worry too much about it at this point. Just try to grasp how it is used even if you aren’t fully sure how it works.

Returning to our current example, suppose that Eve has a ciphertext c obtained by the RSA public key encryption of m. Without the private key, Eve should not be able to decrypt it. And presumably Bob won’t decrypt it for her either. If he will decrypt a multiple of it, however, Eve can recover the original.

For our example, let’s choose our multiple to just be 2. Eve starts by encrypting 2 using (4.1) and the public key to get c_r.

For clarity, let’s call the original ciphertext c₀. If we multiply c₀ and c_r (modulo n), we’ll get a new ciphertext that we’ll call c₁.

${c}_1={c}_0{c}_r\kern0.125em \left(\operatorname{mod}n\right).$

From (4.3), this works out to be

$\begin{array}{l}{c}_1={c}_0{c}_r\kern0.125em \left(\operatorname{mod}n\right)\\ {}={m}^e{r}^e\kern0.125em \left(\operatorname{mod}\kern0.125em n\right)\\ {}={(mr)}^e\kern0.125em \left(\operatorname{mod}n\right).\end{array}$

So how does Eve use this? Suppose that Eve has intercepted one of Alice’s ciphertexts c. Eve takes her computed c_r (again, this is just the value of 2 encrypted under the public key) and then multiplies the two encrypted values together (modulo n). Eve sends this new ciphertext c₁ to Bob.

Bob receives c₁ and decrypts it to mr and converts the integers to bytes. He finds that it does not decrypt to anything legible and assumes that something was damaged in transport. Shrugging his shoulders, he crumples up the paper and throws it in the waste basket. Later that night, Eve’s agent goes through the trash and finds the crumpled up paper. Creating a quick copy, she sends it by secret carrier back to Eve.

Eve now has mr and needs to extract m. No problem. She chose r to be 2. In familiar arithmetic you would divide by r to extract m. But when doing this arithmetic with modulo operations, you have to use a different inverse operation: r−1 (mod n). Fortunately, there are libraries that compute these kinds of numbers for us, like gmpy2.

r_inv_modulo_n = gmpy2.powmod(r, -1, n)

Exercise 4.8. Eve’s Protege

Recreate Eve’s chosen ciphertext attack. Create a sample message in Python, as you have done previously, using the public key to encrypt it. Then, encrypt a value of r (such as 2). Multiply the two numeric versions of the ciphertext together and don’t forget to take the answer modulo n. Decrypt this new ciphertext and try to convert it to bytes. It shouldn’t be anything human readable. Take the numeric version of this decryption and multiply it by the inverse of r (mod n). You should be back to the original number. Convert it to bytes to see the original message.

Common Modulus Attack

Another problem for RSA without padding is the “common modulus” attack. Recall that the n parameter is the modulus and is included in both the public key and private key. For mathematical reasons beyond the scope of this book, if the same RSA message is encrypted by two different public keys with the same n modulus, the message can be decrypted without the private key.

In the chosen ciphertext example, we walked through the math in some detail both because it can be described relatively easily and because it is critical to multiple attacks. For this example, in the interests of simplicity and conserving space, we won’t get into the mathematical details. Instead, use the code in Listing 4-6 to test and explore the attack. If you’re interested in the details of the math, you can read “Common Modulus Attacks on Small Private Exponent RSA and Some Fast Variants (in Practice)” by Hinek and Lam.

1 # Partial Listing: Some Assembly Required

3 # Derived From: https://github.com/a0xnirudh/Exploits-and-Scripts/tree/master/RSA At tacks

4 def common_modulus_decrypt(c1, c2, key1, key2):

5 key1_numbers = key1.public_numbers()

6 key2_numbers = key2.public_numbers()

8 if key1_numbers.n != key2_numbers.n:

9 raise ValueError("Common modulus attack requires a common modulus")

10 n = key1_numbers.n

12 if key1_numbers.e == key2_numbers.e:

13 raise ValueError("Common modulus attack requires different public exponents")

15 e1, e2 = key1_numbers.e, key2_numbers.e

16 num1, num2 = min(e1, e2), max(e1, e2)

18 while num2 != 0:

19 num1, num2 = num2, num1 % num2

20 gcd = num1

22 a = gmpy2.invert(key1_numbers.e, key2_numbers.e)

23 b = float(gcd - (a*e1))/float(e2)

25 i = gmpy2.invert(c2, n)

26 mx = pow(c1, a, n)

27 my = pow(i, int(-b), n)

28 return mx * my % n

Listing 4-6

Common Modulus

Note that in order to test this attack, you will need two public keys with the same modulus (n value) and different public exponents (e values). Recall that e is recommended to always be 65537. But obviously you won’t use that for both keys in this example.

How does one create a public key? In all of our examples so far, we either generated new keys or loaded them from disk.

Recall that the n and e values define the public key. Everything else is just wrappers for convenience. The cryptography module provides an API for creating a key directly from these values. The RSA private key objects have a method called private_numbers, and the RSA public key objects have a method called public_numbers. These methods return data structures with data elements such as n, d, or e. These “numbers” objects can also be used to create the key objects.

In Listing 4-7, we generate a private key and then manually create another key with the same modulus and different public exponent.

1 # Partial Listing: Some Assembly Required

3 private_key1 = rsa.generate_private_key(

4 public_exponent =65537,

5 key_size=2048,

6 backend = default_backend()

7 )

8 public_key1 = private_key1.public_key()

10 n = public_key1.public_numbers().n

11 public_key2 = rsa.RSAPublicNumbers(3, n).public_key(default_backend())

Listing 4-7

Common Modulus Key Generation

Now you should have all the Python code you need to test out this attack.

At this point you might be asking yourself, “how practical is this attack?” In order to carry it out, you have to have the same message encrypted under two keys with the same modulus. Why would the same message ever be encrypted twice under two different keys and why would two different keys ever have the same modulus?

When dealing with cryptography, you should never rely on this kind of thinking. If there is a way for the cryptography to be exploited, the bad guy will figure out a way to exploit it. Let’s start by thinking about how to get the same message encrypted by two different keys.

One possibility is to convince Alice that a new public key has been created and that she needs to switch. If we control the new public key, we can give her a key with n and e values of our choosing.

But if we can control her key, why would we need to use the common modulus attack? Why not just give her a public key that we created and for which we have the paired private key?

It is true that a new private key/public key pair will allow Eve to decrypt any messages Alice sends in the future. But the common modulus attack will allow Eve to potentially determine some messages sent in the past . In our example with Alice infiltrating the cafeteria, the food service probably repeats with some regularity. In fact, as we discussed previously, Eve can already tell if the same message is being resent even if she cannot decrypt it. If Eve observes that the same messages are being sent over and over, the common modulus attack provides a much greater view into the history of what is sent as well as information about messages sent in the future.

Exercise 4.9. Common Modulus Attack

Test out the code in this section by creating a common modulus attack demo.

Exercise 4.10. Common Modulus Use Cases

Write out an additional scenario when the use of the common modulus attack might be useful to an attacker.

The Proof Is in the Padding

As we have just demonstrated, this very raw form of RSA, sometimes referred to as “textbook RSA,” is relatively easy to break. There are two critical problems. As we have already seen, one problem with textbook RSA is that the outputs are deterministic. This makes attacks like the common modulus attack, which require encrypting the same message twice, much easier.

Perhaps the bigger problem is how malleable the messages are. We talked about malleability with symmetric encryption in the previous chapter. With RSA we have similar problems, for example, multiplying the RSA ciphertext and getting a decryptable value.

There are also potential problems with trying to encrypt tiny messages, such as some of the small messages we have encrypted in our exercises. In addition to the brute-force methods in the exercises, there are ways to break smaller messages especially with smaller public exponents (e.g., e = 3).

To reduce or eliminate these problems, practical uses of RSA always utilizes padding with random elements. RSA padding is applied to the plaintext message before encryption by the raw RSA computations we have been working with. The padding ensures that messages are not too small and provide a certain amount of structure that reduces malleability. Also, the randomized elements operate not unlike an IV for symmetric encryption: good randomized padding ensures that each ciphertext produced by the RSA encryption operation, even for the same plaintext, is (with very high probability) unique.

RSA without padding is dangerous enough that the cryptography module does not even have a padding-free RSA operation. It should be absolutely clear to you that you must not use RSA for encryption without padding. While the cryptography module does not allow this, other libraries do. Significantly, this includes OpenSSL.

At the time of this writing, there are two padding schemes that are typically used. The older scheme is called PKCS #1 v1.5 and the other is OAEP, which stands for Optimal Asymmetric Encryption Padding. Either of these padding schemes can be used with the cryptography module as shown in Listing 4-8.

1 from cryptography.hazmat.backends import default_backend

2 from cryptography.hazmat.primitives.asymmetric import rsa

3 from cryptography.hazmat.primitives import serialization

4 from cryptography.hazmat.primitives import hashes

5 from cryptography.hazmat.primitives.asymmetric import padding

7 def main():

8 message = b'test'

10 private_key = rsa.generate_private_key(

11 public_exponent =65537,

12 key_size=2048,

13 backend=default_backend()

14 )

15 public_key = private_key.public_key()

17 ciphertext1 = public_key.encrypt(

18 message,

19 padding.OAEP(

20 mgf = padding.MGF1(algorithm = hashes.SHA256()),

21 algorithm = hashes.SHA256(),

22 label = None # rarely used. Just leave it 'None'

23 )

24 )

26 ###

27 # WARNING: PKCS #1 v1.5 is obsolete and has vulnerabilities

28 # DO NOT USE EXCEPT WITH LEGACY PROTOCOLS

29 ciphertext2 = public_key.encrypt(

30 message,

31 padding.PKCS1v15()

32 )

34 recovered1 = private_key.decrypt(

35 ciphertext1,

36 padding.OAEP(

37 mgf=padding.MGF1(algorithm=hashes.SHA256()),

38 algorithm=hashes.SHA256(),

39 label=None # rarely used.Just leave it 'None'

40 ))

42 recovered2 = private_key.decrypt(

43 ciphertext2,

44 padding.PKCS1v15()

45 )

47 print("Plaintext: {}".format(message))

48 print("Ciphertext with PKCS #1 v1.5 padding(hexlified): {}".format(ciphertext1.hex()))

49 print("Ciphertext with OAEP padding (hexlified): {}".format(ciphertext2.hex()))

50 print("Recovered 1: {}".format(recovered1))

51 print("Recovered 2: {}".format(recovered2))

53 if __name__=="__main__":

54 main()

Listing 4-8

RSA Padding

If you run this demonstration script repeatedly, you will observe that the ciphertext for both padding schemes causes the output to change every time. Consequently, adversaries like Eve cannot execute the chosen ciphertext attack nor the common modulus attack demonstrated earlier in this chapter. She is also unable to use RSA’s deterministic encryption to analyze message patterns, frequency, and so forth.

Padding also solves the problem of losing leading zeros during encryption. Padding ensures that the input is always a fixed size: the bit size of the modulus. So, for example, with padding, the input to RSA encryption with a modulus size of 2048 will always be 256 bytes (2048 bits). Because the size of the output is known, it also allows the plaintext to start with leading zeros. Regardless of whether the combined message starts with 0, the known size means that zeros can be affixed until the correct size is reached.

So everything is fine now, right? Alice and Bob will switch to using padding and Eve will be shut out of their communications?

First of all, please note that padding does not solve either of the man-in-the-middle or authentication problems. Eve can still intercept and change the public key, enabling complete decryption of Alice’s messages. Bob still cannot tell who is sending him messages. These are problems for another chapter.

Second, the astute reader probably noticed the warning in the source code listing. Just in case you glanced over it without paying attention, we will emphasize it again.

Warning: Say “No” to PKCS #1 v1.5

Do not use PKCS #1 v1.5 unless you must do so to be compatible with legacy protocols. It is obsolete and has vulnerabilities (including one we will test in the next section)! For encryption, always use OAEP when possible.

Before moving on from this section, two other comments are in order regarding the use of OAEP:

1.
You may have noticed the “label” parameter to OAEP. This is rarely used and can typically be left as None. Using a label does not increase security, so ignore it for now.
2.
OAEP requires the use of a hashing algorithm. In the example we used SHA-256. Why not SHA-1? Is this related to known weaknesses in SHA-1? No. Actually, there are no known attacks against OAEP that depend on SHA-1’s weaknesses. Because SHA-1 is considered obsolete, it is best to not use it when writing your own code, but if you have to use OAEP with SHA-1 for compatibility reasons or to maintain someone else’s code, it is not known to be less secure than SHA-256 as of the time of this writing.

Exercise 4.11. Getting An Upgrade

Help Alice and Bob out. Rewrite the RSA encryption/decryption program to use the cryptography module instead of gmpy2 operations.

Exploiting RSA Encryption with PKCS #1 v1.5 Padding

This section is going to be exciting and fun! Eve is not a cryptographer and you—because you are reading this book—are probably not a master cryptographer either. However, you and Eve are going to implement an attack designed by a brilliant cryptographer and use it to break Alice and Bob’s cipher.

This attack is not only fun, but it is very real. Not only has it been a real attack in the past, but it even continues to be used today against poorly configured TLS servers. It’s both historical and contemporary at the same time.

The paper in question is “Chosen Ciphertext Attacks Against Protocols Based on the RSA Encryption Standard PKCS #1” by Daniel Bleichenbacher [2]. You can find this paper online, and some readers may be interested in the mathematics behind the attack. In the sections that follow, we are going to walk through this paper creating an implementation of the attack. At the same time, we will try to give some intuition behind certain key concepts. If you find the in-depth details frustrating or uninteresting, you should be able to ignore most of the explanation and just put together a working RSA cracker from the source code listings. We won’t be offended.

There are going to be a lot of code snippets for this example. You should start with Listing 4-9 that initializes a few imports. Don’t forget about the dependencies on other functions we’ve already seen in this chapter. As we work through new snippets, add them to this skeleton.

1 from cryptography.hazmat.primitives.asymmetric import rsa, padding

2 from cryptography.hazmat.primitives import serialization

3 from cryptography.hazmat.primitives import hashes

4 from cryptography.hazmat.backends import default_backend

6 import gmpy2

7 from collections import namedtuple

9 Interval = namedtuple('Interval', ['a','b'])

10 # Imports and dependencies for RSA Oracle Attack

11 # Dependencies: simple_rsa_encrypt(), simple_rsa_decypt()

12 # bytes_to_int()

Listing 4-9

RSA Padding Oracle Attack

Alice and Bob are at it again. This time, though, they’re using RSA with padding. But EATSA is still making bad decisions. They decide to use PKCS #1 v1.5 simply because it requires no parameters. Originally they were going to use OAEP, but the East Antarctica Taskforce for Modern Operational RSA Employment and Better Encryption, Especially in the Field (EATMOREBEEF) apparently argued for weeks about the task force name. Pressing up against a deadline, and unable to agree about which hashing algorithm should be used for OAEP, and whether “EATMOREBEEF” should be used for the label, they threw up their hands and said, “We’re pretty sure PKCS #1 v1.5 is good enough.”

Once again, we find Alice in the West Antarctica spying on her neighbors. This time, however, Alice is posing as a CEO for an ice-making company meeting other executives in the ice industry at a conference in West Antarctica City. Sales of ice have melted in the last few years, and the government, facing its own problems with frozen assets and decreased liquidity, has been either unable or unwilling to offer subsidies. Alice’s mission is to continue crystallizing the dissent against the current party in power, in an attempt to solidify influence in the next election.

After the conference, Alice needs to send Bob a report of CEOs that she has convinced to donate significantly to the opposition party. Alice transmits the following message using RSA with PKCS #1 v1.5: “Jane Winters, F. Roe Zen, and John White.”

Alice whips out a mobile flip phone (they are slowly catching up in technology... no smart phones yet, but they finally did away with carrier penguins). She keys in the message to Bob and it automatically converts it to a number, encrypts it, and transmits it. A few seconds later, her phone vibrates with a new message:

Received: OK

Elsewhere in the city, Eve watches this communication. She has been tracking Alice since crossing the border. But she cannot decrypt the messages. Alice even came with the public key already installed in the phone so Eve can’t give her a fake key either. What can she do?

Fortunately for Eve, she finds out through her own intelligence agency that Alice and Bob are using PKCS #1 v1.5 for the RSA padding. Eve is surprised. After all of the events of the earlier part of this chapter, Eve has been reading up on RSA quite a bit, and she knows that this padding scheme has known vulnerabilities. Why are they using it, she wonders. Did they not get the memo?

Eve has a copy of the Bleichenbacher paper and begins reading. The paper explains that the PKCS #1 v1.5 padding can be broken with an oracle attack similar to the one we saw in the previous chapter.

In this case, Eve needs an oracle to tell her whether or not a given ciphertext (a number) decrypts to something with proper padding. The oracle will not, of course, tell her what the ciphertext decrypted to; all it needs to say is “yes” or “no” with regard to the padding.

Fortunately, Eve has been monitoring EA communications, and it appears that they built an error-reporting system into their technologies. When Alice sends a valid message, she gets back

Received: OK

But when Eve sends a random number (ciphertext), she almost always gets back

Failed: Padding

After sending a thousands of random numbers, she did eventually get back one that answered with the OK message. As far as she could tell, it was not a “real” message (human readable, or one that Bob understood), but it did have the correct padding as reported by the automated processing system.

This is Eve’s oracle. It is all she needs to completely decrypt a ciphertext message.

For convenience in writing her attack program, Eve will start by breaking a message encrypted locally with a self-generated private key. Eve will use a pluggable oracle configuration so that when it’s time to attack Bob, she can simply switch out the oracle used to power the attack. The test oracle uses the real private key to decrypt the message and check whether the message has the proper formatting.

Eve starts reading up on PKCS v1.5 and starts playing around with her own experiments. Creating her own key pair, she encrypts messages with the padding and then examines the output. She encrypts the message “test” and then decrypts the message without removing the padding . Listing 4-10 shows the key snippet of the code that she used.

1 # Partial Listing: Some Assembly Required

3 from cryptography.hazmat.primitives.asymmetric import rsa, padding

4 from cryptography.hazmat.primitives import hashes

5 from cryptography.hazmat.backends import default_backend

6 import gmpy2

8 # Dependencies: int_to_bytes(), bytes_to_int(), and simple_rsa_decrypt()

10 private_key = rsa.generate_private_key(

11 public_exponent=65537,

12 key_size=2048,

13 backend=default_backend()

14 )

15 public_key = private_key.public_key()

17 message = b'test'

19 ###

20 # WARNING: PKCS #1 v1.5 is obsolete and has vulnerabilities

21 # DO NOT USE EXCEPT WITH LEGACY PROTOCOLS

22 ciphertext = public_key.encrypt(

23 message,

24 padding.PKCS1v15()

25 )

27 ciphertext_as_int = bytes_to_int(ciphertext)

28 recovered_as_int = simple_rsa_decrypt(ciphertext_as_int, private_key)

29 recovered = int_to_bytes(recovered_as_int)

31 print("Plaintext: {}".format(message))

32 print("Recovered: {}".format(recovered))

Listing 4-10

Encrypt with Padding

You can see that she is using the cryptography module to create the encryption. But she is using her own simple_rsa_decrypt operation for the decryption in order to preserve the padding.

This is what she sees:

Plaintext: b'test'

Recovered: b'\x02@&\x1cC\xb1\xe4\x0f\x14\xd9\x93oU

\x07\x1b\xfdC\xe1\xe2K\xeeP\xdd\x8b\x10\xf9cZJ\x0c

42\x8e\xbblZ\xfb\x80\x8b\xfcA?p\xac\xba\xf7I\x9e\x

11\x1cn&t\xb8\x15\xbfo\xfe\xcc\xdf\xe7=\xc2\x9e\x

ca<v\xcd\x9ep\xd8\x1c\xf6b2"\x8c\xc0\x1e\xb8\xdb\x

97\x89\xfauj\x8f``\x99m~,\x18h\xc2k6d~qr-\x0c\xb9\

xfe?\xf9\xf9\xa6o\x05\\ZV\xfd4?\x0e;y\xf3\xd3q\xb2

\x94\xf6\xf8~a\xc1eA\xe4\x14\xce\x82\xdcc\xbf4e\xa

e\xa3<"\xcb,L\xd8\xed\xca}\xeb\x82\xa67\x1a\xd1\xc

7)\x13\xc1D)\xe8\x05h\xbe/\x97\xdf>\xf0\xef\xeb\xe

4Q\xc2\x85(*\xdcE\x9ct\x08c0\xb1\x80la\x94_/2\xd4y

\xc7\x95\x01\x90@\xea\x92\xaa\xb8\x18!\xc7\xff\xab

\x03\xea\x8b\xa3\xb4\xf6\xf2\xd6GH\x98-fM\x1c\x99\

x84\x8d4\xaf"\x95\xa7XR(M\x836\xd4\x17\x99m\xa8\x1

a\xb3\x00test'

Eve notices that the actual message is at the end of the padding, consistent with the PKCS #1 v1.5 standard. (From the rest of this section, we will just say “PKCS.”)

She does notice that the first byte of the recovered text is 2. That seems weird to her because the standard says that the padding should start with a 0 and a 2. Where did the initial 0 go?

Then Eve remembers! Of course! Because RSA works with integers instead of bytes, any leading zeros are wiped out. Fortunately, when RSA padding is used, the size of the bytes is fixed to the key size. Eve decides to update her conversion function with an optional parameter for minimum size,⁸ shown in Listing 4-11.

1 # Partial Listing: Some Assembly Required

3 # RSA Oracle Attack Component

4 def int_to_bytes(i, min_size = None):

5 # i might be a gmpy2 big integer; convert back to a Python int

6 i = int(i)

7 b = i.to_bytes((i.bit_length()+7)//8, byteorder="big")

8 if min_size != None and len(b) < min_size:

9 b = b'\x00'*(min_size-len(b)) + b

10 return b

Listing 4-11

Integer to Bytes

Now properly updated, Eve writes her “fake” oracle that she will use just for testing. The code in Listing 4-12 performs a simple RSA decryption, converts the result to bytes (using the minimum size parameter we just implemented), and checks if the first and second bytes are 0 and 2, respectively. Make sure that the new int_to_bytes is working correctly. The old version will always drop the leading zero and the oracle will always report false.

1 # Partial Listing: Some Assembly Required

3 # RSA Oracle Attack Component

4 class FakeOracle:

5 def __init__(self, private_key):

6 self.private_key = private_key

8 def __call__(self, cipher_text):

9 recovered_as_int = simple_rsa_decrypt(cipher_text, self.private_key)

10 recovered = int_to_bytes(recovered_as_int, self.private_key.key_size //8)

11 return recovered [0:2] == bytes([0, 2])

Listing 4-12

Fake Oracle

With an oracle in place, Eve prepares to attack the algorithm described in the paper. The algorithm is described in four steps. We will review each one individually and develop the code incrementally.

Step 1: Blinding

Bleichenbacher’s algorithm requires the blinding step both for setup and for “blinding” the message. However, the remarks section at the end of the algorithm explains that most of this is not necessary for our situation:

Step 1 can be skipped if c is already PKCS-conforming (i.e., when c is an encrypted message). In that case, we set s₀ ← 1.

There are three values that get configured in this step. Because we are dealing with an already PKCS-padded encrypted message, we only need to set these values to the prescribed defaults:

$\begin{array}{c}\kern3.5em {c}_0\leftarrow c{\left({s}_0\right)}^e\kern0.5em \left(\operatorname{mod}\ n\right)\\ {}\kern2.5em {M}_0\leftarrow \left[2B,3B-1\right]\\ {}i\leftarrow 1.\end{array}$

Because s₀ = 1, we can reduce the first assignment to

${c}_0\leftarrow c$

Obviously, 1 to any power is still just 1, so neither the power nor the modulus has any effect.

The M parameter is going to be a list of lists of intervals (more on intervals in a second). This algorithm consists of repeated steps identified by i. M₀ records a list of intervals identified in the step identified by i = 1. In this case, there is only the single interval [2B, 3B – 1].

What is B? As explained earlier in the paper, B is the number of legal values that have the proper padding. It is defined as

$B={2}^{8\left(k-2\right)}.$

Basically, k is the key size in bytes. So, if we’re using a 2048-bit key, k = 256. But why subtract 2?

Let’s break it down this way. For RSA with padding, our plaintext size in bytes is always supposed to be the same as the key size. If we’re using a 2048-bit key, our padded plaintext must be 2048 bits (256 bytes) as well. That means that there are 2²⁰⁴⁸ possible plaintext values.

That isn’t really true, though, is it? We know that the first two bytes must be 0 and 2, and that reduces the number of legal values by 2 × 8 = 16 bits. Thus, B is the maximum number of values for this key size when you account for the first two fixed bytes.

Returning to the intervals, what is 2B and 3B? The intervals in this data structure represent legal values of PKCS numbers in which the actual plaintext message resides. Because the bytes at the beginning are the most significant bytes, the 0 has no impact on the integer number (e.g., 0020 = 20). But the 2 means that any legal number must be at a minimum 2B but must be less than 3B.

Think about it this way. If I told you that a two-digit number must fall between 20 and 30, you would know that there are ten possible values that it could be. Moreover, you know that the minimum value is 2 × 10. This is the same idea.

The way this algorithm works is by narrowing down the legal interval until it is just a single number. That number is the plaintext message!

Eve decides to create a function for each of the steps of the algorithm. Given that there is state data that needs to be shared between these functions (e.g., B, M, etc.), she decides to use a class for storing state. The constructor takes a public key and an oracle. Remember, the oracle simply takes a ciphertext as input and returns true if the ciphertext decrypts to a proper PKCS-padded plaintext.

Now, Eve writes the code for this step (step 1) of the algorithm. This step requires a ciphertext as input (c) and initializes the values of c₀, B, s, and M. Eve also copies n out of the public key in a convenience function called _step1_blinding, as in Listing 4-13.

1 # Partial Listing: Some Assembly Required

3 class RSAOracleAttacker:

4 def __init__(self, public_key, oracle):

5 self.public_key = public_key

6 self.oracle = oracle

8 def _step1_blinding(self, c):

9 self.c0 = c

11 self.B = 2**(self.public_key.key_size-16)

12 self.s = [1]

13 self.M = [ [Interval(2*self.B, (3*self.B)-1)] ]

15 self.i = 1

16 self.n = self.public_key.public_numbers().n

Listing 4-13

RSA Oracle Attack: Step 1

The value of B is computed directly from bits rather than converting from bytes. Everything else is computed exactly as described in the paper.

The Interval data structure in this code is created using the collections.namedtuple factory. Its two values are a (for lower bounds) and b (for upper bounds).

Step 2: Searching for PKCS-Conforming Messages

For this section, we need to dust off our mathematics from about multiplying RSA ciphertexts. Take a quick minute to review (4.3).

Conceptually, step 2 is about searching within the M_i–1 intervals for new PKCS-conforming messages that are a multiples of the original plaintext message m and some other integer s_i.

Figure 4-2 depicts a (simplified) view of the PKCS-conformant space within all possible RSA ciphertext values. An RSA encryption ranges in output from 0 up to 2^k–1 where k is the key size in bits. Regardless of the key size, every number (in hexadecimal) begins with 1 of 16 digits 0 through f. The highlighted slice between 2 and 3 represents RSA ciphertext values that have proper PKCS padding. (This view is overly simplified because, in reality, the correct slice should be from 02 up to 03 out of a range from 00 to ff, so it would actually just be 1 slice out of 256.)

The reason the message space is shown as a ring is because we are dealing with modular (wrap-around) arithmetic. If you take two numbers within this space and multiply them together (modulo n), if the product is greater than n, it just wraps around.

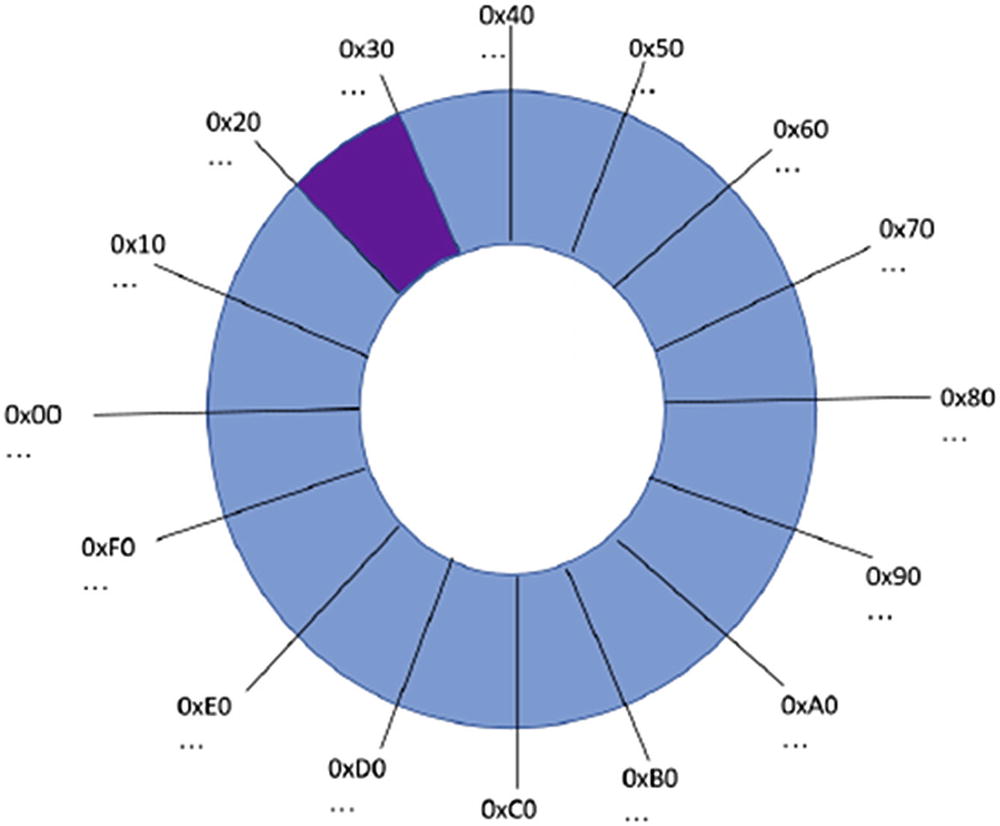
../images/472260_1_En_4_Chapter/472260_1_En_4_Fig2_HTML.jpg — Figure 4-2
Simplified view of PKCS-conformant space

This brings us back to multiplying the plaintext message m by another number. In our simplified view in Figure 4-2, m must be inside the highlighted region somewhere. If we use modular multiplication, multiplying m by certain numbers (modulo n) will produce other numbers that have wrapped around that are also within the same region.

Of course, we don’t know exactly where m is located because all we have is the encrypted version c. All we know is that, because it is PKCS-conformant, it is somewhere within the region. Similarly, because we don’t know where m is, we also have no idea where a multiple of m will land in the ring. The exception, of course, is that using our oracle, we can determine if the multiple landed back inside the PKCS-conformant region!

Using the oracle, then, we will search for an s_i value that, when multiplied by m (modulo n), is PKCS-conformant and thus within the PKCS-conformant region of the RSA message space. We still won’t know where m is, but knowing that it has a multiple that falls within a certain region introduces additional constraints on the interval that contains it. We’ll talk more about those constraints and how to use them in step 3. But for now, let’s find s_i!

Bleichenbacher breaks up finding s_i into three sub-steps:

1.
2a Starting the search is for the very first time we do this operation (i.e., when i = 1).
2.
2b Searching with more than one interval left is for rare cases when we have two intervals instead of just one.
3.
2c Searching with one interval left is for when there is just one interval and i is not 1. This should be all other cases.

Each of these sub-steps requires searching a range of possible s_i values to see if it produces a conformant ciphertext.

Specifically, for each candidate s_i, we encrypt it with RSA to produce c_i.

${c}_i={s}_i^e\kern1em \left(\operatorname{mod}\ n\right).$

We multiply the encrypted s_i value by our original ciphertext c₀ to create a test cipher c_t. Because c₀ is the encryption of the unknown plaintext m₀⁹, we get

$\begin{array}{l}{s}_t={c}_i{c}_0\kern1em \left(\operatorname{mod}\kern0.375em n\right)\\ {}\kern1.625em ={s}_i^e{m}_0^e\kern1em \left(\operatorname{mod}\kern0.375em n\right).\end{array}$

We send c_t to the oracle to test if it is conformant. For our fake oracle, it simply uses the private key to decrypt the c_t and check if the plaintext starts with bytes 0 and 2. (Remember, to break Alice’s messages, we won’t have a private-key-enabled oracle. Instead, we will send the ciphertext to Bob and check for padding error message responses.)

Because each sub-step needs to be able to check a range of s_i values in this way, Eve decides to create a helper function for performing the search. It takes a starting value and an optional inclusive upper bound (as in Listing 4-14).

1 # Partial Listing: Some Assembly Required

3 # RSA Oracle Attack Component, part of class RSAOracleAttacker

4 def _find_s(self, start_s, s_max = None):

5 si = start_s

6 ci = simple_rsa_encrypt(si, self.public_key)

7 while not self.oracle((self.c0 * ci) % self.n):

8 si += 1

9 if s_max and (si > s_max):

10 return None

11 ci = simple_rsa_encrypt(si, self.public_key)

12 return si

Listing 4-14

Find “s”

Using this helper function, the first two sub-steps are very straightforward. Step 2a requires testing all values of s_i ≥ n/(3B) until one of them is conformant. Eve encodes this step as shown in Listing 4-15.

1 # Partial Listing: Some Assembly Required

3 # RSA Oracle Attack Component, part of class RSAOracleAttacker

4 def _step2a_start_the_searching(self):

5 si = self._find_s(start_s=gmpy2.c_div(self.n, 3*self.B))

6 return si

Listing 4-15

Step 2a

Notice that the starting s value is computed as n/(3B) using the c_div function from the gmpy2 module. Because we are working with such big numbers, we cannot trust Python’s built-in floating point. Many of the values we are computing are just ranges and are not guaranteed to be integers, so fractional values are possible. The gmpy2 module provides us with fast operations on very large numbers, including floating point.

The c_div function itself provides division rounding up toward the ceiling. So, for example, c_div(3,4) computes 3/4 and rounds up, returning 1.

Using these RSA concepts, this step searches for values of s_i that multiply c to another PKCS-conformant value. Specifically, for a candidate value of s_i, we RSA encrypt it, then multiply it by the original ciphertext. We use the ceiling because s_i must be an integer and must be greater than or equal to the starting value. Whether the starting value is a whole number or not, the next integer (i.e., ceiling) is the starting point for s_i.

Sub-step 2b is also quite easy to do. This sub-step deals with rare occurrences where the interval for m₀ gets split in two. When this happens, we iterate s_i forward until we find another conforming value (Listing 4-16).

1 # Partial Listing: Some Assembly Required

3 # RSA Oracle Attack Component, part of class RSAOracleAttacker

4 def _step2b_searching_with_more_than_one_interval(self):

5 si = self._find_s(start_s=self.s[-1]+1)

6 return si

Listing 4-16

Step 2b

We will save every s value we find in the self.s array for being able to access these values. In truth, we only ever need the previous value, but we use this idiom to match the way the paper is written.

Finally, the last sub-step, 2c, is a bit more complicated. It requires searching for s across a range of possible values. Recall that there is only one interval found in the previous step and we take the lower bound as a and the upper bound as b. Next, we must iterate through r_i values:

${r}_i\ge 2\frac{b{s}_{i-1}-2B}{n}.$

We use these r_i values to bound both sides of the s_i search:

$\frac{2B+{r}_in}{b}\ge {s}_i<\frac{3B+{r}_in}{a}.$

What we are doing here is picking s_i values within a particular range that will help us continue to narrow down the solution. Bleichenbacher explains in his paper why these bounds work, and we will not repeat his comments here. When we talk about step 3, we will give some further intuition on the entire algorithm that will help to clarify what is happening.

In the meantime, Eve encodes this algorithm as Listing 4-17.

1 # Partial Listing: Some Assembly Required

3 # RSA Oracle Attack Component, part of class RSAOracleAttacker

4 def _step2c_searching_with_one_interval_left(self):

5 a,b = self.M[-1][0]

6 ri = gmpy2.c_div(2*(b*self.s[-1] - 2*self.B),self.n)

7 si = None

9 while si == None:

10 si = gmpy2.c_div((2*self.B+ri*self.n),b)

12 s_max = gmpy2.c_div((3*self.B+ri*self.n),a)

Listing 4-17

Step 2c

13 si = self._find_s(start_s=si, s_max=s_max)

14 ri += 1

15 return si

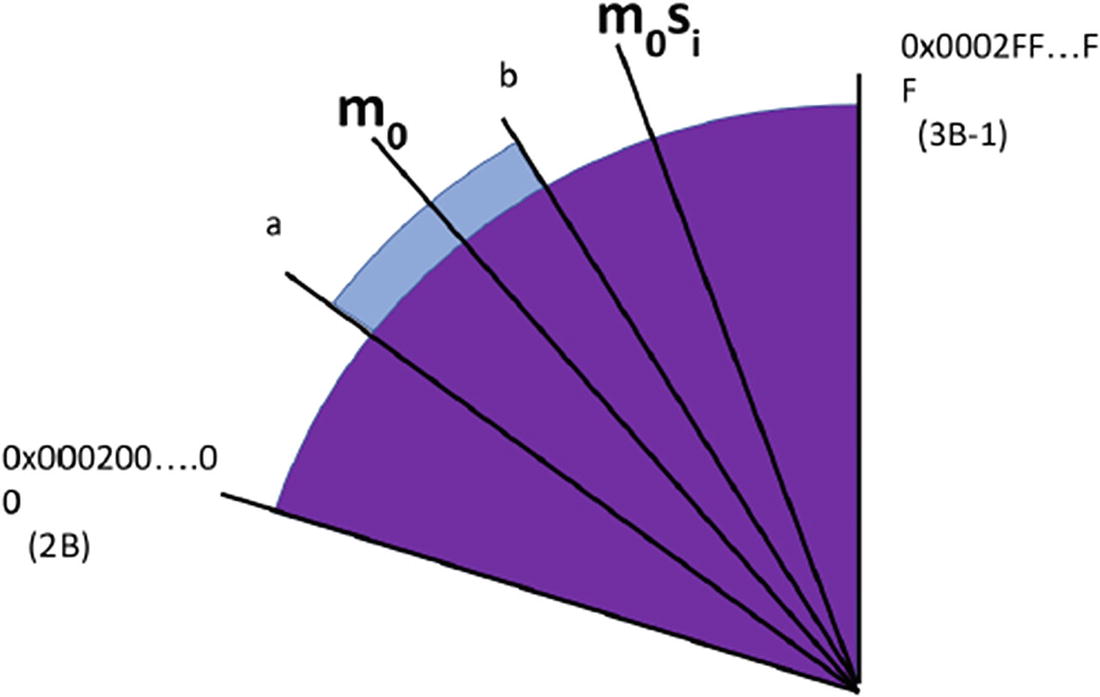
../images/472260_1_En_4_Chapter/472260_1_En_4_Fig3_HTML.jpg — Figure 4-3
Depiction of Bleichenbacher’s attack

As with previous computations, division is handled using gmpy2.c_div. This is very important. If you just use Python’s division operators, you are likely to get incomplete results.

Step 3: Narrowing the Set of Solutions

Once an s_i value has been found from step 2, we update our bounds on the location of m. Before walking through the math, let’s talk about what is going on in this algorithm.

In Figure 4-3 we are again visualizing the slice of the RSA message space ring that contains legitimate PKCS-padded values. The lower bound of this space is numbers beginning with 000200...00 and the inclusive upper bound is 0002FF...FF. The plaintext message m₀ is somewhere in here. At the start of the algorithm, we have no idea where.

However, for each s_i value we find that is conformant, we learn of a new value m₀s_i that is within this region as well (wrapping around because of modulo arithmetic). The fact that we know that m₀s_i (modulo n) falls within a particular range introduces new constraints on where m₀ can be. We are able to use these constraints to calculate a new interval a to b within which m₀ must be.

Once we update the bounds, we can repeat the process using new values of s_i that further tighten the bounds. Eventually, the bounds will restrict m₀ to being a single value. That is the plaintext we’re looking for!

Hopefully this intuition will help even if the following formulas don’t make much sense. Or, it will be helpful if you do try to tackle Bleichenbacher’s paper. In any event, we compute the new upper and lower bounds as follows.

For each a, b interval in the previous M₀ (there will usually be one, but sometimes two), find all integer values of r such that

$\frac{a{s}_i-3B+1}{n}\ge r\le \frac{b{s}_i-2B}{n}.$

For each of these values of a, b, and r, we calculate a new interval. First, we calculate a lower-bound candidate as follows:

${a}_i=\frac{2B+ rn}{si}.$

and an upper-bound candidate

${b}_i=\frac{3B-1+ rn}{si}.$

We define a new interval as [max(a, a_i), min(b, b_i)].

The set of all intervals is inserted into M_i. Again, there is typically only one interval.

Eve encodes this step of the algorithm as in Listing 4-18.

1 # Partial Listing: Some Assembly Required

3 # RSA Oracle Attack Component, part of class RSAOracleAttacker

4 def _step3_narrowing_set_of_solutions(self, si):

5 new_intervals = set()

6 for a,b in self.M[-1]:

7 r_min = gmpy2.c_div((a*si - 3*self.B + 1),self.n)

8 r_max = gmpy2.f_div((b*si - 2*self.B),self.n)

10 for r in range(r_min, r_max+1):

11 a_candidate = gmpy2.c_div((2*self.B+r*self.n),si)

12 b_candidate = gmpy2.f_div((3*self.B-1+r*self.n),si)

14 new_interval = Interval(max(a, a_candidate), min(b, b_candidate))

15 new_intervals.add(new_interval)

16 new_intervals = list(new_intervals)

17 self.M.append(new_intervals)

18 self.s.append(si)

20 if len(new_intervals) == 1 and new_intervals[0].a == new_intervals[0].b:

21 return True

22 return False

Listing 4-18

Step 3

In this code, note that r_max is calculated using f_div. This computes division rounding to the floor instead of the ceiling. We use this value because r is an integer and must be less than or equal to the value.

Once the intervals are computed, the code adds them to the self.M data structure and adds the s_i value to self.s.

Finally, it checks to see if we’ve found a solution. Eve is getting ahead of herself here. This is part of step 4, but it was simply more convenient to put it here.

Step 4: Computing the Solution

As hinted at in previous sections, this algorithm has termination criteria. Hopefully, it is fairly obvious considering the previous discussion. Either

M_i contains only one interval, or
The upper and lower bound in the interval of M_i are the same.

In short, we terminate when the interval that bounds the location of m is reduced to a single number.

We have already seen Eve’s code for checking this condition at the end of step 3. Bleichenbacher’s step 4 also deals with a more general problem than ours and includes steps that are unnecessary for when s₀ is 1. Recall that for processing RSA encryption messages where the plaintext was already PKCS-padded, s₀ was set to 1.

Although it’s somewhat unnecessary, for sake of completeness and consistency, Eve does create a method for step 4 (Listing 4-19).

1 # Partial Listing: Some Assembly Required

3 # RSA Oracle Attack Component, part of class RSAOracleAttacker

4 def _step4_computing_the_solution(self):

5 interval = self.M[-1][0]

6 return interval.a

Listing 4-19

Step 4

That’s it! That’s the entire algorithm! Eve combines these steps into Listing 4-20’s attack method.

1 # Partial Listing: Some Assembly Required

3 # RSA Oracle Attack Component, part of class RSAOracleAttacker

4 def attack(self, c):

5 self._step1_blinding(c)

7 # do this until there is one interval left

8 finished = False

9 while not finished:

10 if self.i == 1:

11 si = self._step2a_start_the_searching()

12 elif len(self.M[ -1]) > 1:

13 si = self._step2b_searching_with_more_than_one_interval()

14 elif len(self.M[-1]) == 1:

15 interval = self.M[-1][0]

16 si = self._step2c_searching_with_one_interval_left()

18 finished = self._step3_narrowing_set_of_solutions(si)

19 self.i += 1

21 m = self._step4_computing_the_solution()

22 return m

Listing 4-20

Attack!

Please note that the attack() method’s input is the ciphertext, but it must already be in integer form. Don’t forget to call bytes_to_int() on the ciphertext first!

Exercise 4.12. Run The Attack!

Take the preceding code and run some experiments with breaking RSA encryption with PKCS padding. You should use the cryptography module to create the encrypted message, convert the encrypted message to an integer, and then use your attack program (and fake oracle) to break the encryption. To begin with, test your program on RSA keys of size 512. This breaks faster and will enable you to validate your code sooner.

Exercise 4.13. Taking The Time

How long does the attack take? Instrument your code with timing checks and a count of how many times the oracle function is called. Run the attack on a suite of inputs and determine the average amount of time required to break keys of sizes 512, 1024, and 2048.

Exercise 4.14. Staying Up To Date

Despite the fact that this attack is over 20 years old, it continues to haunt the Internet. Do a little Google searching and find out about the current state of this attack both in terms of prevention and updated variants. Make sure to find out about the ROBOT attack. We’ll talk about this one again when we discuss TLS.

Additional Notes About RSA

We’ve spent a lot of time on RSA in this chapter, and we haven’t even gotten into much of how it is actually used in practice. RSA, like most asymmetric ciphers, is almost never used to encrypt messages like we had Alice and Bob do throughout the chapter. When it is used, it is typically used to encrypt a session key for a symmetric cipher, or for signatures.

It is, however, critical to understand how asymmetric ciphers work and how they can be broken. Despite all of its weaknesses, RSA is still widely used, often incorrectly. Walking through the exploits and vulnerabilities in this chapter should help put you on the right path.

Here are a few other items for consideration.

Key Management

As with all ciphers, much of their security comes down to correctly creating and safeguarding keys.

When creating an RSA key, make sure to use a library. Do not try to generate the public and private keys yourself. At the same time, keep tabs on any bug reports for the library you do use. For example, some libraries have been found to generate RSA private keys without sufficient randomness, thus producing private keys that were vulnerable to various attacks. You can’t possibly anticipate all of the things that will go wrong, or when the library or algorithm you use will be exposed as vulnerable, so you must “maintain” your cryptography by keeping up to date on known vulnerabilities.

Vulnerabilities can be system-specific. The ROCA vulnerability, for example, was largely confined to certain hardware chips.

It is also important to use the proper parameters when creating an RSA key. The key size should typically be at least 2048 bits unless legacy constraints force you to choose something smaller. And the value of the public exponent e should always be 65537.

You must also be careful to guard and protect private keys and their secrets. Obviously the private key itself should be stored securely and with appropriate permissions. Your private key should, at the very least, be stored with absolutely minimal permissions on the file system. A very sensitive key might need to be stored offline.

You should also consider storing the private key in encrypted form. This will require a password to decrypt the key which can have its own set of difficulties in a fully automated system. However, properly used, it can reduce the risk of a private key being compromised if an attacker gains access to the host system.

Moreover, the private key is made up of a number of component values. In our examples, we could think of d as the private key because that is the value we use to actually decrypt. But in addition to d, care must also be taken not to expose the secrets used to generate it. For example, the modulus n is not, itself, secret, but the two large primes, p and q, that generated it are.

There are additional values generated when creating a private key that will compromise security if disclosed. Along with p and q, these values are not strictly necessary after the key is generated, as everything can be computed from e, d, and n. However, most libraries do keep them as part of the private key both in memory and on disk. You should read your library’s documentation about private key generation and follow recommended handling procedures.

One of the weaknesses of asymmetric cryptography is the inability to “revoke” a private key. If Bob’s private key is compromised, how does Alice know to stop sending data encrypted under the associated public key? In practice, your RSA keys will probably be used in conjunction with certificates, which can include a hierarchy of certificates and keys allowing some keys to be less sensitive than others and also include an expiration date to limit the exposure of a compromised key. More is said on that elsewhere.

Exercise 4.15. Factoring RSA Keys

In this section, we recommended using 2048-bit keys. For this exercise, do an Internet search to find out the current size of keys that can easily be factored. For example, do a search for “factoring as a service” and see how much it costs to factor a 512-bit key.

Exercise 4.16. ROCA Vulnerable Keys

Unless your RSA keys are being generated by certain RSA hardware modules, the keys you have generated for the exercises in this chapter should not be vulnerable to ROCA, but it never hurts to check. For this exercise, visit the online ROCA vulnerability checking site at https://keychest.net/roca#/ and test a couple of keys.

Algorithm Parameters

If there is one thing that you should take away from this chapter, it is this: pay special attention to RSA’s padding parameter . As of the time of this writing, you should use the OAEP padding scheme for encryption operations and the PSS padding scheme for signatures. Do not use PKCS #1 v1.5 unless it is absolutely necessary for legacy applications.

Quantum Cryptography

We don’t have the space to delve into quantum cryptography in this book, but we can’t close out our discussion of RSA without mentioning it. When quantum computing arrives, most of our current asymmetric algorithms will become breakable. RSA is already vulnerable to a number of contemporary attacks, but when quantum computing becomes viable, it will be thoroughly broken. Thus, within the next decade or so, RSA will be completely useless.

Really Short Addendum

If there is one thing to get out of this chapter, it is this: parameters matter, and correct implementations are subtle and evolve over time. The intuition for how asymmetric encryption works and can be used is simple to explain, but there are numerous details that can make one implementation safe and another highly vulnerable.

Choose the right tool for the job, and choose the right parameters for the tool.

Oh, and breaking stuff is fun!

Footnotes

They can still send fake messages pretending to be her, but that was possible with symmetric encryption as well.

It certainly became popular after PKI was invented.

Bob won’t necessarily know who they’re coming from, but that’s a separate (and very interesting) problem. At least he’ll know he’s the only one who can read them.

The message is displayed as the hex representation of its bytes to make it easy to select and paste elsewhere.

Remember Kerckhoff’s principle? Here it is again!

Unless the public key is also guaranteed to be secret, but then we’ve just defeated the purpose of asymmetric keys, in a way, by requiring a secure shared channel for key exchange.

Chosen ciphertext attacks (CCA) are way more complicated than we have space to discuss here. Please consider our CCA discussion to be hyper-simplistic. If you want to know more about CCA and indistinguishability under CCA, Dr. Matthew Green has some great blog posts [7].

In most sources, because the size is fixed, it is specified as the expected size and the code checks to make sure it isn’t too big.

We were just calling this m, but to tie it to the c₀ value, we will refer to it as m₀.

4. Asymmetric Encryption: Public/Private Keys

A Tale of Two Keys

Getting Keyed Up

RSA Done Wrong: Part One

Warning: Do Not Roll Your Own Encryption

Important

Exercise 4.1. Simple RSA Encryption

Stuffing the Outbox

Exercise 4.2. Who Goes There? Bob? Is That You?

Exercise 4.3. What’s The Answer To Life, The Universe, And Everything?

What Makes Asymmetric Encryption Different?

Note: RSA Encrypts Small Things

Pass the Padding

Deterministic Outputs

Exercise 4.4. Brute-Force RSA

Exercise 4.5. Waiting Is The Hardest Part

Exercise 4.6. Dictionary Attacks

Chosen Ciphertext Attack

Exercise 4.7. Homomorphic Property Of Unpadded RSA

Exercise 4.8. Eve’s Protege

Common Modulus Attack

Exercise 4.9. Common Modulus Attack

Exercise 4.10. Common Modulus Use Cases

The Proof Is in the Padding

Warning: Say “No” to PKCS #1 v1.5

Exercise 4.11. Getting An Upgrade

Exploiting RSA Encryption with PKCS #1 v1.5 Padding

Step 1: Blinding

Step 2: Searching for PKCS-Conforming Messages

Step 3: Narrowing the Set of Solutions

Step 4: Computing the Solution

Exercise 4.12. Run The Attack!

Exercise 4.13. Taking The Time

Exercise 4.14. Staying Up To Date

Additional Notes About RSA

Key Management

Exercise 4.15. Factoring RSA Keys

Exercise 4.16. ROCA Vulnerable Keys

Algorithm Parameters

Quantum Cryptography

Really Short Addendum