Many questions that arise naturally in topology are difficult to handle if only the basic definitions and their immediate consequences are used. It is certainly natural to inquire whether two given topological spaces are homeomorphic, and yet this question is hard to answer even for familiar spaces. Intuition suggests that the punctured plane ![]() 2\{(0,0)} is not homeomorphic to the plane
2\{(0,0)} is not homeomorphic to the plane ![]() 2, but a precise proof of this fact using only the foundational material of Chapter II is difficult. A successful approach to such problems involves a principle that at first description may seem unduly abstract. It is the principle of associating with topological objects certain algebraic objects, thus converting topological problems into algebraic problems, which, one hopes, are more tractable. This idea has developed into a whole branch of mathematics, algebraic topology. The purpose of this chapter is to develop an important concrete instance of the general process.
2, but a precise proof of this fact using only the foundational material of Chapter II is difficult. A successful approach to such problems involves a principle that at first description may seem unduly abstract. It is the principle of associating with topological objects certain algebraic objects, thus converting topological problems into algebraic problems, which, one hopes, are more tractable. This idea has developed into a whole branch of mathematics, algebraic topology. The purpose of this chapter is to develop an important concrete instance of the general process.
We begin in Section 1 by introducing the appropriate algebraic concept, that of a group. Sections 2 through 6 form a unit in which the fundamental group of a topological space is introduced and the fundamental group of the circle is computed from a geometric point of view using covering spaces. Several elementary applications are given, such as the Brouwer Fixed Point Theorem in dimension two. In Sections 7 and 8 we discuss homotopic maps and give an alternative computation of the fundamental group of the circle, this time from an analytic point of view. Sections 9 and 10 include deeper applications of the ideas introduced in this chapter. In Section 9 we prove that every vector field on the 2-sphere has a zero, and in Section 10 we prove the deceptively difficult Jordan Curve Theorem, which states that every simple closed curve in the plane has an “inside” and an “outside.”
A group is a set G, and a mapping (a,b) → a * b of G × G into G, that satisfy the following axioms:
Note that the identity of a group is unique. Indeed, if e and e′ both satisfy (1.2), then e = e * e′ = e′.
If both b and b′ are elements of G that satisfy (1.3), then
b = b * e = b * (a * b′) = (b * a) * b′ = e * b′ = b′.
Consequently the element b satisfying (1.3) is unique. It is called the inverse of a and denoted by a–1, so that
a * a−1 = a−1 * a = e, a ![]() G.
G.
By (1.2), e–1 = e.
The group G is commutative, or abelian, if a * b = b * a for all a, b ![]() G.
G.
Examples of groups abound. Here is a list of a few common groups:
(i) The trivial group consisting of only one element, the identity, with the only possible operation, is obviously a commutative group.
(ii) The set ![]() of integers, with the operation of addition, forms an abelian group. The integer 0 is the identity of
of integers, with the operation of addition, forms an abelian group. The integer 0 is the identity of ![]() , and the inverse of m is – m.
, and the inverse of m is – m.
(iii) The set ![]() of real numbers and the set
of real numbers and the set ![]() of complex numbers, with the operation of addition, are commutative groups.
of complex numbers, with the operation of addition, are commutative groups.
(iv) Any real or complex vector space, with the operation of addition, is a commutative group. In particular, ![]() n and
n and ![]() n are commutative groups.
n are commutative groups.
(v) The set of nonzero real numbers, with the operation of multiplication, is a commutative group. The identity is 1, and the inverse of s is 1/s.
(vi) The unit circle S1 in the complex plane, with the operation of multiplication, is a commutative group. The identity is 1, and the inverse of a ![]() S1 is the complex conjugate ā of a.
S1 is the complex conjugate ā of a.
(vii) The set GL(n, ![]() ) of invertible n × n matrices with real entries, with matrix multiplication as the operation, forms a group. If we allow complex entries, we obtain a group GL(n,
) of invertible n × n matrices with real entries, with matrix multiplication as the operation, forms a group. If we allow complex entries, we obtain a group GL(n, ![]() ). These groups are called general linear groups. For n ≥ 2, they are not commutative.
). These groups are called general linear groups. For n ≥ 2, they are not commutative.
(viii) The set Sn of permutations of n objects, with composition as the operation, forms a group called the symmetric group. The group Sn has n! elements. If n ≥ 3, Sn is not commutative.
(ix) The set ![]() n of congruence classes of integers modulo n, with the operation of addition, forms a commutative group of n elements.
n of congruence classes of integers modulo n, with the operation of addition, forms a commutative group of n elements.
A subset H of a group G is a subgroup of G if H forms a group when endowed with the multiplication inherited from G. In order that a subset H of G be a subgroup of G, it is necessary and sufficient that H be “closed” under multiplication and taking inverses, that is, that
For example, ![]() is a subgroup of
is a subgroup of ![]() and
and ![]() is a subgroup of
is a subgroup of ![]() (operation of addition). Subspaces of a vector space are in particular subgroups of the vector space. However, a subgroup of a vector space need not be a subspace, as indicated by the example
(operation of addition). Subspaces of a vector space are in particular subgroups of the vector space. However, a subgroup of a vector space need not be a subspace, as indicated by the example ![]() ⊂
⊂ ![]() .
.
Now let G and H be two groups. A function f from G to H is a homomorphism if
Here the product a * b is taken in G and the product f(a) * f(b) is taken in H. For instance, a map h from ![]() (operation of addition) to the nonzero real numbers (operation of multiplication) is a homomorphism if and only if
(operation of addition) to the nonzero real numbers (operation of multiplication) is a homomorphism if and only if
h(s + t) = h(s)h(t), s, t ![]()
![]() .
.
An example of such a map is given by
h(t) = et, t ![]()
![]() .
.
Some other examples of homomorphisms are as follows:
(i) The map f : ![]() →
→ ![]() defined by
defined by
f(m) = 5m, m ![]()
![]() .
.
(ii) The map f : ![]() → S1 defined by
→ S1 defined by
f(s) = eis, s ![]()
![]() .
.
(iii) The map f : ![]() →
→ ![]() n defined so that f(m) is the congruence class of m (modulo n).
n defined so that f(m) is the congruence class of m (modulo n).
(iv) The map f : ![]() → GL(2,
→ GL(2,![]() ) defined by
) defined by
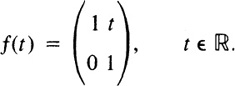
(v) If H is a subgroup of G, then the inclusion map ![]() is a homomorphism.
is a homomorphism.
Let G and H be groups and let f : G → H be a homomorphism. If e is the identity of G and e′ is the identity of H, then f(e) = e′. This follows from the chain of identities
e′ = f(e) * f(e)−1 = f(e * e) * f(e)−1 = f(e) * f(e) * f(e)−1 = f(e).
(Here we ignore the order in which the operations are performed since they are associative.) From the identity e′ = f(e) = f(aa−1) = f(a)f(a−1), we conclude that
f(a−1) = f(a)−1, a ![]() G.
G.
If K is another group and both f : G → H and g : H → K are homomorphisms, then the composition g ∘ f : G → K is also a homomorphism. Indeed,
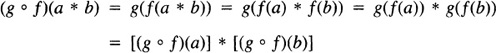
whenever a, b ![]() G.
G.
A homomorphism f : G → H is an isomorphism if f is one-to-one and onto. If there is an isomorphism of G and H, then G and H are said to be isomorphic, written G ≅ H. The composition of two isomorphisms is an isomorphism. Furthermore, the inverse of an isomorphism is an isomorphism. Indeed, if x, y ![]() H, say x = f(a) and y = f(b), then f(a * b) = x * y, so that
H, say x = f(a) and y = f(b), then f(a * b) = x * y, so that
f−1(x * y) = a * b = f−1(x) * f−1(y).
One familiar isomorphism is the map f : ![]() 2 →
2 → ![]() given by
given by
f((x,y)) = x + iy, (x,y) ![]()
![]() 2.
2.
Another example of an isomorphism is the function f from ![]() to the group
to the group ![]() + of positive real numbers, with the operation of multiplication, given by
+ of positive real numbers, with the operation of multiplication, given by
f(t) = et, t ![]()
![]() .
.
1. Prove that any two groups with one element are isomorphic. Prove that any two groups with two elements are isomorphic. Prove that any two groups with three elements are isomorphic.
2. Show that for any fixed positive integer n, there are at most a finite number of nonisomorphic groups of order n. Hint: If α1, . . . ,αn are the elements of the group, then the group is determined by knowing all the products αi * αj, 1 ≤ i ≤ j ≤ n.
3. Find the number of nonisomorphic groups of order 4.
4. Prove that if f is a homomorphism from a group G to a group H, then f(G) is a subgroup of H. Prove that if e is the identity of H, then f–1(e) is a subgroup of G.
5. Let G and H be groups. Define an operation in the Cartesian product G × H by
(a1, b1) * (a2, b2) = (a1, * a2, b1 * b2), a1, a2 ![]() G; b1, b1, b2
G; b1, b1, b2 ![]() H.
H.
Show that endowed with this operation, G × H becomes a group. Show that G × H is commutative if and only if G and H are commutative.
Remark. G × H is the direct product of G and H. If G and H are abelian and if the operations in G and H are denoted by “ + ”, then it is customary to refer to the direct product of G and H as the direct sum of G and H and denote it by G ⊕ H. For example, the group ![]() ⊕
⊕ ![]() is isomorphic to
is isomorphic to ![]() 2 and
2 and ![]() ⊕
⊕ ![]() is isomorphic to the subgroup of integral lattice points in
is isomorphic to the subgroup of integral lattice points in ![]() 2.
2.
Let X be a topological space and let a, b ![]() X. Recall that a path in X from a to b is a map γ : [0,1] → X such that γ(0) = a and γ(1) = b. Two paths γ0 and γ1 from a to b are homotopic with endpoints fixed, written γ0
X. Recall that a path in X from a to b is a map γ : [0,1] → X such that γ(0) = a and γ(1) = b. Two paths γ0 and γ1 from a to b are homotopic with endpoints fixed, written γ0 ![]() γ1 rel{0,1}, if there is a map
γ1 rel{0,1}, if there is a map
such that
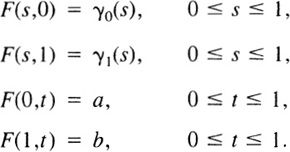
The map F is referred to as a homotopy of γ0 and γ1. For each t ![]() [0,1], the map γt : [0,1] → X defined by
[0,1], the map γt : [0,1] → X defined by
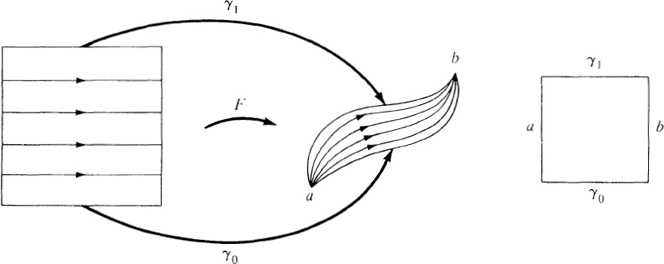
is then a path from a to b. The variable t is to be regarded as a parameter, and the paths γt move “continuously” with t. As the parameter t moves from 0 to 1, the path γ0 is continuously deformed to the path γ1 through the γt’s. Often we shall refer to {γt}0≤t≤1 as a homotopy of γ0 and γ1, understanding that the homotopy F can be recovered from the γt’s by (2.1). The situation may be represented by a square, representing the parameter space, with left edge labeled “a” to indicate that the restriction of the homotopy F to the left edge is the constant path at a, with bottom edge labeled “γ0” to indicate that the restriction of F to the bottom edge coincides with γ0, etc. (see the diagram).
A subset X of ![]() n is convex if, whenever x and y belong to X, then the straight-line interval joining x to y lies in X. In other words, X is convex if, whenever x, y
n is convex if, whenever x and y belong to X, then the straight-line interval joining x to y lies in X. In other words, X is convex if, whenever x, y ![]() X, then tx + (1 – t)y
X, then tx + (1 – t)y ![]() X for 0 ≤ t ≤ 1. The following theorem provides the fundamental example of homotopic paths.
X for 0 ≤ t ≤ 1. The following theorem provides the fundamental example of homotopic paths.
2.1 Theorem: Let X be a convex subset of ![]() n and let a, b
n and let a, b ![]() X. Then any two paths in X from a to b are homotopic in X with endpoints fixed.
X. Then any two paths in X from a to b are homotopic in X with endpoints fixed.
Proof: Let γ0 and γ1 be paths in X from a to b. The homotopy {γt} is defined so that for each fixed s, γt(s) moves from γ0(s) to γ1(s) along the straight-line interval joining the points. An explicit homotopy is given by defining
F(s,t) = γt(s) = (1 − t)γ0(s) + tγ1(s), 0≤ s, t ≤ 1.
One checks that each γt is a path in X from a to b and that the γt move continuously with t, that is, the homotopy F is continuous. ![]()
The remainder of this section is devoted to a series of elementary lemmas, which will form the foundation for the discussion of the fundamental group in Section 3. We fix a topological space X.
2.2 Lemma: The relation γ ![]() α rel{0,1} is an equivalence relation on the set of paths in X from a to b.
α rel{0,1} is an equivalence relation on the set of paths in X from a to b.
Proof: A homotopy of γ to γ is given by γt = γ, 0 ≤ t ≤ 1, so that the relation is reflexive.
Suppose that γ0 ![]() γ1 rel{0,1} and let {γt} be a homotopy of γ0 and γ1. Then by changing the direction of the parameter, we obtain a homotopy t → γ1 – t, 0 ≤ t ≤ 1, of γ1 to γ0. In other words,
γ1 rel{0,1} and let {γt} be a homotopy of γ0 and γ1. Then by changing the direction of the parameter, we obtain a homotopy t → γ1 – t, 0 ≤ t ≤ 1, of γ1 to γ0. In other words,
F(s,t) = γ1 − t(s), 0 ≤ s, t ≤ 1,
is a homotopy of γ1 and γ0. Hence the relation is symmetric.
Suppose that γ0 ![]() γ1 rel{0,1} and γ1
γ1 rel{0,1} and γ1 ![]() γ2 rel{0,1}. Let {γt}0≤t≤1 be the homotopy of γ0 and γ0 and let {αt}0≤t≤1 be the homotopy of γ1 to γ2, so that α0 = γ1 and α1 = γ2. Set
γ2 rel{0,1}. Let {γt}0≤t≤1 be the homotopy of γ0 and γ0 and let {αt}0≤t≤1 be the homotopy of γ1 to γ2, so that α0 = γ1 and α1 = γ2. Set
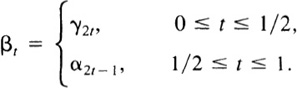
Since γ1 = α0, β1/2 is well defined. The homotopy βt corresponds to deforming γ0 to γ1 at double speed and then deforming γ1 to γ2 at double speed. The map (s,t) → βt(s) is continuous, so that {βt} is indeed a homotopy of γ0 and γ2, and the relation is transitive. ![]()
The equivalence classes of paths in X from a to b modulo this equivalence relation are called the homotopy classes of paths from a to b. The homotopy class of a path γ is denoted by [γ]. Then [γ0] = [γ0] means that γ0 ![]() γ1 rel{0,1}, that is, that γ0 and γ1 are homotopic with endpoints fixed.
γ1 rel{0,1}, that is, that γ0 and γ1 are homotopic with endpoints fixed.
The next lemma shows that any reparametrization of a path lies in the same homotopy class.
2.3 Lemma: Let γ be a path in X from a to b. Let ρ be any map from [0,1] to [0,1] such that ρ(0) = 0 and ρ(1) = 1. Then [γ∘ρ] = [γ].
Proof: Note that γ∘ρ is a path from a to b. It is obtained by running along γ at a varying speed, with perhaps some backsliding. A homotopy of γ to γ∘ρ is given explicitly by
γt(s) = γ((1 − t)s + tρ(s)), 0 ≤ s, t ≤ 1.
This homotopy is precisely the composition of γ and the homotopy αt(s) = (1 − t)s + tρ(s) of ρ, regarded as a path in [0,1] from 0 to 1, and the identity path α0(s) = s from 0 to 1. In particular, γt is well defined and moves continuously with t. ![]()
Now let a, b, c ![]() X, let α be a path from a to b, and let β be a path from b to c. As in Section II.9, we define a path αβ from a to c by
X, let α be a path from a to b, and let β be a path from b to c. As in Section II.9, we define a path αβ from a to c by
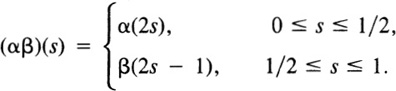
In other words, αβ is obtained by running first along α at double speed and then along β at double speed.
2.4 Lemma: Let a, b, c ![]() X, let α0 and α1 be paths from a to b, and let β0 and β1 be paths from b to c. If [α0] = [α1] and [β0] = [β1] then [α0β0] = [α1β1].
X, let α0 and α1 be paths from a to b, and let β0 and β1 be paths from b to c. If [α0] = [α1] and [β0] = [β1] then [α0β0] = [α1β1].
Proof: If {αt}0≤t≤1 is a homotopy of α0 and α1 and {βt}0≤t≤1 is a homotopy of βO and β1, then {αtβt}0≤t ≤1 is a homotopy of α0β0 and α1β1. ![]()
Lemma 2.4 allows us to define under certain circumstances the products of homotopy classes. If α is a path from a to b and β is a path from b to c, we define
[α][β] = [αβ]
By Lemma 2.4, the class [αβ] does not depend on the representatives of [α] and [β] used to define it.
Consider three paths α, β, and γ such that the terminal point of α coincides with the initial point of β and the terminal point of β coincides with the initial point of γ. Then (αβ)γ and α(βγ) are both defined, and they are given by
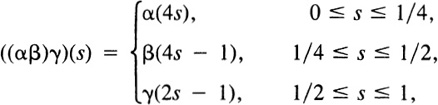
and
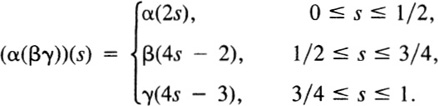
It is easy to give examples of α, β, and γ such that (αβ)γ ≠ α(βγ). In other words, multiplication of paths (when defined) is not an associative operation. However, when we pass to homotopy classes, we do obtain an associative operation.
2.5 Lemma: Let α, β, and γ be paths in X as above, so that (αβ)γ and α(βγ) are defined. Then
(αβ)γ ![]() α(βγ) rel{0,1}.
α(βγ) rel{0,1}.
([α][β][γ]) = [α]([β][γ]).
Proof: Comparing the formulas above for the respective products, we find that
(α(βγ))(s) = ((αβ)γ)(ρ(s)), 0 ≤ s ≤ 1,
where
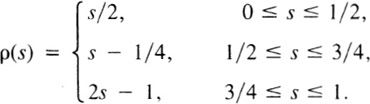
In other words, α(βγ) is a reparametrization of (αβ)γ, so that, by Lemma 2.3, the paths are homotopic with endpoints fixed. ![]()
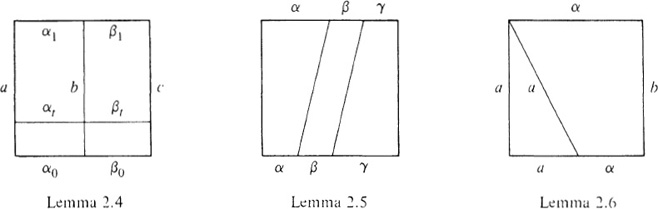
The constant path at the point b will also be denoted by b. It is defined by b(s) = b, 0 ≤ s ≤ 1.
2.6 Lemma: If α is a path from a to b, then
aα ![]() α
α ![]() αb rel{0,1}.
αb rel{0,1}.
In other words,
[a][α] = [α] = [α][b].
Proof: The path aα is given by
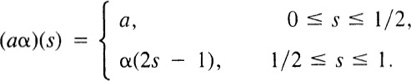
If
then aα = α∘ρ. By Lemma 2.3, aα ![]() α rel{0,1}. Similarly, αb
α rel{0,1}. Similarly, αb ![]() α rel{0,1}.
α rel{0,1}. ![]()
Now let a be a path in X from a to b. As in Section II.9, we define a path α–1 from b to a by
(α–1)(s) = α(1 – s), 0 ≤ s ≤ 1,
so that α–1 corresponds to running backwards along α. In particular, for the constant path b, we have b−1 = b.
2.7 Lemma: Let α0 and α1 be paths in X from a to b. If [α0] = [α1] then [α0–1] = [α1–1].
Proof: If {αt}0≤t≤1 is a homotopy of α0 and α1, then {αt− 1}0≤t≤1 is a homotopy of α1−1 and α0−1. ![]()
Lemma 2.7 allows us to define the inverse of the homotopy class of a path α by
[α]−1 = [α−1].
By the lemma, the homotopy class defining [α]–1 does not depend on the choice of the representative of the homotopy class of α.
The final preparatory lemma asserts that the path obtained by running along α at double speed and then returning backwards along α at double speed is homotopic to a constant path. Note that in a homotopy of a product path, the intermediate stopping points are not required to be held fixed.
2.8 Lemma: Let α be a path in X from a to b. Then αα−1 is homotopic to the constant path at a with endpoints fixed. In other words,
[α][α]−1 = [a]
Proof: For 0 ≤ t ≤ 1, let γt be the path described by running along α at double speed until time t/2, then resting until time 1 − t/2, then returning along α at double speed. The explicit formula for γt is
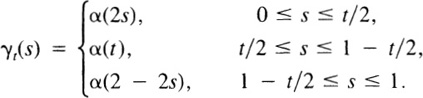
Then γ0 is the constant path at a and γ1 and αα−1. It is easy to check that the γt move continuously with t, so that they form a homotopy. ![]()
1. Suppose that (αβ)γ = α(βγ) for any three paths α, β, and γ in X for which the product is defined. Show that each path comaponent of X consists of a single point.
2. Let X be path-connected and let b ![]() X. Show that every path in X is homotopic with endpoints fixed to a path passing through b.
X. Show that every path in X is homotopic with endpoints fixed to a path passing through b.
3. Let D be an open subset in ![]() n, let α be a path in D from x to y, and set
n, let α be a path in D from x to y, and set
d = inf{|α(s) − w| : w ![]() ∂D, 0 ≤ s ≤ 1}.
∂D, 0 ≤ s ≤ 1}.
Show that if β is any path in D from x to y such that |β(s) − α(s)| < d, 0 ≤ s ≤ 1, then β is homotopic to α with endpoints fixed.
4. A path a in ![]() n, is polygonal if there is a subdivision 0 = s0 < s1 < · · · < sm = 1 of the unit interval such that a maps each interval [sj − 1, sj] onto the straight-line segment from to α(sj – 1) to α(sj). Show that every path in an open subset D of
n, is polygonal if there is a subdivision 0 = s0 < s1 < · · · < sm = 1 of the unit interval such that a maps each interval [sj − 1, sj] onto the straight-line segment from to α(sj – 1) to α(sj). Show that every path in an open subset D of ![]() n, is homotopic in D with endpoints fixed to a polygonal path.
n, is homotopic in D with endpoints fixed to a polygonal path.
5. Show that any path in Sn is homotopic with endpoints fixed to a polygonal path on Sn, where “polygonal” is now interpreted to mean that the path is formed from arcs lying on great circles of Sn.
6. Let (X,d) be a compact metric space and let a, b ![]() X. Let
X. Let ![]() be the set of all paths in X from a to b with the metric
be the set of all paths in X from a to b with the metric
ρ(α, β) = sup{d(α(s), β(s)) : 0 ≤ s ≤ 1}.
Show that two paths α,β ![]()
![]() are homotopic with endpoints fixed if and only if α and β lie in the same path component of
are homotopic with endpoints fixed if and only if α and β lie in the same path component of ![]() .
.
A pointed space is a pair (X,b) consisting of a topological space X and a point b ![]() X. The point b is referred to as the base point of X. A loop in X based at b is a path in X that begins and ends at b. The product of any two loops based at b is well defined, so that the product of the homotopy classes of any two such loops is well defined. Let π1(X,b) denote the set of homotopy classes of loops based at b, together with the multiplication of homotopy classes defined in Section 2.
X. The point b is referred to as the base point of X. A loop in X based at b is a path in X that begins and ends at b. The product of any two loops based at b is well defined, so that the product of the homotopy classes of any two such loops is well defined. Let π1(X,b) denote the set of homotopy classes of loops based at b, together with the multiplication of homotopy classes defined in Section 2.
3.1 Theorem: The set π1(X,b) of homotopy classes of loops based at b, with the operation of multiplication of homotopy classes, is a group.
Proof: Lemma 2.5 shows that the multiplication in π1(X,b) is associative. Lemma 2.6 shows that the homotopy class [b ] of the constant map b is an identity for π1(X,b) Lemma 2.8 shows that the homotopy class [α]−1 of α−1 is an inverse for the homotopy class of α. ![]()
The group π1(X,b) is called the fundamental group of X based at b. If π1(X,b) consists of only the identity, we say that π1(X,b) is trivial and write π1(X,b) ≅ 0. Thus π1(X,b) is trivial if and only if every loop based at b is homotopic with endpoints fixed to the constant loop at b. Theorem 2.1 then yields the following result.
3.2 Theorem: If X s a convex subset of ![]() n, and b
n, and b ![]() X, then π1(X,b) ≅ 0.
X, then π1(X,b) ≅ 0.
Reclining figure eight
It turns out that the fundamental group of a space need not be commutative. For instance, if X is a “figure eight,” then π1(X,b) is isomorphic to a certain non-commutative group, namely, the free group on two generators. This theorem is due to Van Kampen, and a proof will be indicated in the exercises in Section 5. Meanwhile, it will take us some effort to prove that there is a space X such that π1(X,b) is not trivial. The simplest space with a nontrivial fundamental group is the circle S1, and it will be shown in Section 5 that
π1(S1, 1) ≅ ![]() .
.
Now the question arises of how π1(X,b) depends on the base point b. Any loop based at b lies within the path component of b in X. Therefore if c ![]() X lies in a path component different from b, then π1(X,c) is in no way related to π1(X,b). However, if c lies in the same path component as b, then π1(X,c) is isomorphic to π1(X,b). In fact, the following is true.
X lies in a path component different from b, then π1(X,c) is in no way related to π1(X,b). However, if c lies in the same path component as b, then π1(X,c) is isomorphic to π1(X,b). In fact, the following is true.
3.3 Theorem: Let b, c ![]() X and suppose α to be a path in X from b to c. Then for each loop γ based at c, the homotopy class
X and suppose α to be a path in X from b to c. Then for each loop γ based at c, the homotopy class
α*([γ]) = [α][γ][α]−1
is defined and α* is an isomorphism of π1(X,c) and π1(X,b).
Proof: Since the initial and terminal points of the paths match up appropriately, α* is well defined. Since the multiplication of homotopy classes is associative, the parentheses indicating the order of multiplication are omitted.
Suppose that β and γ are both loops at c. From Lemmas 2.6 and 2.8 we obtain
[β][γ] = [β][c][γ] = [β][α]−1[α][γ].
Consequently
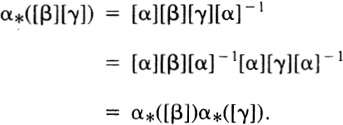
Hence α* is a homomorphism.
Suppose next that the loops β and γ at c satisfy α*([β]) = α*([γ]). Then
[β] = [α]−1[α][β][α]−1[α] = [α]−1[α][γ][α]−1[α] = [γ].
Hence α* is one-to-one.
Finally, let λ be a loop based at b. Then β = (α−1λ)α is a loop based at c that satisfies
α*([β]) = [α][α]−1[λ][α][α]−1 = [λ].
Consequently α* is onto and is an isomorphism. ![]()
If X is path-connected, then the various groups π1(X,b), b ![]() X, are all isomorphic. Thus the isomorphism type of π1(X,b) is well defined; it is called the fundamental group of X, denoted by π1(X). The situation here is slightly peculiar linguistically in that the fundamental group π1(X) is not equal to any of the π1(X,b) but is rather the (common) isomorphism class of all the distinct but isomorphic groups π1(X,b), b
X, are all isomorphic. Thus the isomorphism type of π1(X,b) is well defined; it is called the fundamental group of X, denoted by π1(X). The situation here is slightly peculiar linguistically in that the fundamental group π1(X) is not equal to any of the π1(X,b) but is rather the (common) isomorphism class of all the distinct but isomorphic groups π1(X,b), b ![]() X. In the following development, the assertions to be made about π1(X) will be such assertions as “π1(X) is isomorphic to G,” where G is some concretely described group. This assertion has the precise meaning that, for all b
X. In the following development, the assertions to be made about π1(X) will be such assertions as “π1(X) is isomorphic to G,” where G is some concretely described group. This assertion has the precise meaning that, for all b ![]() X, π1(X,b) is isomorphic to G; the isomorphism holds for all b in X if it holds for any one b in X since all π1(X,b) are isomorphic.
X, π1(X,b) is isomorphic to G; the isomorphism holds for all b in X if it holds for any one b in X since all π1(X,b) are isomorphic.
A space X is simply connected if X is path-connected and π1(X) is trivial. Since any convex subset of ![]() n is path-connected, Theorem 3.2 shows that a convex subset of
n is path-connected, Theorem 3.2 shows that a convex subset of ![]() n is simply connected.
n is simply connected.
There is another way of viewing loops in X based at b, which is convenient for some purposes. Let S1 denote the unit circle in ![]() 2 ≅
2 ≅ ![]() . Then each map
. Then each map
f : S1 → X
satisfying f(1) = b determines a loop α based at b via the formula
α(s) = f(e2πis), 0 ≤ S ≤ 1.
Conversely, any loop α based at b arises from a map f : S1 → X satisfying f(1) = b. The point is that the exponential map s → e2πis is a homeomorphism from the interval [0,1], with the endpoints identified, to the circle S1.
If the loops α0 and α1 based at b are homotopic with endpoints fixed, then the corresponding maps f0, f1 : S1 → X are homotopic relative to the base points 1 ![]() S1 and b
S1 and b ![]() X in the sense that there are maps {ft}0≤t≤1 from S1 to X such that ft(1) = b, 0 ≤ t ≤ 1, and the ft move continuously with t. In other words, there is a map
X in the sense that there are maps {ft}0≤t≤1 from S1 to X such that ft(1) = b, 0 ≤ t ≤ 1, and the ft move continuously with t. In other words, there is a map
F : S1 × [0,1] → X
such that
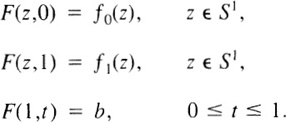
Conversely, if f0 and f1 are homotopic as above, then (s,t) → F(e2πis, t) is a homotopy of α0 and α1 with endpoints fixed.
With this identification in mind, we shall think of maps f : (S1, 1) → (X,b) also as loops in X based at f(1).
1. Prove that if n ≥ 2, then Sn is simply connected. Hint: Use Exercise 2.5 to show that every loop in Sn is homotopic to a loop that does not cover all of Sn.
2. Prove that if there are simply connected open subsets U and V of X such that U ∪ V = X and U ∩ V is nonempty and path-connected, then X is simply connected.
3. A space X is contractible to a point x0 ![]() X with x0 held fixed if there is a map F : X × [0, 1] → X such that
X with x0 held fixed if there is a map F : X × [0, 1] → X such that
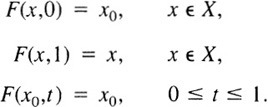
Show that such a space is simply connected.
4. Let X be the comb space, that is, the compact subset of ![]() 2 consisting of the horizontal interval {(x, 0) : 0 ≤ x ≤ 1} and the closed vertical intervals of unit length with lower endpoints at (0,0) and at (0,1/n), 1 ≤ n < ∞.
2 consisting of the horizontal interval {(x, 0) : 0 ≤ x ≤ 1} and the closed vertical intervals of unit length with lower endpoints at (0,0) and at (0,1/n), 1 ≤ n < ∞.
Comb space
Show that X is contractible to (0,0) with (0,0) held fixed. Show that X is not contractible to (0,1) with (0,1) held fixed.
5. A subset W of ![]() n is star-shaped with respect to a point w
n is star-shaped with respect to a point w ![]() W if, whenever y
W if, whenever y ![]() W, then the straight-line segment from w to y is contained in W.
W, then the straight-line segment from w to y is contained in W.
(a) Show that a subset W of ![]() n is convex if and only if it is star-shaped with respect to each of its points.
n is convex if and only if it is star-shaped with respect to each of its points.
(b) Give an example of a star-shaped set that is not convex.
(c) Show that a star-shaped set in ![]() n is contractible to a point.
n is contractible to a point.
(d) Show that a star-shaped set in ![]() n is simply connected.
n is simply connected.
6. Let (X,x0) and (Y,y0) be pointed spaces. Show that π1(X × Y, (x0y0)) is isomorphic to the direct product π1(X,x0) × π1(Y,y0).
7. Prove that the product of simply connected spaces is simply connected.
8. Prove that if n ≥ 3, then ![]() n\{0} is simply connected.
n\{0} is simply connected.
9. Let X be a path-connected topological space and let b, c ![]() X. Let B2 be the closed unit ball in
X. Let B2 be the closed unit ball in ![]() 2, with boundary circle S1. Show that the following are equivalent.
2, with boundary circle S1. Show that the following are equivalent.
(a) X is simply connected.
(b) Any two paths from b to c are homotopic with endpoints fixed.
(c) Every map f : S1 → X extends to a map F : B2 → X.
Let (X,b) and (Y,c) be pointed topological spaces. A map f : (Y,c) → (X,b) is a continuous function f from Y to X that satisfies f(c) = b. We aim to show that any such map induces a homomorphism f* from π1(Y,c) to π1(X,b). Despite the notational similarity, f* is unrelated to the induced map α* of the preceding section. The map f* will be defined in the obvious way, by making the path γ in Y correspond to the path f∘γ in X. That this correspondence respects homotopy classes is the content of the following elementary but useful lemma.
4.1 Lemma: Let X and Y be topological spaces and let f : Y → X be a map. Let α0 and α1 be paths in Y that are homotopic with endpoints fixed. Then f∘α0 and f∘α1 are paths in X that are homotopic with endpoints fixed.
Proof: If {αt}0≤t≤1 is the homotopy of α0 to α1, then the paths {f∘αt}0≤t≤1 form a homotopy of f∘α0 and f∘α1. ![]()
The following corollary to Lemma 4.1 and Theorem 2.1 is sufficiently useful to merit a separate statement.
4.2 Corollary: Let Y be a convex subset of ![]() n let y0, y1
n let y0, y1 ![]() Y, and let f be a map from Y to X. If α and β are paths in Y from y0 to y1, then f∘α is homotopic to f∘β with endpoints fixed.
Y, and let f be a map from Y to X. If α and β are paths in Y from y0 to y1, then f∘α is homotopic to f∘β with endpoints fixed.
Suppose now that c0, c1 ![]() Y and that f is a map from Y to X. If α is a path in Y from c0 to c1, then f*([α]) is defined to be the homotopy class of paths in X from f(c0) to f(c1) that includes f∘α:
Y and that f is a map from Y to X. If α is a path in Y from c0 to c1, then f*([α]) is defined to be the homotopy class of paths in X from f(c0) to f(c1) that includes f∘α:
f*([α]) = [f∘α].
By Lemma 4.1, this definition does not depend on the choice of the representative of the homotopy class [α]. If the path product αβ is defined, then f∘(αβ) = (f∘α)(f∘β), so that
Since the inverse of the path f∘α is f∘(α−1),
f*([α]−1) = f*([α])−1.
Finally,
f*([c] = [f(c)]
whenever c is a constant path in Y.
4.3 Theorem: Let (X,b) and (Y,c) be pointed topological spaces and let f : (Y,c) → (X,b) be a map. Then f* is a homomorphism of π1(Y,c) and π1(X,b). If, furthermore, (W,d) is a pointed topological space and g : (W,d) → (Y,c) is a map, then
(f∘g)* = f*∘g*.
Finally, if X = Y, b = c, and f is the identity map, then f* is the identity isomorphism.
Proof: That f* is a htomomorphism follows from (4.1). The other statements follow directly from the definitions. ![]()
4.4 Corollary: If f : Y → X is a homeomorphism and if c ![]() Y and b = f(c), then f* is an isomorphism of π1(Y,c) and π1(X,b).
Y and b = f(c), then f* is an isomorphism of π1(Y,c) and π1(X,b).
Proof: Since f∘f−1 and f−1∘f are the identity maps of X and Y, respectively, f*∘(f−1)* and (f−1)*∘f* are the identity isomorphisms of π1(X,b) and π1(Y,c), respectively. Since (f−1)* ∘f* is one-to-one, so is f*. Since f* ∘(f−1) * is onto, so is f*. Hence f* is an isomorphism. ![]()
With Corollary 4.4, we have attained the goal indicated at the beginning of the chapter, namely, we have associated to each (pointed) topological space an algebraic object, its fundamental group, in such a way that if two spaces are homeomorphic (via a base-point-preserving homeomorphism), then the algebraic objects are isomorphic. Thus, for instance, two spaces could be shown to be nonhomeomorphic by showing that their fundamental groups were not isomorphic. To give this idea any real significance, it is necessary to be able to compute the fundamental groups of whatever topological spaces one wishes to study. In the following section, we shall show how to determine the fundamental group of the circle S1—it turns out to be (isomorphic to) the group ![]() of integers with addition as the group operation. We focus attention first on the circle S1 because it is obviously the simplest space containing a closed curve without self-intersections. The method used to compute π1(S1) will serve to compute the fundamental group of many other topological spaces. Some applications of the fundamental group to fixed-point theorems and other related results will be presented in Section 6 and later sections.
of integers with addition as the group operation. We focus attention first on the circle S1 because it is obviously the simplest space containing a closed curve without self-intersections. The method used to compute π1(S1) will serve to compute the fundamental group of many other topological spaces. Some applications of the fundamental group to fixed-point theorems and other related results will be presented in Section 6 and later sections.
1. Show that simple connectivity is a topological property.
2. A subspace A of a topological space X is a retract of X if there is a map f : X → A such that f(y) = y for all y ![]() A. The map f is called a retraction of X onto A. Show that the unit sphere Sn in
A. The map f is called a retraction of X onto A. Show that the unit sphere Sn in ![]() n + 1 is a retract of
n + 1 is a retract of ![]() n + 1\{0}.
n + 1\{0}.
3. Let f be a retraction of X onto A and let x0 ![]() A. Let j :
A. Let j : ![]() be the inclusion map. Prove the following:
be the inclusion map. Prove the following:
(a) j* : π1(A,x0) → π1(X,x0) is one-to-one.
(b) f* : π1(X,x0)→ π1(A,x0) is onto.
(c) If X is simply connected, then A is simply connected.
We wish now to compute the fundamental group of the circle S1. This will be accomplished with the aid of the exponential map p : ![]() → S1, defined by
→ S1, defined by
Since the line of proof will be quite general, we axiomatize those properties of the spaces ![]() and S1 and the exponential map p that will be needed.
and S1 and the exponential map p that will be needed.
Let E and X be topological spaces and let p : E → X be a map. An open subset U of X is evenly covered by p if the inverse image p−1(U) is a union of disjoint open subsets of E, each of which is mapped homeomorphically by p onto U. The map p is a covering map if p maps E onto X and if each x ![]() X has an open neighborhood that is evenly covered by p. In this case, E is a covering space over X.
X has an open neighborhood that is evenly covered by p. In this case, E is a covering space over X.
If x ![]() X, the set p−1(x) is called the fiber over x. It is evidently a discrete subspace of E. According to the definition, each x
X, the set p−1(x) is called the fiber over x. It is evidently a discrete subspace of E. According to the definition, each x ![]() X has an open neighborhood U such that p−1(U) is homeomorphic to p−1(x) × U. The subsets of p−1(U) that are mapped homeomorphically onto U are called the sheets of p−1(U). If U is connected, then the sheets of p−1(U) coincide with the connected components of p−1(U).
X has an open neighborhood U such that p−1(U) is homeomorphic to p−1(x) × U. The subsets of p−1(U) that are mapped homeomorphically onto U are called the sheets of p−1(U). If U is connected, then the sheets of p−1(U) coincide with the connected components of p−1(U).
The exponential map p : ![]() → S1 is a covering map. Indeed, let e2πit0
→ S1 is a covering map. Indeed, let e2πit0 ![]() S1, fix 0 < ε < 1/2, and let U = {e2πit : |t − t0| < ε}. Then p−1(U) is the disjoint union of the intervals (m + t0 − ε, m + t0 + ε), m an integer, and each of these intervals is mapped homeomorphically by p onto U. For the purposes of visualizing the covering map, it is convenient to think of
S1, fix 0 < ε < 1/2, and let U = {e2πit : |t − t0| < ε}. Then p−1(U) is the disjoint union of the intervals (m + t0 − ε, m + t0 + ε), m an integer, and each of these intervals is mapped homeomorphically by p onto U. For the purposes of visualizing the covering map, it is convenient to think of ![]() as the helix {(cor(2πt), sin(2πt), t) : − ∞ < t < ∞} in
as the helix {(cor(2πt), sin(2πt), t) : − ∞ < t < ∞} in ![]() 3 by identifying t
3 by identifying t ![]()
![]() with the corresponding point on the helix. The covering map p then projects the helix onto the circle S1 in the x, y-plane.
with the corresponding point on the helix. The covering map p then projects the helix onto the circle S1 in the x, y-plane.
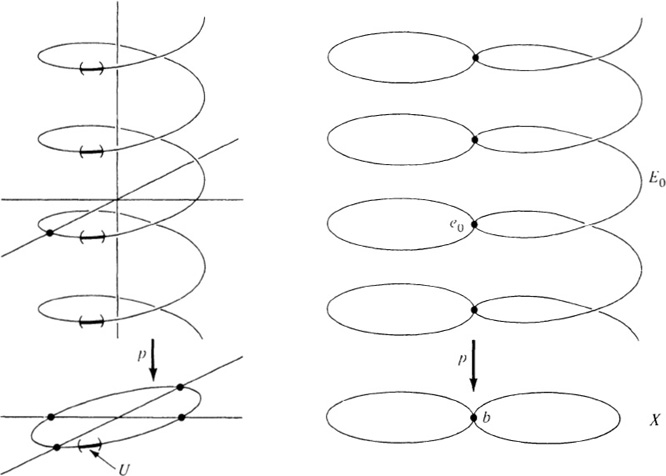
As a second example, let X be a figure eight, consisting of two loops touching at one point b. Let E0 be the space obtained by unwinding one of the loops, so that E0 is a helix with loops attached as indicated in the figure above. If we unwind the loop of E0 touching the base point e0 of E0, we obtain another covering space E over X, as suggested by the figure appearing towards the end of this section. The covering map is the composition of two covering maps, one from E to E0, the other from E0 to X.
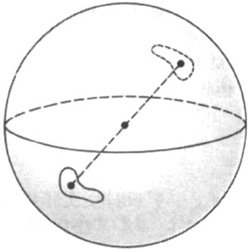
As another example, consider the n-dimensional projective space Pn, defined in Exercise II.13.8. Recall that Pn is the quotient space obtained from the unit sphere Sn in ![]() n + 1 by identifying antipodal points. Let p : Sn → Pn be the quotient map. If x0
n + 1 by identifying antipodal points. Let p : Sn → Pn be the quotient map. If x0 ![]() Sn,
Sn, ![]() > 0 is small, and V = {x
> 0 is small, and V = {x ![]() Sn : |x − x0| < ε}, then U = p(V) is an open subset of Pn and p−1(U) is the disjoint union of V and −V. Since both V and −V are mapped homeomorphically by p onto U, p is a covering map. In this case, every fiber consists of two points.
Sn : |x − x0| < ε}, then U = p(V) is an open subset of Pn and p−1(U) is the disjoint union of V and −V. Since both V and −V are mapped homeomorphically by p onto U, p is a covering map. In this case, every fiber consists of two points.
Products of covering spaces are covering spaces. For instance, if Tn = S1 × . . . × S1 is the n-dimensional torus (product of n circles), then the exponential map p : ![]() n → Tn, defined by
n → Tn, defined by
p(x1, . . . , xn) = (e2πix1, . . . , e2πixn),
is a covering map.
Now let p : E → X be a covering map, let Y be a topological space, and let f : Y → X be a map. For later developments it will be important to determine whether there is a map g : Y → E such that p∘g = f. Such a map g is called a lift of f. The situation may be represented schematically by the diagram
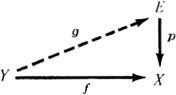
The relation p∘g = f means that the image of a point y ![]() Y is the same whether f is applied directly (the “low road”) or g is applied followed by the projection p (the “high road”). If p∘g = f, the diagram is said to commute.
Y is the same whether f is applied directly (the “low road”) or g is applied followed by the projection p (the “high road”). If p∘g = f, the diagram is said to commute.
The uniqueness of lifts will be handled by the following lemma.
5.1 Lemma: Let p : E → X be a covering map and let Y be a connected topological space. Let f : Y → X be a map and let g, h : Y → E be two lifts of f. If g(y) = h(y) for some point y ![]() Y, then g = h.
Y, then g = h.
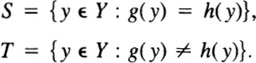
Then S ∪ T = Y and S ∩ T = Ø. We must show that either S = Y or T = Y. Since Y is connected, it suffices to show that S and T are each open.
Let y ![]() Y and let U be an open neighborhood of f(y) that is evenly covered. Let V and W be sheets of p−1(U) provided by the definition of covering map, such that g(y)
Y and let U be an open neighborhood of f(y) that is evenly covered. Let V and W be sheets of p−1(U) provided by the definition of covering map, such that g(y) ![]() V and h(y)
V and h(y) ![]() W. If g(y) = h(y), then V = W, whereas if g(y) ≠ h(y), then V and W are disjoint.
W. If g(y) = h(y), then V = W, whereas if g(y) ≠ h(y), then V and W are disjoint.
Since g and h are continuous at y, there is an open neighborhood N of y such that g(N) ⊂ V and h(N) ⊂ W. If y ![]() T, then V ∩ W = Ø, so that g(z) ≠ h(z) for all z
T, then V ∩ W = Ø, so that g(z) ≠ h(z) for all z ![]() N, and N ⊂ T. It follows that T is open. On the other hand, if y
N, and N ⊂ T. It follows that T is open. On the other hand, if y ![]() S, then V = W. Furthermore, for each z
S, then V = W. Furthermore, for each z ![]() N, g(z) must be that unique point ν
N, g(z) must be that unique point ν ![]() V such that p(ν) = f(z) and h(z) must be that unique point w
V such that p(ν) = f(z) and h(z) must be that unique point w ![]() W such that p(w) = f(z). Since V = W, we conclude that ν = w, so that g = h on N, N ⊂ S, and S is also open.
W such that p(w) = f(z). Since V = W, we conclude that ν = w, so that g = h on N, N ⊂ S, and S is also open. ![]()
5.2 Theorem (Path Lifting Theorem): Let p : E → X be a covering map, let γ : [0,1] → X be a path, and let e0 ![]() E satisfy p(e0) = γ(0). Then there exists a unique path α : [0,1] → E such that α(0) = e0 and p∘α = γ.
E satisfy p(e0) = γ(0). Then there exists a unique path α : [0,1] → E such that α(0) = e0 and p∘α = γ.
Proof: For each x ![]() X, choose an open neighborhood U(x) of x that is evenly covered by p. The open sets γ−1(U(x)), x
X, choose an open neighborhood U(x) of x that is evenly covered by p. The open sets γ−1(U(x)), x ![]() X, form an open cover of [0,1]. Since [0,1] is compact, we can find 0 = s0 < s1 < . . . < sm = 1 and evenly covered open sets U1, . . . , Um such that γ−1(Uj) includes [sj − 1, sj], 1 ≤ j ≤ m. In other words,
X, form an open cover of [0,1]. Since [0,1] is compact, we can find 0 = s0 < s1 < . . . < sm = 1 and evenly covered open sets U1, . . . , Um such that γ−1(Uj) includes [sj − 1, sj], 1 ≤ j ≤ m. In other words,
γ([sj − 1, sj]) ⊂ Uj, 1 ≤ j ≤ m.
The lift is performed now in m steps, as follows.
Since p(e0) = γ(0) ![]() U1, there is an open neighborhood V1, of e0 that is mapped homeomorphically by p onto U1. Define α on the interval [0, s1] such that α(s) is the unique point of V1 covering γ(s). In other words, set
U1, there is an open neighborhood V1, of e0 that is mapped homeomorphically by p onto U1. Define α on the interval [0, s1] such that α(s) is the unique point of V1 covering γ(s). In other words, set
α = (p|ν1)−1∘γ on [0, s1].
Then α(0) = e0 and pºα = γ on [0, s1].
Now perform the same procedure, with e0 = α(0) replaced by α(s1) and U1, replaced by U2, to extend α to the interval [s1, s2]. After m steps, we shall have lifted the entire path α.
The uniqueness of the lifted path α follows from Lemma 5.1. ![]()
Actually, one can lift a family of paths depending continuously on a parameter, so that the lifted paths also depend continuously on the parameter. A version of this principle, which will suffice for our purposes, is as follows.
5.3 Theorem: Let p : E → X be a covering map, let F : [0,1] × [0,1] → X be a map, and let e0 ![]() E satisfy p(e0) = F(0,0). Then there exists a unique lift G : [0,1] × [0,1] → E of F such that G(0,0) = e0.
E satisfy p(e0) = F(0,0). Then there exists a unique lift G : [0,1] × [0,1] → E of F such that G(0,0) = e0.
Proof: The uniqueness again follows from Lemma 5.1.
According to the Path Lifting Theorem, there is a unique path t → et, 0 ≤ t ≤ 1, in E such that p(et) = F(0,t), 0 ≤ t ≤ 1. By the same theorem, there exists for each t a unique path s → G(s,t), 0 ≤ s ≤ 1, such that G(0,t) = et and p(G(s,t)) = F(s,t), 0 ≤ s ≤ 1. This defines the lift G of F. We must show that G is continuous on [0,1] × [0,1].
Let γ : [0,1] → X be the path defined by
γ(s) = F(s, 0), 0 ≤ s ≤ 1.
Consider the construction of the lift α(s) = G(s, 0) given in the proof of Theorem 5.2 and retain the notation of that proof. Since γ−1(Uj) is an open neighborhood of [sj−1, sj], F−1(Uj) includes [sj−1, sj] × [0, ε] for some small ε > 0. Consequently there exists ε > 0 such that
F([sj−1, sj] × [0, ε]) ⊂ Uj, 1 ≤ j ≤ m.
Since e0 ![]() V1, we can assume also that the initial points et belong to V1 for 0 ≤ t ≤ ε since they depend continuously on t. Now, the procedure for constructing the lift shows that
V1, we can assume also that the initial points et belong to V1 for 0 ≤ t ≤ ε since they depend continuously on t. Now, the procedure for constructing the lift shows that
G = (p|ν1)−1∘F on [0, s1] × [0, ε].
In particular, G is continuous on [0, s1] × [0, ε]. Proceeding in this fashion, we find that G is continuous on each rectangle [sj–1, sj] × [0, ε], 1 ≤ j ≤ m, so that G is continuous on [0,1] × [0,ε].
The same proof shows that for each t0 ![]() (0,1], there exists ε > 0 such that G is continuous on the rectangle [0,1] × [t0 − ε, t0 + ε]. (Replace t0 + ε by t0 if t0 = 1.) Consequently G is continuous on [0,1] × [0,1].
(0,1], there exists ε > 0 such that G is continuous on the rectangle [0,1] × [t0 − ε, t0 + ε]. (Replace t0 + ε by t0 if t0 = 1.) Consequently G is continuous on [0,1] × [0,1]. ![]()
Now let (E,e) and (X,b) be pointed spaces and let p : (E,e) → (X,b) be a covering map, that is, p : E → X is a covering map satisfying p(e) = b. Let γ : [0,1] → X be a loop based at b. By the Path Lifting Theorem, there is a unique lift α : [0,1] → E of γ that satisfies α(0) = e. The lift α need not be a loop since it need not terminate at e. However, the terminal point α(1) of α satisfies p(α(1)) = γ(1) = b, so that α(1) lies in the fiber p−1(b) over b.
Suppose now that γ1 is another loop in X based at b such that γ1 is homotopic to γ with endpoints fixed. Let {γt}0≤t≤1 be the homotopy, so that γ0 = γ. Applying Theorem 5.3 to F(s,t) = γt(s), we obtain a map G : [0,1] × [0,1] → E such that G(0,0) = e and p(G(s,t)) = γt(s), 0 ≤ s, t ≤ 1. Then the path αt in E defined by αt(s) = G(s,t), 0 ≤ t ≤ 1, is a lift of γt and α0 = α. We claim that the αt’s all start at e. To see this, observe that the map t → G(0,t) is the unique lift to E, starting at e, of the constant path at b. Hence the lift coincides with the constant path at e and e = G(0,t) = αt(0), 0 ≤ t ≤ 1. Similarly, the map t → G(1,t) is the unique lift to E, starting at G(1,0) = α(1), of the constant path at b. Hence α(1) = G(1,t) = αt(1) for 0 ≤ t ≤ 1 and all of the paths αt terminate at α(1). In particular, the lift α1 of γ1 to E starts at e and terminates at α(1).
We conclude that the terminal point α(1) is the same for all loops in the same homotopy class of γ. This allows us to define a function
Φ : π1(X,b) → p−1(b),
so that Φ([γ]) is the terminal point of the lift of γ to E that starts at e.
As an application, consider the figure eight X and its covering space E given in the illustration. The loop αβ in X lifts to a path in E that begins at e and terminates
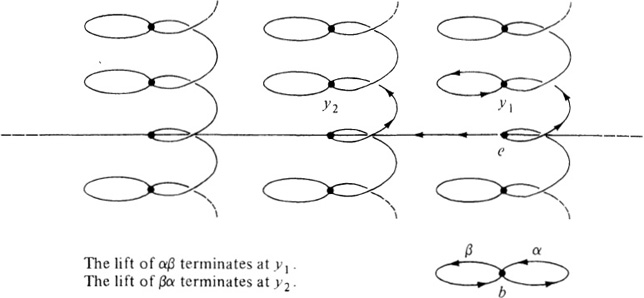
at y1 On the other hand, the loop αβ in X lifts to a path in E that begins at e and terminates at y2. Since y1 ≠ y2, αβ is not homotopic to βα and
[α][β] ≠ [β][α].
Thus we arrive at the striking discovery that the fundamental group of the figure eight is not commutative. By applying the idea used above to more elaborate covering spaces, it is possible to prove Van Kampen’s Theorem, that the fundamental group of the figure eight is the group called the free group on two generators (Exercise 6).
5.4 Theorem: Let p : (E,e) → (X,b) be a covering map and suppose that E is simply connected. Then Φ is a one-to-one correspondence of π1(X,b) and the fiber p−1(b).
Proof: Suppose that y ![]() p−1(b). Let α be a path in E from e to y and set γ = pºα. Then α is the lift of γ to E that starts at e, so that Φ([γ]) = α(1) = γ. Hence the function Φ is onto.
p−1(b). Let α be a path in E from e to y and set γ = pºα. Then α is the lift of γ to E that starts at e, so that Φ([γ]) = α(1) = γ. Hence the function Φ is onto.
Suppose that γ0 and γ1 are loops in X based at b such that Φ([γ0]) = Φ([γ1]). Let α0 and α1 be lifts of γ0 and γ1 respectively, that start at e. Then α0 and α1 have the same terminal point, so that the path α0α1−1 in E is a loop based at e. Since E is simply connected, there is a homotopy F : [0,1] × [0,1] → E of α0α1−1 to the point e. Then p∘F : [0,1] × [0,1] → X is a homotopy of the loop γ0γ1−1 to the point b. Hence [γ0][γ1]−1 = [b] and [y0] = [γ1]. It follows that Φ is one-to-one. ![]()
As a corollary of the proof, we obtain the following.
5.5 Corollary: Let p : (E,e) → (X,b) be a covering map and suppose that E is simply connected. For each point y ![]() p−1(b), let αy be a path in E from e to y and let γy = p∘αy be a loop in X based at b. If γ is any loop in X based at b, then there is a unique loop γy such that γ is homotopic to γy with endpoints fixed.
p−1(b), let αy be a path in E from e to y and let γy = p∘αy be a loop in X based at b. If γ is any loop in X based at b, then there is a unique loop γy such that γ is homotopic to γy with endpoints fixed.
As an example, we apply Theorem 5.4 to the covering map
p : Sn → Pn
discussed earlier in this section. Let e be the north pole of Sn and let b = p(e). Then p−1(b) consists of two points, the north and south poles of Sn. If n ≥ 2, then Sn is simply connected (Exercise 3.1). Consequently Theorem 5.4 applies and π1(Pn, b) has exactly two elements. One element is the identity, and the other element is the homotopy class of p∘α, where α is any path on Sn from the north pole to the south pole. Since any group with two elements is isomorphic to ![]() 2, we obtain
2, we obtain
π1(Pn) ≅ ![]() 2, n ≥ 2.
2, n ≥ 2.
Now we return to the prototypical covering map p : (![]() ,0) → (S1, 1) given by (5.1). Since p−1(1) coincides with the subset
,0) → (S1, 1) given by (5.1). Since p−1(1) coincides with the subset ![]() of
of ![]() consisting of the integers, the elements of the fundamental group π1(S1,1) are in one-to-one correspondence with the integers. We wish to show that this correspondence is a group isomorphism. For this, we consider in detail the procedure by which a loop in S1 determines an integer.
consisting of the integers, the elements of the fundamental group π1(S1,1) are in one-to-one correspondence with the integers. We wish to show that this correspondence is a group isomorphism. For this, we consider in detail the procedure by which a loop in S1 determines an integer.
Let γ be a loop in S1 based at 1. Then the lift of γ is a map
h : [0,1] → ![]()
that satisfies
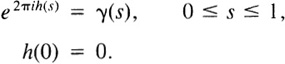
The terminal point h(1) of h is then an integer, which is called the index of γ and denoted by ind(γ). Thus ind(γ) is the element of p−1(0) associated with [γ] by Theorem 5.4.
5.6 Theorem: Two loops α and β in S1 based at 1 are in the same homotopy class if and only if they have the same index. The correspondence
[α] → ind(α)
is an isomorphism of π1(S1, 1) and the integers ![]() .
.
Proof: The only item that remains to be proved is that the correspondence is a homomorphism. To verify this, it suffices to show that
ind(α1α2) = ind(α1) + ind(α2)
whenever α1 and α2 are both loops in S1 based at 1.
Choose maps h1, h2 : [0,1] → ![]() so that h1(0) = h2(0) = 0 and
so that h1(0) = h2(0) = 0 and
αj(S) = e2πihj(s), 0 ≤ s ≤ 1; j = 1,2.
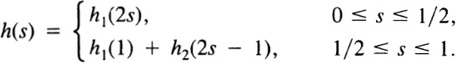
Then h : [0,1] → ![]() is continuous, h(0) = 0, and
is continuous, h(0) = 0, and
(α1α2)(s) = e2πih(s), 0 ≤ s ≤ 1.
Consequently
ind(α1α2) = h(1) = h1(1) + h2(1) = ind(α1) + ind(α2). ![]()
In Chapter IV we shall generalize the notion of index to mappings of the n-sphere. In that context, the integer associated with a map will be called the degree of the map. Thus ind(γ) coincides with the degree deg(γ) of γ, to be defined in Chapter IV. It is a historical accident that the terminology used for curves on the plane differs from that used in higher-dimensional topology.
1. For m an integer, let αm be the loop in S1 defined by
αm(s) = e2πims, 0 ≤ s ≤ 1.
Show that every loop in S1 based at 1 is homotopic with endpoints fixed to precisely one of the loops αm.
2. Suppose that p : (E,e) → (X,b) is a covering map and that E is simply connected. Suppose furthermore that E and X are groups with identities e and b, respectively, and that p is a homomorphism. Suppose finally that for each fixed y ![]() E, the group multiplication z → y * z is a continuous function on E. Prove that the fiber p−1(b) is a subgroup of E, and that
E, the group multiplication z → y * z is a continuous function on E. Prove that the fiber p−1(b) is a subgroup of E, and that
π1(X,b) ≅ p−1(b).
3. Show that the exponential map p : ![]() n → Tn, defined earlier in this section, is a covering map of
n → Tn, defined earlier in this section, is a covering map of ![]() n onto the n-torus Tn. Show that
n onto the n-torus Tn. Show that
π1(Tn) ≅ ![]() ⊕ . . . ⊕
⊕ . . . ⊕ ![]() (n summands).
(n summands).
For each n-tuple (m1, . . . , mn) ![]()
![]() ⊕ . . . ⊕
⊕ . . . ⊕ ![]() , define explicitly a loop in Tn based at (1, . . . ,1) in the corresponding homotopy class.
, define explicitly a loop in Tn based at (1, . . . ,1) in the corresponding homotopy class.
4. Show that the map p : ![]() →
→ ![]() \{0}, defined by
\{0}, defined by
p(z) = ez, z ![]()
![]() ,
,
is a covering map. What is π1(![]() \{0})?
\{0})?
5. Show that the restriction of the map p of Exercise 4 to the horizontal strip E = {x + iy : c < y < d} is a covering map of E over the open annulus {w : ec < |w| < ed}. What is the fundamental group of the open annulus?
What is the fundamental group of a closed annulus?
6. Let X be the figure-eight space, and let α and β be the loops in X indicated in the figure and discussion preceding Theorem 5.4. Show that every element of π1(X) can be expressed uniquely as a finite product
[α]m1[β]m2[α]m3. . . ,
where m1m2, . . . are integers and mj ≠ 0 for j ≥ 2 (m1 = 0 is allowed). Note: This proves Van Kampen’s Theorem, that π1(X) is the free group with generators [α] and [β]. For the uniqueness assertion, construct an appropriate covering space of X.
7. A topological space Y is locally path-connected if for each y ε Y and neighborhood U of y, there exists a neighborhood V of y such that every point of V can be joined to y by a path in U. Let (Y,c) be a pointed topological space such that Y is locally path-connected and simply connected, let p : (E,e) → (X,b) be a covering map.
(a) Show that every map f : (Y,c) → (X,b) can be uniquely lifted to a map g : (Y,c) → (E,b).
(b) Suppose in addition that X is locally path-connected and E is simply connected. Show that if f is a covering map, then g is a homeo-morphism of Y and E. (In other words, a simply connected covering space of a locally path-connected space is unique.)
8. Let p : E → X be a covering map. A map ![]() is a covering transformation if p∘f = f.
is a covering transformation if p∘f = f.
(a) Show that with the operation of composition, the covering transformations form a group.
(b) Show that if X is locally path-connected and E is simply connected, then the group of covering transformations is isomorphic to the fundamental group of X.
9. What are the covering transformations of S2 over P2? of ![]() over S1?
over S1?
10. Let X be a path-connected topological space such that every x ![]() X has an open neighborhood that is simply connected. Fix b ε X and let E be the set of all pairs (x, [γ]), where x
X has an open neighborhood that is simply connected. Fix b ε X and let E be the set of all pairs (x, [γ]), where x ![]() X and γ is a path in X from b to x. For each simply connected open subset U of X and each path γ in X starting at b and terminating at some point γ(1)
X and γ is a path in X from b to x. For each simply connected open subset U of X and each path γ in X starting at b and terminating at some point γ(1) ![]() U, define W(U, γ) to be the set of all pairs (x, [γ][α]) in E such that x
U, define W(U, γ) to be the set of all pairs (x, [γ][α]) in E such that x ![]() U and α is a path in U from γ(1) to x. Prove the following.
U and α is a path in U from γ(1) to x. Prove the following.
(a) The sets W(U, γ) form a base for a topology for E.
(b) The natural projection (x, [γ]) → x of E onto X is a covering map.
(c) E is simply connected.
Remark: By Exercise 7, the space E is essentially unique. It is called the universal covering space of X.
11. Let X be the quotient space obtained from the union of circles {x2 + y2 = 1, z = 1/n} in ![]() 3, for 1 ≤ n ≤ ∞, by identifying the set {(1,0,1/n) : 1 ≤ n ≤ ∞} to a point b. Show that if p : (E,e) → (X,b) is a covering map, then E is not simply connected. (Thus X has no universal covering space. Why does Exercise 10 not apply?)
3, for 1 ≤ n ≤ ∞, by identifying the set {(1,0,1/n) : 1 ≤ n ≤ ∞} to a point b. Show that if p : (E,e) → (X,b) is a covering map, then E is not simply connected. (Thus X has no universal covering space. Why does Exercise 10 not apply?)
Recall that Bn is the closed unit ball in ![]() n. It will be convenient to identify
n. It will be convenient to identify ![]() 2 and
2 and ![]() so that B2 becomes the closed unit disc in the complex plane, with boundary circle S1. The applications to be presented in this section are based on the following theorem.
so that B2 becomes the closed unit disc in the complex plane, with boundary circle S1. The applications to be presented in this section are based on the following theorem.
6.1 Theorem: Let f be a map from B2 to S1 that satisfies f(1) = 1. Then the loop α, defined by
α(s) = f(e2πis), 0 ≤ s ≤ 1,
has index zero:
ind(α) = 0.
Proof: Define a loop β in B2 by
β(s) = e2πis, 0 ≤, s ≤ 1.
Then α = f∘β. Since B2 is convex, Corollary 4.2 shows that α is homotopic with endpoints fixed to the constant loop in S1 at 1. By Theorem 5.6, ind(α) = 0. ![]()
The first application asserts that S1 is not a retract of B2.
6.2 Theorem: There is no map f of B2 onto S1 such that f(z) = z for all z ![]() S1.
S1.
Proof: If there were such a map f, then the loop s → e2πis, 0 ≤ s ≤ 1, in S1 would have index zero, by Theorem 6.1. However, the index of the loop is 1. ![]()
There is another proof of Theorem 6.2, one which illustrates more clearly the method of algebraic topology (sometimes referred to as algebraic arrowology), that is, the converting of topological problems to problems in algebra.
Alternate Proof: Let ![]() be the inclusion map. By Theorem 4.3, the mappings in the following commutative diagram
be the inclusion map. By Theorem 4.3, the mappings in the following commutative diagram
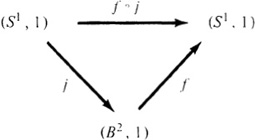
generate the following commutative diagram of group homomorphisms:
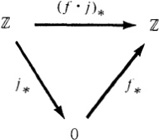
Since f∘j is the identity map of S1, (f∘j)* = f*∘j* is the identity isomorphism of ![]() ≅ π1(S1, 1). However, since π(B2, 1) = 0, both f* and j* are the zero homo-morphisms. Again we have reached a contradiction.
≅ π1(S1, 1). However, since π(B2, 1) = 0, both f* and j* are the zero homo-morphisms. Again we have reached a contradiction. ![]()
A point x ![]() X is a Fixed point of a map f : X → X if f(x) = x. In general, one does not expect a map to have a fixed point. For instance, the antipodal map z → − z of Sn onto Sn has no fixed points. In contrast, the celebrated Brouwer Fixed Point Theorem asserts that every map f : Bn → Bn has a fixed point. We prove this theorem in the special case where n = 2. The general case is treated in Chapter IV.
X is a Fixed point of a map f : X → X if f(x) = x. In general, one does not expect a map to have a fixed point. For instance, the antipodal map z → − z of Sn onto Sn has no fixed points. In contrast, the celebrated Brouwer Fixed Point Theorem asserts that every map f : Bn → Bn has a fixed point. We prove this theorem in the special case where n = 2. The general case is treated in Chapter IV.
6.3 Theorem: Any map f : B2 → B2 has a fixed point.
Proof: Suppose that f has no fixed point. For each z ![]() B2, let g(z) be the point of
B2, let g(z) be the point of
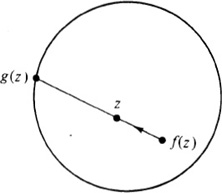
S1 at which the ray issuing from f(z) and passing through z leaves B2. Then g is a continuous map from B2 to S1 (the proof is left as an exercise). Since g(z) = z if z ![]() S1, we obtain a contradiction to Theorem 6.2.
S1, we obtain a contradiction to Theorem 6.2. ![]()
The next application involves a preliminary reduction and then a more detailed analysis of the behavior of the index. Lurking in the background is projective space.
6.4 Theorem (Borsuk-Ulam Theorem): Let f be a map from S2 to ![]() 2. Then there exist antipodal points w and − w in S2 such that f(w) = f(− w).
2. Then there exist antipodal points w and − w in S2 such that f(w) = f(− w).
Proof: Define a map g : S2 → ![]() 2 by
2 by
g(w) = f(w) − f(− w), w ![]() S2.
S2.
We must show that g vanishes at some point of S2. The proof will depend only on the following property of g :
Consider the map h : B2 → ![]() 2 defined by
2 defined by
![]()
Here the nonnegative value of the square root is taken, so that h is obtained from g by flattening the top half of S2 onto the closed disc B2. From (6.1) we have
It suffices to show that any map h from B2 to ![]() 2 satisfying (6.2) vanishes at some point of B2.
2 satisfying (6.2) vanishes at some point of B2.
Suppose that such an h does not vanish on B2. Then
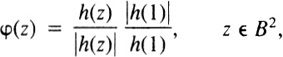
defines a map φ : B2 → S1 which satisfies
By Theorem 6.1, the path
α(s) = φ(e2πis), 0 ≤ s ≤ 1,
has index zero. We aim to obtain a contradiction by showing that the index of α is odd.
Choose k : [0,1] → ![]() such that
such that
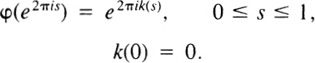
Then ind(α) = k(1). The condition (6.3) shows that
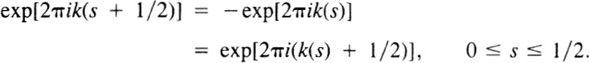
For each fixed s ![]() [0,1/2], the number
[0,1/2], the number
is then an integer. Since the function defined by (6.5) depends continuously on s and has discrete range, it is constant—equal to the integer m, say—so that
k(s + 1/2) – k(s) = m + 1/2, 0 ≤ s ≤ 1/2.
Then
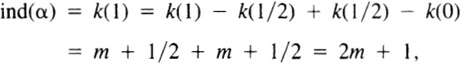
an odd integer. ![]()
6.5 “Corollary”: At any given instant of time, there are two antipodal points on the surface of the earth at which the temperature and the wind speed are the same.
The next result concerns the division of volumes by planes. It derives its picturesque name from its interpretation as the assertion that it is possible, with a single knife stroke, to divide two pieces of bread and a piece of ham each into equal halves, no matter how irregular the three pieces or how askew their relative locations.
6.6 Theorem (Ham Sandwich Theorem): Let U, V, and W be three bounded connected open subsets of ![]() 3. Then there is a plane in
3. Then there is a plane in ![]() 3. that divides each of the sets into two pieces of equal volume.
3. that divides each of the sets into two pieces of equal volume.