CHAPTER 10
Study this chapter to learn about:
The following sections all concern part-to-whole relationships. A part-to-whole relationship can be expressed as a fraction, decimal, percent, or ratio. It may seem simplistic, but envisioning a pie in these questions often helps conceptualize the situation. It’s equally important that you remember that the part must always refer to a whole. People often have a tendency to say things like, “I have one-fourth,” or “Jack has 20%.” But these statements beg the question: one-fourth of what? 20 percent of what? When expressing these relationships algebraically, remember that the part must always be a piece of some quantity.
Fractions
This section discusses fractions. A fraction is a way to represent a piece of a whole. Fractions look like the following:
1 →numerator
4 →denominator
When thinking of fractions, imagine one pie. The denominator tells you how many slices the pie is broken into, and the numerator tells you how many of those slices you have. So the fraction  means you have 1 slice of a pie that has been cut into 4 slices.
means you have 1 slice of a pie that has been cut into 4 slices.
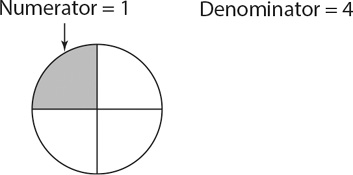
Now let’s look at what happens when the numerator and denominator of a fraction change. Let’s compare  to
to  .
.
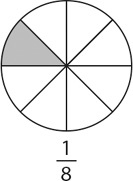
In this case, you are still dealing with one pie, but now the pie is broken up into 8 slices instead of 4. One slice out of 8 is less than 1 slice out of 4. From this, you can derive a general rule:
As the denominator of a positive fraction increases, the value of the fraction decreases.
Now let’s compare 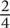 to
to  .
.

Again, each fraction represents one pie, and in both cases, the number of slices is the same. Two slices from a 4-slice pie is more than 1 slice from a 4-slice pie. Thus 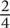 is greater than
is greater than  . From this, you can derive a general rule:
. From this, you can derive a general rule:
As the numerator of a positive fraction increases, the value of the fraction increases.
Quantitative Comparison Strategy: Fractions
When the quantities in a Quantitative Comparison question are fractions, focus on the relationships between numerator and denominator. If the denominators are the same, the fraction with the larger numerator will be greater. If the numerators are the same, the fraction with the smaller denominator will be greater.

SOLUTION: Since the numerators of the fractions are the same, the fraction with the smaller denominator will be greater. 100 < 1002. Thus Quantity A is greater.
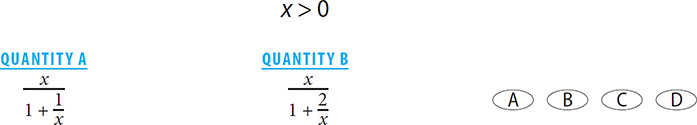
SOLUTION: The fractions in the two quantities have the same numerator. Thus the fraction with the smaller denominator will be greater. Since the numerator in 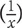 is smaller than the numerator in
is smaller than the numerator in 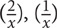 is a smaller fraction, which means the denominator in Quantity A is smaller. Since the denominator in Quantity A is smaller, the value of the fraction in Quantity A is greater. The correct answer is A.
is a smaller fraction, which means the denominator in Quantity A is smaller. Since the denominator in Quantity A is smaller, the value of the fraction in Quantity A is greater. The correct answer is A.
What if the fractions are negative? The opposite relationships apply:
As the denominator of a negative fraction increases, the value of the fraction increases.
As the numerator of a negative fraction increases, the value of the fraction decreases.
To understand why this is the case, compare  and
and 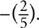 You know that
You know that 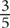 is a larger piece of a pie than is
is a larger piece of a pie than is 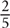 . But since
. But since 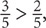 the negative version of
the negative version of 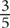 will be more negative than the negative version of
will be more negative than the negative version of 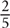 . If
. If 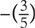 is more negative than
is more negative than  then
then  must be smaller. See the number line below for illustration:
must be smaller. See the number line below for illustration:
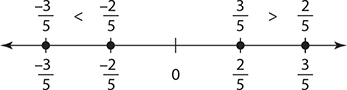
Improper Fractions
Any fraction in which the numerator is larger than the denominator is an improper fraction. Look at the fraction 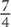 . In this case, the denominator is 4, which means the pie you are working with is cut up into 4 slices. The numerator tells you that you have 7 slices of this pie. If you have 7 slices of a 4-slice pie, then you have more than one pie. In fact, you have one 4-slice pie
. In this case, the denominator is 4, which means the pie you are working with is cut up into 4 slices. The numerator tells you that you have 7 slices of this pie. If you have 7 slices of a 4-slice pie, then you have more than one pie. In fact, you have one 4-slice pie 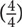 and 3 additional slices of that pie
and 3 additional slices of that pie 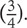
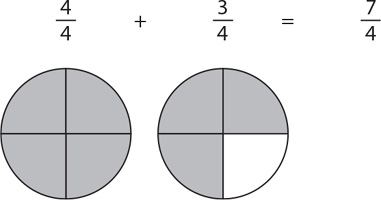
You can write this as a mixed number: 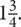 A mixed number is any number that is written as an integer and a fraction. To convert from a mixed number to an improper fraction, do the following:
A mixed number is any number that is written as an integer and a fraction. To convert from a mixed number to an improper fraction, do the following:
1. Multiply the integer by the denominator of the fraction: in this case, 1 × 4 = 4
2. Take that product and add it to the numerator of the fraction: in this case, 4 + 3 = 7
3. Take the result of Step 2 and put it above the original denominator: 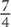 .
.
Skills Check: Improper Fractions
Write each of the following as an improper fraction. See the end of this section for the answers.

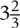

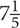

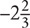
Adding and Subtracting Fractions
When adding or subtracting fractions, your goal is to manipulate the fractions to have the same denominator. If you are asked to solve for  +
+ 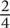 , the answer would be
, the answer would be  since you are adding 1 slice of a 4-slice pie to 2 slices of a 4-slice pie. You will end up with 3 slices of a 4-slice pie, which means you will have
since you are adding 1 slice of a 4-slice pie to 2 slices of a 4-slice pie. You will end up with 3 slices of a 4-slice pie, which means you will have  .
.
However, addition and subtraction of fractions will not always be so straightforward. Sometimes the fractions you are adding or subtracting will have different denominators, for example, 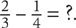 When adding or subtracting fractions with different denominators, you must first find a common denominator. To do so, find the smallest number that is a multiple of both denominators. In this case, the smallest number that is a multiple of 3 and 4 is 12. Now you need to manipulate both fractions to have a denominator of 12. To do so, you will multiply.
When adding or subtracting fractions with different denominators, you must first find a common denominator. To do so, find the smallest number that is a multiple of both denominators. In this case, the smallest number that is a multiple of 3 and 4 is 12. Now you need to manipulate both fractions to have a denominator of 12. To do so, you will multiply.
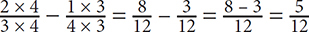
Comparing Fractions with Different Numerators and Denominators
Using a common denominator is also helpful when comparing fractions whose numerators and denominators differ. Look at the following Quantitative Comparison question.

SOLUTION: Express both fractions with a denominator of 72. Quantity A: 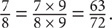 Quantity B:
Quantity B: 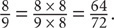 Now the comparison is
Now the comparison is  The fractions have the same denominator, but the numerator of the second fraction is greater. Thus Quantity B is greater.
The fractions have the same denominator, but the numerator of the second fraction is greater. Thus Quantity B is greater.
Multiplying Fractions
The product of two positive fractions will always be smaller than either of the factors, for example, 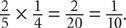
Why is this the case? When you multiply fractions, you are essentially taking a piece of a piece. In other words, multiplying  by
by 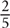 means that you are looking for
means that you are looking for 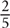 of
of  . Or it can mean that you are taking
. Or it can mean that you are taking  of
of 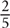 . In either case, the result is a piece of both original fractions, meaning that the result will be smaller than either fraction. Look at the following Quantitative Comparison question.
. In either case, the result is a piece of both original fractions, meaning that the result will be smaller than either fraction. Look at the following Quantitative Comparison question.
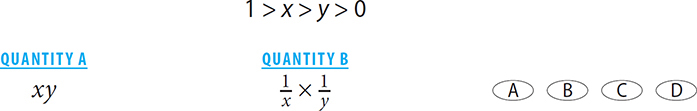
SOLUTION: Since x and y are between 0 and 1, their product must be a fraction. Thus the value in Quantity A must be a fraction. Since x and y are between zero and 1, their respective reciprocals must be greater than 1. Thus the factors of the product in Quantity B are each greater than 1. Since both factors are greater than 1, the product must be greater than 1. Thus Quantity B is greater.
Generally, when multiplying fractions, you should multiply all the numerators and all the denominators. For example:
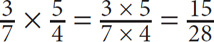
However, sometimes you will be able to reduce the fractions before multiplying:

SOLUTION: Before multiplying, cancel out the common factors:
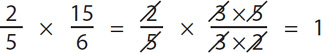
The answer is 1.
Dividing Fractions
When dividing by a fraction, multiply the numerator by the reciprocal of the fraction in the denominator. To find the reciprocal of a fraction, simply switch the terms in the numerator and denominator.
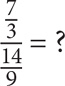
SOLUTION: Multiply 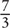 by the reciprocal of
by the reciprocal of 
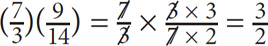
Fractions in Word Problems
Many word problems will test your understanding of fractions in real-world contexts. In many of these questions, you will be given a value for the part and will be asked to solve for the whole or vice versa. In these questions, it is essential to remember the following relationship: part = fraction × whole. As you are given information, track how that information fits into that formula. Look at the following example:
Of the 120 boys in a school,  are taking chemistry. If
are taking chemistry. If 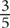 of the students in the school are boys, the number of boys taking chemistry is what fraction of all the students at the school?
of the students in the school are boys, the number of boys taking chemistry is what fraction of all the students at the school?
SOLUTION: You are being asked to solve for the number of boys taking chemistry as a fraction of all students at the school, so the numerator should be “number of boys taking chemistry” and the denominator should be “the number of students in the school.” Now use the information from the question to solve for these values.
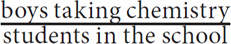
SOLUTION: In the first sentence, you are told that  of all the boys are taking chemistry. Since there are 120 students in the school, the number of boys taking chemistry =
of all the boys are taking chemistry. Since there are 120 students in the school, the number of boys taking chemistry =  × 120 = 90. Now figure out the number of students in the school. The whole is the number of students, the part is the number of boys, and
× 120 = 90. Now figure out the number of students in the school. The whole is the number of students, the part is the number of boys, and 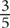 is the fraction. Thus 120 =
is the fraction. Thus 120 = 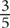 × n, where n is the number of students in the school. Multiply both sides of the equation by
× n, where n is the number of students in the school. Multiply both sides of the equation by 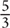 to solve for n:
to solve for n:
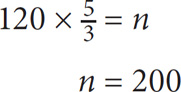
SOLUTION: So the fraction you arrive at is 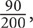 which reduces to
which reduces to 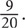
Plugging in Numbers with Fractions
In many fraction questions, you will be given unspecified amounts and asked to solve for a relationship between these amounts. In these situations, the best strategy is to choose values that satisfy the relationships in the question. When plugging in numbers for fraction questions with no specified amounts, keep the following tips in mind:
 When choosing a value, choose a value for the whole. For example, if you are told that
When choosing a value, choose a value for the whole. For example, if you are told that 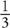 of the employees in a company are administrators and that
of the employees in a company are administrators and that  of the administrators are men, then choose a value for the number of employees (the whole), and not the administrators or men.
of the administrators are men, then choose a value for the number of employees (the whole), and not the administrators or men.
 Choose a value for the whole that will be divisible by the denominators of all the fractions in the question. For example, if you are told that
Choose a value for the whole that will be divisible by the denominators of all the fractions in the question. For example, if you are told that 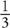 of the employees in a company are administrators and that
of the employees in a company are administrators and that  of the administrators are men, then the value you choose for the number of employees should be divisible by 3 (the denominator of the first fraction) and 4 (the denominator of the second fraction). Good numbers here would be multiples of 12. Why is this strategy important? Because to the extent that it is possible, you want to work with integers. If the number that you choose is not divisible by 3 or 4, then the value for one of the parts will end up being a fraction, and the math will almost certainly be messier.
of the administrators are men, then the value you choose for the number of employees should be divisible by 3 (the denominator of the first fraction) and 4 (the denominator of the second fraction). Good numbers here would be multiples of 12. Why is this strategy important? Because to the extent that it is possible, you want to work with integers. If the number that you choose is not divisible by 3 or 4, then the value for one of the parts will end up being a fraction, and the math will almost certainly be messier.
Let’s look at an example:
Two-thirds of the cars in a lot are sedans, and the rest are trucks. If 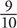 of the sedans are new and
of the sedans are new and 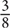 of the trucks are new, what fraction of the cars in the lot are used?
of the trucks are new, what fraction of the cars in the lot are used?
SOLUTION: Since the question does not provide any amounts, you should choose numbers to determine values for the total number of cars and the number of used cars. Based on the first tip provided earlier, you should choose a value for the whole, which in this case is the total number of cars. Based on the second tip, the value you choose should be divisible by 3, 8, and 10. The most obvious value here is 3 × 8 × 10 = 240. If there are 240 cars, then 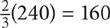 = 160 are sedans, and the other 80 are trucks. Now determine how many sedans and how many trucks are used. If
= 160 are sedans, and the other 80 are trucks. Now determine how many sedans and how many trucks are used. If 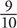 of the sedans are new, then the remaining
of the sedans are new, then the remaining 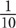 are used.
are used. 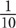 of 160 = 16, so there are 16 used sedans. If
of 160 = 16, so there are 16 used sedans. If 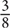 of the trucks are new, then
of the trucks are new, then 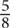 are used.
are used. 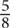 of 80 = 50, so 50 of the trucks are used. In total, there are 50 + 16 = 66 used cars. The final fraction of used cars/total cars
of 80 = 50, so 50 of the trucks are used. In total, there are 50 + 16 = 66 used cars. The final fraction of used cars/total cars 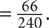 Divide the numerator and denominator by 6 and arrive at
Divide the numerator and denominator by 6 and arrive at 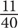 .
.
Decimals
A decimal is another way of representing a fraction, for example,  = 0.25,
= 0.25, 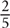 = 0.4, and so on.
= 0.4, and so on.
Place Values
Every digit in a number has a place value. For example, in the number 237.98, 2 is in the hundreds place, 3 is in the tens place, 7 is in the units place, 9 is in the tenths place, and 8 is in the hundredths place.
Place Values and Powers of 10
Look at what happens when you multiply the preceding value by 10:
237.98 × 10 = 2,379.8
Note that the digits haven’t changed, but their place values have! This illustrates an important point: Whenever you multiply or divide a number by a power of 10, the decimal of the number shifts:
If you multiply a number by a positive power of 10, the decimal will move to the right as many places as the value of the exponent.
2.79 × 103 = 2,790
321.98 × 10 = 3,219.8
If you divide a number by a positive power of 10, the decimal will move to the left as many places as the value of the exponent:
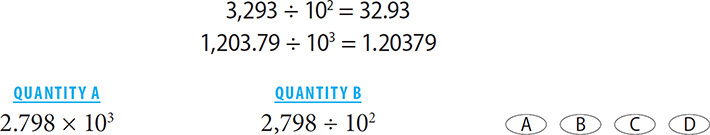
SOLUTION: Move the decimal three places to the right in Quantity A: 2,798. Move the decimal two places to the left in Quantity B: 27.98. Quantity A is greater.
The process also works in reverse. If you are doing calculations with a number that has a lot of zeros to the right or to the left of the decimal, you can use powers of 10 as shorthand for those values:
2,400,000 = 24 × 105
0.00037 = 37 ÷ 105 = 37 × 10–5
Let’s look at a GRE-style example:
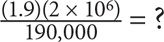
 0.02
0.02
 0.2
0.2
 2
2
 20
20
 200
200
SOLUTION: To make the calculations easier, express the denominator as 1.9 × 105. The fraction now reads:
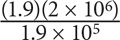
SOLUTION: Divide numerator and denominator by 1.9 to arrive at:
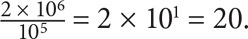 The correct answer is D.
The correct answer is D.

Exercise: Fractions and Decimals
Discrete Quantitative Questions
1. 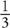 of the cookies in a jar are chocolate chip,
of the cookies in a jar are chocolate chip,  of the remaining cookies are peanut butter, and the rest of the cookies are white chocolate. If 20 cookies are white chocolate, how many cookies are in the jar?
of the remaining cookies are peanut butter, and the rest of the cookies are white chocolate. If 20 cookies are white chocolate, how many cookies are in the jar?
 40
40
 60
60
 70
70
 90
90
 100
100
2. 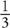 of the 120 marbles in a jar are red. If 20 red marbles are taken out and 40 black marbles are added, what fraction of the marbles in the jar will be red?
of the 120 marbles in a jar are red. If 20 red marbles are taken out and 40 black marbles are added, what fraction of the marbles in the jar will be red?



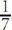





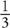
For this question, write your answer in the box.
3. What is 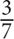 of
of 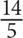 of
of 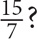
4. 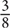 of the students in a school are male, and
of the students in a school are male, and 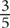 of the male students take calculus. If
of the male students take calculus. If  of the female students take calculus, what fraction of the students at the school do not take calculus?
of the female students take calculus, what fraction of the students at the school do not take calculus?

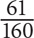

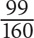

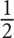

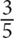

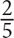
5. Upon winning the lottery, John spent 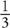 of his winnings on a home and
of his winnings on a home and  of the remaining amount on a car. After these purchases, he had $200,000 left. How much money did John win in the lottery?
of the remaining amount on a car. After these purchases, he had $200,000 left. How much money did John win in the lottery?
 400,000
400,000
 480,000
480,000
 600,000
600,000
 800,000
800,000
 2,400,000
2,400,000
6. Jar X is currently filled to 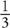 of its capacity with water, and Jar Y is filled to
of its capacity with water, and Jar Y is filled to  of its capacity with water. If Jar Y has double the capacity of Jar X, what fraction of Jar Y would be filled when the contents of Jar X are poured into Jar Y?
of its capacity with water. If Jar Y has double the capacity of Jar X, what fraction of Jar Y would be filled when the contents of Jar X are poured into Jar Y?


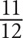

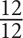

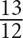

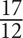
For this question, indicate all of the answer choices that apply.
7. If 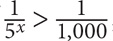 , then x could equal which of the following values?
, then x could equal which of the following values?
 1
1
 2
2
 3
3
 4
4
 5
5
 6
6
8. Which of the following fractions has the greatest value?

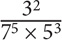

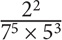

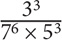

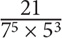

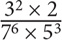
9. A $360,000 inheritance is split equally among three siblings. If one of the siblings splits her share equally among herself and her three children, how much of the inheritance does each of the three children get?
 22,500
22,500
 30,000
30,000
 40,000
40,000
 90,000
90,000
 120,000
120,000
10. Each month, Janet saves 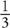 of her paycheck and spends the rest. The amount of money Janet saves in a month is what fraction of the amount that she spends in a year?
of her paycheck and spends the rest. The amount of money Janet saves in a month is what fraction of the amount that she spends in a year?

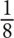

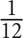

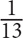

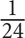

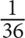
11. Bob, Peter, and Stan are going to combine all their savings to invest in a business. The amount of money in Bob’s savings is  of the amount in Stan’s savings. The amount in Peter’s savings is double the amount in Stan’s savings. If Stan decides to invest only
of the amount in Stan’s savings. The amount in Peter’s savings is double the amount in Stan’s savings. If Stan decides to invest only  of his savings into the business, then the amount that Stan invests will be what fraction of the amount that Bob and Peter invest combined?
of his savings into the business, then the amount that Stan invests will be what fraction of the amount that Bob and Peter invest combined?

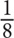

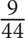

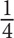

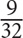

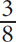
12. All of the following fractions are greater than  EXCEPT
EXCEPT

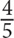

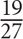

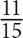

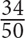

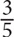
For this question, write your answer in the box.
13. If (1.5 × 104) × 10x = 150, then what is the value of x?

14. After doing the last step of a certain calculation, Bob arrived at an answer of 387. Bob then realized that he had accidentally multiplied by 100 instead of dividing by 100. Had he done the calculations correctly, what would the result have been?
 0.000387
0.000387
 0.00387
0.00387
 0.0387
0.0387
 0.387
0.387
 3.87
3.87
Quantitative Comparison Questions
1. 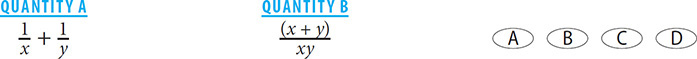
2. 
3. 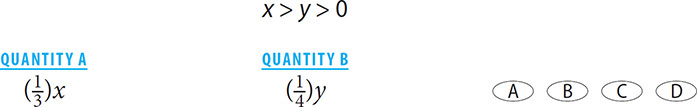
4. 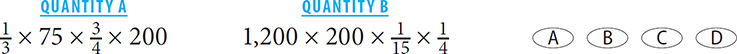
5. 
6. 
7. 
8. 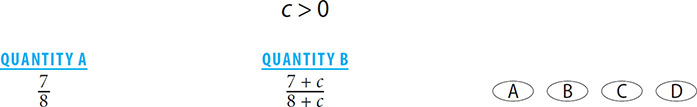
9. 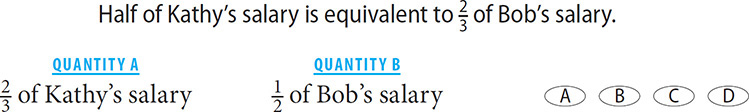
10. 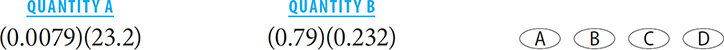
11. 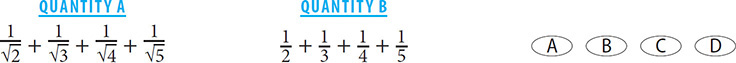
Exercise Answers
Skills Check: Improper Fractions
A. 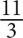
B. 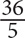
C. 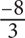
Discrete Quantitative Questions
1. D Since you are not told how many cookies are in the jar, assign a variable: j. Now express the different quantities in terms of j. If 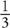 of the cookies are chocolate chip, then chocolate chip cookies =
of the cookies are chocolate chip, then chocolate chip cookies = 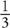 j.
j.  of the remaining cookies are peanut butter. The remaining cookies in the jar =
of the remaining cookies are peanut butter. The remaining cookies in the jar =  j, so the number of peanut butter cookies will be
j, so the number of peanut butter cookies will be  (
( )j = (
)j = ( )j. Finally, you know that the remaining 20 cookies are white chocolate. What is the relationship between all these quantities? They must add up to the total: j. You should thus set up the following relationship:
)j. Finally, you know that the remaining 20 cookies are white chocolate. What is the relationship between all these quantities? They must add up to the total: j. You should thus set up the following relationship: 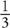 j +
j +  j + 20 = j. Combine like terms:
j + 20 = j. Combine like terms:
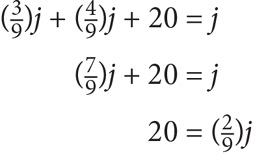
Multiply both sides by 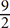 :
:
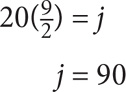
2. B To answer the question, you need a fraction where the numerator will be the number of red marbles left after 20 are removed, and the denominator will be the total number of marbles after 20 red marbles are removed and 40 black marbles are added. The denominator is easier to solve, so start there. After 20 red marbles are taken away, there are 100 total marbles. After 40 black marbles are added, there are 140 total marbles. The denominator of the fraction is 140. To determine a value for the numerator, first determine the number of red marbles before 20 are removed. Red marbles = 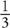 (120) = 40. There are originally 40 red marbles. After 20 are removed, there are 20. Thus the numerator of the fraction is 20. The fraction you are solving for will be
(120) = 40. There are originally 40 red marbles. After 20 are removed, there are 20. Thus the numerator of the fraction is 20. The fraction you are solving for will be 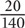 . Reduce and arrive at
. Reduce and arrive at 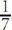 .
.
3. 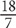 Solution: First reduce, then multiply:
Solution: First reduce, then multiply:
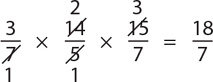
The correct answer is 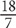 .
.
4. B Since this is a fraction question with no amounts given, you should plug in values. Choose a value for the number of students that will divide evenly by 8, 4, and 5. The best number here is 8 × 4 × 5 = 160. The denominator of the fraction will be 160, and the numerator will be the number of students who do not take calculus. First, determine how many males do not take calculus. The number of male students is 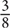 (160) = 60. If
(160) = 60. If 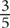 of these students take calculus, then
of these students take calculus, then 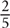 of them do not.
of them do not. 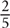 (60) = 24. 24 male students do not take calculus. Now solve for the number of females who do not take calculus. If there are 160 students and
(60) = 24. 24 male students do not take calculus. Now solve for the number of females who do not take calculus. If there are 160 students and 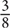 are male, then
are male, then 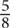 are female.
are female. 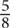 (160) = 100.
(160) = 100.  of these 100 females take calculus, so
of these 100 females take calculus, so  do not.
do not.  (100) = 75. So 75 female students do not take calculus. Add this to 24, which is the number of male students who do not take calculus. 24 + 75 = 99. Thus
(100) = 75. So 75 female students do not take calculus. Add this to 24, which is the number of male students who do not take calculus. 24 + 75 = 99. Thus 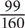 of the students do not take calculus.
of the students do not take calculus.
5. A Represent John’s winnings as w:
the amount spent on his home = 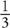 w
w
The amount spent on his car is  of what he did not spend on his home.
of what he did not spend on his home.
Since he spent (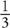 )w on his home, he has (
)w on his home, he has ( )w remaining.
)w remaining.
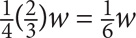
These two amounts + $200,000 will equal the total winnings. Expressed algebraically, the equation is 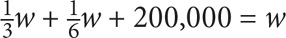 Now solve for w:
Now solve for w:
Multiply across the entire equation by 6:
2w + w + 1,200,000 = 6w
Combine like terms:
1,200,000 = 3w
Divide both sides by 3:
400,000 = w
6. B With so many relationships, this question can be confusing. Start by identifying the whole. The capacity of Jar Y is expressed in terms of the capacity of Jar X, so the capacity of Jar X is the whole. Next, plug in a value for the capacity of Jar X. Remember to choose a value that will be divisible by the denominators of the fractions in the question. In this case, 12 would be a good value for the capacity of Jar X since 12 is divisible by 3 and by 4. If the capacity of Jar X is 12, then the capacity of Jar Y is 24. Jar X is filled to 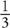 of its capacity, so it has
of its capacity, so it has 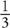 (12) = 4 units of water. Jar Y is filled to
(12) = 4 units of water. Jar Y is filled to  of its capacity, so it has
of its capacity, so it has  (24) = 18 units of water. If the water in Jar X is poured into Jar Y, then Jar Y will have 4 + 18 = 22 units of water. So the capacity of Jar Y is 24, and it will have 22 units of water. Thus the fraction of water in Jar Y =
(24) = 18 units of water. If the water in Jar X is poured into Jar Y, then Jar Y will have 4 + 18 = 22 units of water. So the capacity of Jar Y is 24, and it will have 22 units of water. Thus the fraction of water in Jar Y = 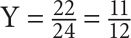 .
.
7. A, B, C, and D The fractions in the given inequality have the same numerator. If two positive fractions have the same numerator, then the fraction with the smaller denominator will be the greater value. Thus 5x must be less than 1,000. Now determine which values in the choices will satisfy the inequality: 5x < 1,000. 54 = 625, so any integer value less than or equal to 4 will satisfy the constraints. However, 55 = 3,125, so 5 and 6 are too large. The correct answers are A, B, C, and D.
8. D Though you can certainly calculate the value of each fraction, such an approach would be time-consuming. Since the question is asking you to compare fractions, identify any choices that have the same numerator or denominator. Notice that all of the fractions in Choices A, B, and D have the same denominator. Among those three choices, the fraction that has the greatest numerator will be the greatest: 21 > 32 > 22. Thus Choice D is the greatest among those three fractions. Now compare C and E. Both fractions have the same denominator, so the fraction with the greater numerator will be larger. 33 > 32 × 2, so the fraction in Choice C is greater than the fraction in Choice E. Now compare C and D. To arrive at an equal denominator in both fractions, multiply the numerator and denominator of the fraction in Choice D by 7:
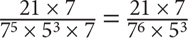
Now that the fractions have the same denominator, compare their numerators:
Choice C: 33
Choice D: 21 × 7
21 × 7 > 33. Thus the fraction in Choice D is greater.
9. B Since $360,000 is split equally among three siblings, each sibling receives 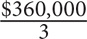 = $120,000. The sibling will then split this $120,000 into 4 parts (herself and her three children), so each child receives
= $120,000. The sibling will then split this $120,000 into 4 parts (herself and her three children), so each child receives 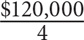 = $30,000.
= $30,000.
10. D Choose a value for Janet’s monthly paycheck. Since the denominator of the fraction is 3, a multiple of 3 would be a smart number. Let’s use 30. If Janet earns $30/month, then she saves $10/month and spends $20/month. If she spends $20 per month, then she spends $20 × 12 = $240/year. The fraction you are solving for is 10/240 = 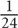 .
.
11. D Since this question has only fractions and no given amounts, plug in numbers. Bob’s and Peter’s savings are given in terms of Stan’s savings, so choose a value for Stan’s savings. Since the fractions in the question have denominators of 3 and 4, choose a multiple of 3 and 4 for Stan’s savings. Let’s use $12. If Stan’s savings is $12, then Bob’s savings is  ($12) = $8 and Peter’s savings is 2($12) = $24. Combined, Peter and Bob will invest $32. Originally, Stan was going to invest all $12, but now he will invest only
($12) = $8 and Peter’s savings is 2($12) = $24. Combined, Peter and Bob will invest $32. Originally, Stan was going to invest all $12, but now he will invest only  of that amount.
of that amount.  (12) = 9, so Stan will invest $9. Stan’s investment as a fraction of Bob’s and Peter’s investments is thus
(12) = 9, so Stan will invest $9. Stan’s investment as a fraction of Bob’s and Peter’s investments is thus 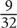 .
.
12. E Recognize that  = 0.66
= 0.66
Now compare the choices:
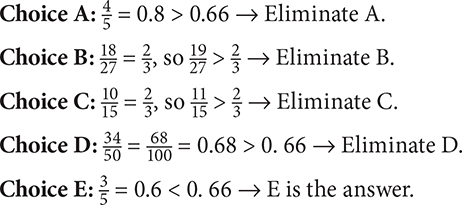
13. –2 Express 1.5 × 104 as 15,000. To go from 15,000 to 150, you must move the decimal two places to the left. Thus x = –2.
14. C Bob accidentally moved the decimal two places to the right instead of two places to the left. To correct the original error, he needs to first move the decimal two places to the left to arrive at 3.87. To do the correct calculation, he must move the decimal two places to the left again, to arrive at 0.0387.
Quantitative Comparison Questions
1. C Add the fractions in Quantity A by finding a common denominator of xy.
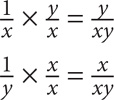
Thus 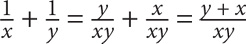 . The two quantities are equal.
. The two quantities are equal.
2. D Choose values for x. The best numbers to consider are 0, 1, and –1. If x = 1, then Quantity A is greater. If x = 0, then the denominator of both quantities will equal 1 and the two fractions will therefore be equal. Since a relationship cannot be determined, the answer is Choice D.
3. A Since x is greater than y, and 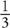 is greater than
is greater than  , the value in Quantity A will be a bigger piece of a bigger whole than the value in Quantity B. Thus Quantity A is greater.
, the value in Quantity A will be a bigger piece of a bigger whole than the value in Quantity B. Thus Quantity A is greater.
4. B To simplify the comparison, divide both quantities by 200. The new comparison is thus:
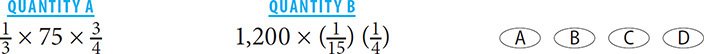
Next, reduce both quantities:
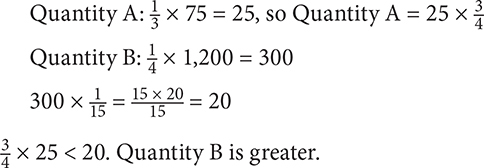
5. C Determining the number of thirds in 7 is the same thing as determining how many times 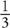 divides into 7. Written as a fraction, this becomes
divides into 7. Written as a fraction, this becomes 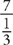 ?. Dividing by a fraction is equivalent to multiplying by the reciprocal of that fraction, so
?. Dividing by a fraction is equivalent to multiplying by the reciprocal of that fraction, so 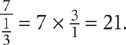 The values in the columns are equal.
The values in the columns are equal.
6. B Instead of calculating a value for Quantity A, look at how the two columns compare. Both fractions in Quantity A are smaller than the fraction in Quantity B. Multiplying two positive fractions will yield only a smaller fraction, so the product of the fractions in Quantity A must be less than 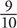 .
.
7. B Since the two fractions have the same numerator, whichever fraction has the smaller denominator will be the greater fraction. 3200 is greater than 2200, so the denominator in Quantity A is greater, meaning that the fraction in Quantity A is smaller.
8. B Choose values for c. Since you are given a range, choose extremes. First choose 1. In this case, the value in Quantity B will be 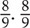 is greater than
is greater than  , so in this case, the value in Quantity B is greater. Now choose a larger value for c: 100.
, so in this case, the value in Quantity B is greater. Now choose a larger value for c: 100. 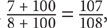 which is greater than
which is greater than  . Both values for c yielded a larger value in Quantity B than in Quantity A.
. Both values for c yielded a larger value in Quantity B than in Quantity A.
9. A Expressed algebraically, the prompt says that 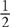 k =
k =  b, where k = Kathy’s salary and b = Bob’s salary. The quantities you are asked to compare are
b, where k = Kathy’s salary and b = Bob’s salary. The quantities you are asked to compare are  k and
k and 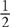 b.
b.  k is greater than
k is greater than 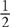 k, and
k, and 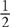 b is less than
b is less than  b. Thus if
b. Thus if 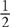 k =
k =  b, then
b, then  k must be greater than
k must be greater than 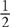 b.
b.
This question can be done quickly if you identify what you are comparing and how those values relate to the given information. Since  is greater than
is greater than 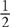 , the value in Quantity A must be greater than half of Kathy’s salary. Since
, the value in Quantity A must be greater than half of Kathy’s salary. Since 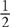 is less than
is less than  , the value in Column B must be less than
, the value in Column B must be less than  of Bob’s salary. If half of Kathy’s salary equals
of Bob’s salary. If half of Kathy’s salary equals  of Bob’s salary, then
of Bob’s salary, then  of Kathy’s salary must be more than
of Kathy’s salary must be more than 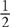 of Bob’s salary.
of Bob’s salary.
10. C You can use your calculator, but it is faster to express both quantities using powers of 10. In Quantity A, there are five digits total to the right of the decimal, so you can express Quantity A as 79 × 232 × 10–5. In Quantity B, there are five digits total to the right of the decimal, so you can express Quantity B as 79 × 232 × 10–5. The two quantities are equal.
11. A In each quantity, the same number of fractions is being added, and the numerators in Quantity A and Quantity B are the same. The difference is the denominators. The denominator of each of the values in Quantity B is greater than each corresponding denominator in Quantity A. If two positive fractions have the same numerator, the fraction with the smaller denominator is larger. Thus each fraction in Quantity A is greater than its corresponding fraction in Quantity B. Quantity A is greater.
Percentages
Part Versus Whole
A percent is another way to express a part-to-whole relationship. Percent literally means “per one hundred” and is used to determine the piece that a quantity represents when the whole is 100. For example, if Bob has 200 pies, and 75% of the pies are blueberry, then the number of blueberry pies is
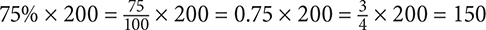
The formula to calculate percent is
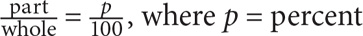
62 is what percent of 1,000?
SOLUTION: Use the percent formula: 62 is the part and 100 is the whole, so:
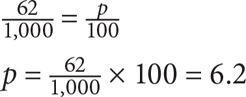
Percent questions can be phrased in a few ways. Let’s look at a few examples and how they fit into the preceding formula.
15 is what percent of 50?
SOLUTION: The part is 15 and the whole is 50. The solution is thus:
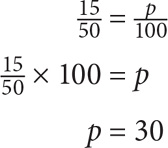
What percent of 200 is 350?
SOLUTION: The part is 350 and the whole is 200 (note that the part can be greater than the whole). The solution is thus:
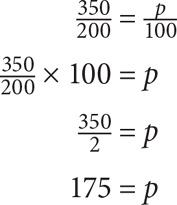
SOLUTION: The part is 540, and the whole is unknown. Thus:
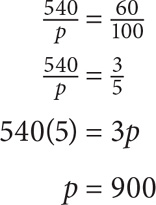
Percent Change
Some GRE questions will ask you to calculate the percent by which a certain value increases or decreases. For example:
If the price of a shirt increased from $80 to $100, then by what percent did the price of the shirt increase?
Any time you are asked to solve for percent change, use the following formula:
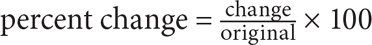
When using this formula, make sure that the denominator is the original value and that the value in the numerator is positive. In the given example, the change is 100 – 80 = 20. The original value is the price of the shirt before the increase, in this case, $80. Thus the percent change = 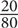 × 100 = 25%.
× 100 = 25%.
In the preceding example, you knew the original value and the new value, and you were asked to solve for the percent change. What if you are told the percent change and are asked to solve for the original or new value? Use the following formulas:
If a quantity increases by p percent, the new quantity will equal (100 + p)% × the original quantity.
If the price of a $3,000 computer increased by 20%, what is the new price?
SOLUTION: Since the price increases by 20%, the new price will be (100% + 20%) × $3,000 = 120% × 3,000 = 1.2 × $3,000 = $3,600.
After a 20% increase, the price of a computer is $3,000. What was the original price of the computer?
SOLUTION: Let o = the original price. Thus
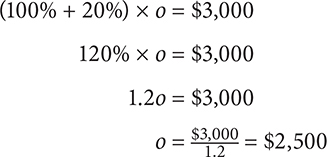
If a quantity decreases by p percent, the new quantity will equal (100 – p)% × the original quantity.
After a 25% decrease, the price of a car was $24,000. What was the original price?
SOLUTION: Let p = the original price of the car. Thus
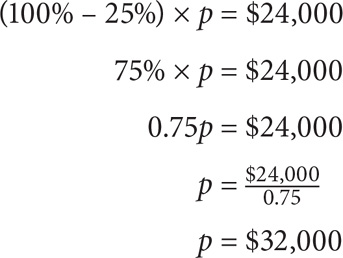
Consecutive Percentages
Certain GRE questions will involve more than one percent change to a value. For example:
On January 1, the price of a certain stock was $400. On January 2, the price of the stock was 20% greater than it was on January 1. On January 3, the price was 20% less than it was on January 2. What was the price of the stock on January 3?
SOLUTION: To answer these questions, you should use the preceding formulas, but keep the following point in mind: Each successive percent change relates to the quantity that immediately precedes it, not to the starting quantity.
It would be wrong to think that the 20% changes cancel each other out and yield a value equal to the original value. This is so because the value that goes up 20% from January 1 to January 2 is different from the value that goes down from January 2 to January 3. Since the percents are pieces of different wholes, they do not simply cancel out. So you should instead use the percent change formulas given in the previous section:
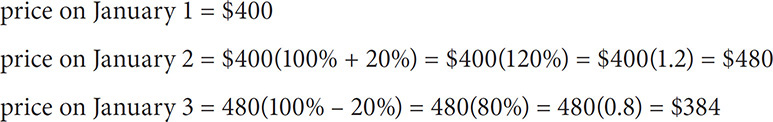
Percent Greater Versus Percent Of
If you don’t read the following question carefully, you might fall for a trap:
150 is what percent greater than 50?
Many test-takers simply use the percent formula for this question:
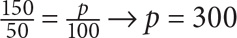
But this is wrong. Why? Because the question is asking, 150 is what percent greater than 50, not what percent of 50. To calculate percent greater, use the following formula:
percent greater = % of – 100%
In the previous example, 150 is 300% of 50, so it is (300% – 100%) = 200% greater than 50.
Plugging in Numbers with Percentages
In the section on fractions and decimals, you read that plugging in numbers was a useful strategy in Discrete Quantitative questions that only give fractions and no specified amounts. The same applies to percent questions. If you see a Discrete Quantitative question with only percents and no actual amounts, plug in 100 for the total.
20% of the employees in a company are managers. 10% of these managers have been with the company for at least 10 years. The number of managers who have not been with the company for at least 10 years is what percent of all the employees?
SOLUTION: Let the total number of employees = 100. Thus the number of managers is 20%(100) = 20. The percentage of managers who have not been with the company for 10 years is 100% – 10% = 90%. Thus the number of managers who have not been with the company for 10 years is 90%(20) = 18. Now the question is, 18 is what percent of 100? The answer is 18 (notice how simple the calculations are when you choose 100!).
Simple and Compound Interest
Though tested rarely, these topics are worthwhile to learn if you are aiming for a high score. The formula for simple interest is
principal × rate × time
If Bob invested $800 at 5% simple annual interest, how much interest did his investment earn after 5 years?
SOLUTION: the interest accrued = principal × rate × time = $800(0.05)5 = $200.
The formula for compound interest is
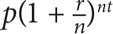
where p = principal, r = rate, n = number of times per year, and t = number of years.
If Bob invested $5,000 at 5% compound annual interest. What was the dollar amount of the investment after 3 years, rounded to the nearest dollar?
SOLUTION: $5,000 = p, 5% = r, n = 1, and t = 3. Thus the amount of the investment is 5,000(1.05)3 = $5,788.125 ≈ $5,788
Quantitative Comparison Strategy: Percentages
Often percent questions in Quantitative Comparison questions will test your ability to differentiate between the original value and new values. When looking at successive percent changes, always keep in mind that each percent change occurs to the previous value, not the original one.

SOLUTION: It may be tempting to assume that the percent changes will offset each other and that the answer is thus C. But the second percent change is on a bigger value than the original percent change. Thus the amount by which the second price decreases is greater than the amount by which the first price increased. Thus the final price must be less than the original price. The correct answer is A.
Exercise: Percentages
Discrete Quantitative Questions
1. 3.4 is what percent of 1,000?
 0.0034
0.0034
 0.034
0.034
 0.34
0.34
 3.4
3.4
 34
34
For this question, write your answer in the box.
2. 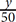 +
+ 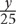 is what percent of
is what percent of 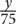 ?
?

3. 3. A shirt originally priced at x dollars is reduced by 20% percent. This new price is then reduced by 40%. The final price of the shirt is what percent of the original price?
 60%
60%
 52%
52%
 48%
48%
 40%
40%
 20%
20%
4. If 10% of a equals 25% of b, then a is what percent of b?
 40
40
 50
50
 140
140
 150
150
 250
250
5. The price of a home in 1997 was 200% greater than the price in 1957. The price in 1957 was 300% greater than the price in 1927. The price of the home in 1997 is what percent greater than the price of the home in 1927?
 500
500
 600
600
 700
700
 1,100
1,100
 1,200
1,200
6. A 30% increase in the price of a shirt is equivalent to $60. If the price of the shirt were reduced by 20% instead of increased by 30%, what would be the price of the shirt?
 240
240
 200
200
 160
160
 120
120
 54
54
7. In 1980, a college had 4,000 students, of whom 30% were women. In 2010, the college had 12,000 students, of whom 60% were women. By what percent did the number of women students in the college increase from 1980 to 2010?
 100
100
 200
200
 400
400
 500
500
 600
600
8. The contents of a jar of jelly that is 40% full are poured into an empty 200-ounce vat, filling it to 25% of capacity. How many jars of jelly would be required to fill three of these vats?
 2
2
 3
3
 4
4
 5
5
 6
6
9. At a certain store, the retail price for a blouse is double the retail price for a T-shirt. If Beth buys a blouse at a 50% discount and a T-shirt at a 25% discount, the amount Beth pays is approximately what percent of the amount she would have paid had there been no discounts?
 58%
58%
 50%
50%
 38%
38%
 30%
30%
 25%
25%
10. In a high school with 500 students, 15% of the students are freshmen. If 50 additional students enroll in the school, how many of those students would have to be freshmen for the number of freshmen to be 20% of the student body?
 10
10
 25
25
 35
35
 100
100
 175
175
11. In a company of 800 employees, 25% hold administrative positions. How many administrative employees would have to be added for the number of administrative employees to be 40% of the total number of employees?
 80
80
 120
120
 200
200
 320
320
 400
400
12. If Bob invests $10,000 at y percent simple annual interest for 5 years, which of the following represents the amount of interest he will have gained after 5 years?
 10,000(1 + y)5
10,000(1 + y)5
 10,000(y)5
10,000(y)5

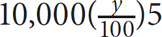
 10,000(y)5
10,000(y)5

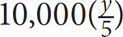
13. In Boronia, all purchases are taxed between 10% and 15%, depending on the type of item purchased. If Bob paid $30 tax for a certain item, which of the following could equal the pretax cost of the item? (Indicate all that apply.)
 150
150
 175
175
 210
210
 270
270
 330
330
For this question, write your answer in the box.
14. Jack invests $5,000 at 4% compound annual interest. Rounded to the nearest units digit, what will be the value of Jack’s investment in 3 years?

15. In 2007, there were 300 juniors and 200 seniors at a high school. In 2008, there were 400 juniors and 250 seniors at the same high school. What was the approximate percent increase in the ratio of juniors to seniors from 2007 to 2008?
 6.5%
6.5%
 6.66%
6.66%
 24%
24%
 25%
25%
 30%
30%
16. A shirt originally cost x dollars. After a y percent increase, the price of the shirt is z dollars. What is x, in terms of y and z?

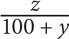

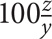

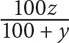

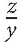

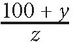
17. Bob sold his car for $20,000. If Bob’s profit was 25% of the purchase price of the car, what was the purchase price of the car?
 $4,000
$4,000
 $8,000
$8,000
 $12,000
$12,000
 $16,000
$16,000
 $18,000
$18,000
For this question, write your answer in the box.
18. If y is 50% greater than x, then y is what percent of 2x?

Quantitative Comparison Questions
1. 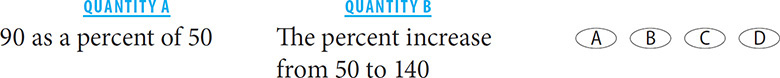
2. 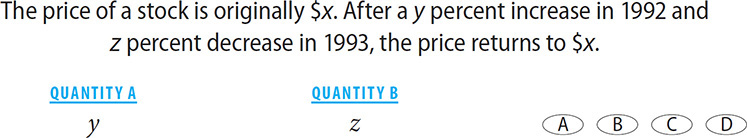
3. 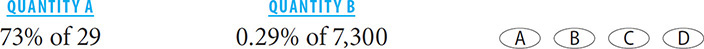
4. 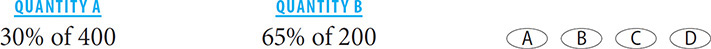
5. 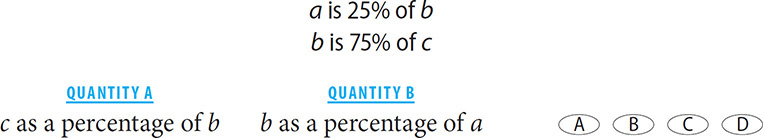
6. 
7. 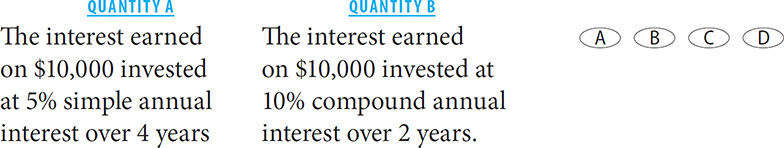
8. 
Exercise Answers
Discrete Quantitative Questions
1. C To calculate percent, use the following formula: 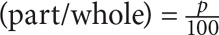 In this question, 3.4 is the part and 1,000 is the whole. Plug these values into the formula and arrive at 0.34.
In this question, 3.4 is the part and 1,000 is the whole. Plug these values into the formula and arrive at 0.34.
2. 450 Since this question has variables in the choices, a good strategy is to plug in a value for y. To make the math simpler, choose a value for y that will divide evenly by 50, 25, and 75: 150. After plugging in 150 for y, the question is 3 + 6 is what percent of 2? Use the percent formula:
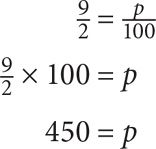
3. C Since this question gives only percents and no actual amounts, plugging in is a useful strategy. Choose a value for the original price of the shirt: 100. After a 20% reduction, the price of the shirt is 80. Taking 40% away from 80 is the same as keeping 60% of 80, so to calculate the price of the shirt after the second reduction, do 0.6(80) = 48. 48 is 48% of 100.
4. E Solution: Plug in values. Let b = 100. If b = 100, then
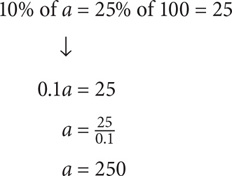
Now use the percent formula: 250 is the part and 150 is the whole:

5. D Let the price of the home in 1927 = $100. The price of the home in 1957 is therefore $100 + 3($100) = $400. The price of the home in 1997 is therefore $400 + 2($400) = $1,200. Now, we need to determine 1,200 is what percent greater than 100. Use the percent greater formula: % greater = % of – 100% = 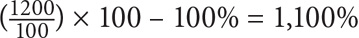 .
.
6. C You are asked to find the price of the shirt after a 20% decrease. In other words, you want to solve for 0.8 (original price). If a 30% increase represents $60, then $60 is 30% of the original price. Algebraically, you can represent this as 0.3x = 60, where x = the original price. Solve for x:
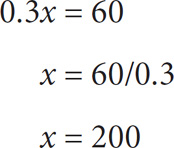
Now reduce 200 by 20%: 200(100% – 20%) = 200(80%) = 200(0.8) = 160.
7. D To solve for percent increase, use the formula 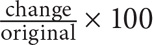 . In this case, the new value is the number of women students at the college in 2010, and the old value is the number of women students at the college in 1980. The number of women students in 2010 is 60% of 12,000 = 0.6(12,000) = 7,200. The number of women students in 1980 is 30% of 4,000 = 0.3(4,000) = 1,200. Plug these values into the formula:
. In this case, the new value is the number of women students at the college in 2010, and the old value is the number of women students at the college in 1980. The number of women students in 2010 is 60% of 12,000 = 0.6(12,000) = 7,200. The number of women students in 1980 is 30% of 4,000 = 0.3(4,000) = 1,200. Plug these values into the formula: 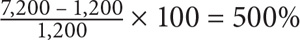 .
.
8. D First, identify what you’re solving for. To fill three 200-ounce vats, you will need 600 ounces of jelly. To determine how many jars of jelly you need, you will need to determine how many ounces are in an individual jar of jelly. Use j to represent this value. You are told that 40% of j will fill a 200-ounce vat to 25% of its capacity. 25% of 200 is 50, so you know that 40% of j = 50. Now solve for j: 0.4j = 50 → j = 125. The number of jars you need will be  . However, since you cannot have a fraction of a jar, you will need 5 jars to yield the necessary amount of jelly to fill the three vats.
. However, since you cannot have a fraction of a jar, you will need 5 jars to yield the necessary amount of jelly to fill the three vats.
9. A Since the question asks for a percent, use the formula 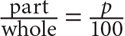 . You must determine the part and the whole. This is a percent question with no actual amounts given, so the best approach is to plug in values. Let the original price of a T-shirt be $100 and the original price of a blouse be $200. After a 50% discount, the blouse will cost $100. After a 25% discount, the T-shirt will cost $75. In total, Beth pays $175. Before the discounts, Beth would have paid $300. Now find $175 as a percentage of $300:
. You must determine the part and the whole. This is a percent question with no actual amounts given, so the best approach is to plug in values. Let the original price of a T-shirt be $100 and the original price of a blouse be $200. After a 50% discount, the blouse will cost $100. After a 25% discount, the T-shirt will cost $75. In total, Beth pays $175. Before the discounts, Beth would have paid $300. Now find $175 as a percentage of $300:
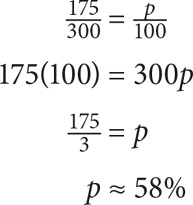
10. C Since you are not told how many additional freshmen enroll in the school, assign a variable: x. You know that after x freshmen enroll in the school, the number of freshmen will be 20% of all students. Since you are given a relationship using percentages, use the formula:
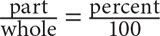
In this case, the part is the number of freshmen after you add x. Of the 500 students, 15% were freshmen, so the original number of freshmen was 0.15(500) = 75. After the change, the number of freshmen is 75 + x. The whole is the total number of students in the school after you add 50: 550. The equation is 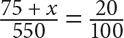 . Reduce
. Reduce 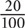 and arrive at
and arrive at 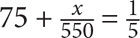 . Cross-multiply: 5(75 + x) = 550. Divide both sides by 5. 75 + x = 110. x = 35.
. Cross-multiply: 5(75 + x) = 550. Divide both sides by 5. 75 + x = 110. x = 35.
11. C If 25% of the original 800 employees are administrative, then there are 0.25(800) = 200 administrative employees. Since you don’t know how many administrative employees you are adding, assign a variable: x. After the increase, there will be 200 + x administrative employees. You know this number will be 40% of the total number of employees. How many total employees will there be? There were originally 800, but if you are adding x administrative employees, then there will be 800 + x total employees. You can therefore create the following equation:
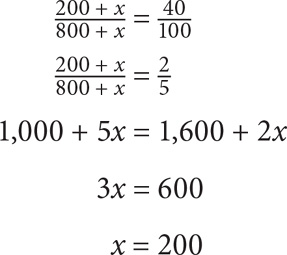
12. C Plug in a value for y. Let y = 5. Now use the simple interest formula:
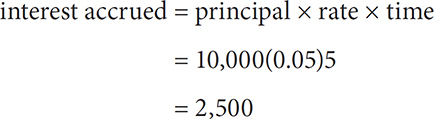
Substitute 5 for y into the choices and see which choice yields a value of 2,500.
13. C and D Since Bob paid $30 in tax, you know that $30 must be between 10% and 15% of the total cost. The cost for which $30 represents a 10% tax will be the higher bound of the price of the item, and the cost for which $30 represents a 15% tax will be the lower bound of the price of the item. Determine these bounds, and find which choices fall within the price range. Let the pretax cost be x. For the 10% tax, you can create the equation: 30 = 0.1x → x = 300. For the 15% tax, you can create the equation 30 = 0.15x → x = 200. Among the choices, the values between 200 and 300 are C and D.
14. $5,624 Use the compound interest formula: P(1 + r)n = new. Thus you arrive at 5,000(1.04)3 = $5,624.
15. B Use the percent change formula: 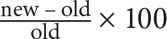 . Note that you are looking for the percent change in the ratios of the two groups, not in their actual values. The ratio of juniors to seniors in 2007 was
. Note that you are looking for the percent change in the ratios of the two groups, not in their actual values. The ratio of juniors to seniors in 2007 was 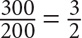 . The ratio of juniors to seniors in 2008 was
. The ratio of juniors to seniors in 2008 was 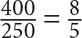 . Plug
. Plug 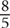 in for the new value and
in for the new value and 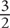 for the old value:
for the old value:
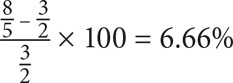
16. C When a Discrete Quantitative question has variables in the question and in the choices, consider plugging in numbers. In the question, the new price of the shirt, z, depends on the original price, x, and the percent increase, y, so choose values for x and y, and let those values determine z. Let x = 100 and y = 25. Thus the new price of the shirt is $125. Plug the values you chose for x and y into the choices, and see which yields you $125.
17. D The formula for calculating profit is p = r – c, where p = profit, r = revenue, and c = cost. The revenue for the car is $20,000. You are told that the profit was 25% of the purchase price. You can express this algebraically as r – c = 0.25c. Now plug in $20,000 for r: 20,000 – c = 0.25c. Solve for c:
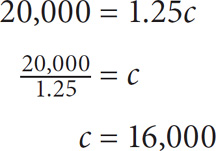
18. 75 Since you are dealing with a percent question with no amounts given, plug in values for the unknowns. Let x = 100. If y is 50% greater than x, then y = 100 + 0.5(100) = 150. You thus want to determine what percent 150 is of 200. Use the formula for calculating percents: 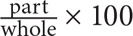 . (150/200) × 100 = 75.
. (150/200) × 100 = 75.
Quantitative Comparison Questions
1. C To arrive at a value for Quantity A, use the percent formula: 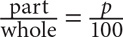 . In this case, 90 is the part and 50 is the whole, so Quantity A is equivalent to
. In this case, 90 is the part and 50 is the whole, so Quantity A is equivalent to 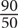 × 100. To arrive at a value for Quantity B, use the percent change formula (difference/original) × 100. The difference between the two numbers is 90. The original number is 50. Plugging these values into the formula, you arrive at
× 100. To arrive at a value for Quantity B, use the percent change formula (difference/original) × 100. The difference between the two numbers is 90. The original number is 50. Plugging these values into the formula, you arrive at 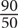 × 100. Column B and Column A have the same value.
× 100. Column B and Column A have the same value.
2. A Option 1: Solve it intuitively.
The price of the stock after a y percent increase is more than the original price of the stock. For a z percent decrease to bring the stock value back to its original price, z% of the price in 1993 must be the same as y% of the price in 1993. Since the value in 1993 is greater than the value in 1992, the whole that z% is taken from is bigger, which means a smaller piece of that whole is needed to arrive at y% of 1992. If you need a smaller piece, that means that z, as a percentage of 1993, is smaller than y, as a percentage of 1992. The answer is A.
Option 2: Plug in numbers.
Since you are dealing with percents, choose $100 for x and 25 for y. Use these values to determine what value for z would bring the price back to $100. If y = 25, then the price in 1992 will be 125. Now solve for z: 25 is what percent of 125? Use the percent formula: 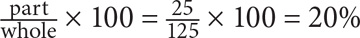 Thus when y = 25, z = 20. Column A is greater.
Thus when y = 25, z = 20. Column A is greater.
3. C Avoid calculating! Notice that the columns have very similar digits, but different place values. Write each column in decimal format and see how the place values compare. Column A can be written as 0.73(29) and Column B can be written as 0.0029(7,300). 0.0029(7,300) = 0.73(29).
4. B 400 is double 200, but 65% is more than double 30%. Thus Quantity B is greater. Note that you can use your calculator here.
5. B Plug in the numbers! The prompt gives you a in terms of b and b in terms of c. Since you can express everything in terms of c, choose a value for c and work backward to get values for a and b. In this case, you should choose a value for c that will divide evenly by 4 twice. Why? Because b =  (c) and a =
(c) and a =  (b). To get integer values for a and b, you will be dividing by 4 and then dividing by 4 again, so a good value for c would be 16. If c = 16, then b = 12. If b = 12, then a = 3. The value in Quantity A is thus
(b). To get integer values for a and b, you will be dividing by 4 and then dividing by 4 again, so a good value for c would be 16. If c = 16, then b = 12. If b = 12, then a = 3. The value in Quantity A is thus 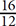 × 100 = 133.3%. The value in Quantity B is thus
× 100 = 133.3%. The value in Quantity B is thus 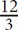 × 100 = 400%. Quantity B is greater.
× 100 = 400%. Quantity B is greater.
6. A Before doing any math, make sure to look at the columns. You are comparing a $40 reduction in the price of the item to a 20% reduction. So you need to determine how 20% of the price compares to $40. The difficulty here is that you only have a range for the price of the item, so you will only be able to arrive at a range for what 20% of the item would be. Let’s see how that range compares to $40. First, assume that the item actually equaled $200. If that’s the case, then a 20% reduction in the item would equal $40. But since the price of the item is less than $200, a 20% reduction in the item would be less than $40. Thus Quantity A is greater.
7. B Don’t calculate! Instead, figure out how the columns relate to each other. First, notice that in both cases, the principal is the same ($10,000). In Column A, the interest earned will be 0.05(10,000)4, which is the same as 20% of 10,000. How does Column B relate to 20% of $10,000? Compound interest accrues on each successive period. For the first period, the interest is 10% of $10,000. For the second period, the interest is 10% of a value that is more than $10,000. The sum of these two quantities will be more than 20% of $10,000. Thus Quantity B is greater.
8. B The fastest way to do this question is to choose values. When choosing values for percent questions, always start by choosing a value for the whole, which in this case is y. Let y = 100, and let x = 80. Now the comparison is 20% more than 80 versus 100. 20% more than 80 is the same as 1.2(80), which equals 96. This value is less than 100. Thus Quantity B is greater.
Ratios
A ratio represents a relationship between two or more quantities. Examples of ratios are
There are 3 boys for every 4 girls.
The preceding can be expressed as “The ratio of boys to girls is 3 to 4.”
A recipe requires 3 parts sugar, 2 parts salt, and 4 parts water.
The above can be expressed as: “The ratio of sugar to salt to water is 3 to 2 to 4.”
Ratios can be represented in a few different ways:
 The word to 3 to 4
The word to 3 to 4
 Using a colon 3:4
Using a colon 3:4
 As a fraction
As a fraction 
The Elements of a Ratio
The relationship that a ratio specifies will be either part-to-part or part-to-whole. An example of a part-to-part ratio is “In a school, there are 7 boys for every 3 girls.” An example of a part-to-whole ratio is “In a school, there are 7 boys for every 10 students.”
Ratios Do Not Specify Amounts!
It is important to remember that a ratio only provides a relationship between quantities, not the actual amounts of each quantity. If the ratio of boys to girls is 7:3, there can be any number of values for boys and girls, as long as those values satisfy the given ratio.
Expressing Ratios
As discussed previously, there are several ways of expressing ratios. For the purpose of the GRE, the best way to express a ratio between two quantities is as a fraction. But before doing so, you must label the units.
If you are told that the ratio of men to women is 1:3, then on your paper, you should label which quantity corresponds with the numerator of the fraction and which quantity corresponds with the denominator of the fraction:
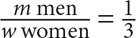
To make the quantities easier to work with algebraically, it’s even better to write:
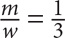 , where m = the number of men and w = the number of women
, where m = the number of men and w = the number of women
Proportions
The simplest types of ratio questions will give you a ratio and the value for one quantity and will ask you to find a value for the other quantity. Whenever you have a ratio with the value for one quantity, set up a proportion.
At a certain university, the ratio of doctoral students to master’s students is 3 to 5. If there are 9,000 doctoral students, how many master’s students are there?

Representing Ratios Algebraically
Recall from the discussion of fractions that the denominator of a fraction specifies the number of slices a pie is cut into, and the numerator represents the number of slices of that pie. In a certain sense, ratios can be thought of in the same way.
If you are given a part:part ratio, such as “The ratio of boys to girls is 3 to 2,” you can think of the number of boys as 3 slices of a pie and the number of girls as 2 slices of the same pie. Since you are not told the value of the slice of the pie, let x represent the quantity of 1 slice. Thus if the ratio of boys to girls is 3 to 2, then:
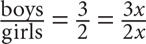
Representing ratios in this way is helpful in the following situations:
Situation 1: When you know values for the parts of a ratio and want to determine the whole, or vice versa.
In a certain business’s budget, the dollar amounts allocated for marketing, product development, and administration are in the ratio 5:3:2. If the business’s budget is $200,000, how much money is allocated for marketing?
Step 1: Since you are not given a value for any of the parts, use x to represent one part. Thus
5x = dollars allocated for marketing
3x = dollars allocated for product development
2x = dollars allocated for administration
Step 2: Identify an algebraic relationship:
The $200,000 budget is split among the three segments, so the sum of the amounts for the three segments will equal $200,000:
5x + 3x + 2x = $200,000
Step 3: Solve for the unknown: you are asked to solve for the amount of money allocated for marketing, so you must solve for 5x. Using the preceding equation:
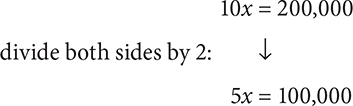
Situation 2: When you do not have quantities for either part of a ratio, but have information about how the ratio changes.
In a certain school, the ratio of students to teachers is 20 to 1. If the school adds 1,000 students and 100 teachers, the new ratio of students to teachers will be 15 to 1. How many students are currently at the school?
Step 1: Set up the original ratio with x representing one slice of the pie
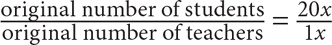
Step 2: Use the quantities from Step 1 to create a proportion
new number of students/new number of teachers = 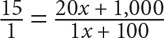 .
.
Step 3: Cross-multiply and solve for 20x (the original number of students)
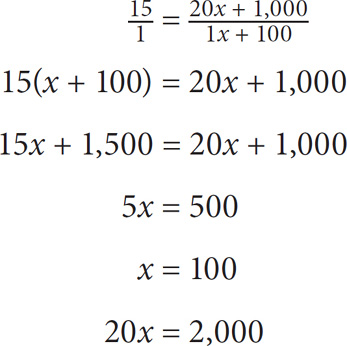
Multiple Ratios with a Common Element
On some GRE questions, you will be given two ratios that share a common part and be asked to solve for the ratio of the other parts. The most efficient way to answer these questions is to manipulate the two ratios so that the common element has the same value in both. How will you do this? By finding the least common multiple of the common element.
At a certain pet store, there are 3 dogs for every 2 cats and 5 cats for every 7 birds. What is the ratio of the number of dogs to the number of birds?
Step 1: Set up the given ratios:
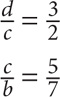
Step 2: Manipulate the ratios so that the quantity for the overlapping element is the same in both ratios.
In the first ratio, there are 2 parts cats, and in the second ratio, there are 5 parts cats. To make the ratios comparable, manipulate the two fractions so that cats will be 5 × 2 = 10 in both fractions.
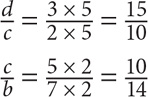
Now that both ratios are in terms of the same number of cats, the ratio of dogs to cats to birds is 15:10:14. The ratio of dogs to birds is thus 15:14.
Exercise: Ratios
Discrete Quantitative Questions
1. Which of the following equals the ratio of 3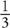 to 2
to 2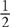 ?
?
 1:3
1:3
 2:5
2:5
 5:2
5:2
 3:4
3:4
 4:3
4:3
For this question, write your answer in the box.
2. A certain exercise regimen suggests that an individual do 3 push-ups for every 2 sit-ups. If John follows this exercise regimen and does 30 sit-ups per day, how many push-ups would he have to do per day?

3. At a certain farm, the ratio of sheep to horses is 4:3. If the farm adds 5 sheep and 5 horses, what will the new ratio of sheep to horses be?
 9:8
9:8
 13:10
13:10
 19:18
19:18
 24:23
24:23
 It cannot be determined from the given information.
It cannot be determined from the given information.
4. If a zoo has 48 chimpanzees and 36 bonobos, then what is the ratio of chimpanzees to bonobos?

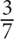

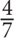

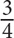

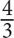

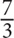
5. In a certain solution, the ratio of water to alcohol is 3:1. If water and alcohol combined make up half of the volume of the solution, what percentage of the solution is water?
 12.5%
12.5%
 25%
25%
 37.5%
37.5%
 50%
50%
 75%
75%
6. At Bridgewood High School, freshmen, sophomores, juniors, and seniors are in the ratio of 3:4:6:7, respectively. Which of the following CANNOT be the total number of students at the school?
 40
40
 80
80
 90
90
 100
100
 140
140
7. A solution of alcohol and water contains alcohol and water in the ratio of 1:8. If the entire solution is 31.5 ounces, how many ounces of water are in the solution?
 4.5
4.5
 9
9
 16
16
 27
27
 28
28
8. At a certain company, the ratio of managers to directors is 5:3. If 10 of the managers become directors, the new ratio will be 7:5. How many managers are currently at the company?
 30
30
 90
90
 140
140
 150
150
 240
240
9. In a certain orchestra, the ratio of cello players to viola players is 4:5. If there are 2 more viola players than cello players, how many viola players are there?
 8
8
 9
9
 10
10
 11
11
 12
12
10. In a certain company, the dollar amounts budgeted for advertising, product development, and administration are 4:3:1, respectively. If the company’s entire budget is $200,000, how much did the company spend on product development?
 25,000
25,000
 50,000
50,000
 75,000
75,000
 80,000
80,000
 100,000
100,000
For this question, indicate all of the answer choices that apply.
11. A certain basket consists of white eggs and brown eggs. If the ratio of white eggs to brown eggs is 4:3, which of the following could be the total number of eggs in the basket?
 5
5
 15
15
 21
21
 70
70
 140
140
 161
161
12. In a stock portfolio of 80 shares, the ratio of shares invested in bonds to shares invested in mutual funds is 1:3. If the number of mutual funds remains the same, how many bonds would have to be added for the ratio of bonds to mutual funds to be 5:6?
 30
30
 40
40
 50
50
 70
70
 80
80
For this question, indicate all of the answer choices that apply.
13. In a certain organization, the ratio of managers to directors is 3:2, and the ratio of directors to administrators is 5:14. Which of the following could be the sum of managers, directors, and administrators in the organization?
 1,060
1,060
 1,300
1,300
 2,120
2,120
 5,300
5,300
 7,200
7,200
14. At a certain school, the ratio of students to teachers is greater than 3:1. If there are 500 students at the school, what is the maximum number of teachers that can be at the school?
 165
165
 166
166
 167
167
 168
168
 169
169
15. If 7a = 6b and ab ≠ 0, what is the ratio of 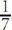 a to
a to  b?
b?

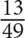

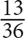

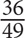

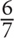

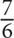
Quantitative Comparison Questions
1. 
2. 
3. 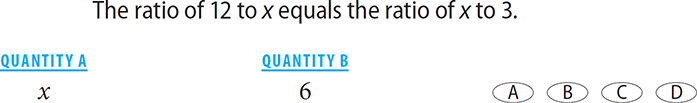
4. 
5. 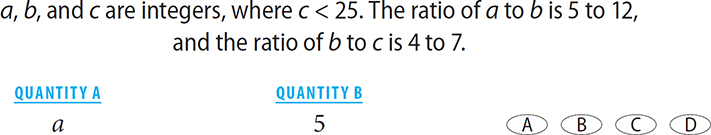
Exercise Answers
Discrete Quantitative Questions
1. E First, convert the fractions in the question to improper fractions: 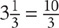 and
and 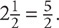 Now express the ratio as a fraction:
Now express the ratio as a fraction: 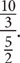 Multiply the numerator by the reciprocal of
Multiply the numerator by the reciprocal of 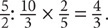
2. 45 First, express the ratio as a fraction: number of push-ups/number of sit-ups = 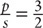 (Note: p = number of push-ups and s = number of sit-ups). Next, set up a proportion:
(Note: p = number of push-ups and s = number of sit-ups). Next, set up a proportion: 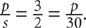 Now cross-multiply to solve for p:
Now cross-multiply to solve for p:
90 = 2p
p = 45
3. E Remember that ratios specify relationships, not values. Let 4x = the original number of sheep and 3x = the original number of horses. The new ratio will be: number of sheep/number of horses = 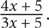 Without knowing how many horses or sheep there were originally, it is not possible to determine the new ratio. Another option is to plug in numbers. If the ratio of sheep to horses is 4:3, then there can be 4 sheep and 3 horses at the farm. In this case, the new ratio will be 9:8. However, the original number of sheep can be 8 and the original number of horses can be 6, in which case the new ratio would be
Without knowing how many horses or sheep there were originally, it is not possible to determine the new ratio. Another option is to plug in numbers. If the ratio of sheep to horses is 4:3, then there can be 4 sheep and 3 horses at the farm. In this case, the new ratio will be 9:8. However, the original number of sheep can be 8 and the original number of horses can be 6, in which case the new ratio would be 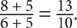 Multiple answers are possible, meaning that a value cannot be determined.
Multiple answers are possible, meaning that a value cannot be determined.
4. D Express the ratio as a fraction: chimpanzees/bonobos = 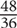 . Reduce:
. Reduce: 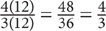
5. C Let the amount of water = 3x and the amount of alcohol = 1x. The sum of water and alcohol is thus 3x + 1x = 4x. Since water and alcohol make up half of the volume of the solution, the volume of the entire solution will be 2(4x) = 8x. To determine water as a percentage of the entire solution’s volume, use the percent formula:
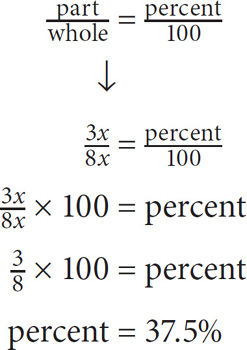
6. C Represent the number of students algebraically:
number of freshmen = 3x
number of sophomores = 4x
number of juniors = 6x
number of seniors = 7x
The total number of students will be the sum of these four groups: 3x + 4x + 6x + 7x = 20x. Since the number of students in the school must be an integer (you can’t have a fraction of a student!) and this integer = 20x, the number of students in the school must be a multiple of 20. Of the choices, the only value that is not a multiple of 20 is 90.
7. E Since you are not given a value for either part, represent the parts algebraically:
ounces of alcohol = 1x and ounces of water 8x
In terms of x, the volume of the solution is 1x + 8x = 9x. Since the solution is 31.5 ounces,
9x = 31.5
x = 3.5
The number of ounces of water is 8x = 8(3.5 ounces) = 28 ounces. The correct answer is Choice E.
8. D Since you are not given a value for either quantity, represent the values algebraically:
number of managers/number of directors = 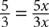
You are told that 10 managers will become directors. Thus after the change, the number of managers will be 5x – 10, and the number of directors will be 3x + 10. Use these values for the second ratio in the question:
new number of managers/new number of directors = 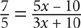
Cross-multiply to solve:
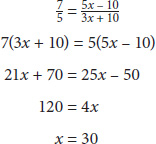
The original number of managers is 5x. Plug in 30 for x: 5(30) = 150.
9. C Since the question provides ratios with no actual values, represent the quantities algebraically:
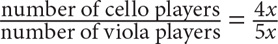
Since the number of viola players = 2 + number cello players, create the equation: 5x = 4x + 2. Solve for x: x = 2. The number of viola players is 5x. Plug in 2 for x. The answer is 5(2) = 10.
10. C Since the question provides ratios with no actual values, represent each part of the budget algebraically:

The sum of these values is 200,000: 4x + 3x + x = 200,000. Manipulate to solve for x:
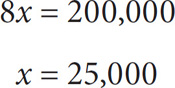
The amount budgeted for product development is 3x = 3(25,000) = 75,000.
11. C, D, E and F Since the question provides ratios with no actual values, represent the parts algebraically: number of 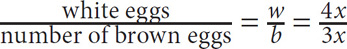 . The total number of eggs in the basket is thus 4x + 3x = 7x. Since it is impossible to have a fraction of an egg, x must be an integer, and thus 7x must be a multiple of 7. The possible values must all be multiples of 7. Among the choices, 21, 70, 140, and 161 are the only multiples of 7.
. The total number of eggs in the basket is thus 4x + 3x = 7x. Since it is impossible to have a fraction of an egg, x must be an integer, and thus 7x must be a multiple of 7. The possible values must all be multiples of 7. Among the choices, 21, 70, 140, and 161 are the only multiples of 7.
12. A Let x be the total number of bonds and 3x be the total number of mutual funds. The sum of these quantities will be 80, the total number of shares. Thus:
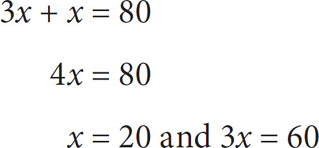
Now that you know how many mutual funds and bonds there were originally, use these values to set up a proportion with the second ratio in the question. Let y = the number of bonds that will be added:
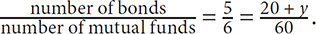
Cross-multiply:
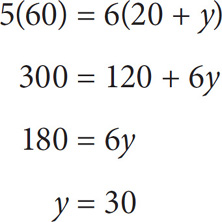
13. A, C, and D Since the ratios share the common element of directors, your first step should be to manipulate the ratios so that the value for the number of directors is the same in both. (Note: In the following ratios, m = the number of managers, d = the number of directors, and a = the number of administrators).
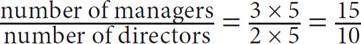
number of directors/number of administrators = 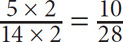
Thus the ratio of managers to directors to administrators is 15:10:28. To determine the possible sum of the three, represent managers as 15x, directors as 10x, and administrators as 28x. The sum of these values is 15x + 10x + 28x = 53x. Since it is impossible to have a fraction of a person, x must be an integer, and thus 53x must be a multiple of 53. The possible values must all be multiples of 53.
14. B Your first step should be to set up a proportion, where s represents the number of students and t represents the number of teachers. However, note that the proportion will be an inequality since the ratio is greater than 3:1:
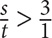
There are 500 students, so 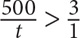 . Cross-multiply to arrive at a range for t: 500 > 3t. Solve for t:
. Cross-multiply to arrive at a range for t: 500 > 3t. Solve for t: 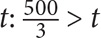 . Since t must be an integer, the greatest value for t will be the greatest integer less than
. Since t must be an integer, the greatest value for t will be the greatest integer less than 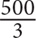 ·
· 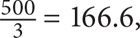 , so the greatest value for t is 166. The correct answer is B.
, so the greatest value for t is 166. The correct answer is B.
15. 15. C The best approach here is to plug in values. Choose a value for a and let that value determine b. If a = 6, then 42 = 6b, and b 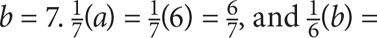
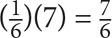 . Now find the ratio of
. Now find the ratio of 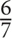 to
to 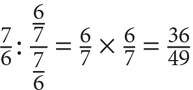 . The correct answer is C.
. The correct answer is C.
Quantitative Comparison Questions
1. B Choose values that satisfy the constraints in the given information: let’s say there are 3 white marbles and 7 black marbles. In this case, the ratio of white marbles to all marbles is  ·
· 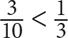 , so for the given values, Quantity B is greater. Choose a “weird” case: 7 is the smallest possible number of black marbles when there are 3 white marbles. Let’s choose a larger value for the number of black marbles. Let there be 3 white marbles and 100 black marbles. In this case, the ratio of white marbles to all marbles is
, so for the given values, Quantity B is greater. Choose a “weird” case: 7 is the smallest possible number of black marbles when there are 3 white marbles. Let’s choose a larger value for the number of black marbles. Let there be 3 white marbles and 100 black marbles. In this case, the ratio of white marbles to all marbles is  ·
· 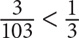 , so Quantity B is still greater.
, so Quantity B is still greater.
2. D Since there are more boys than girls, the current ratio of boys to girls must be greater than 1. The impact of adding 10 girls and 20 boys on the ratio will depend on the original ratio. For example, let’s say there were originally 100 boys and 50 girls. In this case, the original ratio is 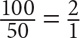 . When 20 boys and 10 girls are added, the new ratio is
. When 20 boys and 10 girls are added, the new ratio is  to 1. In this case, the quantities are equal. Now let’s say the original number of boys was 100 and the original number of girls was 90. In this case, the original ratio is
to 1. In this case, the quantities are equal. Now let’s say the original number of boys was 100 and the original number of girls was 90. In this case, the original ratio is  . The new ratio will be
. The new ratio will be 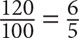 . In this case, Quantity B is greater. Since there is more than one relationship between the quantities, the correct answer is Choice D.
. In this case, Quantity B is greater. Since there is more than one relationship between the quantities, the correct answer is Choice D.
3. D Set the ratios up as fractions: 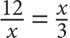 . Next, cross-multiply: x2 = 36. Since the exponent on x is even, x = 6 or –6. The relationship between the columns cannot be determined.
. Next, cross-multiply: x2 = 36. Since the exponent on x is even, x = 6 or –6. The relationship between the columns cannot be determined.
4. C Let the revenue = 5x and the expenses = 4x. Use the profit formula: profit = revenue – expenses. Thus profit = 5x – 4x = x. The ratio of profit to expenses is thus 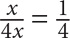 . The two quantities are equal.
. The two quantities are equal.
5. C When you are given two ratios with a common element, you should manipulate the ratios so that the common element has the same value in both ratios. In this case, the common element is b. In the first ratio, 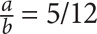 , and in the second ratio,
, and in the second ratio, 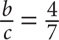 Manipulate the second ratio to make b = 12:
Manipulate the second ratio to make b = 12: 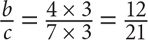 . Thus the ratio of a:b:c = 5:12:21. Since c < 25 and is an integer, c must equal 21. If c = 21, then a = 5.
. Thus the ratio of a:b:c = 5:12:21. Since c < 25 and is an integer, c must equal 21. If c = 21, then a = 5.
 if Quantity A is greater
if Quantity A is greater if Quantity B is greater
if Quantity B is greater if the two quantities are equal
if the two quantities are equal if the relationship between the two quantities cannot be determined
if the relationship between the two quantities cannot be determined