CHAPTER 7
Study this chapter to learn about:
Strategy 1: Plug in numbers
Strategy 2: Back-solve
The following strategies are meant to apply generally to all content areas. Though no GRE question is “designed” for you to use these strategies, they can be effective in situations where no algebraic or conceptual solution is immediately apparent. When working through the questions later in the book, focus on mastering all approaches toward the question—both the algebraic, content-based approach and the “strategic” approach, where possible.
Strategy 1: Plug In Numbers
One of the primary difficulties test-takers have with algebra is its abstract nature. Plugging in numbers helps you get past the abstract by using concrete values in place of variables. You can plug in numbers any time there are variables in the answer choices. This does not mean that you always should plug in numbers in these situations, but it is always an option. Since plugging in numbers requires variables in the answer choices, it can only be used on multiple-choice Discrete Quantitative questions. Let’s look at a sample question and how to answer it by plugging in numbers:
Which of the following equals the average (arithmetic mean) of (a − 2)2 and (a + 2)2?
a2
a2 + 2
a2 + 4
a2 + 2x
a2 + 8x
STEP 1: Choose a value for the variable in the question. When choosing a value for a variable, keep in mind the following recommendations:
Never choose 0 or 1.
Never choose a value that will yield a 0 or 1.
Avoid repeating the same value throughout the question.
Always work with integers.
So what value should you choose for a? Based on number 1, you won’t choose 0 or 1. Based on number 2, you won’t choose 3. Why? Because if you plug in 3 for a, (3 − 2)2 = 12, so 3 yields a value of 1. Based on number 3, you won’t choose 4: (4 – 2)2 = 22. 2 will appear multiple times in the question. So you can’t choose 1, 2, 3, or 4. Go with 5. It does not violate any of the rules given earlier, and it is a prime number, which you generally want. Once you have chosen the value, label it on your paper: a = 5.
STEP 2: Answer the question using the value that you chose. Since you let a = 5, the question now becomes: Which of the following equals the average (arithmetic mean) of (5 − 2)2 and (5 + 2)2? Solve:
(5 − 2)2 = 32 = 9 and (5 + 2)2 = 72 = 49.
The average of 9 and 49 is:
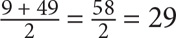
The value above is called the “goal.” Write that answer on your paper and circle it.
STEP 3: Plug the value you chose for the variable into the choices. The choice that yields a value that matches the goal will be the correct answer. This step is straightforward, except for the following caveat: Check all the choices! Occasionally, more than one choice will yield the correct answer, in which case you will need to choose a new value for the variable. This is obviously not an ideal situation, which is why you want to follow the rules in Step 1 about which numbers to avoid.
Here’s the question again:
Which of the following equals the average (arithmetic mean) of (a − 2)2 and (a + 2)2?
a2
a2 + 2
a2 + 4
a2 + 2x
a2 + 8x
SOLUTION: Plug in 5 for a, and identify which choice yields a value of 29.
52 = 25 → No
52 + 2 = 27 → No
52 + 4 = 29 → Yes
52 + 2(5) = 35 → No
52 + 8(5) = 65 → No
The only choice that yields a value that matches the goal is C, so C is the correct answer.
Plugging In Numbers with Multiple Variables
Sometimes, you will have a candidate for plugging in numbers, but there will be more than one variable in the question. Look at the following example:
If a + b = 11c, what is the average of a, b, and c, in terms of c?
3c
3c + 1
4c
5c
5c − 1
When there are multiple variables in a plug-in question, you must choose values that satisfy the restrictions in the question. For example, in the previous question, you cannot simply choose 2 for a, 3 for b, and 5 for c. When you plug those values into the equation, you will arrive at 2 + 3 = 11(5) = 55. This is not a true equation. Instead of arbitrarily choosing values, you must let the values for one or more of the variables determine the other variable. In the previous example, let’s choose values for a and b and let those values determine c.
STEP 1: Choose values for the variables in the question. What values should you choose for a and b? You can choose anything that does not violate the rules outlined in Step 1 of the previous section, but keep in mind that you want c to be an integer. If c = an integer, then 11c must be a multiple of 11. Thus to yield an integer for c, you should choose values for a and b that will sum to a multiple of 11. Let’s choose 9 for a and 13 for b. Those values sum to 22, which is a multiple of 11. Now use these values to solve for c:
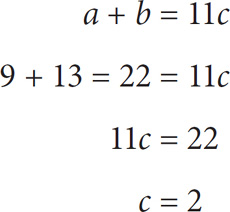
So your values are a = 9, b = 13, c = 2.
STEP 2: Answer the question using the values you chose for the variables. What is the average of 9, 13, and 2?
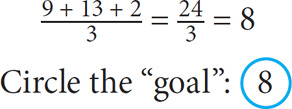
STEP 3: Plug the values into the choices and see which choice yields a value that matches your goal. Here’s the original question again:
If a + b = 11c, what is the average of a, b, and c, in terms of a and b?
3c
3c + 1
4c
5c
5c − 1
Now substitute 2 for c in all the choices and identify which choice matches the target of 8.
3(2) = 6 → No
3(2) + 1 = 7 → No
4(2) = 8 → Yes
5(2) = 10 → No
5(2) – 1 = 9 → No
The only choice that yields a value that matches the target is C.
Strategy 2: Back-Solve
Like plugging in numbers, back-solving is specific to Discrete Quantitative questions. Back-solving is an option when the choices provide values for a variable in the question. Again, back-solving is a way to avoid algebra. Instead of working out the manipulations in the question, you can work backward to determine which choice provides a value that matches the restrictions in the question. Let’s look at an example:
After a 20% decrease, the price of a shirt was $120. What was the original price of the shirt?
$100
$144
$150
$160
$180
Though you can certainly answer this question algebraically, let’s focus on back-solving.
STEP 1: Start with Choice B. Take the value in Choice B and determine how it relates to the information in the question. If the original price of the shirt was $144, then the new price of the shirt would be $144 − 0.2($144) = $115.20. When the original price of the shirt is $144, the reduced price of the shirt ($115.20) is less than $120. Thus $144 is too small a value for the original price of the shirt. Since the value in B is too small, the value in A must be too small as well. The correct answer is C, D, or E.
STEP 2: Back-solve with Choice D. Why Choice D? There are three possibilities: Either D is the answer, D is too small, or D is too big. If D is too small, then the answer must be choice E. If D is too big, then the answer must be choice C. No matter what happens, you won’t have to test choices C and E. Thus by testing B and then D, you ensure that you will never have to test more than two choices.
Let’s see how the value in D relates to the given information. If the original price of the shirt was $160, then the reduced price of the shirt would be $160 − 0.2(160) = $128. $128 is greater than the reduced price in the question. You can thus infer that $160 is too large of a value for the original price of the shirt. The value in Choice D is too large. If the value in Choice D is too large, then the value in Choice E must be too large as well. The correct answer must be C.
Exercise: Two Essential Quantitative Reasoning Strategies
Discrete Quantitative Questions
1. The cost for a phone call is $0.75 for the first minute and $0.50 per minute after the first minute. If a phone call lasted x minutes, what was the cost of the phone call in terms of x?
$0.75
$0.75 + x
$0.75 + 0.5x
$0.75 + 0.5(x – 1)
$1.25x
2. If 2x + 3y = z, what is x in terms of y and z?
z – 3y
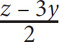
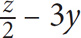
2z – 3y
z + 3y
3. Walking at a constant rate of x miles per hour, it took Jack y hours to travel from his home to his school. In terms of x and y, which of the following is equivalent to half of the distance that Jack traveled?
xy
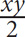
2xy
2(x + y)
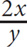
4. The total price for a equally priced shirts was b dollars. In terms of b and a, what is the total price for six of these shirts?
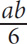
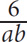
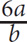
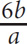
6ab
5. Traveling at a constant rate of 15 miles per hour, it took Bob x hours to go from his home to his school. Traveling at a constant rate of 20 miles per hour, it took Bob x − 1 hours to travel the same route. What is the value of x?
2
3
4
5
6
For this question, indicate all of the answer choices that apply.
6. If xy = 12, and x + y = 7, then y could equal which of the following?
3
4
5
6
7
7. If a2 + b = 7, then b could equal which of the following?
6
8
9
10
11
8. A group of x friends agreed to equally split the bill for a meal that cost y dollars. If z friends decide not to pay how much will each of the remaining friends have to pay, in terms of x, y, and z?
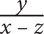
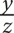
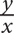
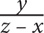
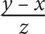
9. A retailer originally bought 50 equally priced phones for a total of z dollars. If he sold each phone for 25% more than he paid for it, then in terms of z, how much was each phone sold for?
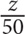
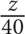
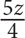
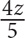
62.5z
10. Sam has y tapes, which is three times as many as Bob and half as many as Tom. In terms of y, how many tapes do Sam, Bob, and Tom have combined?
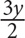
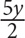
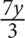
3y
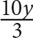
11. A basketball team averaged z points per game for q games. If the team scored 100 points its next game, what was the team’s average in terms of z and q?
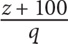
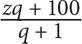
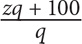
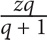
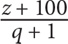
12. If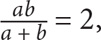 
then what is a in terms of b?
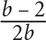
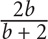
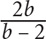
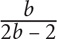
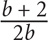
Exercise Answers
Discrete Quantitative Questions
1. D
Step 1: Choose a smart value for x: Let x = 3.
Step 2: Substitute 3 for x in the question and determine the “goal”: The cost of the first minute = $0.75. The cost for the next two minutes = $0.50(2) = $1. The total cost = $1.75. Goal: $1.75
Step 3: Substitute 3 for x in the choices, and identify which choice yields a value that matches your goal: $1.75
The only choice that yields a value of $1.75 is D.
2. C
Step 1: Choose smart values: Let x = 5 and y = 15. Substitute these values to determine a value for z: 2(5) + 3(15) = 60. Thus when x = 5 and y = 15, z = 60.
Step 2: Substitute 5 for x in the question and determine the “goal”: In this case, you want to solve for x, so the goal is simply the value that you chose for x: 5.
Step 3: Substitute 15 for y and 60 for z in the choices, and identify which choice yields a value that matches your goal: 5. The only choice that yields a value of 5 is C.
3. C
Step 1: Choose smart values for x and y: Let x = 10 and y = 5.
Step 2: Substitute 10 for x and 5 for y in the question and determine the “goal.” Since you want half the distance to the school, let’s use these values to get the entire distance, and then divide by 2. In this case, the total distance to the school is (miles/hour) x # of hours = xy = 10 × 5 = 50. Half of the distance is thus 50/2 = 25. The goal is 25.
Step 3: Substitute 10 for x and 5 for y in the choices, and identify which choice yields a value that matches your goal: 25. The only choice that yields a value of 25 is C.
4. D
Step 1: Choose smart values: Let a = 5 and b = 20.
Step 2: Substitute 5 for a and 20 for b in the question and determine the goal: If 5 shirts cost $20, then each shirt is $20/5 = $4. The cost of six shirts will thus be 6 × $4 = 24. The goal is 24.
Step 3: Substitute 5 for a and 20 for b in the choices, and identify which choice yields a value that matches your goal: 24. The only choice that yields a value of 24 is D.
5. C Since the distance for both trips is the same, the answer should provide a value of x that yields the same distance for both trips. You can determine the value of x by back-solving. First, start with 3. If x = 3, then traveling at 15 mph, Bob traveled a distance of 15(3) = 45. Traveling 20 mph for (3 − 1) hours, Bob traveled 40 miles. 3 is too small for the distances to match. Eliminate A and B. Now go to Choice D. If x = 5, then traveling at 15 mph, Bob traveled a distance of 15(5) = 75. Traveling 20 mph for (5 − 1) hours, Bob traveled 80 miles. 5 is too large for the values to match. Eliminate D and E. The answer is C.
6. A and B Back-solving is a good strategy here, but make sure to check all the choices. Try Choice A. If y = 3, then 3x = 12 → x = 4. These values satisfy the equation: x + y = 7. Thus 3 is a potential answer. Go through this process for all the choices. The only other choice that provides a value that will yield a value for x that satisfies both equations is 4. The answer is A and B.
7. A Back-solve by starting with Choice B. If b = 8, then
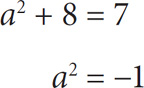
A number raised to an even exponent never yields a negative result. Thus 8 is too large for B. The correct answer must be A.
8. A
Step 1: Choose smart values: Let y = 100, x = 25, and z = 5.
Step 2: Substitute 100 for y, 20 for x, and 5 for z in the question and determine the “goal”: If there were originally 25 people and 5 people dropped out, then the bill will be split among 25 – 5 = 20 people. The total bill is $100, so after the friends drop out, the cost per person will be 100/20 = 5. The goal is 5.
Step 3: Substitute 100 for y, 20 for x, and 5 for z in the choices, and identify which choice yields a value that matches your goal: 5. The only choice that yields a value of 5 is A.
9. B
Step 1: Choose a smart value: Let z = 200.
Step 2: Substitute 200 for z in the question and determine the “goal”: If the retailer paid $200 for 50 phones, then each phone cost $4. If the dealer charged 25% more than he paid for it, he sold each phone for 4 + 0.25(4) = 5. The goal is 5.
Step 3: Substitute 200 for z in the choices, and identify which choice yields a value that matches your goal: 5. The only choice that yields a value of 5 is B.
10. E
Step 1: Choose a smart value: To ensure that the number of tapes that Bob has is an integer, choose a multiple of 3 for y: 6.
Step 2: Substitute 6 for y in the question and determine the “goal”: If Sam has 6 tapes, then Bob has 2 tapes, and Tom has 12 tapes. In total, they have 6 + 2 + 12 = 20 tapes.
Step 3: Substitute 6 for y in the choices, and identify which choice yields a value that matches your goal: 20. The only choice that yields a value of 20 is E.
11. B
Step 1: Choose smart values for z and q: Let z = 80 and q = 5.
Step 2: Substitute 80 for z and 5 for q in the question and determine the “goal”: If the team averaged 80 points per game for 5 games, then its total number of points for those 5 games was 80 × 5 = 400. After the team scored 100 points, its total was 500 and the number of games played was 6. Thus the new average is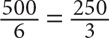 
. The goal is 
.
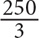Step 3: Substitute 80 for z and 5 for q in the choices, and identify which choice yields a value that matches your goal: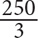 
. The only choice that yields a value of 
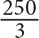is B.
12. C
Step 1: Choose smart values for a and b: Since there is a restriction in the question, choose a value for a and let that value determine b: Let a = 6. Substitute 6 into the given equation to solve for b:
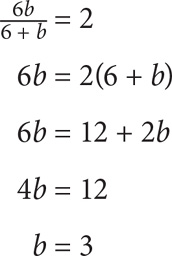
So a = 6, and b = 3.
Step 2: Substitute 6 for a and 3 for b in the question and determine the “goal”: Since the question asks to solve for a, the goal is simply the value of a: 6.
Step 3: Substitute 3 for b in the choices, and identify which choice yields a value that matches your goal: 6. The only choice that yields a value of 6 is C.