CHAPTER 9
Study this chapter to learn about:
On a broad level, you can think of properties of numbers as the branch of math concerned with how numbers behave in certain situations. Though this is an enormous field in formal mathematics, the GRE will be concerned with properties of numbers in the following contexts: divisibility, odds and evens, positives and negatives, and evenly spaced sets. Because these areas are all concerned with concrete mathematical rules and what you can deduce from these rules, questions testing these concepts will often appear in Quantitative Comparison questions or a “must be true” or “could be true” format in Discrete Quantitative questions.
Factors and Multiples
Any whole number is an integer. For example, 2 and –9 are integers, but 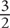 and –7.2 are not. The factors (or divisors) of an integer are the integer values that divide evenly into that number. 2 is a factor of 12 because
and –7.2 are not. The factors (or divisors) of an integer are the integer values that divide evenly into that number. 2 is a factor of 12 because 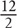 = 6, which is an integer. But 5 is not a factor of 12, because
= 6, which is an integer. But 5 is not a factor of 12, because 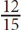 = 2.4, which is not an integer. To determine the factors of a number, you can create a factor table. For example, the factors of 12 are:
= 2.4, which is not an integer. To determine the factors of a number, you can create a factor table. For example, the factors of 12 are:
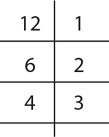
The multiples of an integer are the products that result when that integer is multiplied by another integer. For example, the multiples of 12 are 12(1) = 12, 12(2) = 24, 12(3) = 36, … .
The GRE expresses the preceding relationships in several ways. All of the following sentences mean the same thing:
2 is a factor of 12 |
12 is a multiple of 2 |
2 is a divisor of 12 |
12 is divisible by 2 |
2 divides evenly into 12 |
12 divided by 2 yields an integer |
Many test-takers tend to confuse factors and multiples. If this is the case, think to yourself that there are finite factors and many multiples. The factors are what create a number and the multiples are what result from that number.
Prime Factors and the Factor Tree
Any number will always have 1 and itself as divisors. If an integer is divisible only by 1 and itself, then it is a prime number. Examples of prime numbers are 2, 3, 5, 7, 11, 13, and so on.
A prime factor is any factor of an integer that is also prime. For example, 2 and 3 are prime factors of 12, but 4 is not. There are two important properties about prime factors:
1. Any integer can be expressed as the product of its prime factors. For example: 12 = 2 × 2 × 3.
2. The factors of any integer will be completely determined by the prime factors of that integer. For example, 12 = 2 × 2 × 3. The factors of 12 are 1, 2, 3, (2 × 2), (2 × 3), (2 × 2 × 3).
To determine the prime factors of a number, you should create a factor tree. The following is the factor tree for 240.
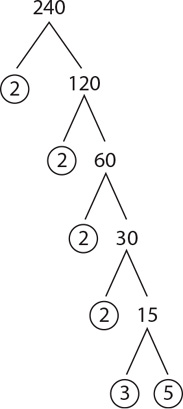
The prime factorization of 240 is thus: (24) × 3 × 5. From Property 2 earlier, you can infer that 40 is a factor of 240 but that 32 is not. Why? Because the prime factors of 40 (2 × 2 × 2 × 5) are contained in the prime factorization of 240, but the prime factors of 32 (2 × 2 × 2 × 2 × 2) are not contained in the prime factorization of 240. One important principle that extends from the preceding explanation is the following:
If a is a factor of b, and b is a factor of c, then a must be a factor of c.
For example, since 40 is a factor of 240, 8 and 5 (which are factors of 40) must also be factors of 240.
If y is divisible by 12, which of the following must be true? Indicate all that apply.
 y is divisible by 24
y is divisible by 24
 y is divisible by 6
y is divisible by 6
 y is divisible by 4
y is divisible by 4
SOLUTION: If y is divisible by 12, then the prime factors of 12 must be prime factors of y. Create a factor tree to determine the prime factors of 12.
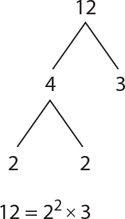
You can therefore infer that y has 2, 2, and 3 in its prime factorization. Since y has 2 × 2 in its prime factorization, y must be divisible by 4. Since y has 2 × 3 in its prime factorization, y must be divisible by 6. The correct answer is B and C.
Greatest Common Factor and Least Common Multiple
The greatest common factor (GCF) of a set of numbers is the largest integer that divides evenly into all the numbers. To determine the greatest prime factor of a set of numbers, break each of the numbers down into their prime factors and circle the shared factors. The product of the shared factors will be the GCF.
For this question, write your answer in the box.
What is the greatest common factor of 12, 72, and 88?

SOLUTION: Determine the prime factors of each of the numbers and circle their common prime factors:
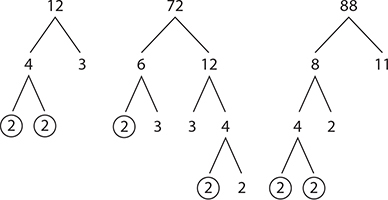
12, 72, and 88 each have two 2s in their prime factorizations. The GCF of the three numbers is thus 2 × 2 = 4.
The least common multiple (LCM) of a set of numbers is the smallest integer that is divisible by all the numbers in the set. The LCM must therefore contain the prime factors of each number in the set. As with the GCF, prime factorization is important for LCM questions.
If x is the smallest integer that is divisible by 9, 12, and 15, what is the value of x?
SOLUTION: You are asked to determine the LCM of 9, 12, and 15. First, break each number down into its prime factorization:
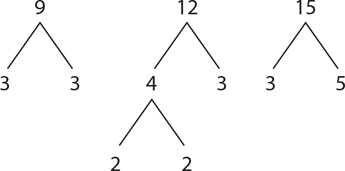
Since x is a multiple of 9, x must have two 3s in its prime factorization. Thus x = 3 × 3 … . Since x is a multiple of 12, x must have two 2s and one 3 in its prime factorization. You know that x already has a 3 in its prime factorization, so to make x a multiple of 12, you only need to add two 2s to its prime factors. Thus x = 3 × 3 × 2 × 2 … . Since x is a multiple of 15, it must have one 3 and one 5 in its prime factorization. You know from earlier that x already has a 3 in its prime factorization, so to make x a multiple of 15, you only need to add one 5 to its prime factors. Thus x = 3 × 3 × 2 × 2 × 5 = 180.
Remainders
Recall that 15 is a multiple of 5 since 5 divides evenly into 15. What about 16? 16 is not a multiple of 5, because 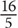 = 3.2, which is a noninteger. When doing division, if the numerator is not divisible by the denominator, the value left over after the denominator divides into the numerator is called the remainder.
= 3.2, which is a noninteger. When doing division, if the numerator is not divisible by the denominator, the value left over after the denominator divides into the numerator is called the remainder.
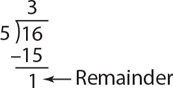
The remainder essentially tells you how many units the numerator is past a given multiple of the denominator. It follows that the remainder must always be smaller than the divisor. Look at the remainders yielded by each of the following:
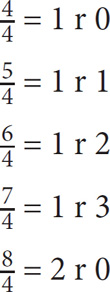
Once you come to  , the remainder cycles back to zero.
, the remainder cycles back to zero.
Unknowns and Remainders
It helps to express remainders algebraically, especially when the numerator of the fraction is an unknown. For example: When x is divided by 7, the remainder is 2. You can translate this to mean: x is two units to the right of a multiple of 7.

As illustrated in the diagram, x can equal 9, 16, 23, 30, 37, and so on. There are infinite values for x, but they are all two units to the right of a multiple of 7.
You can also express the previous mathematical sentence algebraically. Any given multiple of 7 can be expressed as 7I, where I = any integer. Since x is two units to the right of a multiple of 7, it follows that: x = 7I + 2.
When x is divided by 6, the remainder is 2. Which of the following could be a value of x?
 10
10
 12
12
 14
14
 16
16
 18
18
SOLUTION: Express x algebraically: x = 6I + 2. Determine which of the choices will yield an integer value for I.
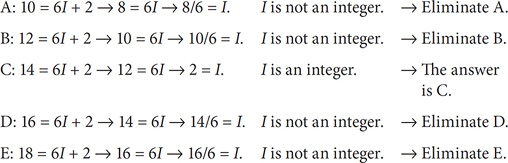
SOLUTION: The correct answer is C.
Exercise: Factors and Multiples
Discrete Quantitative Questions
For each question, select one answer, unless the instructions state otherwise.
1. What is the greatest common factor of 16, 24, and 72?
 2
2
 4
4
 8
8
 12
12
 16
16
For this question, write your answer in the box.
2. What is the least common multiple of 6, 8, and 15?

For Questions 3 and 4, indicate all the answer choices that apply.
3. If x is divisible by 12 and y is divisible by 8, then which of the following must be true?
 xy is a multiple of 48
xy is a multiple of 48
 64 is a factor of xy
64 is a factor of xy
 xy is not divisible by 5
xy is not divisible by 5
 32 is a factor of xy
32 is a factor of xy
4. If a is divisible by 6 and by 8, which of the following must be true?
 a is divisible by 4
a is divisible by 4
 a is divisible by 12
a is divisible by 12
 a is divisible by 48
a is divisible by 48
5. What is the greatest integer, k, such that 5k is a factor of the product of the integers from 1 through 24, inclusive?
 1
1
 2
2
 3
3
 4
4
 5
5
Quantitative Comparison Questions
1. 
2. 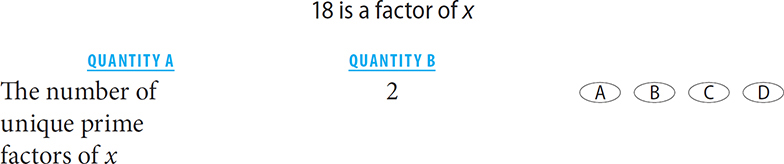
3. 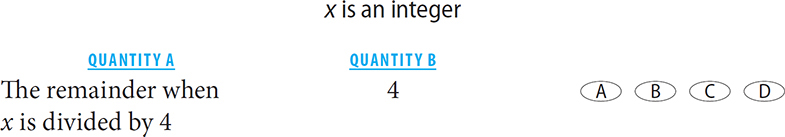
4. 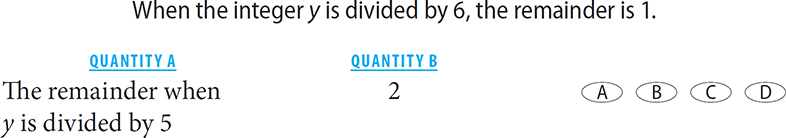
Exercise Answers
Discrete Quantitative Questions
1. C Determine the prime factorization of each of the numbers.
16 = 2 × 2 × 2 × 4
24 = 2 × 2 × 2 × 3
72 = 2 × 2 × 2 × 3 × 3
Each term contains three 2s. The greatest common factor is thus 2 × 2 × 2 = 8.
2. 120 The LCM of a set must contain the prime factorization of each term in the set. First, find the prime factorization of each term in the set:
6 = 2 × 3
8 = 2 × 2 × 2
15 = 5 × 3
The LCM must thus have the factors of 6: 2 × 3. The LCM must have the factors of 8: 2 × 2 × 2. Since 6 contains a 2, the LCM will contain all the factors of 8 and 6 when it has 2 × 2 × 2 × 3 in its prime factorization. For the LCM to contain the factors of 15, an additional 5 is required. Thus the LCM is: 2 × 2 × 2 × 3 × 5 = 120.
3. A and D Since x is divisible by 12, it must contain the prime factors of 12. The prime factorization of 12 is 2 × 2 × 3. Since y is divisible by 8, it must contain the prime factors of 8. The prime factorization of 8 is 2 × 2 × 2. xy must contain all the prime factors of x and all the prime factors of y. Thus the prime factorization of xy must contain 2 × 2 × 2 × 2 × 2 × 3. Note that xy can contain other prime factors as well, but the ones just given are the only prime factors that it has to contain.
Choice A: Since the prime factors of xy can be combined to yield 48, 48 must be a factor of xy, which means xy is a multiple of 48. → Choice A is true.
Choice B: The prime factorization of 64 is 2 × 2 × 2 × 2 × 2 × 2. The factorization 2 × 2 × 2 × 2 × 2 × 3 does not contain the prime factorization of 64. Thus 64 is not necessarily a factor of xy. → Eliminate Choice B.
Choice C: The information in the question tells you which prime factors xy must have, but it does not eliminate the possibility that xy has other factors. Thus it cannot be determined whether 5 is a factor of xy. → Eliminate Choice C.
Choice D: The prime factorization of 32 is 2 × 2 × 2 × 2 × 2. The factorization 2 × 2 × 2 × 2 × 2 × 3 contains the prime factorization of 32. Thus 32 is a factor of xy. → Choice D is true.
The correct answer is A and D.
4. A and B Since this is a “must be true” question, identify only what is necessarily true about a. Since a is a multiple of 6 and 8, a must contain the prime factors of 6 and 8. Though a could equal 6 × 8 = 48, a must equal the LCM of 6 and 8, which is 24. Since a must be a multiple of 24, it must contain the factors of 24. 4 is a factor of 24, so Choice A is true. 12 is a factor of 24, so Choice B is true. 48 is not a factor of 24, so Choice C is not necessarily true. The correct answer is A and B.
5. D For the purpose of this question, let’s express “the product of the integers from 1 through 24, inclusive” as 24!. For 5k to be a factor of 24!, 5k must divide evenly into 24!. For this to be true, the value of k cannot exceed the number of times 5 appears in the prime factorization of 24!. The greatest value for k will thus equal the number of times that 5 appears in the prime factorization of 24!. To determine the number of times that 5 appears in the prime factorization of 24!, look at the multiples of 5 from 1–24, inclusive: 5 = 5(1). 10 = 5(2). 15 = 5(3). 20 = 5(4). There are thus four 5s in the prime factorization of 24!. The maximum value for k is thus 4. The correct answer is D.
Quantitative Comparison Questions
1. C If x is a multiple of 12, then the factors of 12 must be factors of x. Since 3 is a factor of 12, 3 is a factor of x. Thus x divided by 3 yields a remainder of 0. Since 6 is a factor of 12, 6 is a factor of x. Thus x divided by 6 yields a remainder of 0.
2. D Since 18 is a factor of x, the prime factors of 18 must be prime factors of x. The prime factorization of 18 is 3 × 3 × 2. Thus 18 has two unique prime factors, meaning x must have at least two unique prime factors. However, since you have no additional information about x, you do not know whether it has additional prime factors. For example, x could equal 90, which has a prime factorization of 3 × 3 × 2 × 5. In this case, x has three unique factors. The relationship cannot be determined.
3. B The remainder must always be smaller than the divisor. Thus the value in quantity A must be less than 4.
4. D Plug in the numbers. If y = 7, the value in Quantity A is 2. In this case, the two quantities are equal. If y = 13, the value in Quantity A is 3. In this case, Quantity A is greater. The relationship cannot be determined.
Odds and Evens
An even number is any integer that has 2 as a factor; for example, 4, 28, –12, –6, and so on.
An odd number is simply the opposite: any number that does not have 2 as a factor, for example, 1, 9, –13, and so on. The GRE will expect you to know the following rules. Though testing numbers is certainly helpful on these questions, you will ultimately save time on the test by committing these rules to memory!
Addition and Subtraction
Property 1: In addition or subtraction, the result will be even if the numbers being added or subtracted are the same (both odd or both even), and the result will be odd if the numbers being added or subtracted are different (one odd and one even).
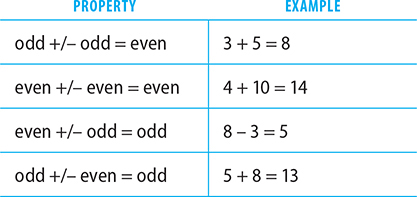
Multiplication
Property 2: For a product to be even, at least one of the factors must be even.
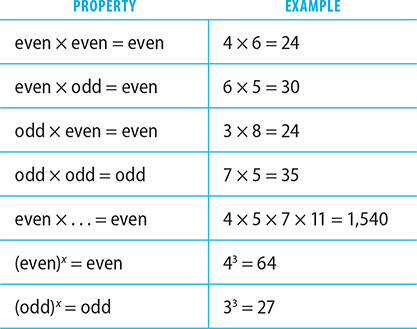
Let’s look at a sample question that tests these properties:
For this question, indicate all of the answer choices that apply.
If x and y are integers and 3x + 2y is even, then which of the following must be true?
 x is even
x is even
 x is odd
x is odd
 xy is even
xy is even
 x + y is even
x + y is even
 x2 is odd
x2 is odd
SOLUTION: Use properties of odds and evens to deduce what must be true about the variables.
3x + 2y = even
Look at each term separately: you don’t know whether 3x is odd or even, since you don’t know whether x is odd or even. However, whether y is odd or even, 2y will always be even since 2y has 2 as a factor. So think of the equation as:
3x + even = even
From the addition and subtraction rules, you know that even + even = even. Therefore, 3x must be even. For the product 3x to be even, the term must have an even factor. 3 is not even, so x must be even.
SOLUTION: The correct answer is A and C
Exercise: Odds and Evens
Discrete Quantitative Questions
1. If x is an integer, and 3x2 is even, then which of the following must be true?
 x + 3 is even
x + 3 is even
 x2 – 1 is even
x2 – 1 is even
 x + 4 is even
x + 4 is even

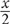 is even
is even

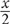 is odd
is odd
2. If –x/7 is even, then which of the following must be true?
 x is odd
x is odd
 x is even
x is even
 x is negative
x is negative
 x is positive
x is positive
 x is a prime number
x is a prime number
For Questions 3 to 6, indicate all of the answer choices that apply.
3. If x and y are integers, and x2 – y2 is even, then which of the following must be true?
 x – y is even
x – y is even
 x + y is even
x + y is even
 (x + y)2 is even
(x + y)2 is even
 xy is even
xy is even

 is even
is even
 x2 – xy is even
x2 – xy is even
4. If x is an even integer, then which of the following must be true?
 x2 + 2 is even
x2 + 2 is even

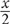 is even
is even

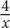 is even
is even
 x7 is even
x7 is even
 x2 is a multiple of 4
x2 is a multiple of 4
5. If x and y are both integers and x(y +3) is odd, then which of the following must be true?
 x is even
x is even
 y is even
y is even
 xy is odd
xy is odd
 xy is even
xy is even
 x is odd
x is odd
 y is odd
y is odd
6. If a, b, and c are positive integers, a + b = 12, and bc = 15, then which of the following must be true?
 b + c is even
b + c is even
 ab is even
ab is even
 ac is odd
ac is odd
 a – c is even
a – c is even
 abc is odd
abc is odd
Exercise Answers
1. C Exponents are irrelevant when considering properties of odds and evens. So if 3x2 is even, then 3x is even. If 3x is even, then 3x must have an even factor. 3 is not even, so x must be even. If x is even, then x + 4 is always even. You may be wondering about Choice D: note that even when x is even, 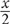 is not always even. For example, if x = 6,
is not always even. For example, if x = 6, 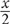 = 3, which is not even.
= 3, which is not even.
2. B Plug in values for x that would satisfy the given information. Try x = 14. In this case, 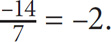 –2 is even, so 14 is a possible value for x. Thus choices B and D are possibilities. However, if x = –14, the given information will still be true:
–2 is even, so 14 is a possible value for x. Thus choices B and D are possibilities. However, if x = –14, the given information will still be true: 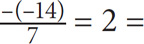 even. Thus x can be positive or negative. Eliminate Choice D. The correct answer is B. An important takeaway from this question is that the sign is irrelevant in odd and even questions.
even. Thus x can be positive or negative. Eliminate Choice D. The correct answer is B. An important takeaway from this question is that the sign is irrelevant in odd and even questions.
3. A, B, C, and F Since exponents are irrelevant when working with odds and evens, the fact that x2 – y2 is even implies that x – y is even. If the difference between two numbers is even, then x and y must both be odd or both be even. For cases where they are both odd or both even, A, B, C, and F will always be true. (You can plug in numbers to confirm.)
4. A, D, and E Evaluate each choice.
Choice A: An even number to any power yields an even. An even + even = even. → A is true.
Choice B: If x is 4, then 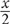 = 2 = even. If x = 6, then
= 2 = even. If x = 6, then 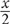 = 3, which is odd. → B is not always true.
= 3, which is odd. → B is not always true.
Choice C: If x is 4, then 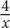 = 1, which is odd. → C is not always true.
= 1, which is odd. → C is not always true.
Choice D: An even to any power yields an even. → D is true.
Choice E: If x is 2, then x2 = 4. 4 is a multiple of 4. If x is 8, then x2 = 64. 64 is a multiple of 4. Both cases lead to the conclusion that x2 is a multiple of 4. → E is true.
5. B, D, and E For a product to be odd, all factors must be odd. Thus x and (y + 3) must be odd. If y + 3 is odd, then y is even. Now evaluate the choices:
Choice A: As previously shown, x is odd. → A is not true.
Choice B: As previously shown, y is even. → B is true.
Choice C: For a product to be odd, all factors must be odd. As previously shown, y is even. Thus xy is even. → C is not true.
Choice D: See the explanation for C. → D is true
Choice E: See the explanation for A. → E is true
Choice F: See the explanation for B. → F is not true
6. A, C, D, and E Since a + b is an even integer, a and b must both be odd or both be even. Since bc is an odd integer, b and c must both be odd. If a + b = even and b = odd, then a = odd. Thus a, b, and c are all odd. Evaluate the choices:
Choice A: odd + odd = even → A is true.
Choice B: odd × odd = odd → B is not true.
Choice C: odd × odd = odd → C is true.
Choice D: odd – odd = even → D is true.
Choice E: odd × odd × odd = odd → E is true.
Positives and Negatives
All About Zero
A number’s position in relation to zero determines its sign. If a number is greater than zero, then it is positive. If a number is less than zero, it is negative.
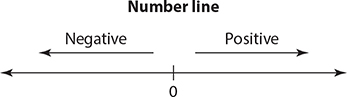
Generally, when you are told or asked whether a term is greater than zero or less than zero, you should interpret it using properties of positives and negatives. For example, if you are told that xy > 0, think of this information as “xy is positive,” and proceed to use the rules covered in this chapter. As with odds and evens, you will need to know certain properties of positive and negative numbers.
Multiplication and Division
When multiplying or dividing two terms, the result will be positive if the terms are the same sign (both positive or both negative) and negative if the two terms are different signs (one positive and one negative).
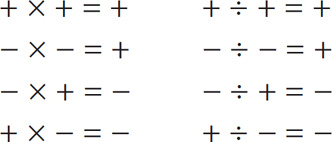
If 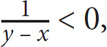 then which of the following must be true?
then which of the following must be true?
 y > 0
y > 0
 x > 0
x > 0
 xy > 0
xy > 0
 y > x
y > x
 x > y
x > y
SOLUTION: If 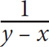 is negative, then the numerator and denominator must have different signs. Since the numerator is positive, y – x must be negative. Algebraically y – x < 0. Add x to both sides: y < x. Of the choices, the only one matching what you have deduced is E.
is negative, then the numerator and denominator must have different signs. Since the numerator is positive, y – x must be negative. Algebraically y – x < 0. Add x to both sides: y < x. Of the choices, the only one matching what you have deduced is E.
If a4b3c7 > 0, then which of the following must be true? (Indicate all the apply.)
 a > 0
a > 0
 b > 0
b > 0
 bc > 0
bc > 0
 b/c > 0
b/c > 0
 ab > 0
ab > 0
 abc > 0
abc > 0
SOLUTION: You are not told the sign of any of the unknowns, but since a is raised to an even exponent, you know that a2 is positive. Thus you have: (+) × (b3) × (c7) > 0. Since + × + = +, it must be true that b3 × c7 is positive. Since b and c are each raised to odd exponents, the signs of b3 and c7 will be the same as the signs of b and c, respectively. Thus you know that bc > 0. If bc > 0, then b and c must have the same sign, meaning that their product and their quotient are positive. The correct answer is C and D.
Many test-takers mistakenly assume that since a4 > 0, a must be greater than zero. However, remember that even exponents hide the sign of the base. Whether the base is positive or negative, the result of a variable raised to an even exponent will always be positive. Thus F is not necessarily true.
Quantitative Comparison Strategy: Positives and Negatives
The GRE loves testing properties of positives and negatives in Quantitative Comparison questions. One important building block of success for the savvy test-taker is to identify situations in which these properties are being tested.
Situation 1 You are told that an unknown is greater than or less than zero.
If the stem says that x > 0, then you know that x is positive. If it says that xy < 0, then you know that xy is negative. Once you recognize that these properties are being tested, you can then start using the rules that have been covered.
Situation 2 One of the quantities has a value of zero.
If you are comparing an unknown to zero, your ultimate goal is to determine the sign of that unknown. Remember that you can determine its sign without knowing its actual value.
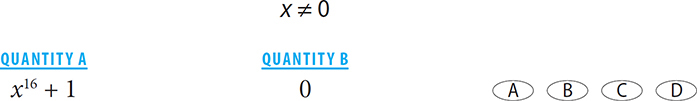
SOLUTION: Since you are comparing (x16 + 1) to zero, you should focus on determining the sign of Quantity A. Since the exponent on x16 is even, x16 > 0. Thus x16 + 1 > 0. The correct answer is Quantity A.
Situation 3 One of the quantities has an even exponent, and the other quantity has an odd exponent.
Since the result of an even exponent hides the sign of the base, and the result of an odd exponent preserves the sign of the base, these properties are fertile ground to test your knowledge of positives and negatives.
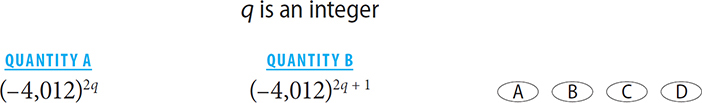
SOLUTION: In both quantities, the base is negative. Since the exponent in Quantity A is even, the value in Quantity A must be positive. Since the exponent in Quantity B is odd, the value in Quantity B must be negative. The correct answer is A.
Finally, when testing numbers for Quantitative Comparison questions testing positives and negatives, you should always test at least one negative case and one positive case. You want to play devil’s advocate, and the best way to do so is by choosing numbers with different signs.
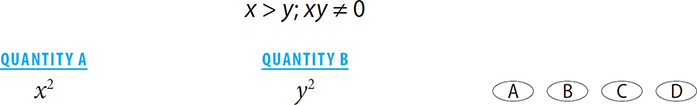
SOLUTION: The even exponents in the quantities should clue you in that the question might be addressing properties of positives and negatives. Let’s thus choose positive and negative cases for x and y:
Case 1: x = 3 and y = 2. Quantity A: 32 = 9. Quantity B: 22 = 4. Quantity A is greater. The answer is A or D.
Case 2: x = 3 and y = –2. Quantity A: 32 = 9. Quantity B: –22 = 4. Quantity A is still greater. Though you might be tempted to stop here and select A, notice that you have not looked at situations where both values are negative.
Case 3: x = –5 and y = –6. Quantity A: –52 = 25. Quantity B: –62 = 36. In this case, Quantity B is greater. A relationship cannot be determined, so the answer is D.
Exercise: Positives and Negatives
Discrete Quantitative Questions
1. If a < b < 0, then which of the following must be true?
 ab < 0
ab < 0
 a + b > 0
a + b > 0

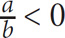
 b – a > 0
b – a > 0
 a – b > 0
a – b > 0
2. If xy > 0 and yz < 0, then which of the following must be negative?
 xyz
xyz
 xy2z
xy2z
 x2y2z
x2y2z
 x2y2z2
x2y2z2

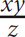
3. If ab2 > 0 and ac < 0, then which of the following must be true? (Indicate all the apply.)
 ab >0
ab >0
 b > 0
b > 0

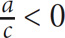
 b2c < 0
b2c < 0
 a(c2) > 0
a(c2) > 0
4. If 0 > x > y, then which of the following must be true? (Indicate all that apply.)
 x2 – y2 < 0
x2 – y2 < 0
 y – x < 0
y – x < 0

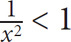

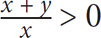
 y2 – x2 < 0
y2 – x2 < 0
5. If 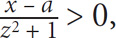 then which of the following must be true?
then which of the following must be true?
 x > 0
x > 0
 x < a
x < a
 x > a
x > a
 xa > 0
xa > 0
 x + a > 0
x + a > 0
6. If xy > 0 and x + y > 0, then which of the following must be true? (Indicate all that apply.)
 x < 0
x < 0
 |x| > |y|
|x| > |y|
 x > 0
x > 0

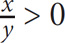
 y > 0
y > 0
Quantitative Comparison Questions
1. 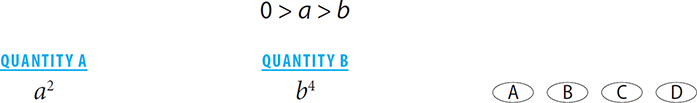
2. 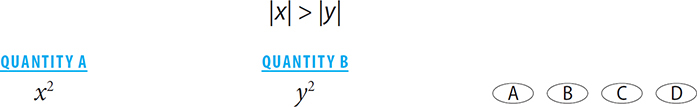
3. 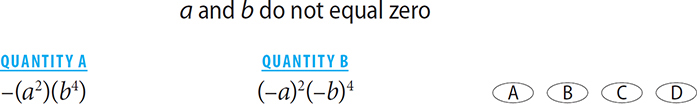
4. 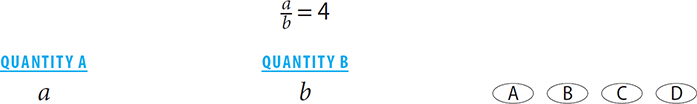
5. 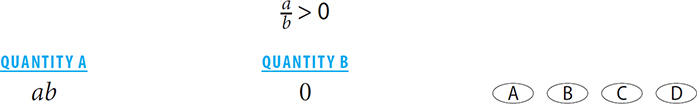
6. 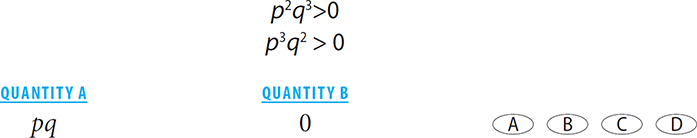
7. 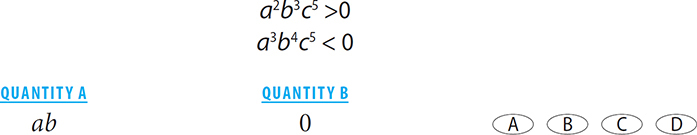
Exercise Answers
Discrete Quantitative Questions
1. D Since a and b are negative, their product and quotient must be positive. Thus eliminate A and C. The sum of two negatives is a negative. Thus eliminate B. For D and E, choose values. Let a = –4 and b = –3. Evaluate the expression in D: –3 – (–4) = –3 + 4 = 1. 1 > 0, so D is true. Evaluate the expression in E: –4 – (–3) = –4 + 3 = –1. –1 is not greater than zero. Eliminate E.
2. B If xy is positive, then x and y must have the same sign. If yz is negative, then y and z must have different signs. If x and y have the same sign and y and z have different signs, then x and z must have different signs, meaning xz < 0. Use this information in each choice. For A, you know that xz < 0, but you do not know the sign of y, so you do not know whether the product is negative. In B, you know that y2 > 0 (because of the even exponent) and that xz < 0. (–)(+) = (–), so Choice B is negative. In C, you know that x2y2 must be positive because of the even exponents, but you do not know the sign of z. In D, all the variables are raised to even exponents, so the result must be positive. In E, you know that xy > 0, but you do not know the sign of the denominator. The only choice that must be negative is B.
3. C, D, and E In the first inequality, you know that a must be positive since b2 is positive. In the second inequality, you know that a and c must have different signs. If a > 0, and a and c have different signs, then c < 0.
4. A, B, and D Since this is a “must be true” question, it is helpful to plug in values for x and y. First, plug in integers, and then fractions.
Case 1: x = –0.5 and y = –0.75. Plug these values into the choices:
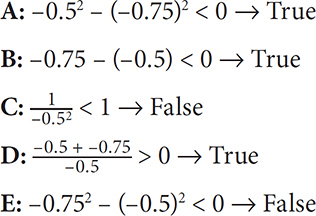
Now plug in integers for the choices that yielded true in Case 1. Let x = –2 and y = –3.
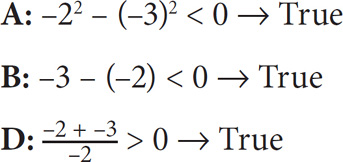
Since 1, 2, and 4 remain true for both conditions, those are the answers.
5. C For a fraction to be positive, the numerator and denominator must have the same sign. Since z is raised to an even exponent, you know that z2 must equal at least zero. Therefore, z2 + 1 must be positive. If the denominator of this fraction is positive, then the numerator is also positive. Thus x – a > 0. Add a to both sides: x > a.
6. C, D, and E If xy > 0, then x and y are both positive or both negative. If x and y are both negative, then x + y < 0. The condition that x and y are both negative does not satisfy the given information. Thus to satisfy the given information, x and y must both be positive. If x and y are both positive, then choices C, D, and E are true.
Quantitative Comparison Questions
1. D Choose values: First, select an integer value for each variable. Let a = –1 and b = –2. In this case, Quantity A = 1, and Quantity B = 16. In this case, Quantity B is greater. Next, choose values that are likely to yield a relationship different than the relationship that the first pair of numbers yielded. To do so, select “weird” numbers. In this case, a good type of “weird” number is a fraction. Let a = 0.25 and let b = 0.5. In this case, Quantity A = 0.0625, and Quantity B = 0.0625. In this case, both quantities are equal. Therefore, a relationship cannot be determined.
2. A Plugging in numbers is a good strategy here. Since the columns have even exponents, the signs will not matter. So choose fractions and integers.
Case 1: x = 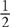 and y =
and y = 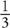 . In this case, the value of column A is
. In this case, the value of column A is  and the value of column B is
and the value of column B is  . Quantity A is greater, so the answer is A or D.
. Quantity A is greater, so the answer is A or D.
Case 2: Plug in new values to prove D: x = 3 and y = 2. In this case, the value of column A is 9, and the value of column B is 4. Quantity A is still greater.
3. B Though it would appear that you do not have sufficient information about a and b, keep in mind that the even exponents and the signs will help you make inferences. In Quantity A, a2 and b4 must be positive (because of the even exponents). Thus their product is positive. Multiply this product by –1, and the result is negative. In Quantity B, –a2 and –b4 are both positive. Thus their product is positive. The value in Column B is greater.
4. D Since 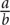 equals a positive number, a and b must have the same sign. However, you do not know what the signs are. If a = 8, then b = 2, and Quantity A is greater. But if a = –8, then b = –2, and Quantity B is greater. There is more than one relationship, so the answer is D.
equals a positive number, a and b must have the same sign. However, you do not know what the signs are. If a = 8, then b = 2, and Quantity A is greater. But if a = –8, then b = –2, and Quantity B is greater. There is more than one relationship, so the answer is D.
5. A If 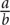 > 0, then a and b must have the same sign. If a and b have the same sign, then their product must be positive. Thus ab > 0, and the correct answer is A.
> 0, then a and b must have the same sign. If a and b have the same sign, then their product must be positive. Thus ab > 0, and the correct answer is A.
6. A Your first step should be to make inferences from the stem. Inequality 1: you know that p2q3 > 0. Because of the even exponent, p2 must be positive. Thus q3 must be positive. If q3 is positive, then q > 0 (remember, odd exponents preserve the sign of the base). Inequality 2: you know that p3q2 > 0. Because of the even exponent, q2 must be positive. Thus p3 must be positive. If p3 is positive, then p > 0. Positive × positive = positive, so pq > 0.
7. B Your first step should be to make inferences from the stem. Inequality 1: because of the even exponent, you know that a2 > 0. Thus b3c5 > 0. Because of the odd exponents, b3 and c5 will have the same signs as b and c, respectively. Thus bc > 0. Inequality 2: because of the even exponent, you know that b4 > 0. Thus a3c5 < 0. Because of the odd exponents, a3 and c5 will have the same signs as a and c, respectively. Thus ac < 0. Now you know that bc > 0 and ac < 0. If bc > 0, then b and c must have the same sign. If ac < 0, then a and c must have different signs. Therefore, a and b must have different signs, and their product must be negative.
Evenly Spaced Sets
An evenly spaced set is any series of numbers in which the spacing between consecutive terms is constant. The most basic example of an evenly spaced set is consecutive integers. In the set 1, 2, 3, 4, 5, the spacing between successive terms is 1. Other examples are:
2, 4, 6, 8 …
10, 15, 20 …
3, 8 13, 18 …
Properties of Evenly Spaced Sets
The GRE will expect you to know certain properties of evenly spaced sets.
Property 1: All the terms in an evenly spaced set can be expressed using one of the terms in the set.
If the sum of three consecutive multiples of 4 is 60, what is the value of the smallest term?
SOLUTION: Approaching this algebraically, you can let a = the smallest term, b = the middle term, and c = the largest term. Therefore, a + b + c = 60. But notice that you have additional information about these variables! Since you are dealing with consecutive multiples of 4, you can let b = a + 4 and c = b + 4 = a + 8. Thus using substitution, you can arrive at one equation with one variable:
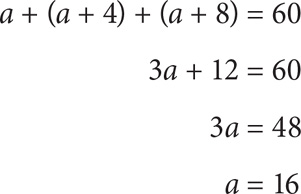
Property 2: The average (arithmetic mean) of an evenly spaced set = the median of the set = the average of the endpoints.
What is the average of x, x + 4, x + 8, x + 12, and x + 16?
SOLUTION: Recognize that each term is 4 greater than the previous term. You thus have an evenly spaced set. To find the average, you need the median, which in this case, is x + 8.
What is the average of the integers from 15–21, inclusive?
SOLUTION: Since average = median for an evenly spaced set, you could list out all the terms and find the median. But a faster approach would be to take the average of the endpoints: 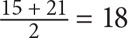 . The average is 18.
. The average is 18.
Property 3: Use the following formula to determine the number of terms in an evenly spaced set:
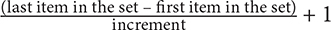
Example: How many integers are there from 6–10, inclusive?
SOLUTION: Note that inclusive means that you will include both endpoints of the set when determining the answer. You might be tempted to simply take the difference of 10 and 6 and arrive at 4 as your answer, but this would omit one of the items. If you list out the numbers, you will see that there are five (6, 7, 8, 9, and 10). Using the preceding formula, you arrive at:
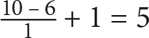
How many multiples of 15 are there from 40–160, inclusive?
SOLUTION: Before using the formula, note that the endpoints of this set are not multiples of 15. To use the formula, you need the endpoints to have the property that the formula specifies (in this case, multiples of 15). Your endpoints will thus be 45 (the smallest multiple of 15 that is greater than 40) and 150 (the greatest multiple of 15 that is less than 160). Now you know that your endpoints are 45 and 150, and the increment between each term in the set is 15. Plug these values into the formula:
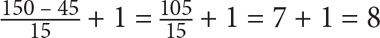
Property 4: To determine the sum of the values in an evenly spaced set, use the average formula: A × N = S.
Properties 2 and 3 specified how to determine the average and number of items in a set, so using these properties, you can determine the sum of a set.
What is the sum of the even integers from 4–180, inclusive?
SOLUTION: Based on Property 4, you should multiply the average and the number of items in the set. From Property 2, you know that the average of an evenly spaced set equals the average of the endpoints: 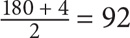 . Using Property 3, you can determine the number of items:
. Using Property 3, you can determine the number of items:
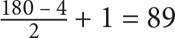
SOLUTION: A × N = S, so 92 × 89 = S = 8,188.
Quantitative Comparison Strategy: Evenly Spaced Sets
Many Quantitative Comparison questions testing evenly spaced sets will give you large sets of values. As is always the case with Quantitative Comparison questions, you should minimize calculations by comparing the quantities and identifying what terms they have in common:
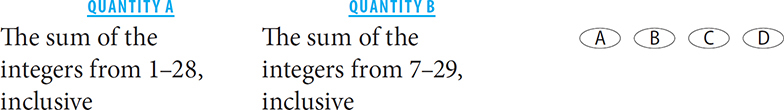
SOLUTION: Instead of calculating, identify similarities between the two columns.
Quantity A can be rewritten as: (1 + 2 + 3 … 6) + (7 + 8 … 28).
Quantity B can be rewritten as: (7 + 8 … 28) + 29.
SOLUTION: The two quantities share the sum of the terms from 7–28, inclusive. You can thus subtract this sum from both quantities. The new comparison is:
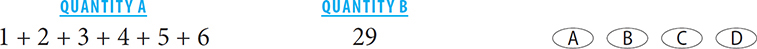
SOLUTION: The value in Quantity A = 21. 21 < 29, so Quantity B is greater.
Exercise: Evenly Spaced Sets
Discrete Quantitative Questions
1. If the sum of four consecutive even integers is 44, what is the value of the second-largest integer in the set?
 10
10
 12
12
 14
14
 16
16
 18
18
2. What is the median value of the integers from 14–80, inclusive?
 43
43
 44
44
 45
45
 46
46
 47
47
For this question, write your answer in the box.
3. How many integers from 1–120, inclusive, are multiples of 3 or 4?

4. How many even multiples of 9 are there from 1–1,000, inclusive?
 55
55
 56
56
 109
109
 110
110
 111
111
5. In a series of six consecutive integers, the sum of the first three integers is 93. What is the sum of the last three integers?
 96
96
 99
99
 102
102
 105
105
 108
108
6. What is the sum of the multiples of 3 from 11–110, inclusive?
 1,980
1,980
 2,057
2,057
 3.228
3.228
 4,573
4,573
 6,050
6,050
For this question, write your answer in the box.
7. How many integers from 5–100 yield a remainder of 1 when divided by 6?

8. In a series of eight consecutive integers, the third term is 7. What is the sum of the eight integers?
 42
42
 56
56
 64
64
 68
68
 72
72
9. What is the difference between the sum of the even integers from 1–100 and the sum of the odd integers from 1–100?
 0
0
 25
25
 26
26
 50
50
 52
52
10. What is the difference between the number of integers from 50–60, inclusive, and the sum of the integers from 50–60, inclusive?
 11
11
 44
44
 55
55
 594
594
 605
605
11. In a series of twenty consecutive integers, the sum of the first two integers is 37. What is the sum of the last three integers in the set?
 107
107
 108
108
 109
109
 110
110
 111
111
Quantitative Comparison Questions
1. 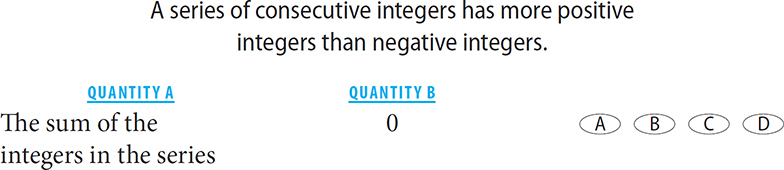
2. 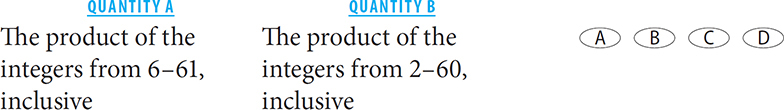
3. 
4. 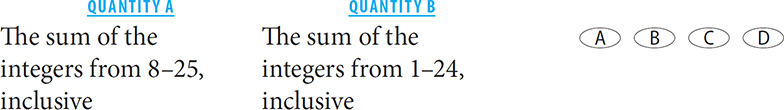
5. 
Exercise Answers
Discrete Quantitative Questions
1. B Let the smallest integer = x. Therefore:
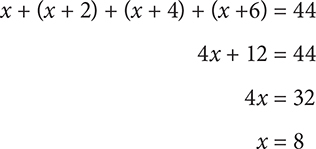
The second-largest integer is x + 4. Substitute 8 for x: 8 + 4 = 12.
2. E Use Property 2: The average (arithmetic mean) of an evenly spaced set = the median of the set = the average of the endpoints. In this question, the fastest way to determine the median is to take the average of the endpoints: 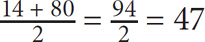 .
.
3. 60 Use Property 3 to determine how many multiples of 3 there are from 1–120, inclusive. The lower bound is 3 and the upper bound is 120. Thus the number of multiples of 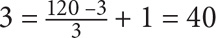 . Now use Property 3 to determine how many multiples of 4 there are from 1–120, inclusive. The lower bound is 4 and the upper bound is 120. Thus the number of multiples of
. Now use Property 3 to determine how many multiples of 4 there are from 1–120, inclusive. The lower bound is 4 and the upper bound is 120. Thus the number of multiples of 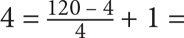 30 → 40 + 30 = 70. But there’s an issue: You have double-counted the multiples of 12. You thus need to determine how many multiples of 12 there are from 1–120, inclusive, and subtract that value from 70. Use Property 3 again: The number of multiples of 12 from 1–120, inclusive, is
30 → 40 + 30 = 70. But there’s an issue: You have double-counted the multiples of 12. You thus need to determine how many multiples of 12 there are from 1–120, inclusive, and subtract that value from 70. Use Property 3 again: The number of multiples of 12 from 1–120, inclusive, is 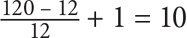 . Thus the answer is 70 – 10 = 60.
. Thus the answer is 70 – 10 = 60.
4. A An even multiple of 9 is any number that has 9 and 2 as factors, in other words, a multiple of 18. You are thus looking for the number of multiples of 18 from 1–1,000, inclusive. The smallest value in the set is 18. The largest value in the set is 990. Substitute these values into the formula from Property 3:
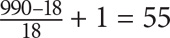
5. C In an evenly spaced set, median = average, so the median of the first three terms will equal 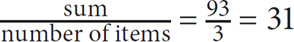 . Since each set has three terms, and all the values are consecutive, the median of the next three terms will be 3 greater than the median of the first three terms: 31 + 3 = 34. Use Property 4 to determine the sum of the last three terms:
. Since each set has three terms, and all the values are consecutive, the median of the next three terms will be 3 greater than the median of the first three terms: 31 + 3 = 34. Use Property 4 to determine the sum of the last three terms:
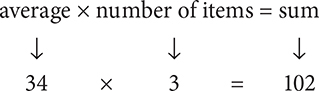
6. A Before using any of the relevant formulas, recognize that since the question concerns multiples of 3, the endpoints are 12 and 108. Based on Property 4: average × number of items = sum. From Property 2, you know that the average of an evenly spaced set equals the average of the endpoints: 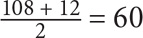 . Using Property 3, you can determine the number of items:
. Using Property 3, you can determine the number of items:
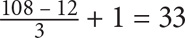
Plug these values into the formula:
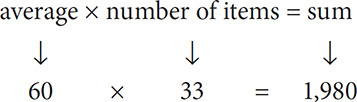
7. 16 Though it might be difficult to see, the numbers in this set are evenly spaced. Think of numbers that yield a remainder of 1 when divided by 6: 7, 13, 19, and so on. The spacing is thus 6. Use Property 3 to determine the number of items in the set:
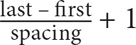
The last term will be the greatest number smaller than 100 that yields a remainder of 1 when divided by 6: 97. The first term will be the smallest number greater than 5 that yields a remainder of 1 when divided by 6: 7. Now plug these values into the formula:
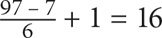
8. D Use Property 4 to determine the sum:
average × number of items = sum
You are told that the set contains eight consecutive integers, so to calculate the sum, you must determine the average. The average of an evenly spaced set = the median. Since the given set has an even number of terms, the median will be the average of the two middle terms (in this case, the 4th and 5th terms). If the third term is 7, then the 4th term is 8 and the 5th term is 9. The average of these two terms is 8.5. Now substitute 8.5 for the average and 8 for the number of items:
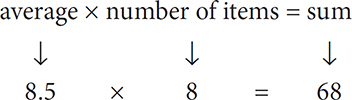
9. D Though you can use the previously discussed formulas, it would be faster to recognize that from 1–100, there are an equal number of odd integers and even integers. Since there are 100 terms in the set, 50 will be odd and 50 will be even. Each even term will be 1 greater than each corresponding odd term. Since there are 50 terms, the sum of the even terms will be 50 more than the sum of the odd terms.
10. D Use Property 3 to determine the number of integers from 50–60, inclusive:
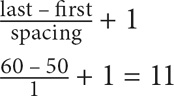
Use Property 4 to determine the sum of the integers in the set:
average × number of items = sum
The average of an evenly spaced set = the average of the endpoints. The endpoints of the set are 50 and 60. Their average is 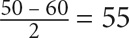 . You know from earlier that the number of items in the set is 11. Plug these values into the formula:
. You know from earlier that the number of items in the set is 11. Plug these values into the formula:
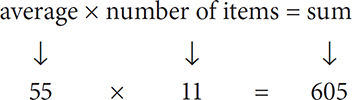
Subtract the sum from the number of items: 605 – 11 = 594.
11. B Let x be the first integer in the set and x + 1 be the next integer. You know:
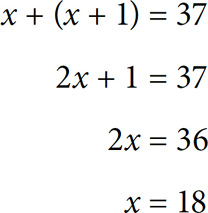
To find the sum of the last three integers, determine the value of the last integer and work from there to get the value of the previous two integers. If the first integer is 18, then the 20th term in the set will be 18 + 19 = 37. The values of the 2nd-to-last and 3rd-to-last terms are 36 and 35, respectively. 35 + 36 + 37 = 108.
Quantitative Comparison Questions
1. A If a series of consecutive integers has more positive than negative numbers, the positive numbers must all offset the negative numbers. Thus the sum of the series will be positive. You can also see this by testing numbers. Try –2, –1, 0, 1, 2, 3. The sum is greater than zero. Try –4, –3, –2, –1, 0, 1, 2, 3, 4, 5. The sum is still greater than zero.
2. B Don’t calculate! Determine how the two columns differ.
Column A can be rewritten as (6 × 7 × 8 … 60) × 61.
Column B can be rewritten as: 2 × 3 × 4 × 5 × (6 × 7 × 8 … 60).
Divide both columns by (6 × 7 × 8 … 60). The new comparison is 61 versus (2 × 3 × 4 × 5). 2 × 3 × 4 × 5 = 120. 120 > 61. Thus the value in Column B is greater.
3. B If given the endpoints of an evenly spaced set, the fastest way to determine the average of the set is to take the average of the endpoints. The average of the integers from 2–20, inclusive is (20 + 2)/2 = 11. Quantity B is greater.
4. B Don’t calculate! Determine how the two quantities differ.
Quantity A can be rewritten as: (8 + 9 + 10 … 24) + 25.
Quantity B can be rewritten as: 1 + 2 + 3 + 4 + 5 + 6 + 7 + (8 + 9 + 10 … 24).
Subtract (8 + 9 + 10 … 24) from both columns. The new comparison is: 25 versus (1 + 2 + 3 + 4 + 5 + 6 + 7). 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28. 28 > 25. Thus Quantity B is greater.
5. A Use the formula from Property 3:
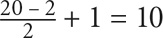
 Factors and multiples
Factors and multiples if Quantity A is greater
if Quantity A is greater if Quantity B is greater
if Quantity B is greater if the two quantities are equal
if the two quantities are equal if the relationship between the two quantities cannot be determined
if the relationship between the two quantities cannot be determined