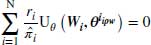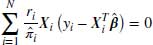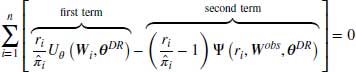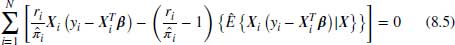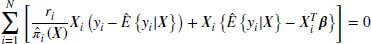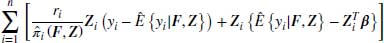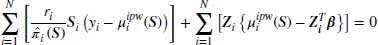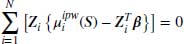8
Doubly robust estimation
- Inverse probability weighting (IPW) weights subjects by the inverse probability of their being observed. In this way, subjects that are fully observed but have a small probability of being fully observed are treated as being representative of those with missing values. Such subjects are given a larger weight to compensate for missing data on subjects who would have similar outcome profiles, but whose data is not available because they dropped out.
- Doubly robust (DR) estimators augment the IPW estimator by making use not only of subjects with fully observed data but also the subjects with partially observed data which are used to predict (or impute) missing outcome values.
-
DR estimators use three models: one, which models the probability of being observed (the missingness model), another which estimates missing values by modeling the relationship between the observed data and the response (the imputation model), and an analysis model which models the overall scientific question of interest.
- With DR estimators, if the imputation model or the missingness model are misspecified (but not both) the resulting estimates will still be unbiased. This provides the statistician with two opportunities to specify a correct model and obtain consistent unbiased estimates.
- Vansteelandt et al. (2010) propose a DR method for dealing with missingness in the response variable, which will be described in this chapter.
8.1 Introduction
Doubly robust (DR) estimators combine three models: an imputation model which models the response variables Y on the covariates X; a missingness model which calculates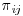 
, the probability of being observed for each subject i at trial visit j; and a final analysis model which is the model that would have been used if there were no missing values in the dataset or, in other words, the model which answers the overall scientific question of interest. With DR methods, either the imputation model or the missingness model, but not both, can be misspecified and the trialist will still obtain unbiased estimates, thus giving the analyst two opportunities to correctly specify a model and get valid, consistent results. DR estimators augment the inverse probability weighted estimator by adding a term based on an imputation model that has an expected value of zero, if the inverse probability weighting (IPW) model is correctly specified. DR estimators can be more efficient than IPW estimators, which is not surprising because they make use of not only the fully observed subjects but also the information contained in partially observed subjects. We will first introduce the concept of IPW estimators before going on to describe DR estimation. We will also discuss the assumptions, advantages and limitations of each of these methods in turn.
The chapter will then focus on a particular implementation of DR estimation proposed by Vansteelandt et al. (2010) before finally providing example code showing how to implement this method in SAS. The code described here can also be implemented using a macro called “Vansteelandt_method.sas” which is available at the Drug Information Association (DIA) Special Working Group on Missing Data web page on the www.missingdata.org.uk site. As explained in Chapter 7, we feel that it is useful to provide sample code to show the reader how to implement this method using standard SAS procedures not only for ease of interpretation but also for use if an independent programmed quality control (QC) check is needed to support the validity of the analysis performed using the macro. Section 8.5 will provide SAS code fragments and results obtained from the analysis of two illustrative clinical trial datasets referred to throughout the book: the illustrative insomnia and mania datasets.
8.2 Inverse probability weighted estimation
Inverse probability weighted estimators are a form of complete case analysis that can give unbiased estimates when the missing at random (MAR) assumption holds. Here,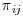 
, the probability of subject i being observed at the jth occurrence, is calculated separately for each visit j and the inverse of this probability is then applied to the outcome model for subject i. As often is the case, we are interested in estimating parameters which will be valid for the entire population of interest, extending inference not only for populations of subjects represented by those subjects fully observed, but also to those with missing data. Weighting subjects with the inverse of the probability of being observed results in constructing a “pseudo-population” in which subjects with certain covariate profiles who were under-represented in the observed data receive higher weights. Conversely, those kinds of subjects that were over-represented in the observed data receive lower weight. With IPW, then, patients who were actually observed, but had low probability of being observed, are treated as being representative of subjects with missing outcomes in the data, who would have similar outcome profiles, had they been observed, and as such receive a higher weight (Robins et al., 1994).
The intuition behind IPW methods is very clearly explained in a simple example by Carpenter and Kenward (2006), which we will reiterate here. In this example, the target for the inference is the mean of the response, and the IPW estimator is defined in Equation 8.1.
Here ri is an indicator variable which is 1 when the ith subject is observed and 0 otherwise; yi is the outcome or response for ith subject and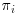 
is the probability of being observed that is computed based on some fully observed covariate X with 3 possible levels (A, B and C). Example data is illustrated in Table 8.1.
Table 8.1 IPW example used in Carpenter and Kenward (2006).
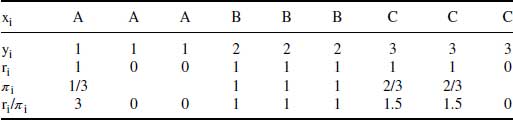
Table 8.1 presents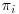 
, the probability of being observed for each level of the covariate xi. As can be seen, the mean of the outcome variable yi is 2 for the full data (including both complete and incomplete cases). This “full data mean” is an unbiased estimate of the true mean in the population. If complete cases only are used, the estimated mean would be 2 1/6, which probably overestimates the true mean. The bias is caused by the fact that subjects with xi = “A” (which has lower expected outcome) are represented in the observed sample by a single subject, whereas the category xi = “C” with higher expected outcome is represented by two subjects (over-represented compared with the group with xi = “A”). However, if for the observed cases, the outcome is weighted by 
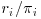(the inverse probability of being observed), we see that the estimated mean is 2 ((3 + 2 + 2 + 2 + 4.5 + 4.5)/9), and the bias is removed.
Of course, the example above is a very simple one. However, we can still see how IPW estimators, by weighting the outcome by the inverse probability, put higher importance on the observations that have a low probability of being observed. In this way, we can estimate the true parameter of interest in the entire population of observed and missing observations.
8.2.1 Inverse probability weighting estimators for estimating equations
The objective of most clinical trials is not to estimate a simple population mean but rather to estimate some (functions of) model parameters, so as to quantify, for example, the effect of treatment versus control. We can show that for such functions the same logic applies with regard to IPW estimators.
In the following explanation we use a similar notation to Daniel and Kenward (2012). For a parametric or non-parametric model, the form of the IPW estimator is as shown in Equation 8.2.
where Wi is the complete data vector Wi = (XTi, YTi)T ; Xi are the fully observed baseline and post-baseline covariates;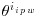 
is the vector of parameters which we wish to estimate; ri is an indicator variable which takes the value 1 when yi is observed and 0 otherwise, 
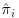is the estimated probability of yi being observed, and 
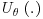is the score function. If we take the Gaussian case then the IPW estimation of the parameters 
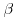are the solution to the following normal estimating equations for 
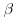over the observed cases:
For Equation 8.3 we can see that the parameter estimates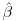 
are consistent as long as the estimates for 
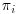are consistent, that is, as long as the missingness model for 
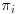is correctly specified (Robins et al., 1994).
With repeated measures, such as a clinical trial with more than one post-baseline visit,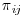 
(the probability for subject i being observed at visit j), is estimated by creating dichotomous variables Rij which indicate patient i being observed at visit j and then performing a separate logistic regression for each visit j using Rij as the response. These probabilities can then be transformed into the vertical format of one observation per subject/visit to give the overall weight 
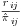in the IPW model.
Of course, as mentioned above, the obvious limitation to this approach is that the model for the probability of being observed has to be correct in order for the resulting estimator to be unbiased. If the wrong model is used for estimating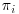 
, then the observations will be weighted incorrectly and so will not be able to properly represent the missing data. As, in practice, there is no way of knowing if the probability model is correct, this assumption may be rather strong, thus limiting the use of the IPW method. Also, if an observation has a very small estimated probability of being observed, the inverse weight on this observation will be extremely large and so could unduly dominate the analysis. This concept is slightly counterintuitive, as it means that the more accurately the IPW model predicts the probability of subjects who are the most representative of the missing observations, the more unstable the IPW solution becomes. However, it is hard to adjust for bias caused by missing subjects when there are only very few corresponding observed representatives in the sample, as it is hard to make inference based on small sample size in general, and it is impossible in the extreme case when there are no observed representatives corresponding to certain kinds of missing data. Note that probabilities estimated close to the boundaries (0 or 1) may simply reflect the non-probabilistic mechanism behind generation of missing values. This may happen if there is a provision in the protocol that investigators should discontinue a subject from the study once a certain criteria has been met as in this case, the logic of IPW does not apply. Because of these issues great care needs to be taken by the trialist when using IPW estimation to ensure that one or a small number of cases are not receiving extremely large weights or zero probability. Kang and Schafer (2007) suggest techniques such as the truncation of large weights to avoid a small subset of subjects dominating the analysis, or revision of the missingness model if either of these situations is encountered. They also advise against the removal of subjects which receive extreme weights, which is a warning we would like to reiterate here. Although removal of outliers may be a valid approach in other modeling methods, in the case of IPW estimation, the subjects who receive the highest weights are likely to be the subjects we are most interested in modeling, as they are the most representative of the missing subjects and so their removal could result in a biased model.
8.2.2 Summary of inverse probability weighting advantages
- IPW is designed to correct for the bias inherent in available cases or complete cases analysis by incorporating a missingness model, and weighting cases according to their probability of being observed.
- When the model for missingness is correctly specified and the missingness mechanism is MAR, this method will give unbiased estimates.
8.2.3 Inverse probability weighting disadvantages
- The model for missingness must be correctly specified. If this model is misspecified then the resulting estimates may be biased. This is because if the model is incorrect then the resulting probabilities of being observed will also be misspecified, which will result in the incorrect weights being given to the observations.
- If the model is approximately correct but some observations have a very low probability of being observed, those observations will receive a very large weight which, while approximately correctly estimated, may inappropriately dominate the analysis.
- As with all missing data approaches, the analysis model (the model that would have been used in the event of no missingness) must also be correctly specified in order to give unbiased estimates.
8.3 Doubly robust estimation
We describe double robustness in the framework used by Robins et al. (1994) for estimating regression coefficients pertaining to the population from incomplete data. We also follow the framework of Vansteelandt et al. (2010).
DR methods require three models to be specified: one that explains the missingness in the data (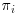
or missingness model), one which describes the population of responses (imputation model) and the model that would have been used if there were no missing values in the data (analysis model). As mentioned in the previous section, in order for the IPW estimator to be consistent, the model for the probability of being observed 
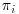has to be correctly specified. The final analysis model must also be correctly specified. Equally, for imputation methods such as multiple imputation, (MI, described in Chapter 6) both the model for imputing the missing values and the final analysis model must be correctly specified in order to obtain consistent estimators. DR methods build on the IPW estimator to include a model for the missing data given the observed (which could be, e.g., a linear regression, generalized estimating equations (GEEs) and so on or even MI) and are more robust to model misspecification than IPW or imputation methods alone.
Because the main section of this chapter describes the implementation of the method proposed in Section 4.2 of Vansteelandt et al. (2010), we will explain DR methods following Vansteelandt et al. (2010), where the assumption is that all baseline and post-baseline covariates are fully observed and so missingness is only permissible in the response variable Y. Their paper also describes an extension of this estimator where the covariates can contain missing values as long as the response is fully observed. Note that there are many possible ways of obtaining a DR estimator. For example, Teshome et al. (2011) suggested novel DR methods that combine MI with GEEs, Daniel and Kenward (2012) proposed a DR version of MI where missingness is confined to the response variable and Tchetgen (2009) implemented a likelihood-based approach to double robustness. We describe the implementation of Vansteelandt et al. as it can be implemented using standard SAS procedures and provides DR estimates which are calculated in a transparent manner and can be easily reproduced if a QC check is required.
8.3.1 Doubly robust methods explained
This section will explain how DR estimators offer greater protection against model misspecification than other methods. A formal description of the DR method can be seen in the formula below:
where Wobs refers to the observed part of the complete data W and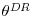 
to the vector of parameter estimates estimated using this approach. Note that 
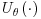is the score function for the full data, not just the observed data. Only the observed cases are used because this function is multiplied by ri, and ri = 1 only when the data is observed.
Equation 8.4 above has two parts which we will hereafter refer to as the first term and the second term. The first term of this DR estimator is the IPW estimator described in Section 8.2, which inversely weights the observed responses in the dataset.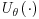 
is the final analysis model or in other words the model that would have been used if the data had been fully observed. In the second term, 
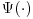represents the model for the missing data given the observed. We refer to 
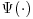as the imputation model; in the literature this is also referred to as the probability of data (POD) model or the propensity model (Daniel and Kenward, 2012; Kang and Schafer, 2007). The model in the second term includes data from both fully observed subjects and those with missing values and thus has the potential to improve the efficiency of the IPW estimator. Because its expectation is zero (provided the model for missingness is correct) the overall estimator remains consistent (Molenberghs and Kenward, 2007, pp. 130–132).
8.3.1.1 Linear regression example
The general DR case described in Equation 8.4 can be re-written as in Equation 8.5 for the case of linear regression. To simplify notation, we omit the visit index j in the equations below for outcomes yij and missingness indicators Rij, with the understanding that each specified model is a linear regression model for a particular visit. In Equation 8.5, X is an N× (S+1) matrix which has N observations and S parameters where the first column of X is a column of 1s to allow for an intercept term. The 0 on the right-hand side of the equation is also a vector of zeros which has N elements. Note that Equation 8.5 can be evaluated using only observed data and each of the N observations contributes non-trivially to Equation 8.5: the missing cases contribute 0 to the first term because ri = 0, but have non-zero contributions to the augmented part. Non-missing cases contribute to both terms.
If we assume that the missingness model is correctly specified, we can see that the expected value of the second term is zero because
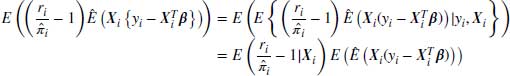
Note that we can separate the first expectation and drop its conditioning on Y because of MAR. Under the weak law of large numbers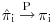 
and the first expectation tends to 
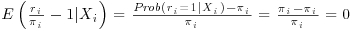(Kang and Schafer, 2007). Because the second term of Equation 8.5 is zero in expectation, we are now just left with the first term which we already noted is the IPW estimator and provides consistent estimates as long as the missingness model is correctly specified. Thus we see from Equation 8.5 that when the missingness model is correctly specified we get unbiased estimates of the parameter estimates 
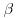regardless of the imputation model used.
Now, if we multiply out the second term of Equation 8.5, we can see that Equation 8.5 can be written as in Equation 8.6.
If we now assume that the imputation model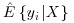 
is correctly specified we can see that the expected value of the residual term in the first term of Equation 8.6, which amounts to the residual of a linear regression, is zero and only the second term remains. Because the imputation model is correctly specified, the predicted values of yi will be consistent and so the solution to the equation described by the second term of Equation 8.6 will provide consistent estimates regardless of the missingness model. Hence, DR estimators provide consistent estimates when either the missingness model or the imputation model or both are correctly specified.
8.3.2 Advantages of doubly robust methods
- DR methods provide consistent estimates, if either the missingness model or the imputation model (model of the observed data given the missingness) is correct. This offers more protection against model misspecification than other missing data approaches such as IPW, mixed models for repeated measures with categorical time effects (MMRM) or imputation alone.
8.3.3 Limitations of doubly robust methods
- As with all missing data methods, the final analysis model, that is, the model that would have been used if there were no missingness, must be correctly specified if the resulting estimates are to be unbiased.
- The missingness mechanism is assumed to be MAR.
- As DR methods incorporate the IPW estimator in their methodology they attract the limitations mentioned in Section 8.2, mainly that subjects with a very low probability of being observed will receive large weights which may dominate the analysis. Because of this, care must also be taken when implementing DR methods.
8.4 Vansteelandt et al. method for doubly robust estimation
Section 4.2 of Vansteelandt et al. (2010) describes a form of DR estimation that can easily be performed using standard statistical techniques such as logistic regression and GLM, and can be implemented in SAS using standard procedures such as PROC LOGISTIC and PROC MIXED. Vansteelandt et al. (2010) describe their DR method for the non-longitudinal case only. Hernández and O'Kelly have implemented an extension of this method for use on longitudinal data, available as the Vansteelandt_method.sas macro from the www.missingdata.org.uk site. We first describe the Vansteelandt et al. method. We then explain the extended method used to provide consistent estimates for longitudinal analysis.
As stated in Section 8.3, the Vansteelandt et al. method is valid when there is missingness in the response variable only. It is assumed that all covariates are fully observed and estimates will only be consistent if this is the case.
Vansteelandt et al. (2010) divide all the available covariates X into two sets. The first, which we will refer to as Z, are the covariates whose coefficients we wish to estimate (e.g., the measure of treatment effect); these variables are to be included in the final analysis model. The second group of covariates, F, explains the relationship between the response variable, Y, and the missingness in the data. We are not directly interested in evaluating the relationship between F and Y. Because F helps explain the missingness in the data, these variables should be included in the missingness and imputation models but not the final analysis model. In the description of the Vansteelandt et al. method below, we see that in computing the IPW estimator in step 1 both the covariates F and Z are used to model the missingness in Y and they are also used in the model which imputes the values of Y (the imputation model). However, only the covariates Z are used in the final model described in step 3 as these are the only covariates of primary interest. Note that some variables in which we are directly interested may also predict the missingness in Y. If this is the case, these variables should be included in the subset Z, so that they will be used in all the three models described below. Only variables whose relationship with Y we are not directly interested in calculating, but which predict the missingness in Y, should be included in F.
The procedure as laid out in Section 4.2 of Vansteelandt et al. (2010) for calculating a DR estimator is as follows:
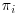denote the fitted probability for each subject i.
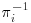as calculated in step 1. Let 
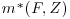denote the fitted values of the response yi for all subjects, that is, those which were fully observed and also those who had missing values for yi.
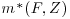as calculated in step 2. Fit another GLM for all subjects (both fully observed and those that had a missing outcome) to the new response 
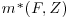using only the covariates Z.8.4.1 Theoretical justification for the Vansteelandt et al. method
Equation 8.7 is a reiteration of Equation 8.6 showing the covariate space spanned by X split into the two subspaces: Z (covariates whose relationship with response we are interested in evaluating) and F (covariates which further help to explain the relationship between the response Y and the missingness) described in the previous section.
Here 
refers to the model for the probability of being observed, and again 
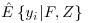refers to the imputation model, both of which may be estimated using all available covariates F and Z.
The Vansteelandt et al. method proposes a special case of Equation 8.7 and suggests the use of the IPW estimator to calculate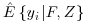 
. This can be seen in Equation 8.8 where S describes the full covariate space enhanced by a column of 1s to allow for an intercept term in the models (1, F, Z). In this case we can see that when 
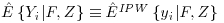, the first term in Equation 8.8 is zero. This is because 
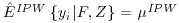, therefore the first sum in Equation 8.8 comprises estimating equations for the IPW model evaluated at its solution 
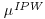, which of course is 0; therefore the first term of Equation 8.8 vanishes.
Because of the above, Equation 8.8 can then be simplified to the unweighted equations described in Equation 8.9 where both the fully observed subjects and subjects with missing outcomes whose values have been predicted through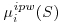 
all contribute to the overall coefficient estimates.
As we can see, Equation 8.9 is exactly the estimating procedure in Vansteelandt et al. whereby the IPW estimator is calculated for the full covariate space S = (1, F, Z). The fitted values from this are then used as the response for an unweighted regression on all the observations for the covariates of interest Z. This last model is the one that must also be correct if the estimate is to be DR.
As noted in Vansteelandt et al. (2010), this method will also work in a more general framework of GEEs where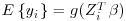 
and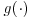 
is an inverse link function.
8.4.2 Implementation of the Vansteelandt et al. method for doubly robust estimation
The macro to implement the Vansteelandt et al. method was written with the aim of facilitating DR estimation in longitudinal clinical trials. Missingness for a visit is estimated given baseline and available post-baseline data. In addition, the overall results from the macro provide the trialist with a report showing the estimated change from baseline by treatment group for each visit, as well as the difference between treatment and control effects for each visit. This report indicates the mean, standard error and the upper and lower 95% confidence limits of each estimate as well as the p-value for the significance of the difference between treatment levels at each visit compared to baseline. In the case of a binary response, the macro will report both the log odds and the odds for treatment effects for each visit as well as the difference in log odds and the odds ratio for each visit.
Thus the SAS macro extends the DR method outlined in Vansteelandt et al. (2010) to allow for longitudinal analysis; it also provides bootstrap estimates of the standard errors of estimated treatment effects.
8.4.2.1 Bootstrap estimates of the variance
It is clear that the standard SAS output for the variance of the estimators using the Vansteelandt et al. method will underestimate the true variance, as the response values for the final analysis GLM (step 3, Section 8.4) are the predicted values from a previous, often very similar, weighted GLM (step 2, Section 8.4). Because of this, the estimate of the standard error from the standard output could not be used. The standard errors of the estimated treatment effect are obtained using non-parametric bootstrap procedure: the procedure is run on multiple datasets, each dataset consisting of a sample with replacement from the original set of subjects. The mean of the parameter estimates denoted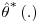 
is then calculated as: 
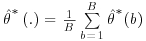where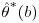 
refers to the parameter estimate for the bootstrap sample b. Note that this estimate is produced by applying the entire four-step DR procedure as described earlier in this section, including re-estimation of IP weights, to each bootstrap sample. The standard error of the parameter estimate is calculated as 
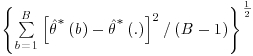where B denotes the total number of bootstrap samples. In addition to capturing all the sources of variability in the estimated parameters, the bootstrap estimate of the standard error has the advantage that no assumptions about the distribution of the data are made. The procedure is non-parametric and it mimics the true sampling distribution of the test statistic with the distribution of the estimates from multiple bootstrap (re)samples. The confidence interval for 
is then calculated using a normal approximation based on the bootstrap estimate of the standard error. The random seed used to generate the bootstrapped datasets and also the number of bootstrap samples required can be specified by the trialist in the macro call to ensure fully reproducible results.
Bootstrap theory states that the estimates of the standard error are asymptotically unbiased, meaning that estimates are valid under the assumption of infinite bootstrap samples. If too few samples are taken, the estimate of the standard error is not guaranteed to be unbiased. Efron and Tibshirani (1993, pp. 50–53) suggest that for the majority of examples between 50 and 200 bootstrap samples will provide satisfactory results. They also suggest that the number of bootstrap samples needed to obtain acceptable results can be effectively estimated by calculating the coefficient of variation (the ratio of the standard deviation to the expected value of the standard deviation). In this way the statistician can calculate the difference between the true standard error to its estimated value and can decide whether a larger number of bootstrap samples B are needed (the smaller the coefficient of variation the better). Because of this we recommend that care be taken when deciding the number of bootstrap samples used to calculate the standard error of estimates 
and in particular we caution against using too few samples.
8.4.2.2 Missingness model for longitudinal data
Recall that for each subject i at visit j,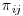 
is the probability of being observed. In order to calculate 
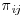, a separate logistic regression is run for each visit, j, where the response Rij is an indicator variable with value 1 if the outcome is observed for subject i at visit j, and 0 otherwise. The default missingness model implemented by the macro for visit j includes baseline covariates plus, if available, post-baseline and response variables for visits 0 to j−1. Monotone missingness, where data is missing for a subject after a given time point, is assumed. In other words, it is assumed that once data is missing for a subject at a particular visit, data for all subsequent visits are also missing. For each visit, the probability of being observed is conditional on being observed at previous visits and so any subject that is missing at visit j will not be included in the probability calculation in subsequent visits. To calculate the full unconditional probability of being observed at visit j, the product of the probabilities for the current and previous visits for each subject i are calculated: 
. It is the inverse of this product that is used as the weights for the first GLM (described in step 2 of Section 8.4).
It is possible for the response variable for some bootstrap samples at a particular post-baseline visit to be either fully observed or contain only missing values. If this is the case then the response variable for that visit will only have one level (it will contain either 1 for every subject or 0 for every subject) and so PROC LOGISTIC will fail, as it will only have one group, not two, to model. The macro will automatically check if a visit is fully observed for the original or any bootstrap dataset. If it is, then the 
for visit j will be updated with the probability for the previous visit. As there was no change in subject dropout between the visits, there is thus no change in the estimate of the cumulative probability of being observed. If the response variable for a given bootstrap dataset contains only missing values, that bootstrap dataset will be deleted, as the weighted GLM (described in step 2 of Section 8.4) will not run for a dataset with no response values.
Another common issue addressed by the macro is non-convergence of PROC LOGISTIC due to quasi or complete separation of data points, which can result in unreliable predicted values for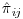 
. If this issue is encountered at a particular visit – and with the bootstrap sampling we find in practice that it does occur – the macro will continue to the next calculable visit and calculate the probability of being observed at the current visit conditional on all the previous fully observed/non-converging visits. The probability of being observed is then pooled across the current visit j and previous q−1 fully observed/non-converging visits as 
. The unconditional probability of being observed at each visit is then calculated by calculating the product of the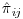 
over the j visits as before. More details on the calculation of these models can be found in the “Users Guidebook for Vansteelandt” also available on the www.missingdata.org.uk website.
8.4.2.3 Final analysis model
As discussed in Section 8.4 the final analysis model should only include covariates which are needed to gain the desired estimate, usually an estimate of treatment effect. The Vansteelandt et al. method macro calculates least-squares means for each treatment group effect at each visit, and the differences between these least-squared means. The statistician can specify other explanatory covariables for this analysis model, for example, baseline and demographic or medical history variables. We would, in general, advise against the addition of any post-baseline variables in this model as they may dilute the estimated treatment effect and render it difficult to interpret. For example, if a post-baseline variable were related to the response and also to treatment then its inclusion would lead to underestimating the effect of treatment (Vansteelandt et al., 2010). Also, including too many coefficients in the final analysis model can lead to model over-specification which may inflate the variance of the estimates (Freund et al., 2006, pp. 238–240).
8.4.2.4 Characteristics of Vansteelandt et al. method macro for calculating doubly robust estimates of treatment effects
Here we will summarize the main characteristics of the Vansteelandt et al. method macro.
Non-monotone missing data
How regression parameters are estimated
Restrictions on regression parameters
Missing covariates
Binary covariates
Binary responses
Auxiliary variables
8.5 Implementing the Vansteelandt et al. method via SAS
This section will provide code fragments showing how to calculate the Vansteelandt et al. method for two illustrative clinical trial datasets referred to throughout the book: mania (a binary outcome) and insomnia (a continuous outcome).
8.5.1 Mania dataset
As mentioned previously, the mania dataset is an illustrative dataset that is patterned after typical clinical data studying mania in an adult population with bipolar disorder (see Section 1.10.3). The response variable in this trial data is a binary variable derived from the Young Mania Rating Scale (YMRS). For the YMRS scale, lower scores are better. We suppose that the purpose of the trial in the case of this dataset is to compare the treatment effect of a mania treatment of a type similar to valproate to a control drug such as lithium.
As in Chapter 7, the code excerpts in this section will refer to the example data in both vertical (one observation per subject and visit) and horizontal formats (one observation per subject). See Section 1.10.3 for a description of variables included in the dataset.
8.5.1.1 Implementing the Vansteelandt et al. method for the illustrative mania dataset
The following section will show the equivalent analysis for a continuous response. A full implementation of the Vansteelandt et al. method for the mania trial data can be seen in Appendix 8.A. Appendix 8.A also gives code implementing the equivalent analysis using the macro described in Section 8.4 above. We assume that the data are monotone missing and the dataset in its horizontal format is called maniah.
As we estimate the variance of the DR estimates using the bootstrap, all calculations are done on a set of bootstrap samples of the original data. Bootstrap samples are drawn in SAS Code Fragment 8.1. One hundred bootstrap samples equal to the number of subjects in the original data (1100 subjects) are taken. As stated in Section 8.4 we would recommend that at least 100 samples be taken to ensure that the estimates of the standard error are consistent and unbiased.
SAS Code Fragment 8.1 Take a bootstrap sample.
ODS LISTING CLOSE; PROC SURVEYSELECT DATA=maniah METHOD = urs SAMPSIZE=1100 REP=100 SEED=883960001 OUT=ymrs_boot_samples OUTHITS; RUN; ODS LISTING; |
We then create the missingness indicators Rij which are 1 if the response (resp_1,…,resp_5) is observed for subject i at visit j and 0 if the response is missing (see SAS Code Fragment 8.2).
SAS Code Fragment 8.2 Simple macro to create missingness indicators.
*Create missingness indicators for each visit Rij which take the value 1 if the response is observed and 0 if not; %MACRO create_missing_indicators(); DATA ymrs_boot_samples; SET ymrs_boot_samples; %DO i=1 %TO 5; IF resp_&i EQ . THEN r_&i = 0;ELSE r_&i = 1; %END; OUTPUT; RUN; %MEND create_missing_indicators; %create_missing_indicators(); |
A logistic regression is then run for each visit separately. For each visit, only subjects who were observed at previous visits are included in the model. Hence the model for each visit calculates the conditional probability of being observed at the current visit given the subject was observed at previous visits.
When the logistic regression shown in SAS Code Fragment 8.3 was run on the original data (maniah dataset) for the first visit the following warning message was received.
WARNING: There is possibly a quasi-complete separation of data points. The maximum likelihood estimate may not exist.
SAS Code Fragment 8.3 Code to calculate the probability of being observed at the first visit.
*Run logistic regression for being observed at visits 1; ODS LISTING CLOSE; PROC LOGISTIC DATA=maniah DESCENDING; CLASS trt resp_0 country; MODEL r_1=base_ymrs resp_0 trt country; BY replicate; OUTPUT OUT=p_1 P=prob_1; ODS OUTPUT CONVERGENCESTATUS =convstat; RUN; QUIT; ODS LISTING; |
This warning can occur because a linear combination of covariates exists that can perfectly predict the response and so PROC LOGISTIC will not give reliable estimates, as the maximum likelihood cannot be calculated if there is no overlap in the distribution of the two groups. Thus, the predicted probabilities from an analysis with this warning message cannot be used. In the case of non-convergence, such as this, we continue to the next visit which did converge for the original dataset (maniah), which in our example is Visit 2. The code to implement the logistic regression on the bootstrapped datasets for Visit 2 can be seen in SAS Code Fragment 8.4.
SAS Code Fragment 8.4 Code to calculate the probability of being observed at the first or the second visit.
*Run logistic regression for being observed at visits 1 or 2; ODS LISTING CLOSE; PROC LOGISTIC DATA=ymrs_boot_samples DESCENDING; CLASS trt resp_0 country; MODEL r_2=base_ymrs resp_0 trt country; BY replicate; OUTPUT OUT=p_2 P=prob_2; ODS OUTPUT CONVERGENCESTATUS =convstat; RUN; QUIT; ODS LISTING; |
The analysis performed in SAS Code Fragment 8.4 calculates the probability of a subject being observed at either Visit 1 or Visit 2. Since some subjects will have missing values for Visit 1, no covariates relating to Visit 1 were included in the model. To approximate the probability of being observed at Visit 1, we apportion the predicted probability of being observed at Visits 1 or 2 by estimating each visit's probability as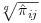 
, where q is the number of visits we are pooling across (two in this case). The unconditional probability of being observed at Visit 2 is then 
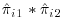. The probabilities for Visits 3, 4 and 5 are calculated similarly to those for Visits 1 and 2. SAS Code Fragment 8.5 describes how to calculate the overall probability of being observed at Visits 1, 2 and 3.
SAS Code Fragment 8.5 Code to calculate the unconditional probability of being observed at each visit.
*Calculate the product of the probabilities of being observed from visits 1 to j-1; *PROC LOGISTIC for visit 1 didn't converge so pooled probability is sqrt(prob_2); DATA p_2; SET p_2; prob_2=SQRT(prob_2); RUN; *The unconditional probability of being observed at visit 2 is prob(observed at visit 1) * prob(observed at visit 2),since the data are monotone missing; DATA overall_probability; SET p_2; prob_1=prob_2; prob_2 = prob_1*prob_2; RUN; *Likewise for visit 3 the overall probability of being observed at visit 3 is the probability of being observed at visit 1*visit 2*visit3 as the data are monotone missing; DATA overall_probability; MERGE overall_probability p_3; BY replicate subjid trt; *prob 2 is now prob_1*prob2; prob_3 = prob_2*prob_3; RUN; |
Once the probability of being observed at each visit has been calculated, the inverse of this probability needs to be obtained (SAS Code Fragment 8.6). The inverse probability weight each subject will receive at each visit has now been calculated, and it is these weights which will be used in the GLM referred to in step 2 of the description of the Vansteelandt et al. method in Section 8.4.
SAS Code Fragment 8.6 Calculate the inverse probability of being observed.
*Get the inverse probability of being observed at each visit; %MACRO get_inverse_prob(); DATA overall_probability; SET overall_probability; %DO i = 1 %TO 5; inverse_prob_&i = 1/prob_&i; %END; RUN; %MEND get_inverse_prob; %get_inverse_prob(); |
Before the GLM can be performed the data must first be converted to vertical format, one record per visit per subject. SAS Code Fragment 8.7 shows how to do this for our example. Once the data are in vertical format, a weighted logistic regression is performed using PROC GLIMMIX (although the model does not include a random effect). This step models the binary response, resp, on all available covariates: base_ymrs, country and trt. Note that the IPW is included in this model by use of the “WEIGHT inverse_prob”; statement.
SAS Code Fragment 8.7 Convert the dataset to vertical format and run the weighted imputation model.
*Convert the data back to vertical format; DATA ymrs_boot_vert; SET ymrs_boot_samples; %MACRO makevert(); %DO i=1 %TO 5; resp=resp_&i; r=r_&i; inverse_prob=inverse_prob_&i; visit=&i; OUTPUT; DROP resp_&i r_&i inverse_prob_&i; %END; %MEND makevert; %makevert(); RUN; *Sort the data appropriately; PROC SORT DATA=ymrs_boot_vert; BY replicate DESCENDING trt DESCENDING visit; RUN; *Run a weighted GLM (to get the IPW predictions). This model can make use of both baseline and post-baseline variables; ODS LISTING CLOSE; PROC GLIMMIX DATA=ymrs_boot_vert; CLASS trt visit country; MODEL resp=base_ymrs country trt trt*visit/DIST=binomial LINK=logit; BY replicate; WEIGHT inverse_prob; OUTPUT OUT=first_glm_out PRED(ILINK)=pred; RUN; ODS LISTING; |
The predicted probability obtained from the logistic regression shown in SAS Code Fragment 8.7 is then used as the new response for a second logistic regression (the final analysis model) as described in Section 8.4. Because the mania dataset has a binary response, the final analysis model uses the equivalent binominal notation where the response is written in the form of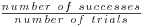 
, where the number of successes is the probability of being a responder on the mania scale (the response from the model in SAS Code Fragment 8.7) and the number of trials for each subject/visit is one. SAS Code Fragment 8.8 runs the final analysis model. Note that the covariates in this model are only those for which we are directly interested in calculating coefficients, in this case trt and visit. The LSMEANS statement with the DIFFS qualifier provides estimates of the expected log odds of response for each treatment group, and of the difference between two groups at each visit for each bootstrap dataset. The “/ODDS ODDSRATIO” in the LSMEANS statement provides these results on the odds scale as well as the log odds scale.
SAS Code Fragment 8.8 Set the predicted outcome from the imputation model as the new response and run the final analysis model.
*set new response to be the predicted response from the previous GLM;
DATA ymrs_boot_vert;
MERGE ymrs_boot_vert first_glm_out(KEEP=pred replicate subjid
visit);
BY replicate visit subjid;
resp=pred;
DROP pred;
RUN;
PROC SORT DATA= ymrs_boot_vert;
BY replicate DESCENDING trt DESCENDING visit;
RUN;
*Run the second logistic regression using the predicted probability of being observed obtained from the first logistic regression. To do this, need to use the binomial notation where the probability is the number of successes and 1 is the number of trials;
DATA ymrs_boot_vert;
SET ymrs_boot_vert;
denom=1;
RUN;
*Run final analysis model using only the covariates for which coefficient are required(in this case treatment effects are each visit);
ODS LISTING CLOSE;
PROC GLIMMIX DATA= ymrs_boot_vert;
CLASS trt visit;
MODEL resp/denom=trt visit trt*visit/DIST=binomial LINK=logit;
BY replicate;
LSMEANS trt*visit /odds ODDSRATIO cl DIFF=control("1" "5");
OUTPUT OUT=YMRS_Final_Analysis_out PRED(ILINK)=pred;
ODS OUTPUT DIFFS=diffs LSMEANS=lsms;
RUN;
QUIT;
ODS LISTING;
|
The DR estimate of the mean and standard error of the effect of valproate over lithium for the mania dataset is calculated as the mean and standard deviation of the estimates over all the bootstrap datasets. SAS Code Fragment 8.9 shows how to obtain the overall DR estimates of the mean and standard error of the effects of valproate and lithium at the final visit, which are easily calculated using PROC MEANS (see Appendix 8.B for SAS code which shows that this is equivalent to calculating the formula described in Section 8.4).
SAS Code Fragment 8.9 Use LSMEANS to get the treatment effect at the final visit for each bootstrap sample and PROC MEANS to get the overall estimate of treatment effect.
*Get overall estimates of mean and standard error of treatment effect at final visit; *Dataset "lsms" contains the estimates of the treatment effect for each visit over the 100 bootstrap samples Here, we are interested in the final visit; DATA lsms; SET lsms; IF visit NE 5 THEN DELETE; RUN; PROC SORT DATA=lsms; BY trt; RUN; *Get the mean and standard error of estimates over the bootstrap samples to get the overall bootstrapped estimate; PROC MEANS DATA=lsms; VAR estimate; BY trt; *stddev gives the bootstrap standard error of the overall estimate(arithmetically identical to that specified in section 8.4); OUTPUT OUT=lsm_estimates MEAN=lsm STDDEV=se; RUN; |
The DR estimates for the effect of experimental and control treatment groups, as well as the difference between these at the final visit, can be seen in Table 8.2. The code to perform the equivalent analysis using the Vansteelandt et al. method macro can also be seen in Appendix 8.A. From Table 8.2 we can see that the results of this analysis are in line with the MI analysis on this dataset shown in Table 6.5 which reports a treatment difference in the LSMEANS estimate of 0.1 and also shows no evidence of a significant difference between treatments at the final visit (p-value = 0.0849).
Table 8.2 Results for Vansteelandt et al. method for mania dataset: least-squares means (LSMEANS) estimate of treatment (TRT) effects and the difference between treatments in the logit of the probability of response at Visit 5.
The results of the DR approach are reasonably consistent with those of MI in Table 6.5 (p = 0.0849), given that a different model was used for Table 6.5.
8.5.2 Insomnia dataset
This section will show the equivalent DR analysis for data with a continuous response and will use the insomnia trial data described as an illustrative example in Section 1.10.2. The primary efficacy variable for the insomnia data is the total sleep time (TST). The insomnia trial contains data for six visits in total, one baseline and five post-baseline visits. Two secondary efficacy variables: sleep quality score (SQS) and morning sleepiness score (MSS) were also measured as part of this trial. However, because the values for SQS and MSS contain missing values they cannot be used in the Vansteelandt et al. analysis, as it is an assumption of this method that all covariates are fully observed. Because of this, analysis for this data will model the primary efficacy TST based on the baseline MSS score and the treatment by visit effect only. Section 1.10.2 includes a description of all variables in the dataset.
Again, the following is given as an illustrative example only. It should be noted that if a dataset has a high number of explanatory variables with missing values, this implementation of the Vansteelandt et al. method will be at a disadvantage compared to, for example, MI. This is because MI can, for example, make use of post-baseline data from incompletely observed subjects to give potentially less biased or more precise estimates of the response.
Since this implementation uses the bootstrap to estimate variance, the procedure is repeated for a number of bootstrap samples. As a first step, therefore, a number of bootstrap samples of the dataset should be taken with replacement, each sample having the same number of subjects per treatment group as the original dataset. The probability of being observed at each visit,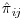 
, should then be calculated using PROC LOGISTIC and the overall probabilities for each subject i of being observed at visit j should be calculated as 
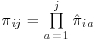. The inverse of the unconditional probabilities, 
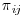, are the weights that should be used in the first GLM. The SAS code to perform this analysis for the insomnia data is provided in Appendix 8.C. It is similar to that for the mania example in Section 8.5 and so will not be repeated here.
Because the response for the insomnia data is continuous we can control for random differences between the two treatment groups at baseline by including the baseline TST score in our models. As often in clinical trials, we will use as the efficacy parameter the change from baseline in the response variable. SAS Code Fragment 8.10 shows how the change in TST from baseline (called tstc below) and the imputation model is calculated for the insomnia data.
SAS Code Fragment 8.10 Imputation model for each bootstrap sample.
*The response of interest is the change from baseline; DATA tst_boot_vert; SET tst_boot_vert; tstc= tst - tst_0; RUN; *Step 2: Run a weighted GLM (to get the IPW predictions) this model should be based on all variables if dataset has (fully observed) baseline and post-baseline variables; ODS LISTING CLOSE; PROC MIXED DATA= tst_boot_vert ORDER=data; CLASS trt visit; MODEL tstc=base_mss trt visit trt*visit/SOLUTION OUTP=first_glm_out; BY replicate; WEIGHT prob; RUN; QUIT; ODS LISTING; |
Both the imputation and final analysis models can be calculated using, for example, PROC MIXED (although the model is a linear regression and not a mixed model). As in the mania example, the predicted change in tst from baseline should be used as the new response variable for the final analysis model (see SAS Code Fragment 8.11).
SAS Code Fragment 8.11 Final analysis model to calculate the treatment change from baseline.
*set new response to be the predicted response from the previous GLM;
DATA tst_boot_vert;
MERGE tst_boot_vert first_glm_out(KEEP=pred replicate subjid
visit);
BY replicate visit subjid;
tstc=pred;
DROP pred;
RUN;
PROC SORT DATA=tst_boot_vert;
BY replicate DESCENDING trt DESCENDING visit;
RUN;
*Run final analysis model using only the relevant covariates;
ODS LISTING CLOSE;
PROC MIXED DATA=tst_boot_vert order=data;
CLASS trt visit;
MODEL tstc= base_mss trt visit trt*visit /SOLUTION
OUTP=final_analysis_out;
BY replicate;
LSMEANS trt*visit /CL DIFF=CONTROL("1" "5");
ODS OUTPUT DIFFS=diffs LSMEANS=lsms;
RUN;
QUIT;
ODS LISTING;
|
The DR estimates of the mean and standard error of the treatment effects and difference in the change of these effects from baseline can be calculated at the final visit using PROC MEANS as shown in Section 8.5. The results of this analysis for the insomnia data at the final visit can be seen in Table 8.3.
Table 8.3 Results for Vansteelandt et al. method for insomnia dataset: least-squares means (LSMEANS) estimate of treatment effects (change from baseline in TST) and the difference between treatments at Visit 5.
Comparing these results with those of the MI Method 3 performed in Chapter 6 (see Table 6.2), we can see that overall both mean estimates are quite close with the DR method estimating a mean difference of 21.3 and MI a difference of 19.3. Both analyses also conclude that there is evidence to suggest a significant difference in treatment levels at the final visit (p-value = 0.0039 and 0.0025 for DR and MI, respectively).
Appendix 8.A How to implement Vansteelandt et al. method for mania dataset (binary response)
Mania dataset: Vansteelandt et al. method “by hand”
*The following code will run the Vansteelandt et al. method for the Mania Dataset with binary response;
*Create 100 bootstrap samples with replacement. Each bootstrap sample is the same size as the original data;
ODS LISTING CLOSE;
PROC SURVEYSELECT DATA=maniah METHOD = urs SAMPSIZE= 1100
REP=100 SEED=883960001 OUT=ymrs_boot_samples OUTHITS;
RUN;
ODS LISTING;
DATA ymrs_boot_samples;
SET ymrs_boot_samples;
DROP numberhits;
RUN;
*Create missingness indicators for each visit rij which take the value 1 if the response is observed and 0 if not;
%MACRO create_missing_indicators();
DATA ymrs_boot_samples;
SET ymrs_boot_samples;
%DO i=1 %TO 5;
IF resp_&i NE . THEN r_&i = 1;ELSE r_&i = 0;
%END;
OUTPUT;
RUN;
%mend create_missing_indicators;
%create_missing_indicators();
*Run logistic regression for each visit;
ODS LISTING CLOSE;
PROC LOGISTIC DATA=ymrs_boot_samples DESCENDING;
CLASS trt resp_0 country;
MODEL r_2=base_ymrs resp_0 trt country;
BY replicate;
OUTPUT OUT=p_2 P=prob_2;
ODS OUTPUT CONVERGENCESTATUS =convstat;
RUN;
QUIT;
ODS LISTING;
*if subject was missing at previous visit then delete that observation, probability at Visit 2 is conditional on being observed
at Visit 1;
DATA ymrs_boot_temp;
SET ymrs_boot_samples;
IF r_2 EQ 0 THEN DELETE;
RUN;
*Estimate the probability of being observed at Visit 3;
ODS LISTING CLOSE;
PROC LOGISTIC DATA= ymrs_boot_temp DESCENDING;
CLASS trt resp_0 resp_1 country;
MODEL r_3= base_ymrs resp_0 resp_2 trt country;
BY replicate;
OUTPUT OUT=p_3 P=prob_3;
ODS OUTPUT CONVERGENCESTATUS =convstat;
RUN;
QUIT;
ODS LISTING;
DATA ymrs_boot_temp;
SET ymrs_boot_temp;
IF r_3 EQ 0 THEN DELETE;
RUN;
*Estimate the probability of being observed at Visit 4;
ODS LISTING CLOSE;
PROC LOGISTIC DATA= ymrs_boot_temp DESCENDING;
CLASS resp_0 resp_2 resp_3 trt country;
MODEL r_4= base_ymrs resp_0 resp_2 resp_3 trt country;
BY replicate;
OUTPUT OUT=p_4 P=prob_4;
ODS OUTPUT CONVERGENCESTATUS =convstat;
RUN;
QUIT;
ODS LISTING;
*The default model for the final visit doesn't converge so instead we use baseline values and trt only;
ODS LISTING CLOSE;
PROC LOGISTIC DATA= ymrs_boot_temp DESCENDING;
CLASS resp_0;
MODEL r_5= base_ymrs resp_0;
BY replicate;
OUTPUT OUT=p_5 P=prob_5;
ODS OUTPUT CONVERGENCESTATUS =convstat;
RUN;
QUIT;
ODS LISTING;
*Before merging probabilities for each visit first need to sort them;
%MACRO sortdata();
%DO i = 2 %TO 5;
PROC SORT DATA = p_&i;
BY replicate subjid trt;
RUN;
DATA p_&i;
SET p_&i;
KEEP replicate subjid trt prob_&i;
RUN;
%END;
%MEND sortdata;
%sortdata();
*Calculate the product of the probabilities of being observed from Visits 1 to j-1;
*PROC LOGISTIC for Visit 1 didn't converge so pooled probability is sqrt(prob_2). Perform this calculation;
DATA p_2;
SET p_2;
prob_2=SQRT(prob_2);
RUN;
*Start with the probability of being observed at the first visit. The overall probability of being observed at Visit 2 is the probability of being observed at Visit 1*Visit 2 as the data are monotone missing;
DATA overall_probability;
SET p_2;
prob_1=prob_2;
prob_2 = prob_1*prob_2;
RUN;
*Likewise for Visit 3 the overall probability of being observed at Visit 3 is the probability of being observed at Visit 1*Visit 2*Visit3 as the data are monotone missing;
DATA overall_probability;
MERGE overall_probability p_3;
BY replicate subjid trt;
*prob 2 is now prob_1*prob2;
prob_3 = prob_2*prob_3;
RUN;
*The same applies for visit 4;
DATA overall_probability;
MERGE overall_probability p_4;
BY replicate subjid trt;
*prob 3 is now prob_1*prob2*prob_3;
prob_4 = prob_3*prob_4;
RUN;
*And also for visit 5;
DATA overall_probability;
MERGE overall_probability p_5;
BY replicate subjid trt;
*prob 4 is now prob_1*prob2*prob_3*prob_4;
prob_5 = prob_4*prob_5;
RUN;
*Calculate the inverse probability of being observed at each visit;
%MACRO get_inverse_prob();
DATA overall_probability;
SET overall_probability;
%DO i = 1 %TO 5;
prob_&i = 1/prob_&i;
%END;
RUN;
%MEND get_inverse_prob;
%get_inverse_prob();
*Append inverse probabilities to the original dataset;
PROC SORT DATA=YMRS_BOOT_SAMPLES;
BY replicate subjid trt;
RUN;
PROC SORT DATA=overall_probability;
BY replicate subjid trt;
RUN;
DATA ymrs_boot_samples;
MERGE ymrs_boot_samples overall_probability;
BY replicate subjid trt;
RUN;
*Convert the data back to vertical format;
DATA ymrs_boot_vert;
SET ymrs_boot_samples;
%MACRO makevert();
%DO i=1 %TO 5;
resp=resp_&i;
r=r_&i;
prob=prob_&i;
visit=&i;
OUTPUT;
DROP resp_&i R_&i prob_&i;
%END;
%MEND makevert;
%makevert();
RUN;
*Make sure data are sorted appropriately;
PROC SORT DATA=ymrs_boot_vert;
BY replicate descending trt descending visit;
RUN;
*Run a weighted GLM (to get the IPW predictions) this model should be based on all variables if dataset has (fully observed) baseline and post-baseline variables;
ODS LISTING CLOSE;
PROC GLIMMIX DATA=ymrs_boot_vert;
CLASS trt visit country;
MODEL resp=base_ymrs country trt trt*visit/DIST=binomial LINK=logit;
BY replicate;
WEIGHT prob;
OUTPUT OUT=first_glm_out PRED(ILINK)=pred ;
RUN;
ODS LISTING;
*Now take the predicted response from dataset "first_glm_out" and use it as the new response;
PROC SORT DATA=first_glm_out;
BY replicate visit subjid;
RUN;
PROC SORT DATA= ymrs_boot_vert;
BY replicate visit subjid;
RUN;
*set new response to be the predicted response from the previous GLM;
DATA ymrs_boot_vert;
MERGE ymrs_boot_vert first_glm_out(keep=pred replicate subjid visit);
BY replicate visit subjid;
resp=pred;
DROP pred;
RUN;
PROC SORT DATA=ymrs_boot_vert;
BY replicate DESCENDING trt DESCENDING visit;
RUN;
*Run the second logistic regression using the predicted probability of being observed obtained from the first logistic regression. To do this, need to use the binomial notation where the probability is the number of successes and 1 is the number of trials;
DATA ymrs_boot_vert;
SET ymrs_boot_vert;
denom=1;
RUN;
*Run final analysis model using only the covariates for which coefficient are required (in this case treatment effects are each visit);
ODS LISTING CLOSE;
PROC GLIMMIX DATA=ymrs_boot_vert;
CLASS trt visit;
MODEL resp/denom=trt visit trt*visit/DIST=binomial LINK=logit;
BY replicate;
LSMEANS trt*visit /odds ODDSRATIO CL DIFF=control("1" "5");
OUTPUT OUT=YMRS_Final_Analysis_out PRED(ILINK)=pred;
ODS OUTPUT DIFFS=diffs LSMEANS=lsms;
RUN;
QUIT;
ODS LISTING;
*Calculate overall estimates of mean and standard error of treatment effect at final visit;
*Dataset "lsms" contains the estimates of the treatment effect for each visit over the 100 bootstrap samples. We are interested in the final visit;
DATA lsms;
SET lsms;
IF visit NE 5 THEN DELETE;
RUN;
PROC SORT DATA=lsms;
BY trt;
RUN;
*Get the mean and standard error of estimates over the bootstrap samples to get the overall bootstrapped estimate;
PROC MEANS DATA=lsms;
VAR estimate;
BY trt;
*stddev gives the bootstrap standard error of the overall estimate
(this is the same as working out the formula given in section 8.4)
See appendix 8.B for proof.;
OUTPUT OUT=lsm_estimates MEAN=lsm STDDEV=se;
RUN;
*Show estimates of the difference in the treatment groups;
DATA diffs;
SET diffs;
IF visit NE 5 THEN DELETE;
RUN;
PROC MEANS DATA=diffs;
VAR estimate;
OUTPUT OUT=trt_diff_estimates MEAN=trt_diff STDDEV=diff_SE;
RUN;
*calculate the p-value of treatment difference at last visit;
DATA trt_diff_estimates;
SET trt_diff_estimates;
t_Value= trt_diff/diff_SE;
p_value=(1-probt(abs(t_value),5490))*2;
RUN;
*odds ratio of estimates;
DATA lsm_estimates;
SET lsm_estimates;
or=exp(lsm);
RUN;
DATA trt_diff_estimates;
SET trt_diff_estimates;
or =exp(trt_diff);
RUN;
Identical implementation via a SAS macro by the authors, available from DIA pages at missingdata.org.uk
%INCLUDE "vansteelandt_method.sas"; %INCLUDE "VansteelandtSubMacros.sas"; %vansteelandt_method(datain=maniav, trtname=trt, subjname=subjid, visname=visit, basecont=%str(base_YMRS), baseclass=%str(country), postclass=%str(),seed=883960001,nboot=100,visit_basecont_5=%str (base_YMRS,visit_baseclass_5=%str(RESP_0),primaryname=resp, analcovarcont=%str(), analcovarclass=%str(),trtref=1, dataout=test_vans_predicted, resout=test_vans_results );
Appendix 8.B SAS code to calculate estimates from the bootstrapped datasets
Bootstrap SE as per equation in Section 8.4.2.1 are equivalent to PROC MEANS using the option “STDDEV” for mania example
/*ASIDE: The following code will show the estimate of the standard error using the formula in section 8.4 is the same as that from using the stddev option in PROC MEANS for the LS means of treatment at the final visit*/ DATA bootse; MERGE lsm_estimates (KEEP=trt lsm) lsms; BY trt; RUN; DATA bootse; SET bootse; diff=estimate-lsm; *to calculate the numerator[θ\hat(b)- θ\hat(.)]^2; diff2=diff*diff; KEEP trt lsm estimate diff diff2; RUN; PROC MEANS DATA=bootse; VAR diff2; BY trt; *Calculate Σ_(b=1)^B[θ\hat(b)- θ\hat(.)]^2; OUTPUT OUT=lsm_sum SUM=sumls; RUN; DATA lsm_sum; SET lsm_sum; *Calculate Σ_(b=1)^B[θ\hat(b)- θ\hat(.)]^2/B-1 B is 10; sumls=sumls/9; RUN; DATA lsm_sum; SET lsm_sum; *Calculate the standard error of the estimates [Σ_(b=1)^B[θ\hat(b)- θ\hat(.)]^2/B-1]^1/2; sumls=sqrt(sumls); *sumls gives the same estimate of the standard error as above in proc means (See dataset “lsm_estimates”); RUN;
Appendix 8.C How to implement Vansteelandt et al. method for insomnia dataset
Insomnia dataset: Vansteelandt et al. method “by hand” (continuous response)
*The following code will run the Vansteelandt et al. method for the Mania dataset;
*Create 100 bootstrap samples with replacement. Each bootstrap sample is the same size as the original data (640 observations);
ODS LISTING CLOSE;
PROC SURVEYSELECT DATA=sleeph METHOD = urs SAMPSIZE= 640
REP=100 SEED=883960001 OUT=tst_boot_samples OUTHITS;
RUN;
ODS LISTING;
DATA tst_boot_samples;
SET tst_boot_samples;
DROP numberhits;
RUN;
*Create missingness indicators for each visit Rij which take the value 1 if the response is observed and 0 if not;
%MACRO create_missing_indicators();
DATA tst_boot_samples;
SET tst_boot_samples;
%DO i=1 %TO 5;
IF tst_&i NE . THEN r_&i = 1;ELSE r_&i = 0;
%END;
OUTPUT;
RUN;
%MEND create_missing_indicators;
%create_missing_indicators();
*First visit was fully observed and so proc logistic cannot be run, so the probability of being observed at visit 1 is 1 the first logistic regression is for visit 2;
*Run logistic regression for each visit;
ODS LISTING CLOSE;
PROC LOGISTIC DATA=tst_boot_samples DESCENDING;
CLASS trt;
MODEL r_2=tst_0 base_mss trt;
BY replicate;
OUTPUT OUT=p_2 P=prob_2;
ODS OUTPUT CONVERGENCESTATUS =convstat;
RUN;
QUIT;
ODS LISTING;
*if subject was missing at previous visit then delete that observation, probability at visit 3 is conditional on being observed at visit 1 and visit 2;
DATA tst_boot_temp;
SET tst_boot_samples;
IF r_2 EQ 0 THEN DELETE;
RUN;
ODS LISTING CLOSE;
PROC LOGISTIC DATA=tst_boot_temp DESCENDING;
CLASS trt;
MODEL r_3= tst_0 tst_2 base_mss trt;
BY replicate;
OUTPUT OUT=p_3 P=prob_3;
ODS OUTPUT CONVERGENCESTATUS =convstat;
RUN;
QUIT;
ODS LISTING;
DATA tst_boot_temp;
SET tst_boot_temp;
IF r_3 EQ 0 THEN DELETE;
RUN;
ODS LISTING CLOSE;
PROC LOGISTIC DATA=tst_boot_temp DESCENDING;
CLASS trt;
MODEL r_4= tst_0 tst_2 tst_3 base_mss trt;
BY replicate;
OUTPUT OUT=p_4 P=prob_4;
ODS OUTPUT CONVERGENCESTATUS =convstat;
RUN;
QUIT;
ODS LISTING;
DATA tst_boot_temp;
SET tst_boot_temp;
IF r_4 EQ 0 THEN DELETE;
RUN;
ODS LISTING CLOSE;
PROC LOGISTIC DATA=tst_boot_temp DESCENDING;
CLASS trt;
MODEL r_5= tst_0 tst_2 tst_3 tst_4 base_mss trt;
BY replicate;
OUTPUT OUT=p_5 P=prob_5;
ODS OUTPUT CONVERGENCESTATUS =convstat;
RUN;
QUIT;
ODS LISTING;
*Before merging probabilities for each visit first need to sort them;
%MACRO sortdata();
%DO i = 2 %TO 5;
PROC SORT DATA = p_&i;
BY replicate subjid trt;
RUN;
DATA p_&i;
SET p_&i;
KEEP replicate subjid trt prob_&i;
RUN;
%END;
%MEND sortdata;
%sortdata();
*Calculate the product of the probabilities of being observed from visits 1 to j-1;
*As the first visit was fully observed, give each subject a probability of 1 make a dataset with probabilities 1 for each subject;
DATA p_1;
SET p_2 (KEEP=replicate subjid trt);
prob_1=1;
RUN;
DATA overall_probability;
MERGE p_1 p_2;
BY replicate subjid trt;
*the overall probability of being observed at visit 2 is the
probability of being observed at visit 1*visit 2, as the data
are monotone missing;
prob_2 = prob_1*prob_2;
RUN;
*Likewise for visit 3 the overall probability of being observed at visit 3 is the probability of being observed at visit 1*visit 2*visit3 as the data are monotone missing;
DATA overall_probability;
MERGE overall_probability p_3;
BY replicate subjid trt;
*prob 2 is now prob_1*prob2;
prob_3 = prob_2*prob_3;
RUN;
*The same applies for visit 4;
DATA overall_probability;
MERGE overall_probability p_4;
BY replicate subjid trt;
*prob 3 is now prob_1*prob2*prob_3;
prob_4 = prob_3*prob_4;
RUN;
*And also for visit 5;
DATA overall_probability;
MERGE overall_probability p_5;
BY replicate subjid trt;
*prob 4 is now prob_1*prob2*prob_3*prob_4;
prob_5 = prob_4*prob_5;
RUN;
*Calculate the inverse probability of being observed at each visit;
%MACRO get_inverse_prob();
DATA overall_probability;
SET overall_probability;
%DO i = 1 %TO 5;
prob_&i = 1/prob_&i;
%END;
RUN;
%MEND get_inverse_prob;
%get_inverse_prob();
*Append inverse probabilities to the original dataset;
PROC SORT DATA=tst_boot_samples;
BY replicate subjid trt;
RUN;
PROC SORT DATA=overall_probability;
BY replicate subjid trt;
RUN;
DATA tst_boot_samples;
MERGE tst_boot_samples overall_probability;
BY replicate subjid trt;
RUN;
*Convert the data back to vertical format;
DATA tst_boot_vert;
SET tst_boot_samples;
%MACRO makevert();
%DO i=1 %TO 5;
tst=tst_&i;
r=r_&i;
prob=prob_&i;
visit=&i;
OUTPUT;
DROP tst_&i r_&i prob_&i;
%END;
%MEND makevert;
%makevert();
RUN;
*Make sure data are sorted appropriately;
PROC SORT DATA=tst_boot_vert;
BY replicate descending trt descending visit;
RUN;
*The response of interest is the change from baseline;
DATA tst_boot_vert;
SET tst_boot_vert;
tstc= tst - tst_0;
RUN;
*Run a weighted GLM (to get the IPW predictions) this model should be based on all variables if dataset has (fully observed) baseline and post-baseline variables;
ODS LISTING CLOSE;
PROC MIXED DATA= tst_boot_vert ORDER=data;
CLASS trt visit;
MODEL tstc=base_mss trt visit trt*visit/SOLUTION OUTP=first_glm_out;
BY replicate;
WEIGHT prob;
RUN;
QUIT;
ODS LISTING;
*Now take the predicted response from dataset "first_glm_out" and use it as the new response;
PROC SORT DATA=first_glm_out;
BY replicate visit subjid;
RUN;
PROC SORT DATA=tst_boot_vert;
BY replicate visit subjid;
RUN;
*set new response to be the predicted response from the previous GLM;
DATA tst_boot_vert;
MERGE tst_boot_vert first_glm_out(keep=pred replicate subjid visit);
BY replicate visit subjid;
tstc=pred;
DROP pred;
RUN;
PROC SORT DATA=tst_boot_vert;
BY replicate DESCENDING trt DESCENDING visit;
RUN;
*Run final analysis model using only the covariates for which coefficient are required (in this case treatment effects are each visit);
ODS LISTING CLOSE;
PROC MIXED DATA=tst_boot_vert order=data;
CLASS trt visit;
MODEL tstc= base_mss trt visit trt*visit /SOLUTION
OUTP=final_analysis_out;
BY replicate;
LSMEANS trt*visit /CL DIFF=control("1" "5");
ODS OUTPUT DIFFS=diffs LSMEANS=lsms;
RUN;
QUIT;
ODS LISTING;
*Get overall estimates of mean and variance of treatment effect at final visit;
*Dataset "lsms" contains the estimates of the treatment effect for each visit over the 100 bootstrap samples. We are interested in the final visit;
DATA lsms;
SET lsms;
IF visit NE 5 THEN DELETE;
RUN;
PROC SORT DATA=lsms;
BY trt;
RUN;
*Get the mean and standard error of estimates over the bootstrap samples to get the overall bootstrapped estimate;
PROC MEANS DATA=lsms;
VAR estimate;
BY trt;
*stddev gives the bootstrap standard error of the overall estimate
(this is the exact same as working out the formula given in
section 8.4) See appendix 8.B for proof.;
OUTPUT OUT=lsm_estimates MEAN=lsm STDDEV=se;
RUN;
*Show estimates of the difference in the treatment groups;
DATA diffs;
SET diffs;
IF visit NE 5 THEN DELETE;
RUN;
PROC MEANS DATA=diffs;
VAR estimate;
OUTPUT OUT=trt_diff_estimates MEAN=trt_diff STDDEV=diff_SE;
RUN;
*calculate the p-value of treatment difference at last visit;
DATA trt_diff_estimates;
SET trt_diff_estimates;
t_Value= trt_diff/diff_SE;
p_value=(1-probt(abs(t_value),5490))*2;
RUN;
PROC CONTENTS DATA = trt_diff_estimates; RUN;
Identical implementation via a SAS macro by the authors, available from DIA pages at missingdata.org.uk
%INCLUDE "vansteelandt_method.sas"; %INCLUDE "VansteelandtSubMacros.sas"; %vansteelandt_method( datain=sleepv, trtname=trt, subjname=subjid, visname=visit, basecont=%str(base_mss), seed=883960001, nboot=100,debug=0, primaryname=tst, analcovarcont=%str(base_mss), trtref=1, dataout=Sleep_vans_predicted, resout=Sleep_vans_results );
References
Carpenter JR, Kenward MG (2006) A comparison of multiple imputation and doubly robust estimation for analyses with missing data. Journal of the Royal Statistical Society Series A 169: 571–584.
Daniel R, Kenward MG (2012) A method for increasing the robustness of multiple imputation. Computational Statistics and Data Analysis 56: 1624–1643.
Efron B, Tibshirani RJ (1993) An Introduction to the Bootstrap. Chapman and Hall/CRC, Boca Raton, FL.
Freund RJ, Wilson WJ, Sa P (2006) Regression Analysis: Statistical Modelling of a Response Variable. Academic Press, San Diego, CA.
Kang JDY, Schafer JL (2007) Demystifying double robustness: a comparison of alternative strategies for estimating a population mean from incomplete data. Statistical Science 22(4): 523–539.
Molenberghs G, Kenward MG (2007) Missing Data in Clinical Studies. John Wiley & Sons Ltd., West Sussex.
Robins J, Rotnitzky A, Zhao L (1994) Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association 89(427): 846–866.
Tchetgen E (2009) A simple implementation of doubly robust estimation in logistic regression with covariates missing at random. Journal of Epidemiology 20: 391–394.
Teshome B, Molenberghs G, Sotto C, Kenward MG (2011) Doubly robust and multiple-imputation-based generalized estimating equations. Journal of Biopharmaceutical Statistics 21: 202–225.
Vansteelandt S, Carpenter J, Kenward MG (2010) Analysis of incomplete data using inverse probability weighting and doubly robust estimators. Methodology: European Journal of Research Methods for the Behavioral and Social Sciences 6(1): 37–48.
Table of SAS Code Fragments