Die endlichdimensionale kontinuierliche Optimierung behandelt die Minimierung oder Maximierung einer Zielfunktion in einer endlichen Anzahl kontinuierlicher Entscheidungsvariablen. Wichtige Anwendungen finden sich nicht nur bei linearen Modellen (wie in einfachen Modellen zur Gewinnmaximierung in Produktionsprogrammen oder bei Transportproblemen [24]), sondern auch bei diversen nichtlinearen Modellen aus Natur-, Ingenieur- und Wirtschaftswissenschaften. Dazu gehören geometrische Probleme, mechanische Probleme, Parameter-Fitting-Probleme, Schätzprobleme, Approximationsprobleme, Datenklassifikation und Sensitivitätsanalyse. Als Lösungswerkzeug benutzt man sie außerdem bei nichtkooperativen Spielen [35], in der robusten Optimierung [35] oder bei der Relaxierung diskreter und gemischt-ganzzahliger Optimierungsprobleme [32].
Das vorliegende einführende Kapitel motiviert in Abschn. 1.1 zunächst die grundlegende Terminologie und Notation von Optimierungsproblemen anhand diverser Beispiele und grenzt die endlichdimensionale glatte gegen die unendlichdimensionale und die nichtglatte Optimierung ab. Abschn. 1.2 widmet sich danach der Frage, unter welchen Voraussetzungen Optimierungsprobleme überhaupt lösbar sind (eine weitaus ausführlichere Darstellung von Lösbarkeitsfragen findet der interessierte Leser in [33]). Abschließend stellt Abschn. 1.3 einige Rechenregeln und Umformungen für Optimierungsprobleme bereit, die im Rahmen dieses Lehrbuchs eine Rolle spielen werden.
1.1 Beispiele und Begriffe
In der Optimierung vergleicht man verschiedene Alternativen bezüglich eines Zielkriteriums und sucht unter allen betrachteten Alternativen eine beste. Anhand des folgenden Beispiels eines nichtlinearen Optimierungsproblems in zwei Variablen, das sich mit Mitteln der Schulmathematik lösen lässt, führen wir zunächst einige grundlegende Begriffe ein.
1.1.1 Beispiel (Konservendose – glatte Optimierung)
Aus A Maßeinheiten (z. B. Quadratzentimeter) Blech sei eine Konservendose mit maximalem Volumen zu konstruieren. Die Dose sei als Zylinder mit Deckel und Boden modelliert, ist also durch zwei Angaben charakterisiert, nämlich ihren Radius r und ihre Höhe h. Die Dose besitzt dann das Volumen V(r, h) = πr2h und die Oberfläche 2πrh + 2πr2.
 in der durch die Nebenbedingungen beschriebenen Menge
in der durch die Nebenbedingungen beschriebenen Menge
Wie in diesem Beispiel lassen sich in Problemen der kontinuierlichen Optimierung die Alternativen stets geometrisch als „Punkte in einem Raum“ interpretieren, hier im zweidimensionalen euklidischen Raum  . Da genau diese geometrische Entsprechung auf Optimalitätsbedingungen und numerische Verfahren führen wird, adressieren wir die Elemente von M im Folgenden nicht als zulässige Alternativen, sondern als zulässige Punkte
. Die Menge M werden wir zulässige Menge
nennen.
. Da genau diese geometrische Entsprechung auf Optimalitätsbedingungen und numerische Verfahren führen wird, adressieren wir die Elemente von M im Folgenden nicht als zulässige Alternativen, sondern als zulässige Punkte
. Die Menge M werden wir zulässige Menge
nennen.
 der reellen Zahlen. Diese Funktion nennen wir Zielfunktion. Im vorliegenden Beispiel ist dies die Volumenfunktion
der reellen Zahlen. Diese Funktion nennen wir Zielfunktion. Im vorliegenden Beispiel ist dies die Volumenfunktion



Während in  über die Werte von r und h eine Entscheidung getroffen werden soll, ist der Wert von A exogen vorgegeben. Wir nennen r und h daher Entscheidungsvariablen
und A einen Parameter
. Zur Übersichtlichkeit notiert man die Entscheidungsvariablen häufig wie in
über die Werte von r und h eine Entscheidung getroffen werden soll, ist der Wert von A exogen vorgegeben. Wir nennen r und h daher Entscheidungsvariablen
und A einen Parameter
. Zur Übersichtlichkeit notiert man die Entscheidungsvariablen häufig wie in  unterhalb der Optimierungsvorschrift „max“ oder „min“.
unterhalb der Optimierungsvorschrift „max“ oder „min“.
Ein Punkt  heißt optimal für ein allgemeines Optimierungsproblem P, wenn kein Punkt x ∈ M einen besseren Zielfunktionswert besitzt. Bei Maximierungsproblemen bedeutet dies gerade, dass die Ungleichung
heißt optimal für ein allgemeines Optimierungsproblem P, wenn kein Punkt x ∈ M einen besseren Zielfunktionswert besitzt. Bei Maximierungsproblemen bedeutet dies gerade, dass die Ungleichung  für alle x ∈ M erfüllt ist, und bei Minimierungsproblemen kehrt sich diese Ungleichung um. Der zugehörige optimale Wert
von P ist die Zahl
für alle x ∈ M erfüllt ist, und bei Minimierungsproblemen kehrt sich diese Ungleichung um. Der zugehörige optimale Wert
von P ist die Zahl  . Während ein Optimierungsproblem durchaus mehrere optimale Punkte besitzen kann, ist der optimale Wert immer eindeutig.
. Während ein Optimierungsproblem durchaus mehrere optimale Punkte besitzen kann, ist der optimale Wert immer eindeutig.

Um nun einen optimalen Punkt und den optimalen Wert von  zu bestimmen, gehen wir in diesem einführenden Beispiel etwas lax vor und bedienen uns unter anderem des aus der Schulmathematik bekannten Konzepts der Kurvendiskussion, das erst in Abschn. 2.1 (in viel allgemeinerem Rahmen) behandelt wird.
zu bestimmen, gehen wir in diesem einführenden Beispiel etwas lax vor und bedienen uns unter anderem des aus der Schulmathematik bekannten Konzepts der Kurvendiskussion, das erst in Abschn. 2.1 (in viel allgemeinerem Rahmen) behandelt wird.





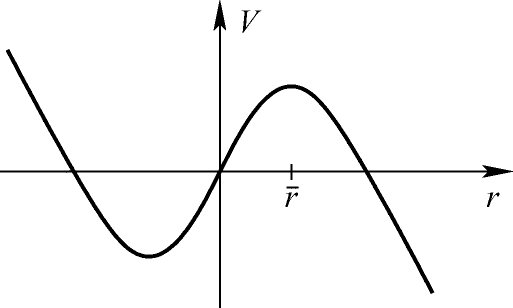
Dosenvolumen in Abhängigkeit vom Radius



 nicht als Maximalpunkt infrage kommt. Wegen
nicht als Maximalpunkt infrage kommt. Wegen  und
und  sind als Ergebnis einer Kurvendiskussion aber sowohl x1 als auch x3 Kandidaten für Maximalpunkte von f. Allerdings ist x3 nur unter allen Punkten aus seiner „Nachbarschaft“ (also z. B. einem kleinen Intervall um x3) der beste Punkt, während x1 unter allen Punkten in
sind als Ergebnis einer Kurvendiskussion aber sowohl x1 als auch x3 Kandidaten für Maximalpunkte von f. Allerdings ist x3 nur unter allen Punkten aus seiner „Nachbarschaft“ (also z. B. einem kleinen Intervall um x3) der beste Punkt, während x1 unter allen Punkten in  optimal ist.
optimal ist.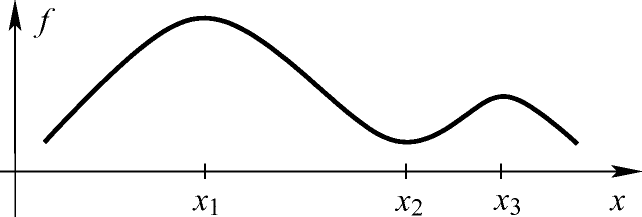
Ein globaler und ein lokaler Maximalpunkt

Lokale und globale Minimalität
1.1.2 Definition (Minimalpunkte und Minimalwerte)
Gegeben seien eine Menge von zulässigen Punkten  und eine Zielfunktion
und eine Zielfunktion  .
.
- a)
 heißt lokaler Minimalpunkt
von f auf M, falls eine Umgebung U von
heißt lokaler Minimalpunkt
von f auf M, falls eine Umgebung U von  mit
existiert.
mit
existiert.
- b)
 heißt globaler Minimalpunkt
von f auf M, falls man in (a)
heißt globaler Minimalpunkt
von f auf M, falls man in (a)  wählen kann.
wählen kann. - c)
Ein lokaler oder globaler Minimalpunkt heißt strikt, falls in (a) bzw. (b) für
 sogar die strikte Ungleichung > gilt.
sogar die strikte Ungleichung > gilt. - d)
Zu jedem globalen Minimalpunkt
 heißt
heißt  globaler Minimalwert
, und zu jedem lokalen Minimalpunkt
globaler Minimalwert
, und zu jedem lokalen Minimalpunkt  heißt
heißt  lokaler Minimalwert.
lokaler Minimalwert.
Damit die Forderung
 sinnvoll ist, muss der Bildbereich von f geordnet sein. Zum Beispiel ist die Minimierung von
sinnvoll ist, muss der Bildbereich von f geordnet sein. Zum Beispiel ist die Minimierung von  zunächst nicht sinnvoll. Allerdings befasst sich das Gebiet der Mehrzieloptimierung
damit, wie man solche Probleme trotzdem behandeln kann (für eine kurze Einführung s. z. B. [24]).
zunächst nicht sinnvoll. Allerdings befasst sich das Gebiet der Mehrzieloptimierung
damit, wie man solche Probleme trotzdem behandeln kann (für eine kurze Einführung s. z. B. [24]).Jeder globale Minimalpunkt ist auch lokaler Minimalpunkt.
Strikte globale Minimalpunkte sind eindeutig, und strikte lokale Minimalpunkte sind lokal eindeutig.
Lokale und globale Maximalpunkte sind analog definiert. Da die Maximalpunkte von f genau die Minimalpunkte von −f sind, reicht es, Minimierungsprobleme zu betrachten. Achtung: Dabei ändert sich allerdings das Vorzeichen des Optimalwerts, denn es gilt
 . Dies wird in Abb. 1.4 illustriert und in Übung 1.1.3 sowie etwas allgemeiner in Übung 1.3.1 bewiesen.
. Dies wird in Abb. 1.4 illustriert und in Übung 1.1.3 sowie etwas allgemeiner in Übung 1.3.1 bewiesen.Wegen der ähnlichen Notation besteht eine Verwechslungsgefahr zwischen dem Minimalwert
 und der zugrunde liegenden Minimierungsaufgabe P (vgl. die Diskussion in Beispiel 1.1.1).
und der zugrunde liegenden Minimierungsaufgabe P (vgl. die Diskussion in Beispiel 1.1.1).
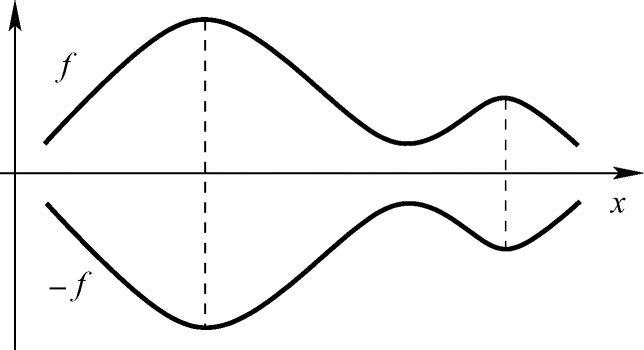
Maximierung von f durch Minimierung von −f
1.1.3 Übung
Gegeben seien eine Menge von zulässigen Punkten  und eine Zielfunktion
und eine Zielfunktion  . Zeigen Sie:
. Zeigen Sie:
- a)
Die globalen Maximalpunkte von f auf M sind genau die globalen Minimalpunkte von −f auf M.
- b)Sofern f globale Maximalpunkte besitzt, gilt für den globalen Maximalwert

Per Definition 1.1.2 lassen sich lokale bzw. globale Minimalpunkte in den wenigsten Fällen berechnen. Stattdessen werden wir in Kap. 2 und 3 ableitungsbasierte Optimalitätsbedingungen und darauf aufbauende Lösungsverfahren entwickeln. Diese sind naturgemäß nicht anwendbar, wenn die definierenden Funktionen des betrachteten Optimierungsproblems nicht differenzierbar sind. Das folgende Beispiel zeigt allerdings, dass sich nichtdifferenzierbare Optimierungsprobleme in wichtigen Fällen in äquivalente differenzierbare Probleme umwandeln lassen.
1.1.4 Beispiel (Diskrete Approximation – glatte vs. nichtglatte Optimierung)
 , 1 ≤ j ≤ m. Gesucht ist eine Gerade, die diese Punkte „möglichst gut“ annähert. Setzt man eine Gerade der Form y = ax + b an, so ist also ein
, 1 ≤ j ≤ m. Gesucht ist eine Gerade, die diese Punkte „möglichst gut“ annähert. Setzt man eine Gerade der Form y = ax + b an, so ist also ein  gesucht, das die Norm des Fehlervektors minimiert:
gesucht, das die Norm des Fehlervektors minimiert:
 das Problem
das Problem
 im Nullpunkt nicht differenzierbar ist. Man spricht dann von einem nichtglatten Optimierungsproblem
. Die meisten in diesem Lehrbuch vorgestellten Techniken werden sich allerdings auf glatte Optimierungsprobleme beziehen, bei denen mindestens erste Ableitungen der beteiligten Funktionen existieren
. Dies ist keine zu starke Einschränkung, da sich etwa das obige Problem zu einem äquivalenten glatten Problem umformen lässt: Nach Übung 1.3.4 ändern sich die optimalen Punkte nicht, wenn man in der Zielfunktion die Wurzel weglässt. Die neue Zielfunktion ist dann überall differenzierbar. Mit der Setzung
im Nullpunkt nicht differenzierbar ist. Man spricht dann von einem nichtglatten Optimierungsproblem
. Die meisten in diesem Lehrbuch vorgestellten Techniken werden sich allerdings auf glatte Optimierungsprobleme beziehen, bei denen mindestens erste Ableitungen der beteiligten Funktionen existieren
. Dies ist keine zu starke Einschränkung, da sich etwa das obige Problem zu einem äquivalenten glatten Problem umformen lässt: Nach Übung 1.3.4 ändern sich die optimalen Punkte nicht, wenn man in der Zielfunktion die Wurzel weglässt. Die neue Zielfunktion ist dann überall differenzierbar. Mit der Setzung  , 1 ≤ j ≤ m, besitzt sie die Struktur
, 1 ≤ j ≤ m, besitzt sie die Struktur  , und man spricht von einem Kleinste-Quadrate-Problem
.
, und man spricht von einem Kleinste-Quadrate-Problem
. erhält man das nichtglatte unrestringierte Problem
erhält man das nichtglatte unrestringierte Problem



Dass endlichdimensionale Optimierungsprobleme auch „unendliche Aspekte“ besitzen können, zeigt das nächste Beispiel. Dort treten im Gegensatz zu Beispiel 1.1.1 nicht endlich viele (nämlich drei), sondern unendlich viele Ungleichungsrestriktionen auf, und dies in natürlicher Weise.
Wir folgen dort und im Folgenden außerdem einer in der mathematischen Literatur üblichen Konstruktion für Verneinungen und benutzen beispielsweise den künstlichen Begriff „nichtleer“ anstelle von „nicht leer“, damit klar ist, worauf das „nicht“ sich bezieht.
1.1.5 Beispiel (Kontinuierliche Approximation – semi-infinite Optimierung)
 , eine glatte Funktion
, eine glatte Funktion  sowie eine Familie glatter Funktionen a(p, ·) mit Scharparameter
sowie eine Familie glatter Funktionen a(p, ·) mit Scharparameter  (z. B. für m = 1 Polynome
(z. B. für m = 1 Polynome  vom Höchstgrad n − 1). Gesucht ist die beste Approximation an f auf Z durch eine Funktion a(p, ·) in der Tschebyscheff-Norm. Eine Formulierung als Optimierungsproblem lautet
vom Höchstgrad n − 1). Gesucht ist die beste Approximation an f auf Z durch eine Funktion a(p, ·) in der Tschebyscheff-Norm. Eine Formulierung als Optimierungsproblem lautet

Das abschließende Beispiel dieses Abschnitts illustriert den Fall der unendlichdimensionalen Optimierung, den dieses Lehrbuch nicht thematisieren wird, obwohl sich einige Techniken vom endlichdimensionalen Fall auf ihn übertragen lassen (für Details s. z. B. [19]). Das folgende von Johann Bernoulli im Jahre 1696 gestellte Optimierungsproblem gilt als wesentlicher Ausgangspunkt zur Entwicklung der gesamten Analysis.
1.1.6 Beispiel (Brachistochrone – Variationsrechnung, infinite Optimierung)
Gegeben seien zwei Punkte A und B in einer senkrecht stehenden Ebene mit B seitlich unterhalb von A. Gesucht ist eine Kurve durch A und B, so dass ein sich unter dem Einfluss der Gravitation entlang dieser Kurve bewegender Massenpunkt den Weg von A nach B in kürzestmöglicher Zeit zurücklegt.

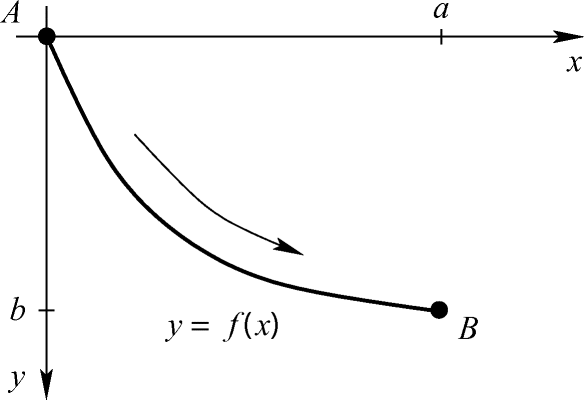
Problem der Brachistochrone

1.2 Lösbarkeit
Ob ein Optimierungsproblem überhaupt optimale Punkte besitzt, liegt nicht immer auf der Hand und muss bei vielen Lösungsverfahren vorab vom Anwender selbst geprüft werden. Eine ausführliche Diskussion dieser Problematik findet sich in [33], während wir hier nur auf die wesentlichen Punkte eingehen.
 und die Funktion
und die Funktion  lässt sich jedenfalls jedem Minimierungsproblem
lässt sich jedenfalls jedem Minimierungsproblem
 als untere Schranke
für f auf M, falls
als untere Schranke
für f auf M, falls
 , falls
, fallsv ≤ f(x) für alle x ∈ M gilt (d. h., v ist selbst untere Schranke von f auf M) und
α ≤ v für alle unteren Schranken α von f auf M gilt.
 von f auf M als kleinste obere Schranke definiert.
von f auf M als kleinste obere Schranke definiert.1.2.1 Beispiel
Es gilt  und
und  .
.


1.2.2 Beispiel
Es gilt  und
und  .
.
Der „verallgemeinerte Minimalwert“  von P ist also stets ein Element der erweiterten reellen Zahlen
von P ist also stets ein Element der erweiterten reellen Zahlen
 . In der Analysis wird gezeigt (z. B. [17]), dass das so definierte Infimum ohne Voraussetzungen an f und M stets existiert und eindeutig bestimmt ist. Außerdem wird dort eine Charakterisierung von Infima bewiesen, die wir nachfolgend benutzen werden: Das Infimum einer nichtleeren Menge reeller Zahlen ist genau diejenige ihrer Unterschranken, die sich durch Elemente der Menge beliebig genau approximieren lässt. Für die hier betrachteten Infima von Funktionen auf Mengen bedeutet dies, dass für
. In der Analysis wird gezeigt (z. B. [17]), dass das so definierte Infimum ohne Voraussetzungen an f und M stets existiert und eindeutig bestimmt ist. Außerdem wird dort eine Charakterisierung von Infima bewiesen, die wir nachfolgend benutzen werden: Das Infimum einer nichtleeren Menge reeller Zahlen ist genau diejenige ihrer Unterschranken, die sich durch Elemente der Menge beliebig genau approximieren lässt. Für die hier betrachteten Infima von Funktionen auf Mengen bedeutet dies, dass für  genau dann
genau dann  gilt, wenn v ≤ f(x) für alle x ∈ M gilt und wenn eine Folge (xk) ⊆ M mit
gilt, wenn v ≤ f(x) für alle x ∈ M gilt und wenn eine Folge (xk) ⊆ M mit  existiert. Dabei schreiben wir hier und im Folgenden kurz (xk) für eine Folge
existiert. Dabei schreiben wir hier und im Folgenden kurz (xk) für eine Folge  sowie limk für
sowie limk für  .
.
1.2.3 Definition (Lösbarkeit)
Das Minimierungsproblem P heißt lösbar
, falls ein  mit
mit  existiert.
existiert.
Lösbarkeit von P bedeutet also, dass das Infimum von f auf M als Zielfunktionswert eines zulässigen Punkts realisiert werden kann, dass also das Infimum angenommen wird. Um anzudeuten, dass das Infimum angenommen wird, schreiben wir  anstelle von
anstelle von  .
.
1.2.4 Beispiel
Es gilt  mit
mit  , aber es gibt kein
, aber es gibt kein  mit
mit  .
.
Der folgende Satz besagt (wenig überraschend), dass man zur Lösbarkeit genauso gut die Existenz eines globalen Minimalpunkts fordern kann (zum Beweis s. [33]).
1.2.5 Satz
Das Minimierungsproblem P ist genau dann lösbar, wenn es einen globalen Minimalpunkt besitzt.
Es gilt
 .
.Dies entspricht per Definition dem trivial erscheinenden Fall
 , ist aber nicht immer leicht zu erkennen. Wenn etwa in Beispiel 1.1.1 (z. B. aus Marketinggründen) die zusätzliche Restriktion r ≥ 1 eingeführt wird, dann besitzt
, ist aber nicht immer leicht zu erkennen. Wenn etwa in Beispiel 1.1.1 (z. B. aus Marketinggründen) die zusätzliche Restriktion r ≥ 1 eingeführt wird, dann besitzt  im Fall A < 2π keine zulässigen Punkte. Hinreichende Bedingungen für die Lösbarkeit von P werden natürlich stets
im Fall A < 2π keine zulässigen Punkte. Hinreichende Bedingungen für die Lösbarkeit von P werden natürlich stets  fordern.
fordern.Es gilt
 .Bei stetiger Zielfunktion f muss M in diesem Fall unbeschränkt sein. Beispielsweise ist die Menge der zulässigen Punkte des Optimierungsproblems
.Bei stetiger Zielfunktion f muss M in diesem Fall unbeschränkt sein. Beispielsweise ist die Menge der zulässigen Punkte des Optimierungsproblems aus Beispiel 1.1.1 unbeschränkt (Übung 1.2.7). Dass
aus Beispiel 1.1.1 unbeschränkt (Übung 1.2.7). Dass  trotzdem lösbar ist, zeigt andererseits, dass eine unbeschränkte Menge nicht notwendigerweise die Lösbarkeit verhindert. Als hinreichende Bedingung für Lösbarkeit bietet es sich trotzdem an, M als beschränkt vorauszusetzen. Man fordert also, dass sich ein Radius R > 0 finden lässt, so dass die Kugel um den Nullpunkt mit Radius R die Menge M umschließt:
trotzdem lösbar ist, zeigt andererseits, dass eine unbeschränkte Menge nicht notwendigerweise die Lösbarkeit verhindert. Als hinreichende Bedingung für Lösbarkeit bietet es sich trotzdem an, M als beschränkt vorauszusetzen. Man fordert also, dass sich ein Radius R > 0 finden lässt, so dass die Kugel um den Nullpunkt mit Radius R die Menge M umschließt:

Ein endliches Infimum
 wird nicht angenommen.
wird nicht angenommen.Grund dafür kann wiederum eine unbeschränkte Menge M sein, etwa bei der Funktion f(x) = ex auf der Menge
 . Aber auch für beschränkte Mengen M ist dieser Effekt möglich, etwa wenn Teile des Rands nicht zu M gehören, wie für f(x) = x und M = (0, 1]. Hier gibt es zu jedem Lösungskandidaten x ∈ M eine Verbesserungsmöglichkeit (Abb. 1.6).Als Gegenmittel kann man M als abgeschlossen voraussetzen, d. h., für alle Folgen (xk) ⊆ M mit
. Aber auch für beschränkte Mengen M ist dieser Effekt möglich, etwa wenn Teile des Rands nicht zu M gehören, wie für f(x) = x und M = (0, 1]. Hier gibt es zu jedem Lösungskandidaten x ∈ M eine Verbesserungsmöglichkeit (Abb. 1.6).Als Gegenmittel kann man M als abgeschlossen voraussetzen, d. h., für alle Folgen (xk) ⊆ M mit gelte
gelte  (z. B. ist M = (0, 1] wegen (1/k) ⊆ M und
(z. B. ist M = (0, 1] wegen (1/k) ⊆ M und  nicht abgeschlossen). Falls M durch endlich viele Ungleichungen und Gleichungen beschrieben ist, d. h., falls
mit endlichen Indexmengen I und J gilt, dann ist die Stetigkeit der Funktionen
nicht abgeschlossen). Falls M durch endlich viele Ungleichungen und Gleichungen beschrieben ist, d. h., falls
mit endlichen Indexmengen I und J gilt, dann ist die Stetigkeit der Funktionen
 , i ∈ I, und
, i ∈ I, und  , j ∈ J, hinreichend für die Abgeschlossenheit von M (Übung 1.2.11). Wenn M gleichzeitig beschränkt und abgeschlossen ist, heißt M auch kompakt
.Schließlich ist es möglich, dass ein endliches Infimum selbst auf einer nichtleeren und kompakten Menge M nicht angenommen wird, nämlich wenn f Sprungstellen besitzt. Zum Beispiel besitzt die Funktionkeinen globalen Minimalpunkt auf der nichtleeren und kompakten Menge M = [−1, 1], denn wieder gibt es zu jedem Lösungskandidaten eine Verbesserungsmöglichkeit (Abb. 1.7). Als Gegenmittel kann man f als stetig voraussetzen.
, j ∈ J, hinreichend für die Abgeschlossenheit von M (Übung 1.2.11). Wenn M gleichzeitig beschränkt und abgeschlossen ist, heißt M auch kompakt
.Schließlich ist es möglich, dass ein endliches Infimum selbst auf einer nichtleeren und kompakten Menge M nicht angenommen wird, nämlich wenn f Sprungstellen besitzt. Zum Beispiel besitzt die Funktionkeinen globalen Minimalpunkt auf der nichtleeren und kompakten Menge M = [−1, 1], denn wieder gibt es zu jedem Lösungskandidaten eine Verbesserungsmöglichkeit (Abb. 1.7). Als Gegenmittel kann man f als stetig voraussetzen.

Unlösbarkeit wegen fehlender Abgeschlossenheit von M
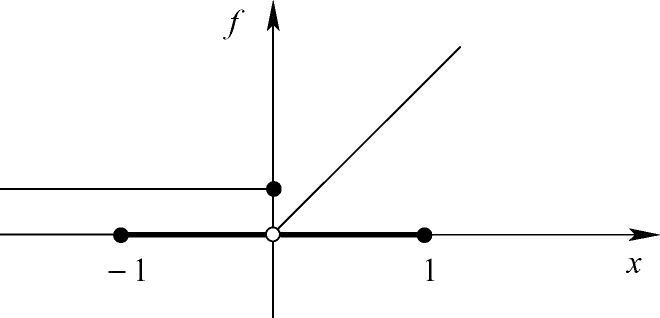
Unlösbarkeit wegen Sprungstelle von f
Der folgende grundlegende Satz zur Existenz von Minimal- und Maximalpunkten zeigt, dass unter den oben motivierten „Mitteln gegen Unlösbarkeit“ tatsächlich stets optimale Punkte existieren. Eine Version des Satzes, die unter schwächeren Voraussetzungen an f noch die Existenz von Minimalpunkten (aber nicht von Maximalpunkten) garantiert, findet sich in [35].
1.2.6 Satz (Satz von Weierstraß)
Die Menge  sei nichtleer und kompakt, und die Funktion
sei nichtleer und kompakt, und die Funktion  sei stetig. Dann besitzt f auf M (mindestens) einen globalen Minimalpunkt und einen globalen Maximalpunkt.
sei stetig. Dann besitzt f auf M (mindestens) einen globalen Minimalpunkt und einen globalen Maximalpunkt.
Beweis.
 . Wegen
. Wegen  gilt
gilt  . Zu zeigen ist die Existenz eines
. Zu zeigen ist die Existenz eines  in M mit
in M mit  Da v Infimum ist, existiert eine Folge (xk) ⊆ M mit
Da v Infimum ist, existiert eine Folge (xk) ⊆ M mit  . In der Analysis wird bewiesen (im Satz von Bolzano-Weierstraß; z. B. [18]), dass jede in einer kompakten Menge M liegende Folge (xk) eine in M konvergente Teilfolge besitzt. Um nicht eine mühsame Teilfolgennotation benutzen zu müssen, wählen wir unsere Folge (xk) direkt als eine solche konvergente Folge, es existiert also ein
. In der Analysis wird bewiesen (im Satz von Bolzano-Weierstraß; z. B. [18]), dass jede in einer kompakten Menge M liegende Folge (xk) eine in M konvergente Teilfolge besitzt. Um nicht eine mühsame Teilfolgennotation benutzen zu müssen, wählen wir unsere Folge (xk) direkt als eine solche konvergente Folge, es existiert also ein  mit
mit  . Aufgrund der Stetigkeit von f auf M gilt nun
. Aufgrund der Stetigkeit von f auf M gilt nun
 wählen. Der Beweis zur Existenz eines globales Maximalpunkts verläuft analog.
wählen. Der Beweis zur Existenz eines globales Maximalpunkts verläuft analog.Obwohl Satz 1.2.6 einerseits viele praktische Anwendungen besitzt, sind seine Voraussetzungen andererseits selbst bei manchen einfachen lösbaren Problemen verletzt, beispielsweise beim Problems  aus Beispiel 1.1.1.
aus Beispiel 1.1.1.
1.2.7 Übung
Zeigen Sie, dass die Menge der zulässigen Punkte des Optimierungsproblems  aus Beispiel 1.1.1 zwar nichtleer und abgeschlossen, aber unbeschränkt ist.
aus Beispiel 1.1.1 zwar nichtleer und abgeschlossen, aber unbeschränkt ist.
Für Probleme ohne Nebenbedingungen, sogenannte unrestringierte Probleme,
gilt  (etwa in Beispiel 1.1.4). Auch dann ist M zwar nichtleer und abgeschlossen, aber nicht beschränkt. Daher ist Satz 1.2.6 auf kein unrestringiertes Problem anwendbar.
(etwa in Beispiel 1.1.4). Auch dann ist M zwar nichtleer und abgeschlossen, aber nicht beschränkt. Daher ist Satz 1.2.6 auf kein unrestringiertes Problem anwendbar.
Um den Satz von Weierstraß für Probleme mit unbeschränkter Menge M anwendbar zu machen, bedient man sich eines Tricks und betrachtet untere Niveaumengen (lower level sets) von f. In deren sowie einigen späteren Definitionen werden wir den Definitionsbereich von f nicht mit M, sondern mit X bezeichnen, da er nicht unbedingt die zulässige Menge eines Optimierungsproblems sein muss.
1.2.8 Definition (Untere Niveaumenge)
 ,
,  und
und  heißt
heißt
 schreiben wir auch kurz
schreiben wir auch kurz
1.2.9 Beispiel
1.2.10 Übung
Für eine abgeschlossene Menge  sei die Funktion
sei die Funktion  stetig. Zeigen Sie, dass dann die Mengen
stetig. Zeigen Sie, dass dann die Mengen  für alle
für alle  abgeschlossen sind.
abgeschlossen sind.
1.2.11 Übung
 und endliche Indexmengen I und J seien die Funktionen
und endliche Indexmengen I und J seien die Funktionen  , i ∈ I, und
, i ∈ I, und  , j ∈ J, stetig. Zeigen Sie, dass dann die Menge
, j ∈ J, stetig. Zeigen Sie, dass dann die Menge

 ausdrücken (in [33] werden aber noch interessantere Eigenschaften der Menge S gezeigt).
ausdrücken (in [33] werden aber noch interessantere Eigenschaften der Menge S gezeigt).1.2.12 Lemma
Für ein  sei
sei  . Dann gilt
. Dann gilt  .
.
Beweis.
Wegen  gibt es einen Punkt
gibt es einen Punkt  in M mit
in M mit  . Nun sei
. Nun sei  ein beliebiger globaler Minimalpunkt von P. Dann gilt
ein beliebiger globaler Minimalpunkt von P. Dann gilt  und
und  , also
, also  .
.
Das Konzept der unteren Niveaumengen erlaubt es, in einer hinreichenden Bedingung zur Lösbarkeit von P das Zusammenspiel der Eigenschaften der Zielfunktion f und der zulässigen Menge M zu berücksichtigen.
1.2.13 Satz (Verschärfter Satz von Weierstraß)
Für eine (nicht notwendigerweise beschränkte oder abgeschlossene) Menge  sei
sei  stetig, und mit einem
stetig, und mit einem  sei
sei  nichtleer und kompakt. Dann besitzt f auf M (mindestens) einen globalen Minimalpunkt.
nichtleer und kompakt. Dann besitzt f auf M (mindestens) einen globalen Minimalpunkt.
Beweis.
1.2.14 Übung
Zeigen Sie, dass die Voraussetzungen von Satz 1.2.13 schwächer sind als die von Satz 1.2.6, dass sie also unter den Voraussetzungen von Satz 1.2.6 stets erfüllbar sind.
Die Verschärfung von Satz 1.2.13 gegenüber Satz 1.2.6 bezieht sich darauf, dass die uns interessierende Aussage des Satzes von Weierstraß, nämlich die Existenz eines globalen Minimalpunkts, auch unter der schwächeren Voraussetzung von Satz 1.2.13 folgt. Da nun allerdings keine Aussage mehr zur Existenz eines globalen Maximalpunkts von P getroffen werden kann, sind die beiden Sätze genau genommen unabhängig voneinander.
1.2.15 Beispiel
1.2.16 Übung
Zeigen Sie die Lösbarkeit des Optimierungsproblems  aus Beispiel 1.1.1 mit Hilfe von Satz 1.2.13.
aus Beispiel 1.1.1 mit Hilfe von Satz 1.2.13.
1.2.17 Korollar (Verschärfter Satz von Weierstraß für unrestringierte Probleme)
Die Funktion  sei stetig, und mit einem
sei stetig, und mit einem  sei
sei  nichtleer und kompakt. Dann besitzt f auf
nichtleer und kompakt. Dann besitzt f auf  (mindestens) einen globalen Minimalpunkt.
(mindestens) einen globalen Minimalpunkt.
Beweis.
Satz 1.2.13 mit  .
.
1.2.18 Beispiel
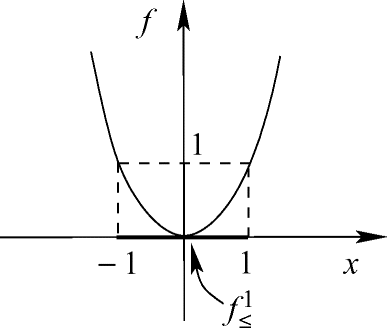
Für f(x) = (x − 5)2 ist ![$f_{\le}^1 = \left[ 4,6\right]$](../images/439970_1_De_1_Chapter/439970_1_De_1_Chapter_TeX_IEq139.png) nichtleer und kompakt, also besitzt f nach Korollar 1.2.17 einen globalen Minimalpunkt auf
nichtleer und kompakt, also besitzt f nach Korollar 1.2.17 einen globalen Minimalpunkt auf  .
.
1.2.19 Beispiel
Mit f(x) = ex gilt  für alle α ≤ 0 sowie
für alle α ≤ 0 sowie ![$f_{\le}^\alpha = \left( -\infty, \log(\alpha)\right]$](../images/439970_1_De_1_Chapter/439970_1_De_1_Chapter_TeX_IEq142.png) für alle α > 0. Daher ist
für alle α > 0. Daher ist  für kein α nichtleer und kompakt, Korollar 1.2.17 also nicht anwendbar. f besitzt auch tatsächlich keinen globalen Minimalpunkt auf
für kein α nichtleer und kompakt, Korollar 1.2.17 also nicht anwendbar. f besitzt auch tatsächlich keinen globalen Minimalpunkt auf  .
.
1.2.20 Beispiel
Für f(x) = sin(x) ist Korollar 1.2.17 ebenfalls nicht anwendbar, da alle Mengen  mit
mit  unbeschränkt oder leer sind. f besitzt aber trotzdem globale Minimalpunkte auf
unbeschränkt oder leer sind. f besitzt aber trotzdem globale Minimalpunkte auf  .
.
Im Folgenden geben wir ein einfaches Kriterium an, aus dem die Kompaktheit von  mit jedem
mit jedem  folgt. Dadurch kann man die Voraussetzungen von Satz 1.2.13 und Korollar 1.2.17 garantieren, ohne ein explizites Niveau α angeben zu müssen.
folgt. Dadurch kann man die Voraussetzungen von Satz 1.2.13 und Korollar 1.2.17 garantieren, ohne ein explizites Niveau α angeben zu müssen.
1.2.21 Definition (Koerzivität)
 und eine Funktion
und eine Funktion  . Falls für alle Folgen (xk) ⊆ X mit
. Falls für alle Folgen (xk) ⊆ X mit  auch
auch
1.2.22 Beispiel
f(x) = (x − 5)2 ist koerziv auf  .
.
1.2.23 Beispiel
f(x) = ex ist nicht koerziv auf  , wohl aber auf der Menge
, wohl aber auf der Menge  .
.
1.2.24 Übung
Gegeben sei die quadratische Funktion  mit einer symmetrischen (n, n)-Matrix A (d. h., es gilt
mit einer symmetrischen (n, n)-Matrix A (d. h., es gilt  ) und
) und  . Zeigen Sie, dass q genau dann koerziv auf
. Zeigen Sie, dass q genau dann koerziv auf  ist, wenn A positiv definit ist (d. h. wenn
ist, wenn A positiv definit ist (d. h. wenn  für alle
für alle  gilt; Details zu positiv definiten Matrizen finden sich in Abschn. 2.1.4).
gilt; Details zu positiv definiten Matrizen finden sich in Abschn. 2.1.4).
1.2.25 Beispiel
Auf kompakten Mengen X ist jede Funktion f trivialerweise koerziv.
Zur Formulierung von Beispiel 1.2.25 sei angemerkt, dass wir den Begriff „trivial
“ in diesem Lehrbuch sparsam benutzen. Er bezeichnet nicht Aussagen, die aus Sicht des Autors „leicht“ zu beweisen sind, sondern solche, die wegen einer logischen Trivialität gelten. Zum Beispiel ist die Aussage „Alle grünen Kühe können fliegen“ trivialerweise wahr, denn um sie zu widerlegen, müsste man eine grüne Kuh finden, die nicht fliegen kann. Da man aber schon keine grüne Kuh findet, braucht man nicht noch darüber hinaus nach einer grünen Kuh zu suchen, die nicht fliegen kann. Damit lässt die Aussage sich aus einem trivialen Grund nicht widerlegen und ist folglich wahr. In Beispiel 1.2.25 lautet die analoge Argumentation, dass in einer kompakten Menge X keine einzige Folge (xk) mit  liegt. Um zu zeigen, dass f nicht koerziv ist, müsste aber eine solche Folge existieren und außerdem noch
liegt. Um zu zeigen, dass f nicht koerziv ist, müsste aber eine solche Folge existieren und außerdem noch  erfüllen. Letzteres ist aber irrelevant, weil schon die Existenz der Folge nicht vorliegt. Folglich ist f auf X aus einem trivialen Grund koerziv.
erfüllen. Letzteres ist aber irrelevant, weil schon die Existenz der Folge nicht vorliegt. Folglich ist f auf X aus einem trivialen Grund koerziv.
Im Satz von Weierstraß können wir nun im Sinne der folgenden beiden Resultate die Beschränktheit von M durch die Koerzivität von f auf M ersetzen. Beweise dazu finden sich beispielsweise in [33].
1.2.26 Lemma
Die Funktion  sei stetig und koerziv auf der (nicht notwendigerweise beschränkten) abgeschlossenen Menge
sei stetig und koerziv auf der (nicht notwendigerweise beschränkten) abgeschlossenen Menge  . Dann ist die Menge
. Dann ist die Menge  für jedes Niveau
für jedes Niveau  kompakt.
kompakt.
Hieraus und aus dem Satz von Weierstraß folgt das zweite Resultat, das insbesondere ein häufig einsetzbares Kriterium zum Nachweis der Lösbarkeit unrestringierter Optimierungsprobleme liefert.
1.2.27 Korollar
Es sei M nichtleer und abgeschlossen, aber nicht notwendigerweise beschränkt. Ferner sei die Funktion  stetig und koerziv auf M. Dann besitzt f auf M (mindestens) einen globalen Minimalpunkt.
stetig und koerziv auf M. Dann besitzt f auf M (mindestens) einen globalen Minimalpunkt.
1.3 Rechenregeln und Umformungen
Dieser Abschnitt führt eine Reihe von Rechenregeln und äquivalenten Umformungen von Optimierungsproblemen auf, die im Rahmen dieses Lehrbuchs von Interesse sind. Die Existenz aller auftretenden Optimalpunkte und -werte wird in diesem Abschnitt ohne weitere Erwähnung vorausgesetzt und muss bei Anwendung der Resultate zunächst zum Beispiel mit den Techniken aus Abschn. 1.2 garantiert werden. Die Übertragung der Resultate zu Optimalwerten auf Fälle von nicht angenommenen Infima und Suprema ist dem Leser als weitere Übung überlassen.
1.3.1 Übung (Skalare Vielfache und Summen)
Gegeben seien  und
und  Dann gilt:
Dann gilt:
- a)
 .
. - b)
 .
. - c)
 .
. - d)
In (c) kann die strikte Ungleichung > auftreten.
1.3.2 Übung (Separable Zielfunktion auf kartesischem Produkt)
 ,
,  ,
,  und
und  . Dann gilt
. Dann gilt
1.3.3 Übung (Vertauschung von Minima und Maxima)
Es seien  ,
,  , M = X × Y und
, M = X × Y und  gegeben. Dann gilt:
gegeben. Dann gilt:
- a)

- b)

- c)

- d)
In (c) kann die strikte Ungleichung > auftreten.
1.3.4 Übung (Monotone Transformation)
 und einer Funktion f : M → Y mit
und einer Funktion f : M → Y mit  sei
sei  eine streng monoton wachsende Funktion. Dann gilt
eine streng monoton wachsende Funktion. Dann gilt
1.3.5 Übung (Epigraphumformulierung)
 und eine Funktion
und eine Funktion  . Dann sind die Probleme
. Dann sind die Probleme

- a)
Für jeden lokalen bzw. globalen Minimalpunkt
 von P ist
von P ist  lokaler bzw. globaler Minimalpunkt von
lokaler bzw. globaler Minimalpunkt von  .
. - b)
Für jeden lokalen bzw. globalen Minimalpunkt
 von
von  ist
ist  lokaler bzw. globaler Minimalpunkt von P.
lokaler bzw. globaler Minimalpunkt von P. - c)
Die Minimalwerte von P und
 stimmen überein.
stimmen überein.
1.3.6 Definition (Parallelprojektion)
 . Dann heißt
. Dann heißt
 .
.1.3.7 Übung (Projektionsumformulierung)
 und eine Funktion
und eine Funktion  , die nicht von den Variablen aus
, die nicht von den Variablen aus  abhängt. Dann sind die Probleme
abhängt. Dann sind die Probleme

- a)
Für jeden lokalen bzw. globalen Minimalpunkt
 von P ist
von P ist  lokaler bzw. globaler Minimalpunkt von
lokaler bzw. globaler Minimalpunkt von  .
. - b)
Für jeden lokalen bzw. globalen Minimalpunkt
 von
von  existiert ein
existiert ein  , so dass
, so dass  lokaler bzw. globaler Minimalpunkt von P ist.
lokaler bzw. globaler Minimalpunkt von P ist. - c)
Die Minimalwerte von P und
 stimmen überein.
stimmen überein.
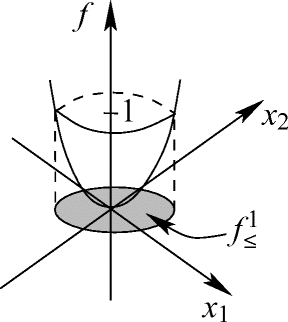
![$f_{\le}^1 = \left[-1,1\right],\ f_{\le}^0 = \left\lbrace 0 \right\rbrace$](../images/439970_1_De_1_Chapter/439970_1_De_1_Chapter_TeX_IEq98.png)













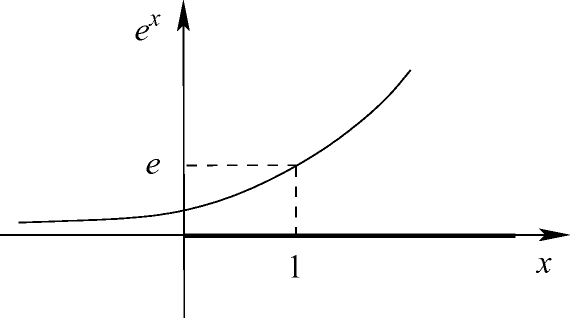

![$$
\textrm{lev}_{\le}^e(f,M)\ =\ \lbrace x \in M \vert\ e^x \leq e \rbrace\ =\ \lbrace x\ge0 \vert\ x \leq 1 \rbrace\ =\ \left[ 0,1 \right]
$$](../images/439970_1_De_1_Chapter/439970_1_De_1_Chapter_TeX_Equao.png)