Unrestringierte Optimierung

Nichtlineare Optimierungsprobleme ohne Restriktionen besitzen die Form

$P:\quad \min\,f(x)$

mit einer Funktion $f:\mathbb R^n\to\mathbb R$ . Das Problem P wird auch unrestringiertes Optimierungsproblem genannt. Allgemeiner werden manchmal auch Probleme mit offener zulässiger Menge M als unrestringiert bezeichnet. In der Tat lassen sich die im folgenden Abschn. 2.1 besprochenen Optimalitätsbedingungen ohne Weiteres auf diesen Fall übertragen, was wir aus Gründen der Übersichtlichkeit aber nicht explizit angeben werden. Abschn. 2.2 diskutiert ausführlich verschiedene numerische Lösungsverfahren für unrestringierte Optimierungsprobleme, die auf den zuvor hergeleiteten Optimalitätsbedingungen basieren.

2.1 Optimalitätsbedingungen

Zur Herleitung von ableitungsbasierten notwendigen bzw. hinreichenden Optimalitätsbedingungen führen wir in Abschn. 2.1.1 zunächst das ableitungsfreie Konzept der sogenannten Abstiegsrichtung für eine Funktion f an einer Stelle $\bar x\in\mathbb R^n$ ein. Für jede differenzierbare Funktion f lässt sich mit Hilfe der (mehrdimensionalen) ersten Ableitung von f an $\bar x$ eine hinreichende Bedingung dafür angeben, dass eine Richtung Abstiegsrichtung für f an $\bar x$ ist, woraus wir in Abschn. 2.1.2 als zentrale notwendige Optimalitätsbedingung die Fermat’sche Regel herleiten werden.

Die dafür erforderliche Definition der mehrdimensionalen ersten Ableitung führt auf den Begriff des Gradienten der Funktion f an $\bar x$ , der selbst ein Vektor der Länge n ist. Die in Abschn. 2.1.3 diskutierten geometrischen Eigenschaften solcher Gradienten sind grundlegend für das Verständnis sowohl der Optimalitätsbedingungen als auch der numerischen Verfahren in Abschn. 2.2.

Sofern f zweimal differenzierbar ist, lässt sich die obige hinreichende Bedingung für die Abstiegseigenschaft einer Richtung durch Informationen über die zweite Ableitung von f an $\bar x$ verfeinern, was eine stärkere notwendige Optimalitätsbedingung als die Fermat’sche Regel liefert, nämlich die in Abschn. 2.1.4 besprochene notwendige Optimalitätsbedingung zweiter Ordnung. Durch eine einfache Modifikation wird sich aus dieser Bedingung auch eine hinreichende Optimalitätsbedingung konstruieren lassen. Allerdings wird zwischen der notwendigen und der hinreichenden Optimalitätsbedingung zweiter Ordnung eine „Lücke“ klaffen. Wir diskutieren kurz, warum dies keine gravierenden Konsequenzen hat. Der abschließende Abschn. 2.1.5 reißt kurz an, wie die Optimalitätsbedingungen sich vereinfachen, wenn die Zielfunktion f zusätzlich konvex auf $\mathbb R^n$ ist.

2.1.1 Abstiegsrichtungen

Um zu klären, welche notwendigen Bedingungen die Funktion f an einem Minimalpunkt erfüllen muss, geht man nach folgendem Ausschlussprinzip vor: Wenn man den Punkt $\bar x\in\mathbb R^n$ entlang einer Richtung $d\in\mathbb R^n$ verlassen kann, während die Funktionswerte (zumindest zunächst) fallen, dann kommt $\bar x$ offensichtlich nicht als Minimalpunkt infrage. Die Punkte, die man beim Verlassen von $\bar x$ entlang d besucht, lassen sich per Punktrichtungsform einer Geraden explizit als $\bar x + td$ mit Skalaren t ≥ 0 adressieren.

2.1.1 Definition (Abstiegsrichtung)

Es seien $f:\mathbb R^n\to\mathbb R$ und $\bar x\in\mathbb R^n$ . Ein Vektor $d\in\mathbb R^n$ heißt Abstiegsrichtung für f in $\bar x$ , falls

$\exists\ \check{\kern-1pt t} >0\quad \forall\ t\in(0,\check{\kern-1pt t}):\quad f(\bar x + td)\ <\ f(\bar x)$

gilt.

2.1.2 Übung

Für $f:\mathbb R^n\to\mathbb R$ sei $\bar x$ ein lokaler Minimalpunkt. Zeigen Sie, dass dann keine Abstiegsrichtung für f in $\bar x$ existiert.

Im Folgenden werden wir die nur von der eindimensionalen Variable t abhängige Funktion $f(\bar x + td)$ genauer untersuchen und geben ihr dazu eine eigene Bezeichnung.

2.1.3 Definition (Eindimensionale Einschränkung)

Gegeben seien $f:\mathbb R^n\to\mathbb R$ , ein Punkt $\bar x\in\mathbb R^n$ und ein Richtungsvektor $d\in\mathbb R^n$ . Die Funktion

$\upvarphi_d:\ \mathbb R^1\to\mathbb R^1,\quad t\mapsto f(\bar x + td)$

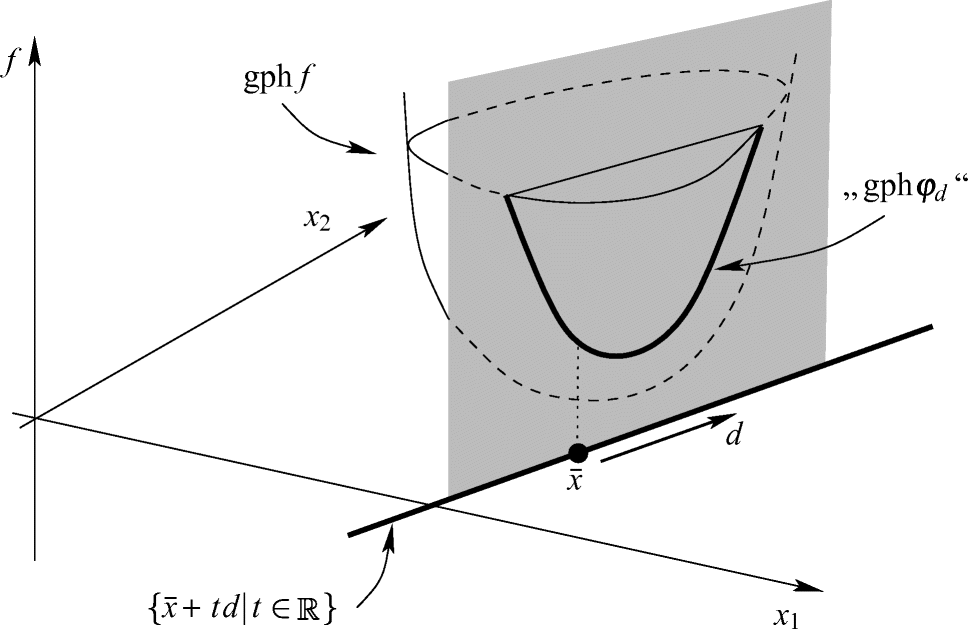
heißt eindimensionale Einschränkung von f auf die durch $\bar x$ in Richtung d verlaufende Gerade.

Abb. 2.1 veranschaulicht, wie man sich die Entstehung des Graphen der Funktion φ_d aus dem der Funktion f für n = 2 geometrisch vorstellen kann: Der Punkt $\bar x$ und die Richtung d definieren die Gerade $\{\bar x + td|\ t\in\mathbb R\}$ im zweidimensionalen Raum der Argumente, und φ_d beschreibt die Auswertung der Funktion f genau auf den Punkten dieser Geraden. Den Graphen gph φ_d von φ_d erhält man geometrisch also, indem man über der Geraden eine „senkrechte Ebene“ errichtet und diese mit dem Graphen gphf von f schneidet. Tatsächlich ist gph φ_d aber natürlich keine Teilmenge des $\mathbb R^3$ , wie es in Abb. 2.1 dargestellt ist, sondern Teilmenge des zweidimensionalen Raums, der mit der konstruierten „senkrechten Ebene“ übereinstimmt.

../images/439970_1_De_2_Chapter/439970_1_De_2_Fig1_HTML.png — Abb. 2.1
Eindimensionale Einschränkung

Offensichtlich gilt $\upvarphi_d(0)=f(\bar x)$ für jede Richtung $d\in\mathbb R^n$ . Daher ist d genau dann Abstiegsrichtung für f in $\bar x$ , wenn

$\exists\ \check{\kern-1pt t}>0\quad \forall\ t\in(0,\check{\kern-1pt t}):\quad \upvarphi_d(t)\ <\ \upvarphi_d(0)$

gilt.

2.1.2 Optimalitätsbedingung erster Ordnung

Im Folgenden werden wir eine Bedingung herleiten, die an jedem lokalen Minimalpunkt von f notwendigerweise erfüllt sein muss. Da sie Informationen aus ersten Ableitungen von f benutzt, spricht man von einer notwendigen Optimalitätsbedingung erster Ordnung. Um später (in Satz 3.3.21) eine Anwendung der folgenden Grundüberlegungen auch auf gewisse nichtglatte Probleme zuzulassen, führen wir sie unter einer sehr schwachen Voraussetzung an die Funktion f ein, nämlich ihrer einseitigen Richtungsdifferenzierbarkeit.

Zur Motivation dieses Konzepts betrachten wir zunächst den Fall, in dem f differenzierbar an einem betrachteten Punkt $\bar x\in\mathbb R^n$ ist. Als Verknüpfung von f mit der affin-linearen Funktion $\bar x + td$ ist dann auch die eindimensionale Einschränkung φ_d an $\bar t=0$ differenzierbar. Ihre Ableitung $\upvarphi_d'(0)$ gibt an, mit welcher Steigung die Funktionswerte von f sich ändern, wenn man $\bar x$ in Richtung d verlässt. Diese Ableitung

$\upvarphi_d'(0)\ =\ \lim_{t\to 0}\,\frac{f(\bar x + td)-f(\bar x)}t$

heißt Richtungsableitung von f an $\bar x$ in Richtung d.

Es erscheint plausibel, dass im Fall $\upvarphi_d'(0)<0$ die Funktionswerte von φ_d bei wachsendem t zunächst fallen, dass ein solches d also eine Abstiegsrichtung ist. Da negative Werte von t für dieses Argument aber gar keine Rolle spielen, benötigt man tatsächlich nicht die Richtungsableitung von f, sondern nur das folgende Konzept.

2.1.4 Definition (Einseitige Richtungsableitung)

Eine Funktion $f:\mathbb R^n\to\mathbb R$ heißt an $\bar x\in\mathbb R^n$ in eine Richtung $d\in\mathbb R^n$ einseitig richtungsdifferenzierbar , wenn der Grenzwert

$f'(\bar x,d)\ :=\ \lim_{t\searrow 0}\,\frac{f(\bar x + td)-f(\bar x)}t$

existiert. Der Wert $f'(\bar x,d)$ heißt dann einseitige Richtungsableitung . Die Funktion f heißt an $\bar x$ einseitig richtungsdifferenzierbar , wenn f an $\bar x$ in jede Richtung $d\in\mathbb R^n$ einseitig richtungsdifferenzierbar ist, und f heißt einseitig richtungsdifferenzierbar, wenn f an jedem $\bar x\in\mathbb R^n$ einseitig richtungsdifferenzierbar ist.

Die obigen Schreibweisen für die auftretenden Limiten bedeuten expliziter das Folgende: Richtungsdifferenzierbarkeit von f an $\bar x$ in Richtung d besagt, dass für alle Folgen $(t^k)\subseteq\mathbb R\setminus\{0\}$ mit $\lim_k t^k=0$ der Grenzwert

$\lim_k\,\frac{f(\bar x + t^k d)-f(\bar x)}{t^k}$

existiert und identisch ist. Diesen Grenzwert nennen wir $\upvarphi_d'(0)$ . Hingegen bedeutet die einseitige Richtungsdifferenzierbarkeit von f an $\bar x$ in Richtung d, dass nur für alle Folgen $(t^k)\subseteq\{t\in\mathbb R|\,t>0\}$ mit $\lim_k t^k=0$ der Grenzwert

$\lim_k\,\frac{f(\bar x + t^k d)-f(\bar x)}{t^k}$

zu existieren und identisch zu sein braucht. Diesen Grenzwert bezeichnen wir mit $f'(\bar x,d)$ .

Offensichtlich ist jede an $\bar x$ in Richtung d richtungsdifferenzierbare Funktion f an $\bar x$ in Richtung d auch einseitig richtungsdifferenzierbar mit $f'(\bar x,d)=\upvarphi_d'(0)$ . Damit ist insbesondere jede an $\bar x$ differenzierbare Funktion f dort auch einseitig richtungsdifferenzierbar. Allerdings umfasst die Klasse der einseitig richtungsdifferenzierbaren Funktionen auch sehr viele nichtdifferenzierbare Funktionen, etwa alle auf $\mathbb R^n$ konvexen Funktionen (Abschn. 2.1.5 und [34]) sowie Maxima endlich vieler glatter Funktionen (Übung 2.1.12). Als einfaches Beispiel ist $f(x)=|x|$ an $\bar x=0$ weder differenzierbar noch richtungsdifferenzierbar, aber einseitig richtungsdifferenzierbar.

2.1.5 Lemma

Die Funktion { $f:\mathbb R^n\to\mathbb R$ sei an $\bar x\in\mathbb R^n$ in Richtung $d\in\mathbb R^n$ einseitig richtungsdifferenzierbar mit $f'(\bar x,d)<0$ . Dann ist d Abstiegsrichtung für f in $\bar x$ .

Beweis.

Angenommen, d sei keine Abstiegsrichtung für f in $\bar x$ . Dann existiert kein $\check{\kern-1pt t}>0$ , so dass für alle $t\in(0,\check t)$ die Ungleichung $f(\bar x + td)< f(\bar x)$ erfüllt ist. Insbesondere erfüllt für jedes $k\in\mathbb N$ mindestens ein t^k ∈ (0, 1/k) die Ungleichung $f(\bar x + t^k d)\ge f(\bar x)$ . Für jedes $k\in\mathbb N$ gilt dann wegen t^k > 0 auch

$\frac{f(\bar x + t^k d)-f(\bar x)}{t^k}\ \ge\ 0,$

und die einseitige Richtungsdifferenzierbarkeit von f an $\bar x$ in Richtung d liefert

$f'(\bar x,d)\ =\ \lim_k\,\frac{f(\bar x + t^k d)-f(\bar x)}{t^k}\ \ge\ 0.$

Dies steht jedoch im Widerspruch zur Voraussetzung $f'(\bar x,d)<0$ . Demnach ist die Annahme falsch und die Behauptung bewiesen.

Aus Übung 2.1.2 und Lemma 2.1.5 folgt sofort das nächste Resultat.

2.1.6 Lemma

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei an einem lokalen Minimalpunkt $\bar x\in\mathbb R^n$ einseitig richtungsdifferenzierbar. Dann gilt $f'(\bar x,d)\ge0$ für jede Richtung $d\in\mathbb R^n$ .

Lemma 2.1.5 und 2.1.6 motivieren die folgende Definitionen.

2.1.7 Definition (Abstiegsrichtung erster Ordnung)

Für eine am Punkt $\bar x\in\mathbb R^n$ in Richtung $d\in\mathbb R^n$ einseitig richtungsdifferenzierbare Funktion $f:\mathbb R^n\to\mathbb R$ heißt d Abstiegsrichtung erster Ordnung , falls $f'(\bar x,d)<0$ gilt.

2.1.8 Definition (Stationärer Punkt – unrestringierter Fall)

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei an $\bar x\in\mathbb R^n$ einseitig richtungsdifferenzierbar. Dann heißt $\bar x$ stationärer Punkt von f, falls $f'(\bar x,d)\ge0$ für jede Richtung $d\in\mathbb R^n$ gilt.

In dieser Terminologie besagt Lemma 2.1.5, dass jede Abstiegsrichtung erster Ordnung tatsächlich eine Abstiegsrichtung im Sinne von Definition 2.1.1 ist. Die Definition der Stationarität eines Punkts aus Definition 2.1.8 lautet gerade, dass an ihm keine Abstiegsrichtung erster Ordnung existieren darf, und Lemma 2.1.6 sagt aus, dass jeder lokale Minimalpunkt einer dort einseitig richtungsdifferenzierbaren Funktion auch stationär ist.

Um Lemma 2.1.6 algorithmisch ausnutzen zu können, benötigen wir eine einfache Formel für $f'(\bar x,d)$ und kehren daher wieder zu einer in $\bar x$ differenzierbaren Funktion f zurück. Wir betrachten als Richtungsvektor zunächst speziell den i-ten Einheitsvektor d = e_i (setzen also d_i = 1 und d_j = 0 für alle j ≠ i). Dann ist $f'(\bar x,e_i)$ die partielle Ableitung von f bezüglich der Variable x_i , die man alternativ auch mit $\partial_{x_i}\ f(\bar x)$ bezeichnet. Als erste Ableitung einer partiell differenzierbaren Funktion $f:\mathbb R^n\to\mathbb R$ an $\bar x$ betrachtet man den Zeilenvektor

$Df(\bar x)\ :=\ (\,\partial_{x_1}\,f(\bar x),\,\ldots\,,\partial_{x_n}\,f(\bar x)\,)$

oder auch sein Transponiertes $\nabla f(\bar x):=(Df(\bar x))^\intercal$ . Der Spaltenvektor $\nabla f(\bar x)$ wird als Gradient von f an $\bar x$ bezeichnet. Im Hinblick auf spätere Konstruktionen halten wir fest, dass der Gradient $\nabla f(\bar x)$ zwar einerseits nur eine Liste von partiellen Ableitungsinformationen ist, andererseits aber genau wie $\bar x$ als ein n-dimensionaler Vektor interpretiert werden darf.

Für eine vektorwertige Funktion $f:\mathbb R^n\to\mathbb R^m$ mit partiell differenzierbaren Komponenten $f_1,\,\ldots\,,f_m$ definiert man die erste Ableitung als

$Df(\bar x)\ :=\ \begin{pmatrix}Df_1(\bar x)\\\vdots\\Df_m(\bar x)\end{pmatrix}.$

Diese (m, n)-Matrix heißt Jacobi-Matrix oder Funktionalmatrix von f an $\bar x$ . Gelegentlich werden wir auch für vektorwertige Funktionen f die Notation $\nabla f(\bar x):=(Df(\bar x))^\intercal$ benutzen.

Eine wichtige Rechenregel für differenzierbare Funktionen ist die Kettenregel, deren Beweis man z. B. in [18] findet.

2.1.9 Satz (Kettenregel)

Es seien $g:\mathbb R^n\to\mathbb R^m$ differenzierbar an $\bar x\in\mathbb R^n$ und $f:\mathbb R^m\to\mathbb R^k$ differenzierbar an $g(\bar x)\in\mathbb R^m$ . Dann ist $f\circ g:\mathbb R^n\to\mathbb R^k$ differenzierbar an $\bar x$ mit

$D(\ f\circ g)(\bar x)\ =\ Df(g(\bar x))\cdot Dg(\bar x).$

Ein wesentlicher Grund dafür, die Jacobi-Matrix einer Funktion wie oben zu definieren, besteht darin, dass die Kettenregel dann völlig analog zum eindimensionalen Fall ( $n=m=k=1$ ) formuliert werden kann, obwohl das auftretende Produkt ein Matrixprodukt ist.

Bei der Anwendung der Kettenregel auf die Funktion $\upvarphi_d(t)=f(\bar x + td)$ gilt k = m = 1 und $g(t)=\bar x + td$ . Als Jacobi-Matrix von g erhält man

$Dg(t)\ =\ d$

und damit

$\upvarphi_d'(0)\ =\ Df(\bar x)\,d.$

Das Matrixprodukt aus der Kettenregel wird in diesem speziellen Fall also zum Produkt des Zeilenvektors $Df(\bar x)$ mit dem Spaltenvektor d.

Für zwei allgemeine (Spalten-)Vektoren $a,b\in\mathbb R^n$ nennt man den so definierten Term

$a^\intercal b\ =\ \sum_{i\,=\,1}^n\,a_i\,b_i$

auch (Standard-)Skalarprodukt von a und b. Eine alternative Schreibweise dafür ist

$\langle a,b\rangle\ :=\ a^\intercal b.$

Wir erhalten also

$\upvarphi_d'(0)\ =\ \langle\nabla f(\bar x),d\rangle$

und können damit zunächst Lemma 2.1.5 umformulieren.

2.1.10 Lemma

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei am Punkt $\bar x\in\mathbb R^n$ differenzierbar, und für die Richtung $d\in\mathbb R^n$ gelte $\langle\nabla f(\bar x),d\rangle<0$ . Dann ist d Abstiegsrichtung für f in $\bar x$ .

Für eine an $\bar x$ differenzierbare Funktion f ist d offensichtlich genau dann Abstiegsrichtung erster Ordnung im Sinne von Definition 2.1.7, wenn $\langle\nabla f(\bar x),d\rangle<0$ gilt.

2.1.11 Bemerkung

Nachfolgend wird wichtig sein, wie die Bedingung $\langle\nabla f(\bar x),d\rangle<0$ geometrisch zu interpretieren ist. Für zwei Vektoren $a,b\in\mathbb R^n$ besitzt das Skalarprodukt $\langle a,b\rangle$ neben der algebraischen Definition zu $a^\intercal b$ nämlich auch die Darstellung

$\langle a,b\rangle\ =\ \|a\|_2\cdot\|b\|_2\cdot\cos(\,\angle(a,b)\,)$

(2.1)

(z. B. [8]). Dabei bezeichnet $\angle(a,b)$ den Winkel zwischen den beiden Vektoren a und b. Dieser lässt sich für n-dimensionale Vektoren a und b definieren, indem man ihn in der Ebene misst, die von a und b aufgespannt wird (also in der Menge ${\{\lambda a + \mu b|\, \lambda,\mu\in\mathbb R\}}$ ). Im Ausnahmefall, in dem die Vektoren a und b linear abhängig sind, spannen sie zwar keine Ebene auf, aber der Winkel zwischen a und b kann dann nur null (falls sie in die gleiche Richtung zeigen) oder π (falls sie in entgegengesetzte Richtungen zeigen) betragen. In diesen Fällen gilt $\cos(\,\angle(a,b)\,)= + 1$ bzw. $\cos(\,\angle(a,b)\,)=-1$ .

Aus der Darstellung (2.1) erhalten wir die Bedingung $\langle a,b\rangle<0$ also genau dann, wenn $\cos (\,\angle(a,b)\,)<0$ gilt, d. h. genau für $\angle(a,b)\in(\pi,2\pi)$ . Mit anderen Worten ist das Skalarprodukt der Vektoren a und b genau dann negativ, wenn sie einen stumpfen Winkel miteinander bilden. Analog ist das Skalarprodukt genau für einen spitzen Winkel bildende Vektoren positiv sowie genau für senkrecht zueinander stehende Vektoren null.

Insbesondere ist d genau dann eine Abstiegsrichtung erster Ordnung für f in $\bar x$ , wenn d einen stumpfen Winkel mit dem Gradienten $\nabla f(\bar x)$ bildet. Wir werden später sehen, dass unter gewissen Zusatzvoraussetzungen auch Richtungen d Abstiegsrichtungen sein können, die senkrecht zum Vektor $\nabla f(\bar x)$ stehen.

Auch für nur einseitig richtungsdifferenzierbare Funktionen lassen sich manchmal einfache Formeln für die einseitige Richtungsableitung angeben.

2.1.12 Übung

Gegeben seien $\bar x\in\mathbb R^n$ , eine endliche Indexmenge K und an $\bar x$ differenzierbare Funktionen $f_k:\mathbb R^n\to\mathbb R$ , k ∈ K. Zeigen Sie, dass dann die Funktion $f(x):=\max_{k\in K}\,f_k(x)$ an $\bar x$ einseitig richtungsdifferenzierbar ist und dass mit $K_\star(\bar x)=\{k\in K|\,f_k(\bar x)=f(\bar x)\}$

$f'(\bar x,d)\ =\ \max_{k\in K_\star(\bar x)}\langle \nabla f_k(\bar x),d\rangle$

für jede Richtung $d\in\mathbb R^n$ gilt.

Wir können nun die zentrale Optimalitätsbedingung für unrestringierte glatte Optimierungsprobleme beweisen.

2.1.13 Satz (Notwendige Optimalitätsbedingung erster Ordnung – Fermat’sche Regel)

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei differenzierbar an einem lokalen Minimalpunkt $\bar x\in\mathbb R^n$ . Dann gilt $\nabla f(\bar x)=0$ .

Beweis.

Nach Lemma 2.1.6 ist $\bar x$ ein stationärer Punkt von f. Aufgrund der Darstellung der Richtungsableitung per Kettenregel gilt für jede Richtung $d\in\mathbb R^n$ also

$0\ \le\ \upvarphi_d'(0)\ =\ \langle\nabla f(\bar x),d\rangle.$

Insbesondere gilt dies auch für die Wahl des Vektors $d=-\nabla f(\bar x)$ , also

$0\ \le\ \langle\nabla f(\bar x),-\nabla f(\bar x)\rangle\ =\ -\|\nabla f(\bar x)\|_2^2\ \le\ 0.$

Es folgt $\|\nabla f(\bar x)\|_2=0$ und (wegen der Definitheit der Norm) $\nabla f(\bar x)=0$ .

Die Fermat’sche Regel wird als Optimalitätsbedingung erster Ordnung bezeichnet, da sie von ersten Ableitungen der Funktion f Gebrauch macht. Sie motiviert die folgende Definition.

2.1.14 Definition (Kritischer Punkt)

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei an $\bar x\in\mathbb R^n$ differenzierbar. Dann heißt $\bar x$ kritischer Punkt von f, wenn $\nabla f(\bar x)=0$ gilt.

In dieser Terminologie ist nach der Fermat’schen Regel jeder lokale Minimalpunkt einer differenzierbaren Funktion notwendigerweise kritischer Punkt.

2.1.15 Übung

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei differenzierbar an einem Punkt $\bar x\in\mathbb R^n$ . Zeigen Sie, dass $\bar x$ genau dann stationärer Punkt von f ist, wenn er kritischer Punkt von f ist.

Übung 2.1.15 begründet, weshalb in der Literatur zur glatten unrestringierten Optimierung die Begriffe des stationären und des kritischen Punkts synonym gebraucht werden. Für nichtglatte oder restringierte glatte Probleme ist der Zusammenhang zwischen der durch das Fehlen einer Abstiegsrichtung erster Ordnung definierten Stationarität und einer algebraischen Optimalitätsbedingung (analog zur Kritikalität $\nabla f(\bar x)=0$ ) allerdings weniger übersichtlich ([34] und Kap. 3). Die Begriffe der Stationarität und der Kritikalität werden in der Literatur aber nicht einheitlich gebraucht.

2.1.16 Beispiel

Für den (globalen) Minimalpunkt $\bar x=0$ von $f_1(x)=x_1^2 + x_2^2$

rechnet man sofort $\nabla f_1(\bar x)=0$ nach. Für die beiden Funktionen $f_2(x)=-x_1^2-x_2^2$

und

ist $\bar x=0$ allerdings ebenfalls kritischer Punkt, obwohl $\bar x$ kein lokaler Minimalpunkt ist. In der Tat liefert beispielsweise die Richtung $d=(0,1)^\intercal$ für die eindimensionale Einschränkung beider Funktionen

$\upvarphi_d(t)\ =\ f_i(\bar x + td)\ =\ f_i(0,t)\ =\ -t^2, \qquad i=2,3,$

so dass man $\bar x=0$ in diese Richtung verlassen kann, während die Funktionswerte fallen (damit ist d zwar Abstiegsrichtung, aber nicht Abstiegsrichtung erster Ordnung). Für f₂ ist dies sogar in jeder beliebigen Richtung der Fall, da f₂ an $\bar x=0$ offensichtlich einen Maximalpunkt besitzt. Bei f₃ wachsen hingegen in Richtung $d=(1,0)^\intercal$ die Funktionswerte an. In diesem Fall spricht man von einem Sattelpunkt von f₃.

2.1.17 Definition (Sattelpunkt)

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei an $\bar x\in\mathbb R^n$ differenzierbar. Dann heißt $\bar x$ Sattelpunkt von f, falls $\bar x$ zwar kritischer Punkt von f, aber weder lokaler Minimal- noch lokaler Maximalpunkt ist.

Beispiel 2.1.16 illustriert, dass die Fermat’sche Regel nur eine notwendige Optima- litätsbedingung ist. Sie besagt zwar, dass ein lokaler Minimalpunkt von f notwendigerweise kritischer Punkt ist, aber die Eigenschaft, ein kritischer Punkt zu sein, ist nicht hinreichend für Minimalität.

Damit ist klar, dass kritische Punkte lediglich Kandidaten für Minimalpunkte von f sind, aber auch beispielsweise Maximal- oder Sattelpunkten entsprechen können. Algorithmus 2.1 beschreibt ein auf dieser Beobachtung basierendes konzeptionelles Verfahren zur Minimierung mit Hilfe kritischer Punkte. Es nutzt die notwendige Optimalitätsbedingung, um unter allen zulässigen Punkten (also allen Punkten in $\mathbb R^n$ ) diejenigen „auszusieben“, die nicht als Kandidaten für Minimalpunkte infrage kommen. „Nur“ unter den restlichen Punkten muss dann noch ein Minimalpunkt gesucht werden.

Hier und im Folgenden nennen wir ein Optimierungsproblem P differenzierbar, wenn es durch differenzierbare Funktionen beschrieben wird. Im vorliegenden unrestringierten Fall betrifft dies natürlich nur die Differenzierbarkeit der Zielfunktion f.

Algorithmus 2.1: Konzeptioneller Algorithmus zur unrestringierten nichtlinearen Minimierung mit Informationen erster Ordnung

Input : Lösbares unrestringiertes differenzierbares Optimierungsproblem P

Output : Globaler Minimalpunkt $x^\star$ von f über $\mathbb R^n$

1 begin

2 Bestimme alle kritischen Punkte von f, d. h. die Lösungsmenge K der Gleichung $\nabla f(x)=0$ .

3 Bestimme einen Minimalpunkt $x^\star$ von f in K.

4 end

Algorithmus 2.1 besitzt drei Nachteile, die seine Anwendung auf praktische Probleme behindern. Zunächst muss die Lösbarkeit des Problems P a priori bekannt sein, etwa durch Anwendung der Kriterien aus Abschn. 1.2. Beispielsweise besitzt die Funktion $f(x)=x^3/3-x$ genau die beiden kritischen Punkte x¹ = −1 und x² = 1, wobei x² den kleineren Funktionswert besitzt und damit den Output von Algorithmus 2.1 bildet. Allerdings ist f auf $\mathbb R$ nicht nach unten beschränkt und besitzt damit keinen globalen Minimalpunkt. Diese Unlösbarkeit kann von Algorithmus 2.1 nicht identifiziert werden.

Der zweite Nachteil von Algorithmus 2.1 besteht darin, dass er alle kritischen Punkte bestimmen muss. Bei einer nichtlinearen Kritische-Punkt-Gleichung ∇f(x) = 0 ist aber selten klar, wie alle Lösungen bestimmt werden können. Falls kritische Punkte übersehen werden, besteht die Gefahr, dass der Output von Algorithmus 2.1 kein globaler Minimalpunkt ist.

Als dritter Nachteil ist anzuführen, dass bei komplizierten Funktionen f schon die Berechnung eines einzigen kritischen Punkts sehr aufwendig sein kann.

Algorithmus 2.1 lässt sich demnach immerhin auf lösbare Optimierungsprobleme anwenden, deren kritische Punkte etwa durch Fallunterscheidung komplett und außerdem explizit berechenbar sind. Dies trifft leider oft nur auf niedrigdimensionale Probleme mit „übersichtlicher“ Zielfunktion zu.

2.1.18 Übung

Betrachten Sie noch einmal das Datenapproximationsproblem aus Beispiel 1.1.4 mit der euklidischen Norm, also das auch als Problem der linearen Regression bekannte unrestringierte Optimierungsproblem

$\min_{a,b}\ \left\|\begin{pmatrix}ax_1 + b-y_1\\\vdots\\ax_m + b-y_m\end{pmatrix}\right\|_2$

für gegebene Datenpunkte $(x_j,y_j)\in\mathbb R^2$ , 1 ≤ j ≤ m. Warum ist nicht garantiert, dass sich die Fermat’sche Regel auf jeden lokalen Minimalpunkt dieses Problems anwenden lässt?

Berechnen Sie alle kritischen Punkte des nach Übung 1.3.4 äquivalenten und auch als Kleinste-Quadrate-Problem bekannten Optimierungsproblems

$\min_{a,b}\ \left\|\begin{pmatrix}ax_1 + b-y_1\\\vdots\\ax_m + b-y_m\end{pmatrix}\right\|_2^2$

unter der Voraussetzung, dass mindestens zwei der Stützstellen x_j, 1 ≤ j ≤ m, voneinander verschieden sind.

2.1.3 Geometrische Eigenschaften von Gradienten

Um die geometrische Interpretation des Gradienten $\nabla f(\bar x)$ vollständig zu verstehen, bringen wir ihn mit der unteren Niveaumenge

$f^{f(\bar x)}_\le\ =\ \{x\in\mathbb R^n|\ f(x)\le f(\bar x)\}$

in Verbindung. Sie ist für Minimierungsverfahren von grundlegender Bedeutung, da einerseits offensichtlich $\bar x\in f^{f(\bar x)}_\le$ gilt und im Vergleich zu $\bar x$ „bessere“ Punkte x gerade solche sind, die die strikte Ungleichung $f(x)< f(\bar x)$ erfüllen. Eine Abstiegsrichtung d für f in $\bar x$ sollte also in das „Innere“ von $f^{f(\bar x)}_\le$ zeigen. Abb. 2.2 illustriert, wie eine solche Menge für eine nichtlineare Funktion f aussehen kann, wobei zwei verschiedene Punkte x¹ und x² so gewählt sind, dass $f^{f(x^1)}_\le=f^{f(x^2)}_\le$ gilt.

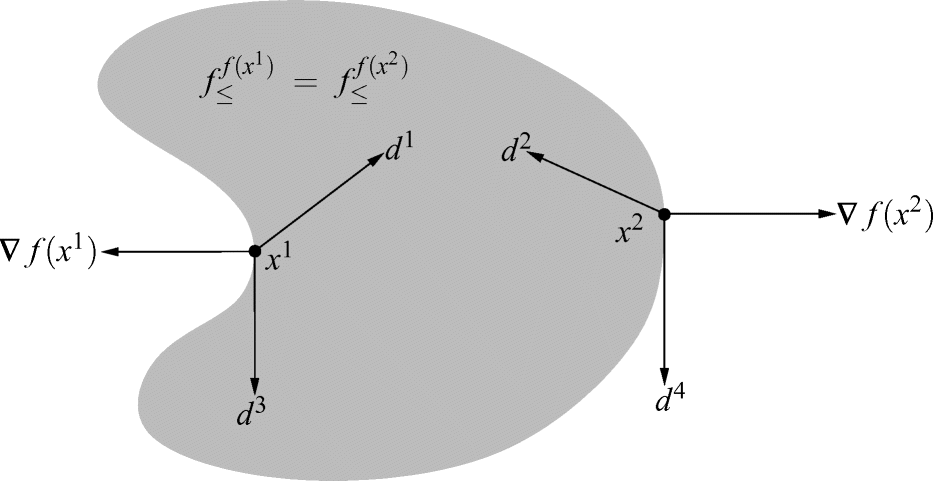
../images/439970_1_De_2_Chapter/439970_1_De_2_Fig2_HTML.png — Abb. 2.2
Gradienten und Abstiegsrichtungen

Völlig analog zu Lemma 2.1.10 und Definition 2.1.7 kann man zeigen, dass jeder Vektor $d\in\mathbb R^n$ mit $\langle\nabla f(\bar x),d\rangle > 0$ eine Anstiegsrichtung erster Ordnung ist. Da für einen nichtkritischen Punkt $\bar x$ die Gradientenrichtung $d=\nabla f(\bar x)$ die strikte Ungleichung

$\langle\nabla f(\bar x),\nabla f(\bar x)\rangle\ =\ \|\nabla f(\bar x)\|_2^2\ >\ 0$

erfüllt, ist $d=\nabla f(\bar x)$ also eine Anstiegsrichtung erster Ordnung für f in $\bar x$ und zeigt damit sicherlich aus $f^{f(\bar x)}_\le$ heraus.

In der Tat lässt sich sogar zeigen, dass $\nabla f(\bar x)$ senkrecht auf dem Rand von $f^{f(\bar x)}_\le$ steht. Um dies korrekt zu begründen, muss man einen Tangentialkegel an die Menge $f^{f(\bar x)}_\le$ im Punkt $\bar x$ definieren, was wir auf Abschn. 3.1.2 verschieben, in dem Tangentialkegel an allgemeine Mengen eingeführt werden (Übung 3.2.9).

Plausibel ist zumindest, dass der Tangentialkegel, also die um $\bar x$ linearisierte Menge $f^{f(\bar x)}_\le$ , etwas mit der Linearisierung der Ungleichung zu tun hat, durch die die Menge definiert ist. In der Tat liegt für t > 0 und eine Richtung $d\in\mathbb R^n$ der Punkt $\bar x + td$ in $f^{f(\bar x)}_\le$ , falls $f(\bar x + td)\le f(\bar x)$ gilt. Mit der eindimensionalen Einschränkung lässt sich dies auch als $\upvarphi_d(t)\le\upvarphi_d(0)$ schreiben. Eine Linearisierung dieser Ungleichung um $\bar t=0$ , also die Taylor-Entwicklung erster Ordnung (s. auch Satz 2.1.19a) mit unterschlagenem Restglied, führt auf

$\upvarphi_d(0) + \upvarphi_d'(0)\,t\ \le\ \upvarphi_d(0),$

woraus für jedes t > 0 die Bedingung $\langle\nabla f(\bar x),d\rangle=\upvarphi_d'(0)\le0$ folgt. Mit den Ergebnissen aus Abschn. 3.2.2 werden wir in Übung 3.2.9 tatsächlich zeigen können, dass an einem nichtkritischen Punkt $\bar x$ der Tangentialkegel an die Menge $f^{f(\bar x)}_\le$ im Punkt $\bar x$ durch

$\{d\in\mathbb R^n|\ \langle\nabla f(\bar x),d\rangle\le0\}$

gegeben ist. Jede Richtung d aus dem Rand des Tangentialkegels erfüllt daher ${\langle\nabla f(\bar x),d\rangle=0}$ , steht also senkrecht auf dem Gradienten $\nabla f(\bar x)$ . Folglich zeigt $\nabla f(\bar x)$ nicht nur aus $f^{f(\bar x)}_\le$ heraus, sondern steht auch senkrecht zum Rand dieser Menge (bzw. ihres Tangentialkegels).

Abb. 2.2 illustriert dies für die Punkte x¹ und x². Da d¹ und d² stumpfe Winkel mit ∇f(x¹) bzw. ∇f(x²) bilden, sind sie Abstiegsrichtungen erster Ordnung für f in x¹ bzw. x². Offensichtlich gerät man entlang dieser Richtungen auch (zunächst) ins Innere der Menge $f^{f(x^1)}_\le=f^{f(x^2)}_\le$ . Der Vektor d³ steht senkrecht auf ∇f(x¹), ist also keine Abstiegsrichtung erster Ordnung. Dass er dennoch als Abstiegsrichtung fungiert, ist der „nichtkonvexen Krümmung“ des Rands dieser Menge um x¹ zu verdanken. Andererseits steht der Vektor d⁴ zwar ebenfalls senkrecht auf ∇f(x²), kommt als Abstiegsrichtung aber offensichtlich nicht infrage. Mit diesen beiden Effekten werden wir uns in Abschn. 2.1.4 genauer befassen.

Während wir bislang nur das Vorzeichen der Richtungsableitung $\upvarphi_d'(0)=f'(\bar x,d)=\langle\nabla f(\bar x),d\rangle$ betrachtet haben, untersuchen wir abschließend noch, wie man den tatsächlichen An- oder Abstieg der Funktionswerte von $\bar x$ aus in Richtung d quantifizieren kann. Das Problem hierbei ist, dass zu jedem Vektor d ≠ 0 auch etwa der Vektor 2d in dieselbe Richtung zeigt, sich beim Austausch von d gegen 2d aber der Wert der Richtungsableitung verdoppelt. Um einen eindeutigen Wert der Richtungsableitung zu erhalten, liegt es nahe, nur solche Richtungen d zu betrachten, die die Länge eins besitzen, also $\|d\|_2=1$ erfüllen. Dies entspricht der natürlichen Forderung, dass ein Schritt der Länge t von $\bar x$ in Richtung d zu einem Punkt $\bar x + td$ führt, der tatsächlich den Abstand t von $\bar x$ besitzt (denn mit $\|d\|_2=1$ gilt $\|(\bar x + td)-\bar x\|_2=t\|d\|_2=t$ ).

Für solche normierten Richtungen d liefert die Cauchy-Schwarz-Ungleichung (die sofort aus der Darstellung (2.1) des Skalarprodukts folgt)

$-\|\nabla f(\bar x)\|_2 = -\|\nabla f(\bar x)\|_2\cdot \|d\|_2 \le \langle\nabla f(\bar x),d\rangle \le \|\nabla f(\bar x)\|_2\cdot \|d\|_2 = \|\nabla f(\bar x)\|_2\,,$

und die Unter- und Oberschranken werden genau für linear abhängige d und $\nabla f(\bar x)$ angenommen. Wegen $\nabla f(\bar x)\neq{}0$ wird die kleinstmögliche Steigung $-\|\nabla f(\bar x)\|_2$ daher mit

$d\ =\ -\frac{\nabla f(\bar x)}{\|\nabla f(\bar x)\|_2}$

realisiert und die größtmögliche $+ \|\nabla f(\bar x)\|_2$ mit

$d\ = + \frac{\nabla f(\bar x)}{\|\nabla f(\bar x)\|_2}.$

Insbesondere entspricht die Länge $\|\nabla f(\bar x)\|_2$ des Gradienten genau dem größtmöglichen Anstieg der Funktion f von $\bar x$ aus, und die Richtung des Gradienten zeigt in die zugehörige Richtung des steilsten Anstiegs.

Analog zeigt $-\nabla f(\bar x)$ in die Richtung des steilsten Abstiegs von f in $\bar x$ . Dies wird in Abschn. 2.2 auf ein grundlegendes numerisches Verfahren führen. In der Tat arbeitet man numerisch allerdings nicht mit normierten Richtungsvektoren, da beispielsweise die Länge $\|\nabla f(x)\|_2$ der negativen Gradientenrichtung gerade in der Nähe der gesuchten kritischen Punkte nahe bei null liegt, und die Division $-\nabla f(x)/\|\nabla f(x)\|_2$ dann numerisch instabil wäre.

2.1.4 Optimalitätsbedingungen zweiter Ordnung

Zur Herleitung der Fermat’schen Regel haben wir in Abschn. 2.1.2 ausgenutzt, dass an lokalen Minimalpunkten keine Abstiegsrichtungen erster Ordnung existieren können. Übung 2.1.2 schließt in lokalen Minimalpunkten allerdings jegliche Abstiegsrichtungen aus, und in Beispiel 2.1.16 sowie mit der Richtung d³ in Abb. 2.2 haben wir gesehen, dass es noch andere als Abstiegsrichtungen erster Ordnung gibt. Die im aktuellen Abschnitt hergeleiteten Optimalitätsbedingungen zweiter Ordnung basieren auf dem Konzept der Abstiegsrichtungen zweiter Ordnung.

Um es einzuführen, setzen wir f im Folgenden als mindestens zweimal differenzierbar am betrachteten Punkt $\bar x\in\mathbb R^n$ voraus. Dann ist auch die eindimensionale Einschränkung φ_d an $\bar t=0$ zweimal differenzierbar. Ihre zweite Ableitung $\upvarphi_d''(0)$ ist ein Maß für die Krümmung von φ_d in $\bar t=0$ . Aus Abschn. 2.1.2 ist bekannt, dass φ_d im Fall ${\upvarphi_d'(0)<0}$ von $\bar t=0$ aus für wachsende Werte von t zunächst fällt und analog dass φ_d im Fall $\upvarphi_d'(0)>0$ von $\bar t=0$ aus für wachsende Werte von t zunächst steigt. Im Grenzfall $\upvarphi'_d(0)=0$ erscheint es plausibel, dass für $\upvarphi_d''(0)<0$ die Funktionswerte von φ_d bei wachsendem t zunächst fallen, dass ein solches d also eine Abstiegsrichtung ist. Um auch dies tatsächlich nachzuweisen, benötigen wir den aus der Analysis bekannten und beispielsweise in [16, 17, 28] bewiesenen Satz von Taylor in folgender Form, wobei der Begriff univariat sich darauf bezieht, dass die betrachtete Funktion von einer nur eindimensionalen Variable abhängt.

2.1.19 Satz (Entwicklungen erster und zweiter Ordnung per univariatem Satz von Taylor)

a)
Es sei $\upvarphi:\mathbb R\to\mathbb R$ differenzierbar an $\bar t$ . Dann gilt für alle $t\in\mathbb R$
$\upvarphi(t)\ =\ \upvarphi(\bar t) + \upvarphi'(\bar t)(t-\bar t) + o(|t-\bar t|),$
wobei $o(|t-\bar t|)$ einen Ausdruck der Form $\omega(t)\cdot|t-\bar t|$ mit $\lim_{t\to\bar t}\omega(t)=\omega(\bar t)=0$ bezeichnet.
b)
Es sei $\upvarphi:\mathbb R\to\mathbb R$ zweimal differenzierbar an $\bar t$ . Dann gilt für alle $t\in\mathbb R$
$\upvarphi(t)\ =\ \upvarphi(\bar t) + \upvarphi'(\bar t)(t-\bar t) + {\textstyle\frac12}\upvarphi''(\bar t)(t-\bar t)^2 + o(|t-\bar t|^2),$
wobei $o(|t-\bar t|^2)$ einen Ausdruck der Form $\omega(t)\cdot|t-\bar t|^2$ mit $\lim_{t\to\bar t}\omega(t)=\omega(\bar t)=0$ bezeichnet.

2.1.20 Lemma

Für $f:\mathbb R^n\to\mathbb R$ , einen Punkt $\bar x\in\mathbb R^n$ und eine Richtung $d\in\mathbb R^n$ seien $\upvarphi'_d(0)=0$ und $\upvarphi_d''(0)<0$ . Dann ist d Abstiegsrichtung für f in $\bar x$ .

Beweis.

Wie im Beweis zu Lemma 2.1.5 nehmen wir an, dass d keine Abstiegsrichtung ist. Dann existiert für jedes $k\in\mathbb N$ wieder ein t^k ∈ (0, 1/k) mit

$\upvarphi_d(t^k)\ =\ f(\bar x + t^k d)\ \ge\ f(\bar x)\ =\ \upvarphi_d(0).$

Satz 2.1.19b mit φ = φ_d und $\bar t=0$ liefert außerdem für jedes $k\in\mathbb N$

$\upvarphi_d(t^k)\ =\ \upvarphi_d(0) + \upvarphi_d'(0)\,t^k + {\textstyle\frac12}\upvarphi_d''(0)(t^k)^2 + o((t^k)^2).$

Zusammen mit der Voraussetzung $\upvarphi_d'(0)=0$ und t^k ≠ 0 erhalten wir insgesamt für jedes $k\in\mathbb N$

$0\ \le\ \frac{\upvarphi_d(t^k)-\upvarphi_d(0)}{(t^k)^2}\ =\ {\textstyle\frac12}\upvarphi_d''(0) + \omega(t^k)$

mit $\lim_k\omega(t^k)=\omega(0)=0$ . Im Grenzübergang gilt also

$0\ \le\ {\textstyle\frac12}\upvarphi_d''(0),$

was aber im Widerspruch zur Voraussetzung $\upvarphi_d''(0)<0$ steht. Demnach ist d Abstiegsrichtung.

2.1.21 Lemma

Für $f:\mathbb R^n\to\mathbb R$ sei $\bar x$ ein lokaler Minimalpunkt. Dann gilt $\nabla\,f(\bar x)=0$ , und jede Richtung $d\in\mathbb R^n$ erfüllt $\upvarphi_d''(0)\ge0$ .

Beweis.

Zunächst liefert Satz 2.1.13, dass $\nabla f(\bar x)=0$ gilt und damit insbesondere auch $\upvarphi_d'(0)=\langle\nabla f(\bar x),d\rangle=0$ . Aus Übung 2.1.2 und Lemma 2.1.20 folgt daher die Behauptung.

Um Lemma 2.1.21 ausnutzen zu können, benötigen wir eine einfache Formel für $\upvarphi_d''(0)$ , also für die Ableitung der bereits per Kettenregel berechneten ersten Ableitung

$\upvarphi_d'(t)\ =\ \langle\nabla f(\bar x + td),d\rangle\ =\ \sum_{i\,=\,1}^n\partial_{x_i}f(\bar x + td)\,d_i$

an der Stelle $\bar t=0$ . Aus nochmaliger Anwendung der Kettenregel folgt

$\upvarphi_d''(t)\ =\ \sum_{i\,=\,1}^n\left(D\partial_{x_i}\ f(\bar x + td)\,d\right)\,d_i\ =\ \sum_{i\,=\,1}^n\sum_{j\,=\,1}^n\partial_{x_j}\partial_{x_i}\ f(\bar x + td)\,d_j\,d_i$

und damit

$\upvarphi_d''(0)\ =\ \sum_{i\,=\,1}^n\sum_{j\,=\,1}^n\partial_{x_j}\partial_{x_i}\ f(\bar x)\,d_j\,d_i\,.$

In dieser noch etwas unübersichtlichen Formel für $\upvarphi_d''(0)$ treten jedenfalls partielle zweite Ableitungen von f auf. Um eine übersichtlichere Formel für $\upvarphi_d''(0)$ zu finden, führen wir eine „n-dimensionale zweite Ableitung“ von f ein. Eine naheliegende Möglichkeit dafür ist es, die erste Ableitung der ersten Ableitung zu bilden, also die Jacobi-Matrix des Gradienten von f: Die (n, n)-Matrix

$D^2 f(\bar x)\ :=\ D\nabla f(\bar x)\ =\ \begin{pmatrix} \partial_{x_1}\partial_{x_1}\ f(\bar x) & \cdots & \partial_{x_n}\partial_{x_1}\ f(\bar x)\\ \vdots & & \vdots\\ \partial_{x_1}\partial_{x_n}\ f(\bar x) & \cdots & \partial_{x_n}\partial_{x_n}\ f(\bar x)\\ \end{pmatrix}$

heißt Hesse-Matrix von f an $\bar x$ . Als zweite Ableitung sind in ihr Krümmungsinformationen von f an $\bar x$ codiert.

Nach den Regeln der Matrix-Vektor-Multiplikation gilt für jeden Vektor $d\in\mathbb R^n$ gerade

$d^\intercal D^2 f(\bar x)d\ =\ \sum_{i\,=\,1}^n\sum_{j\,=\,1}^n\partial_{x_j}\partial_{x_i}\ f(\bar x)\,d_j\,d_i\ =\ \upvarphi_d''(0),$

womit die gesuchte einfache Darstellung von $\upvarphi_d''(0)$ vorliegt. Damit können wir Lemma 2.1.20 umformulieren.

2.1.22 Lemma

Für $f:\mathbb R^n\to\mathbb R$ , einen Punkt $\bar x\in\mathbb R^n$ und eine Richtung $d\in\mathbb R^n$ seien $\langle\nabla f(\bar x),d\rangle=0$ und $d^\intercal D^2f(\bar x)d<0$ . Dann ist d Abstiegsrichtung für f in $\bar x$ .

Dies motiviert die folgende Definition.

2.1.23 Definition (Abstiegsrichtung zweiter Ordnung)

Zu $f:\mathbb R^n\to\mathbb R$ und $\bar x\in\mathbb R^n$ heißt jeder Richtungsvektor $d\in\mathbb R^n$ mit $\langle\nabla f(\bar x),d\rangle=0$ und $d^\intercal D^2f(\bar x)d<0$ Abstiegsrichtung zweiter Ordnung für f in $\bar x$ .

2.1.24 Beispiel

Die Funktionen $f_1(x)=x_1^2 + x_2^2$

und

aus Beispiel 2.1.16 besitzen an $\bar x=0$ den Gradienten $\nabla f(\bar x)=0$ und die Hesse-Matrizen

$D^2f_1(0)=\begin{pmatrix}2 & 0\\0 & 2\end{pmatrix},\qquad D^2f_2(0)=\begin{pmatrix}-2 & 0\\0 & -2\end{pmatrix},\qquad D^2f_3(0)=\begin{pmatrix}2 & 0\\0 & -2\end{pmatrix}.$

Für $d=(0,1)^\intercal$ folgt

$\langle \nabla f_2(0),d\rangle\ =\ \langle \nabla f_3(0),d\rangle\ =\ \langle 0,d\rangle\ =\ 0$

und

$d^\intercal D^2f_2(0)d\ =\ d^\intercal D^2f_3(0)d\ =\ -2\ <\ 0,$

so dass d Abstiegsrichtung zweiter Ordnung für f₂ und f₃ in $\bar x=0$ ist.

2.1.25 Beispiel

In Beispiel 2.1.24 ist die Bedingung $\langle\nabla f(\bar x),d\rangle=0$ aus Definition 2.1.23 erfüllt, weil schon $\nabla f(\bar x)=0$ gilt. Es gibt aber auch Abstiegsrichtungen zweiter Ordnung im Fall $\nabla f(\bar x)\neq{}0$ , nämlich solche, die orthogonal zu $\nabla f(\bar x)$ stehen. Dies veranschaulicht etwa die Richtung d³ in Abb. 2.2. Die dortige Richtung d⁴ verdeutlicht andererseits, dass die bloße Orthogonalität natürlich nicht ausreicht. Die „nichtkonvexe Krümmung“ des Rands der Menge $f^{f(x^1)}_\le=f^{f(x^2)}_\le$ an x¹ entspricht gerade der Bedingung $(d^3)^\intercal D^2f(x^1)d^3<0$ , die d³ laut Definition 2.1.23 zu einer Abstiegsrichtung zweiter Ordnung macht. Dieser Zusammenhang wird noch klarer werden, wenn wir diese Bedingungen mit den Eigenwerten der Matrix $D^2f(x^1)$ in Verbindung gebracht haben.

Das folgende Beispiel belegt, dass nicht jede Abstiegsrichtung entweder von erster oder von zweiter Ordnung ist.

2.1.26 Beispiel

Für jede Abstiegsrichtung zweiter Ordnung d ist offenbar auch ihre „Gegenrichtung“ −d eine Abstiegsrichtung zweiter Ordnung. Daher ist beispielsweise d = −1 für die Funktion f(x) = x³ an $\bar x=0$ zwar eine Abstiegsrichtung, aber weder von erster noch von zweiter Ordnung.

Die per Formel für $\upvarphi_d''(0)$ explizitere Formulierung von Lemma 2.1.21 besagt, dass an einem lokalen Minimalpunkt $\bar x$ von f notwendigerweise $\nabla f(\bar x)=0$ und $d^\intercal D^2f(\bar x)d\ge0$ für alle $d\in\mathbb R^n$ gilt. In der linearen Algebra wird letztere Bedingung an die Matrix $D^2f(\bar x)$ positive Semidefinitheit genannt und kurz mit $D^2f(\bar x)\succeq0$ bezeichnet. Damit erhalten wir aus Lemma 2.1.21 folgendes Resultat.

2.1.27 Satz (Notwendige Optimalitätsbedingung zweiter Ordnung)

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei zweimal differenzierbar an einem lokalen Minimalpunkt $\bar x\in\mathbb R^n$ . Dann gilt $\nabla f(\bar x)=0$ und $D^2f(\bar x)\succeq0$ .

Um Satz 2.1.27 praktisch anwenden zu können, muss die Bedingung $D^2f(\bar x)\succeq0$ überprüfbar sein. Nach Definition der positiven Semidefinitheit wären dazu aber unendlich viele Ungleichungen zu garantieren. Glücklicherweise stellt die lineare Algebra eine Charakterisierung von positiver Semidefinitheit zur Verfügung, sofern die Matrix $D^2f(\bar x)$ symmetrisch ist (d. h., es gilt $D^2f(\bar x)=D^2f(\bar x)^\intercal$ ). Nach dem aus der Analysis bekannten Satz von Schwarz (z. B. [18]) ist Letzteres der Fall, wenn f nicht nur zweimal differenzierbar, sondern sogar zweimal stetig differenzierbar ist (kurz: $f\in C^2(\mathbb R^n,\mathbb R)$ ).

Es sei daran erinnert, dass λ ein Eigenwert zum Eigenvektor v ≠ 0 von $D^2f(\bar x)$ ist, wenn $D^2f(\bar x)v=\lambda v$ gilt (eine Motivation dafür wird z. B. im Anhang von [24] gegeben). Obwohl Eigenwerte im Allgemeinen komplexe Zahlen sein können, wird in der linearen Algebra gezeigt (z. B. [8, 20]), dass Eigenwerte symmetrischer Matrizen stets reell sind. Insbesondere kann man dann ihre Vorzeichen betrachten. Eine symmetrische Matrix ist in der Tat genau dann positiv semidefinit, wenn ihre sämtlichen Eigenwerte nichtnegativ sind (z. B. [8, 20]). Demnach dürfen wir für jede C²-Funktion f die Bedingung $D^2f(\bar x)\succeq0$ verifizieren, indem wir die n Eigenwerte der Matrix $D^2f(\bar x)$ berechnen und auf Nichtnegativität überprüfen.

2.1.28 Beispiel

Alle drei Funktionen f₁, f₂ und f₃ aus Beispiel 2.1.24 sind zweimal stetig differenzierbar an $\bar x=0$ , so dass die positive Semidefinitheit ihrer Hesse-Matrizen mit Hilfe der Eigenwerte geprüft werden kann. Von den drei Hesse-Matrizen ist nur $D^2f_1(0)$ positiv semidefinit. Daher kann man mit Satz 2.1.27 ausschließen, dass f₂ und f₃ an $\bar x=0$ lokale Minimalpunkte besitzen.

Beispiel 2.1.28 zeigt, dass Satz 2.1.27 die Kandidatenmenge für lokale Minimalpunkte gegenüber der Fermat’schen Regel stark reduzieren kann. Darauf basiert der konzeptionelle Algorithmus 2.2, der im Vergleich zu Algorithmus 2.1 das entsprechend „feinere Sieb“ zum Einsatz bringt. Die drei Hauptnachteile von Algorithmus 2.1, nämlich die fehlende Identifizierung der Unlösbarkeit des Optimierungsproblems, die Notwendigkeit, die Kandidatenmenge K komplett zu berechnen, sowie die Schwierigkeit, überhaupt kritische Punkte zu bestimmen, werden auch durch Algorithmus 2.2 nicht ausgeräumt. Sein Vorteil gegenüber Algorithmus 2.1 ist die üblicherweise erheblich kleinere Menge K.

Algorithmus 2.2: Konzeptioneller Algorithmus zur unrestringierten nichtlinearen Minimierung mit Informationen zweiter Ordnung

Input : Lösbares unrestringiertes zweimal stetig differenzierbares Optimierungsproblem P

Output : Globaler Minimalpunkt $x^\star$ von f über $\mathbb R^n$

1 begin

2 Bestimme alle kritischen Punkte mit positiv semidefiniter Hesse-Matrix von f, d. h. die Lösungsmenge K der beiden Bedingungen $\nabla f(x)=0$ und $D^2f(x)\succeq0$ .

3 Bestimme einen Minimalpunkt $x^\star$ von f in K.

4 end

Leider sind lokale Minimalpunkte durch die notwendige Bedingung aus Satz 2.1.27 nach wie vor nicht charakterisiert, denn etwa für $f_4(x)=x_1^2-x_2^4$

gilt ∇f₄(0) = 0, und die Hesse-Matrix

$D^2f_4(0)\ =\ \begin{pmatrix}2 & 0\\0 & 0\end{pmatrix}$

ist positiv semidefinit, aber $\bar x=0$ ist trotzdem kein lokaler Minimalpunkt von f. Dies führt auf die Frage nach einer hinreichenden Bedingung für lokale Minimalität.

Analog zu unseren bisherigen Betrachtungen ließe sich vermuten, dass f sicherlich dann einen lokalen Minimalpunkt an $\bar x$ besitzt, wenn für alle $d\in\mathbb R^n$ die eindimensionale Einschränkung φ_d an $\bar t$ einen lokalen Minimalpunkt besitzt. Die folgende Übung zeigt allerdings, dass diese Vermutung falsch ist.

2.1.29 Übung (Beispiel von Peano)

Zeigen Sie, dass die Funktion $f(x)=(x_1^2-x_2)\cdot(x_1^2-3x_2)$ zwar keinen lokalen Minimalpunkt bei $\bar x=0$ besitzt, dass aber für jede Richtung $d\in\mathbb R^n$ die eindimensionale Einschränkung φ_d an $\bar t=0$ einen lokalen Minimalpunkt aufweist.

Übung 2.1.29 illustriert einen Effekt, der für univariate Funktionen (also für n = 1) nicht auftreten kann: Der Funktionswert an $\bar x$ wird durch Funktionswerte an Punkten unterschritten, die nicht entlang einer Geraden durch $\bar x$ liegen, sondern entlang einer Parabel durch $\bar x$ . In der Tat gilt in Übung 2.1.29 für die Richtung d, die an $\bar x$ tangential zu dieser Parabel liegt, $\upvarphi_d''(0)=0$ , während alle anderen Richtungen $\upvarphi_d''(0)>0$ erfüllen.

Um einen lokalen Minimalpunkt $\bar x$ durch Informationen zweiter Ordnung zu garantieren, sollte man also ausschließen, dass für eine Richtung d nur $\upvarphi_d''(0)=0$ gilt. Dies ist (neben der notwendigerweise aufzustellenden Bedingung $\nabla f(\bar x)=0$ ) gleichbedeutend mit der Forderung, jede Richtung d sei Anstiegsrichtung zweiter Ordnung, also

$d^\intercal D^2f(\bar x) d\ >\ 0\ \text{ f\"{u}r alle }\ d\neq{}0,$

was in der linearen Algebra als positive Definitheit von $D^2f(\bar x)$ bezeichnet wird, kurz $D^2f(\bar x) \succ 0$ . Falls die Hesse-Matrix wegen zweimaliger stetiger Differenzierbarkeit von f an $\bar x$ symmetrisch ist, wird positive Definitheit dadurch charakterisiert, dass alle Eigenwerte von $D^2f(\bar x)$ strikt positiv sind (z. B. [8, 20]).

Der Beweis der resultierenden hinreichenden Optimalitätsbedingung zweiter Ordnung benutzt wieder den Satz von Taylor. Aus Übung 2.1.29 erschließt sich allerdings, dass univariate Versionen dieses Satzes, also Entwicklungen entlang von Geraden, nicht hilfreich sein werden.

Zum Glück lässt der Satz von Taylor sich auch im multivariaten Fall formulieren (ein Beweis wird z. B. in [16, 18] gegeben).

2.1.30 Satz (Entwicklungen erster und zweiter Ordnung per multivariatem Satz von Taylor)

a)
Es sei $f:\mathbb R^n\to\mathbb R$ differenzierbar in $\bar x$ . Dann gilt für alle $x\in\mathbb R^n$
$f(x)\ =\ f(\bar x) + \langle\nabla f(\bar x),x-\bar x\rangle + o(\|x-\bar x\|),$
wobei $o(\|x-\bar x\|)$ einen Ausdruck der Form $\omega(x)\cdot\|x-\bar x\|$ mit $\lim_{x\to\bar x}\omega(x)=\omega(\bar x)=0$ bezeichnet.
b)
Es sei $f:\mathbb R^n\to\mathbb R$ zweimal differenzierbar in $\bar x$ . Dann gilt für alle $x\in\mathbb R^n$
$f(x)\ =\ f(\bar x) + \langle\nabla f(\bar x),x-\bar x\rangle + {\textstyle\frac12}(x-\bar x)^\intercal D^2f(\bar x)(x-\bar x) + o(\|x-\bar x\|^2),$
wobei $o(\|x-\bar x\|^2)$ einen Ausdruck der Form $\omega(x)\cdot\|x-\bar x\|^2$ mit $\lim_{x\to\bar x}\omega(x)=\omega(\bar x)=0$ bezeichnet.

Im Beweis des folgenden Satzes werden wir außerdem mit

$B_\le(\bar x,r)\ =\ \{x\in\mathbb R^n|\ \|x-\bar x\|\le r\}$

eine Kugel mit Radius r um $\bar x$ bezeichnen und mit

$B_=(\bar x,r)\ =\ \{x\in\mathbb R^n|\ \|x-\bar x\| = r\}$

ihren Rand, also die Sphäre mit Radius r um $\bar x$ (wobei die Wahl der Norm $\|\cdot\|$ keine Rolle spielt).

2.1.31 Satz (Hinreichende Optimalitätsbedingung zweiter Ordnung)

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei an $\bar x\in\mathbb R^n$ zweimal differenzierbar, und es gelte $\nabla f(\bar x)=0$ und $D^2f(\bar x)\succ0$ . Dann ist $\bar x$ ein strikter lokaler Minimalpunkt von f.

Beweis.

Der Beweis wird per Widerspruch geführt. Angenommen, $\bar x$ sei kein strikter lokaler Minimalpunkt von f. Falls $\bar x$ kein kritischer Punkt von f ist, liegt bereits ein Widerspruch vor, so dass wir im Folgenden $\nabla f(\bar x)=0$ voraussetzen dürfen. Da $\bar x$ kein strikter lokaler Minimalpunkt ist, existiert per Definition 1.1.2 zu jeder Umgebung U von $\bar x$ ein $x_U\in U\setminus\{\bar x\}$ mit $f(x_U)\le f(\bar x)$ . Insbesondere existiert zu jeder Umgebung $U_k=B_\le(\bar x,1/k)$ mit $k\in\mathbb N$ ein Punkt $x^k\neq\bar x$ mit $f(x^k)\le f(\bar x)$ . Aus der speziellen Wahl der Umgebungen folgt außerdem $\lim_k x^k=\bar x$ .

Folglich bilden die Werte $t^k:=\|x^k-\bar x\|$ eine Nullfolge positiver Zahlen, die Richtungen

$d^k\ :=\ \frac{x^k-\bar x}{t^k}\ =\ \frac{x^k-\bar x}{\|x^k-\bar x\|}$

sind wohldefiniert und normiert, und es gilt $x^k=\bar x + t^k d^k$ für alle $k\in\mathbb N$ . Dass alle Richtungen d^k normiert sind, bedeutet gerade, dass die Folge (d^k) in der Einheitssphäre B₌(0, 1) liegt. Da diese eine kompakte Menge ist, besitzt die Folge (d^k) mindestens einen Häufungspunkt d ∈ B₌(0, 1) (nach dem Satz von Bolzano-Weierstraß; z. B. [18]). Nach Übergang zu einer entsprechenden Teilfolge erhalten wir die Existenz von Folgen (t^k) und (d^k) mit $\lim_k t^k=0$ , $\lim_k d^k=d$ , $\|d\|=1$ und

$f(x^k)\ =\ f(\bar x + t^k d^k)\ \le\ f(\bar x)$

für alle $k\in\mathbb N$ . Satz 2.1.30b liefert nun für alle $k\in\mathbb N$

$0\ \ge\ \frac{f(\bar x + t^k d^k)-f(\bar x)}{(t^k)^2}\ =\ {\textstyle\frac12} (d^k)^\intercal D^2f(\bar x) d^k + \omega(t^k),$

wobei die Funktion ω(t) für t → 0 gegen ω(0) = 0 strebt. Wegen $\lim_k t^k=0$ folgt im Grenzübergang also

$0\ \ge\ d^\intercal D^2f(\bar x)d.$

Aufgrund von $\|d\|=1$ widerspricht dies aber der Voraussetzung $D^2f(\bar x)\succ0$ .

2.1.32 Bemerkung

Die notwendigen Optimalitätsbedingungen erster und zweiter Ordnung lassen sich samt ihrer Beweise problemlos auf Funktionale auf Banach-Räumen $f:X\to\mathbb R$ übertragen, also auf eine große Klasse unendlichdimensionaler Optimierungsprobleme. Die Verallgemeinerung hinreichender Bedingungen ist hingegen nur mit zusätzlichem Aufwand möglich. Hauptgrund hierfür ist, dass die Einheitssphäre in einem Banach-Raum nur in Spezialfällen kompakt ist (für Details s. z. B. [4, 19]).

2.1.33 Übung

Zeigen Sie, dass der in Übung 2.1.18 unter der Voraussetzung, dass mindestens zwei der Stützstellen x_j, 1 ≤ j ≤ m, voneinander verschieden sind, berechnete eindeutige kritische Punkt des Kleinste-Quadrate-Problems

$\min_{a,b}\ \left\|\begin{pmatrix}ax_1 + b-y_1\\\vdots\\ax_m + b-y_m\end{pmatrix}\right\|_2^2$

ein strikter lokaler Minimalpunkt ist.

2.1.34 Bemerkung

Man kann sich fragen, warum es bei den Optimalitätsbedingungen zweiter Ordnung zwar eine notwendige und eine hinreichende Version gibt, bei den Bedingungen erster Ordnung aber nur die Fermat’sche Regel als notwendige Bedingung. Dazu sei daran erinnert, dass der Beweis der Fermat’schen Regel auf Lemma 2.1.6 für einseitig richtungsdifferenzierbare Funktionen basiert, also auf der Notwendigkeit von Stationarität für jeden lokalen Minimalpunkt. Im glatten Fall besagt dies, dass an einem lokalen Minimalpunkt $\bar x$ von f notwendigerweise die Ungleichungen $\langle\nabla f(\bar x),d\rangle\ge0$ für alle $d\in\mathbb R^n$ gelten.

Würde man hier zur Konstruktion einer womöglich hinreichenden Optimalitätsbedingung erster Ordnung analog zu den Bedingungen zweiter Ordnung die nichtstrikte durch eine strikte Ungleichung ersetzen, erhielte man $\langle\nabla f(\bar x),d\rangle>0$ für alle $d\in\mathbb R^n\setminus\{0\}$ . Diese Bedingung ist aber für keinen Vektor $\nabla f(\bar x)$ erfüllbar und daher nutzlos.

Das Problem liegt dabei in der Glattheitsvoraussetzung an die Funktion f. Für lediglich einseitig richtungsdifferenzierbare Funktionen lässt sich sehr wohl zeigen, dass aus $f'(\bar x,d)>0$ für alle $d\in\mathbb R^n\setminus\{0\}$ die (strikte) lokale Minimalität von $\bar x$ für f folgt und dass diese Bedingung auch erfüllbar ist (z. B. für $f(x)=|x|$ und $\bar x=0$ ).

Für restringierte glatte Probleme werden wir in Korollar 3.2.68 wiederum eine hinreichende Optimalitätsbedingung erster Ordnung angeben können, weil (etwas lax formuliert) die dafür benötigte Nichtglattheit durch den Rand der zulässigen Menge bereitgestellt wird.

Da die hinreichende Bedingung aus Satz 2.1.31 etwas mehr liefert als gewünscht, nämlich sogar strikte lokale Minimalpunkte, kann man von ihr keine Charakterisierung lokaler Minimalität erwarten. Andererseits liefert diese hinreichende Bedingung auch keine Charakterisierung für strikte Minimalität, denn sie kann an strikten lokalen Minimalpunkten verletzt sein (z. B. für f(x) = x⁴ und $\bar x=0$ ).

Zwischen notwendigen und hinreichenden Optimalitätsbedingungen zweiter Ordnung klafft in diesem Sinne also eine Lücke. Die folgenden Ergebnisse zeigen allerdings, dass diese Lücke für „sehr viele“ Optimierungsprobleme keine Rolle spielt. Als Konsequenz daraus befassen wir uns weder mit Optimalitätsbedingungen noch mit Abstiegsrichtungen dritter und höherer Ordnung, obwohl sich diese mit Hilfe der entsprechenden Taylor-Entwicklungen durchaus angeben ließen. Für die folgende Definition sei daran erinnert, dass eine quadratische Matrix nichtsingulär heißt, wenn keiner ihrer Eigenwerte null ist.

2.1.35 Definition (Nichtdegenerierte kritische und Minimalpunkte)

Die Funktion $f:\mathbb R^n\to\mathbb R$ sei an $\bar x$ zweimal differenzierbar mit $\nabla f(\bar x)=0$ . Dann heißt $\bar x$

a)
nichtdegenerierter kritischer Punkt , falls $D^2f(\bar x)$ nichtsingulär ist,
b)
nichtdegenerierter lokaler Minimalpunkt , falls $\bar x$ lokaler Minimalpunkt und nichtdegenerierter kritischer Punkt ist.

Beispielsweise ist der Sattelpunkt $\bar x=0$ von $f_3(x)=x_1^2-x_2^2$ ein nichtdegenerierter kritischer Punkt, während der Sattelpunkt $\bar x=0$ ein degenerierter kritischer Punkt von $f_4(x)=x_1^2-x_2^4$ ist.

Nichtdegenerierte lokale Minimalpunkte lassen sich durch Eigenschaften von Gradient und Hesse-Matrix charakterisieren.

2.1.36 Lemma

Der Punkt $\bar x$ ist genau dann nichtdegenerierter lokaler Minimalpunkt von f, wenn $\nabla f(\bar x)=0$ und $D^2f(\bar x)\succ0$ gilt.

Beweis.

Für einen lokalen Minimalpunkt $\bar x$ gilt nach Satz 2.1.27 $\nabla f(\bar x)=0$ und $D^2f(\bar x)\succeq0$ . Wenn $\bar x$ außerdem nichtdegenerierter kritischer Punkt ist, dann besitzt $D^2f(\bar x)$ keinen verschwindenden Eigenwert, ist also positiv definit.

Es seien andererseits $\nabla f(\bar x)=0$ und $D^2f(\bar x)\succ0$ . Dann ist $\bar x$ nach Satz 2.1.31 ein lokaler Minimalpunkt. Da eine positiv definite Matrix nichtsingulär ist, ist dieser lokale Minimalpunkt auch nichtdegeneriert.

In einem gewissen Sinne, den wir nur kurz motivieren, besitzen „fast alle“ C²-Funktionen ausnahmslos nichtdegenerierte kritische Punkte. Etwas genauer ausgedrückt ist die Teilmenge

$\mathcal F\ =\ \{f\in C^2(\mathbb R^n,\mathbb R)|\ \text{alle kritischen Punkte von}\ \textit{f}\ \text{sind nichtdegeneriert}\}$

der Menge aller C²-Funktionen „sehr groß“. In der Tat macht man sich leicht die Äquivalenz

$f\in\mathcal F\quad\Leftrightarrow\quad\forall\ x\in\mathbb R^n:\quad \|\nabla f(x)\| + |\det(D^2f(x))|\ >\ 0$

klar, so dass $\mathcal F$ in einer passend gewählten Topologie auf dem Funktionenraum $C^2(\mathbb R^n,\mathbb R)$ (die für die Definition einer Umgebung einer Funktion auch ihre ersten und zweiten Ableitungen berücksichtigt) eine offene Menge sein wird. Benutzt man dafür die starke Whitney-Topologie ( $C^2_s$

-Topologie), dann gilt sogar das folgende Ergebnis, für dessen tiefliegenden Beweis wir auf [22] verweisen.

2.1.37 Satz

$\mathcal F$ ist $C^2_s$ -offen und -dicht in $C^2(\mathbb R^n,\mathbb R)$ .

Im Sinne von Satz 2.1.37 ist es also eine schwache Voraussetzung, die Nichtdegeneriertheit eines kritischen Punkts und insbesondere die Nichtdegeneriertheit eines lokalen Minimalpunkts zu fordern.

Abschließend halten wir fest, dass analog zu den Interpretationen von Vorzeichen und Wert des Skalarprodukts $\langle\nabla f(\bar x),d\rangle$ auch nicht nur die Vorzeichen von Eigenwerten von $D^2f(\bar x)$ wichtige Informationen enthalten, sondern auch deren tatsächlichen Werte. Dazu sei λ ein Eigenwert von $D^2f(\bar x)$ , und d mit $\|d\|_2=1$ sei ein zugehöriger Eigenvektor. Dann gilt

$\upvarphi''_d(0)\ =\ d^\intercal D^2f(\bar x)d\ =\ d^\intercal(\lambda d)\ =\ \lambda\,\|d\|_2^2\ =\ \lambda,$

so dass man die Größe des Eigenwerts λ als ein Maß für die Krümmung der eindimensionalen Einschränkung φ_d an $\bar t=0$ interpretieren kann.

Zudem ist für symmetrische (n, n)-Matrizen aus der linearen Algebra bekannt, dass die n Eigenvektoren der n Eigenwerte paarweise orthogonal zueinander gewählt werden können (z. B. [8, 20]). Dadurch lässt sich die lokale Struktur von f um einen nichtdegenerierten kritischen Punkt sehr genau beschreiben.

Letztlich ermöglichen es diese Zusammenhänge auch, in kritischen Punkten Abstiegsrichtungen zweiter Ordnung explizit anzugeben. Dazu sei ein kritischer Punkt $\bar x$ von f mit $D^2f(\bar x)\not\succeq0$ gegeben, d. h., $D^2f(\bar x)$ besitzt (mindestens) einen negativen Eigenwert λ. Jeder zugehörige Eigenvektor d ist dann Abstiegsrichtung zweiter Ordnung, denn er erfüllt $\langle \nabla f(\bar x),d\rangle=0$ und

$d^\intercal D^2f(\bar x)d\ =\ \lambda\ <\ 0.$

2.1.38 Übung

Zeigen Sie, dass an einem nichtdegenerierten Sattelpunkt sowohl eine Abals auch eine Anstiegsrichtung zweiter Ordnung existieren.

2.1.5 Konvexe Optimierungsprobleme

Abschn. 2.1 hat mit Hilfe von ersten und zweiten Ableitungen einer Funktion Optimalitätsbedingungen für ihre lokalen Minimalpunkte angegeben. Da Ableitungen nur lokale Information über eine Funktion enthalten, kann man auch nicht mehr erwarten, sofern man nicht eine zusätzliche globale Eigenschaft der Funktion fordert. Eine solche ist die Konvexität. Da konvexe Optimierungsprobleme ausführlich in [33] behandelt werden, stellen wir im Folgenden nur einige wesentliche Resultate zusammen und verweisen für Beweise und weitergehende Überlegungen auf [33].

2.1.39 Definition (Konvexe Mengen und Funktionen)

a)
Eine Menge $X \subseteq \mathbb R^n$ heißt konvex , falls
$\forall\ x,y \in X,\ \lambda \in (0,1):\quad (1-\lambda)x + \lambda y \in X$
gilt (d. h., die Verbindungsstrecke von je zwei beliebigen Punkten in X gehört komplett zu X; Abb. 2.3).
b)
Für eine konvexe Menge $X\subseteq\mathbb R^n$ heißt eine Funktion $f:X\to\mathbb R$ konvex (auf X) , falls
$\forall\ x,y \in X ,\ \lambda \in (0,1):\quad f(\,(1-\lambda)x + \lambda y\,)\ \leq\ (1-\lambda)f(x) + \lambda f(y)$
gilt (d. h., der Funktionsgraph von f verläuft unter jeder seiner Sekanten; Abb. 2.4).

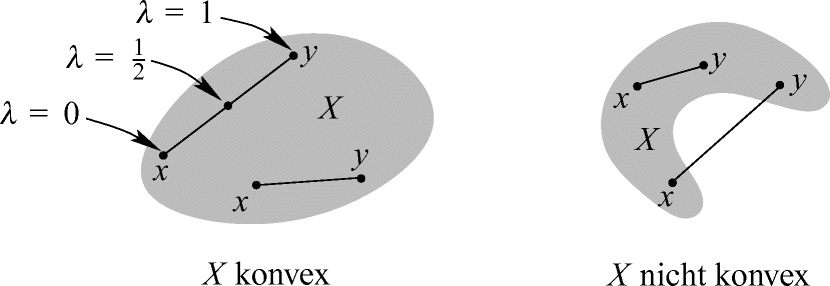
../images/439970_1_De_2_Chapter/439970_1_De_2_Fig3_HTML.png — Abb. 2.3
Konvexität von Mengen in $\mathbb R^2$

Abb. 2.3
Konvexität von Mengen in $\mathbb R^2$

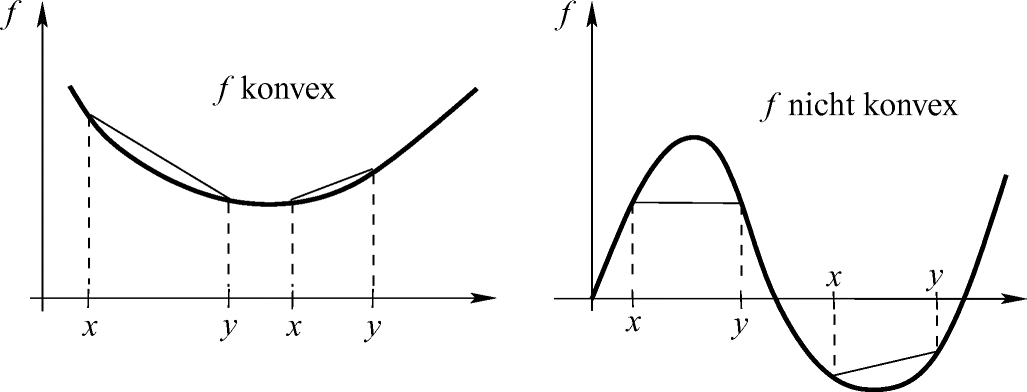
../images/439970_1_De_2_Chapter/439970_1_De_2_Fig4_HTML.png — Abb. 2.4
Konvexität von Funktionen auf $\mathbb R$

Abb. 2.4
Konvexität von Funktionen auf $\mathbb R$

Während die Konvexität einer Funktion geometrisch dadurch definiert ist, dass ihr Graph unter jeder ihrer Sekanten verläuft, lässt sich Konvexität einer stetig differenzierbaren Funktion f dadurch charakterisieren, dass ihr Graph über den Graphen jeder ihrer Linearisierungen verläuft. Dazu betrachten wir für f die multivariate Taylor-Entwicklung erster Ordnung aus Satz 2.1.30a um einen Punkt x, die besagt, dass für alle $y\in\mathbb R^n$ die Darstellung

$f(y)\ =\ f(x) + \langle\nabla f(x),y-x\rangle + o(\|y-x\|)$

gilt. Zur Linearisierung unterschlagen wir den Fehlerterm $o(\|y-x\|)$ und erhalten die (in y lineare) Funktion $f(x) + \langle\nabla f(x),y-x\rangle$ als Approximation von f im Punkt x. Die angekündigte Charakterisierung von Konvexität stetig differenzierbarer Funktionen (kurz: f ∈ C¹) lautet damit wie folgt.

2.1.40 Satz ( $\boldsymbol{C}^\textbf{1}$ -Charakterisierung von Konvexität)

Auf einer konvexen Menge $X\subseteq\mathbb R^n$ ist eine Funktion $f\in C^1(X,\mathbb R)$ genau dann konvex, wenn

$\forall\ x,y\in X:\quad f(y)\ \ge\ f(x) + \langle\nabla f(x),y-x\rangle$

gilt.

Der zentrale Satz für stetig differenzierbare konvexe unrestringierte Optimierungsprobleme ist die folgende weitreichende Verschärfung der Fermat’schen Regel.

2.1.41 Korollar

Die Funktion $f\in C^1(\mathbb R^n,\mathbb R)$ sei konvex. Dann sind die kritischen Punkte von f genau die globalen Minimalpunkte von f.

Beweis.

Dass jeder globale Minimalpunkt kritischer Punkt von f ist, folgt aus Satz 2.1.13. Andererseits erfüllt jeder Punkt $\bar x$ mit $\nabla f(\bar x)=0$ nach Satz 2.1.40

$\forall\ y\in\mathbb R^n:\quad f(y)\ \ge\ f(\bar x) + \langle\underbrace{\nabla f(\bar x)}_{=\ 0},y-\bar x\rangle\ =\ f(\bar x)$

und ist damit globaler Minimalpunkt.

Das Problem der globalen Minimierung stetig differenzierbarer konvexer Funktionen ist also äquivalent zu einem Nullstellenproblem, nämlich zur Lösung der Gleichung ∇f(x) = 0.

Obwohl notwendige oder hinreichende Optimalitätsbedingungen zweiter Ordnung im konvexen Fall offenbar überflüssig sind, spielen Hesse-Matrizen dennoch eine wichtige Rolle, nämlich um ein einfaches Kriterium zum Nachweis der Konvexität zweimal stetig differenzierbarer Funktionen anzugeben.

2.1.42 Satz ( $\boldsymbol{C}^\textbf{2}$ -Charakterisierung von Konvexität)

Eine Funktion $f\in C^2(\mathbb R^n,\mathbb R)$ ist genau dann konvex, wenn

$\forall\ x\in\mathbb R^n:\quad D^2f(x)\ \succeq\ 0$

gilt.

Zum Abschluss dieses Abschnitts betrachten wir für $f\in C^2(\mathbb R^n,\mathbb R)$ einen nichtdegenerierten lokalen Minimalpunkt $\bar x$ von f, d. h., an ihm gelte $D^2f(\bar x)\succ0$ . Wegen der Stetigkeit von D²f und der stetigen Abhängigkeit der Eigenwerte symmetrischer Matrizen von den Matrixeinträgen [36] gilt auch D²f(x) ≻ 0 für die x aus einer ganzen Umgebung von $\bar x$ . Nach Satz 2.1.42 ist f also lokal um den nichtdegenerierten lokalen Minimalpunkt $\bar x$ konvex.

2.1.43 Übung

Gegeben sei die quadratische Funktion $q(x)=\frac12x^\intercal Ax + b^\intercal x$ mit $A=A^\intercal\succ0$ und $b\in\mathbb R^n$ . Zeigen Sie, dass q eine auf $\mathbb R^n$ konvexe Funktion ist und dass ihr eindeutiger Minimalpunkt

$x^\star\ =\ -A^{-1} b$

mit Minimalwert

$q(x^\star)\ =\ -{\textstyle\frac12}\, b^\intercal A^{-1} b$

lautet.

Angemerkt sei, dass die Funktion q aus Übung 2.1.43 nach [33] sogar gleichmäßig konvex ist.

2.1.44 Übung

Zeigen Sie, dass die Zielfunktion des Optimierungsproblems

$\min_{a,b}\ \left\|\begin{pmatrix}ax_1 + b-y_1\\\vdots\\ax_m + b-y_m\end{pmatrix}\right\|_2^2$

aus Übung 2.1.18 konvex ist, und bestimmen Sie unter der Voraussetzung, dass mindestens zwei der Stützstellen x_j, 1 ≤ j ≤ m, voneinander verschieden sind, den eindeutigen globalen Minimalpunkt sowie den globalen Minimalwert.

2.2 Numerische Verfahren

In diesem Abschnitt entwickeln wir numerische Verfahren zur Minimierung einer glatten Funktion $f:\mathbb R^n\to\mathbb R$ , wobei der vage Begriff „glatt“ bedeuten wird, dass die jeweils benötigten Stetigkeits- und Differenzierbarkeitsvoraussetzungen stets erfüllt sind. Alle vorgestellten Verfahren gehen von einem vom Benutzer bereitgestellten Startpunkt x⁰ aus und erzeugen daraus iterativ eine Folge (x^k), deren Häufungspunkte zumindest kritische Punkte von f sind, also Nullstellen des Gradienten ∇f. Wir werden sehen, dass diese Folge unter gewissen Voraussetzungen sogar konvergiert, und dass ihr Grenzpunkt üblicherweise ein lokaler Minimalpunkt von f sein wird. Nicht erwarten kann man, so numerisch einen globalen Minimalpunkt von f zu finden, sofern nicht zusätzliche globale Informationen über f vorliegen. Für Verfahren der globalen Optimierung verweisen wir stattdessen auf [33].

Abschn. 2.2.1 wird zunächst als sehr allgemeinen Rahmen ein sogenanntes Abstiegsverfahren einführen, ohne es bereits explizit auszugestalten. Trotzdem wird es möglich sein, hinreichende Bedingungen für das Terminieren dieses Verfahrens zu formulieren, die wir später für die explizit angegebenen Verfahren überprüfen können. Die neuen Iterierten werden dabei durch eine Kombination von Suchrichtungsvektoren und Schrittweiten entlang dieser Suchrichtungen generiert, und die genannten hinreichenden Bedingungen sind die sogenannte Gradientenbezogenheit der Suchrichtungsfolge sowie die Effizienz der Schrittweitenfolge. Abschn. 2.2.2 stellt drei Möglichkeiten zur Bestimmung effizienter Schrittweitenfolgen vor, die danach in den konkreten Abstiegsverfahren zum Einsatz kommen können.

In Abschn. 2.2.3 untersuchen wir die naheliegendste Wahl zur Konstruktion gradientenbezogener Suchrichtungsfolgen, was auf das Gradientenverfahren führt. Es erweist sich in der Praxis allerdings als sehr langsam, was wir zunächst durch die Einführung verschiedener Konvergenzgeschwindigkeiten quantifizieren. Mit der geometrischen Einsicht, dass der Hauptgrund für die Langsamkeit des Gradientenverfahrens in der mangelnden Verwertung von Krümmungsinformation der Zielfunktion liegt, modifizieren wir es in Abschn. 2.2.4 zur Klasse der Variable-Metrik-Verfahren.

Ein wichtiger Vertreter dieser Verfahrensklasse ist das in Abschn. 2.2.5 besprochene Newton-Verfahren. Obwohl seine quadratische Konvergenzgeschwindigkeit sehr hoch ist, besitzt es den entscheidenden Nachteil, unter oft nur sehr unrealistischen Voraussetzungen ein Abstiegsverfahren zu sein. Wir modifizieren unseren Ansatz daher weiter und geben in Abschn. 2.2.6 zunächst sehr allgemeine Voraussetzungen an, unter denen Variable-Metrik-Verfahren wenigstens superlinear konvergieren, bevor Abschn. 2.2.7 darauf basierend die Quasi-Newton-Verfahren einführt.

Dass die Quasi-Newton-Verfahren auf Krümmungsinformation aus Approximationen der Hesse-Matrix der Zielfunktion angewiesen sind, kann bei hochdimensionalen Optimierungsproblemen zu Speicherplatzproblemen führen. Daher versuchen wir, das Gradientenverfahren auch durch matrixfreie Verfahren zu verbessern. Überraschenderweise lässt sich durch eine geschickte Kombination von Gradienteninformationen so viel Krümmungsinformation gewinnen, dass tatsächlich solche Verfahren existieren. Dies sind die auf dem in Abschn. 2.2.8 erklärten Konzept der konjugierten Richtungen basierenden und in Abschn. 2.2.9 eingeführten Konjugierte-Gradienten-Verfahren.

Abschn. 2.2.10 widmet sich abschließend den Trust-Region-Verfahren, die im Gegensatz zu den anderen besprochenen Abstiegsverfahren nicht zuerst eine Suchrichtung und dann eine Schrittweite, sondern erst einen Suchradius und dann die Richtung zur neuen Iterierten bestimmen.

2.2.1 Abstiegsverfahren

Neben der Stetigkeit der Zielfunktion f werden wir im gesamten Abschn. 2.2 fordern, dass die untere Niveaumenge $f_\le^{f(x^0)}$ zum Startpunkt $x^0\in\mathbb R^n$ beschränkt ist. Falls diese Voraussetzung verletzt sein sollte, sind die vorgestellten Konvergenzbeweise nicht durchführbar, und die betrachteten Verfahren können dann nur als Heuristiken angesehen werden. Nach Lemma 1.2.26 ist die Voraussetzung aber zum Beispiel für jeden beliebigen Startpunkt x⁰ erfüllt, wenn f auf $\mathbb R^n$ koerziv ist.

Als ersten Grund für die Einführung dieser Voraussetzung stellen wir fest, dass für beschränktes $f_\le^{f(x^0)}$ eine stetige Funktion f nach Korollar 1.2.17 einen globalen Minimalpunkt besitzt und dass dann insbesondere die Gleichung ∇f(x) = 0 überhaupt lösbar ist.

2.2.1 Bemerkung

Für beschränktes $f_\le^{f(x^0)}$ ist die Funktion f also nach unten beschränkt. In der Literatur wird für Konvergenzbeweise manchmal auch nur diese schwächere Voraussetzung benutzt. Allerdings wird die dadurch später getroffene Voraussetzung der Lipschitz-Stetigkeit des Gradienten ∇f auf $f_\le^{f(x^0)}$ in vielen Anwendungen zu einer starken oder sogar unerfüllbaren Voraussetzung (s. dazu Bemerkung 2.2.11).

Als erste algorithmische Idee könnte man versuchen, die Gleichung ∇f(x) = 0 mit dem aus der Numerik bekannten Newton-Verfahren

$x^{k + 1}\ =\ x^k\ -\ (D^2f(x^k))^{-1}\nabla f(x^k),\quad k=0,1,2,\,\ldots\,$

zu lösen (für eine geometrische Interpretation s. [24, 33]). Vorteil wäre eine hohe Konvergenzgeschwindigkeit, falls x⁰ nahe genug an einer Lösung liegt. Nachteilig ist, dass x⁰ nicht in der Nähe einer Lösung zu liegen braucht, dass die Hesse-Matrix $D^2f(x^k)$

nicht notwendig invertierbar sein muss (und eventuell schwer auszuwerten) und dass das Newton-Verfahren auch gegen lokale Maximalpunkte und Sattelpunkte konvergieren kann.

Obwohl wir wegen der hohen lokalen Konvergenzgeschwindigkeit in Abschn. 2.2.5 ausführlich auf die Idee des Newton-Verfahrens zurückkommen werden, betrachten wir stattdessen zunächst Verfahren, die in jedem Iterationsschritt einen Abstieg im Zielfunktionswert erzeugen, für die also

$\forall\ k\in\mathbb N_0:\quad f(x^{k + 1})\ <\ f(x^k)$

gilt. Solche Verfahren können nur „unter sehr unglücklichen Umständen“ gegen lokale Maximalpunkte konvergieren (z. B. falls x⁰ bereits zufällig lokaler Maximalpunkt ist oder falls man bei einem langen Abstiegsschritt einen lokalen Minimalpunkt überspringt und zufällig einen lokalen Maximalpunkt trifft), und aus geometrischen Überlegungen heraus ist die Konvergenz gegen Sattelpunkte unwahrscheinlich (x⁰ müsste in einer nicht volldimensionalen Mannigfaltigkeit liegen, damit ein Abstiegsverfahren gegen einen Sattelpunkt konvergiert, was wegen stets präsenter kleiner numerischer Störungen nicht zu erwarten ist).

Ein allgemeines Abstiegsverfahren ist in Algorithmus 2.3 formuliert. In seinem Input sowie nachfolgend sprechen wir etwas lax von einem „C¹-Optimierungsproblem P“, wenn die definierenden Funktionen von P stetig differenzierbar sind.

Aus theoretischer Sicht würde häufig sogar nur die Differenzierbarkeit genügen. In Anwendungen sind differenzierbare Funktionen aber typischerweise auch stetig differenzierbar, so dass diese Voraussetzung üblich ist und keine entscheidende Einschränkung darstellt.

Algorithmus 2.3: Allgemeines Abstiegsverfahren

Input : C¹-Optimierungsproblem P

Output : Approximation $\bar x$ eines kritischen Punkts von f (falls das Verfahren terminiert; Korollar 2.2.10)

1 begin

2 Wähle einen Startpunkt x⁰, eine Toleranz $\varepsilon>0$ und setze $k=0$ .

3 While $\|\nabla f(x^k)\|>\varepsilon$ do

4 Wähle $x^{k + 1}$ mit $\ f(x^{k + 1})<f(x^k)\$ .

5 Ersetze k durch $k + 1$ .

6 end

7 Setze $\bar x=x^k$ .

8 end

Verschiedene Abstiegsverfahren unterscheiden sich durch die Wahl von x^k + 1 in Zeile 4 von Algorithmus 2.3. Im Folgenden werden wir zunächst unabhängig von der speziellen Ausgestaltung der Zeile 4 schwache Bedingungen an die Wahl von x^k + 1 herleiten, die garantieren, dass Algorithmus 2.3 tatsächlich nach endlich vielen Schritten terminiert.

Für den Fall, in dem diese schwachen Bedingungen verletzt sind, versieht man Algorithmus 2.3 häufig noch mit einer „Notbremse“, nämlich mit dem zusätzlichen Abbruchkriterium $k> k_\textrm{max}$ mit einer hohen Iterationszahl $k_\textrm{max}$ (wie etwa $k_\textrm{max}=10^4\cdot n$ ). Vom Output $\bar x$ kann man dann natürlich nicht erwarten, einen kritischen Punkt von f zu approximieren, aber immerhin erfüllt er die Ungleichung $f(\bar x)< f(x^0)$ . Zur Übersichtlichkeit werden wir im Folgenden auf die explizite Betrachtung der „Notbremse“ verzichten.

2.2.2 Bemerkung

In der Praxis ist man manchmal schon damit zufrieden, irgendeinen Punkt $\bar x$ mit besserem Zielfunktionswert als x⁰ zu finden, also mit $f(\bar x)< f(x^0)$ . Dafür genügen offenbar endlich viele Schritte jedes Abstiegsverfahrens (wie auch bei Verbesserungsheuristiken [24]), ohne dass das Abbruchkriterium in Zeile 3 erfüllt zu sein braucht. Die Implementierung der oben beschriebenen „Notbremse“ liefert bei jedem Abstiegsverfahren garantiert einen solchen Output $\bar x$ .

In Zeile 3 des allgemeinen Abstiegsverfahrens 2.3 testet man als Abbruchkriterium $\|\nabla f(x^k)\|>\varepsilon$ mit einer Toleranz ɛ > 0, da man nicht erwarten kann, numerisch einen kritischen Punkt exakt zu bestimmen (eine While-Schleife zur Bedingung $\|\nabla f(x^k)\|>0$ würde in den meisten Fällen also nie abbrechen). Der generierte Output $\bar x$ mit $\|\nabla f(\bar x)\|\le\varepsilon$ ist dann natürlich nur die Approximation eines kritischen Punkts.

Um zu garantieren, dass Algorithmus 2.3 nach endlich vielen Iterationen terminiert, muss man nachweisen können, dass unabhängig von der Wahl von ɛ ein $k\in\mathbb N$ mit $\|\nabla f(x^k)\|\le\varepsilon$ existiert. Dies ist sicher dann gewährleistet, wenn die Folge (∇f(x^k)) gegen den Nullvektor konvergiert. Es genügt aber beispielsweise auch, dass diese Folge den Nullvektor lediglich als Häufungspunkt besitzt. Da andererseits für vorgegebenes ɛ > 0 im Fall der Terminierung von Algorithmus 2.3 gar keine unendliche Folge erzeugt werden würde, werden wir für die folgenden Konvergenzuntersuchungen künstlich ɛ = 0 setzen und von den erhaltenen Resultaten auf die endliche Terminierung im Fall ɛ > 0 schließen.

Zunächst untersuchen wir, ob die Iterierten x^k selbst sowie ihre Funktionswerte konvergieren.

2.2.3 Lemma

Für beschränktes $f_\le^{f(x^0)}$ bricht die von Algorithmus 2.3 mit ɛ = 0 erzeugte Folge (x^k) entweder nach endlich vielen Schritten mit einem kritischen Punkt ab, oder sie besitzt mindestens einen Häufungspunkt in $f_\le^{f(x^0)}$ , und die Folge der Funktionswerte (f(x^k)) ist konvergent.

Beweis.

Aufgrund der Abstiegseigenschaft in Zeile 4 liegen alle Iterierten x^k in der Menge $f_\le^{f(x^0)}$ . Diese ist als beschränkt vorausgesetzt und nach Übung 1.2.10 außerdem abgeschlossen, insgesamt also kompakt. Nach dem Satz von Bolzano-Weierstraß (z. B. [18]) besitzt die Folge (x^k) also mindestens einen Häufungspunkt in $f_\le^{f(x^0)}$ . Außerdem ist die Folge (f(x^k)) monoton fallend und durch den globalen Minimalwert von f nach unten beschränkt, also konvergent.

Die folgende Übung zeigt, dass aus Lemma 2.2.3 noch nicht folgt, dass ein Häufungspunkt der Iterierten x^k existiert, der auch kritischer Punkt von f ist.

2.2.4 Übung

Betrachten Sie die Funktion f(x) = x², den Startpunkt x⁰ = 3 sowie die Iterierten $x^k=(-1)^k(1 + 1/k)$ , $k\in\mathbb N$ . Zeigen Sie, dass die Iterierten die Abstiegsbedingung aus Zeile 4 von Algorithmus 2.3 erfüllen, dass sie zwei Häufungspunkte besitzen, dass aber keiner davon kritischer Punkt von f ist.

Um Bedingungen an die Wahl von x^k + 1 in Zeile 4 von Algorithmus 2.3 herzuleiten, die dessen Terminieren gewährleisten, stellen wir zunächst fest, dass man ohne Einschränkung

$x^{k + 1}\ =\ x^k + t^k d^k$

(2.2)

mit t^k > 0 und $d^k\in\mathbb R^n$ ansetzen darf, denn durch passende Wahlen von t^k und d^k lässt sich jede neue Iterierte x^k + 1 in dieser Form realisieren. Eine einfache Möglichkeit dafür wäre es, $d^k=x^{k + 1}-x^k$ und t^k = 1 zu setzen; nachfolgend werden wir d^k und t^k aber geschickter wählen.

Die Wahl der neuen Iterierten x^k + 1 wird durch den Ansatz (2.2) in zwei separate Operationen aufgeteilt, nämlich die Bestimmung einer Suchrichtung d^k und die einer Schrittweite t^k. Die klassischen Optimierungsverfahren, auf die wir uns zunächst konzentrieren werden, bestimmen erst eine Suchrichtung d^k und dann eine Schrittweite t^k. Man spricht daher auch von Suchrichtungsverfahren mit Schrittweitensteuerung. Die Grundidee der moderneren Trust-Region-Verfahren, die wir in Abschn. 2.2.10 besprechen werden, besteht darin, erst einen Suchradius t^k und dann eine Abstiegsrichtung d^k zu berechnen.

Wir beginnen mit Suchrichtungsverfahren. Im Folgenden sei d^k eine Abstiegsrichtung erster Ordnung für f in x^k, es gelte also $\langle\nabla f(x^k),d^k\rangle<0$ . Wir suchen nach schwachen Bedingungen an die Wahl von t^k und d^k, die $\lim_k \nabla f(x^k)=0$ garantieren, also $\nabla f(x^\star)=0$ für jeden Häufungspunkt $x^\star$ der Folge (x^k).

Wegen der in Lemma 2.2.3 gezeigten Konvergenz der Folge (f(x^k)) konvergieren jedenfalls die Differenzen $f(x^k + \,t^k d^k)-f(x^k)$ gegen null. Nach dem Satz von Taylor (Satz 2.1.30) stimmt der tatsächliche Abstieg $f(x^k + t^k d^k)-f(x^k)<0$

ungefähr mit dem „Abstieg erster Ordnung“ $t^k \langle\nabla f(x^k),d^k\rangle<0$ überein, woraus wir durch geeignete Voraussetzungen die Konvergenz der ∇f(x^k) gegen null schließen können. Zunächst fordern wir, dass der tatsächliche Abstieg eine Unterschranke an den Abstieg erster Ordnung liefert, dass die Werte von f also hinreichend schnell fallen:

$\exists\ c_1>0\ \forall k\in\mathbb N:\quad f(x^k + t^k d^k)-f(x^k)\ \le\ c_1\cdot t^k \langle\nabla f(x^k),d^k\rangle.$

(2.3)

Wegen $0> f(x^k + t^k d^k)-f(x^k)\to0$ und $c_1\cdot t^k \langle\nabla f(x^k),d^k\rangle<0$ liefert das Sandwich-Theorem

$\lim_k\, t^k \langle\nabla f(x^k),d^k\rangle\ =\ 0.$

(2.4)

Um hieraus zu schließen, dass schon $\lim_k\nabla f(x^k)=0$ gilt, müssen wir Bedingungen an die Folgen (t^k) und (d^k) aufstellen, die ausschließen, dass der Grenzwert in (2.4) aus anderen Gründen null wird.

Um wenigstens $\lim_k \langle\nabla f(x^k),d^k\rangle=0$ schließen zu können, darf jedenfalls (t^k) nicht zu schnell gegen null konvergieren, muss also genügend groß bleiben. Wir fordern daher

$\exists\ c_2>0\ \forall k\in\mathbb N:\quad t^k\ \ge\ -c_2\cdot\frac{\langle\nabla f(x^k),d^k\rangle}{\|d^k\|_2^2},$

(2.5)

wobei wir die Motivation der Division durch $\|d^k\|_2^2$ für einen Moment zurückstellen. Wegen

$\underbrace{t^k \langle\nabla f(x^k),d^k\rangle}_{<\ 0,\ \to\ 0}\ \le\ -c_2\left(\frac{\langle\nabla f(x^k),d^k\rangle}{\|d^k\|_2}\right)^2\ <\ 0$

liefert das Sandwich-Theorem dann

$\lim_k\,\frac{\langle\nabla f(x^k),d^k\rangle}{\|d^k\|_2}\ =\ 0.$

(2.6)

Für dieses Ergebnis reicht es sogar, nur eine Kombination von (2.3) und (2.5) zu fordern.

2.2.5 Definition (Effiziente Schrittweiten)

Es sei (d^k) eine Folge von Abstiegsrichtungen erster Ordnung, und (t^k) erfülle

$\exists\ c>0\ \forall\ k\in\mathbb N:\quad f(x^k + t^k d^k)-f(x^k)\ \le\ -c\cdot\left(\frac{\langle\nabla f(x^k),d^k\rangle}{\|d^k\|_2}\right)^2.$

Dann heißt (t^k) effiziente Schrittweitenfolge (für (d^k)).

Das folgende Ergebnis beweist man wie oben mit dem Sandwich-Theorem.

2.2.6 Satz

Die Menge $f_\le^{f(x^0)}$ sei beschränkt, (d^k) sei eine Folge von Abstiegsrichtungen erster Ordnung, und (t^k) sei eine effiziente Schrittweitenfolge. Dann gilt (2.6).

Nun benötigen wir noch eine Bedingung an die Folge (d^k), die $\lim_k\nabla f(x^k)=0$ garantiert. Dazu stellen wir fest, dass (2.6) zwar unter der gewünschten Bedingung $\lim_k\nabla f(x^k)=0$ gilt (weil alle Vektoren $d^k/\|d^k\|_2$ die Länge eins besitzen und damit eine beschränkte Folge bilden), dass (2.6) aber auch dadurch erfüllt sein kann, dass nicht die Längen der Vektoren ∇f(x^k) gegen null gehen, sondern ihre Richtungen im Grenzüber- gang senkrecht zu einem Grenzpunkt der Folge $(d^k/\|d^k\|_2)$ stehen. In diesem Sinne müssen wir also ausschließen, dass die Vektoren ∇f(x^k) und $d^k/\|d^k\|_2$ „asymptotisch senkrecht“ aufeinander stehen. Ohne die Division von d^k durch $\|d^k\|_2$ würde man dann insbesondere den Fall d^k→0 ausschließen, was aber bereits für die Wahl $d^k=-\nabla f(x^k)$ wegen des gewünschten Verhaltens der Folge (∇f(x^k)) sinnlos wäre.

Die stumpfen Winkel zwischen ∇f(x^k) und $d^k/\|d^k\|_2$ dürfen also nicht gegen einen rechten Winkel konvergieren. Äquivalent können wir fordern, dass die negativen Werte $\cos\left(\,\angle(\nabla f(x^k),d^k/\|d^k\|_2)\,\right)$ nicht gegen null konvergieren. Dazu setzen wir die Existenz einer Konstante c > 0 voraus, so dass alle $k\in\mathbb N$ die Ungleichung

$\cos\left(\,\angle\left(\nabla f(x^k),\,\frac{d^k}{\|d^k\|_2}\right)\,\right)\ \le\ -c$

erfüllen. Aufgrund der Darstellung des Skalarprodukts aus (2.1) ist diese Ungleichung äquivalent zu

$\frac{\left\langle\nabla f(x^k),\frac{d^k}{\|d^k\|_2}\right\rangle}{\left\|\frac{d^k}{\|d^k\|_2}\right\|_2}\ \le\ -c\cdot\|\nabla f(x^k)\|_2,$

wobei wir die Ungleichung mit dem Faktor $\|\nabla f(x^k)\|_2$ durchmultipliziert haben, um den Fall $\|\nabla f(x^k)\|_2=0$ abzufangen. Dies rechtfertigt die folgende Definition.

2.2.7 Definition (Gradientenbezogene Suchrichtungen)

Die Folge von Suchrichtungen (d^k) heißt gradientenbezogen , falls

$\exists\ c>0\ \forall\ k\in\mathbb N:\quad \frac{\langle\nabla f(x^k),d^k\rangle}{\|d^k\|_2}\ \le\ -c\cdot\|\nabla f(x^k)\|_2$

gilt.

2.2.8 Übung

Zeigen Sie, dass die Folge der Suchrichtungen $d^k=-\nabla f(x^k)$ , $k\in\mathbb N$ , gradientenbezogen ist.

Wir können nun das folgende zentrale Ergebnis zum allgemeinen Abstiegsverfahren zeigen.

2.2.9 Satz

Die Menge $f_\le^{f(x^0)}$ sei beschränkt, und in Zeile 4 von Algorithmus 2.3 sei $x^{k + 1}=x^k + t^k d^k$ mit einer gradientenbezogenen Suchrichtungsfolge (d^k) und einer effizienten Schrittweitenfolge (t^k) gewählt. Für ɛ = 0 stoppt dann das Verfahren entweder nach endlich vielen Schritten mit einem kritischen Punkt, oder die Folge (x^k) besitzt einen Häufungspunkt, und für jeden solchen Punkt $x^\star$ gilt $\nabla f(x^\star)=0$ .

Beweis.

Aus Lemma 2.2.3 wissen wir, dass das Verfahren entweder nach endlich vielen Schritten mit einem kritischen Punkt abbricht oder die Folge (x^k) einen Häufungspunkt in $f_\le^{f(x^0)}$ besitzt. Es bezeichne $x^\star$ einen beliebigen solchen Häufungspunkt. Satz 2.2.6, die Definition der Gradientenbezogenheit sowie das Sandwich-Theorem liefern nun die Behauptung.

Dass Algorithmus 2.3 nach endlichen vielen Schritten mit einer exakten Lösung abbricht, ist natürlich kaum zu erwarten, wird in Satz 2.2.9 aber als Alternative angeführt, damit man andernfalls über Häufungspunkte einer „echten“ Folge sprechen kann.

Für den Fall, dass in $f_\le^{f(x^0)}$ nur ein einziger kritischer Punkt $x^\star$ liegt, muss dieser der globale Minimalpunkt von f sein, und jeder Häufungspunkt der Folge (x^k) aus Satz 2.2.9 stimmt mit $x^\star$ überein. Dies bedeutet, dass dann sogar $\lim_k x^k=x^\star$ gilt.

2.2.10 Korollar

2.2.2 Schrittweitensteuerung

Während die Existenz einer gradientenbezogenen Suchrichtungsfolge nach Übung 2.2.8 klar ist, müssen wir uns noch mit der Konstruktion effizienter Schrittweiten befassen. Ob solche existieren, ist zunächst nicht klar, da die Bedingungen (2.3) und (2.5) grob gesagt gleichzeitig Ober- und Unterschranken an t^k fordern und damit vielleicht nicht simultan erfüllbar sind. Im Folgenden sei der Index $k\in\mathbb N$ der besseren Übersichtlichkeit halber fest und unterschlagen, d. h., wir setzen x = x^k, t = t^k und d = d^k.

In der Tat werden wir die Effizienz von drei beliebten Schrittweitenstrategien nachweisen, nämlich der Wahl exakter Schrittweiten t_e, gewisser konstanter Schrittweiten t_c sowie der Armijo-Schrittweiten t_a. Allgemein bezeichnet man die Wahl geeigneter Schrittweiten auch als Schrittweitensteuerung (line search).

Als grundlegende Voraussetzung für die zugehörigen Effizienzbeweise werden wir die Lipschitz-Stetigkeit des Gradienten ∇f auf der Menge $f^{f(x^0)}_\le$ benötigen. Dazu sei daran erinnert, dass eine Funktion $F:D\to\mathbb R^m$ Lipschitz-stetig auf $D\subseteq\mathbb R^n$ (bezüglich der euklidischen Norm) heißt, falls

$\exists\ L>0\ \forall\ x,y\in D:\quad \|F(x)-F(y)\|_2\ \le\ L\cdot \|x-y\|_2$

gilt. Da C¹-Funktionen auf kompakten Mengen immer Lipschitz-stetig sind (z. B. [12]), ist ∇f bei beschränkter Menge $f_\le^{f(x^0)}$ zum Beispiel für jede C²-Funktion f Lipschitz-stetig auf $f_\le^{f(x^0)}$ . Dieses Wissen schließt leider nicht automatisch die Kenntnis der Größe der Konstante L ein, was uns später bei der Wahl konstanter Schrittweiten t_c ein Problem bereiten wird.

2.2.11 Bemerkung

Für beschränkte (und daher kompakte) Mengen $f_\le^{f(x^0)}$ ist die Voraussetzung der Lipschitz-Stetigkeit von ∇f auf $f_\le^{f(x^0)}$ also eine schwache Voraussetzung. Dies wäre nicht der Fall, wenn wir anstelle der Beschränktheit von $f_\le^{f(x^0)}$ z. B. nur gefordert hätten, dass f auf $\mathbb R^n$ nach unten beschränkt ist (vgl. dazu Bemerkung 2.2.1).

Beweistechnisch werden wir im folgenden Lemma die Lipschitz-Stetigkeit von ∇f auf einer konvexen Menge ausnutzen müssen, was bei der Menge $f_\le^{f(x^0)}$ aber nicht notwendigerweise gegeben ist. Daher werden wir sie sogar auf der konvexen Hülle $\textrm{conv}(f_\le^{f(x^0)})$ von $f_\le^{f(x^0)}$ fordern, also auf der kleinsten konvexen Obermenge von $f_\le^{f(x^0)}$ .

2.2.12 Bemerkung

Bei beschränktem (und daher kompaktem) $f_\le^{f(x^0)}$ ist die Menge $\textrm{conv}(f_\le^{f(x^0)})$ ebenfalls kompakt, so dass die Forderung der Lipschitz-Stetigkeit von ∇f auch auf $\textrm{conv}(f_\le^{f(x^0)})$ eine schwache Voraussetzung ist.

Das folgende Ergebnis besagt, dass man bei Lipschitz-stetigem Gradienten den Fehlerterm $o(\|x-\bar x\|)$ aus der multivariaten Taylor-Entwicklung erster Ordnung (Satz 2.1.30a) betraglich durch einen quadratischen Term nach oben abschätzen kann.

2.2.13 Lemma

Auf einer konvexen Menge $D\subseteq\mathbb R^n$ sei f differenzierbar mit Lipschitz-stetigem Gradienten ∇f und zugehöriger Lipschitz-Konstante L > 0. Dann gilt

$\forall\,\bar x,x\in D:\quad |f(x)-f(\bar x)-\langle\nabla f(\bar x),x-\bar x\rangle|\ \le\ \frac{L}2\|x-\bar x\|_2^2\,.$

Beweis.

Für $\bar x$ und x aus D folgt wegen der Konvexität von D für alle t ∈ [0, 1]

$\bar x + t(x-\bar x)\ =\ (1-t)\bar x + tx\ \in\ D,$

so dass wir die Lipschitz-Stetigkeit von ∇f für alle Punkte $\bar x + t(x-\bar x)$ mit t ∈ [0, 1] ausnutzen können. Wir fassen den Punkt x als den für t = 1 auftretenden Endpunkt der Strecke

$[\bar x,x]\ =\ \{\bar x + t(x-\bar x)|\ t\in[0,1]\}$

auf und betrachten den Fehlerterm zusätzlich entlang dieser Strecke. Er erfüllt

$f(\bar x + t(x-\bar x))-f(\bar x)-\langle\nabla f(\bar x),\bar x + t(x-\bar x)-\bar x\rangle\ =\ f(\bar x + t(x-\bar x))-f(\bar x)-t\langle\nabla f(\bar x),x-\bar x\rangle.$

Aufgrund von

$\frac{d}{dt}(\,f(\bar x + t(x-\bar x))-f(\bar x)-t\langle\nabla f(\bar x),x-\bar x\rangle\,)\ =\ \langle\nabla f(\bar x + t(x-\bar x))-\nabla f(\bar x),x-\bar x\rangle$

können wir daher den Fehlerterm bei t = 1 „künstlich kompliziert“ als

$\begin{aligned}f(x)-f(\bar x)-\langle\nabla f(\bar x),x-\bar x\rangle\ =\ \int_0^1\langle\nabla f(\bar x + t(x-\bar x))-\nabla f(\bar x),x-\bar x\rangle\, dt\end{aligned}$

schreiben. Die Dreiecksungleichung für Integrale, die Cauchy-Schwarz-Ungleichung sowie die Lipschitz-Stetigkeit von ∇f liefern somit

$\begin{aligned}|f(x)-f(\bar x)-\langle\nabla f(\bar x),x-\bar x\rangle| & \le \int_0^1|\langle\nabla f(\bar x + t(x-\bar x))-\nabla f(\bar x),x-\bar x\rangle|\, dt\\ & \le \int_0^1 \|\nabla f(\bar x + t(x-\bar x))-\nabla f(\bar x)\|_2\cdot\|x-\bar x\|_2\, dt\\ & \le \int_0^1 L\cdot t\cdot \|x-\bar x\|_2^2\, dt\ =\ L\|x-\bar x\|_2^2\cdot \int_0^1 t\, dt\\ & = \frac{L}2\|x-\bar x\|_2^2\,.\end{aligned}$

Exakte Schrittweiten

Zu $x\in f_\le^{f(x^0)}$ sei eine Abstiegsrichtung erster Ordnung d für f in x gegeben. Wegen $\upvarphi_d'(0)=\langle\nabla f(x),d\rangle<0$ gilt $\upvarphi_d(t)<\upvarphi_d(0)$ für kleine positive t. Für beschränktes $f_\le^{f(x^0)}$ besitzt φ_d nach dem Satz von Weierstraß sogar globale Minimalpunkte t_e > 0, die exakte Schrittweiten genannt werden. Per Definition der eindimensionalen Einschränkung φ_d erfüllen sie

$f(x + t_ed)\ =\ \min_{t>0}\,f(x + td).$

Eine wichtige und im Folgenden häufig benutzte Eigenschaft jeder exakten Schrittweite ist die laut Fermat’scher Regel sowie Kettenregel gültige Beziehung

$0\ =\ \upvarphi_d'(t_e)\ =\ \langle\nabla f(x + t_e d),d\rangle.$

(2.7)

Eine exakte Schrittweite zu berechnen, um den größtmöglichen Abstieg von x aus entlang d zu erzielen, ist im Allgemeinen sehr aufwendig, so dass wir dieses Konzept meist nur für theoretische Zwecke benutzen werden und später stattdessen zu inexakten Schrittweiten übergehen werden. Bei spezieller Struktur von f lassen sich aber exakte Schrittweiten manchmal leicht berechnen, wie zum Beispiel die folgende Übung zeigt.

2.2.14 Übung

Gegeben sei die quadratische Funktion $q(x)={\textstyle\frac12} x^\intercal Ax + b^\intercal x$ mit $A=A^\intercal\succ0$ und $b\in\mathbb R^n$ , die nach Übung 1.2.24 koerziv und nach Übung 2.1.43 konvex ist. Zeigen Sie, dass für jedes $x\in\mathbb R^n$ und jede Abstiegsrichtung erster Ordnung d für q in x die exakte Schrittweite eindeutig zu

$t_e\ =\ -\frac{\langle Ax + b,d\rangle}{d^\intercal Ad}$

bestimmt ist.

2.2.15 Satz

Die Menge $f_\le^{f(x^0)}$ sei beschränkt, die Funktion ∇f sei Lipschitz-stetig auf $\textrm{conv}(f_\le^{f(x^0)})$ , und (d^k) sei eine Folge von Abstiegsrichtungen erster Ordnung. Dann ist jede Folge von exakten Schrittweiten $(t_e^k)$ effizient.

Beweis.

Der Index $k\in\mathbb N$ sei wieder fest und unterschlagen. Da man von x⁰ aus nur Abstiege ausgeführt hat, liegen sowohl x als auch x + t_ed in der Menge $f_\le^{f(x^0)}$ . Es sei L > 0 eine nach Voraussetzung existierende Lipschitz-Konstante von ∇f auf $\textrm{conv}(f_\le^{f(x^0)})$ . Aus der Cauchy-Schwarz-Ungleichung folgt dann zunächst

$\begin{aligned}0 = \,& \upvarphi_d'(t_e)\ =\ \langle\nabla f(x + t_e d),d\rangle\ =\ \langle\nabla f(x + t_ed)-\nabla f(x),d\rangle + \langle\nabla f(x),d\rangle\\ \le \,& \|\nabla f(x + t_ed)-\nabla f(x)\|_2\cdot\|d\|_2 + \langle\nabla f(x),d\rangle\ \le\ L\cdot t_e \|d\|_2^2 + \langle\nabla f(x),d\rangle.\end{aligned}$

Demnach erfüllt t_e die Bedingung (2.5) mit $c_2=L^{-1}$ , also

$t_e\ \ge\ -\frac{\langle\nabla f(x),d\rangle}{L\cdot\|d\|_2^2}\ =:\ t_c\,.$

Die positive Hilfsgröße t_c lässt sich ebenfalls als Schrittweite auffassen, was wir später ausnutzen werden.

Wegen x, $x + t_ed\in f^{f(x^0)}_\le$ liegt der Punkt x + td für alle t ∈ (0, t_e) in $\textrm{conv}(f_\le^{f(x^0)})$ . Lemma 2.2.13 liefert daher für diese t

$f(x + td)-f(x)-t\langle\nabla f(x),d\rangle\ \le\ |f(x + td)-f(x)-t\langle\nabla f(x),d\rangle|\ =\ t^2\frac{L}2\|d\|_2^2.$

Für t_c folgt daraus

$\begin{aligned}f(x + t_cd)-f(x) \le \,& t_c\left(\,\langle\nabla f(x),d\rangle + t_c\frac{L}2\|d\|_2^2\,\right)\\ = \,& -\frac{\langle\nabla f(x),d\rangle}{L\cdot\|d\|_2^2}\left(\,\langle\nabla f(x),d\rangle-\frac{\langle\nabla f(x),d\rangle}{L\cdot\|d\|_2^2}\cdot\frac{L}2\|d\|_2^2\,\right)\\ = \,& -\frac1{2L}\left(\frac{\langle\nabla f(x),d\rangle}{\|d\|_2}\right)^2.\end{aligned}$

Wegen t_c > 0 und der globalen Minimalität der exakten Schrittweite t_e für φ_d(t) über t > 0 erhalten wir schließlich

$f(x + t_ed)-f(x)\ \le\ f(x + t_c d)-f(x)\ \le\ -\frac1{2L}\left(\frac{\langle\nabla f(x),d\rangle}{\|d\|_2}\right)^2,$

so dass mit der von $k\in\mathbb N$ unabhängigen Konstante c = (2L)⁻¹ die Behauptung folgt.

Damit ist neben der Existenz gradientenbezogener Suchrichtungen auch die Existenz effizienter Schrittweiten gezeigt, weshalb insbesondere Satz 2.2.9 nicht trivialerweise gilt (weil er nicht „von der leeren Menge handelt“).

Konstante Schrittweiten

Falls die Funktion f keine besondere Struktur aufweist (wie etwa in Übung 2.2.14), lohnt sich üblicherweise der Aufwand nicht, in jedem Iterationsschritt eine exakte Schrittweite $t_e^k$ zu berechnen. Da man weniger an Minimalpunkten der Hilfsfunktionen $\upvarphi_{d^k}$ interessiert ist als an denen von f, benutzt man dann lieber inexakte Schrittweiten, die ebenfalls effizient, aber erheblich leichter zu berechnen sind.

Eine zunächst naheliegend erscheinende Möglichkeit dafür besteht darin, anstelle von $t_e^k$

die im Beweis von Satz 2.2.15 aufgetretenen und leicht berechenbaren Hilfsgrößen

$t_c^k\ =\ -\frac{\langle\nabla f(x^k),d^k\rangle}{L\cdot\|d^k\|_2^2}$

als Schrittweiten zu benutzen, denn dort wurde insbesondere auch die Effizienz der Folge $(t^k_c)$

gezeigt. Im speziellen Fall $d^k=-\nabla f(x^k)$ gilt sogar

$t_c^k\ =\ \frac1L,$

so dass die Folge der Schrittweiten dann konstant ist.

Leider lässt sich diese Wahl algorithmisch nur umsetzen, wenn eine Lipschitz-Konstante L > 0 von ∇f auf $\textrm{conv}(f_\le^{f(x^0)})$ explizit bekannt ist. Mit gewissem Aufwand und unter Einsatz der Intervallarithmetik [33] lassen sich Lipschitz-Konstanten in der Tat häufig ermitteln. Während allerdings nur kleinstmögliche Lipschitz-Konstanten das Verhalten von ∇f gut beschreiben, muss man sich dann oft mit groben Überschätzungen von L zufrieden geben. Die entsprechenden Schrittweiten $t_c^k$ können dadurch sehr klein werden, so dass die Iteration langsamer als nötig voranschreitet.

Es sei betont, dass eine explizite Kenntnis von L im Effizienzbeweis für die exakten Schrittweiten in Satz 2.2.15 nicht erforderlich war.

Armijo-Schrittweiten

Eine in modernen Implementierungen von Optimierungsverfahren sehr beliebte inexakte Schrittweitensteuerung geht auf eine Idee von Armijo zurück: Zu $x\in f^{f(x^0)}_\le$ seien d eine Abstiegsrichtung erster Ordnung und σ ∈ (0, 1). Dann existiert ein $\check{\kern-1pt t}>0$ , so dass für alle $t\in(0,\check{\kern-1pt t})$ die Werte φ_d(t) unter der „nach oben gedrehten Tangente“ $\upvarphi_d(0) + t\upsigma \upvarphi_d'(0)$ liegen, so dass also

$f(x + td)\ \le\ f(x) + t\upsigma \langle\nabla f(x),d\rangle$

gilt (Abb. 2.5).

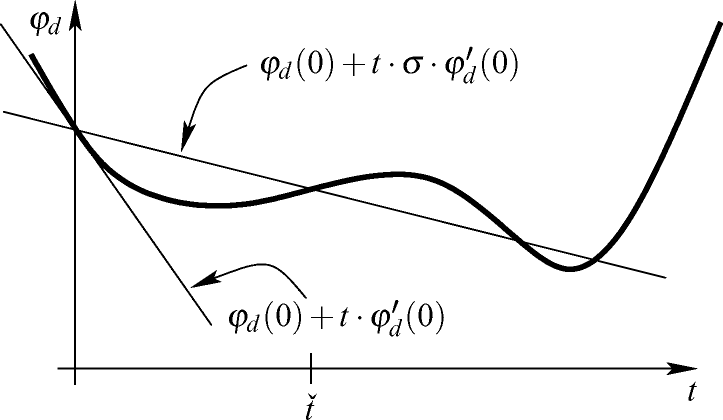
../images/439970_1_De_2_Chapter/439970_1_De_2_Fig5_HTML.png — Abb. 2.5
Armijo-Regel

Offensichtlich erfüllt jedes solche t die Bedingung (2.3) mit c₁ = σ. Wie kann man unter diesen Schrittweiten aber ein t_a > 0 so wählen, dass außerdem (2.5) erfüllt ist? Dies realisiert die in Algorithmus 2.4 angegebene Armijo-Regel mit einer Backtracking Line Search genannten Idee.

Algorithmus 2.4: Armijo-Regel

Input : C¹-Funktion f und $x,d\in\mathbb R^n$ mit $\langle\nabla f(x),d\rangle<0$

Output : Armijo-Schrittweite t_a

1 begin

2 Wähle $\sigma,\rho\in(0,1)$ sowie $\gamma>0$ (alle unabhängig von x und d).

3 Wähle eine Startschrittweite $t^0\ge-\gamma\,\langle\nabla f(x),d\rangle/\|d\|_2^2$ und setze $\ell=0$ .

4 While $f(x + t^\ell d)\,>\,f(x) + t^\ell\sigma \langle\nabla f(x),d\rangle$ do

5 Setze $t^{\ell + 1}=\rho\, t^\ell$ .

6 Ersetze ℓ durch $\ell + 1$ .

7 end

8 Setze $t_a=t^\ell$ .

9 end

2.2.16 Satz

Die Menge $f_\le^{f(x^0)}$ sei beschränkt, die Funktion ∇f sei Lipschitz-stetig auf $\textrm{conv}(f_\le^{f(x^0)})$ , und (d^k) sei eine Folge von Abstiegsrichtungen erster Ordnung. Dann ist die Folge der Armijo-Schrittweiten $(t_a^k)$ aus Algorithmus 2.4 (mit unabhängig von k gewählten Parametern σ, ρ und γ) wohldefiniert und effizient.

Beweis.

Der Index $k\in\mathbb N$ sei wieder fest und unterschlagen. Wegen ρ ∈ (0, 1) gilt in Algorithmus 2.4 $\lim_\ell t^\ell=0$ , also existiert ein $\ell_0\in\mathbb N$ mit $t^{\ell_0}\in (0,\check{\kern-1pt t})$ (Abb. 2.5). Die Abbruchbedingung in Zeile 4 von Algorithmus 2.4 ist folglich nach endlich vielen Schritten erfüllt, und die Folge der Armijo-Schrittweiten ist damit wohldefiniert.

Da nach den Vorüberlegungen (2.3) mit c₁ = σ für t_a erfüllt ist, bleibt noch (2.5) zu zeigen. Falls Algorithmus 2.4 bereits bei $\ell=0$ abbricht, so gilt (2.5) mit c₂ = γ. Im Folgenden sei also $t_a=t^\ell$ mit $\ell>0$ . Da $t^{\ell-1}$ das Abbruchkriterium noch nicht erfüllt hatte, gilt

$f(x + t^{\ell-1}d)\ >\ f(x) + t^{\ell-1}\upsigma \langle\nabla f(x),d\rangle.$

(2.8)

Um die vorausgesetzte Lipschitz-Bedingung auf $\textrm{conv}(f_\le^{f(x^0)})$ einzusetzen, unterscheiden wir nun zwei Fälle, wobei $[x,x + t^{\ell-1}d]$ die Strecke $\{\,x + td|\,t\in[0,t^{\ell-1}]\,\}$ bezeichne.

Fall 1: $\ [x,x + t^{\ell-1}d]\,\subseteq\,\textrm{conv}(f_\le^{f(x^0)})$

Nach dem Mittelwertsatz existiert ein θ ∈ (0, 1) mit

$f(x + t^{\ell-1}d)\ =\ f(x) + t^{\ell-1} \langle\nabla f(x + \theta t^{\ell-1}d,d\rangle.$

Wegen (2.8) und $t^{\ell-1}>0$ folgt daraus

$\upsigma \langle\nabla f(x),d\rangle\ <\ \langle\nabla f(x + \theta t^{\ell-1}d),d\rangle,$

also mittels Cauchy-Schwarz-Ungleichung und Lipschitz-Bedingung

$(\upsigma-1)\langle\nabla f(x),d\rangle\ <\ \langle\nabla f(x + \theta t^{\ell-1}d)-\nabla f(x),d\rangle\ \le\ L\cdot\theta t^{\ell-1}\|d\|_2^2\ \le\ Lt^{\ell-1}\|d\|_2^2.$

Wir erhalten

$t_a\ =\ \rho\cdot t^{\ell-1}\ \ge\ -\frac{\rho(1-\upsigma)}{L}\frac{\langle\nabla f(x),d\rangle}{\|d\|_2^2}.$

Fall 2: $\ [x,x + t^{\ell-1}d]\,\not\subseteq\,\textrm{conv}(f_\le^{f(x^0)})$

Die Lipschitz-Abschätzung ist in diesem Fall nicht auf ganz $[x,x + t^{\ell-1}d]$ garantiert. Mit einer exakten Schrittweite t_e liegen allerdings sowohl x als auch x + t_ed in $f_\le^{f(x^0)}$ und demnach die Strecke [x, x + t_ed] in $\textrm{conv}(f_\le^{f(x^0)})$ . Die Voraussetzung des zweiten Falls impliziert daher $t_e\le t^{\ell-1}$ . Mit der Schrittweite $t_c\le t_e$ aus dem Beweis zu Satz 2.2.15 folgt

$t_a\ =\ \rho\, t^{\ell-1}\ \ge\ \rho\, t_e\ \ge\ \rho\, t_c\ =\ -\frac{\rho}{L}\frac{\langle\nabla f(x),d\rangle}{\|d\|_2^2} \ \ge\ -\frac{\rho(1-\upsigma)}{L}\frac{\langle\nabla f(x),d\rangle}{\|d\|_2^2}.$

Insgesamt ist (2.5) also in jedem Fall mit

$c_2\ =\ \min\left\{\,\gamma,\,\frac{\rho(1-\upsigma)}L\,\right\}$

erfüllt. Da c₁ und c₂ unabhängig von k sind, folgt die Behauptung.

Angemerkt sei, dass die konkrete Größe der Lipschitz-Konstante L auch für diesen Effizienzbeweis irrelevant war.

In der Praxis haben sich Werte σ ∈ [0.01, 0.2] und ρ = 0.5 bewährt. Statt t⁰ in Algorithmus 2.4 per γ zu bestimmen, wird häufig t⁰ : = 1 gesetzt. Die folgende Übung zeigt, dass Algorithmus 2.4 dann aber nicht notwendigerweise terminiert.

2.2.17 Übung

Zeigen Sie für die Funktion $f(x)={\textstyle\frac12} x^2$ , den Startpunkt x⁰ = −3, die Richtungen $d^k=2^{-k}$ sowie $\upsigma={\textstyle\frac12}$ , dass der durch die Wahl t⁰ : = 1 modifizierte Algorithmus 2.4 nicht zu einer effizienten Schrittweitenfolge führt.

Man sollte t⁰ also so initialisieren, wie in Algorithmus 2.4 angegeben, wobei sich die Wahl γ = 10⁻⁴ bewährt hat. Es ist außerdem nicht schwer zu sehen, dass sich die Armijo-Regel auch für nur einseitig richtungsdifferenzierbare Funktionen einsetzen lässt, indem man das Skalarprodukt $\langle\nabla f(\bar x),d\rangle$ durch $f'(\bar x,d)$ ersetzt. Davon werden wir in Abschn. 3.3.6 Gebrauch machen.

2.2.3 Gradientenverfahren

Nach dieser Vorarbeit können wir mit Algorithmus 2.5 ein implementierbares numerisches Minimierungsverfahren angeben, nämlich das Gradientenverfahren . Es ist auch unter der Bezeichnung Cauchy-Verfahren bekannt, und ferner aufgrund seiner geometrischen Grundidee (Abschn. 2.1.3) als Verfahren des steilsten Abstiegs .

Algorithmus 2.5: Gradientenverfahren

Input : C¹-Optimierungsproblem P

Output : Approximation $\bar x$ eines kritischen Punkts von f (falls das Verfahren terminiert; Satz 2.2.18)

1 begin

2 Wähle einen Startpunkt x⁰, eine Toleranz $\varepsilon>0$ und setze $k=0$ .

3 While $\|\nabla f(x^k)\|>\varepsilon$ do

4 Setze $d^k=-\nabla f(x^k)$ .

5 Bestimme eine Schrittweite t^k.

6 Setze $x^{k + 1}=x^k + t^k d^k$ .

7 Ersetze k durch $k + 1$

6 end

9 Setze $\bar x=x^k$ .

10 end

2.2.18 Satz

Die Menge $f_\le^{f(x^0)}$ sei beschränkt, die Funktion ∇f sei Lipschitz-stetig auf $\textrm{conv}(f_\le^{f(x^0)})$ , und in Zeile 5 seien exakte Schrittweiten $(t_e^k)$ oder Armijo-Schrittweiten $(t_a^k)$ gewählt. Dann terminiert Algorithmus 2.5 für jedes ɛ > 0 nach endlich vielen Schritten. Falls eine Lipschitz-Konstante L > 0 zur Lipschitz-Stetigkeit von ∇f auf $\textrm{conv}(f_\le^{f(x^0)})$ bekannt ist, dann gilt dieses Ergebnis auch für die dann berechenbaren konstanten Schrittweiten $t_c^k=L^{-1}$ , $k\in\mathbb N$ .

Beweis.

Die Behauptungen folgen aus Korollar 2.2.10, Übung 2.2.8, Satz 2.2.15 sowie Satz 2.2.16.

Bei der Anwendung auf konvex-quadratische Zielfunktionen f sind sogar noch bessere Konvergenzaussagen für das Gradientenverfahren möglich. Zur Vorbereitung erinnern wir an die Definition der Spektralnorm einer (nicht notwendigerweise quadratischen) Matrix A als

$\|A\|_2\ :=\ \max\{\|Ad\|_2\,|\ \|d\|_2=1\}.$

Aus dieser Definition folgt für jeden Vektor d ≠ 0 sofort die Abschätzung

$\|Ad\|_2\ =\ \left\|A\,\frac{d}{\|d\|_2}\right\|_2\,\|d\|_2\ \le\ \|A\|_2\,\|d\|_2$

(2.9)

(und für d = 0 gilt sie ohnehin).

2.2.19 Übung

Gegeben sei die quadratische Funktion $q(x)={\textstyle\frac12} x^\intercal Ax + b^\intercal x$ mit $A=A^\intercal$ und $b\in\mathbb R^n$ . Zeigen Sie, dass der Gradient ∇q auf ganz $\mathbb R^n$ Lipschitz-stetig mit $L=\|A\|_2$ ist.

2.2.20 Beispiel

Für die Funktion $q(x)={\textstyle\frac12} x^\intercal Ax + b^\intercal x$ mit $A=A^\intercal\succ0$ und $b\in\mathbb R^n$ erzeugt das Gradientenverfahren eine sogar gegen den globalen Minimalpunkt von q konvergente Folge von Iterierten (x^k), wenn entweder exakte, konstante oder Armijo-Schrittweiten gewählt werden.

In der Tat ist q nach Übung 1.2.24 koerziv, weshalb zu jedem $x^0\in\mathbb R^n$ die untere Niveaumenge $q_\le^{q(x^0)}$ beschränkt ist. Ferner ist ∇q nach Übung 2.2.19 sogar auf ganz $\mathbb R^n$ Lipschitz-stetig mit $L=\|A\|_2$ . Die erwähnten Schrittweitenwahlen sind demnach effizient, so dass nach Satz 2.2.9 jeder Häufungspunkt der vom Gradientenverfahren für q erzeugten Iterierten x^k ein kritischer Punkt von q ist. Übung 2.1.43 zeigt außerdem, dass der einzige kritische Punkt $x^\star=-A^{-1} b$ von q mit dem eindeutigen globalen Minimalpunkt übereinstimmt. Damit konvergiert die Folge der Iterierten (x^k), und ihr Grenzpunkt ist globaler Minimalpunkt von q.

Nach Übung 2.2.14 ist bei jeder Abstiegsrichtung erster Ordnung für q in x die (eindeutige) exakte Schrittweite

$t_e\ =\ -\frac{\langle Ax + b,d\rangle}{d^\intercal Ad},$

beim Gradientenverfahren also

$t_e\ =\ \frac{\|\nabla q(x)\|_2^2}{Dq(x)A\nabla q(x)}$

mit ∇q(x) = Ax + b.

Wegen der expliziten Kenntnis der Lipschitz-Konstante $L=\|A\|_2$ ist schließlich auch die Wahl der konstanten Schrittweite $t_c=\|A\|_2^{-1}$ möglich. Mit der Berechnung der Spektralnorm $\|A\|_2$ einer symmetrischen und positiv definiten Matrix A als größtem Eigenwert $\lambda_\textrm{max}(A)$ von A werden wir uns in Bemerkung 2.2.38 befassen.

Aufgrund der Konvergenzresultate sowie wegen seiner einfachen Implementierbarkeit wird das Gradientenverfahren in der Praxis gerne benutzt. Allerdings hat die Strategie, in jedem Schritt lokal den steilsten Abstieg zu wählen (eine Greedy-Strategie), den Nachteil, dass das Verfahren häufig sehr langsam konvergiert. Man kann daher oft nur grobe Toleranzen ɛ > 0 vorgeben, wenn das Verfahren nach einer vertretbaren Zeit terminieren soll.

Geometrisch lässt sich die Langsamkeit des Gradientenverfahrens mit Hilfe der Ergebnisse aus Abschn. 2.1.3 begründen (Abb. 2.6): Falls die Höhenlinien von f die Form lang gezogener Ellipsen mit einem Minimalpunkt $x^\star$ in deren gemeinsamem Zentrum besitzen, dann zeigt −∇f(x^k) typischerweise nicht in die Richtung von $x^\star$ . Die Iterierten springen dadurch entlang einer Zickzacklinie, weshalb man in Anlehnung an die englischsprachige Literatur auch vom Zigzagging-Effekt spricht.

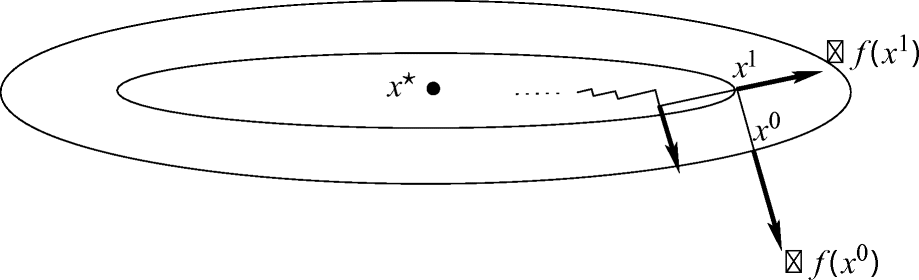
../images/439970_1_De_2_Chapter/439970_1_De_2_Fig6_HTML.png — Abb. 2.6
Zigzagging-Effekt

Um bessere Verfahren zu konstruieren, benötigen wir zunächst eine Klassifikation von Konvergenzgeschwindigkeiten.

2.2.21 Definition (Konvergenzgeschwindigkeiten)

Es sei (x^k) eine konvergente Folge mit Grenzpunkt $x^\star$ . Sie heißt

a)
linear konvergent , falls
$\exists\ 0< c<1,\ k_0\in\mathbb N\quad \forall\ k\ge k_0:\quad\|x^{k + 1}-x^\star\|\ \le\ c\cdot\|x^k-x^\star\|,$
b)
superlinear konvergent , falls
$\exists\ c^k\searrow0,\ k_0\in\mathbb N\quad \forall\ k\ge k_0:\quad\|x^{k + 1}-x^\star\|\ \le\ c^k\cdot\|x^k-x^\star\|,$
c)
quadratisch konvergent , falls
$\exists\ c>0,\ k_0\in\mathbb N\quad \forall k\ge k_0:\quad \|x^{k + 1}-x^\star\|\ \le\ c\cdot\|x^k-x^\star\|^2.$

Es ist nicht schwer zu sehen, dass quadratische Konvergenz superlineare Konvergenz impliziert und dass Letztere lineare Konvergenz nach sich zieht. Während superlineare Konvergenz „schnell“ und quadratische Konvergenz „sehr schnell“ sind, kann lineare Konvergenz bei einer Konstante c ≈ 1 sehr langsam sein.

Wir weisen darauf hin, dass die Punkte x^k in Definition 2.2.21 nicht notwendigerweise Iterierte eines Abstiegsverfahrens zu sein brauchen. Insbesondere kann man für ein Abstiegsverfahren auch die Konvergenzgeschwindigkeit der Funktionswerte f(x^k) gegen einen Grenzwert $f(x^\star)$ messen.

In der Tat zeigt der folgende Satz, dass das Gradientenverfahren schon für sehr angenehme Funktionen nur linear konvergente Funktionswerte der Iterierten besitzt, und zwar mit einer Konstante c, die sehr nahe bei eins liegen kann.

Konkret betrachten wir die konvex-quadratische Funktion $q(x)={\textstyle\frac12} x^\intercal Ax + b^\intercal x$ mit $A=A^\intercal\succ0$ sowie $b\in\mathbb R^n$ und bezeichnen den größten und den kleinsten Eigenwert der Matrix A mit $\lambda_\textrm{max}$ bzw. $\lambda_\textrm{min}$ . Nach Beispiel 2.2.20 konvergieren die Iterierten des Gradientenverfahrens mit exakten Schrittweiten gegen den globalen Minimalpunkt $x^\star=-A^{-1} b$ von q, und die Stetigkeit von q impliziert die Konvergenz der Funktionswerte q(x^k) gegen $q(x^\star)=-{\textstyle\frac12} b^\intercal A^{-1} b$ . Wir betrachten nun die Konvergenzgeschwindigkeit dieser Funktionswerte.

Dazu benötigen wir folgendes Ergebnis, das zum Beispiel in [16] bewiesen wird.

2.2.22 Lemma (Kantorowitsch-Ungleichung)

Es sei $A=A^\intercal\succ0$ mit maximalem und minimalem Eigenwert $\lambda_\textrm{max}$ bzw. $\lambda_\textrm{min}$ . Dann gilt für jedes $v\in\mathbb R^n\setminus\{0\}$

$\frac{v^\intercal A^{-1} v\cdot v^\intercal A v}{\|v\|_2^4}\ \le\ \frac{(\lambda_\textrm{max} + \lambda_\textrm{min})^2}{4\,\lambda_\textrm{max}\,\lambda_\textrm{min}}.$

2.2.23 Satz

Auf die konvex-quadratische Funktion $q(x)={\textstyle\frac12} x^\intercal Ax + b^\intercal x$ mit $A=A^\intercal\succ0$ und $b\in\mathbb R^n$ werde das Gradientenverfahren mit exakten Schrittweiten und ɛ = 0 angewendet. Dann gilt für alle $k\in\mathbb N$

$|q(x^{k + 1})-q(x^\star)|\ \le\ \left(\frac{\lambda_\textrm{max}-\lambda_\textrm{min}}{\lambda_\textrm{max} + \lambda_\textrm{min}}\right)^2|q(x^k)-q(x^\star)|.$

Beweis.

Es sei $k\in\mathbb N$ fest gewählt. Zur Übersichtlichkeit unterschlagen wir im Folgenden den Index k und setzen $x^+:=x^{k + 1}$ . Da $q(x^\star)$ globaler Minimalwert von q ist, sind die Beträge in der behaupteten Ungleichung überflüssig. Wegen $x^+=x-t_e\nabla q(x)$ und

$t_e\ =\ \frac{\|\nabla q(x)\|_2^2}{Dq(x)A\nabla q(x)}$

gilt

$q(x^+)-q(x^\star)\ =\ q(x)-t_e\|\nabla q(x)\|_2^2 + \frac{t^2_e}2\,Dq(x)A\nabla q(x)-q(x^\star)\ =\ q(x)-q(x^\star)-\frac12\frac{\|\nabla q(x)\|_2^4}{Dq(x)A\nabla q(x)}$

sowie

$q(x)-q(x^\star)\ =\ {\textstyle\frac12}\,Dq(x)A^{-1}\nabla q(x),$

wie man durch Ausmultiplizieren der rechten Seite leicht nachrechnet. Es folgt

$\frac{q(x^+)-q(x^\star)}{q(x)-q(x^\star)}\ =\ 1-\frac{\frac12\frac{\|\nabla q(x)\|_2^4}{Dq(x)A\nabla q(x)}}{q(x)-q(x^\star)} \ =\ 1-\frac{\|\nabla q(x)\|_2^4}{Dq(x)A^{-1}\nabla q(x)\cdot Dq(x)A\nabla q(x)}.$

Da das Gradientenverfahren im Fall ∇q(x) = 0 vor der Berechnung von x⁺ terminiert hätte, lässt sich Lemma 2.2.22 mit v = ∇q(x) ≠ 0 anwenden, und wir erhalten

$\begin{aligned}\frac{q(x^+)-q(x^\star)}{q(x)-q(x^\star)}\ \le\ 1-\frac{4\,\lambda_\textrm{max}\,\lambda_\textrm{min}}{(\lambda_\textrm{max} + \lambda_\textrm{min})^2}\ =\ \left(\frac{\lambda_\textrm{max}-\lambda_\textrm{min}}{\lambda_\textrm{max} + \lambda_\textrm{min}}\right)^2.\end{aligned}$

Satz 2.2.23 besagt zunächst nur, dass die Funktionswerte der Iterierten im Gradientenverfahren unter den dortigen Voraussetzungen mindestens linear mit der Konstante

$c\ =\ \left(\frac{\lambda_\textrm{max}-\lambda_\textrm{min}}{\lambda_\textrm{max} + \lambda_\textrm{min}}\right)^2$

konvergieren, was noch nicht ausschließt, dass das Verfahren trotzdem schneller läuft. Die numerische Erfahrung mit dem Gradientenverfahren zeigt allerdings, dass lineare Konvergenz mit der berechneten Konstante üblicherweise realisiert wird. Entscheidend ist hierbei, dass durch die passende Wahl der Matrix A Konstanten c beliebig nahe bei eins erzeugt werden können und man dadurch beliebig langsame lineare Konvergenz des Gradientenverfahrens erreicht. Dass $\lambda_\textrm{min}$ dazu im Vergleich zu $\lambda_\textrm{max}$ sehr klein werden muss, schlägt sich geometrisch in „sehr lang gezogenen“ Niveaumengen von q nieder, wie sie bereits als Höhenlinien in Abb. 2.6 illustriert wurden.

2.2.24 Bemerkung (Ellipsodiale Niveaumengen und Eigenwerte)

Da das Verständnis des Zusammenhangs zwischen Eigenwerten und Niveaumengen auch für den folgenden Abschnitt wesentlich ist, wiederholen wir an dieser Stelle kurz einige Grundlagen zu den ellipsodialen Niveaumengen

$q^\alpha_=\ :=\ \{x\in\mathbb R^n|\,q(x)=\alpha\}$

konvex-quadratischer Funktionen $q(x)={\textstyle\frac12} x^\intercal Ax + b^\intercal x$ mit $A=A^\intercal\succ0$ und $b\in\mathbb R^n$ .

Nach Übung 2.1.43 ist $\alpha_\textrm{min}=-{\textstyle\frac12} b^\intercal A^{-1} b$ das Minimalniveau von q, und den zugehörigen Minimalpunkt $x^\star=-A^{-1} b$ können wir als Mittelpunkt jedes Ellipsoids $q^\alpha_=$ mit $\alpha>\alpha_\textrm{min}$ auffassen. Für jedes solche α kann man von diesem Mittelpunkt $x^\star$ aus in eine beliebige vorgegebene Richtung $d\in\mathbb R^n$ „laufen“ und wird sicher die Niveaumenge $q_=^\alpha$ treffen. Allerdings wird die Größe der entsprechenden Schrittweite t > 0 mit $x^\star + td\in q_=^\alpha$ im Allgemeinen von der Richtung d abhängen. In Formeln ausgedrückt ist dies die Frage nach dem zu d gehörigen t > 0 mit

$\begin{aligned}\alpha\ =\ q(x^\star + td) = \,& {\textstyle\frac12}(x^\star + td)^\intercal A(x^\star + td) + b^\intercal(x^\star + td)\\ = \,& {\textstyle\frac12}(x^\star)^\intercal A(x^\star) + td^\intercal Ax^\star + {\textstyle\frac12} t^2d^\intercal A d + b^\intercal x^\star + tb^\intercal d\\ = \,& \left({\textstyle\frac12}(x^\star)^\intercal A(x^\star) + b^\intercal x^\star\right) + td^\intercal A(-A^{-1} b) + {\textstyle\frac12} t^2d^\intercal A d + tb^\intercal d\\ = \,& -{\textstyle\frac12} b^\intercal A^{-1} b-td^\intercal b + {\textstyle\frac12} t^2d^\intercal A d + tb^\intercal d\\ = \,& \alpha_\textrm{min} + {\textstyle\frac12} t^2d^\intercal A d.\end{aligned}$

Wählt man als Richtung d speziell einen auf Länge eins normierten Eigenvektor v der Matrix A, so folgt mit dem zugehörigen Eigenwert λ weiter

$\alpha-\alpha_\textrm{min}\ =\ {\textstyle\frac12} t^2v^\intercal A v\ =\ {\textstyle\frac12} t^2v^\intercal (\lambda v)\ =\ {\textstyle\frac12}\lambda t^2\|v\|_2^2\ =\ {\textstyle\frac12}\lambda t^2$

und damit

$t\ =\ \sqrt{\frac{2(\alpha-\alpha_\textrm{min})}{\lambda}},$

wobei wir benutzt haben, dass λ wegen der positiven Definitheit von A positiv ist. Die hergeleitete Formel für t besagt, dass es in Richtung eines Eigenvektors v von A (einer Hauptachse des Ellipsoids) von der Wurzel des Kehrwerts des zugehörigen Eigenwerts abhängt, wann die Menge $q_=^\alpha$ getroffen wird. Für Eigenwerte nahe bei null ist der Weg also sehr weit, während er für große Eigenwerte kurz ist. Die Länge eines solchen Wegs wird auch als Länge der durch v bestimmten Halbachse des zugehörigen Ellipsoids bezeichnet.

Dies erklärt letztendlich, dass einer großen Diskrepanz zwischen $\lambda_\textrm{min}$ und $\lambda_\textrm{max}$ eine große Diskrepanz zwischen längster und kürzester Halbachse jedes Ellipsoids entspricht, das eine Niveaumenge von q bildet, dass also die Niveaumengen von q geometrisch „sehr lang gezogen“ sind.

2.2.25 Übung

Berechnen Sie für eine Matrix $A=A^\intercal\succ0$ die Längen der Halbachsen des Ellipsoids $\{x\in\mathbb R^n|\,x^\intercal Ax=1\}$ .

2.2.26 Übung

Zu einer Matrix $A=A^\intercal\succ0$ mit maximalem und minimalem Eigenwert $\lambda_\textrm{max}$ bzw. $\lambda_\textrm{min}$ heißt $\kappa:=\lambda_\textrm{max}/\lambda_\textrm{min}$ Konditionszahl von A. Bei einer Konditionszahl nahe bei eins spricht man von einer gut konditionierten Matrix. Drücken Sie den Linearitätsfaktor des Gradientenverfahrens aus Satz 2.2.23 mit Hilfe der Konditionszahl aus. Wie wirkt sich demnach die Güte der Kondition von A auf die Geschwindigkeit des Verfahrens aus?

2.2.4 Variable-Metrik-Verfahren

Satz 2.2.23 zur langsamen Konvergenz des Gradientenverfahrens und seine geometrische Interpretation (Abb. 2.6) legen die Idee nahe, die Abstiegsrichtung $d^k=-\nabla f(x^k)$ durch eine Richtung zu ersetzen, die Krümmungsinformation über f berücksichtigt. Dies lässt sich wie folgt bewerkstelligen.

Nach Satz 2.2.23 minimiert das Gradientenverfahren (mit exakten Schrittweiten) eine konvex-quadratische Funktion $q(x)={\textstyle\frac12} x^\intercal Ax + b^\intercal x$ in einem einzigen Schritt, wenn der kleinste und größte Eigenwert $\lambda_\textrm{min}$ bzw. $\lambda_\textrm{max}$ von A übereinstimmen. Dann stimmen natürlich auch alle Eigenwerte von A miteinander überein, so dass q sphärenförmige Niveaumengen besitzt.

Die geometrische Hauptidee der folgenden Verfahren ist es, bei der Minimierung einer (nicht notwendigerweise konvex-quadratischen) C¹-Funktion f an jeder Iterierten x^k ein jeweils neues Koordinatensystem so einzuführen, dass f um x^k in den neuen Koordinaten möglichst sphärenförmige Niveaumengen besitzt. In den neuen Koordinaten ist folglich ein Abstieg in die negative Gradientenrichtung sinnvoll. Wenn die Koordinatentransformation linear ist, werden wir eine einfache Darstellung dieser Suchrichtung in den originalen Koordinaten herleiten können, so dass der explizite Gebrauch der Koordinatentransformation danach nicht mehr nötig ist.

Abb. 2.7 verdeutlicht die Konstruktion zunächst am Beispiel einer konvex-quadratischen Funktion $q(x)={\textstyle\frac12} x^\intercal Ax + b^\intercal x$ , wobei wir vernachlässigen, dass der Punkt, an dem die Suchrichtung berechnet werden soll, eine Iterierte ist, und ihn stattdessen mit $\bar x$ bezeichnen. Links sind ellipsenförmige Niveaulinien von q dargestellt, für die das Gradientenverfahren von $\bar x$ aus zu langsamer Konvergenz führen würde. Ein sowohl von der Orientierung als auch von der Skalierung her zu den Niveaulinien „passenderes“ Koordinatensystem ist gestrichelt eingezeichnet, und die neuen Koordinaten sind mit y₁ und y₂ anstelle von x₁ und x₂ bezeichnet. (Man könnte zusätzlich als Ursprung des neuen Koordinatensystems den gemeinsamen Mittelpunkt der Ellipsen wählen, was sich aber später als unnötig erweisen würde.)

../images/439970_1_De_2_Chapter/439970_1_De_2_Fig7_HTML.png — Abb. 2.7
Koordinatentransformation in der Variable-Metrik-Idee

Für dieses konkrete Koordinatensystem liest man aus der Abbildung als mögliche neue „Einheitsvektoren“

$b^1\ =\ \begin{pmatrix}\,\,\,\frac12\\[2pt]-\frac12\end{pmatrix}\quad\text{und}\quad b^2\ =\ \begin{pmatrix}1\\1\end{pmatrix}$

ab. In der Sprache der linearen Algebra sind b¹ und b² Basisvektoren des neuen Koordinatensystems. Mit ihrer Hilfe lassen sich zu jedem Punkt $x\in\mathbb R^2$ seine Koordinaten y₁ und y₂ bezüglich des neuen Koordinatensystems bestimmen, denn diese erfüllen das lineare Gleichungssystem

$x\ =\ y_1b^1 + y_2b^2\ =\ By$

mit der Matrix $B:=(b^1,b^2)$

. Beispielsweise erfüllen die neuen Koordinaten y₁ und y₂ des Punkts $x=(1,0)^\intercal$ das System

$\begin{pmatrix}1\\0\end{pmatrix}\ =\ \begin{pmatrix}\;\,\frac12 & 1\\-\frac12 & 1\end{pmatrix}\begin{pmatrix}y_1\\y_2\end{pmatrix},$

woraus y₁ = 1 und $y_2=\frac12$ folgt. In der Tat muss man zur Bestimmung neuer Koordinaten nicht notwendigerweise Gleichungssysteme lösen. Da die Vektoren b¹ und b² eine Basis des $\mathbb R^2$ bilden, ist die Matrix B invertierbar, und die Vorschrift y = B⁻¹x liefert zu jedem $x\in\mathbb R^2$ explizit die neuen Koordinaten y.

Die Abbildung $x\mapsto B^{-1} x$ ist die gesuchte lineare Koordinatentransformation. Sie transformiert die Geometrie der linken Seite aus Abb. 2.7 in die der rechten Seite.

Insbesondere wird durch die Transformation der Punkt $\bar x$ , an dem wir eine dem negativen Gradienten von q überlegene Abstiegsrichtung suchen, auf den Punkt $\bar y$ abgebildet. In den neuen Koordinaten y sind die Höhenlinien von q kreisförmig, so dass von $\bar y$ aus die negative Gradientenrichtung zum Minimalpunkt zeigt. Entscheidend dabei ist, wie die „Funktion q in neuen Koordinaten“ explizit lautet, von der hier die Höhenlinien betrachtet werden und deren Gradient berechnet werden soll. Wegen

$q(x)\ =\ q(By)\ =\ (q\circ B)(y)$

ist $\widetilde q:=q\circ B$ diese gesuchte Darstellung von q in neuen Koordinaten, und $\nabla\,\widetilde q(\bar y)$ ist die gesuchte Gradientenrichtung in $\bar y$ .

In einem letzten Schritt möchten wir die in den neuen Koordinaten gefundene Richtung wieder in die originalen Koordinaten zurücktransformieren, wobei die Rücktransformation der Geometrie der rechten Seite aus Abb. 2.7 in die der linken Seite durch die Abbildung $y\mapsto By$ realisiert wird. Um den resultierenden Vektor $B\nabla\,\widetilde q(\bar y)$ in originalen Koordinaten darzustellen, benutzen wir die Kettenregel und erhalten für jedes $y\in\mathbb R^2$

$D\widetilde q(y)\ =\ D[q(B(y))]\ =\ Dq(By)B\ =\ Dq(x)B,$

also insbesondere $\nabla\widetilde q(\bar y)=B^\intercal\nabla q(\bar x)$ und

$B\nabla\widetilde q(\bar y)\ =BB^\intercal\nabla q(\bar x)\ =\ \frac14\begin{pmatrix}5 & 3\\3 & 5\end{pmatrix}\nabla q(\bar x).$

Für den allgemeinen Fall n ≥ 1 und ohne grafische Veranschaulichung ist an dieser Stelle leider noch unklar, wie die Matrix B konstruiert werden soll. Auch im Allgemeinen existiert aber stets ein rechtwinkliges Koordinatensystem, das zur Lage der ellipsodialen Niveaumengen von q „passend ausgerichtet“ ist. Seine Achsen entsprechen gerade den Hauptachsen dieser Ellipsoide, also den durch die Eigenvektoren $v^1,\,\ldots\,,v^n$ von A gegebenen Richtungen (da A symmetrisch ist, existieren in der Tat genau n verschiedene und paarweise senkrecht zueinander stehende Eigenvektoren von A). Wie in Abb. 2.7 verzichten wir allerdings darauf, den Mittelpunkt der Ellipsoide (also den Minimalpunkt von q) mit dem Koordinatenursprung des neuen Koordinatensystems zu identifizieren.

Wir benötigen ferner noch eine „passende Skalierung“ der Achsen, um im neuen Koordinatensystem sphärenförmige Niveaumengen zu erhalten. Dazu wählen wir auf Länge eins normierte Eigenvektoren und suchen zu den einzelnen Vektoren passende (positive) Skalierungsfaktoren, d. h., das neue Koordinatensystem soll als „Einheitsvektoren“ die Vektoren $b^i:=c_iv^i$

, i = 1, … , n, mit passend gewählten Faktoren $c_1,\,\ldots\,,c_n>0$ besitzen. Die neuen Koordinaten $y_1,\,\ldots\,,y_n$ eines Punkts $x\in\mathbb R^n$ erfüllen dann jedenfalls das System

$x\ =\ y_1b^1 + \ldots + y_nb^n\ =\ y_1c_1v^1 + \ldots + y_nc_nv^n\ =\ V\begin{pmatrix}c_1y_1\\\vdots\\c_ny_n\end{pmatrix},$

wobei wir die Matrix $V:=(v^1,\,\ldots\,,v^n)$ eingeführt haben. Mit der Diagonalmatrix

$C\ :=\ \begin{pmatrix}c_1 &&\\&\ddots &\\&&c_n\end{pmatrix}$

lässt das System sich noch kompakter als x = VCy schreiben, und man kann für die Matrix $B:=(b^1,\,\ldots\,,b^n)$ die Darstellung B = VC ablesen. In neuen Koordinaten lautet die Funktion q also $\widetilde q(y)=q(By)$ mit B = VC.

Um die Skalierungsfaktoren $c_1,\,\ldots\,,c_n$ zu berechnen, mit denen $\widetilde q$ sphärenförmige Niveaumengen besitzt, sorgen wir dafür, dass die Hesse-Matrix von $\widetilde q$ identische Eigenwerte besitzt. Diese Matrix lesen wir aus

$\widetilde q(y)\ =\ q(By)\ =\ {\textstyle\frac12} (By)^\intercal A(By) + b^\intercal(By)\ =\ {\textstyle\frac12} y^\intercal B^\intercal A By + b^\intercal By$

$D^2\widetilde q(y)\ =\ B^\intercal A B\ =\ C V^\intercal A V C$

ab.

Im nächsten Schritt hilft uns der Spektralsatz weiter, nach dem die in $D^2\widetilde q(y)$ auftretende Matrix $V^\intercal A V$ mit der Diagonalmatrix

$\Lambda\ =\ \begin{pmatrix}\lambda_1 &&\\&\ddots &\\&&\lambda_n\end{pmatrix}$

der Eigenwerte von A übereinstimmt. Dies ist nicht schwer zu sehen, denn die Normiertheit und paarweise Orthogonalität der Eigenvektoren implizieren einerseits $(v^i)^\intercal v^i=\|v^i\|_2^2=1$ für alle i = 1, … , n sowie andererseits $(v^i)^\intercal v^j=0$ für alle i ≠ j. Daher gilt

$V^\intercal A V\ =\ V^\intercal(Av^1,\,\ldots\,,Av^n)\ =\ \begin{pmatrix}(v^1)^\intercal\\\vdots\\(v^n)^\intercal\end{pmatrix}(\lambda_1v^1,\,\ldots\,,\lambda_nv^n)\ =\ \Lambda$

und damit

$D^2\widetilde q(y)\ =\ CV^\intercal A V C\ =\ C\Lambda C\ =\ \begin{pmatrix}\lambda_1c_1^2 &&\\&\ddots &\\&&\lambda_nc_n^2\end{pmatrix},$

weshalb $\widetilde q$ etwa für die Wahlen $c_i:=1/\sqrt{\lambda_i}$ , i = 1, … , n, sphärenförmige Niveaumengen besitzt. Mit den Definitionen

$\Lambda^{\frac12}\ :=\ \begin{pmatrix}\sqrt{\lambda_1} &&\\&\ddots &\\&&\sqrt{\lambda_n}\end{pmatrix}$

und $\Lambda^{-\frac12} := (\Lambda^{\frac12})^{-1}$ lässt sich dieser Zusammenhang auch kurz als $C=\Lambda^{-\frac12}$ schreiben, so dass die gesuchte Matrix

$B\ =\ VC\ =\ V\Lambda^{-\frac12}$

lautet.

Als Rücktransformation des Gradientenvektors $\nabla\widetilde q(\bar y)$ in originale Koordinaten erhalten wir wie oben den Vektor $BB^\intercal\nabla q(\bar x)$ , wobei die Matrix $BB^\intercal$ jetzt wie folgt geschrieben werden kann:

$BB^\intercal\ =\ VC(VC)^\intercal\ =\ VC^2V^\intercal\ =\ V\Lambda^{-1} V^\intercal.$

Um zu sehen, dass diese Matrix mit A⁻¹ identisch ist, invertieren wir beide Seiten der nach dem Spektralsatz gültigen Gleichung $V^\intercal A V=\Lambda$ zu

$V^{-1} A^{-1} V^{-\intercal}\ =\ \Lambda^{-1}.$

Isolieren von A⁻¹ aus dieser Gleichung liefert

$A^{-1}\ =\ V\Lambda^{-1} V^\intercal\ =\ BB^\intercal.$

Die gewünschte Suchrichtung an der Stelle $\bar x$ lautet demnach $-A^{-1}\nabla q(\bar x)$ .

Für eine nicht notwendigerweise konvex-quadratische Funktion $f\in C^1(\mathbb R^n,\mathbb R)$ ist abschließend noch zu klären, wie man an einer Stelle $x\in\mathbb R^n$ ein Koordinatensystem einführen kann, in dem f möglichst sphärenförmige Niveaumengen besitzt. Beschränkt man sich darauf, approximativ eine Konstruktion wie bei konvex-quadratischen Funktionen zu benutzen, motiviert dies die folgende Definition.

2.2.27 Definition (Gradient bezüglich einer positiv definiten Matrix)

Für $f\in C^1(\mathbb R^n,\mathbb R)$ und eine (n, n)-Matrix $A=A^\intercal\succ0$ heißt

$\nabla_Af(x)\ :=\ A^{-1}\nabla f(x)$

Gradient von f bezüglich A an x.

Die verschiedenen Variable-Metrik-Verfahren unterscheiden sich durch die Wahl der Matrix A, mit deren Hilfe die Suchrichtung −∇_Af(x) gebildet wird. Für jedes $A=A^\intercal\succ0$ ist diese Suchrichtung an einem nichtkritischen Punkt x jedenfalls eine Abstiegsrichtung erster Ordnung, denn da mit A auch A⁻¹ positiv definit ist, gilt

$\langle\nabla f(\bar x),-\nabla_Af(\bar x)\rangle\ =\ -\nabla f(\bar x)^\intercal A^{-1} \nabla f(\bar x)\ <\ 0.$

Um den Begriff „variable Metrik“ zu motivieren, stellen wir zunächst fest, dass jede Matrix $A=A^\intercal\succ0$ auch ein Skalarprodukt und eine Norm definiert.

2.2.28 Übung

Zeigen Sie, dass für jedes $A=A^\intercal\succ0$ die Funktion $\langle x,y\rangle_A:=x^\intercal A y$ ein Skalarprodukt auf $\mathbb R^n$ ist.

2.2.29 Übung

Zeigen Sie, dass für jedes $A=A^\intercal\succ0$ und das von A induzierte Skalarprodukt $\langle \cdot,\cdot\rangle_A$ die Funktion

$\|x\|_A\ :=\ \sqrt{\langle x,x\rangle_A}$

eine Norm auf $\mathbb R^n$ ist.

Das von A induzierte Skalarprodukt und die von A induzierte Norm erlauben es, weitere Einblicke zu gewinnen.

2.2.30 Übung

Zeigen Sie, dass unter den Voraussetzungen von Satz 2.2.23 für alle $x\in\mathbb R^n$

${\textstyle\frac12}\|x-x^\star\|_A^2\ =\ q(x)-q(x^\star)$

gilt.

Wegen Übung 2.2.30 macht Satz 2.2.23 auch eine Aussage über die Konvergenzgeschwindigkeit der Iterierten (und nicht nur ihrer Funktionswerte) des Gradientenverfahrens, sofern man die passende Norm wählt. Da aber die quadrierten Abstände der Iterierten zum Grenzpunkt linear konvergieren, erhält man daraus eine sogar noch langsamere als lineare (nämlich eine sog. sublineare) Konvergenz der Iterierten selbst.

2.2.31 Übung

Zeigen Sie unter den Voraussetzungen von Beispiel 2.2.20 für die exakte Schrittweite des Gradientenverfahrens die Formel

$t_e\ =\ \frac{\|\nabla q(x)\|_2^2}{\|\nabla q(x)\|_A^2}\,.$

2.2.32 Übung

Zeigen Sie für das durch $A=A^\intercal\succ0$ induzierte Skalarprodukt $\langle \cdot,\cdot\rangle_A$ und die induzierte Norm $\|\cdot\|_A$ die Cauchy-Schwarz-Ungleichung:

$\forall\ x,y\in\mathbb R^n:\quad |\,\langle x,y\rangle_A\,|\ \le\ \|x\|_A\cdot\|y\|_A\,,$

und die Abschätzung ist scharf.

Da die Niveaumengen $\{x\in\mathbb R^n|\ \|x\|_A\le c\}$ mit c > 0 Ellipsoide sind, werden die Abstände um $\bar x$ in der Norm $\|\cdot\|_A$ unterschiedlich gewichtet. Das folgende Lemma zeigt, dass bezüglich dieser neuen Abstände der Vektor ∇_Af(x) eine „Richtung steilsten Abstiegs“ ist.

2.2.33 Lemma

Es sei ∇f(x) ≠ 0. Dann löst der Vektor

$d\ =\ -\nabla_Af(x)\,/\,\|\nabla_Af(x)\|_A$

das Problem

$\min\ \langle\nabla f(x),d\rangle \quad\text{ s.t. }\quad \|d\|_A=1,$

und zwar mit optimalem Wert $-\|\nabla_A f(x)\|_A$ .

Beweis.

Laut Übung 2.2.32 gilt auch für das Skalarprodukt $\langle\cdot,\cdot\rangle_A$ die Cauchy-Schwarz-Ungleichung, also für alle d mit $\|d\|_A=1$

$\langle\nabla f(x),d\rangle\ =\ \langle\nabla_A f(x),d\rangle_A\ \ge\ -\|\nabla_A f(x)\|_A\cdot\|d\|_A\ =\ -\|\nabla_A f(x)\|_A,$

wobei diese Abschätzung scharf ist. Daraus folgen die Behauptungen.

Bekanntlich lässt sich mit Hilfe jeder Norm $\|\cdot\|$ auf $\mathbb R^n$ auch eine Metrik auf $\mathbb R^n$ einführen, indem der Abstand zweier Punkte x und y zu $\|x-y\|$ definiert wird. Diese Metrik werden wir nicht explizit benutzen, sie erklärt aber die benutzte Terminologie: Verfahren, die in jeder Iteration eine neue Matrix $A^k=(A^k)^\intercal\succ0$ wählen und damit die Suchrichtung $-\nabla_{A^k} f(x^k)$ definieren, heißen Variable-Metrik-Verfahren. Algorithmus 2.6 setzt diese Idee um.

In Zeile 2 von Algorithmus 2.6 wählt man häufig A⁰ = E, also als erste Suchrichtung die Gradientenrichtung $d^0=-\nabla f(x^0)$ . In Zeile 3 wäre ein konsistenteres Abbruchkriterium eigentlich $\|\nabla_{A^k} f(x^k)\|_{A^k}\le\varepsilon$ , aber wegen

Algorithmus 2.6: Variable-Metrik-Verfahren

Input : C¹-Optimierungsproblem P

Output : Approximation $\bar x$ eines kritischen Punkts von f (falls das Verfahren terminiert; Satz 2.2.37)

1 begin

2 Wähle einen Startpunkt x⁰, eine Matrix $A^0=(A^0)^\intercal\succ0$ , eine Toleranz $\varepsilon>0$ und setze $k=0$ .

3 While $\|\nabla f(x^k)\|_2>\varepsilon$ do

4 Setze $d^k=-\nabla_{A^k} f(x^k)$ .

5 Bestimme eine Schrittweite t^k.

6 Setze $x^{k + 1}=x^k + t^k d^k$ .

7 Wähle $A^{k + 1}=(A^{k + 1})^\intercal\succ0$ .

8 Ersetze k durch $k + 1$ .

9 end

10 Setze $\bar x=x^k$ .

11 end

$\|\nabla_{A^k} f(x^k)\|_{A^k}\ =\ \sqrt{Df(x^k)(A^k)^{-1}\nabla f(x^k)}\ =\ \|\nabla f(x^k)\|_{(A^k)^{-1}}$

und der Äquivalenz von $\|\cdot\|_{(A^k)^{-1}}$ und $\|\cdot\|_2$ (d. h., es gibt Konstanten $c_1,c_2>0$

, so dass alle $x\in\mathbb R^n$ die Abschätzungen $c_1\|x\|_{(A^k)^{-1}}\le\|x\|_2\le c_2\|x\|_{(A^k)^{-1}}$ erfüllen) kann man ebensogut das angegebene und weniger aufwendigere Kriterium testen. In Zeile 4 berechnet man die Suchrichtung d^k numerisch nicht durch die eine Matrixinversion enthaltende Definition $-(A^k)^{-1}\nabla f(x^k)$ , sondern weniger aufwendig als Lösung des linearen Gleichungssystems $A^k d=-\nabla f(x^k)$ .

Möchte man die Konvergenz von Variable-Metrik-Verfahren im Sinne von Satz 2.2.9 garantieren, benötigt man neben der Effizienz der Schrittweiten auch die Gradientenbezogenheit der Suchrichtungen. Diese muss man noch fordern.

2.2.34 Definition (Gleichmäßig positiv definite und beschränkte Matrizen)

Eine Folge (A^k) symmetrischer (n, n)-Matrizen heißt gleichmäßig positiv definit und beschränkt, falls

$\exists\ 0< c_1\le c_2\ \forall\ d\in B_=(0,1),\ k\in\mathbb N:\quad c_1\ \le\ d^\intercal A^k d\ \le\ c_2$

gilt.

Beispielsweise bilden die Matrizen

$A^k\ =\ \begin{pmatrix}k & 0\\0 & \frac1k\end{pmatrix},\quad k\in\mathbb N,$

eine Folge, die weder gleichmäßig positiv definit noch beschränkt ist.

2.2.35 Übung

Die Folge (A^k) sei gleichmäßig positiv definit und beschränkt mit Konstanten c₁ und c₂ . Zeigen Sie, dass dann die Folge $\left((A^k)^{-1}\right)$ gleichmäßig positiv definit und beschränkt mit Konstanten 1/c₂ und 1/c₁ ist. Zeigen Sie außerdem, dass die Folge $(\lambda_\textrm{max}\left((A^k)^{-1}\right)$ der größten Eigenwerte von $\left((A^k)^{-1}\right)$ durch 1/c₁ nach oben beschränkt ist.

2.2.36 Satz

Die Folge (A^k) sei gleichmäßig positiv definit und beschränkt. Dann ist die Folge (d^k) mit $d^k=-(A^k)^{-1}\nabla f(x^k)$ , $k\in\mathbb N$ , gradientenbezogen.

Beweis.

Es sei $k\in\mathbb N$ . Im Fall ∇f(x^k) = 0 ist nichts zu zeigen, daher sei im Folgenden ∇f(x^k) ≠ 0. Nach Übung 2.2.35 gilt zunächst

$\langle\nabla f(x^k),d^k\rangle\ =\ -Df(x^k)(A^k)^{-1}\nabla f(x^k)\ \le\ -\frac1{c_2}\,\|\nabla f(x^k)\|_2^2$

sowie nach (2.9)

$\|d^k\|_2\ \le\ \|(A^k)^{-1}\|_2\cdot\|\nabla f(x^k)\|_2\ \le\ \frac1{c_1}\,\|\nabla f(x^k)\|_2,$

wobei wir Übung 2.2.35 nun zur Abschätzung der Spektralnorm $\|A\|_2=\lambda_\textrm{max}(A)$ für eine symmetrische positiv definite Matrix A benutzt haben (Bemerkung 2.2.38). Da der Zähler des ersten Bruchs bei der folgenden Abschätzung negativ ist, folgt für alle $k\in\mathbb N$

$\begin{aligned}\frac{\langle\nabla f(x^k),d^k\rangle}{\|d^k\|_2}\ \le\ -\frac{c_1}{c_2}\,\frac{\|\nabla f(x^k)\|_2^2}{\|\nabla f(x^k)\|_2}\ =\ -c\cdot \|\nabla f(x^k)\|_2.\end{aligned}$

2.2.37 Satz

Die Menge $f_\le^{f(x^0)}$ sei beschränkt, die Funktion ∇f sei Lipschitz-stetig auf $\textrm{conv}(f_\le^{f(x^0)})$ , die Folge (A^k) sei gleichmäßig positiv definit und beschränkt, und in Zeile 5 seien exakte Schrittweiten $(t_e^k)$ oder Armijo-Schrittweiten $(t_a^k)$ gewählt. Dann terminiert Algorithmus 2.5 für jedes ɛ > 0 nach endlich vielen Schritten.

Beweis.

Die Behauptung folgt aus Korollar 2.2.10, Satz 2.2.36, Satz 2.2.15 sowie Satz 2.2.16.

2.2.38 Bemerkung (Spektralnorm und Eigenwerte)

Da die in Abschn. 2.2.3 eingeführte Spektralnorm

$\|A\|_2\ :=\ \max\{\|Ad\|_2\,|\ \|d\|_2=1\}$

einer Matrix A der Optimalwert eines restringierten nichtlinearen Optimierungsproblems ist, werden wir sie mit den Techniken aus Kap. 3 explizit zu

$\|A\|_2\ =\ \sqrt{\lambda_\textrm{max}(A^\intercal A)}$

berechnen können, wobei $\lambda_\textrm{max}(A^\intercal A)$ den größten Eigenwert der positiv semidefiniten Matrix $A^\intercal A$ bezeichnet (Beispiel 3.2.45). Dass die Menge der Eigenwerte einer Matrix auch als Spektrum von A bezeichnet wird, erklärt die Terminologie für $\|A\|_2$ .

Da im Fall $A=A^\intercal$ die Eigenwerte von $A^\intercal A=A^2$ gerade die quadrierten Eigenwerte von A sind, folgt dann

$\|A\|_2\ =\ \sqrt{\lambda_\textrm{max}(A^\intercal A)}\ =\ \sqrt{\left(\lambda_\textrm{max}(A)\right)^2}\ =\ |\lambda_\textrm{max}(A)|$

und im Fall A ≻ 0 auch das oben benutzte $\|A\|_2=\lambda_\textrm{max}(A)$ .

Mit den in diesem Abschnitt erläuterten Techniken lässt sich die explizite Formel für $\|A\|_2$ bei Matrizen A von vollem Spaltenrang zumindest motivieren. Dann ist die Matrix $A^\intercal A$ nämlich sogar positiv definit, und wir können mit Hilfe der Matrix Λ der Eigenwerte von $A^\intercal A$ sowie der Matrix V der zugehörigen Eigenvektoren die Matrix

$(A^\intercal A)^{-\frac12}\ :=\ V\Lambda^{-\frac12}V^\intercal$

definieren. Die Substitution $d=(A^\intercal A)^{-\frac12}\eta$ mit $\eta\in\mathbb R^n$ führt dann zu

$\|Ad\|_2^2\ =\ d^\intercal A^\intercal Ad\ =\ \eta^\intercal (A^\intercal A)^{-\frac12}(A^\intercal A)(A^\intercal A)^{-\frac12}\eta\ =\ \|\eta\|_2^2.$

Wegen

$\|A\|_2\ =\ \max\{\|Ad\|_2\,|\ \|d\|_2=1\}\ =\ \max\{\|\eta\|_2\,|\ \|(A^\intercal A)^{-\frac12}\eta\|_2=1\}$

entspricht die Spektralnorm von A also gerade der „maximalen Verzerrung“ des Ellipsoids

$\{\eta\in\mathbb R^n|\ \eta^\intercal(A^\intercal A)^{-\frac12}(A^\intercal A)^{-\frac12}\eta=1\}\ =\ \{\eta\in\mathbb R^n|\ \eta^\intercal(A^\intercal A)^{-1}\eta=1\}.$

Wie in Bemerkung 2.2.24 und Übung 2.2.25 gesehen besitzt die längste Halbachse dieses Ellipsoids die Länge

$\frac1{\sqrt{\lambda_\textrm{min}((A^\intercal A)^{-1})}}\ =\ \sqrt{\lambda_\textrm{max}(A^\intercal A)},$

was dem behaupteten Wert von $\|A\|_2$ entspricht und wobei wir benutzt haben, dass die Eigenwerte der positiv definiten Matrix $(A^\intercal A)^{-1}$ genau die Kehrwerte der Eigenwerte von $A^\intercal A$ sind. Zumindest für n = 2 und n = 3 ist zwar geometrisch einsichtig, dass die größte Verzerrung eines Ellipsoids in der Tat entlang der längsten Halbachse auftritt, dies ist allerdings noch kein Beweis, sondern nur eine Motivation. Der Beweis wird wie erwähnt in Beispiel 3.2.45 geführt.

2.2.5 Newton-Verfahren mit und ohne Dämpfung

Wählt man in Algorithmus 2.6 für $f\in C^2(\mathbb R^n,\mathbb R)$ in jedem Schritt $A^k=D^2f(x^k)$ , so erhält man das bereits zu Beginn von Abschn. 2.2.1 kurz erwähnte Newton-Verfahren, sofern die Matrizen $D^2f(x^k)$ positiv definit sind. Allerdings werden die Newton-Schritte durch den Faktor t^k, der üblicherweise im Intervall (0, 1) liegt, „gedämpft“. Man spricht dann vom gedämpften Newton-Verfahren . Wir haben bereits angeführt, dass das Newton-Verfahren nur für x⁰ hinreichend nahe bei einer Lösung $x^\star$ wohldefiniert und schnell ist. Etwas genauer gilt Folgendes.

Ist $x^\star$ nichtdegenerierter lokaler Minimalpunkt von f, dann gilt aus den bereits am Ende von Abschn. 2.1.5 aufgeführten Stetigkeitsgründen D²f(x) ≻ 0 für alle x aus einer Umgebung von $x^\star$ . Für x⁰ aus dieser Umgebung kann man also $A^k=D^2f(x^k)$

setzen und erhält ein wohldefiniertes Abstiegsverfahren. Ferner sind die Suchrichtungen $d^k=-(D^2f(x^k))^{-1}\nabla f(x^k)$ gradientenbezogen, falls f um $x^\star$ gleichmäßig konvex ist, d. h. falls für eine Umgebung U von $x^\star$

$\exists\ c>0\ \forall\ x\in U,\ d\in B_=(0,1):\quad c\ \le\ d^\intercal D^2f(x)d$

gilt [33]. Die für diese Folgerung nach Satz 2.2.36 noch erforderliche Beschränktheit der Folge $(D^2f(x^k))$

resultiert dabei aus der Stetigkeit von D²f. Die Nichtdegeneriertheit des lokalen Minimalpunkts $x^\star$ gilt bei gleichmäßig konvexem f automatisch.

Die Dämpfung des Newton-Verfahrens hat den Vorteil, dass der Konvergenzradius (also der mögliche Abstand von x⁰ zu $x^\star$ ) etwas größer wird. Andererseits ist zunächst nicht klar, ob die Dämpfung nicht auch die lokale Konvergenz verlangsamt. Das ungedämpfte Newton-Verfahren konvergiert unter schwachen Voraussetzungen jedenfalls quadratisch.

2.2.39 Satz (Quadratische Konvergenz des Newton-Verfahrens)

Die durch

$x^{k + 1}\ =\ x^k-(D^2f(x^k))^{-1}\nabla f(x^k)$

definierte Folge (x^k) konvergiere gegen einen nichtdegenerierten lokalen Minimalpunkt $x^\star$ , und D²f sei Lipschitz-stetig auf einer konvexen Umgebung von $x^\star$ . Dann konvergiert die Folge (x^k) quadratisch gegen $x^\star$ .

Beweis.

Zunächst gilt per Definition des Newton-Verfahrens

$\|x^{k + 1}-x^\star\|_2\ =\ \|x^k-(D^2f(x^k))^{-1}\nabla f(x^k)-x^\star\|_2\,.$

(2.10)

Der Beweis der quadratischen Konvergenz basiert auf einer Taylor-Entwicklung erster Ordnung von ∇f(x^k) um $x^\star$ in (2.10) sowie der quadratischen Abschätzung des dabei entstehenden Fehlerterms mit Hilfe von Lemma 2.2.13. Da wir im Rahmen dieses Lehrbuchs nur Taylor-Entwicklungen von reellwertigen (und nicht von vektorwertigen) Funktionen betrachtet haben, gehen wir wie folgt vor: Für jedes i ∈ {1, … , n} erfüllt der Fehlerterm

$w_i\ :=\ \partial_{x_i}f(x^k)- \partial_{x_i}f(x^\star)-\langle\nabla\partial_{x_i}f(x^\star),x^k-x^\star\rangle$

nach Satz 2.1.30a

$w_i\ =\ o(\|x^k-x^\star\|).$

Außerdem ist die Funktion $\nabla\partial_{x_i}f$ Lipschitz-stetig mit Konstante L > 0 auf der konvexen Umgebung D von $x^\star$ , auf der auch die Lipschitz-Stetigkeit von D²f mit Konstante L > 0 vorausgesetzt ist, also die Bedingung

$\forall\,x,y\in D:\quad \|D^2f(x)-D^2f(y)\|_2\ \le\ L\|x-y\|_2\,.$

In der Tat gilt wegen $\|A\|_2=\max_{\|d\|_2=1}\|Ad\|_2$ und $\|e_i\|_2=1$ für alle x, y ∈ D

$\|\nabla\partial_{x_i}f(x)-\nabla\partial_{x_i}f(y)\|_2\ =\ \|(D^2f(x)-D^2f(y))e_i\|_2\ \le\ \|D^2f(x)-D^2f(y)\|_2\ \le\ L\|x-y\|_2\,.$

Für alle hinreichend großen $k\in\mathbb N$ liegen die Iterierten x^k in D, so dass Lemma 2.2.13 für den Fehlerterm dann sogar

$|w_i|\ \le\ \frac{L}2\|x^k-x^\star\|_2^2$

liefert. Mit dem Vektor aller Fehlerterme

$w\ =\nabla f(x^k)-\nabla f(x^\star)-D^2f(x^\star)(x^k-x^\star)\ =\ \nabla f(x^k)-D^2f(x^\star)(x^k-x^\star)$

können wir nun ∇f(x^k) in (2.10) ersetzen und abschätzen, wobei wir benutzen, dass $\|(D^2f(x^k))^{-1}\|_2$ aus Stetigkeitsgründen auf einer Umgebung von $x^\star$ durch eine Konstante c > 0 beschränkt ist:

$\begin{aligned}\|x^{k + 1}-x^\star\|_2 = \,& \|x^k-(D^2f(x^k))^{-1}\nabla f(x^k)-x^\star\|_2\\ = \,& \|x^k-x^\star -(D^2f(x^k))^{-1}\left(D^2f(x^\star)(x^k-x^\star) + w\right)\|_2\\ = \,& \|(D^2f(x^k))^{-1}\left((D^2f(x^k)-D^2f(x^\star))(x^k-x^\star) + w\right)\|_2\\ \le \,& \|(D^2f(x^k))^{-1}\|_2\left(\|(D^2f(x^k)-D^2f(x^\star))(x^k-x^\star)\|_2 + \|w\|_2\right)\\ \le \,& c\left(\|D^2f(x^k)-D^2f(x^\star)\|_2\|x^k-x^\star\|_2 + \|w\|_2\right)\\ \le \,& c\left(L\|x^k-x^\star\|_2^2 + \frac{L\sqrt{n}}2\|x^k-x^\star\|_2^2\right)\\ = \,& c\left(L + \frac{L\sqrt{n}}2\right)\|x^k-x^\star\|_2^2.\end{aligned}$

Damit ist die Behauptung bewiesen.

2.2.40 Bemerkung

Die Voraussetzungen von Satz 2.2.39 lassen sich noch erheblich abschwächen. Erstens gilt die Aussage für jeden nichtdegenerierten kritischen Punkt $x^\star$ , also nicht nur für lokale Minimalpunkte. Zweitens werden wir in Satz 2.2.48 sehen, dass die Konvergenz der Folge (x^k) bereits impliziert, dass der Grenzpunkt $x^\star$ ein nichtdegenerierter kritischer Punkt ist.

Die Konvergenzgeschwindigkeit überträgt sich aus Satz 2.2.39 natürlich auf das gedämpfte Newton-Verfahren, falls man mit einem $k_0\in\mathbb N$ für alle k ≥ k₀ nur t^k = 1 wählt. Die folgende Übung gibt eine natürliche Bedingung dafür an.

2.2.41 Übung

Für $f\in C^2(\mathbb R^n,\mathbb R)$ liege x in einer genügend kleinen Umgebung eines nichtdegenerierten lokalen Minimalpunkts, und die Suchrichtung d werde mit dem gedämpften Newton-Verfahren per Armijo-Regel mit t⁰ = 1 und $\upsigma<\frac12$ bestimmt. Zeigen Sie, dass dann $\langle\nabla f(x),d\rangle<0$ gilt und dass die Armijo-Regel die Schrittweite t_a = 1 wählt.

2.2.42 Übung

Zeigen Sie, dass das ungedämpfte Newton-Verfahren für die Funktion $q(x)={\textstyle\frac12}\,x^\intercal Ax + b^\intercal x$ mit $A=A^\intercal\succ 0$ und $b\in\mathbb R^n$ von jedem Startpunkt $x^0\in\mathbb R^n$ aus nach einem Schritt den globalen Minimalpunkt von q liefert.

2.2.43 Übung

Für $f\in C^2(\mathbb R^n,\mathbb R)$ sei eine Iterierte x^k mit $D^2f(x^k)\succ0$ gegeben. Zeigen Sie, dass dann die vom Newton-Verfahren erzeugte Suchrichtung d^k der eindeutige lokale Minimalpunkt der konvex-quadratischen Funktion

$q(d)\ =\ f(x^k) + \langle\nabla f(x^k),d\rangle + {\textstyle\frac12}\, d^\intercal D^2f(x^k)d$

ist.

Die Grundidee des Newton-Verfahrens, die Nullstellensuche von ∇f iterativ durch die Bestimmung von Nullstellen linearer Approximationen an ∇f zu ersetzen, lässt sich laut Übung 2.2.43 also auch so interpretieren, dass das Newton-Verfahren zur Minimierung von f in jeder Iteration den Minimalpunkt einer quadratischen Approximation an f berechnet. Auf diese Interpretation werden wir später bei der Betrachtung von CG-, Trust-Region- und SQP-Verfahren zurückkommen.

Wir erwähnen kurz eine wichtige Modifikation des Newton-Verfahrens für Zielfunktionen f mit der besonderen Struktur aus Kleinste-Quadrate-Problemen wie in Beispiel 1.1.4 und Übung 2.1.18, also $f(x)={\textstyle\frac12}\|r(x)\|_2^2$ mit einer glatten Funktion $r:\mathbb R^n\to\mathbb R^m$ . Falls r linear ist, spricht man von einem linearen Kleinste-Quadrate-Problem (z. B. [24, 25]). Da sich f dann leicht als konvex-quadratisch identifizieren lässt (Übung 2.1.44), ist dieser Fall numerisch sehr effizient behandelbar [25]. Für nichtlineare Kleinste-Quadrate-Probleme berechnet man per Ketten- und Produktregel die Hesse-Matrix

$D^2f(x)\ =\ \nabla r(x)\, Dr(x) + \sum_{j=1}^mr_j(x)\,D^2r_j(x).$

(2.11)

Grundidee des zentralen Verfahrens zur Lösung nichtlinearer Kleinste-Quadrate-Probleme, nämlich des Gauß-Newton-Verfahrens , ist es nun, in Algorithmus 2.6 nicht wie beim Newton-Verfahren $A^k=D^2f(x^k)$

zu wählen, sondern $A^k=\nabla r(x^k)\, Dr(x^k)$ . Dass die restlichen Summanden in der Darstellung von $D^2f(x^k)$

eine untergeordnete Rolle spielen, kann zum einen daran liegen, dass für m ≥ n üblicherweise ein Punkt $x^\star$ mit $r(x^\star)=0$ approximiert wird, so dass die Werte $r_j(x^k)$

fast verschwinden, oder zum anderen daran, dass die Krümmungen der Funktionen r_j an $x^\star$ vernachlässigbar sind, so dass sich die Matrizen $D^2r_j(x^k)$

in der Nähe der Nullmatrix aufhalten.

Obwohl zum Aufstellen von A^k im Gauß-Newton-Verfahren also nur Ableitungsinformationen erster Ordnung (die Matrix Dr(x^k)) erforderlich sind, lässt sich unter bestimmten Zusatzvoraussetzungen sogar quadratische Konvergenz zeigen [25]. Zusätzlich sind die Suchrichtungen d^k im Gauß-Newton-Verfahren im Gegensatz zum allgemeinen Newton-Verfahren garantiert Abstiegsrichtungen (erster Ordnung), so dass eine Schrittweitensteuerung etwa per Armijo-Regel möglich ist.

Sollte die Jacobi-Matrix Dr(x^k) nicht den vollen Rang besitzen oder zumindest schlecht konditioniert sein, so lässt das Gauß-Newton-Verfahren sich durch die Wahl ${A^k=\nabla r(x^k)\, Dr(x^k) + \upsigma^k E}$ mit gewissen σ^k > 0 und der Einheitsmatrix E passender Dimension stabilisieren, was auf das Levenberg-Marquardt-Verfahren führt. Eine alternative Formulierung dieses Verfahrens kann als Vorläufer der in Abschn. 2.2.10 vorgestellten Trust-Region-Verfahren aufgefasst werden (für Einzelheiten s. [25]).

2.2.44 Übung

Zeigen Sie für Kleinste-Quadrate-Probleme die Darstellung der Hesse-Matrix D²f(x) aus (2.11).

2.2.6 Superlineare Konvergenz

Falls im Newton-Verfahren x⁰ zu weit von einem nichtdegenerierten Minimalpunkt entfernt liegt, ist $D^2f(x^k)$ nicht notwendigerweise positiv definit und die Newton-Richtung $d^k=-(D^2f(x^k))^{-1}\nabla f(x^k)$ entweder nicht definiert oder nicht notwendigerweise eine Abstiegsrichtung. Man versucht daher, das Newton-Verfahren zu globalisieren , d. h. Konvergenz im Sinne von Satz 2.2.9 gegen einen lokalen Minimalpunkt von jedem Startpunkt $x^0\in\mathbb R^n$ aus zu erzwingen (was nicht zu verwechseln ist mit der Konvergenz gegen einen globalen Minimalpunkt; für solche Verfahren s. [33]).

Ein erster Ansatz dazu besteht darin, in Zeile 2 von Algorithmus 2.6 A⁰ = E zu wählen sowie in Zeile 7 (ähnlich wie im Levenberg-Marquardt-Verfahren)

$A^{k + 1}\ =\ D^2f(x^{k + 1}) + \upsigma^{k + 1}\cdot E$

mit einem so großen Skalar σ^k + 1, dass A^k + 1 positiv definit ist (Übung 2.2.45).

Dann gilt $d^0=-\nabla f(x^0)$ , und bei Konvergenz gegen einen nichtdegenerierten lokalen Minimalpunkt kann man σ^k = 0 für alle hinreichend großen k wählen (d. h., das Verfahren startet als Gradientenverfahren und geht nach endlich vielen Schritten in das gedämpfte Newton-Verfahren über). Unter geeigneten Voraussetzungen kann man superlineare Konvergenz des Verfahrens zeigen (z. B. Satz 2.2.48). Ein Nachteil des Verfahrens besteht darin, dass die Bestimmung von σ^k sehr aufwendig sein kann: Man halbiert oder verdoppelt z. B. σ^k so lange, bis ein Test auf positive Definitheit von $D^2f(x^k) + \upsigma^k E$ erfolgreich ist. Das Verfahren wird in dieser Form daher in der Praxis nicht verwendet.

2.2.45 Übung

Es seien A eine symmetrische (n, n)-Matrix und E die (n, n)-Einheitsmatrix. Zeigen Sie, dass für alle hinreichend großen $\upsigma\in\mathbb R$ die Matrix A + σE positiv definit ist.

Im Folgenden werden wir Verfahren kennenlernen, die nicht nach endlich vielen Schritten, sondern nur asymptotisch in das gedämpfte Newton-Verfahren übergehen. Für diese lässt sich immerhin noch superlineare Konvergenz zeigen. Der entsprechende Konvergenzsatz erfordert einige Vorbereitungen.

Zunächst besitzt die Folge der Iterierten (x^k) nach Satz 2.2.9 einen Häufungspunkt, und jeder solche Häufungspunkt ist kritisch, sofern die Menge $f_\le^{f(x^0)}$ beschränkt ist und gradientenbezogene Suchrichtungen sowie effiziente Schrittweiten benutzt werden. Die Gradientenbezogenheit der Suchrichtungen wird durch Satz 2.2.36 für gleichmäßig positiv definite und beschränkte (A^k) garantiert. Dass die Folge (x^k) tatsächlich konvergiert, können wir mit den Mitteln dieses Lehrbuchs nur in einfachen Fällen zeigen (z. B. falls f einen eindeutigen kritischen Punkt besitzt), werden es für die nachfolgenden Untersuchungen der Konvergenzgeschwindigkeit aber voraussetzen.

Dazu setzen wir zur Abkürzung

$H^k\ :=\ t^k\left(A^k\right)^{-1},$

d. h., in Zeile 6 von Algorithmus 2.6 wählt man die neue Iterierte als

$x^{k + 1}\ =\ x^k-H^k\nabla f(x^k).$

(2.12)

Wir werden außerdem benutzen, dass die Definition der superlinearen Konvergenz einer gegen $x^\star$ konvergenten Folge (x^k) (Definition 2.2.21b) zu

$\limsup_k\,\frac{\|x^{k + 1}-x^\star\|}{\|x^k-x^\star\|}\ =\ 0$

äquivalent ist.

2.2.46 Lemma

Die Folge (x^k) sei nach der Vorschrift (2.12) gebildet und gegen $x^\star$ konvergent. Ferner seien die Folgen $\left(\|H^k\|_2\right)$ und $\left(\|\left(H^k\right)^{-1}\|_2\right)$ beschränkt. Dann gilt:

a)
$\nabla f(x^\star)=0$
b)
$\limsup_k\,\|x^{k + 1}-x^\star\|_2/\|x^k-x^\star\|_2\ \le\ \limsup_k\,\|E-H^k D^2f(x^\star)\|_2$

Beweis.

Wegen

$0\ =\ x^\star-x^\star\ =\ \lim_k\,(x^k-x^{k + 1})\ =\ \lim_k\,H^k\nabla f(x^k)$

und der Beschränktheit von $\left(\|(H^k)^{-1}\|_2\right)$ gilt

$\|\nabla f(x^k)\|_2\ =\ \|(H^k)^{-1} H^k\nabla f(x^k)\|_2\ \le\ \|(H^k)^{-1}\|_2\cdot\|H^k\nabla f(x^k)\|_2\ \to\ 0$

und damit auch

$\|\nabla f(x^\star)\|_2\ =\ \lim_k\,\|\nabla f(x^k)\|_2\ =\ 0,$

also Aussage a.

Dies impliziert mit $z(s)=x^\star-s (x^k-x^\star)$

$\begin{aligned}\|x^{k + 1}-x^\star\|_2 = \,& \|x^k-x^\star-H^k\nabla f(x^k)\|_2\\ = \,& \left\|x^k-x^\star-H^k\int_0^1D^2f(z(s))(x^k-x^\star)\,ds\right\|_2\\ = \,& \left\|x^k-x^\star-H^k\left(D^2f(x^\star)(x^k-x^\star) + \int_0^1\left(D^2f(z(s))-D^2f(x^\star)\right)(x^k-x^\star)\,ds\right)\right\|_2\\ \le \,& \|E-H^k D^2f(x^\star)\|_2\cdot\|x^k-x^\star\|_2 + \|H^k\|_2\cdot\left\|\int_0^1\left(D^2f(z(s))-D^2f(x^\star)\right)(x^k-x^\star)\,ds\right\|_2.\end{aligned}$

Es folgt

$\frac{\|x^{k + 1}-x^\star\|_2}{\|x^k-x^\star\|_2}\ \le\ \|E-H^k D^2f(x^\star)\|_2 + \|H^k\|_2\cdot\left\|\int_0^1\left(D^2f(z(s))-D^2f(x^\star)\right) \frac{x^k-x^\star}{\|x^k-x^\star\|_2} \,ds\right\|_2.$

Da die Folgen $\left(\|H^k\|_2\right)$ und $\left(x^k-x^\star/\|x^k-x^\star\|_2\right)$ beschränkt sind und

$D^2f(z(s))-D^2f(x^\star)\ =\ D^2f(x^\star + s(x^k-x^\star))-D^2f(x^\star)$

für jedes s ∈ [0, 1] gegen die Nullmatrix konvergiert, resultiert Aussage b.

2.2.47 Lemma

Für zwei (n, n)-Matrizen A und B sei $\,L:=\|E-AB\|_2<1\,$ . Dann gilt:

a)
A und B sind nichtsingulär.
b)
$\|A\|_2\ \le\ (1 + L)\cdot\|B^{-1}\|_2$ .
c)
$\|A^{-1}\|_2\ \le\ \|B\|_2/(1-L)$ .

Beweis.

Wegen $\|E-AB\|_2<1$ sind die Eigenwerte von E − AB betraglich echt kleiner als eins (Beispiel 3.2.45). Damit kann die Matrix AB nicht den Eigenwert null besitzen, ist also nichtsingulär. Folglich sind auch A und B nichtsingulär, und Aussage a ist gezeigt.

Aussage b folgt aus

$\begin{aligned}\|A\|_2 = \,& \|ABB^{-1}\|_2\ \le\ \|AB\|_2\cdot\|B^{-1}\|_2\ =\ \|E-(E-AB)\|_2\cdot\|B^{-1}\|_2\\ \le \,& \left(\|E\|_2 + \|E-AB\|_2\right)\cdot\|B^{-1}\|_2\ =\ (1 + L)\cdot\|B^{-1}\|_2.\end{aligned}$

Schließlich seien C : = AB und z ∈ B₌(0, 1) ein Vektor mit $\|C^{-1} z\|_2=\|C^{-1}\|_2$ . Dann gilt mit u : = C⁻¹z und $v:=(E-C)u=u-z$

$\|v\|_2\ \le\ \|E-C\|_2\cdot\|u\|_2\ =\ L\cdot \|C^{-1}\|_2$

und daher

$\|C^{-1}\|_2\ =\ \|u\|_2\ =\ \|v + z\|_2\ \le\ \|v\|_2 + \|z\|_2\ \le\ L\cdot\| C^{-1} \|_2 + 1.$

Es folgt

$\| B^{-1} A^{-1} \|_2 \ =\ \| C^{-1} \|_2 \ \le\ \frac1{1-L}\,,$

also

$\| A^{-1} \|_2 \ =\ \| BB^{-1} A^{-1} \|_2 \ \le\ \| B \|_2 \cdot\| B^{-1} A^{-1} \|_2 \ \le\ \frac{\| B \|_2 }{1-L}$

und damit Aussage c.

2.2.48 Satz

Die Folge (x^k) sei nach der Vorschrift (2.12) gebildet und gegen $x^\star$ konvergent. Ferner sei $\,L:=\limsup_k\,\| E-H^k D^2f(x^\star) \|_2 <1\,$ . Dann gelten die folgenden Aussagen:

a)
$D^2f(x^\star)$ ist nichtsingulär.
b)
$\nabla f(x^\star)=0$ .
c)
(x^k) konvergiert mindestens linear gegen $x^\star$ .
d)
Es gilt L = 0 genau im Fall von $\lim_k H^k=\left(D^2f(x^\star)\right)^{-1}$ , und in diesem Fall konvergiert (x^k) superlinear gegen $x^\star$ .

Beweis.

Wegen $\,\limsup_k\,\| E-H^k D^2f(x^\star) \|_2 <1\,$ existiert ein $k_0\in\mathbb N$ , so dass für alle k ≥ k₀

$\| E-H^k D^2f(x^\star) \|_2 \ <\ 1$

erfüllt ist. Nach Lemma 2.2.47a ist daher $D^2f(x^\star)$ nichtsingulär, was Aussage a beweist, und außerdem ist für k ≥ k₀ auch H^k nichtsingulär. Aus Lemma 2.2.47b und c folgt nun die Beschränktheit der Folgen $\left(\|H^k\|_2\right)$ und $\left(\|\left(H^k\right)^{-1}\|_2\right)$ , so dass Lemma 2.2.46a Aussage b liefert. Nach Lemma 2.2.46b haben wir ferner

$\limsup_k\,\frac{\| x^{k{ + }1}-x^\star \|_2 }{\| x^k-x^\star \|_2 }\ \le\ L,$

womit auch Aussage c bewiesen ist. Für L = 0 folgt daraus offensichtlich superlineare Konvergenz.

Den Rest von Aussage d zeigt man wie folgt. Mit $\bar H:=(D^2f(x^\star))^{-1}$ gilt

$\| \bar H-H^k \|_2 \ =\ \| (E-H^k\bar H^{-1})\bar H \|_2 \ \le\ \| E-H^k\bar H^{-1} \|_2 \cdot\| \bar H \|_2$

sowie

$\| E-H^k D^2f(x^\star) \|_2 \ =\ \| (\bar H-H^k)D^2f(x^\star) \|_2 \ \le\ \| \bar H-H^k \|_2 \cdot\| D^2f(x^\star) \|_2 .$

Damit erhalten wir

$\limsup_k\,\| E-H^k D^2f(x^\star) \|_2 \ =\ 0$

genau für

$\begin{aligned}\lim_k\, H^k\ =\ \bar H=(D^2f(x^\star))^{-1}.\end{aligned}$

Nach Satz 2.2.48 sollte Algorithmus 2.6 also asymptotisch in das ungedämpfte Newton-Verfahren übergehen, um superlineare Konvergenz zu garantieren. Wegen

$H^k\ =\ t^k\cdot (A^k)^{-1}$

sind natürliche Bedingungen dafür $\lim_k t^k=1$ und $\lim_k A^k= D^2f(x^\star)$ . Das zu Beginn dieses Kapitels vorgeschlagene Verfahren erreicht dies mit hohem Aufwand bereits nach endlich vielen Schritten, ist in diesem Sinne also nicht effizient.

2.2.7 Quasi-Newton-Verfahren

Woher nimmt man aber sonst die Matrizen A^k mit $\lim_k A^k = D^2f(x^\star)$ ? Ein möglicher Ansatz dazu besteht darin, zunächst das Sekantenverfahren zur Nullstellensuche einer Funktion von $\mathbb R^1$ nach $\mathbb R^1$ zu betrachten. Im Hinblick auf Optimierungsverfahren sei dies die Funktion $\nabla f=f'$ für eine zu minimierende Funktion $f:\mathbb R\to\mathbb R$ . Das Sekantenverfahren unterscheidet sich vom Newton-Verfahren dadurch, dass die linearen Approximationen an $f'$

, deren Nullstellen berechnet werden, nicht durch Tangenten an $f'$

, sondern durch Sekanten gegeben sind. In der Tat approximiert man die Tangente an $f'$

in einem Iterationspunkt x^k + 1 mit der Sekante an den Funktionsgraphen durch die beiden Punkte $(x^k,f'(x^k))$

und $(x^{k + 1},f'(x^{k + 1}))$ (Abb. 2.8).

../images/439970_1_De_2_Chapter/439970_1_De_2_Fig8_HTML.png — Abb. 2.8
Grundidee des Sekantenverfahrens

Die dabei entstehende Gerade besitzt offenbar die Steigung

$a^{k + 1}\ =\ \frac{f'(x^{k + 1})-f'(x^k)}{x^{k + 1}-x^k}\,,$

und die Folge dieser Sekantensteigungen scheint die für die superlineare Konvergenz gewünschte Eigenschaft zu besitzen, die Tangentensteigung im Lösungspunkt $x^\star$ zu approximieren, also die Eigenschaft $a^k\to f''(x^\star)$ . In Analogie dazu bezeichnet man für n ≥ 1 die Gleichung

$\nabla f(x^{k + 1})-\nabla f(x^k)\ =\ A^{k + 1}\cdot(x^{k + 1}-x^k)$

(2.13)

als Sekantengleichung oder Quasi-Newton-Bedingung an die (n, n)-Matrix A^k + 1. Man zählt leicht nach, dass (2.13) n Gleichungen für die n² Einträge von A^k + 1 liefert. Selbst wenn man A^k + 1 als symmetrisch voraussetzt, sind noch immer n(n + 1)/2 Einträge zu bestimmen, was für n > 1 mit n Gleichungen nicht eindeutig möglich ist. Aus diesem Grunde existieren viele Möglichkeiten, verschiedene Quasi-Newton-Verfahren anzugeben.

Die Grundidee der folgenden Verfahren besteht darin, die Matrix A^k + 1 nicht in jedem Iterationsschritt komplett neu zu berechnen, sondern sie als möglichst einfaches Update der Matrix A^k aus dem vorherigen Schritt aufzufassen. Als erfolgreicher Ansatz hat sich dabei erwiesen, mit A⁰ ≻ 0 zu starten und in Zeile 7 von Algorithmus 2.6 die Matrix A^k + 1 aus A^k durch Addition einer symmetrischen Matrix vom Rang eins oder zwei zu gewinnen:

$A^{k + 1}\ =\ A^k + \alpha_k(u^k)(u^k)^\intercal + \beta_k(v^k)(v^k)^\intercal$

mit Skalaren α_k, $\beta_k\in\mathbb R$ und Vektoren u^k, $v^k\in\mathbb R^n$ , die so gewählt sind, dass A^k + 1 die Sekantengleichung (2.13) erfüllt.

Die auftretenden Matrizen sind dabei von der Bauart $ab^\intercal$ mit zwei Spaltenvektoren a und b. Eine solche Matrix besitzt stets höchstens den Rang eins und heißt dyadisches Produkt der Vektoren a und b. In unserer Anwendung gilt zusätzlich b = a, so dass das dyadische Produkt auch eine symmetrische Matrix ist.

Mit den Abkürzungen

$s^k\ :=\ x^{k + 1}-x^k\qquad\text{und}\qquad y^k\ :=\ \nabla f(x^{k + 1})-\nabla f(x^k)$

lautet die Sekantengleichung (2.13) für die so definierte Matrix A^k + 1

$y^k\ =\ \Big(A^k + \alpha_k(u^k)(u^k)^\intercal + \beta_k(v^k)(v^k)^\intercal \Big)\cdot s^k.$

Im Folgenden sei $k\in\mathbb N$ fest und unterschlagen. Dann folgt

$y-As\ =\ (\alpha\cdot u^\intercal s)\cdot u + (\beta\cdot v^\intercal s)\cdot v.$

Durch Abgleich der beiden Summanden in der linken und rechten Seite dieser Gleichung kann man auf die naheliegende Wahl u: = y und v : = As verfallen. Die passenden Koeffizienten auf der rechten Seite erhält man dann offensichtlich für die Wahlen

$\alpha\ :=\ \frac1{y^\intercal s}\qquad\text{und}\qquad \beta\ :=\ -\frac1{s^\intercal As},$

sofern die auftretenden Nenner nicht verschwinden. Die entstehende Update-Formel

$A^+\ =\ A + \frac{yy^\intercal}{y^\intercal s}\ -\ \frac{As\,s^\intercal A}{s^\intercal As}$

(2.14)

(wobei A⁺ für A^k + 1 steht) heißt BFGS-Update (nach Broyden, Fletcher, Goldfarb und Shanno, die die Formel unabhängig voneinander im Jahre 1970 fanden [5, 9, 14, 29]).

Da man in Zeile 4 von Algorithmus 2.6 die Suchrichtung

$d^k\ =\ -\left(A^k\right)^{-1}\nabla f(x^k)$

wählt, wäre es günstig, die Matrix $\left(A^k\right)^{-1}$ explizit angeben zu können. Wegen der einfachen Struktur des Rang-2-Updates ist dies hier in der Tat möglich, und zwar mit Hilfe der Sherman-Morrison-Woodbury-Formel .

2.2.49 Übung (Sherman-Morrison-Woodbury-Formel)

a)
Zeigen Sie für eine nichtsinguläre (n, n)-Matrix A und Vektoren $b,c\in\mathbb R^n$ , dass $A + b\,c^\intercal$ genau dann nichtsingulär ist, wenn $1 + c^\intercal A^{-1}b$ nicht verschwindet.
b)
Beweisen Sie die Sherman-Morrison-Woodbury-Formel für eine (n, n)-Matrix A und Vektoren $b,c\in\mathbb R^n$ , wobei A und $A + b\,c^\intercal$ nichtsingulär seien:
$(A + b\,c^\intercal)^{-1}\ =\ A^{-1}\ -\ \frac{A^{-1}b\,c^\intercal A^{-1}}{1 + c^\intercal A^{-1}b}.$

Übung 2.2.49 liefert eine Update-Formel für die inversen Matrizen

$B\ :=\ A^{-1}\quad\text{und}\quad B^+\ :=\ \left(A^+\right)^{-1},$

nämlich

$B^+_\textrm{BFGS}\ =\ B + \frac{ss^\intercal}{s^\intercal y}\ -\ \frac{By\,y^\intercal B}{y^\intercal By} + rr^\intercal$

mit

$r\ :=\ \sqrt{y^\intercal By}\cdot\left(\frac{s}{s^\intercal y}-\frac{By}{y^\intercal By}\right).$

Durch diese Kenntnis der inversen Matrizen muss man in Algorithmus 2.6 zur Bestimmung der Suchrichtung in Zeile 4 lediglich Matrix-Vektor-Produkte berechnen, anstatt lineare Gleichungssysteme zu lösen. In Zeile 2 wählt man daher eine Matrix B⁰ ≻ 0 anstelle von A⁰. In Zeile 4 setzt man

$d^k\ =\ -B^k\cdot\nabla f(x^k),$

und in Zeile 7 wählt man $B^{k + 1}=B^{k + 1}_\textrm{BFGS}$ .

Nach dieser Umstellung des Verfahrens von Matrizen A auf deren Inverse B kann man sich fragen, warum man die Herleitung eines Rang-2-Updates nicht direkt für die Inversen vorgenommen hat. Die Sekantengleichung y = As ist ja offenbar äquivalent zu s = By. Führt man dieselbe Konstruktion eines Updates wie oben für A analog für B aus, erhält man natürlich dieselbe Formel wie in (2.14), nur mit vertauschten Vektoren s und y:

$B^+_\textrm{DFP}\ =\ B + \frac{ss^\intercal}{s^\intercal y}\ -\ \frac{By\,y^\intercal B}{y^\intercal By}.$

Dieses DFP-Update (nach Davidon und Fletcher/Powell [6, 10]) unterscheidet sich vom BFGS-Update lediglich durch den Term $rr^\intercal$ . Die Einführung eines zusätzlichen Parameters $\theta\in\mathbb R$ liefert die Updates der Broyden-Familie

$B^+_\theta\ =\ B^+_\textrm{DFP} + \theta\cdot rr^\intercal.$

Offenbar gilt $B^+_0=B^+_\textrm{DFP}$ und $B^+_1=B^+_\textrm{BFGS}$ . Für die Wahl

$\theta\ =\ \frac{s^\intercal y}{s^\intercal y-y^\intercal B y}$

berechnet man

$B^+_\textrm{SR1}\ :=\ B^+_\theta\ =\ B + \frac{(s-By)(s-By)^\intercal}{(s-By)^\intercal y},$

so dass die Update-Matrix nur den Rang 1 besitzt. Man spricht dann vom SR1-Update (SR1 = symmetric rank 1).

Zur Division durch die Zahlen $s^\intercal y$ und $y^\intercal B y$ in den Update-Formeln lässt sich Folgendes anmerken. In Lemma 2.2.51 werden wir zeigen, dass für θ ≥ 0 mit B⁰ auch alle iterierten Matrizen B^k positiv definit sind, sofern $(s^k)^\intercal y^k$ positiv ist. Insbesondere gilt dann y^k ≠ 0 und $(y^k)^\intercal B^k y^k>0$ .

Die entscheidende Frage ist also, ob $(s^k)^\intercal y^k$ stets positiv ist. Zumindest für konvex-quadratische Funktionen $q(x)=\frac12x^\intercal Ax + b^\intercal x$ mit $A=A^\intercal\succ0$ haben wir

$y^k\ =\ \nabla q(x^{k + 1})-\nabla q(x^k)\ =\ (Ax^{k + 1} + b)-(Ax^k + b)\ =\ A(x^{k + 1}-x^k)\ =\ As^k$

(d. h., A erfüllt in jeder Iteration die Sekantengleichung), woraus

$(s^k)^\intercal y^k\ =\ (s^k)^\intercal A s^k\ >\ 0$

folgt. Mit etwas größerem Aufwand kann man dieses Resultat auch für lokal gleichmäßig konvexe Funktionen f zeigen. Unabhängig davon ist $(s^k)^\intercal y^k$ auch dann positiv, wenn man exakte Schrittweiten $t^k_e$

wählt.

2.2.50 Übung

In der k-ten Iteration eines Quasi-Newton-Verfahrens seien B^k ≻ 0 und

$\begin{aligned}d^k = \,& -B^k\nabla f(x^k)\,,\\ x^{k + 1} = \,& x^k + t^k d^k\,,\\ y^k = \,& \nabla f(x^{k + 1})-\nabla f(x^k)\\ \text{sowie}\quad s^k = \,& x^{k + 1}-x^k.\end{aligned}$

Zeigen Sie, dass bei Wahl von exakten Schrittweiten $t^k=t^k_e$

die Ungleichung

$(y^k)^\intercal s^k\ >\ 0$

gilt.

Die Anwendung der Armijo-Regel mit Backtracking Line Search garantiert ebenfalls die Positivität von $(s^k)^\intercal y^k$ [25].

Offenbar „erben“ die Matrizen $B^+_\theta$ für alle $\theta\in\mathbb R$ Symmetrie von B. Mit einer symmetrischen Matrix B⁰ sind also alle iterierten Matrizen B^k ebenfalls symmetrisch. Für die Vererbung von positiver Definitheit gilt folgendes Ergebnis.

2.2.51 Lemma

Es sei θ ≥ 0 beliebig. Dann gilt unter den Bedingungen B ≻ 0 und $s^\intercal y>0$ auch $B^+_\theta\succ0$ .

Beweis.

Für alle w ≠ 0 gilt

$w^\intercal B^+_\theta w\ =\ w^\intercal Bw + \frac{(w^\intercal s)^2}{s^\intercal y}\ -\ \frac{(w^\intercal B y)^2}{y^\intercal By} + \theta\cdot (w^\intercal r)^2.$

$w^\intercal Bw\ -\ \frac{(w^\intercal B y)^2}{y^\intercal By}\ =\ \|w\|_B^2\ -\ \frac{\langle w,y\rangle_B^2}{\|y\|_B^2}$

nach der Cauchy-Schwarz-Ungleichung nichtnegativ ist und dasselbe für die anderen beiden Summanden gilt, ist $w^\intercal B^+ w$ nichtnegativ.

Wir müssen nun noch zeigen, dass $w^\intercal B^+ w$ tatsächlich positiv ist. Dies ist im Fall

$\|w\|_B^2\ -\ \frac{\langle w,y\rangle_B^2}{\|y\|_B^2}\ >\ 0$

gewährleistet. Falls dieser Ausdruck andererseits verschwindet, so existiert nach der Cauchy-Schwarz-Ungleichung wegen w ≠ 0 ein λ ≠ 0 mit w = λy. In diesem Fall erhalten wir

$\frac{(w^\intercal s)^2}{s^\intercal y}\ =\ \lambda^2\,s^\intercal y\ >\ 0,$

also ebenfalls die Behauptung.

Angemerkt sei, dass die Voraussetzung θ ≥ 0 aus Lemma 2.2.51 zwar für den SR1-Update nicht garantiert ist, er in der Praxis aber dennoch häufig gute Ergebnisse liefert.

Wählt man exakte Schrittweiten $t^k=t^k_e$

, $k\in\mathbb N$ , so berechnet man für beliebiges $\theta\in\mathbb R$ leicht die Suchrichtung

$d^{k + 1}\ =\ -B^{k + 1}_\theta\nabla f(x^{k + 1})\ =\ \left(\frac{(y^k)^\intercal d^k}{\sqrt{(y^k)^\intercal B y^k}}- \theta(r^k)^\intercal\nabla f(x^{k + 1})\right)\cdot r^k.$

Da nur der Koeffizient des Vektors r^k von θ abhängt, ist die Suchrichtung für jedes $\theta\in\mathbb R$ identisch. Weil man aber entlang dieser Richtung exakt eindimensional minimiert, liefern alle Verfahren der Broyden-Familie identische Lösungsfolgen (x^k).

Dieses überraschende Ergebnis wird dadurch relativiert, dass man in der Praxis meist nicht exakt, sondern inexakt eindimensional minimiert, etwa per Armijo-Schrittweitensteuerung mit Backtracking Line Search. Bei inexakter Schrittweitenwahl können sich die Lösungsfolgen in der Tat ganz erheblich unterscheiden. Während zum Beispiel das DFP-Update dazu tendiert, schlecht konditionierte Matrizen B^k zu erzeugen, verhält sich das BFGS-Update für Probleme mittlerer Größe numerisch oft sehr robust. Hierbei bedeutet „mittlere Größe“, dass der Platzbedarf zur Speicherung der Matrizen B^k nicht zu hoch wird (etwa in Bezug auf die Größe des Arbeitsspeichers).

Leider lässt sich nicht zeigen, dass die Matrizen B^k stets gegen $(D^2f(x^\star))^{-1}$ streben, wie es zur Anwendung von Satz 2.2.48 zur superlinearen Konvergenz wünschenswert wäre. Mit einer recht technischen Verallgemeinerung von Satz 2.2.48 lässt sich für $\lim_k t^k=1$ trotzdem die superlineare Konvergenz der BFGS- und DFP-Verfahren nachweisen, falls $(B^k)^{-1}$ und $D^2f(x^\star)$ wenigstens entlang der Suchrichtungen d^k asymptotisch gleich sind (für Einzelheiten s. [25])

2.2.8 Konjugierte Richtungen

Für viele Anwendungsprobleme ist die Anzahl der Variablen so hoch, dass sich zwar Vektoren der Länge n wie x^k und d^k noch gut abspeichern lassen, die Speicherung der n(n + 1)/2 Einträge von Matrizen wie B^k aber zu einem Platzproblem führt. Um auch für solch hochdimensionale Probleme effizientere Verfahren als das Gradientenverfahren herzuleiten, befassen wir uns in diesem Abschnitt mit der besonderen Rolle, die Orthogonalität bezüglich eines Skalarprodukts $\langle\cdot,\cdot\rangle_A$ spielt.

2.2.52 Definition (Konjugiertheit bezüglich einer positiv definiten Matrix)

Es sei A eine (n, n)-Matrix mit $A=A^\intercal\succ0$ . Zwei Vektoren $v,w\in\mathbb R^n$ heißen konjugiert bezüglich A , falls $\,\langle v,w\rangle_A=0\,$ gilt.

Im Folgenden betrachten wir das allgemeine Abstiegsverfahren

$x^{k + 1}\ =\ x^k + t^k_e\,d^k$

mit exakten Schrittweiten $t^k_e$

und Abstiegsrichtungen erster Ordnung d^k für die konvex-quadratische Funktion

$q(x)\ =\ {\textstyle\frac12}\,x^\intercal Ax + b^\intercal x$

mit $A=A^\intercal\succ0$ und $b\in\mathbb R^n$ . Als erstes Ergebnis wird sich herausstellen, dass bezüglich A konjugierte Suchrichtungen viel schneller zur Identifikation eines globalen Minimalpunkts führen als etwa die negativen Gradientenrichtungen von q.

2.2.53 Übung

Für $k\in\mathbb N$ seien $d^0,\,\ldots\,,d^k$ paarweise konjugiert bezüglich A und sämtlich ungleich null. Zeigen Sie:

a)
Die Vektoren $d^0,\,\ldots\,,d^k$ sind linear unabhängig. Insbesondere gilt k < n.
b)
Für k = n − 1 gilt
$A^{-1}\ =\ \sum_{\ell=0}^{n-1}\,\frac{(d^\ell)(d^\ell)^\intercal}{(d^\ell)^\intercal A (d^\ell)}.$

2.2.54 Lemma

Für $k\in\mathbb N$ seien $d^0,\,\ldots\,,d^k$ paarweise konjugiert bezüglich A. Dann gilt

$\forall\ 0\le\ell\le k:\quad \langle\nabla q(x^{k + 1}),d^\ell\rangle\ =\ 0.$

Beweis.

Für $\ell=k$ resultiert die Behauptung aus (2.7), denn die exakte Schrittweite $t^k_e$

erfüllt

$0\ =\ \upvarphi_{d^k}'(t^k_e)\ =\ \langle\nabla q(x^k + t^k_e d^k),d^k\rangle\ =\ \langle\nabla q(x^{k + 1}),d^k\rangle.$

Für alle $0\le\ell\le k-1$ gilt

$x^{k + 1}\ =\ x^k + t^k_e d^k\ =\ x^{\ell + 1} + \sum_{j=\ell + 1}^k\,t^j_e\, d^j,$

also

$\nabla q(x^{k + 1})-\nabla q(x^{\ell + 1})\ =\ (Ax^{k + 1} + b)-(Ax^{\ell + 1} + b)\ =\ \sum_{j=\ell + 1}^k\,t^j_e Ad^j$

und somit wegen $0=\upvarphi_{d^\ell}'(t^\ell_e)=\langle\nabla q(x^{\ell + 1}),d^\ell\rangle$ und der Konjugiertheit der Vektoren $d^{\ell + 1},\,\ldots\,,d^k$ zu $d^\ell$

$\begin{aligned}\langle\nabla q(x^{k + 1}),d^\ell\rangle\ =\ \langle\nabla q(x^{k + 1})-\nabla q(x^{\ell + 1}),d^\ell\rangle\ =\ \sum_{j=\ell + 1}^k\,t^j_e (d^j)^\intercal A d^\ell\ =\ 0.\end{aligned}$

2.2.55 Satz

Die Vektoren $d^0,\,\ldots\,,d^{n-1}$ seien paarweise konjugiert bezüglich A und sämtlich ungleich null. Dann ist xⁿ der globale Minimalpunkt von q.

Beweis.

Nach Übung 2.2.53 sind die Vektoren $d^\ell$ , $0\le\ell\le n-1$ , linear unabhängig, und nach Lemma 2.2.54 gilt

$\forall\ 0\le\ell\le n-1:\quad \langle\nabla q(x^n),d^\ell\rangle\ =\ 0.$

Demnach verschwindet der Vektor ∇q(xⁿ), und xⁿ ist der eindeutige globale Minimalpunkt von q (Übung 2.1.43).

Satz 2.2.55 besagt, dass ein Abstiegsverfahren für die konvex-quadratische Funktion q bei exakter Schrittweitensteuerung und paarweise konjugierten Suchrichtungen nach höchstens n Schritten den globalen Minimalpunkt von q findet („höchstens“, weil ein x^k mit k < n zufällig schon ein Minimalpunkt sein kann). Da für ein Abstiegsverfahren wegen $f(x^{k + 1})< f(x^k)$ stets $t^k_e\cdot d^k=x^{k + 1}-x^k\neq{}0$ gilt, kann insbesondere keiner der Vektoren d^k verschwinden.

Im nächsten Schritt suchen wir nach Möglichkeiten, konjugierte Suchrichtungen explizit zu erzeugen. Der folgende Satz besagt, dass man konjugierte Richtungen zum Beispiel aus den Quasi-Newton-Verfahren der Broyden-Familie erhält.

2.2.56 Satz

Für θ ≥ 0 werde Algorithmus 2.6 mit $t^k=t^k_e$ und $B^{k + 1}=B^{k + 1}_\theta$ auf $q(x)=\frac12x^\intercal A x + b^\intercal x$ mit $A=A^\intercal\succ0$ angewendet, und für ein $k\in\mathbb N$ seien die Iterierten $x^0,\,\ldots\,,x^k$ paarweise verschieden. Dann sind die Richtungen $d^0,\,\ldots\,,d^{k-1}$ paarweise konjugiert bezüglich A und sämtlich von null verschieden.

Beweis.

Wir halten zunächst folgende Beziehungen fest: Per Definition gilt für alle $k\in\mathbb N$

$\begin{aligned}d^k = \,& -B^k\nabla q(x^k),\end{aligned}$

(2.15)

$\begin{aligned}x^{k + 1} = \,& x^k + t^k_e d^k\end{aligned}$

(2.16)

und damit

$\begin{aligned}s^k := \,& x^{k + 1}-x^k\ =\ t^k_e d^k,\end{aligned}$

(2.17)

$\begin{aligned}y^k := \,& \nabla q(x^{k + 1})-\nabla q(x^k)\ =\ As^k.\end{aligned}$

(2.18)

Die Sekantengleichung (2.13) ist außerdem äquivalent zu

$B^{k + 1} y^k\ =\ s^k,$

(2.19)

und die Exaktheit der Schrittweite liefert

$\langle\nabla q(x^{k + 1}),d^k\rangle\ =\ \upvarphi'_{d^k}(t^k_e)\ =\ 0.$

(2.20)

Die Verfahren der Broyden-Familie mit θ ≥ 0 sind nach Lemma 2.2.51 Abstiegsverfahren. Solange ein solches Verfahren nicht abbricht, erzeugt es paarweise verschiedene Iterierte, so dass die Voraussetzung des Satzes für den Beginn jeder vom Verfahren generierten Folge (x^k) erfüllt ist. Wegen (2.16) sind daher alle Richtungen $d^0,\,\ldots\,,d^{k-1}$ von null verschieden.

Wir zeigen nun die folgende dreiteilige Hilfsbehauptung, deren erster Teil mit der zu zeigenden Hauptbehauptung übereinstimmt:

$\begin{aligned}\forall\ 0\le\ell\le k-1:\qquad (d^k)^\intercal A d^\ell = \,& 0,\end{aligned}$

(2.21)

$\begin{aligned}\langle\nabla q(x^k),d^\ell\rangle = \,& 0,\end{aligned}$

(2.22)

$\begin{aligned}B^k y^\ell = \,& s^\ell.\end{aligned}$

(2.23)

Für $\ell=k-1$ sieht man diese Behauptung folgendermaßen: Wegen $x^k\neq x^{k-1}$ und (2.16) kann $t^{k-1}_e$ nicht verschwinden. Damit gilt

$\begin{aligned}(d^k)^\intercal A d^{k-1} \stackrel{(2.17)}{=} \,& (d^k)^\intercal A\frac{s^{k-1}}{t^{k-1}_e} \ \stackrel{\textrm{(2.15), (2.18)}}{=}\ -\frac1{t^{k-1}_e}\langle\nabla q(x^k),B^k y^{k-1}\rangle\\ \stackrel{\textrm{(2.19)}}{=} \,& -\frac1{t^{k-1}_e}\langle\nabla q(x^k),s^{k-1}\rangle\ \stackrel{(2.17)}{=} \ -\langle\nabla q(x^k),d^{k-1}\rangle \stackrel{\textrm{(2.20)}}{=}\ 0.\end{aligned}$

Hieraus folgen (2.21) und (2.22). Die Gl. (2.23) stimmt für $\ell=k-1$ gerade mit der Sekantengleichung (2.19) überein.

Die verbleibenden Fälle behandeln wir per vollständiger Induktion über k. Für k = 1 ist die Hilfsbehauptung nur für $\ell=0$ zu zeigen, was wegen $\ell=k-1$ aber gerade geschehen ist. Die Hilfsbehauptung gelte nun für ein $k\in\mathbb N$ und soll für k + 1 bewiesen werden. Wir müssen also die Eigenschaften (2.21) bis (2.23) mit k + 1 anstelle von k für alle $0\le\ell\le k$ zeigen. Um die zu zeigenden Eigenschaften von denen aus der Induktionsvoraussetzung unterscheiden zu können, werden wir sie ab jetzt mit (2.21) $_{^{k + 1}}$ bis (2.23) $_{^{k + 1}}$ bzw. (2.21)_k bis (2.23)_k adressieren.

Der Fall $\ell=k$ ist durch die obige Überlegung bereits bewiesen. Es sei also $0\le\ell\le k-1$ . Es gilt

$(y^k)^\intercal B^k y^\ell\stackrel{(2.23)_k}{=}(y^k)^\intercal s^\ell\stackrel{(2.18)}{=} (s^k)^\intercal A s^\ell\stackrel{(2.17)}{=}t^k_e t^\ell_e (d^k)^\intercal A d^\ell\stackrel{(2.21)_k}{=}\ 0$

sowie analog

$(s^k)^\intercal y^\ell\ =\ (s^k)^\intercal A s^\ell\ =\ 0.$

Daraus folgt

$B^{k + 1} y^\ell\ =\ B^{k + 1}_\theta y^\ell\ =\ B^k y^\ell + \underbrace{\frac{s^k(s^k)^\intercal y^\ell}{(s^k)^\intercal y^k}}_{=\ 0} -\underbrace{\frac{B^k y^k(y^k)^\intercal B^k y^\ell}{(y^k)^\intercal B^k y^k}}_{=\ 0} + \theta r^k\underbrace{(r^k)^\intercal y^\ell}_{=\ 0} \ \stackrel{(2.23)_k}{=}\ s^\ell$

und damit (2.23) $_{^{k + 1}}$ . Ferner gilt

$(d^{k + 1})^\intercal Ad^\ell\ =\ \frac1{t^\ell_e}(d^{k + 1})^\intercal A s^\ell\ =\ -\frac1{t^\ell_e} \langle\nabla q(x^{k + 1}),\underbrace{B^{k + 1} y^\ell}_{=\ s^\ell}\rangle\ =\ -\langle\nabla q(x^{k + 1}),d^\ell\rangle,$

so dass auch (2.21) $_{^{k + 1}}$ bewiesen ist, sobald wir (2.22) $_{^{k + 1}}$ gezeigt haben. Wegen

$\langle\nabla q(x^{k + 1}),d^\ell\rangle\ =\ \langle A(x^k + t^k_e d^k) + b,d^\ell\rangle\ =\ \langle\nabla q(x^k),d^\ell\rangle + t^k_e (d^k)^\intercal A d^\ell$

folgt Letzteres aber aus den Induktionsvoraussetzungen (2.21)_k und (2.22)_k.

Bei Wahl exakter Schrittweiten minimieren die Quasi-Newton-Verfahren der Broyden-Familie konvex-quadratische Funktionen also in höchstens n Schritten. Für eine beliebige C²-Funktion f lässt sich das dahingehend interpretieren, dass sie die lokale quadratische Approximation an f in n Schritten minimieren, im Hinblick auf Übung 2.2.43 also einen Schritt des Newton-Verfahrens simulieren. Unter geeigneten Voraussetzungen und mit Neustarts nach jeweils n Schritten konvergieren sie daher „n-Schritt-quadratisch“ (für Details s. [25]).

2.2.9 Konjugierte-Gradienten-Verfahren

Wie bereits angemerkt möchte man bei hochdimensionalen Problemen vermeiden, Matrizen wie die B^k in den Quasi-Newton-Verfahren abzuspeichern. Man sucht daher nach matrixfreien Möglichkeiten, konjugierte Richtungen zu erzeugen. Verfahren, die iterativ konjugierte Richtungen erzeugen, nennt man Konjugierte-Gradienten-Verfahren oder kurz CG-Verfahren (CG = conjugate gradients).

Wir betrachten weiterhin die konvex-quadratische Funktion

$q(x)\ =\ {\textstyle\frac12}\,x^\intercal Ax + b^\intercal x$

mit $A=A^\intercal\succ0$ sowie $b\in\mathbb R^n$ und bilden die Folge (x^k) mit exakten Schrittweiten. Gesucht sind Möglichkeiten, konjugierte Suchrichtungen (d^k) zu erzeugen.

Nachdem wir bereits die Iterierten x^k grundsätzlich rekursiv aus früheren Iterierten sowie bei Quasi-Newton-Verfahren die Matrizen B^k rekursiv aus früheren Matrizen konstruiert haben, wird die Grundidee dazu im Folgenden sein, auch die Suchrichtungen d^k rekursiv zu wählen, nämlich als Kombination des aktuellen negativen Gradienten −∇q(x^k) und der letzten Suchrichtung d^k − 1 mit Hilfe eines noch zu bestimmenden „Gewichts“ $\alpha_k\in\mathbb R$ zu

$d^k\ =\ -\nabla q(x^k) + \alpha_k\cdot d^{k\,-\,1},\quad k=1,2,\,\ldots\,$

Zu Beginn dieser Rekursion setzen wir

$d^0\ =\ -\nabla q(x^0).$

Das folgende Lemma wird zur Bestimmung der Werte α_k wesentlich sein.

2.2.57 Lemma

Es seien $d^0,\,\ldots\,,d^{k\,-\,1}$ paarweise konjugiert bezüglich A und $x^1,\,\ldots\,,x^k$ schon generiert mit $x^\ell\neq x^{\ell-1}$ für $1\le\ell\le k$ . Dann ist d^k genau dann konjugiert zu einem $d^\ell$ mit $0\le\ell\le k-1$ , wenn

$\langle\nabla q(x^{\ell + 1})-\nabla q(x^\ell),d^k\rangle\ =\ 0$

erfüllt ist.

Beweis.

Aus

$\langle\nabla q(x^{\ell + 1})-\nabla q(x^\ell),d^k\rangle\ =\ t^\ell_e (d^\ell)^\intercal A d^k$

folgt wegen $t^\ell_e\neq 0$ die Behauptung.

2.2.58 Satz

Unter den Voraussetzungen von Lemma 2.2.57 ist die Richtung $d^k = -\nabla q(x^k) + \alpha_k\cdot d^{k-1}$ genau für

$\alpha_k\ =\ \frac{\|\nabla q(x^k)\|^2_2}{\|\nabla q(x^{k-1})\|^2_2}$

konjugiert zu den Vektoren $d^0,\,\ldots\,,d^{k-1}$ .

Beweis.

Wir beweisen die Behauptung per vollständiger Induktion über k. Im Fall k = 1 ist d¹ nach Lemma 2.2.57 genau dann konjugiert zu d⁰, wenn

$\begin{aligned}0 = \,& \langle\nabla q(x^1)-\nabla q(x^0),d^1\rangle\ =\ \langle\nabla q(x^1) + d^0,-\nabla q(x^1) + \alpha_1d^0\rangle\\ = \,& -\|\nabla q(x^1)\|_2^2 + \alpha_1\|\nabla q(x^0)\|_2^2\end{aligned}$

gilt, wobei die letzte Gleichheit aus zweifacher Anwendung von (2.7) folgt.

Für k > 1 zeigen wir nur die Konjugiertheit von d^k und d^k − 1 und überlassen dem Leser die restlichen Fälle als Übung. Nach Lemma 2.2.57 ist d^k genau dann konjugiert zu d^k − 1, wenn

$\begin{aligned}0 = \,& \langle\nabla q(x^k)-\nabla q(x^{k-1}),d^k\rangle\ =\ \langle\nabla q(x^k)-\nabla q(x^{k-1}),-\nabla q(x^k) + \alpha_k d^{k-1}\rangle\\ = \,& -\|\nabla q(x^k)\|_2^2 + \underbrace{\langle\nabla q(x^{k-1}),\nabla q(x^k)\rangle}_{=:\ T_1} -\alpha_k\underbrace{\langle q(x^{k\,-\,1}),d^{k-1}\rangle}_{=:\ T_2}\end{aligned}$

gilt. Aus

$\begin{aligned}T_1 = \,& \langle\nabla q(x^k),\alpha_{k-1}d^{k-2}-d^{k-1}\rangle\ =\ \alpha_{k-1}\langle\nabla q(x^{k-1}) + t^{k-1}_eAd^{k-1},d^{k-2}\rangle\ \stackrel{\textrm{Ind.vor.}}{=}\ 0\\ \textrm{und}\quad T_2 = \,& \langle\nabla q(x^{k-1}),-\nabla q(x^{k-1}) + \alpha_{k-1}d^{k-2}\rangle\ =\ -\|\nabla q(x^{k-1})\|_2^2\end{aligned}$

folgt die Behauptung.

Algorithmus 2.7: CG-Verfahren von Fletcher-Reeves

Input : C¹-Optimierungsproblem P

Output : Approximation $\bar x$ eines kritischen Punkts von f (falls das Verfahren terminiert [25, Th. 5.7])

1 begin

2 Wähle einen Startpunkt x⁰, eine Toleranz $\varepsilon>0$ und setze $d^0=-\nabla f(x^0)$ sowie $k=0$ .

3 While $\|\nabla f(x^k)\|>\varepsilon$ do

4 Setze $x^{k + 1}=x^k + t_e^k d^k$ .

5 Setze $\ d^{k + 1}=-\nabla f(x^{k + 1}) + \left(\|\nabla f(x^{k + 1})\|^2_2/\|\nabla f(x^k)\|^2_2\right)\cdot d^k$ .

6 Ersetze k durch $k + 1$ .

7 end

8 Setze $\bar x=x^k$ .

9 end

Satz 2.2.58 motiviert den Algorithmus 2.7, da er für $f(x)=q(x)=\frac12 x^\intercal A x + b^\intercal x$ mit $A=A^\intercal\succ0$ nach höchstens n Schritten den globalen Minimalpunkt liefert. Man benutzt dieses Verfahren zum Beispiel zur Lösung hochdimensionaler linearer Gleichungssysteme Ax = b durch den Kleinste-Quadrate-Ansatz , also per Minimierung von $\|r(x)\|_2^2$ mit dem Residuum r(x) = Ax − b.

Wegen Rundungsfehlern (vor allem aufgrund der Division durch $\|\nabla f(x^k)\|_2^2$ ) bricht das Verfahren aber selten tatsächlich nach n Schritten ab, so dass auch seine Konvergenzgeschwindigkeit untersucht wurde. Es stellt sich heraus, dass sie von der Wurzel der Konditionszahl (also dem Quotienten aus größtem und kleinstem Eigenwert) der Matrix $A^\intercal A$ abhängt. Es bietet sich daher an, das Gleichungssystem Ax = b zunächst so äquivalent umzuformen, dass diese Konditionszahl sinkt. Dies ist als Präkonditionierung bekannt. Für eine kurze Einführung dazu sei auf [16] verwiesen.

2.2.59 Bemerkung

Der Kleinste-Quadrate-Ansatz per CG-Verfahren zur Lösung linearer Gleichungssysteme Ax = b lässt sich auch auf überbestimmte Gleichungssysteme anwenden, die keine Lösung besitzen. Man gibt sich dann mit dem x zufrieden, das $\|r(x)\|_2^2$ minimiert, auch wenn der Optimalwert nicht null lautet.

Für unterbestimmte Gleichungssysteme besteht andererseits die Möglichkeit, unter allen Lösungen von Ax = b eine spezielle auszuwählen. Oft wählt man dazu das „kleinste“ x in dem Sinne, dass $\|x\|_2$ über dem Lösungsraum minimiert wird. Dies führt allerdings auf ein restringiertes Optimierungsproblem (Kap. 3).

Entscheidend für die Einsetzbarkeit von Algorithmus 2.7 ist, dass für f = q nirgends explizit die Matrix A eingeht, aber trotzdem bezüglich A konjugierte Suchrichtungen erzeugt werden. Man kann das Verfahren also auch für beliebige C¹-Funktionen formulieren, wobei in Zeile 4 die exakte Schrittweite $t^k_e$ im Allgemeinen durch eine inexakte wie die Armijo-Schrittweite $t^k_a$ ersetzt werden muss. Unter geeigneten Voraussetzungen erhält man wieder, dass n CG-Schritte einen Newton-Schritt simulieren, also „n-Schritt-quadratische Konvergenz“. Dazu empfiehlt sich nach je n Schritten ein „Neustart“, indem man $d^{k\cdot n}=-\nabla f(x^{k\cdot n})$ für $k\in\mathbb N$ setzt.

Schließlich rechnet man im Fall f = q leicht die Beziehungen

$\frac{\|\nabla f(x^{k + 1})\|^2_2}{\|\nabla f(x^k)\|^2_2}\ =\ \frac{\langle\nabla f(x^{k + 1}),\nabla f(x^{k + 1})-\nabla f(x^k)\rangle}{\langle d^k,\nabla f(x^{k + 1})-\nabla f(x^k)\rangle}\ =\ \frac{\langle\nabla f(x^{k + 1}),\nabla f(x^{k + 1})-\nabla f(x^k)\rangle}{\|\nabla f(x^k)\|^2_2}$

nach. Für f ≠ q sind diese Gleichheiten hingegen nicht notwendigerweise gültig, so dass man in Algorithmus 2.7 beim Ersetzen von $\|\nabla f(x^{k + 1})\|^2_2/\|\nabla f(x^k)\|^2_2$ durch diese Ausdrücke andere Verfahren erhält, nämlich die CG-Verfahren von Hestenes-Stiefel bzw. von Polak-Ribière (für Details s. [25]).

2.2.10 Trust-Region-Verfahren

Im Gegensatz zu klassischen Suchrichtungsverfahren wählen Trust-Region-Verfahren erst den Suchradius t und dann die Suchrichtung d (formal gilt also d = d(t) anstatt t = t(d)). Dazu benutzt man in Iteration k des allgemeinen Abstiegsverfahrens aus Algorithmus 2.3 wie folgt ein quadratisches Modell für f.

Nach dem Satz von Taylor (Satz 2.1.30b) gilt für $f\in C^2(\mathbb R^n,\mathbb R)$

$f(x^k + d)\ \approx\ f(x^k) + \langle\nabla f(x^k),d\rangle + {\textstyle\frac12} d^\intercal D^2f(x^k) d.$

Mit

, $b^k=\nabla f(x^k)$ und einer symmetrischen Matrix A^k (zum Beispiel, aber nicht notwendigerweise, $A^k=D^2f(x^k)$

) nennt man die Funktion

$m^k(d)\ :=\ c^k + \langle b^k,d\rangle + {\textstyle\frac12} d^\intercal A^k d$

ein lokales quadratisches Modell für f um x^k. Diese Bezeichnung motiviert sich aus den Gleichheiten $m^k(0)=f(x^k)$

und $\nabla m^k(0)=\nabla f(x^k)$ sowie aus der Tatsache, dass m^k die Funktion f im Allgemeinen nur für d aus einer hinreichend kleinen Umgebung des Nullpunkts „gut“ beschreibt.

Man betrachtet daher m^k nur für $\|d\|_2\le t^k$ mit einem hinreichend kleinen Suchradius t^k. Falls das Verhalten von m^k auf $B_\le(0,t^k)$ „gut“ ist, nennt man $B_\le(0,t^k)$ eine „vertrauenswürdige Umgebung“, also eine Trust Region . Um hierbei den Begriff „gut“ zu quantifizieren, bestimmt man einen optimalen Punkt d^k des Trust-Region-Hilfsproblems

$TR^k:\qquad\min_{d\in\mathbb R^n}\,m^k(d)\quad\text{ s.t. }\quad \|d\|_2\le t^k.$

Der Quotient

$r^k\ :=\ \frac{f(x^k)-f(x^k + d^k)}{m^k(0)-m^k(d^k)}$

aus tatsächlichem und erwartetem Abstieg im Zielfunktionswert gibt dann ein Maß für die Güte des lokalen Modells an. Zu beachten ist dabei, dass die Differenz $m^k(0)-m^k(d^k)$

stets positiv ist, und zwar selbst dann, wenn die Matrix A^k nicht positiv definit ist. In der Tat würde die Ungleichung $m^k(0)-m^k(d^k)\le0$ wegen der Zulässigkeit von d = 0 für TR^k die Identität von m^k(0) und $m^k(d^k)$

implizieren, so dass neben d^k auch d = 0 Minimalpunkt von TR^k wäre. Da die Restriktion von TR^k an d = 0 nicht aktiv ist, würde daraus $0=\nabla m^k(0)=\nabla f(x^k)$ folgen, im Widerspruch dazu, dass das allgemeine Abstiegsverfahren 2.3 in diesem Fall bereits terminiert hätte.

Ein Wert r^k < 0 impliziert daher $f(x^k + d^k)> f(x^k)$ , d. h., $x^{k + 1}=x^k + d^k$ würde einen Anstieg im Zielfunktionswert liefern. Folglich ist die Trust Region zu groß, und ihr Radius t^k muss verkleinert werden.

Liegt andererseits r^k nahe bei eins, dann beschreibt das lokale Modell die Funktion f sehr gut; man setzt $x^{k + 1}=x^k + d^k$ und vergrößert in der nächsten Iteration probeweise den Trust-Region-Radius t^k.

Details zu diesem Vorgehen, vor allem zur Annahme von Schritten und zur Veränderung von t^k bei anderen Werten von r^k, gibt Algorithmus 2.8. Insbesondere für r^k ≥ 1/4 wird t^k dort nicht verkleinert, und der Schritt wird angenommen, für r^k < 0 wird t^k verkleinert, und der Schritt wird abgelehnt, und für r^k ∈ [0, 1/4) wird t^k verkleinert, und der Schritt wird dann abgelehnt, wenn r^k ≤ η gilt.

Algorithmus 2.8: Trust-Region-Verfahren

Input : C¹-Optimierungsproblem P

Output : Approximation $\bar x$ eines kritischen Punkts von f (falls das Verfahren terminiert; Satz 2.2.63)

1 begin

2 Wähle einen Startpunkt x⁰, eine Matrix $A^0=(A^0)^\intercal$ , eine Toleranz $\varepsilon>0$ , einen Maximalradius $\check{\kern-1pt t}>0$ , einen Startradius $t^0\in(0,\check{\kern-1pt t})$ , einen Parameter $\eta\in[0,1/4)$ und setze $k=0$ .

3 While $\|\nabla f(x^k)\|_2>\varepsilon$ do

4 Berechne einen (inexakten) Optimalpunkt d^k von TR^k und setze

$r^k\ =\ \frac{f(x^k)-f(x^k + d^k)}{m^k(0)-m^k(d^k)}.$

5 If $r^k<\frac14$ then

6 Setze $t^{k + 1}=\frac14\|d^k\|_2$ .

7 else

8 If ${r^k} > \frac{3}{4}\;{\bf{and}}\;{\left\| {{{\rm{d}}^{\rm{k}}}} \right\|_2} = {{\rm{t}}^{\rm{k}}}$ then

9 Setze $t^{k + 1}=\min\{2t^k,\check{\kern-1pt t}\}$ .

10 else

11 Setze $t^{k + 1} = t^k$ .

12 end

13 end

14 If $r^k>\eta$ thend

15 Setze $x^{k + 1}=x^k + d^k$ .

16 else

17 Setze $x^{k + 1}=x^k$ .

18 end

19 Wähle $A^{k + 1}=(A^{k + 1})^\intercal$ .

20 Ersetze k durch $k + 1$ .

21 end

22 Setze $\bar x=x^k$ .

23 end

Abb. 2.9 zeigt eine mögliche neue Iterierte $x^{k + 1}_{TR}$ eines Trust-Region-Verfahrens im Vergleich zu einer neuen Iterierten eines Suchrichtungsverfahrens $x^{k + 1}_{SR}$ mit gleicher Schrittweite. Zumindest in diesem Beispiel führt der Trust-Region-Schritt näher an den Minimalpunkt von f als der Suchrichtungsschritt.

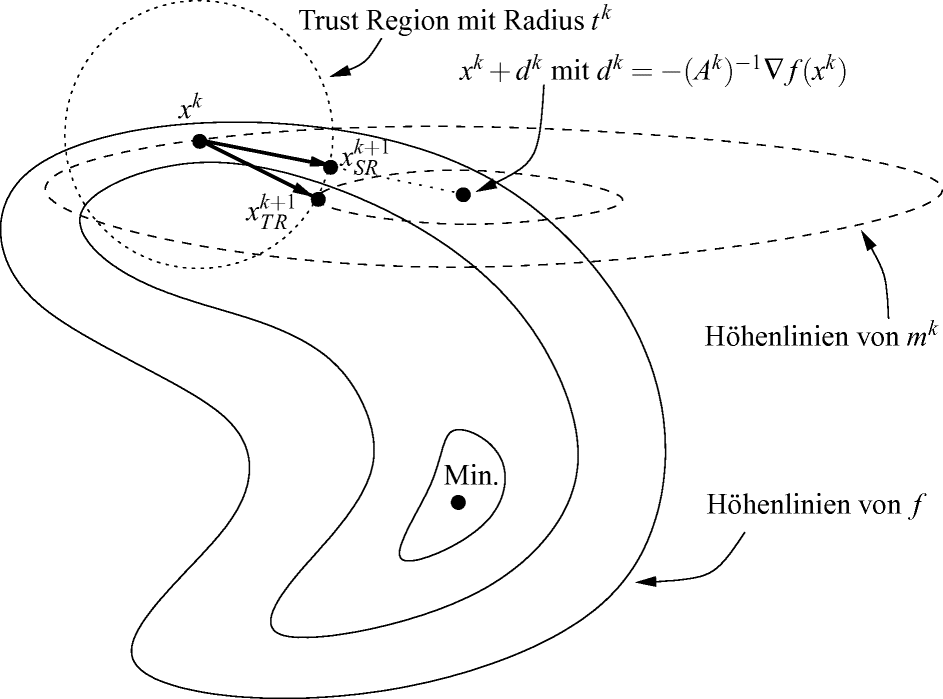
../images/439970_1_De_2_Chapter/439970_1_De_2_Fig9_HTML.png — Abb. 2.9
Schritte von Suchrichtungs- und Trust-Region-Verfahren

Je nach Wahl der Matrizen A^k + 1 in Zeile 19 von Algorithmus 2.8 spricht man von Trust-Region-Newton-Verfahren, Trust-Region-BFGS-Verfahren usw. Ein entscheidender Vorteil von Trust-Region-Verfahren gegenüber Variable-Metrik-Verfahren besteht allerdings darin, dass die Matrizen A^k nicht positiv definit zu sein brauchen.

Insbesondere für A^k≡0 erhält man ein „Trust-Region-Gradientenverfahren“ mit dem Hilfsproblem

$TR^k:\qquad\min_{d\in\mathbb R^n}\, m^k(d)=f(x^k) + \langle\nabla f(x^k),d\rangle\quad\text{ s.t. }\quad \|d\|_2\le t^k.$

Analog zu den Überlegungen in Abschn. 2.1.3 folgt für dessen Minimalpunkt allerdings sofort

$d^k\ =\ -\frac{t^k}{\|\nabla f(x^k)\|_2}\nabla f(x^k)\,,$

so dass hier lediglich ein übliches Gradientenverfahren mit einer speziellen Schrittweitensteuerung entsteht. Von einem solchen Verfahren ist wegen Satz 2.2.23 keine schnelle Konvergenz zu erwarten.

Wir betrachten daher wieder den Fall einer symmetrischen Matrix A^k ≠ 0. Das Problem TR^k zu lösen, kann schwer sein, insbesondere für eine indefinite Matrix A^k. Analog zur inexakten eindimensionalen Minimierung bei Suchrichtungsverfahren genügt allerdings auch hier eine inexakte Lösung von TR^k, um globale Konvergenz zu gewährleisten.

Eine Möglichkeit dafür besteht darin, die zulässige Menge von TR^k stark zu verkleinern und beispielsweise nur nichtnegative Vielfache der beim „Trust-Region-Gradientenverfahren“ gefundenen Suchrichtung zuzulassen:

$\begin{aligned}TR^k_C:\qquad\min_{d,s}\,m^k(d) \quad\text{ s.t. }\quad \,& \|d\|_2\le t^k\,,\quad d=s\cdot\left(-\frac{t^k}{\|\nabla f(x^k)\|_2}\cdot\nabla f(x^k)\right)\\ \,& s\ge0.\end{aligned}$

Dieses Problem (bei dem der Index C daher rührt, dass das Gradientenverfahren auch als Cauchy-Verfahren bezeichnet wird) ist offenbar äquivalent zu

$\min_{s\in\mathbb R}\,m^k\left(-\frac{s\cdot t^k}{\|\nabla f(x^k)\|_2}\cdot\nabla f(x^k)\right)\quad\text{ s.t. }\quad 0\le s\le 1,$

also zu

$\min_{s\in\mathbb R}\ \widetilde m^k(s)\quad\text{ s.t. }\quad 0\le s\le 1$

mit

$\begin{aligned}\widetilde m^k(s) := \,& m^k\left(-\frac{s\cdot t^k}{\|\nabla f(x^k)\|_2}\cdot\nabla f(x^k)\right)\\ = \,& f(x^k)-s\cdot t^k \|\nabla f(x^k)\|_2 + s^2\cdot \frac{(t^k)^2}{2\|\nabla f(x^k)\|_2^2}\,Df(x^k)A^k\nabla f(x^k).\end{aligned}$

Zur Lösung dieses eindimensionalen Optimierungsproblems sind zwei Fälle zu unterscheiden.

Fall 1: $\ Df(x^k)A^k\nabla f(x^k)\le 0$

Dann gilt für alle s ∈ [0, 1]

$\frac{d}{ds}\,\widetilde m^k(s)\ =\ \underbrace{-t^k\|\nabla f(x^k)\|_2}_{<\ 0} + \underbrace{s\,\frac{(t^k)^2}{\|\nabla f(x^k)\|_2^2}\,Df(x^k)A^k\nabla f(x^k)}_{\le\ 0},$

so dass die Funktion $\widetilde m^k$ auf s ∈ [0, 1] streng monoton fällt, ihren Minimalpunkt also in $s^\star=1$ besitzt.

Fall 2: $\ Df(x^k)A^k\nabla f(x^k)> 0$

In diesem Fall ist die Funktion $\widetilde m^k$ konvex-quadratisch, und Minimalpunkt ist entweder ihr Scheitelpunkt

$s^\star\ =\ \frac{\|\nabla f(x^k)\|_2^3}{t^k Df(x^k)A^k\nabla f(x^k)}$

oder $s^\star=1$ , je nachdem, welcher Wert kleiner ist.

Insgesamt löst also der Punkt

$d^k_C\ :=\ -\frac{s^k\,t^k}{\|\nabla f(x^k)\|_2}\nabla f(x^k)$

mit

$s^k\ :=\ \begin{cases}1\,,& \text{falls }\ Df(x^k)A^k\nabla f(x^k)\le 0\\ \min\left\{\,\frac{\|\nabla f(x^k)\|_2^3}{t^k Df(x^k)A^k\nabla f(x^k)}\,,\,1\,\right\}\,,&\text{sonst}\end{cases}$

das Problem $TR^k_C$

2.2.60 Definition (Cauchy-Punkt)

Der Punkt $x^{k + 1}_C=x^k + d^k_C$ heißt Cauchy-Punkt zu x^k und t^k.

2.2.61 Übung

Zeigen Sie, dass der Vektor $d^k=d^k_C$

die Ungleichung

$m^k(0)-m^k(d^k)\ \ge\ c\cdot\|\nabla f(x^k)\|_2\cdot\min\left\{\,t^k\,,\,\frac{\|\nabla f(x^k)\|_2}{\|A^k\|_2}\,\right\}$

(2.24)

mit c = 1/2 erfüllt.

2.2.62 Bemerkung

Die exakte Lösung $d^k_e$ von TR^k erfüllt wegen der Zulässigkeit von $d^k_C$ für TR^k die Ungleichung $m^k(d^k_e)\le m^k(d^k_C)$ und damit nach Übung 2.2.61 ebenfalls (2.24) mit c = 1/2.

Wir können nun einen Satz zur globalen Konvergenz formulieren [25, Th. 4.5 und 4.6].

2.2.63 Satz

Die Menge $f_\le^{f(x^0)}$ sei beschränkt, die Funktion ∇f sei Lipschitz-stetig auf $\textrm{conv}(f_\le^{f(x^0)})$ , die Folge $(\|A^k\|_2)$ sei beschränkt, und die Folge (d^k) der inexakten Lösungen von TR^k erfülle (2.24) mit c > 0. Dann gilt in Algorithmus 2.8:

a)
Für η = 0 ist $\liminf_k\,\|\nabla f(x^k)\|_2=0$ (d. h., (x^k) besitzt einen Häufungspunkt $x^\star$ mit $\nabla f(x^\star)=0$ ).
b)
Für η ∈ (0, 1/4) ist $\lim_k\,\nabla f(x^k)=0$ (d. h., alle Häufungspunkte von (x^k) sind kritisch).

Nach Übung 2.2.61, Bemerkung 2.2.62 und Satz 2.2.63 liefern sowohl die inexakten Lösungen $d^k_C$ als auch die exakten Lösungen $d^k_e$ von TR^k globale Konvergenz. Während die exakte Lösung $d^k_e$ wie erwähnt schwer berechenbar sein kann, ist das Ausweichen auf die inexakte Lösung $d^k_C$ selten ratsam, da die Matrix A^k lediglich die Länge von $d^k_C$ beeinflusst und man so im Wesentlichen nach wie vor das Gradientenverfahren erhält.

Wir betrachten daher noch zwei in der Praxis gebräuchliche inexakte Approximationen für einen Optimalpunkt d^k von TR^k, für die ebenfalls $m^k(d^k)\le m^k(d^k_C)$ und damit (2.24) mit c = 1/2 gilt (für Details zu Konvergenzaussagen s. [25]). Die erste Möglichkeit besitzt als einschränkende Voraussetzung die positive Definitheit der Matrizen A^k, die zweite hingegen nicht.

Dogleg-Methode

Im Folgenden seien wieder $k\in\mathbb N$ fest und unterschlagen sowie A positiv definit. Wir fragen zunächst danach, wie die exakten Lösungen d_e(t) von TR sich bei variierendem t ≥ 0 verhalten. Per Definition löst d_e(t) das Problem

$TR:\qquad \min_{d\in\mathbb R^n}\, c + b^\intercal d + {\textstyle\frac12} d^\intercal A d\quad\text{ s.t. }\quad \|d\|_2\le t$

mit c = f(x) und b = ∇f(x). Für t nahe bei null ist der Term $d^\intercal A d$ gegenüber $b^\intercal d$ vernachlässigbar, so dass d_e(t) dann ungefähr mit der Lösung von

$\min_{d\in\mathbb R^n}\, c + b^\intercal d\quad\text{ s.t. }\quad \|d\|_2\le t,$

also mit $-t\nabla f(x)/\|\nabla f(x)\|_2$ , übereinstimmt. Ist t andererseits hinreichend groß, so erfüllt der unrestringierte Minimalpunkt von $c + b^\intercal d + {\textstyle\frac12} d^\intercal A d$ , nämlich

$d_A\ :=\ -A^{-1}\nabla f(x),$

die Nebenbedingung $\|d\|_2\le t$ von TR. Für wachsende t ≥ 0 beschreiben die Punkte x + d_e(t) also typischerweise eine Kurve von x nach x + d_A, wie sie in Abb. 2.10 dargestellt ist.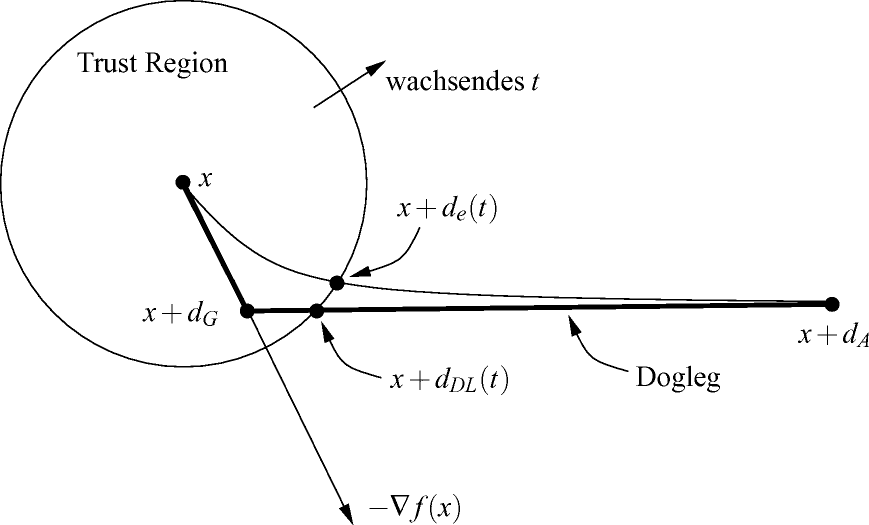

../images/439970_1_De_2_Chapter/439970_1_De_2_Fig10_HTML.png — Abb. 2.10
Approximation der Kurve $\{x + d_e(t)|\,t\ge0\}$ per Dogleg

Abb. 2.10
Approximation der Kurve $\{x + d_e(t)|\,t\ge0\}$ per Dogleg

Die Dogleg-Methode approximiert diese Kurve durch einen Polygonzug von x nach x + d_A mit zwei Segmenten, wobei als Zwischenpunkt x + d_G mit dem exakten Minimalpunkt d_G von m entlang −∇f(x) gewählt wird, den man zu

$d_G\ =\ -\frac{\|\nabla f(x)\|_2^2}{Df(x)A\nabla f(x)}\,\nabla f(x)$

berechnet. Formal lautet der Polygonzug damit $\{\,x + \widetilde d(s)|\ s\in[0,2]\,\}$ mit

$\widetilde d(s)\ =\ \begin{cases}s\cdot d_G\,, & 0\le s\le 1\\ d_G + (s-1)(d_A-d_G)\,,& 1\le s\le 2.\end{cases}$

2.2.64 Übung

Zeigen Sie für $A=A^\intercal\succ0$ :

a)
$\|\widetilde d(s)\|_2$ ist monoton wachsend in s.
b)
$m(\widetilde d(s))$ ist monoton fallend in s.

Nach Übung 2.2.64a schneidet der Polygonzug im Fall $\|d_A\|_2< t$ den Rand der Trust Region gar nicht und sonst in genau einem Punkt. Dieser ist aus

$\begin{array}{ll} \|s\cdot d_G\|_2\ =\ t\,, & \text{falls }\ t<\|d_G\|_2\\[1ex] \|d_G + (s-1)(d_A-d_G)\|_2\ =\ t\,, & \text{sonst} \end{array}$

leicht berechenbar. Aus Übung 2.2.64b folgt ferner, dass die Lösung des auf den Polygonzug eingeschränkten Problems TR im Fall $\|d_A\|_2< t$ gerade d_A ist und im Fall $\|d_A\|_2\ge t$ der obige Schnittpunkt des Polygonzugs mit dem Rand der Trust Region. Die jeweilige Lösung ist die von der Dogleg-Methode gewählte inexakte Lösung d_DL(t) für TR, mit der die neue Iterierte x + d_DL(t) generiert wird.

Minimierung auf einem zweidimensionalen Teilraum

Die inexakte Lösung von TR durch die Dogleg-Methode kann verbessert werden, indem man TR nicht auf den eindimensionalen Polygonzug einschränkt, sondern auf den zweidimensionalen Teilraum, der von d_G und d_A aufgespannt wird. In diesem Raum liegen insbesondere alle Punkte des Polygonzugs. Man erhält das Hilfsproblem

$\min_{d\in\mathbb R^n}\, m(d)\quad\text{ s.t. }\quad \|d\|_2\le t\,,\quad d\in\textrm{bild}(\nabla f(x),\,A^{-1}\nabla f(x)),$

also ein Problem in zwei Variablen, das wieder explizit lösbar ist.

Ein Hauptvorteil dieses Ansatzes besteht darin, dass er sich im Gegensatz zur Dogleg-Methode sinnvoll auf indefinite Matrizen A erweitern lässt. Für Details sei auf [25] verwiesen.

Literatur

4.
Bonnans, J.F., Shapiro, A.: Perturbation Analysis of Optimization Problems. Springer, New York (2000).Crossref
5.
Broyden, C.G.: The convergence of a class of double-rank minimization algorithms. J. I. Math.App., 6, 76–90 (1970).zbMATH
6.
Davidon, W.C.: Variable metric method for minimization. SIAM J. Optimiz. 1, 1–17 (1991).MathSciNetCrossref
8.
Fischer, G.: Lineare Algebra. SpringerSpektrum, Berlin (2014).Crossref
9.
Fletcher, R.: A new approach to variable metric algorithms. Compu. J. 13, 317–322 (1970).Crossref
10.
Fletcher, R., Powell, M.J.D.: A rapidly convergent descent method for minimization. Compu. J.6, 163–168 (1963).MathSciNetCrossref
12.
Geiger, C., Kanzow, C.: Numerische Verfahren zur Lösung unrestringierter Optimierungsaufgaben. Springer, Berlin (1999), 115.Crossref
14.
Goldfarb, D.: A family of variable metric updates derived by variational means. Math. Compu.,24, 23–26 (1970).Crossref
16.
Güler, O.: Foundations of Optimization. Springer, Berlin (2010).Crossref
17.
Heuser, H.: Lehrbuch der Analysis, Teil 1. SpringerVieweg, Wiesbaden, (2009).zbMATH
18.
Heuser, H.: Lehrbuch der Analysis, Teil 2. SpringerVieweg, Wiesbaden (2008).Crossref
19.
Jahn, J.: Introduction to the Theory of Nonlinear Optimization. Springer, Berlin (1994).Crossref
20.
Jänich, K.: Lineare Algebra. Springer, Berlin (2008).Crossref
22.
Jongen, H.Th., Jonker, P., Twilt, F.: Nonlinear Optimization in Finite Dimensions. Kluwer, Dordrecht (2000).zbMATH
24.
Nickel, S., Stein, O., Waldmann, K.-H.: Operations Research. Springer-Gabler, Berlin (2014).Crossref
25.
Nocedal, J., Wright, S.: Numerical Optimization. Springer, New York (2006).zbMATH
28.
Rudin, W.: Principles of Mathematical Analysis. McGraw-Hill, New York (1976).zbMATH
29.
Shanno, D.F.: Conditioning of quasi-Newton methods for function minimization. Math. Comput. 24, 647–656 (1970).MathSciNetCrossref
33.
Stein, O.: Grundzüge der Globalen Optimierung. SpringerSpektrum, Berlin (2018).zbMATH
34.
Stein, O.: Konvexe Analysis. Vorlesungsskript, Karlsruher Institut für Technologie (KIT) (2017).
36.
Werner, J.: Numerische Mathematik II. Vieweg-Verlag, Braunschweig, (1992).zbMATH

2. Unrestringierte Optimierung

2.1 Optimalitätsbedingungen

2.1.1 Abstiegsrichtungen

2.1.1 Definition (Abstiegsrichtung)

2.1.2 Übung

2.1.3 Definition (Eindimensionale Einschränkung)

2.1.2 Optimalitätsbedingung erster Ordnung

2.1.4 Definition (Einseitige Richtungsableitung)

2.1.5 Lemma

Beweis.

2.1.6 Lemma

2.1.7 Definition (Abstiegsrichtung erster Ordnung)

2.1.8 Definition (Stationärer Punkt – unrestringierter Fall)

2.1.9 Satz (Kettenregel)

2.1.10 Lemma

2.1.11 Bemerkung

2.1.12 Übung

2.1.13 Satz (Notwendige Optimalitätsbedingung erster Ordnung – Fermat’sche Regel)

Beweis.

2.1.14 Definition (Kritischer Punkt)

2.1.15 Übung

2.1.16 Beispiel

2.1.17 Definition (Sattelpunkt)

Algorithmus 2.1: Konzeptioneller Algorithmus zur unrestringierten nichtlinearen Minimierung mit Informationen erster Ordnung

2.1.18 Übung

2.1.3 Geometrische Eigenschaften von Gradienten

2.1.4 Optimalitätsbedingungen zweiter Ordnung

2.1.19 Satz (Entwicklungen erster und zweiter Ordnung per univariatem Satz von Taylor)

2.1.20 Lemma

Beweis.

2.1.21 Lemma

Beweis.

2.1.22 Lemma

2.1.23 Definition (Abstiegsrichtung zweiter Ordnung)

2.1.24 Beispiel

2.1.25 Beispiel

2.1.26 Beispiel

2.1.27 Satz (Notwendige Optimalitätsbedingung zweiter Ordnung)

2.1.28 Beispiel

Algorithmus 2.2: Konzeptioneller Algorithmus zur unrestringierten nichtlinearen Minimierung mit Informationen zweiter Ordnung

2.1.29 Übung (Beispiel von Peano)

2.1.30 Satz (Entwicklungen erster und zweiter Ordnung per multivariatem Satz von Taylor)

2.1.31 Satz (Hinreichende Optimalitätsbedingung zweiter Ordnung)

Beweis.

2.1.32 Bemerkung

2.1.33 Übung

2.1.34 Bemerkung

2.1.35 Definition (Nichtdegenerierte kritische und Minimalpunkte)

2.1.36 Lemma

Beweis.

2.1.37 Satz

2.1.38 Übung

2.1.5 Konvexe Optimierungsprobleme

2.1.39 Definition (Konvexe Mengen und Funktionen)

2.1.40 Satz (-Charakterisierung von Konvexität)

2.1.41 Korollar

Beweis.

2.1.42 Satz (-Charakterisierung von Konvexität)

2.1.43 Übung

2.1.44 Übung

2.2 Numerische Verfahren

2.2.1 Abstiegsverfahren

2.2.1 Bemerkung

Algorithmus 2.3: Allgemeines Abstiegsverfahren

2.2.2 Bemerkung

2.2.3 Lemma

Beweis.

2.2.4 Übung

2.2.5 Definition (Effiziente Schrittweiten)

2.2.6 Satz

2.2.7 Definition (Gradientenbezogene Suchrichtungen)

2.2.8 Übung

2.2.9 Satz

Beweis.

2.2.10 Korollar

2.2.2 Schrittweitensteuerung

2.2.11 Bemerkung

2.2.12 Bemerkung

2.2.13 Lemma

Beweis.

2.1.40 Satz ( $\boldsymbol{C}^\textbf{1}$ -Charakterisierung von Konvexität)

2.1.42 Satz ( $\boldsymbol{C}^\textbf{2}$ -Charakterisierung von Konvexität)