1
ANCIENT WORLD
LAYING THE FOUNDATIONS
FOR CENTURIES THERE have been debates over what makes humans unique among the animals. Biologists frequently insist that there is nothing special about the species Homo sapiens. The term ‘exceptionalism’ is used in biology circles in a derogatory fashion to describe the attempt to give us a special status. And, certainly, there are few human abilities that aren’t duplicated in some fashion by other animals. However, Homo sapiens far exceeds other species in its collective capabilities to adapt its environment for life, and the driver for this ability seems to be creativity.
This remarkable trait was present when Homo sapiens first evolved, over 200,000 years ago. Creativity means that humans do not simply accept things as they are and live in the present, but can think outside the moment and ask questions such as ‘Why does that happen?’ or ‘What if I did this?’ or ‘What could I do to make things different?’
When early humans looked beyond scratching an existence to the full might of nature – from the Sun and the stars to the devastating power of lightning and hurricanes – the first responses to the question ‘Why does that happen?’ involved deities or magic. The assumption was that there had to be supernatural forces, capable of actions that were forever beyond our understanding, even if they perhaps could be placated by human rituals. However, with the establishment of static gatherings of people in the early cities, there was an opportunity to begin to take what we would now consider a more scientific approach.
First came the use of numbers (although arguably a separate discipline to science, mathematics is so tightly tied to the sciences that we will be considering it an integral part of Scientifica Historica). More accurately, what seems to have come first was the tally, a mechanism for counting that did not require numbers. Say, for example, a neighbour borrowed some loaves of bread and you wanted to make sure that your loaves were all replaced. Without numbers, you could put a pebble in a safe place for each loaf the neighbour took. When they handed over a replacement loaf, you would throw away a pebble corresponding to it until there were no pebbles left.
We don’t know for certain how long such systems were used as they leave no permanent record, but a number of ancient bones have been discovered that appear to have tally marks on them. The Ishango bone, which is over 20,000 years old, is a baboon’s leg bone, found on what is now the border of Uganda and the Democratic Republic of the Congo. It has a series of notches carved into it, which are widely interpreted as being a tally. The even older Lebombo bone, dating back over 40,000 years, also has a series of notches, though there is more dispute about their nature.
Tally markers can preserve information remarkably well, as witnessed by the fact that these bones still exist so long after they were first created. Such bones can be considered the earliest ancestor of a written record. Of a similar age to the Lebombo bone are some of the early cave paintings, which provide another form of communication that had the potential to establish traditions across a period of time.
Keeping a long-term written record may not have had significance for the makers of the bone tallies, but as cities and trade grew, the need for accounting meant that records began to be kept. At the time, these may simply have been markers of financial transactions, however the ability to keep information to a later date, and to share it, would be crucial for the development of a scientific view of the world.
FOUR VIEWS OF THE ISHANGO BONE, CA. 20,000–18,000 BCE
The series of notches on this baboon leg bone are thought to be tally marks, housed in the Royal Belgian Institure of Natural Sciences.
From tallies to writing
Over the centuries, straightforward pictures and simple notch-based tallies developed into pictograms. As the name suggests, pictograms were image-based, but unlike cave paintings they were stylised into a standard form to represent individual concepts. Some modern Chinese characters still take this form – the character for ‘door’ for example, looks a little like a door.
With some thought, pictograms could also be used to convey less concrete notions. For example, a series of pictograms could be used to communicate the process of putting bread into a basket. If we see a loaf of bread, then a hand, then a loaf in a basket, the message is fairly clear. (For a modern example of a message using pictograms, think of an IKEA instruction sheet.) In that basic form there is no separate symbol to display the concept of ‘in’ or ‘into’, meaning that we need an awful lot of pictograms. There would need to be, for example, a different symbol for a loaf in a basket and for a dog in a basket. But it is not hard to imagine something like an arrow being used to indicate the relationship of ‘in’, after which we just need the pictograms for bread (or dog) and basket with that linking arrow image. A symbol such as this arrow is known as an ideogram, as it indicates something significantly more abstract than an object or an action.
It was this kind of gradual abstraction that led to the formation of proto-writing, the precursor to modern scripts, which seems to have developed at least 6,000 years ago. One early example appearing to carry such proto-writing is a set of tablets found in Tărtăria, located in modern-day Romania, in what was once Transylvania. These are clay tablets marked with a mix of pictograms, lines and symbols. As we don’t know what they mean, it’s possible they were purely decorative, but they are usually assumed to be a precursor to writing, putting across information in a more structured fashion than simple decoration.
In some ways similar, Egyptian hieroglyphs also combined pictograms and ideograms, but did so with more distinct structures. The symbols were not restricted to words, but could also form parts of words, making it possible to build compound words from a mix of symbols, requiring a stock of fewer distinct images. We tend to think of hieroglyphics as the standard script of ancient Egypt because it is what we see on ancient tombs and wall paintings, but in fact it was developed as a formal means of writing for special settings and was too complex for everyday use. Another system, hieratic, was developed in parallel and involved far fewer, more stylised symbols – similar to Chinese characters – which could be written more quickly than hieroglyphs.
However, the Egyptians were not to the first to develop a stylised writing system. Another of the ancient powers of the region, the Sumerian civilisation (which later developed into the Babylonians), devised their cuneiform script around 3600 BCE, making it the earliest known writing system. This script originally combined stylus marks representing numbers with a pictogram-based form of writing. A millennium later, it had become more stylised, with all characters made up of combinations of wedge-shaped marks produced on clay tablets using a stylus: this was the origin of the words ‘style’ and ‘stylised’.
TRADITIONAL CHINESE ‘DOOR’ CHARACTER
Although very stylised, the door character bears a resemblance to a traditional door with a transom.
The European alphabet has a Greek name (alpha and beta are the first two letters of the Greek alphabet), but a more complex background. It seems to have originally derived from the proto-Canaanite abjad. An abjad is like an alphabet but without vowels, which are implied or shown by accent markers – both Arabic and Hebrew use modern abjads. The proto-Canaanite abjad was in use in parts of the Middle East from around 3,500 years ago. Used by the Phoenicians, it was the source of both Greek and Aramaic letters. Greek, though, appears to have been the first true alphabet, with vowels represented by separate characters, originating about 1000 BCE.
The alphabet used in most Western countries is often called Latin or Roman; our upper-case letters are pretty much the same as those used for carving inscriptions by the Romans – their equivalent of Egyptian hieroglyphs. (The character set is not identical, as the Romans didn’t have separate letters J and U, using I and V, which were easier to carve.) Like the Egyptians with hieratic, the Romans also had an everyday set of characters, known as Roman cursive, which morphed into our lower-case letters. For the Romans these were two totally separate styles which would not be mixed, but after the fall of the Roman Empire various options of combining them were tried, such as using capitals to emphasise new sections of writing, or to pick out nouns (as is still the case in modern German).
When first introduced, though, these letters would not have been called upper case and lower case. This terminology dates from the moveable type printing era, when pages of type were set using individual metal letters, bound together to form a page (see here). The two kinds of character were kept in separate boxes, with the basic letters (technically referred to as minuscule) in a lower case and the fancier capital versions in a higher ‘upper case’.
Why is the development of writing so important? Because without writing, it is hard to see how a scientific tradition could be built. Stories of the gods at work in the heavens or throwing lightning do not need precision. They benefit, if anything, from the embellishment and modification that inevitably accompanies an oral tradition. As verbal stories are passed from person to person, less and less of the original remains. But for scientific ideas to be tested and built on, nothing else could match the unchanging foundation provided by the written word.
FRESCO FROM THE TOMB OF NEFERTARI, TWELFTH CENTURY BCE
The burial chamber of Nefertari in the Valley of the Queens, Luxor, features excerpts and scenes from several chapters of the Book of the Dead. Here, three genii guard the Second Gate of the Kingdom of Osiris.
GREEK STELE, 163/4 CE
Stelae were stone slabs with inscriptions often used as grave or boundary markers. This stele records the eponymous archon (chief magistrate), Philisteides, and the kosmetes (military trainer of young men), Claudius, at the top, beneath is a list of trainers and trainees, as well as a variety of festivals and events.
THE LYON TABLET, 48 CE
The Latin text reproduces emperor Caludius’s speech in favour of some leading citizens from Gaul being allowed to sit on the Senate.
The permanence of clay
As we have seen, the earliest written records were not books, but pieces of clay. Working on a far greater scale than the Tărtăria tablets, the Sumerians and the later Babylonians of Mesopotamia produced vast quantities of clay tablets, originally for accounting purposes. These blocks of clay could be easily marked using the stylus-end ‘cuneiform’ markers which were first used to represent numbers, but soon also used in combination to form the stylised characters derived from earlier pictograms.
If the markings were just a temporary note, the clay could be moistened, wiped and reused – but by baking the clay tablet in an oven it became a permanent store of the information recorded on it. It would be an exaggeration to describe these tablets as scientific, but some did give guidance on, for example, practical mathematics. They did not contain mathematical proofs, but there were examples of Pythagorean triples – collections of numbers such as 3, 4, 5 and 8, 15, 17, which reflect the relationship of lengths of the sides of a right-angled triangle that would later be proved in Pythagoras’s theorem.
ASSYRIAN CLAY TABLETS
An accounting tablet (above) from Anatolia, ca. twentieth – nineteenth century BCE, and an astronomical tablet (below) from Nineveh, whose date and origin is debated.
Unknown
EDWIN SMITH PAPYRUS, CA. 1600 BCE
The 4.7 metre (15 foot)-long scroll may have originated in Thebes and was bought by American archeologist Edwin Smith in 1862.
Remarkably, these numerical records date back around 3,800 years. Such tablets also began to be used to record what we would now think of as scientific data, specifically astronomical observations. This information provided the basis both for calendars and for astrological use – there is no evidence at this stage of the application of scientific theories – yet like the invention of writing itself, such collections of data were necessary precursors to the scientific approach.
Similar practical examples (rather than work that had a detailed theoretical basis) began to crop up in the Egyptian civilisation. Practical geometry was an essential for both the measurement of fields and the construction of buildings, again bringing in the guidance of Pythagorean triples. And medicine took the first steps in its long journey from magic to science. The oldest-known example of a written document giving medical guidance with some resemblance of a scientific approach – although not long enough to be considered a true book – is the Egyptian Edwin Smith papyrus, which is around 3,600 years old. It takes the form of a papyrus scroll around 4.7 metres (15 feet) in length, and deals primarily with injuries and surgical techniques, though it does also include a number of magic spells intended for medical purposes.
China was the next of the great civilisations to venture into proto-scientific fields, with mathematical documents dating back at least 3,000 years. It would be relatively late coming to physical or biological sciences, however, as there were philosophical barriers in the way of accepting a purely mechanistic view of the world. India, too, would produce impressive mathematical and later astronomical works from around 500 BCE, which would feed into the development of modern science.
However, the foundations of the approach that has come to dominate science worldwide were primarily developed in ancient Greece. The Greeks built on mathematical ideas from Babylonia and Egypt, but they would take the lead in attempting to build a rational explanation for nature that would eventually become science. They were also the earliest to produce what is close to the modern concept of a science book, though many of the early examples no longer survive.
The early Greeks
The Greek philosopher Thales of Miletus was one of the first to move away from ascribing the forces and structures of nature to the mythical actions of the gods, constructing instead a philosophy that built on theories of the interaction of natural objects. Thales was alive at the same time as the now better-known Pythagoras, who was born around 570 BCE and whose school put numbers at the centre of the explanation of the universe.
With many of the early Greek philosophers it is difficult to know exactly which ideas belonged to the big names that get remembered and which were produced by their followers. Using a famous name added weight to an argument (rather like having a celebrity endorse a product today), and it was common to deploy the big names in a piece of writing even if they weren’t directly involved. We know that Pythagoras did not come up with the mathematical theorem named after him. As we have seen, Pythagorean triples predated him by 1,000 years, and proofs of the theorem were developed well before he was born. It is possible, though, that he was responsible for the first scientific theorising on the nature of music, showing how specific ratios of lengths of vibrating objects (strings or organ pipes, for example) produced notes that sounded harmonic and pleasant.
With the output of Thales and Pythagoras we have the problem that not a single piece of their writing has survived. Everything we know is hearsay. Among the earliest extant examples of what could be considered scientific books is the Hippocratic Corpus, a collection of disparate works on the subject of medicine, which includes the famous Hippocratic Oath requiring a physician to behave ethically with patients. Again, we don’t know if the fifth-century BCE Greek physician Hippocrates of Kos wrote any of the 60 or so titles in this collection. Certainly, the majority of the volumes date back to his period and a little later, though the last was added as much as nine centuries afterwards.
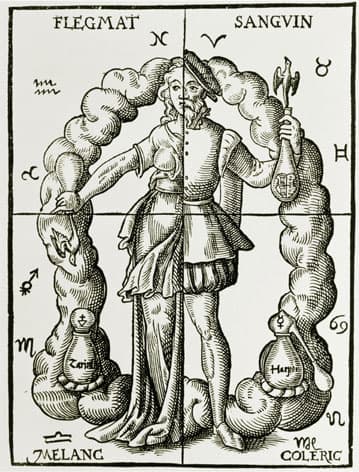
Because of having multiple authors over a period of time, the Corpus is a mix of ideas with no consistency of viewpoint: some of its texts are aimed at other physicians, others at lay readers. If these books can be considered amongst the earliest of scientific titles, they very much take the form of a compendium presenting competing theories, rather than providing the reader with the scientific consensus of the time. There was no ‘standard text’ here. However, some ideas were better supported than others, notably that of the ‘four humours’ – blood, yellow bile, black bile and phlegm – fluids in the body which it was believed, incorrectly, had to be kept in balance for health. This led to such treatments as bloodletting to reduce an ‘excess’ of blood – a life-threatening and useless practice that would remain central to medical work all the way through to the nineteenth century. Like the earlier Egyptian medical documents, these books were originally produced in the form of scrolls, though later editions would see them copied into the familiar codex book form, where eventually all the books of the Corpus would be made available as a single volume.
François Langlois (after Claude Vignon),
PYTHAGORAS, SEVENTEENTH CENTURY
An etching of an imagined Pythagoras (ca. 570–495 BCE).
Hippocrates
HIPPOCRATIC CORPUS, FRANCISCUS MINUTIUS CALVUS, 1525
The title page of a 1525 edition of the Corpus, translated from Greek into Latin by Marcus Fabius Calvus.
Unknown
THE GUILD BOOK OF THE BARBER SURGEONS OF YORK, FIFTEENTH CENTURY
This text for surgeons shows the four medical humours.
Leonhard Thurneisser
THE BOOK OF ALCHEMY, 1574
Above, an illustration of the four humours (phlegm, blood, black bile and yellow bile) within a half female and half male figure.
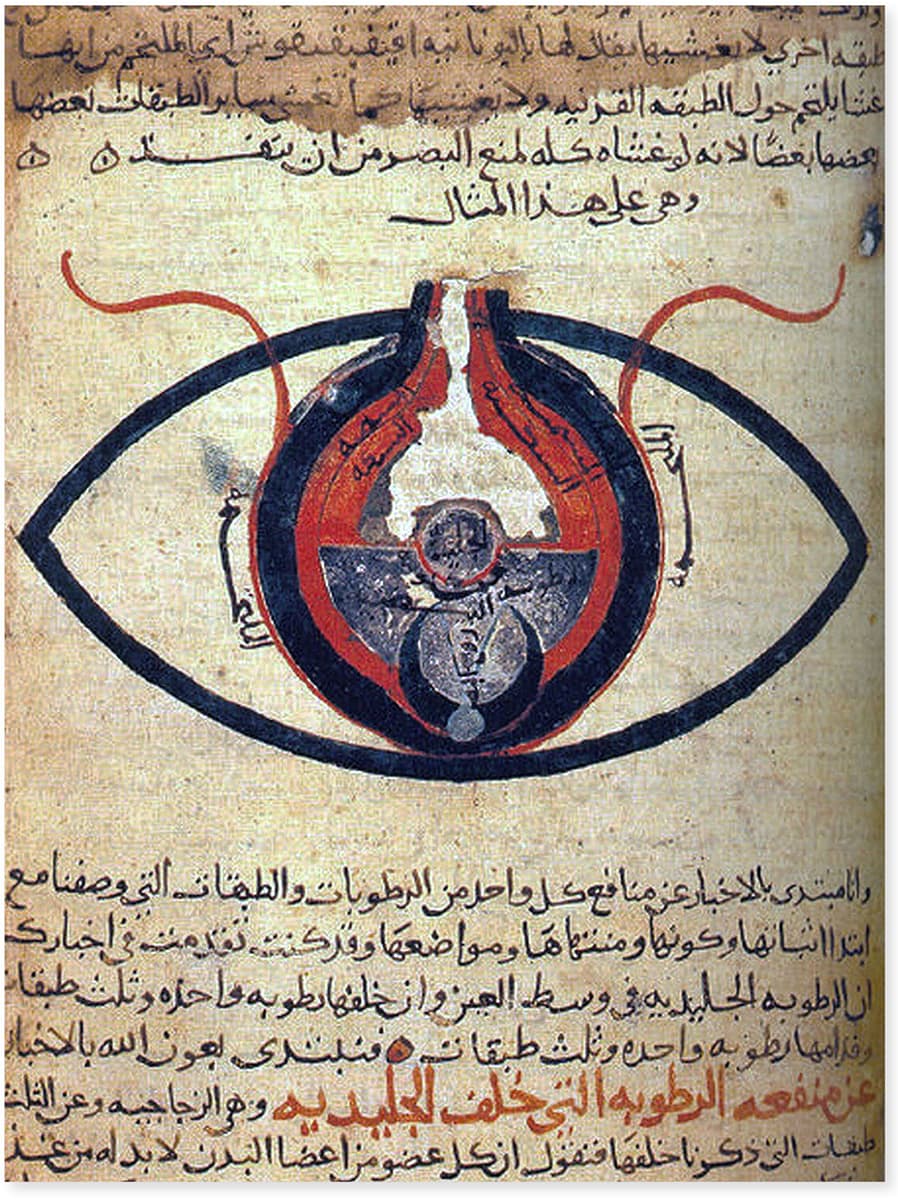
Unknown
THE GUILD BOOK OF THE BARBER SURGEONS OF YORK, FIFTEENTH CENTURY
Left, a ‘phlebotomy chart’ for bleeding.
The survival of books from this period is very much hit and miss (and far more miss than hit). In modern times, many of the books that are conventionally published will be produced in the thousands. However, prior to the printing press, each volume had to be painstakingly copied by hand. It’s entirely possible that initially only a handful of copies of a title may have existed, though if a title became successful there would be a branching out of copies, copies of copies, and so on.
Though this copying process helped preserve some text it also presented a distinct danger to the accuracy of the contents. Copyists regularly introduced variations in the text, either accidentally or intentionally if they disagreed with the message. Examples of deliberate later additions and ‘improvements’ are often found in much-copied ancient works, where modern analysis can show how the original message was modified to match the cultural requirements of a later period. This presented a particular danger for scientific books where preserving the detail was essential. However, copying did at least mean that there were fall-backs if an original book was lost. A much greater danger than either errors or deliberate changes introduced in copying was the instability of ancient societies – and no better example of this can be found than the fate of the Library of Alexandria.
The eighth wonder of the ancient world
We’re used to being told of the seven wonders of the ancient world: the Great Pyramid of Giza, the Hanging Gardens of Babylon, the Temple of Artemis at Ephesus, the Statue of Zeus at Olympia, the Mausoleum at Halicarnassus, the Colossus of Rhodes and the Pharos at Alexandria. Indubitably many of these structures were impressive. This was particularly true of by far the most ancient of the seven, the Great Pyramid, which is not just the only one to survive to the present day, but would also continue to be the tallest man-made structure in the world from its construction around 4,500 years ago all the way up to 1311, when Lincoln Cathedral became the first of many churches and subsequent towers to top it. However, in terms of lasting value to civilisation, surely by far the greatest wonder of the ancient world was the Library of Alexandria.
Alexandria, said to have been founded by the Macedonian king and conqueror Alexander the Great in 332 BCE, was the cultural centre of the European, Middle Eastern and North African world in this period. Located on the northern coast of Egypt, the location cemented Alexander’s integration of Egypt into the Greek civilisation. It’s not clear exactly when the library was first opened – it is believed to be sometime between 300 and 250 BCE – but it was the ancient equivalent of a national library such as the British Library or the US Library of Congress, intended as much as possible to collect all the books of its culture. In fact, the Library of Alexandria had a wider remit still, no longer conceivable in the modern world: the intention was to collect all the world’s wisdom. Any books that arrived in the city – on a ship, for example – would be copied, with the original retained by the library and the copy returned to the (presumably disgruntled) owners.
The library’s books were largely held in the form of papyrus scrolls. The number of books it contained will never be known, as the catalogue has been lost. Claims from relatively near to the time of the library’s destruction put the number in the high 400,000s, though modern estimates, inevitably little more than educated guesswork, place the number at anywhere between 40,000 and 400,000. Whichever end of the scale is accurate, it was a huge number of books for the time, which inevitably would have included all the major scientific literature of the classical world.
Today we only have a small fraction of those early texts, partly due to the library’s destruction, when a significant part of the collection was lost. This involved a number of unrelated attacks on Alexandria when the library suffered collateral damage, rather than the single burning that has often been depicted. Thankfully, some books did survive to be translated and appreciated by the Arabic-speaking scholars between the eighth and fourteenth centuries. These texts travelled to the West, preserving works of the most influential scientific ancient Greek philosopher: Aristotle.
Unknown
BURNING BOOKS IN THE LIBRARY OF ALEXANDRIA, ENGRAVING, SIXTEENTH CENTURY
A representation of the books in the library being burned – in reality this was less of a single organised burning, more the result of repeated damage.
Otto von Corven
A HALL IN THE LIBRARY OF ALEXANDRIA, NINETEENTH CENTURY
An imagined scene in the library, where scholars converse over scrolls, which can be seen stacked end-on in the shelves on the far wall.
Aristotle’s universe
Born in 384 BCE in Stagira in Greece and educated at Plato’s Academy in Athens, Aristotle is said to have been tutor to Alexander the Great. In recent years, Aristotle has had something of a bad press amongst science writers, and it has become popular to deride his lack of a modern scientific approach. It’s certainly true that some of Aristotle’s theories on nature were far more driven by the ancient Greek tradition of deciding what was correct by intellectual debate than they were by observation and experiment. Infamously, Aristotle is said to have pronounced that women have fewer teeth than men, based purely on his philosophical arguments, rather than actually bothering to check and discover that, in fact, women and men have exactly the same number of teeth.
Nonetheless, though Aristotle’s ideas on science have been almost universally shown to be incorrect, it would be unfair to ignore his books, as he was a hugely influential figure. The concepts that he developed (often based on older ideas, but refined in Aristotle’s approach), would continue to be supported for nearly 2,000 years. These notably included the model of the universe that had the Earth at the centre with the Sun, planets and stars travelling around it on crystal spheres, and the five-element theory, which considered everything on Earth to be made from earth, water, air and fire, with a fifth element (quintessence) limited to the heavenly bodies.
Of the volumes of Aristotle’s scientific work that have survived, one of the most influential was the Physics. Given the modern usage of the word, the title is misleading. The book deals with the nature of change and motion (something of an obsession in Greek scientific philosophy, particularly after the Eleatic school had decided that movement was an illusion and didn’t exist). Where now the mechanics of motion is a subset of physics, Aristotle had in mind not just the physical mechanisms of the motion of bodies but of all things involved in movement and change – so his ‘physics’ took in aspects of what now would be regarded as biology (and, inevitably, philosophy too, as Aristotle’s Physics was, in the end, philosophy applied to scientific topics rather than science in the modern sense).
Guillaume de Conches
DE PHILOSOPHIA MUNDI, 1276–7
Below left, the world (universe) according to Aristotle from this French medieval scholastic’s book.
Raphael
THE SCHOOL OF ATHENS, 1509–11
This fresco (below right) from the Apostolic Palace in the Vatican includes over 20 philosophers, with Plato and Aristotle (shown here) central.
In the eight books of the Physics, Aristotle introduced the notion of matter and explored the nature of motion. Though his concepts have all been proved wrong, they tie together into a rational whole. In fact, this strong interlinking of his concepts is one of the reasons that his model of the universe (the solar system in modern terms) with the Earth at its centre rather than the Sun, persisted so long.
If we only consider the Sun and the Earth, it seems logical that the Sun travels around the Earth: that’s certainly what it appears to do. Of course, we now know that the Sun’s motion in the sky is due to the Earth turning, but we still say for convenience that ‘the Sun rises’ not, ‘the Sun becomes visible over the horizon due to the turning of the Earth’. However, when using Aristotle’s model where all heavenly bodies turn around the Earth, the motion of the planets with orbits outside of the Earth’s – Mars, for instance – seems bizarre. These planets appear to occasionally reverse their motion through space. The whole business is greatly simplified if we assume that the Sun is at the centre of the solar system, where the odd reversals of planets like Mars is explained by the relative motion around the Sun at different rates of the Earth and Mars.
However, if the Earth were not at the centre of things, Aristotle’s grand plan built up in the Physics would have fallen apart. He argued that matter has natural tendencies. Of the four earthly elements, he believed that earth and water have an in-built tendency to head for the centre of the universe, while air and fire tend to move away from it. So, he argued, heavy objects, containing more earth-like matter, would naturally fall towards the Earth. The more matter, the stronger the tendency, and the faster they would fall. As Galileo demonstrated nearly 2,000 years later, this simply isn’t true, but it wasn’t such a bad assumption. Feathers do fall slower than rocks – but unfortunately not for the reason that Aristotle devised.
In the second volume of Physics, Aristotle examined causes, separating, for example, the cause of something existing, both in terms of its material and its form, from what we would normally think of as cause – making it happen – and finally coming to the type of cause that has caused many problems in the development of science, the teleological cause – the purpose behind its existence. We now only see a teleological cause (in science, at least) when there is intervention in nature by a thinking entity. A computer has a teleological cause – it was made for a purpose – but earthquakes, say, or evolution, aren’t created with a goal in mind. They don’t have a purpose. But assumptions of a teleological cause have proved a significant problem in the development of some areas of science, and can continue to be a problem when religious beliefs are not separated from scientific theories.
The Physics goes on to consider everything from infinity to the nature of motion. Another example of the interlocking nature of Aristotle’s grand vision is the way that he used his (incorrect) understanding of motion to argue against the existence of atoms. Although we tend to think of atoms as being a modern concept, the fifth-century BCE ancient Greek philosophers Leucippus and his pupil Democritus had argued that matter was made of tiny fragments, which were so small that they were uncuttable – atomos in Greek. If there were atoms, then there had to be a void – a space containing nothing where there were gaps between atoms. (The early atomic theory assumed that each atom was a different shape, and there are very few shapes that can be packed together to fill space without there being any gaps.) But Aristotle argued that such a void could not exist. Fascinatingly, in doing so, he pretty much came up with Newton’s first law of motion – albeit for the purposes of showing that the idea was ludicrous.
Aristotle
PHYSICS, COPY, THIRTEENTH CENTURY
A thirteenth-century Latin version of Aristotle’s fourth century BCE Physics, translated from Arabic in the twelfth century by Gerard of Cremona.
Aristotle said that if there were a void, ‘no one could say why something moved will come to rest somewhere; why should it do so here rather than there? Hence it will either remain at rest or must move on to infinity unless something stronger hinders it.’ His version of physics assumed that for something to keep moving, it must be pushed. When we stop pushing it, it naturally comes to a stop. This was, for example, what happened to a cart. But what about an arrow in flight? Why did it keep moving after it left the bowstring? To explain this, Aristotle decided that the air must continue to push the arrow after it left the bow. But if there were a total void, it seemed to him that there was nothing to influence the moving object in any way, which seemed so counter-intuitive that he dismissed the idea of a vacuum. Aristotle’s physics matched what was observed in everyday life, but he couldn’t accept that the underlying reality could be different from this, so the void – and therefore the existence of atoms – had to go.
Physics was by no means the limit of Aristotle’s many books on scientific subjects. He wrote significantly more titles on biology and zoology than physics and cosmology. Yet the Physics stands out because Aristotle’s views on cosmology, motion and mechanics sat at the heart of the Western understanding of the universe right through to the sixteenth and seventeenth centuries. Other titles were, in their way, also influential. For example, Aristotle’s History of Animals gave us the approach of grouping animals by similar characteristics, and by contrast with the Physics it was less philosophical and more focused on observation, recording a considerable amount of accurate data on a range of species. However, History of Animals is still less significant as a scientific work than the Physics, despite having far more in it that is correct. In the twentieth century, the physicist Ernest Rutherford is said to have remarked, ‘All science is either physics or stamp collecting.’ The implication of this distinctly snippy remark is that real science has to include explanations and theories; it should not just be the collection of data. Books like History of Animals were important, but certainly fall more into the stamp-collecting camp than anything else.
The elements of mathematics
For a book with lasting influence, it is hard to beat Euclid’s Elements, written around 290 BCE. This multi-volume masterpiece would still be used as a textbook at the start of the twentieth century – and even now has a strong influence on the underlying foundation of mathematics in axioms and proofs. The topic of the book is one that centuries of children have found painful at school, yet it was one of the earliest aspects of mathematics to be studied as it was so practically useful: it is geometry.
Euclid
THE ELEMENTS OF GEOMETRY, JOHN DAYE, 1570
Frontispiece of first English translation by Henry Billingsley of Euclid’s work from ca. 300 BCE, printed in London, with a preface by Elizabethan mathematician and occultist John Dee.
Euclid
THE ELEMENTS OF GEOMETRY, COPY, 888
A page of the oldest surviving manuscript of the Elements, the D’Orville Euclid, written by ‘Stephanos the clerk’, showing a detail of Pythagoras’s theorem.
Euclid
THE ELEMENTS OF GEOMETRY, ERHARD RATDOLT, 1482
The first printed edition of the Elements (top left).
Euclid
THE ELEMENTS OF GEOMETRY, COPY, THIRTEENTH CENTURY
An Arabic translation by Persian polymath Nasir al-Din al-Tusi (top right).
Euclid
THE ELEMENTS OF GEOMETRY, PICKERING, 1847
An elegant English translation by Oliver Byrne, which uses coloured graphics to illustrate the proofs (left).
Geometry literally means measuring the Earth. It was devised to help make the measurements required to divide up land and construct buildings, bringing together the concepts of linear dimensions and of measuring angles. The ancient Egyptians made extensive use of geometry, but their approach was purely pragmatic. They used what worked without worrying about why it did so. What the Greeks brought to the table, and what was crystallised in the Elements, was a step-by-step process of logical construction and proof. It was a move from rule-of-thumb practice to the more precise requirements of science. Euclid did not originate the concept of geometric proofs, but what he did in the tour-de-force that is the Elements was bring together a whole range of constructions and proofs, building the whole in incremental stages, starting with the most basic of assumptions.
We refer to Euclid as the author of the Elements, but there is a degree of uncertainty over whether or not Euclid existed at all as a person. The biographical details we have for him all seem to have been later imaginings. It has been suggested that the Elements might have been the work of a group, rather than an individual, who picked the name Euclid as a tribute to the (definitely real) earlier philosopher Euclid of Megara. Whether or not the Euclid of the Elements truly existed, though, this was a breakthrough book.
The Elements consists of a total of 13 volumes. It starts with ‘postulates and common notions’ – what mathematicians would now call axioms, the essential assumptions on which the constructions and proofs (or ‘propositions’) that follow would be based. Axioms are apparently simple statements such as, for example, the idea that a straight line can be drawn between any two points. The book then goes on to give constructions using a straight edge and a pair of compasses of, for example, a circle, and begins to build its geometric theorems, from the famous Pythagoras’s theorem to those giving the relationship between pairs of triangles with similar proportions. Each of the proofs ends with the Greek letters OEΔ, which in Latin translation would become the familiar QED for quod erat demonstrandum, roughly ‘what was to be shown’.
The Elements not only provided the tools necessary for much practical geometry, but laid out the pattern for constructing mathematical proofs, building on simpler proofs to reach more complex conclusions. In its later volumes, the book also contains other mathematical principles, including some basic aspects of prime numbers, lowest common denominators and highest common factors. It explores irrational numbers such as the square root of 2, which can’t be made from a ratio of whole numbers, and covers a small amount of 3D geometry, such as the volumes of simple 3D shapes and the construction of the so-called Platonic solids, where each side is made up of an identical flat shape.
The Elements was one of the many ancient Greek books that were lost after the fall of Greek civilisation, but came back to the West via Arabic translations in the early Middle Ages. Because of its continued importance – the Elements, for example, was central to the mathematics part of the European university syllabuses for centuries – the Elements had many translations and was one of the earliest scientific books to be mass-produced in printed form, rather than hand-copied.
Moving the world
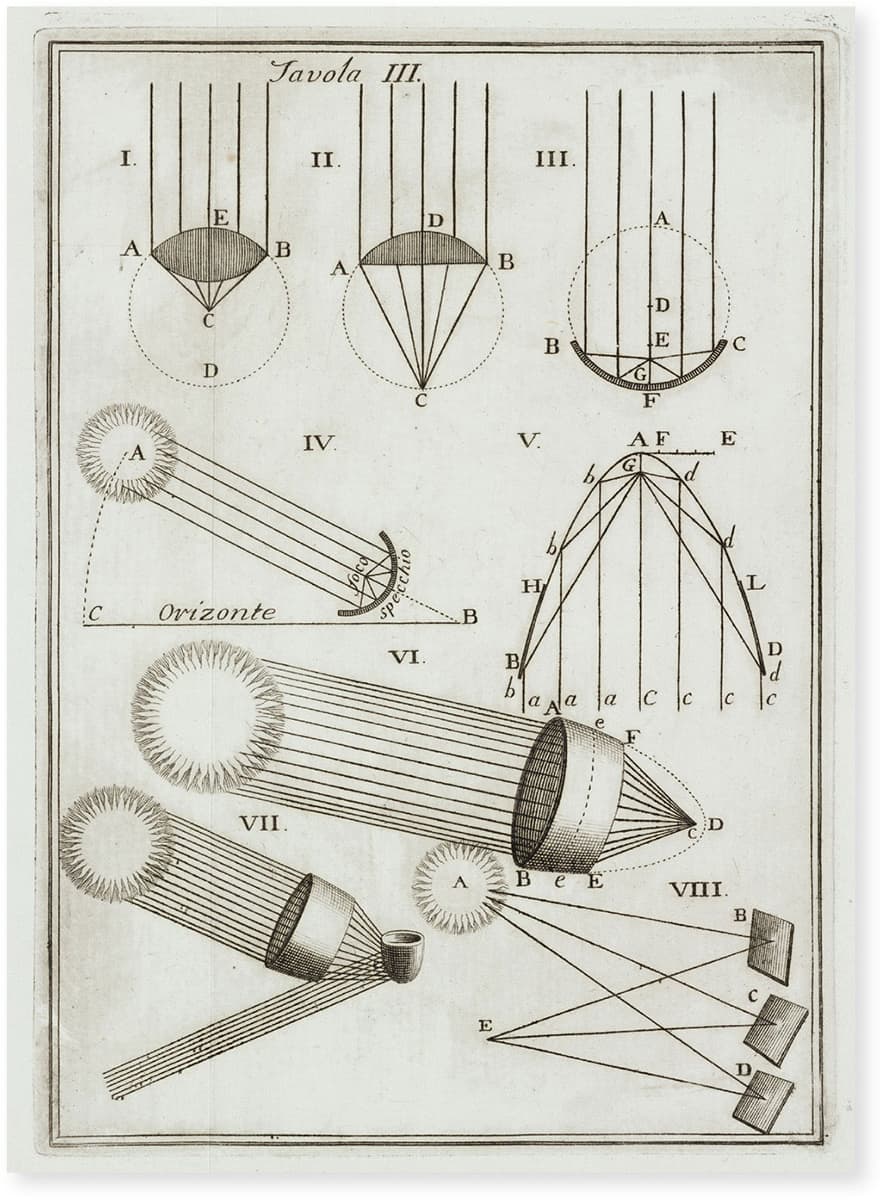
We also shouldn’t overlook the impact of the books of Archimedes, the mathematician and engineer who lived from around 287 to 212 BCE, when it is said he was killed by a Roman invader on Syracuse. Archimedes was without doubt a leading mathematician, who worked on geometry, spirals and the value of pi, and was responsible for an ancestor of integral calculus used for calculating areas and volumes of shapes.
We tend to remember Archimedes for the legend of him leaping from his bath shouting ‘Eureka!’, and for his claim that with a fulcrum and a long-enough lever, he could move the Earth. Best known of his engineering feats are his screw-based pump and the ‘Archimedes principle’ – his method to measure the volume of an irregularly shaped object (that Eureka moment), which he famously used to test the gold content of a crown. The crown had been supplied to King Hiero, who wanted to check if the goldsmith had dishonestly replaced some of the gold with another metal. By combining the crown’s weight with its volume, Archimedes was able to work out its density and show that it was not pure gold. This was a limited example of a wider principle he determined, that an object dipped into a fluid is pushed up by a force equal to the weight of the water it displaces. Archimedes also devised a number of weapons of war, including a death ray in the form of mirrors used to focus the rays of the Sun to start a fire on a ship.
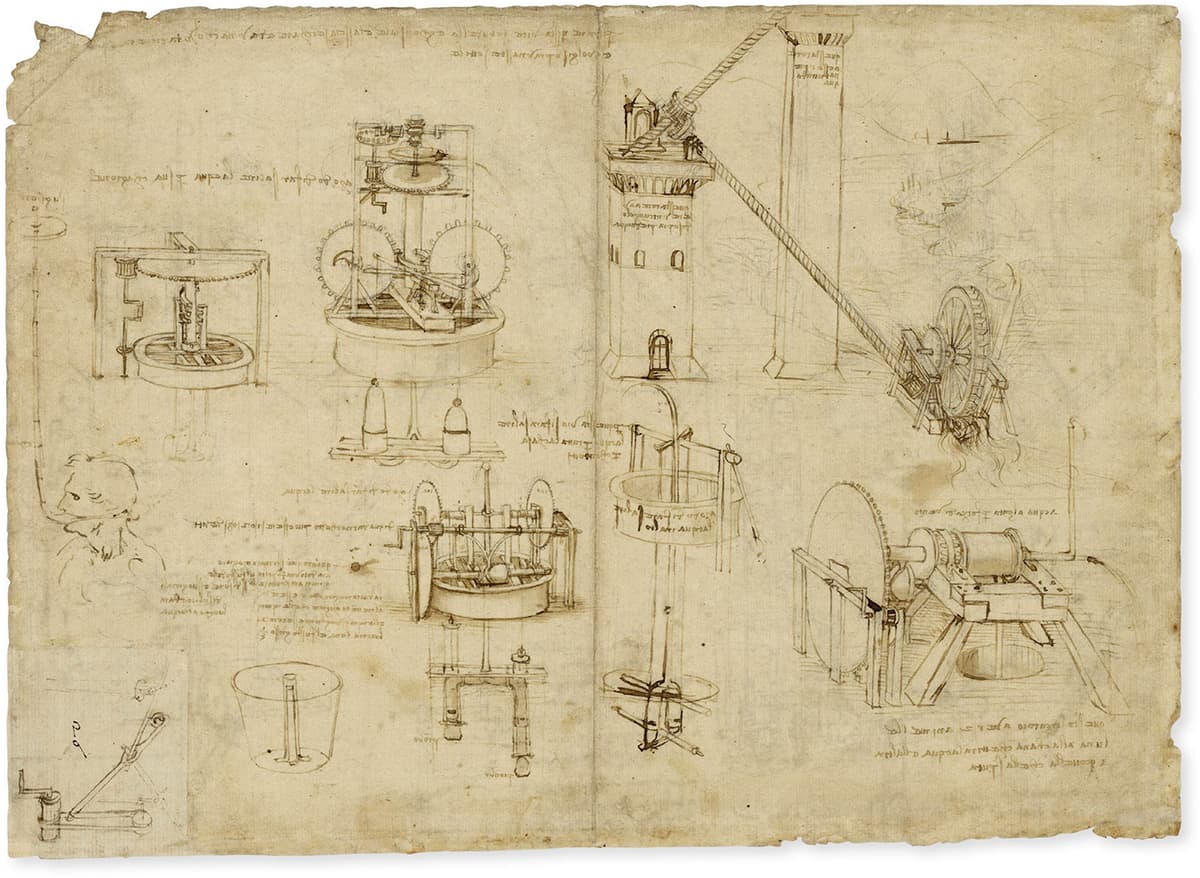
Leonardo da Vinci
CODEX ATLANTICUS, 1478–1519
A page from one of da Vinci’s notebooks showing machines for lifting and pumping water. Leonardo drew on ideas from Archimedes and others.
Giammaria Mazzuchelli
NOTIZIE ISTORICHE DI ARCHIMEDE, RIZZARDI, 1737
An illustration from Mazzuchelli’s book Historical and critical information about the life, inventions and writings of Archimedes of Syracuse.
A relatively high number of Archimedes’ books have survived, notably The Sand-Reckoner (see here), On Floating Bodies, On the Sphere and the Cylinder, On Spirals and On the Equilibrium of Planes. They cover the physics of floating bodies, a range of geometric techniques for calculating sizes of objects, and, notably, in The Sand-Reckoner, the calculation of the number of grains of sand that would fill the universe as a way to demonstrate extending the Greek number system.
Although it may not have included anything original, or directly had an influence on the development of science, one remarkable Roman work from this period also deserves a mention. Roman civilisation was too focused on practical and militaristic goals to deliver any new science. Rome did introduce the codex, making books far more practical to read, but interesting scientific examples from Roman authors are few and far between. The exception is ‘De Rerum Natura’ (On the Nature of Things) by Titus Lucretius Carus, written in the first century BCE. This takes the form of a long poem made up of 7,400 lines, based on the natural philosophy of Epicurus, a Greek philosopher from the third century BCE, whose ideas included atomism. Lucretius’s poem takes in everything from the nature of space and matter to agriculture and disease. Other books of the period, most notably Pliny’s massive Naturalis Historia, collected together existing scientific knowledge, but added little or nothing new.
Archimedes
ON THE SPHERE AND THE CYLINDER, CA. 1450
Renaissance painter Piero della Francesca was also a mathematician; he translated into Latin a number of works by Archimedes and added illustrations to help explain the mathematical theorems.
Titus Lucretius Carus
‘DE RERUM NATURA’, PAULUS FRIDENPERGER, 1486
A page from an early printed version of Lucretius’s first century BCE poem.
Wheels within wheels
By the second century CE, Greece was part of the Roman Empire. The most prolific medical author of the ancient world, Galen, was one of the empire’s most famous physicians. Born in the Greek city of Pergamon in 129 CE, Galen stuck largely to the theories of Hippocrates and his followers, though he did have significantly more experience of anatomy than his predecessors – albeit his knowledge was largely based on monkeys and pigs, so suffered a little when applied to humans. There was a slightly more scientific basis to some elements of his medicine, notably in his suggestion that the arteries carry blood. His vast corpus of books would go on to influence the practice of medicine through to the seventeenth century.
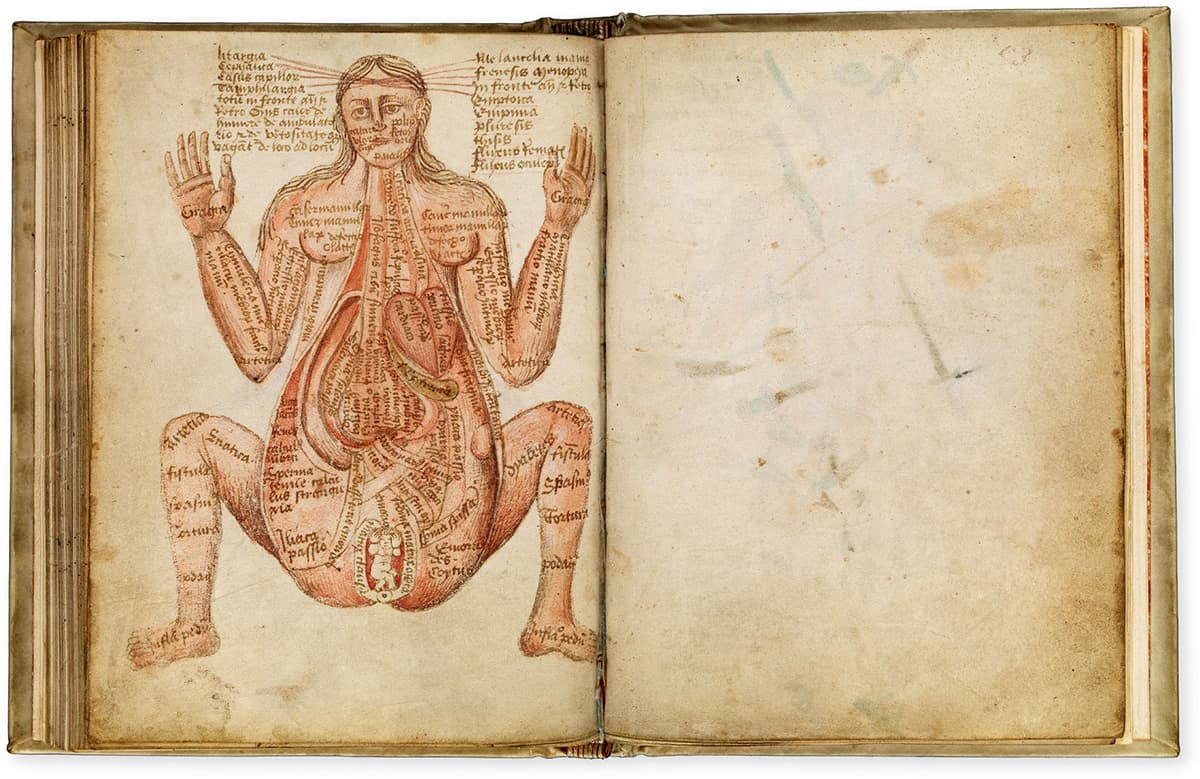
Pseudo-Galen
ANATHOMIA, FIFTEENTH CENTURY
Galen, like many classical authors, had a number of texts attributed to him. This page depicts a pregnant woman.
Guy of Pavia
LIBER NOTABILIUM PHILIPPI SEPTIMI, 1345
Above, a dissection from the abdomen of a cadaver from a book claiming to be taken from Galen’s work, housed in the Musée Condé, Chantilly.
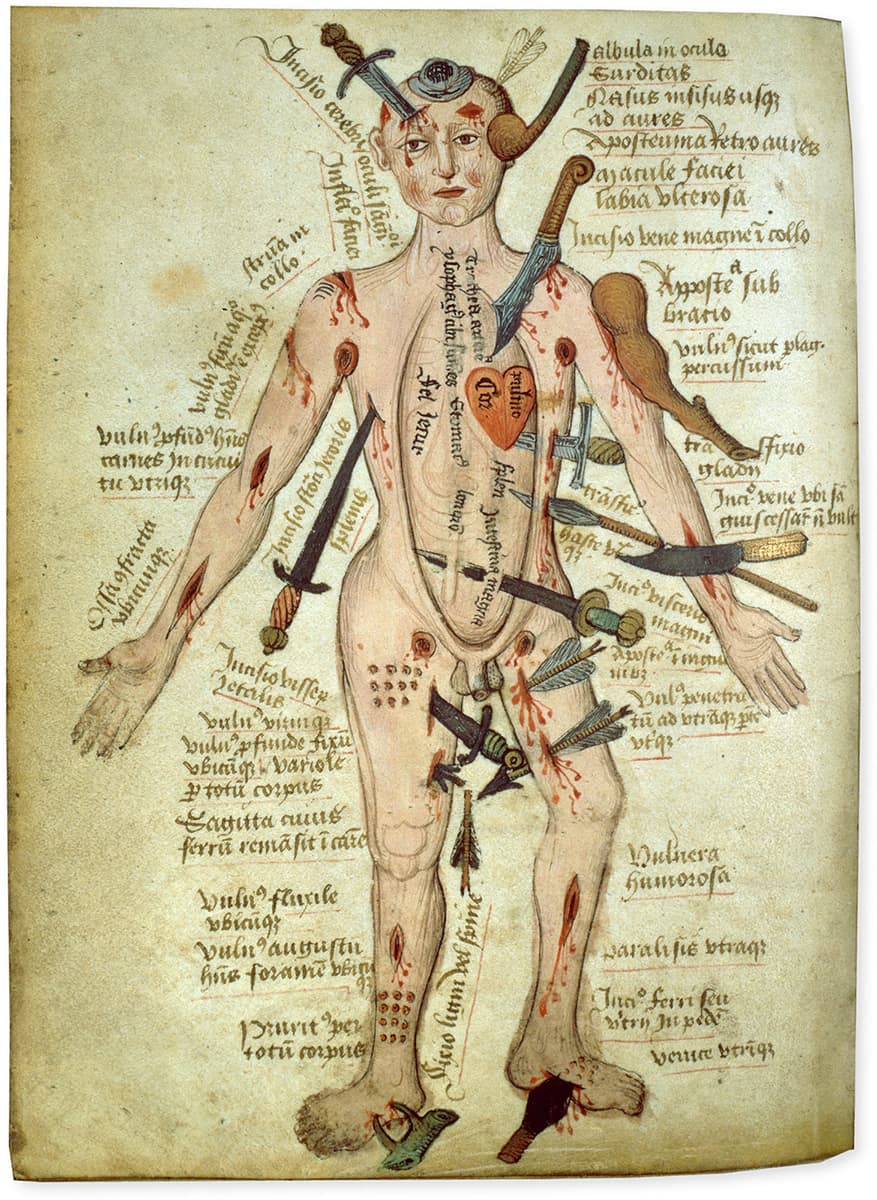
Pseudo-Galen
ANATHOMIA, FIFTEENTH CENTURY
A ‘wound man’ from the same volume as the image opposite.
Bartolomeu Velho
COSMOGRAPHIA, 1568
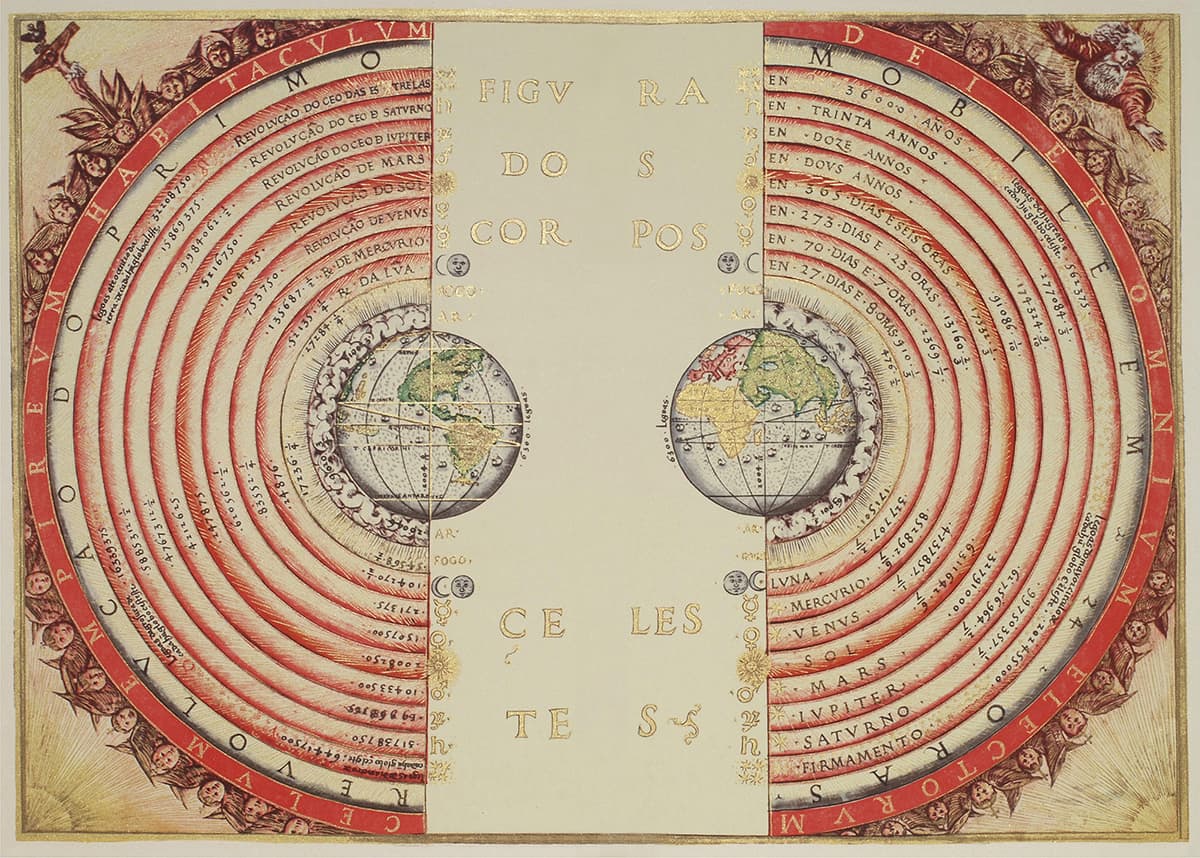
Ptolemy’s geocentric universe (without the epicycles) drawn by this Portuguese cosmographer and cartographer.
Another book from the same time would also have a long impact: based on Aristotle’s physics, it succeeded in keeping alive an incorrect view of the structure of the solar system for 1,500 years. This was the book now known as the Almagest, written by the Egyptian-Greek astronomer Ptolemy. The name Almagest – translating as ‘The Greatest’ – is not Greek (or Egyptian), but Arabic, as the book was introduced to the West, like so many Greek texts, via an Arabic translation.
Dating to around 150 CE, the Almagest was actually titled Mathēmatikē Syntaxis in the original Greek (roughly, ‘Mathematical Treatise’). The title might seem odd given it dealt with astronomy, but we need to remember that until the nineteenth century, astronomy and cosmology were considered part of mathematics, not the physical sciences where they have now been more sensibly reassigned.
This hugely influential book in 13 volumes starts by describing the Earth-centred view of the universe that Aristotle had made the standard model, and goes on to cover the motions of the Sun and planets – including the related concepts as seen from the Earth of, for example, eclipses, the equinoxes and the solstices. Ptolemy also described the constellations and put together a catalogue of the fixed stars. This catalogue was not all Ptolemy’s own work, but was largely based on an earlier catalogue by the ancient Greek astronomer Hipparchus that was already around 280 years old.
As we have seen, there was a problem arising from the requirement of Aristotelian cosmology that everything orbited around the Earth: the way that planets outside the Earth’s orbit would suddenly reverse their direction in so-called retrograde motion. To offer a scientific explanation of how this was possible, Ptolemy was forced to introduce a series of fixes to the older, simple Aristotelian model that had each orbiting planet embedded in a nested crystal sphere.
Andreas Cellarius
HARMONIA MACROCOSMICA, JOHANNES JANSSONIUS, 1660
Cellarius’s The Celestial Atlas, or the Harmony of the Universe depicted the world systems of Ptolemy, Tycho Brahe and Nicolaus Copernicus.
Ingeniously (if painfully), Ptolemy managed to match observation, and to keep the (also incorrect) assumption that all orbits had to be circular as this was the ‘perfect’ shape and the heavens required perfection. He did this using a structure known as epicycles. The idea was that instead of Mars, say, simply travelling around the Earth in a circular motion – which it clearly didn’t – there was instead an empty point in space that orbited the Earth, called a ‘deferent’. Mars then orbited that moving empty point in space in another circular orbit (an epicycle). It was the original case of ‘wheels within wheels’. To make things even more complex, because this model still didn’t quite match what was observed, Ptolemy stated that instead of travelling on circles around the Earth, deferents orbited a point a little way from the Earth called the ‘eccentric’.
If, frankly, eccentric sounds the ideal word for such a contrived structure, the complexity of Ptolemy’s model was necessary to make actual observation fit with the Aristotelian model of the universe. Even today scientists can get very attached to their theories, and in the light of contradictory evidence will repeatedly modify aspects of the theory to keep it working. This has happened, for example, several times with the Big Bang theory, which is still our best idea of the way that the universe came into being, but has had to be patched up repeatedly to match observations.
Andreas Cellarius
HARMONIA MACROCOSMICA, JOHANNES JANSSONIUS, 1660
A further engraving by Cellarius setting Ptolemy’s structure for the universe against the constellations of the zodiac.
PTOLEMY, FIFTEENTH CENTURY
In this illustration from Gautier de Metz’s Image du Monde (Image of the World), Ptolemy is mistakenly depicted as a king as he observes the heavens.
Andreas Cellarius
HARMONIA MACROCOSMICA, JOHANNES JANSSONIUS, 1660
The engraving above illustrates the planetary motions in eccentric and epicyclical orbits, while the engraving opposite is of the early Christian view of the structure of the universe.
Mathematics in the early years of the first millennium was not limited to Ptolemy’s epicycles or the geometrical wonders of the Elements and was being studied around the world. Several other important mathematical volumes would emerge during this period. The earliest of these, developed over a long period starting several centuries earlier but coming to final fruition around 200 CE, was the anonymously authored Jiuzhang Suanshu (The Nine Chapters on the Mathematical Art), a summary of state-of-the-art mathematics in China. The approach taken in the book was one of problem-solving – a more pragmatic one than that of the Elements with its formal proofs, but using significantly more mathematical logic than was present in the simple use of Pythagorean triples in Sumerian clay tablets. Given this practical approach, it’s not surprising that Jiuzhang Suanshu gives us such day-to-day requirements of an early civilisation as measuring the areas of shapes (and, yes, calculating the size of Pythagorean triangles), computations required for trade and taxation, and basic equations. It also includes some slightly more abstract concepts, such as square and cube roots and the volumes of solid objects.
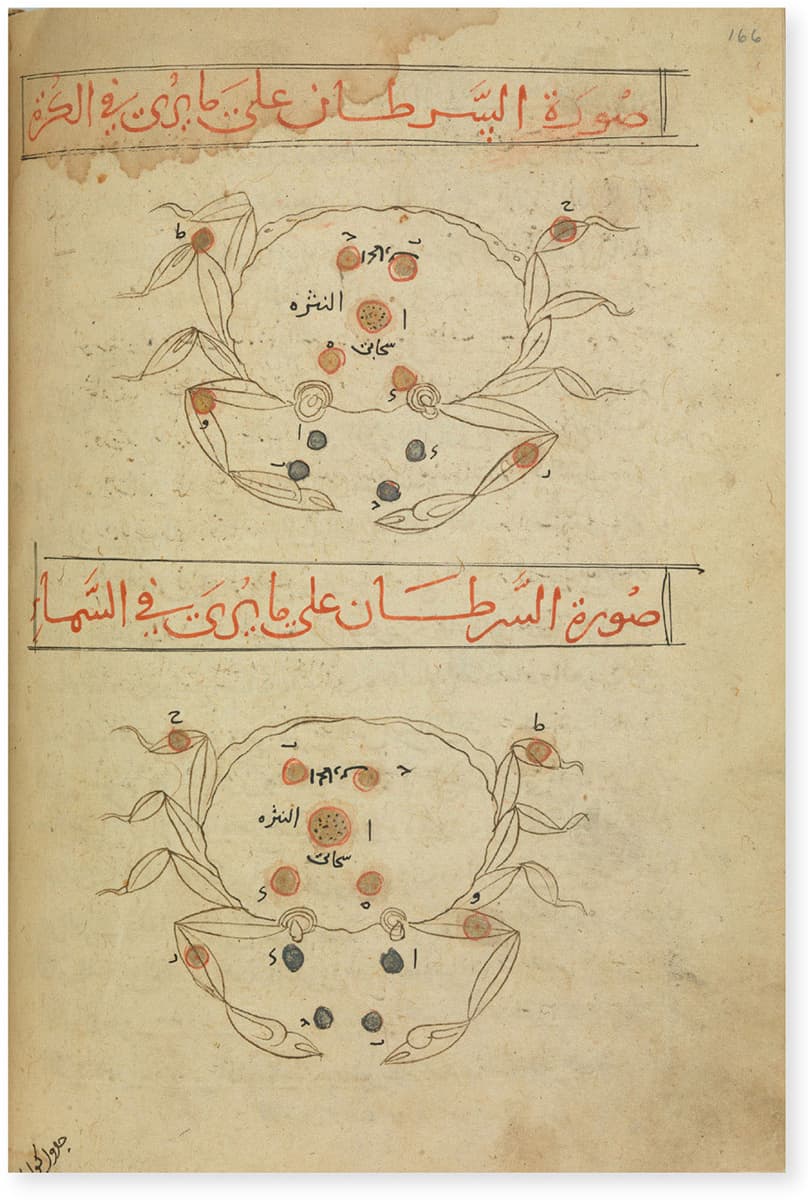
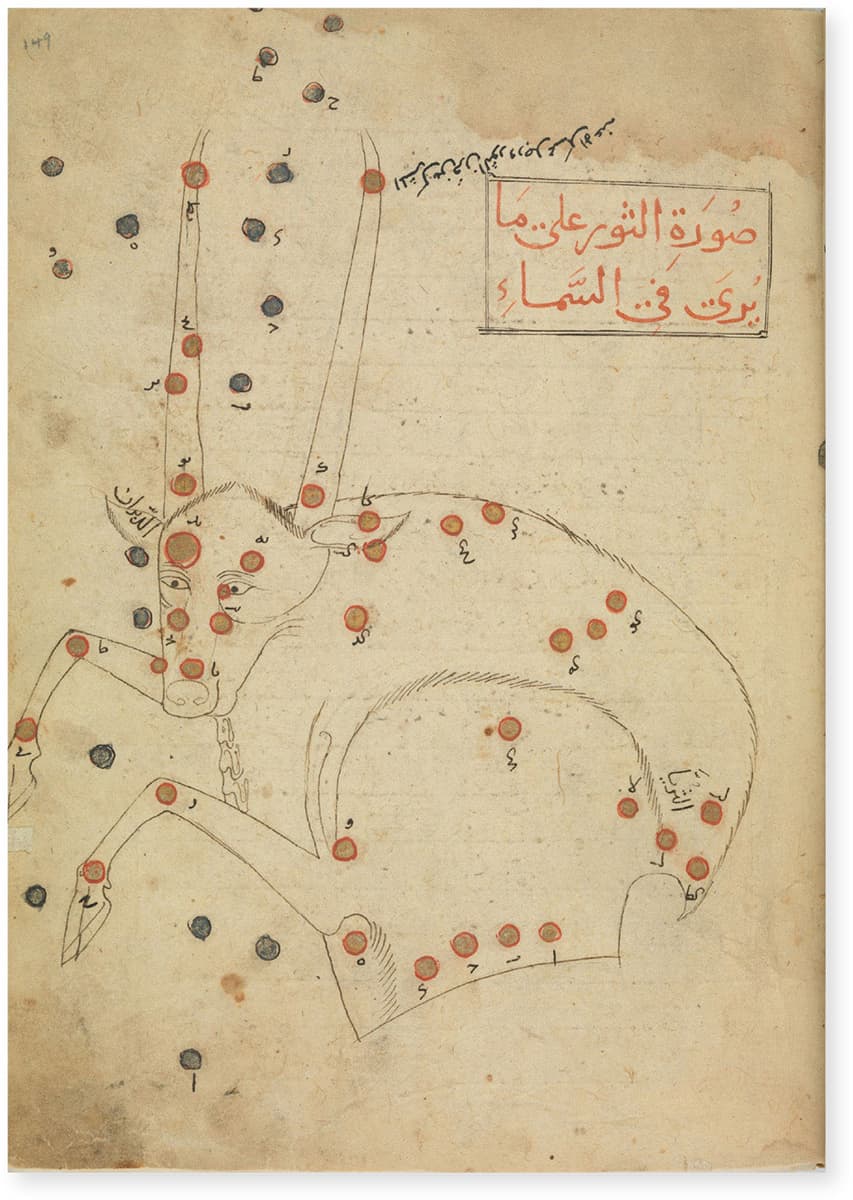
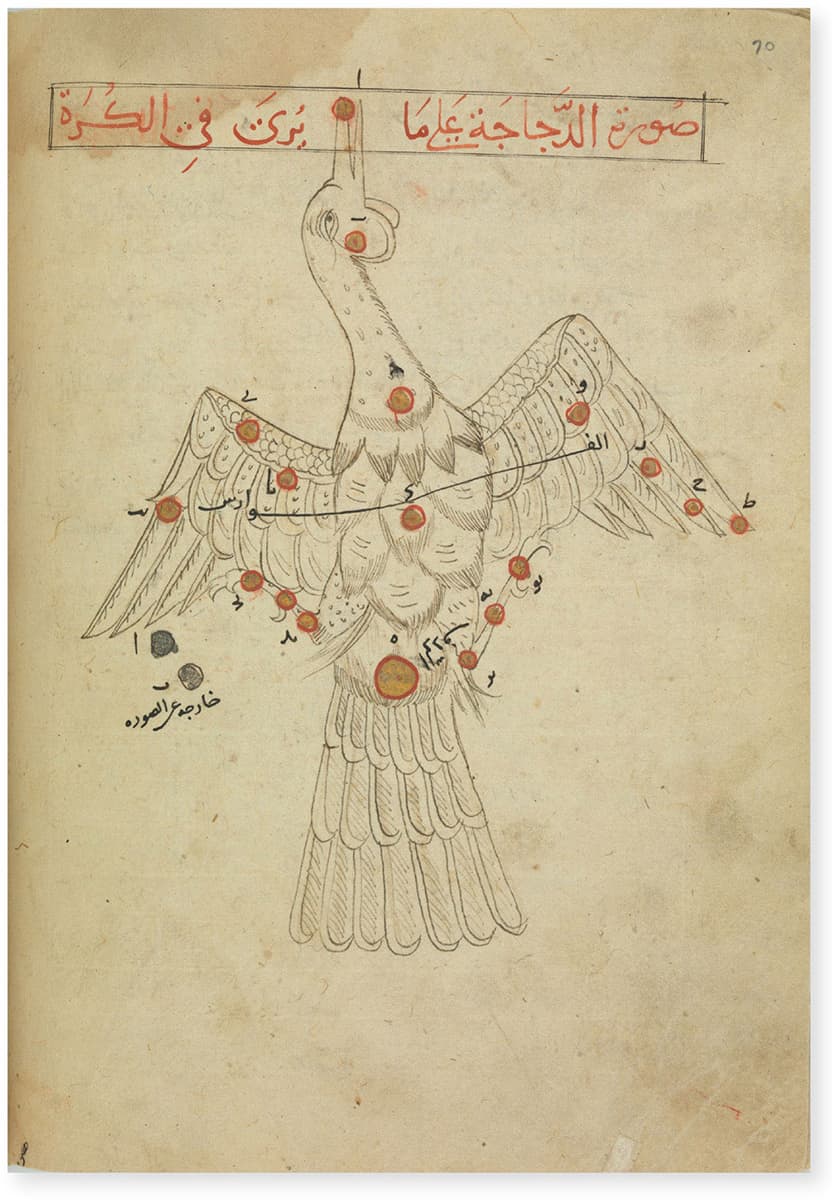
Abd al-Rahman al-Sufi
KITAB SUWAR AL-KAWAKIB AL-ATHABITA, FIFTEENTH CENTURY
Based on Ptolemy’s Almagest, this late fifteenth-century Iranian text illustrates 48 constellations including Cancer and Taurus and opposite Aquila.
There is no surviving book to attribute to her, but it’s important that we also note the late-Greek philosopher and mathematician Hypatia, who lived in Alexandria from the middle of the fourth century. Hypatia was known to have written a number of commentaries and is thought to have edited the Almagest. Historically, women’s contribution to science, and science writing, has only relatively recently become commonplace, as it is only recently that women have had the same opportunities as men. Hypatia provides our first certain example. This doesn’t mean that Hypatia was the first woman to write science books; all the way up to the nineteenth century it was not uncommon for books by women to be published anonymously or under a pseudonym (think, for instance, of the Brontë sisters, who initially wrote as Currer, Ellis and Acton Bell). It is only in recent years that women writers have produced influential science books with anything like the same frequency as men. This move towards gender equality has come significantly later than it did for fiction authors, though thankfully considerable progress has now been made. For the moment, though, female writers will be thin on the ground.
Unknown
JIUZHANG SUANSHU, SIXTEENTH CENTURY
Late edition, showing the method of estimating pi by drawing a polygon with more and more sides, making an increasingly accurate approximation to a circle.
Mathematical transformations
Just as the Elements would have a huge influence on Western mathematics, Jiuzhang Suanshu was central to China’s mainstream development of maths. Like China, India also had a flourishing ancient mathematical tradition, but there, individual mathematicians were given more credit, and so, unlike the anonymous Jiuzhang Suanshu, we know quite a lot about the author of a key Indian mathematical work, Brāhmasphuṭasiddhānta (roughly, ‘The established (or improved) treatise of Brahma’), dating to 628. Its author was Brahmagupta, born around 598, who like many mathematicians of the time studied astronomy as well as mathematics – the book often uses astronomical examples in its content.
As was the case with the Chinese book, this was mathematics presented as statement of fact, rather than as a result of logical proof, and it was provided in an unusually complex fashion, as Brāhmasphuṭasiddhānta was written in the form of poetry. The book was important not only for its various geometric results, but also for its developments in algebra, including one of the two solutions to the quadratic equation familiar to high-school students. Probably the book’s most important innovation was in dealing with non-positive integers. It covered negative numbers, a concept not then widely in use, and treated zero as a number, rather than a simple placeholder for numbers with no value in a particular column. Brahmagupta didn’t get this entirely right – he thought that 0 ÷ 0 = 0. However, this was still a major development in mathematical thought. The use of zero would be essential for the development of modern mathematics.
The concept of zero as a number (as opposed to a placeholder) originated in India, as did the useful Hindu numerals, but they would come to the West through the thriving new academic centres of the Islamic world. A text that would have significant influence was Al-kitāb al-mukhtaṣar fī ḥisāb al-ğabr wa’l-muqābala (The Compendious Book on Calculation by Completing and Balancing), written around 820 in Arabic by Abu Ja’far Muḥammad ibn Mūsā al-Khwārizmī and translated into Latin by Robert of Chester in 1145. We have few reliable biographical details about al-Khwārizmī. He was born in Persia around 780, possibly in Baghdad, and definitely worked in Caliph al-Mamun’s Baghdad House of Wisdom, as the Al-kitāb al-mukhtaṣar was dedicated to the caliph.
Pṛthūdhaka
COMMENTARY ON BRĀHMASPHUṬASIDDHĀNTA, TENTH CENTURY
A commentary on Brahmagaputa’s celebrated work of 628, with annotation by its translator into English, Henry Thomas Colebrooke.
The author and his book give us two technical mathematical terms: ‘algorithm’, from the Latinised version of al-Khwārizmī’s name, Algorithmi; and ‘algebra’, from the ‘al-ğabr’ of the title. It is in the exploration of algebra that this book proved such a success. Al-Khwārizmī was not the first to work on algebraic problems outside India. The third-century Greek philosopher Diophantus had dealt with algebraic equations with powers of a variable value in his book Arithmetica, but he did not attempt to produce generalised solutions that would work for any equation of the same form. Al-Khwārizmī’s version of algebra was in some ways more different from our current approach than that of Diophantus – al-Khwārizmī only works in terms of words, where Diophantus used something closer to a modern equation – but, crucially, al-Khwārizmī dealt with general solutions, so his approach could be applied to a wide range of possibilities.
Another important book by the same author, preserved only in a Latin translation, Algoritmi de numero Indorum (Al-Khwārizmī Concerning the Hindu Art of Reckoning), was a description of the Indian number system (which as we have seen would become known as Arabic numerals in the West, because of the route they took). However, this content proved less significant in terms of the wider development of mathematics, as Indian/Arabic numerals were not widely adopted in the West until Fibonacci’s Liber Abaci (see here) reintroduced the numbering system at the start of the thirteenth century.
Abū Ja’far Muḥammad ibn Mūsā al-Khwārizmī
AL-KITĀB AL-MUKHTAṢARFī ḤISĀB AL-ĞABR WA’L-MUQĀBALA, CA. 1145
A page from Robert of Chester’s translation, which he produced when living in Segovia in Spain.
Arabic optics and medicine
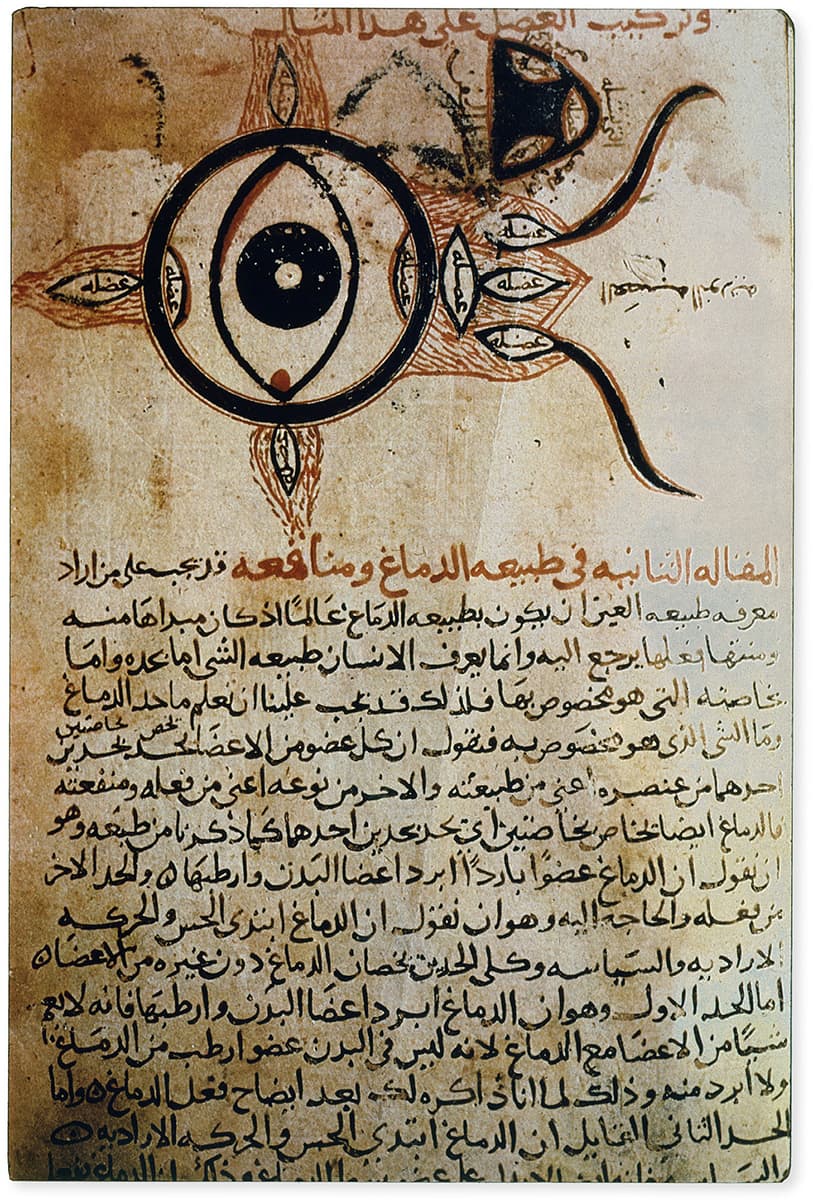
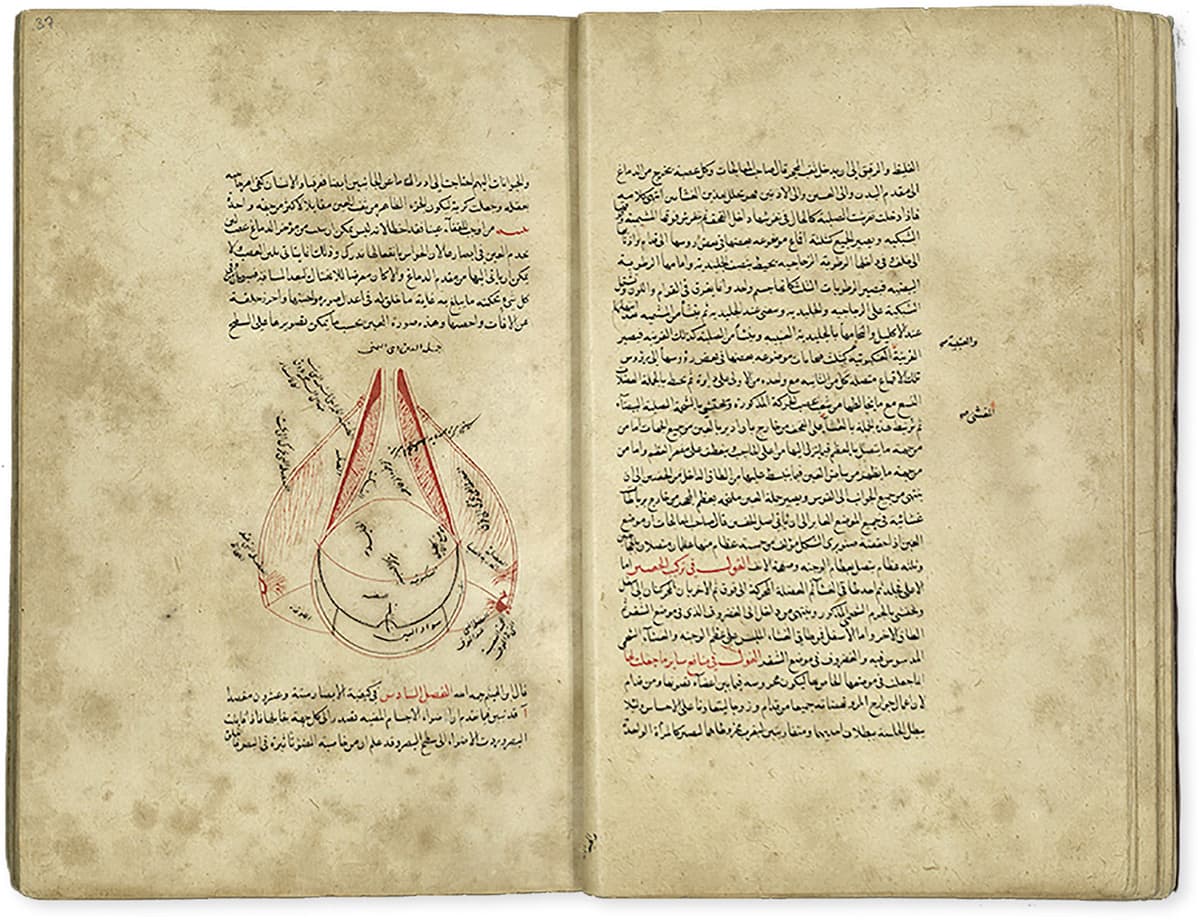
A major figure in the translation of ancient Greek texts into Arabic was Ḥunayn ibn Isḥāq, born in Al-Hira, in what is now Iraq, in 809. Ibn Isḥāq was a physician, so had a particular interest in medical sources, though he translated a wider range of scientific documents. However, he was also responsible for his own contribution to science writing, notably in Al-Ashr Makalat Fi’l’ayn (The Book of the Ten Treatises on the Eye), which has been described as the earliest extant systematic textbook on ophthalmology. There is no doubt that ibn Isḥāq was heavily influenced by ancient Greek texts, particularly Galen, who he widely referenced, but there are also elements of Al-Ashr Makalat Fi’l’ayn which seem to be original observations from ibn Isḥāq’s experimental work, including some impressive illustrations.
Mathematics and medicine were not all that was being produced in the thriving Islamic culture and being passed on to the West. There were a number of titles that covered optics and light, notably those written by Abū ‘Alī al-Ḥasan ibn al-Haytham, whose name was Latinised to Alhazen. Born in what is now Basra in Iraq in 965, al-Haytham was said to have had a similar character to Leonardo da Vinci, the Italian Renaissance polymath who took on roles designing anything from bridges to war machines despite having no previous experience.
According to legend, al-Haytham bit off more than he could chew by promising the Caliph al-Hakim that he could divert the Nile to control flooding and irrigation. Failing to do so, al-Haytham is said to have pretended to be insane, a pretence he had to maintain for years until the caliph’s death. What we know more certainly is that al-Haytham wrote a number of books, including Mizan al-Hikmah (Scale of Wisdom) and particularly notably Kitāb al-Manā
ir (Book of Optics), which contain a wide range of experimentally-based observations on light, both in the way it reflects from mirrors – flat and curved – and is refracted (bent) when passing from one material to another. Al-Haytham even used the refraction of the atmosphere that allows light to continue in the sky after the Sun is below the horizon to estimate the thickness of the atmosphere.
Al-Haytham’s work would be highly influential on medieval Western optics, but even more impact was felt from another Arabic text, ibn Sīnā’s al-Qānūn fī al-Ṭibb, known in the West as Avicenna’s Canon of Medicine. Ibn Sīnā – whose full name was Abū ‘Alī al-Ḥusayn ibn ‘Abd Allāh ibn al-Ḥasan ibn ‘Alī ibn Sīnā – was born around 980 in what is now Uzbekistan, though his work as a physician was primarily in Persia. The five volumes of the Canon of Medicine would become central to medical practice both in the Islamic world and Europe.
Like many of the originators of great science books of the period, ibn Sīnā used information from the best of ancient Greek writing on the topic – taking in the work of Hippocrates and Galen, including the four humours, and mixing in Aristotle’s natural philosophy. He then added in his own ideas to make a heady mixture that would importantly include both a guide to natural substances with medical properties (the Materia Medica) and a formulary describing the manufacture of compound drugs. Although a wide range of these would no longer now be considered effective (or even safe), some indubitably had a genuine medical benefit.
Ḥunayn Ibn-Isḥāq
AL-ASHR MAKALAT FI’L’AYN, TWELFTH CENTURY
A twelfth-century copy of the ninth-century work Al-Ashr Makalat Fi’l’ayn on the structure, diseases and treatment of the eye.
Ḥunayn Ibn-Isḥāq
AL-ASHR MAKALAT FI’L’AYN, TWELFTH CENTURY
A page from one of two known manuscript copies of the ninth-century work Al-Ashr Makalat Fi’l’ayn showing a schema of the eye.
Ibn Al-Haytham
KITĀB AL-MANĀ
IR, THIRTEENTH CENTURY
A thirteenth-century copy of the tenth/eleventh-century work Kitāb al-Manā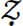ir on light and optics, revised by Kamal al-Din al-Farisi, here showing the optical workings of the eye.
Ibn Sīnā
AL-QĀNŪN FĪ AL-ṬIBB, 1632
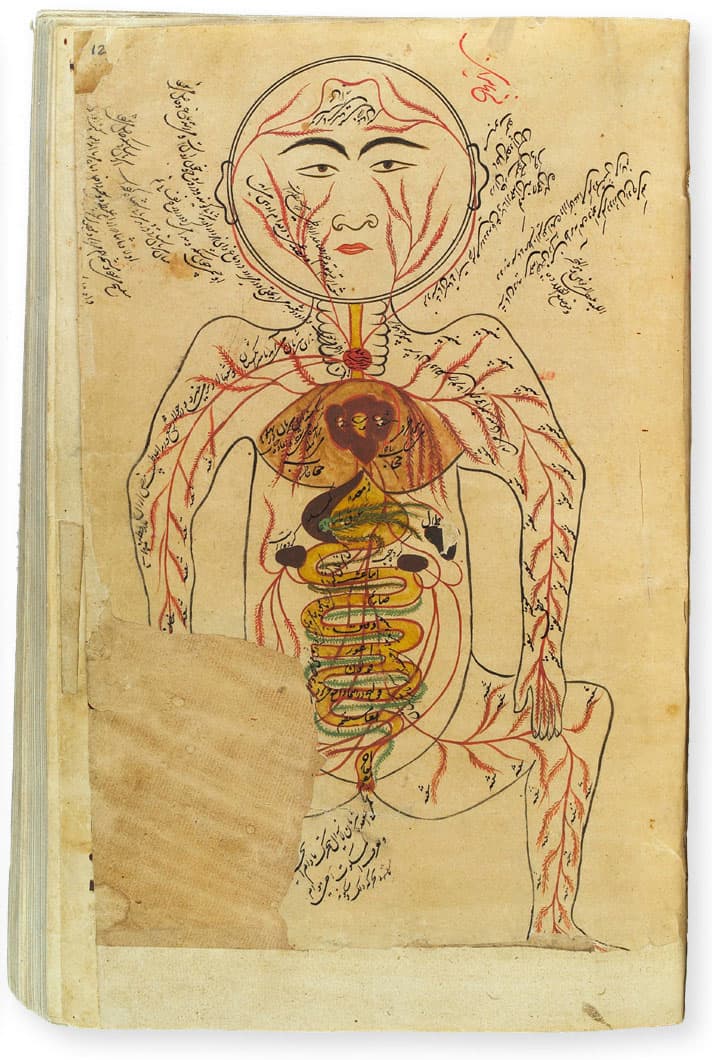
A copy of the eleventh-century work al-Qānūn fī al-Ṭibb. The cover shows a doctor taking a woman’s pulse; inner pages show internal organs and the nervous system.
Mathematics moves on
While the Arabic-speaking world was spreading the word for mathematics that at least in part originated in India, Indian mathematicians were not standing still. By the twelfth century, another mathematical genius was rivalling Brahmagupta. His name was Bhāskara, often known as Bhāskara II to avoid confusion with a seventh-century mathematician. Born in 1114, probably in the modern state of Karnataka, Bhāskara is known for a single important work, the Siddhānta Śiromaṇī, a name not dissimilar to Ptolemy’s Almagest in meaning, translating as ‘Crown of Treatises’.
The four parts of the book cover arithmetic and measurement, algebra, the movement of the planets and the rotation of the heavens. The first volume has many practical applications, such as the calculation of interest, but also includes more sophisticated number theory concepts such as zero and negative numbers. (Like Brahmagupta, Bhāskara had problems with 0 ÷ 0, in his case declaring the result to be infinite.) However, more impressive was the algebra in the second volume, which covers a far wider range of equations than earlier texts and develops some early ideas on what would become calculus (though there is no evidence that the subsequent seventeenth-century development of calculus as we now know it was influenced by this book). Much of the astronomical work in the book was based on existing models, both from ancient Greece and earlier Indian philosophers, but Bhāskara seems to have improved on their calculations to give more accurate values.
Mathematical skill was also central to a highly influential work from this period – Fibonacci’s Liber Abaci (Book of Calculation), written in 1202. Properly Leonardo of Pisa, Fibonacci (a nickname based on ‘son of Bonacci’) was a master Italian mathematician who was born in Pisa around 1175. Like most mathematical books of the period, the Liber Abaci contains practical mathematical tips on, for example, the calculation of interest. It also came closer to our modern representation of fractions. Before Fibonacci, these were written out as the Greeks had as combinations of 1/x rather than having larger numbers above the dividing line. So, for instance, what we would denote 3/4, prior to Fibonacci could only be represented as 1/2 + 1/4. Liber Abaci also introduced the Fibonacci series – the series produced by adding together the previous two numbers that begins 1, 1, 2, 3, 5, 8, 13, 21… which Fibonacci illustrated with the growth in population from a breeding pair of rabbits.
Bhāskara II
LILAVATI, 1650
A page from Lilavati, the first volume of Siddhānta Śiromaṇī. It uses the Pythagorean theorem to work out a problem where a snake is heading from a pillar to its hole and a peacock has to fly down along the hypotenuse to catch it.
However, the book’s main claim to fame was in succeeding where translations of Al-kitāb al-mukhtaṣar (see here) hadn’t in spreading the use of Arabic numerals into Europe, which Fibonacci accurately described as ‘Indian style’. At the time, numbers were either written out as words or represented using the clumsy Roman numerals, making the more modern system so much more practical. As we have seen, Liber Abaci was not the first foreign book to praise the benefits of the Indian system – in fact, they had already been highlighted as far back as 662 by a Syrian bishop – but it seems to have been the one that really lit the spark for the use of these representations.
Along with numerals, Liber Abaci introduced the use of the zero to Europe, an essential for the development of modern mathematics. The zero proved more popular initially with mathematicians than it did with accountants. It was easy to change a zero into a 6, 8 or 9 in a manuscript, so it was treated with suspicion. In 1299, for example, the council of the Italian city of Florence banned the use of Indian numerals in accounts for this reason. Even as late as the sixteenth century, a Belgian priest informed his suppliers that they should only use words as numerical values in their contracts.
Bhāskara II
LILAVATI, 1650
This page features another example of Pythagoras’s theorem.
Leonardo of Pisa (Fibonacci)
LIBER ABACI, 1227
Pages from the book that introduced the Fibonacci series and popularized Arabic/Indian numerals, showing fractions, in the collection of the Biblioteca Nazionale Centrale, Florence.
Against all odds
By the thirteenth century, when Fibonacci was writing, an increasing number of Europeans were producing books that primarily commented on ancient Greek and Islamic science, but also added new ideas of their own. Few of these books have had a lasting impact, but the Opus Majus of Roger Bacon is worth picking out, both as one of the most impressive examples of its kind and also because of Bacon’s remarkable story.
A Franciscan friar based mostly in the English city of Oxford, Bacon was born in either 1214 or 1220 (there are two interpretations of his only autobiographical comment). Bacon seems to have had a driven personality. Despite a ruling from the head of his order that friars should not write books, Bacon was determined to produce a scientific encyclopaedia and looked for political support in the church to enable him to do so. The French cardinal Guy de Foulques had shown an interest in Bacon’s work, so Bacon asked de Foulques to get him an exception from the rule and some funding. Unfortunately, the request seems to have become garbled along the way; after two years, de Foulques finally replied giving his support to Bacon and asking that the (non-existent) book be sent to him immediately. To make matters worse, de Foulques told Bacon to do this secretly, so gave him no defence against the Franciscan prohibition of writing books and provided no cash, which was a disaster as Bacon had already used up his inheritance.
ROGER BACON, 1617
No contemporary images are known to exist of this thirteenth-century English friar, proto-scientist and author; this illustration is from Symbola Aureae Mensae by Michael Maier (1568–1622).
Roger Bacon
OPUS MAJUS, FIFTEENTH CENTURY
This copy of Bacon’s Opus Majus was donated to the Bodleian Library, Oxford, in 1634, where it has remained ever since.
Roger Bacon
OPUS MAJUS, THIRTEENTH CENTURY
The earliest known copy of some of Bacon’s work, housed in the British Library, London. The page shown is from part five of the Opus Majus, titled ‘Tractatus perspective’.
With things looking dire, Bacon had a stroke of luck. To wide surprise, de Foulques was elected Pope, as Clement IV. Bacon obtained formal papal blessing on his venture and decided to write a proposal for his great encyclopaedia, intending to provide a covering letter and a short synopsis of the book. To say Bacon got carried away would be an understatement: his proposal ended up 500,000 words long. While this was being copied, he started on the covering letter – which also became a major manuscript. And this happened once again – all in two years from 1266 to 1267. These three volumes became known as the Opus Majus (Great Work), Opus Minus (Lesser Work) and Opus Tertius (Third Work). Between them they included mathematics and astronomy, optics, geography, philosophy and much more – notably including a section describing the importance of experience and experiment to understanding nature, rather than relying purely on philosophical musing.
Bacon sent off the first two volumes of his vast proposal to the Pope – it’s likely the third was still being copied at this point. Before he could get a response, however, the news broke that the Pope had died. In all likelihood, Clement never saw Bacon’s remarkable books. Clement’s successor as Pope had no interest in science, and, according to legend, by his order Bacon was imprisoned for his actions for as much as 13 years. At the time, Bacon’s books were suppressed, but remarkably they survived and provide an exceptional picture of the science of the period. While Bacon contributed some original ideas, particularly on calendar reform and the nature of light, and even dared to question some of Aristotle’s thinking, the importance of the Opus Majus is in the scale of Bacon’s vision.
The books covered in this chapter, important though they were, were restricted in the number of people they could reach, both by limited literacy and the need to manually copy each volume. However, in the next chapter, with the advent of the printing press and more widespread literacy, we will see books that increasingly bore fruit.