Summary. The law of large numbers and the central limit theorem are two of the principal results of probability theory. The weak law of large numbers is derived from the mean-square law via Chebyshev’s inequality. The central limit theorem is proved using the continuity theorem for moment generating functions. A short account is presented of Cramér’s large deviation theorem for sums of random variables. Convergence in distribution (or ‘weak convergence’) is introduced, and the continuity theorem for characteristic functions stated.

8.1 The law of averages

We aim in this chapter to describe the two main limit theorems of probability theory, namely the ‘law of large numbers’ and the ‘central limit theorem’. We begin with the law of large numbers.

Here is an example of the type of phenomenon which we are thinking about. Before writing this sentence, we threw a fair die one million times (with the aid of a computer, actually) and kept a record of the results. The average of the numbers which we threw was 3.500867. Since the mean outcome of each throw is , this number is not too surprising. If x_i is the result of the ith throw, most people would accept that the running average

(8.1)

approaches the mean value as n gets larger and larger. Indeed, the foundations of probability theory are based upon our belief that sums of the form (8.1) converge to some limit as . It is upon the ideas of ‘repeated experimentation’ and ‘the law of averages’ that many of our notions of chance are founded. Accordingly, we should like to find a theorem of probability theory which says something like ‘if we repeat an experiment many times, then the average of the results approaches the underlying mean value’.

With the above example about throwing a die in the backs of our minds, we suppose that we have a sequence of independent and identically distributed random variables, each having mean value μ. We should like to prove that the average

(8.2)

converges as to the underlying mean value μ. There are various ways in which random variables can be said to converge (advanced textbooks generally list four to six such ways). One simple way is as follows.

Definition 8.3

We say that the sequence of random variables converges in mean square to the (limit) random variable Z if

(8.4)

If this holds, we write ‘ in mean square as ’.

Here is a word of motivation for this definition. Remember that if Y is a random variable and , then Y equals 0 with probability 1. If , then it follows that tends to 0 (in some sense) as .

Example 8.5

Let Z_n be a discrete random variable with mass function

Then Z_n converges to the constant random variable 2 in mean square as , since

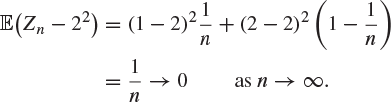
It is often quite simple to show convergence in mean square: just calculate a certain expectation and take the limit as . It is this type of convergence which appears in our first law of large numbers.

Theorem 8.6 (Mean-square law of large numbers)

Let be a sequence of independent random variables, each with mean μ and variance . The average of the first n of the X_i satisfies, as ,

(8.7)

Proof

This is a straightforward calculation. We write

for the nth partial sum of the X_i. Then

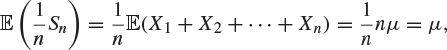
and so

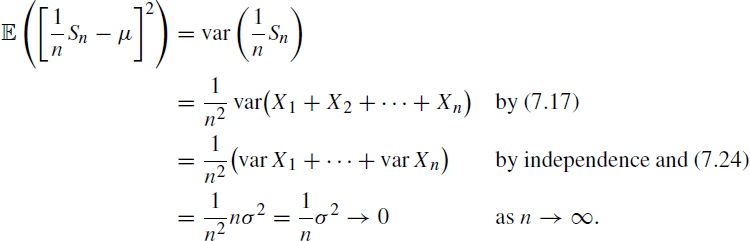
Hence, in mean square as .

It is customary to assume that the random variables in the law of large numbers are identically distributed as well as independent. We demand here only that the X_i have the same mean and variance.

Exercise 8.8

Let Z_n be a discrete random variable with mass function

Show that Z_n converges to 0 in mean square if and only if .

Exercise 8.9

Let be a sequence of random variables which converges to the random variable Z in mean square. Show that in mean square as , for any real numbers a and b.

Exercise 8.10

Let N_n be the number of occurrences of 5 or 6 in n throws of a fair die. Use Theorem 8.6 to show that, as ,

Exercise 8.11

Show that the conclusion of the mean-square law of large numbers, Theorem 8.6, remains valid if the assumption that the X_i are independent is replaced by the weaker assumption that they are uncorrelated.

8.2 Chebyshev’s inequality and the weak law

The earliest versions of the law of large numbers were found in the eighteenth century and dealt with a form of convergence different from convergence in mean square. This other mode of convergence also has intuitive appeal and is defined in the following way.

Definition 8.12

We say that the sequence of random variables converges in probability to Z as if

(8.13)

If this holds, we write ‘ in probability as ’.

Condition (8.13) requires that for all small positive δ and ε and all sufficiently large n, it is the case that with probability at least .

It is not clear at first sight how the two types of convergence (in mean square and in probability) are related to one another. It turns out that convergence in mean square is a more powerful property than convergence in probability, and we make this more precise in the next theorem.

Theorem 8.14

If is a sequence of random variables and in mean square as , then in probability also.

The proof of this follows immediately from a famous inequality which is usually ascribed to Chebyshev but which was discovered independently by Bienaymé and others, and is closely related to Markov’s inequality, Theorem 7.63. There are many forms of this inequality in the probability literature, and we feel that the following is the simplest.

Theorem 8.15 (Chebyshev’s inequality)

If Y is a random variable and , then

(8.16)

Proof

By Markov’s inequality, Theorem 7.63, applied to the positive random variable ,

as required.

Proof of Theorem 8.14

We apply Chebyshev’s inequality to the random variable to find that

If in mean square as , the right-hand side tends to 0 as , and so the left-hand side tends to 0 for all as required.

The converse of Theorem 8.14 is false: there exist sequences of random variables which converge in probability but not in mean square (see Example 8.19).

The mean-square law of large numbers, Theorem 8.6, combines with Theorem 8.14 to produce what is commonly called the ‘weak law of large numbers’.

Theorem 8.17 (Weak law of large numbers)

Let be a sequence of independent random variables, each with mean μ and variance . The average of the first n of the X_i satisfies, as ,

(8.18)

The principal reason for stating both the mean-square law and the weak law are historical and traditional—the first laws of large numbers to be proved were in terms of convergence in probability. There is also a good mathematical reason for stating the weak law separately—unlike the mean-square law, the conclusion of the weak law is valid without the assumption that the X_i have finite variance so long as they all have the same distribution. This is harder to prove than the form of the weak law presented above, and we defer its proof until Section 8.5 and the treatment of characteristic functions therein.

There are many forms of the laws of large numbers in the literature, and each has a set of assumptions and a set of conclusions. Some are difficult to prove (with weak assumptions and strong conclusions) and others can be quite easy to prove (such as those above). Our selection is simple but contains a number of the vital ideas. Incidentally, the weak law is called ‘weak’ because it may be formulated in terms of distributions alone. There is a more powerful ‘strong law’ which concerns intrinsically the convergence of random variables themselves.

Example 8.19

Here is an example of a sequence of random variables which converges in probability but not in mean square. Suppose that Z_n is a random variable with mass function

Then, for and all large n,

giving that in probability. On the other hand

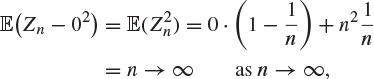
so Z_n does not converge to 0 in mean square.

Exercise 8.20

Prove the following alternative form of Chebyshev’s inequality: if X is a random variable with finite variance and , then

Exercise 8.21

Use Chebyshev’s inequality to show that the probability that in n throws of a fair die the number of sixes lies between and is at least .

Exercise 8.22

Show that if in probability then, as ,

for any real numbers a and b.

8.3 The central limit theorem

Our second main result is the central limit theorem. This also concerns sums of independent random variables. Let be independent and identically distributed random variables, each with mean μ and non-zero variance . We know from the law of large numbers that the sum is about as large as for large n, and the next natural problem is to determine the order of the difference . It turns out that this difference has order .

Rather than work with the sum S_n directly, we work with the so-called standardized version of S_n,

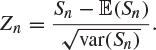
(8.23)

This is a linear function of S_n, where a_n and b_n have been chosen in such a way that and . Note that

Also,

and so

(8.24)

It is a remarkable fact that the distribution of Z_n settles down to a limit as . Even more remarkable is the fact that the limiting distribution of Z_n is the normal distribution with mean 0 and variance 1, irrespective of the original distribution of the X_i. This theorem is one of the most beautiful in mathematics and is known as the ‘central limit theorem’.

Theorem 8.25 (Central limit theorem)

Let be independent and identically distributed random variables, each with mean μ and non-zero variance . The standardized version

of the sum satisfies, as ,

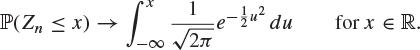
(8.26)

The right-hand side of (8.26) is just the distribution function of the normal distribution with mean 0 and variance 1, and thus (8.26) may be written as

where Y is a random variable with this standard normal distribution.

Special cases of the central limit theorem were proved by de Moivre (in about 1733) and Laplace, who considered the case when the X_i have the Bernoulli distribution. Lyapunov proved the first general version in about 1901, but the details of his proof were very complicated. Here we shall give an elegant and short proof based on the method of moment generating functions. As one of our tools, we shall use a special case of a fundamental theorem of analysis, and we present this next without proof. There is therefore a sense in which our ‘short and elegant’ proof does not live up to that description: it is only a partial proof, since some of the analytical details are packaged elsewhere.

Theorem 8.27 (Continuity theorem)

Let be a sequence of random variables with moment generating functions and suppose that, as ,

Then

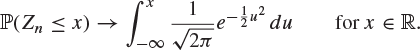
In other words, the distribution function of Z_n converges to the distribution function of the normal distribution if the moment generating function of Z_n converges to the moment generating function of the normal distribution. We shall use this to prove the central limit theorem in the case when the X_i have a common moment generating function

although we stress that the central limit theorem is valid even when this expectation does not exist so long as both the mean and the variance of the X_i are finite.

Proof of Theorem 8.25

Let . Then are independent and identically distributed random variables with mean and variance given by

(8.28)

and moment generating function

Now,

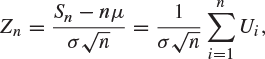
giving that Z_n has moment generating function

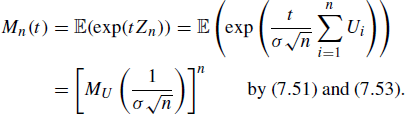
(8.29)

We need to know the behaviour of for large n, and to this end we use Theorem 7.55 to expand as a power series about :

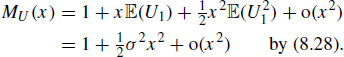
Substitute this into (8.29) with and t fixed to obtain

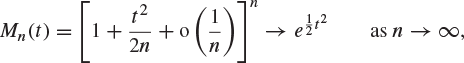
and the result follows from Theorem 8.27. This proof requires the existence of for values of t near 0 only, and this is consistent with the discussion before Theorem 7.49. We shall see in Example 8.54 how to adapt the proof without this assumption.

Example 8.30 (Statistical sampling)

The central limit theorem has many applications in statistics, and here is one such. An unknown fraction p of the population are jedi knights. It is desired to estimate p with error not exceeding by asking a sample of individuals (it is assumed they answer truthfully). How large a sample is needed?

Solution

Suppose a sample of n individuals is chosen. Let X_i be the indicator function of the event that the ith such person admits to being a jedi knight, and assume the X_i are independent, Bernoulli random variables with parameter p. Write

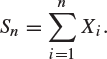
(8.31)

We choose to estimate p with the ‘sample mean’ , which, following statistical notation, we denote as .

We wish to choose n sufficiently large that . This cannot be done, since is a random variable which may (albeit with only small probability) take a value larger than for any given n. The accepted approach is to set a maximal level of probability at which an error is permitted to occur. By convention, we take this to be , and we are thus led to the following problem: find n such that

By (8.31), S_n is the sum of independent, identically distributed random variables with mean p and variance . The above probability may be written as

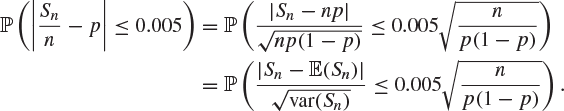
By the central limit theorem, converges in distribution to the normal distribution, and hence the final probability may be approximated by an integral of the normal density function. Unfortunately, the range of this integral depends on p, which is unknown.

Since for ,

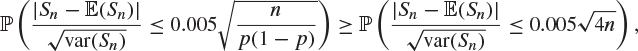
and the right-hand side is approximately , where N is normal with mean 0 and variance 1. Therefore,

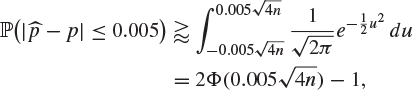
where Φ is the distribution function of N. On consulting statistical tables, we find this to be greater than if , which is to say that .

Exercise 8.32

A fair die is thrown 12,000 times. Use the central limit theorem to find values of a and b such that

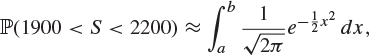
where S is the total number of sixes thrown.

Exercise 8.33

For , let X_n be a random variable having the gamma distribution with parameters n and 1. Show that the moment generating function of is

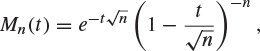
and deduce that, as ,

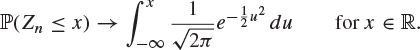
8.4 Large deviations and Cramér’s theorem

Let S_n be the sum of n independent, identically distributed random variables with mean μ and variance . The weak law of large numbers asserts that S_n has approximate order . By the central limit theorem, the deviations of S_n are typically of the order . It is unlikely that S_n will deviate from its mean by more than order with . The study of such unlikely events has proved extremely fruitful in recent decades. The following theorem, proved in its original form by Cramér in 1938, is of enormous practical use within the modern theory of ‘large deviations’, despite the low probability of the events under study.

Let be independent, identically distributed random variables, and . For simplicity, we assume that the X_i have common mean 0; if this does not hold, we replace X_i by . We shall assume quite a lot of regularity on the distribution of the X_i, namely that the common moment generating function satisfies for values of t in some neighbourhood of the origin. Let . The function is strictly increasing on , so that if and only if . By Markov’s inequality, Theorem 7.63,

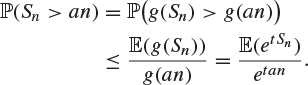
By Theorem 7.52, , and so

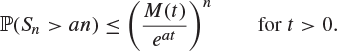
This provides an upper bound for the chance of a ‘large deviation’ of S_n from its mean 0, in terms of the arbitrary constant . We minimize the right-hand side over t to obtain

(8.34)

This is an exponentially decaying bound for the probability of a large deviation.

It turns out that, neglecting sub-exponential corrections, the bound (8.34) is an equality, and this is the content of Cramér’s theorem, Theorem 8.36. The precise result is usually stated in logarithmic form. Let , and define the so-called Fenchel–Legendre transform of Λ by

(8.35)

The function is illustrated in Figure 8.1.

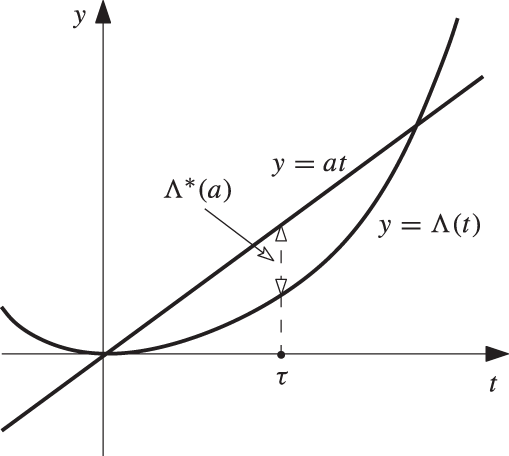
**Fig. 8.1** The function 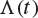plotted against the line 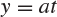, in the case when 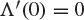. The point 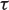marks the value of t at which 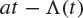is a maximum, and this maximum is denoted .

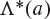Theorem 8.36 (Large deviation theorem)

Let be independent, identically distributed random variables with mean 0, whose common moment generating function is finite in some neighbourhood of the origin. Let be such that . Then and

(8.37)

That is to say, decays to 0 in the manner of . If , then for all n. Theorem 8.36 accounts for deviations above the mean. For deviations below the mean, the theorem may be applied to the sequence .

Partial Proof

We begin with some properties of the function . First,

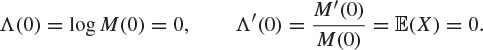
Next,

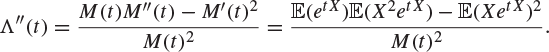
By the Cauchy–Schwarz inequality, Theorem 7.30, applied to the random variables and , the numerator is positive. Therefore, Λ is a convex function wherever it is finite (see Exercise 7.73).

We turn now to Figure 8.1. Since Λ is convex with , and since , the supremum of over is unchanged by the restriction . That is,

(8.38)

Next, we show that under the conditions of the theorem. By Theorem 7.55,

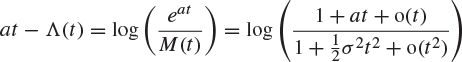
for small positive t, where . This is where we have used the assumption that on a neighbourhood of the origin. For sufficiently small positive t,

whence by (8.38).

It is immediate from (8.34) and (8.38) that

(8.39)

The proof of the sharpness of the limit in (8.37) is more complicated, and is omitted. A full proof may be found in Grimmett and Stirzaker (2001, Sect. 5.11).

Example 8.40

Let X be a random variable with distribution

and moment generating function

Let . By (8.35), the Fenchel–Legendre transformation of is obtained by maximizing over the variable t. The function Λ is differentiable, and therefore the maximum may be found by calculus. We have that

Setting this equal to 0, we find that

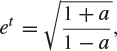
and hence

Let be the sum of n independent copies of X. By the large deviation theorem, Theorem 8.36,

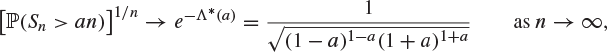
(8.41)

for .

Exercise 8.42

Find the Fenchel–Legendre transform in the case of the normal distribution with mean 0 and variance 1.

Exercise 8.43

Show that the moment generating function of a random variable X is finite on a neighbourhood of the origin if and only if there exist such that for .

Exercise 8.44

Let be independent random variables with the Cauchy distribution, and let . Find for .

8.5 Convergence in distribution, and characteristic functions

We have now encountered the ideas of convergence in mean square and convergence in probability, and we have seen that the former implies the latter. To these two types of convergence we are about to add a third. We motivate this by recalling the conclusion of the central limit theorem, Theorem 8.25: the distribution function of the standardized sum Z_n converges as to the distribution function of the normal distribution. This notion of the convergence of distribution functions may be set in a more general context as follows.

Definition 8.45

The sequence is said to converge in distribution, or to converge weakly, to Z as if

where C is the set of reals at which the distribution function is continuous. If this holds, we write .

The condition involving points of continuity is an unfortunate complication of the definition, but turns out to be desirable (see Exercise 8.56).

Convergence in distribution is a property of the distributions of random variables rather than a property of the random variables themselves, and for this reason, explicit reference to the limit random variable Z is often omitted. For example, the conclusion of the central limit theorem may be expressed as ‘Z_n converges in distribution to the normal distribution with mean 0 and variance 1’.

Theorem 8.14 asserts that convergence in mean square implies convergence in probability. It turns out that convergence in distribution is weaker than both of these.

Theorem 8.46

If is a sequence of random variables and in probability as , then .

The converse assertion is generally false; see the forthcoming Example 8.49 for a sequence of random variables which converges in distribution but not in probability. The next theorem describes a partial converse.

Theorem 8.47

Let be a sequence of random variables which converges in distribution to the constant c. Then Z_n converges to c in probability also.

Proof of Theorem 8.46

Suppose in probability, and write

for the distribution functions of Z_n and Z. Let , and suppose that F is continuous at the point z. Then

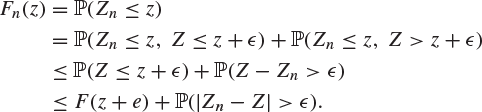
Similarly,

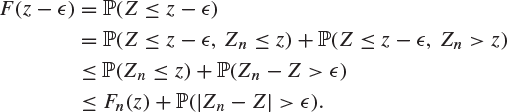
Thus

(8.48)

We let and throughout these inequalities. The left-hand side of (8.48) behaves as follows:

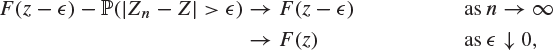
where we have used the facts that in probability and that F is continuous at z, respectively. Similarly, the right-hand side of (8.48) satisfies

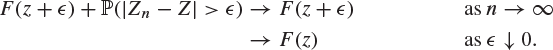
Thus, the left- and right-hand sides of (8.48) have the same limit , implying that the central term satisfies as . Hence .

Proof of Theorem 8.47

Suppose that . It follows that the distribution function F_n of Z_n satisfies

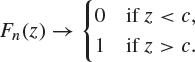
Thus, for ,

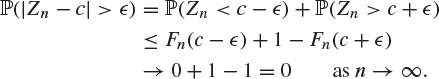
The following is an example of a sequence of random variables which converges in distribution but not in probability.

Example 8.49

Let U be a random variable which takes the values and 1, each with probability . We define the sequence by

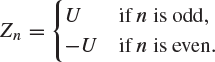
It is clear that , since each Z_n has the same distribution. On the other hand

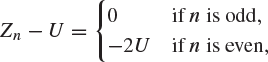
so that for all m. Hence, Z_n does not converge to U in probability.

Finally, we return to characteristic functions. In proving the central limit theorem we employed a result (Theorem 8.27) linking the convergence of moment generating functions to convergence in distribution. This result is a weak form of the so-called continuity theorem, a more powerful version of which we present next (the proof is omitted).

Theorem 8.50 (Continuity theorem)

Let be random variables with characteristic functions . Then if and only if

This is a difficult theorem to prove—see Feller (1971, p. 481). We close the section with several examples of this theorem in action.

Example 8.51

Suppose that and . Prove that .

Solution

Let be the characteristic function of Z_n and the characteristic function of Z. By the continuity theorem, Theorem 8.50, as . The characteristic function of is

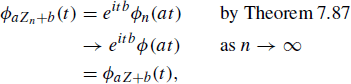
and the result follows by another appeal to Theorem 8.50. A direct proof of this fact using distribution functions is messy when a is negative.

Example 8.52 (The weak law)

Here is another proof of the weak law of large numbers, Theorem 8.17, for the case of identically distributed random variables. Let be independent and identically distributed random variables with mean μ, and let

By Theorem 7.87, the characteristic function of U_n is given by

(8.53)

where is the common characteristic function of the X_i. By Theorem 7.85,

Substitute this into (8.53) to obtain

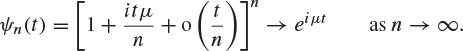
The limit here is the characteristic function of the constant μ, and thus the continuity theorem, Theorem 8.50, implies that . A glance at Theorem 8.47 confirms that the convergence takes place in probability also, and we have proved a version of the weak law of large numbers. This version differs from the earlier one in two regards—we have assumed that the X_i are identically distributed, but we have made no assumption that they have finite variance.

Example 8.54

Central limit theorem. Our proof of the central limit theorem in Section 8.3 was valid only for random variables which possess finite moment generating functions. Very much the same arguments go through using characteristic functions, and thus Theorem 8.25 is true as it is stated.

Exercise 8.55

Let be independent random variables, each having the Cauchy distribution. Show that converges in distribution to the Cauchy distribution as . Compare this with the conclusion of the weak law of large numbers.

Exercise 8.56

Let X_n, Y_n, Z be ‘constant’ random variables with distributions

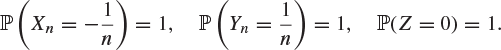
Show that

but .

This motivates the condition of continuity in Definition 8.45. Without this condition, it would be the case that but .

8.6 Problems

1. Let be independent random variables, each having the uniform distribution on the interval , and let . Show that

(a) in probability as ,

(b) in probability as ,

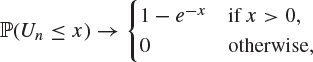
so that U_n converges in distribution to the exponential distribution as .

2. By applying the central limit theorem to a sequence of random variables with the Bernoulli distribution, or otherwise, prove the following result in analysis. If and , then

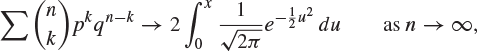
where the summation is over all values of k satisfying .

3. Let X_n be a discrete random variable with the binomial distribution, parameters n and p. Show that converges to p in probability as .

4. Binomial–Poisson limit. Let Z_n have the binomial distribution with parameters n and , where λ is fixed. Use characteristic functions to show that Z_n converges in distribution to the Poisson distribution, parameter λ, as .

5. By applying the central limit theorem to a sequence of random variables with the Poisson distribution, or otherwise, prove that

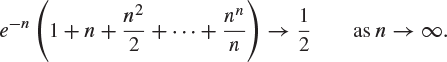
6. (a) Let and

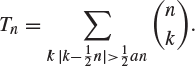
By considering the binomial distribution or otherwise, show that

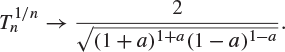
(b) Find the asymptotic behaviour of , where and

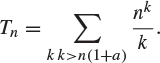
7. Use the Cauchy–Schwarz inequality to prove that if in mean square and in mean square, then in mean square.

8. Use the Cauchy–Schwarz inequality to prove that if in mean square, then . Give an example of a sequence such that in probability but does not converge to .

9. 8.6.9 If in probability and in probability, show that in probability.

10. Let and be independent random variables each having mean μ and non-zero variance . Show that

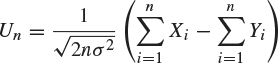
satisfies, as ,

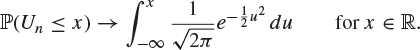
11. Adapt the proof of Chebyshev’s inequality to show that, if X is a random variable and , then

for any function which satisfies

(a) for ,

(b) for ,

12. Let X be a random variable which takes values in the interval only. Show that

if .

13. Show that in probability if and only if

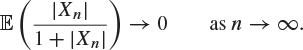
14. Let be a sequence of random variables which converges in mean square. Show that as .

If and for all n, show that the correlation between X_n and X_m converges to 1 as .

15. Let Z have the normal distribution with mean 0 and variance 1. Find and , and find the probability density function of .

*16. Let be independent random variables each having distribution function F and density function f. The order statistics of the subsequence are obtained by rearranging the values of the X_i in non-decreasing order. That is to say, is set to the smallest observed value of the X_i, is set to the second smallest value, and so on, so that . The sample median Y_n of the sequence is the ‘middle value’, so that Y_n is defined to be

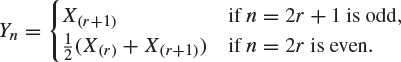
Assume that is odd, and show that Y_n has density function

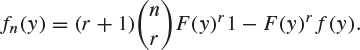
Deduce that, if F has a unique median m, then

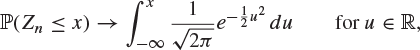
where .

17. The sequence of independent, identically distributed random variables is such that

If f is a continuous function on , prove that

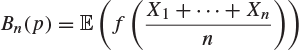
is a polynomial in p of degree at most n. Use Chebyshev’s inequality to prove that for all p with , and any ,

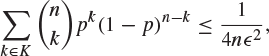
where . Using this and the fact that f is bounded and uniformly continuous in , prove the following version of the Weierstrass approximation theorem:

(Oxford 1976F)

18. Let Z_n have the geometric distribution with parameter , where λ is fixed. Show that converges in distribution as , and find the limiting distribution.

*19. Let and be two sequences of independent random variables with

and

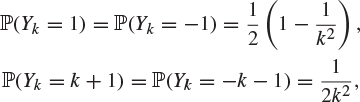
for . Let

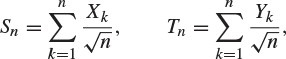
and let Z denote a normally distributed random variable with mean 0 and variance 1. Prove or disprove the following:

State carefully any theorems which you use. (Oxford 1980F)

(a) S_n converges in distribution to Z,

(b) the mean and variance of T_n converge to the mean and variance of Z,

*20. Let X_j, , be independent identically distributed random variables with probability density function , . Show that the characteristic function of is . Consider a sequence of independent trials where the probability of success is p for each trial. Let N be the number of trials required to obtain a fixed number of k successes. Show that, as p tends to zero, the distribution of tends to the distribution of Y with . (Oxford 1979F)

21. Let be independent and identically distributed random variables such that

Derive the moment generating function of the random variable , where are constants. In the special case for , show that Y_n converges in distribution as to the uniform distribution on the interval .

22. X and Y are independent, identically distributed random variables with mean 0, variance 1, and characteristic function . If and are independent, prove that

By making the substitution or otherwise, show that, for any positive integer n,

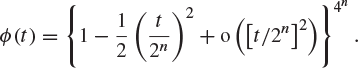
Hence, find the common distribution of X and Y. (Oxford 1976F)

23. Let and be the real and imaginary parts, respectively, of the characteristic function of the random variable X. Prove that

Hence, find the variance of and the covariance of and in terms of u and v.

Consider the special case when X is uniformly distributed on . Are the random variables (i) uncorrelated, (ii) independent? Justify your answers. (Oxford 1975F)

(a) ,

(b) .

24. State the central limit theorem.

The cumulative distribution function F of the random variable X is continuous and strictly increasing. Show that is uniformly distributed. Find the probability density function of the random variable , and calculate its mean and variance. Let be a sequence of independent random variables whose corresponding cumulative distribution functions are continuous and strictly increasing. Let

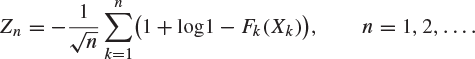
Show that, as , converges in distribution to a normal distribution with mean zero and variance one. (Oxford 2007)