The number of permutations of n distinct objects is
and is pronounced ‘n factorial’. The number of ordered subsequences of length r from these n objects is 
, which may be written as
If the ordering of these r objects is not important, then any of the 
possible orderings gives rise to the same subset, and the number of such combinations is then
This is usually called the binomial coefficient, written as
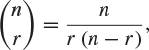
and pronounced ‘n choose r’. It is useful to note that
|
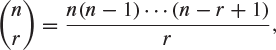
(A.1) |
since this formal definition makes sense even when n is a general real number.
There are entire volumes devoted to combinatorial identities. Of the many such identities we highlight one, namely the following:
|
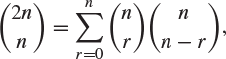
(A.2) |
the proof of which is left as a small exercise.
The binomial theorem states that
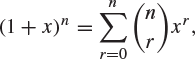
valid for 
and 
. There is a more general version that holds even when n is fractional, or even negative.
Theorem A.3 (Extended binomial theorem)
Let 
. We have that
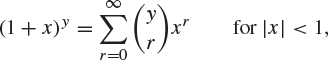
where the binomial coefficients are given by (A.1).
It is often necessary to compare the rate of growth of 
with polynomial and exponential functions of n. The requisite formula is called Stirling’s formula.
Theorem A.4 (Stirling’s formula)
We have that
where 
means 
.
A ‘short’ proof of Stirling’s formula has been given by Romik (2000), and a proof of a slightly weaker result without the identification of the constant 
is provided in Norris (1997, Sect. 1.12).
Partial proof
We prove only the weaker ‘logarithmic asymptotic’
|
(A.5) |
Since 
is increasing on the interval 
, we have that
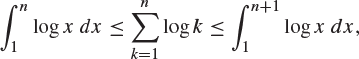
which is to say that
Equation (A.5) follows by dividing by 
and letting 
.
Readers are referred to Graham et al. (1994) for further information about these and related topics.