We say that the sequence 
satisfies a difference equation if
|
(B.1) |
where 
is a given sequence of real numbers and 
. We generally suppose that 
, and in this case we call (B.1) a difference equation of order k. Difference equations occur quite often in the study of random processes, particularly random walks, and it is useful to be able to solve them. We describe here how to do this.
Just as in solving differential equations, we require boundary conditions in order to solve difference equations. To see this, note that (B.1) may be rewritten as
|
(B.2) |
since 
. Thus, if we know the values of 
, equation (B.2) with 
provides the value of xk. Next, equation (B.2) with 
tells us the value of 
, and so on. That is to say, there is a unique solution of (B.1) with specified values for 
. It follows that, if 
, the general solution of (B.1) contains exactly k independent arbitrary constants, and so exactly k independent boundary conditions are required in order to solve (B.1) explicitly.
The principal step involved in solving (B.1) is to find the roots of the auxiliary equation
|
(B.3) |
a polynomial in θ of degree k. We denote the (possibly complex) roots of this polynomial by 
. The general solution of (B.1) is given in the next theorem.
Theorem B.4
Let 
be a sequence of real numbers with 
.
(a) If the roots 
of the auxiliary equation are distinct, the general solution of (B.1) is
|
(B.5) |
where 
are arbitrary constants.
(b) More generally, if 
are the distinct roots of the auxiliary equation and mi is the multiplicity of 
for 
, the general solution of (B.1) is
|
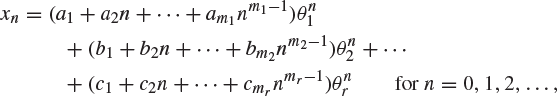
(B.6) |
where the k numbers 
are arbitrary constants.
The auxiliary equation may not possess k real roots, and thus some or all of 
may have non-zero imaginary parts. Similarly, the arbitrary constants in Theorem B.4 need not necessarily be real, and the general solution (B.6) is actually the general solution for complex solutions of the difference equation (B.1). If we seek real solutions only of (B.1), then this fact should be taken into account when finding the values of the constants.
We do not prove this theorem, but here are two ways of going about proving it, should one wish to do so. The first way is constructive, and uses the generating functions of the sequences of ai and xi (see Hall (1967, p. 20)). The second way is to check that (B.5) and (B.6) are indeed solutions of (B.1) and then to note that they contain the correct number of arbitrary constants.
Here is an example of the theorem in action.
Example B.7
Find the solution of the difference equation
subject to the boundary conditions 
, 
, 
.
Solution
The auxiliary equation is
with roots 
. The general solution is therefore
where the constants a, b, c are found from the boundary conditions to be given by 
, 
, 
.
An important generalization of Theorem B.4 deals with difference equations of the form
|
(B.8) |
where g is a given function of n, not always equal to 0. There are two principal steps in solving (B.8). First, we find a solution of (B.8) by any means available, and we call this a particular solution. Secondly, we find the general solution to the difference equation obtained by setting 
for all n:
this solution is called the complementary solution.
Theorem B.9
Suppose that 
is a given sequence of real numbers and that 
. The general solution of (B.8) is
|
(B.10) |
where 
is the complementary solution and 
is a particular solution.
This may be proved in the same general way as Theorem B.4. We finish with an example.
Example B.11
Find the solution of the difference equation
|
(B.12) |
subject to the boundary conditions 
, 
.
Solution
The right-hand side of (B.12) is a polynomial function of n, and this suggests that there may be a particular solution which is a polynomial. Trial and error shows that
is a particular solution. The general solution of the difference equation
is
where a and b are arbitrary constants. It follows that the general solution of (B.12) is
The constants a and b are found from the boundary conditions to be given by 
, 
.