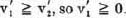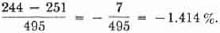It must be understood, however, that α( ), β(
), β( ) do not disclose which strategy of the opponent will inflict this (maximum) loss upon the player who is using
) do not disclose which strategy of the opponent will inflict this (maximum) loss upon the player who is using  or
or  . It is, in particular, not at all certain that if the opponent uses some particular good strategy, i.e. an
. It is, in particular, not at all certain that if the opponent uses some particular good strategy, i.e. an 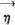 0 in
0 in 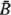 or a
or a  0 in Ā, this in itself implies the maximum loss in question. If a (not good)
0 in Ā, this in itself implies the maximum loss in question. If a (not good)  or
or 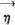 is used by the player, then the maximum loss will occur for those if
is used by the player, then the maximum loss will occur for those if 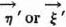 of the opponent, for which
of the opponent, for which
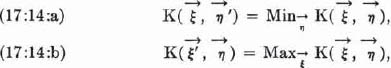
i.e. if 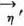 is optimal against the given
is optimal against the given  optimal against the given
optimal against the given  . And we have never ascertained whether any fixed
. And we have never ascertained whether any fixed 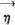 0 or
0 or  0 can be optimal against all
0 can be optimal against all  or
or 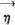 .
.
17.10.2. Let us therefore call an 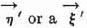 which is optimal against all
which is optimal against all  or
or 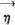 —i.e. which fulfills (17:14:a), or (17:14:b) in 17.10.1. for all
—i.e. which fulfills (17:14:a), or (17:14:b) in 17.10.1. for all  ,
, 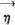 —permanently optimal. Any permanently optimal
—permanently optimal. Any permanently optimal 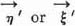 is necessarily good; this should be clear conceptually and an exact proof is easy.3 But the question remains: Are all good strategies also permanently optimal? And even: Do any permanently optimal strategies exist?
is necessarily good; this should be clear conceptually and an exact proof is easy.3 But the question remains: Are all good strategies also permanently optimal? And even: Do any permanently optimal strategies exist?
In general the answer is no. Thus in Matching Pennies or in Stone, Paper, Scissors, the only good strategy (for player 1 as well as for player 2) is 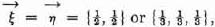 respectively.1 If player 1 played differently—e.g. always “heads”2 or always “stone”2—then he would lose if the opponent countered by playing “tails”3 or “paper.”3 But then the opponent’s strategy is not good—i.e.
respectively.1 If player 1 played differently—e.g. always “heads”2 or always “stone”2—then he would lose if the opponent countered by playing “tails”3 or “paper.”3 But then the opponent’s strategy is not good—i.e. 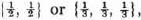 respectively—either. If the opponent played the good strategy, then the player’s mistake would not matter.4
respectively—either. If the opponent played the good strategy, then the player’s mistake would not matter.4
We shall get another example of this—in a more subtle and complicated way—in connection with Poker and the necessity of “bluffing,” in 19.2 and 19.10.3.
All this may be summed up by saying that while our good strategies are perfect from the defensive point of view, they will (in general) not get the maximum out of the opponent’s (possible) mistakes,—i.e. they are not calculated for the offensive.
It should be remembered, however, that our deductions of 17.8. are nevertheless cogent; i.e. a theory of the offensive, in this sense, is not possible without essentially new ideas. The reader who is reluctant to accept this, ought to visualize the situation in Matching Pennies or in Stone, Paper, Scissors once more; the extreme simplicity of these two games makes the decisive points particularly clear.
Another caveat against overemphasizing this point is: A great deal goes, in common parlance, under the name of “offensive,” which is not at all “offensive” in the above sense,—i.e. which is fully covered by our present theory. This holds for all games in which perfect information prevails, as will be seen in 17.10.3.5 Also such typically “aggressive” operations (and which are necessitated by imperfect information) as “bluffing” in Poker.6
17.10.3. We conclude by remarking that there is an important class of (zero-sum two-person) games in which permanently optimal strategies exist. These are the games in which perfect information prevails, which we analyzed in 15. and particularly in 15.3.2., 15.6., 15.7. Indeed, a small modification of the proof of special strict determinateness of these games, as given loc. cit., would suffice to establish this assertion too. It would give permanently optimal pure strategies. But we do not enter upon these considerations here.
Since the games in which perfect information prevails are always specially strictly determined (cf. above), one may suspect a more fundamental connection between specially strictly determined games and those in which permanently optimal strategies exist (for both players). We do not intend to discuss these things here any further, but mention the following facts which are relevant in this connection:
(17:G:a) |
It can be shown that if permanently optimal strategies exist (for both players) then the game must be specially strictly determined. |
(17:G:b) |
It can be shown that the converse of (17:G:a) is not true. |
(17:G:c) |
Certain refinements of the concept of special strict determinateness seem to bear a closer relationship to the existence of permanently optimal strategies. |
17.11. The Interchange of Players. Symmetry
17.11.1. Let us consider the role of symmetry, or more generally the effects of interchanging the players 1 and 2 in the game Γ. This will naturally be a continuation of the analysis of 14.6.
As was pointed out there, this interchange of the players replaces the function 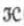 (τ1, τ2) by –
(τ1, τ2) by –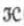 (τ2, τ1). The formula (17:2) of 17.4.1. and 17.0. shows that the effect of this for K(
(τ2, τ1). The formula (17:2) of 17.4.1. and 17.0. shows that the effect of this for K( ,
, 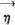 ) is to replace it by – K(
) is to replace it by – K(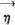 ,
,  ). In the terminology of 16.4.2., we replace the matrix (of
). In the terminology of 16.4.2., we replace the matrix (of  (τ1, τ2) cf. 14.1.3.) by its negative transposed matrix.
(τ1, τ2) cf. 14.1.3.) by its negative transposed matrix.
Thus the perfect analogy of the considerations in 14. continues; again we have the same formal results as there, provided that we replace 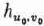 (Cf. the previous occurrence of this in 17.4. and 17.8.)
(Cf. the previous occurrence of this in 17.4. and 17.8.)
We saw in 14.6. that this replacement of  (τ1, τ2) by –
(τ1, τ2) by – (τ2, τ1) carries v1, v2 into –v2, –v1. A literal repetition of those considerations shows now that the corresponding replacement of K(
(τ2, τ1) carries v1, v2 into –v2, –v1. A literal repetition of those considerations shows now that the corresponding replacement of K( ,
, 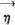 ) by –K (
) by –K (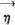 ,
,  ) carries
) carries 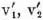 into –v2, –v1. Summing up: Interchanging the players 1, 2, carries v1, v2,
into –v2, –v1. Summing up: Interchanging the players 1, 2, carries v1, v2, 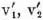 into –v2, –v1, –
into –v2, –v1, –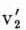 , –
, –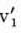 ,.
,.
The result of 14.6. established for (special) strict determinateness was that v = v1 = v2 is carried into –v = –v1 = –v2. In the absence of that property no such refinement of the assertion was possible.
At the present we know that we always have general strict determinateness, so that 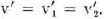 Consequently this is carried into
Consequently this is carried into 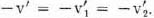
Verbally the content of this result is clear: Since we succeeded in defining a satisfactory concept of the value of a play of Γ (for the player 1), v′, it is only reasonable that this quantity should change its sign when the roles of the players are interchanged.
17.11.2. We can also state rigorously when the game Γ is symmetric. This is the case when the two players 1 and 2 have precisely the same role in it,—i.e. if the game Γ is identical with that game which obtains from it by interchanging the two players 1, 2. According to what was said above, this means that
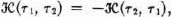
or equivalently that

This property of the matrix 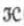 (τ1, τ2) or of the bilinear form K (
(τ1, τ2) or of the bilinear form K ( ,
, 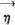 ) was introduced in 16.4.4, and called skew-symmetry.1,2
) was introduced in 16.4.4, and called skew-symmetry.1,2
In this case v1, v2 must coincide with –v2, –v1; hence v1 = –v2, and since v1 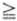 v2, so v1
v2, so v1 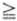 0. But v′ must coincide with –v′; therefore we can even assert that
0. But v′ must coincide with –v′; therefore we can even assert that
v′ = 0.3
So we see: The value of each play of a symmetrical game is zero.
It should be noted that the value v′ of each play of a game Γ could be zero without Γ being symmetric. A game in which v′ = 0 will be called fair.
The examples of 14.7.2., 14.7.3. illustrate this: Stone, Paper, Scissors is symmetric (and hence fair); Matching Pennies is fair (cf. 17.1.) without being symmetric.4
In a symmetrical game the sets Ā, 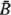 of (17:B:a), (17:B:b) in 17.8. are obviously identical. Since Ā =
of (17:B:a), (17:B:b) in 17.8. are obviously identical. Since Ā = 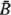 we may put
we may put  =
= 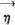 in the final criterion (17:D) of 17.9. We restate it for this case:
in the final criterion (17:D) of 17.9. We restate it for this case:
(17:H) |
In a symmetrical game,  belongs to Ā if and only if this is true: For each τ2 = 1, · · · β2 for which belongs to Ā if and only if this is true: For each τ2 = 1, · · · β2 for which 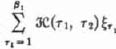 does not assume its minimum (in τ2) we have does not assume its minimum (in τ2) we have  |
Using the terminology of the concluding remark of 17.9., we see that the above condition expresses this:  is optimal against itself.
is optimal against itself.
17.11.3. The results of 17.11.1., 17.11.2.—that in every symmetrical game v′ = 0—can be combined with (17:C:d) in 17.8. Then we obtain this:
(17:I) |
In a symmetrical game each player can, by playing appropriately, avoid loss1 irrespective of what the opponent does. |
We can state this mathematically as follows:
If the matrix 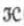 (τ1, τ2) is skew-symmetric, then there exists a vector
(τ1, τ2) is skew-symmetric, then there exists a vector  in
in 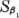 with
with
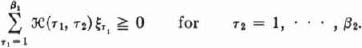
This could also have been obtained directly, because it coincides with the last result (16:G) in 16.4.4. To see this it suffices to introduce there our present notations: Replace the i, j, a(i, j) there by our τ1, τ2, 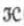 (τ1, τ2) and the
(τ1, τ2) and the 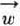 there by our
there by our  .
.
It is even possible to base our entire theory on this fact, i.e. to derive the theorem of 17.6. from the above result. In other words: The general strict determinateness of all Γ can be derived from that one of the symmetric ones. The proof has a certain interest of its own, but we shall not discuss it here since the derivation of 17.6. is more direct.
The possibility of protecting oneself against loss (in a symmetric game) exists only due to our use of the mixed strategies  ,
, 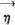 (cf. the end of 17.7.). If the players are restricted to pure strategies τ1, τ2 then the danger of having one’s strategy found out, and consequently of sustaining losses, exists. To see this it suffices to recall what we found concerning Stone, Paper, Scissors (cf. 14.7. and 17.1.1.). We shall recognize the same fact in connection with Poker and the necessity of “bluffing” in 19.2.1.
(cf. the end of 17.7.). If the players are restricted to pure strategies τ1, τ2 then the danger of having one’s strategy found out, and consequently of sustaining losses, exists. To see this it suffices to recall what we found concerning Stone, Paper, Scissors (cf. 14.7. and 17.1.1.). We shall recognize the same fact in connection with Poker and the necessity of “bluffing” in 19.2.1.
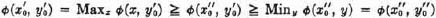 ,
,
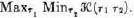
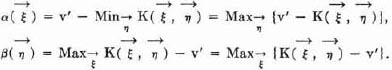
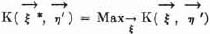
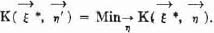
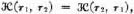
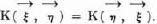

 ), β(
), β( ) do not disclose which strategy of the opponent will inflict this (maximum) loss upon the player who is using
) do not disclose which strategy of the opponent will inflict this (maximum) loss upon the player who is using  or
or 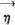 . It is, in particular, not at all certain that if the opponent uses some particular good strategy, i.e. an
. It is, in particular, not at all certain that if the opponent uses some particular good strategy, i.e. an 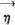 0 in
0 in 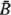 or a
or a  0 in Ā, this in itself implies the maximum loss in question. If a (not good)
0 in Ā, this in itself implies the maximum loss in question. If a (not good)  or
or 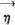 is used by the player, then the maximum loss will occur for those if
is used by the player, then the maximum loss will occur for those if 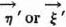 of the opponent, for which
of the opponent, for which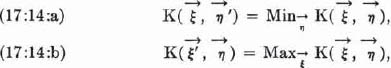
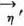 is optimal against the given
is optimal against the given 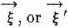 optimal against the given
optimal against the given 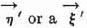 which is optimal against all
which is optimal against all 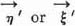 is necessarily good; this should be clear conceptually and an exact proof is easy.
is necessarily good; this should be clear conceptually and an exact proof is easy.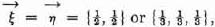 respectively.
respectively.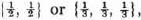 respectively—either. If the opponent played the good strategy, then the player’s mistake would not matter.
respectively—either. If the opponent played the good strategy, then the player’s mistake would not matter.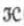 (τ1, τ2) by –
(τ1, τ2) by –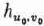 (Cf. the previous occurrence of this in 17.4. and 17.8.)
(Cf. the previous occurrence of this in 17.4. and 17.8.)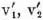 into –v2, –v1. Summing up: Interchanging the players 1, 2, carries v1, v2,
into –v2, –v1. Summing up: Interchanging the players 1, 2, carries v1, v2, 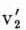 , –
, –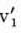 ,.
,.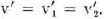 Consequently this is carried into
Consequently this is carried into 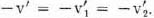
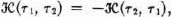

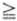 v2, so v1
v2, so v1 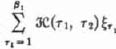 does not assume its minimum (in τ2) we have
does not assume its minimum (in τ2) we have 
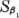 with
with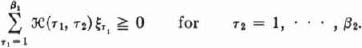
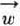 there by our
there by our 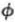 (x),
(x),  and
and  . Then
. Then 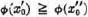 and
and 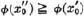 . Hence
. Hence 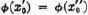 .
.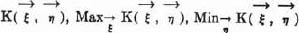 in 17.4., the functions
in 17.4., the functions 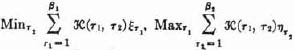 in 17.5.2. The variables of all these functions are
in 17.5.2. The variables of all these functions are 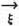 or
or 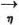 or both, with respect to which subsequent maxima and minima are formed.
or both, with respect to which subsequent maxima and minima are formed.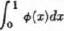 is a constant.
is a constant.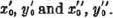 Then:
Then: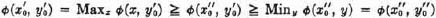 ,
,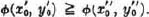 Similarly
Similarly 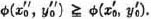
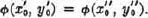
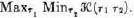
 1 a particular opening move—i.e. choice at
1 a particular opening move—i.e. choice at  1—of “white,” i.e. player 1. Then Γ
1—of “white,” i.e. player 1. Then Γ But we prefer the simpler notation
But we prefer the simpler notation  1 is an exception from (8:B:a) in 8.3.1.; cf. the remark concerning this (8:B:a) in footnote 1 on p. 63, and also footnote 4 on p. 69.
1 is an exception from (8:B:a) in 8.3.1.; cf. the remark concerning this (8:B:a) in footnote 1 on p. 63, and also footnote 4 on p. 69.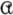 1, which is a subpartition of
1, which is a subpartition of 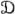 1(k1) unlike
1(k1) unlike 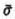 1 = 1, · · · , α1;
1 = 1, · · · , α1; 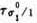 must be treated in this case as a constant.
must be treated in this case as a constant.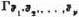 in 15.3.1. In the partition and set terminology: For v = 0 (10:1:f), (10:1:g) in 10.1.1. show that Ω has only one element, say
in 15.3.1. In the partition and set terminology: For v = 0 (10:1:f), (10:1:g) in 10.1.1. show that Ω has only one element, say 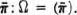 So
So  play the role indicated above.
play the role indicated above. in 15.3.1.
in 15.3.1. is one of
is one of  k; every value of
k; every value of 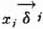 as scalar multipliers.
as scalar multipliers. 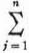 is a vector summation.
is a vector summation.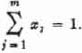
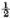 , whatever the opponent’s conduct.
, whatever the opponent’s conduct.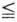 his probability of winning. That he cannot win, means that the former is
his probability of winning. That he cannot win, means that the former is 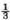 ,
,  and
and 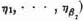 it is perfectly admissible to view each as a single variable in the maxima and minima which we are now forming. Their domains are, of course, the sets
it is perfectly admissible to view each as a single variable in the maxima and minima which we are now forming. Their domains are, of course, the sets 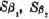 which we introduced in 17.2.
which we introduced in 17.2.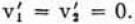
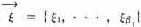 with the components
with the components 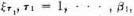 also contains τ1; but there is a fundamental difference. In
also contains τ1; but there is a fundamental difference. In 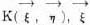 is a variable, while τ1 is, so to say, a variable within the variable.
is a variable, while τ1 is, so to say, a variable within the variable. 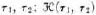 is a function of τ1, τ2 while K(
is a function of τ1, τ2 while K(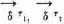 represent.
represent.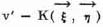 for player 1 and (–v′) – (–K(
for player 1 and (–v′) – (–K(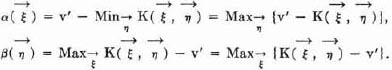
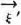 is analogous.
is analogous.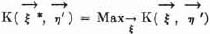
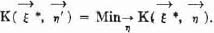
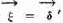 = {1, 0} or [1, 0, 0], respectively.
= {1, 0} or [1, 0, 0], respectively.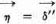 = [0, 1] or [0, 1, 0], respectively.
= [0, 1] or [0, 1, 0], respectively.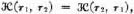
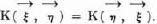
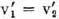 . Without this—i.e. without the general theorem (16:F) of 16.4.3.—we should assert for the
. Without this—i.e. without the general theorem (16:F) of 16.4.3.—we should assert for the 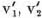 only the same which we obtained above for the v1, v2:
only the same which we obtained above for the v1, v2: 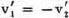 and since
and since