C Differentiation Techniques for Machine Learning
In this appendix we present the basic differentiation techniques that are required to understand how linear regression can be used to build predictive analytics models. In particular we explain what a derivative is, how to calculate derivatives for continuous functions, the chain rule for differentiation, and what a partial derivative is.
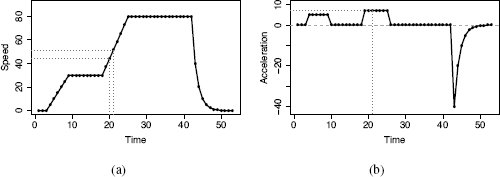
(a) The speed of a car during a journey along a minor road before joining a highway and finally coming to a sudden halt; (b) the acceleration, the derivative of speed with respect to time, for this journey.
To begin, imagine a car journey where we start out driving on a minor road at about 30mph and then move onto a highway, where we drive at about 80mph before noticing an accident and braking suddenly. Figure C.1(a)[551] shows a profile of the speed during this journey measured at different points in time. Figure C.1(b)[551] shows a profile of the acceleration during this journey. We can see that when the car is driving at a constant speed, on the minor road or the highway, acceleration is zero as the speed is not changing. In contrast, acceleration has modest positive values when we are taking off initially and slightly larger positive values when we increase speed on reaching the highway. The sudden braking at the end of the journey results in large negative values that slowly taper off to match the speed profile in Figure C.1(a)[551].
Acceleration is a measure of the rate of change of speed over time. We can say more formally that acceleration is, in fact, the derivative of speed with respect to time. Differentiation is the set of techniques from calculus (the branch of mathematics that deals with how things change) that allows us to calculate derivatives. In an example like the car journey just described, where we have a set of discrete measurements, calculating the derivative is simply a matter of determining the difference between subsequent pairs of measurements. For example, the derivative of speed with respect to time at time index 21 is the speed at time index 21 minus the speed at time index 20, which is 44.28 − 51.42 = 7.14. These values are marked in Figure C.1[551]. All the values of acceleration have been calculated in this way.
C.1 Derivatives of Continuous Functions
While it is interesting to see how derivatives can be calculated for discrete examples, it is much more common that we need to calculate the derivative of a continuous function. A continuous function, f(x), generates an output for every value of a variable x based on some expression involving x. For example:
f(x) = 2x + 3
f(x) = x2
f(x) = 3x3 + 2x2 − x − 2
are continuous functions with a single variable x. Graphs of these functions are shown in Figure C.2[553]. Each graph also shows the derivative of the function. We will return to these shortly.
The function f(x) = 2x + 3 is known as a linear function because the output is a combination of only additions and multiplications1 involving x. The other two functions are known as polynomial functions as they include addition, multiplication, and raising to exponents. Of those, f(x) = x2 is an example of a second order polynomial function, also known as a quadratic function, as its highest exponent is 2, and f(x) = 3x3 + 2x2 − x − 2 is a third order polynomial function, also known as a cubic function, as its highest exponent is 3.
Looking first at Figure C.2(a)[553], the function here is very simple, f(x) = 2x + 3, which results in a straight diagonal line. A straight diagonal line gives us a constant rate of change (in this case an increase of 2 in the value of the function for every change of 1 in x), so the derivative of this function with respect to x is just a constant. This is represented by the horizontal dashed line.
We can intuitively see from Figure C.2(b)[553] for f(x) = x2 that the rate of change of the value of this function is likely to be high at the steep edges of the curve and low at the bottom (imagine a ball rolling around inside this shape!). This intuition is mirrored in the derivative of the function with respect to x. We can see that at the left hand side of the graph (for large negative values of x), the rate of change has a high negative value, while at the right hand side of the graph (for large positive values of x), the rate of change has a large positive value. In the middle of the graph, at the bottom of the curve, the rate of change is zero. It should be no surprise to learn that the derivative of the function with respect to x also gives us the slope of the function at that value of x. The shape of the derivative in Figure C.2(c)[553] can be understood similarly.
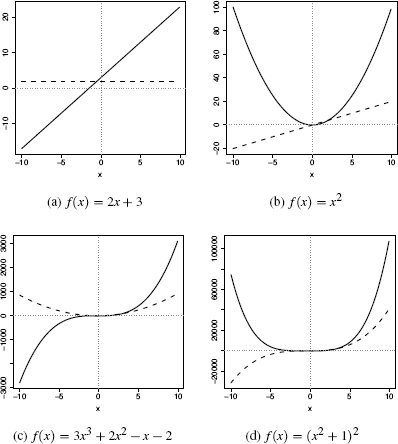
Examples of continuous functions (shown as solid lines) and their derivatives (shown as dashed lines).
To actually calculate the derivative, referred to as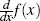 
, of a simple continuous function, f(x), we use a small number of differentiation rules:
| 1. |  |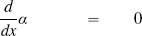
(where α is any constant) |
| 2. |  |
|
| 3. |  |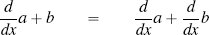
(where a and b are expressions that may or may not contain x) |
| 4. |  |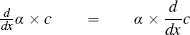
(where α is any constant and c is an expression containing x) |
Applying these rules to the first of our previous examples, f(x) = 2x + 3 (Figure C.2(a)[553]), we first apply Rule 3 to split this function into two parts, 2x
and 3, and then apply differentiation rules to each. By Rule 2 we can differentiate 2x to 2 (remember that x is really x1). The 3 is a constant, so by Rule 1 differentiates to zero. The derivative of the function, then, is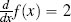 
.
For the last function, f(x) = 3x3 + 2x2 − x − 2 (Figure C.2(c)[553]), we first apply Rule 3 to divide this into four parts: 3x3, 2x2, x, and 2. Applying Rule 2 to each of the first three parts gives 9x2, 4x, and −1. The final part, 2, is a constant and so differentiates to zero. The derivative of this function then is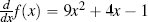 
.
We can see from these examples that calculating derivatives of simple functions is a matter of, fairly mechanically, applying these four simple rules. Calculating the derivatives of the other two functions are left as exercises for the reader. Some of the functions that we will encounter later on in this chapter will be a little more complex, and we need two more differentiation rules to handle these.
C.2 The Chain Rule
The function f(x) = (x2 + 1)2 (shown in Figure C.2(d)[553]) cannot be differentiated using the rules just described because it is a composite function—it is a function of a function. We can rewrite f(x) as f(x) = (g (x))2 where g(x) = x2 + 1. The differentiation chain rule allows us to differentiate functions of this kind.2 The chain rule is
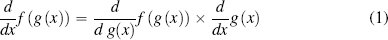
The differentiation is performed in two steps. First, treating g(x) as a unit, we differentiate f (g(x)) with respect to g(x), and then we differentiate g(x) with respect to x, in both cases using the differentiation rules from the previous section. The derivative of f (g(x)) with respect to x is the product of these two pieces.
Applying this to the example f(x) = (x2 + 1)2 we get
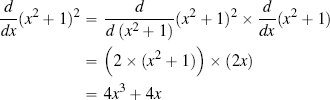
Figure C.2(d)[553] shows this example function and its derivative calculated using the chain rule.
C.3 Partial Derivatives
Some functions are not defined in terms of just one variable. For example, f(x, y) = x2 − y2 + 2x + 4y − xy + 2 is a function defined in terms of two variables, x and y. Rather than defining a curve (as was the case for all the previous examples), this function defines a surface, as shown in Figure C.3(a)[556]. Using partial derivatives offers us an easy way to calculate the derivative of a function like this. A partial derivative (denoted by the symbol ∂) of a function of more than one variable is its derivative with respect to one of those variables with the other variables held constant.
For the example function f (x, y) = x2 − y2 + 2x + 4y − xy + 2, we get two partial derivatives:
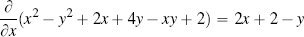
where the terms y2 and 4y are treated as constants as they do not include x, and
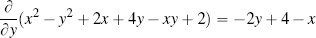
where the terms x2 and 2x are treated as constants as they do not include y. Figures C.3(b)[556] and C.3(c)[556] show these partial derivatives.
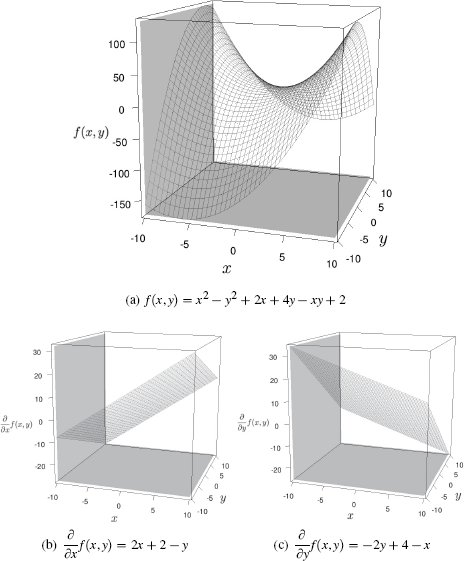
(a) A continuous function in two variables, x and y; (b) the partial derivative of this function with respect to x; and (c) the partial derivative of this function with respect to y.
_______________
1 Note that subtraction is viewed as addition of negative numbers, and division is seen as multiplication by reciprocals, so both are also allowed.
2 This is not to be confused with the probability chain rule discussed in Section B.3[548]. These are two completely different operations.