1 How the notation used in the book relates to the elements of a dataset.
1.1 Predictive data analytics moving from data to insight to decision.
1.2 The two steps in supervised machine learning.
1.3 Striking a balance between overfitting and underfitting when trying to predict age from income.
1.4 A diagram of the CRISP-DM process that shows the six key phases and indicates the important relationships between them. This figure is based on Figure 2 of Wirth and Hipp (2000).
2.1 The different data sources typically combined to create an analytics base table.
2.2 The hierarchical relationship between an analytics solution, domain concepts, and descriptive features.
2.3 Example domain concepts for a motor insurance fraud prediction analytics solution.
2.4 Sample descriptive feature data illustrating numeric, binary, ordinal, interval, categorical, and textual types.
2.5 Modeling points in time using an observation period and an outcome period.
2.6 Observation and outcome periods defined by an event rather than by a fixed point in time (each line represents a prediction subject and stars signify events).
2.7 Modeling points in time for a scenario with no real outcome period (each line represents a customer, and stars signify events).
2.8 Modeling points in time for a scenario with no real observation period (each line represents a customer, and stars signify events).
2.9 A subset of the domain concepts and related features for a motor insurance fraud prediction analytics solution.
2.10 A subset of the domain concepts and related features for a motor insurance fraud prediction analytics solution.
2.11 A subset of the domain concepts and related features for a motor insurance fraud prediction analytics solution.
2.12 A summary of the tasks in the Business Understanding, Data Understanding, and Data Preparation phases of the CRISP-DM process.
3.1 Visualizations of the continuous and categorical features in the motor insurance claims fraud detection ABT in Table 3.2[58].
3.2 Histograms for six different sets of data, each of which exhibit well-known, common characteristics.
3.3 (a) Three normal distributions with different means but identical standard deviations; (b) three normal distributions with identical means but different standard deviations.
3.4 An illustration of the 68−95−99.7 rule. The gray region defines the area where 95% of values in a sample are expected.
3.5 Example scatter plots for pairs of features from the dataset in Table 3.7[78], showing (a) the strong positive covariance between HEIGHT and WEIGHT; (b) the strong negative covariance between SPONSORSHIP EARNINGS and AGE; and (c) the lack of strong covariance between HEIGHT and AGE.
3.6 A scatter plot matrix showing scatter plots of the continuous features from the professional basketball team dataset in Table 3.7[78].
3.7 Examples of using small multiple bar plot visualizations to illustrate the relationship between two categorical features: (a) the CAREER STAGE and SHOE SPONSOR features; and (b) the POSITION and SHOE SPONSOR features. All data comes from Table 3.7[78].
3.8 Examples of using stacked bar plot visualizations to illustrate the relationship between two categorical features: (a) CAREER STAGE and SHOE SPONSOR features; and (b) POSITION and SHOE SPONSOR features, all from Table 3.7[78].
3.9 Example of using small multiple histograms to visualize the relationship between a categorical feature and a continuous feature. All examples use data from the professional basketball team dataset in Table 3.7[78]: (a) a histogram of the AGE feature; (b) a histogram of the HEIGHT feature; (c) histograms of the AGE feature for instances displaying each level of the POSITION feature; and (d) histograms of the HEIGHT feature for instances displaying each level of the POSITION feature.
3.10 Using box plots to visualize the relationships between categorical and continuous features from Table 3.7[78]: (a) the relationship between the POSITION feature and the AGE feature; and (b) the relationship between the POSITION feature and the HEIGHT feature.
3.11 A scatter plot matrix showing scatter plots of the continuous features from the professional basketball team dataset in Table 3.7[78] with correlation coefficients included.
3.12 Anscombe’s quartet. For all four samples, the correlation measure returns the same value (0.816) even though the relationship between the features is very different in each case.
3.13 The effect of using different numbers of bins when using binning to convert a continuous feature into a categorical feature.
3.14 (a)–(c) Equal-frequency binning of normally distributed data with different numbers of bins; (d)–(f) the same data binned into the same number of bins using equal-width binning. The dashed lines illustrate the distribution of the original continuous feature values, and the gray boxes represent the bins.
4.1 Cards showing character faces and names for the Guess Who game.
4.2 The different question sequences that can follow in a game of Guess Who beginning with the question Does the person wear glasses?
4.3 The different question sequences that can follow in a game of Guess Who beginning with the question Is it a man?
4.4 Two decision trees (a) and (b) that are consistent with the instances in the spam dataset; (c) the path taken through the tree shown in (a) to make a prediction for the query instance SUSPICIOUS WORDS = true, UNKNOWN SENDER = true, CONTAINS IMAGES = true.
4.5 The entropy of different sets of playing cards measured in bits.
4.6 (a) A graph illustrating how the value of a binary log (the log to the base 2) of a probability changes across the range of probability values; (b) the impact of multiplying these values by −1.
4.7 How the instances in the spam dataset split when we partition using each of the different descriptive features from the spam dataset in Table 4.2[121].
4.8 The decision tree after the data has been split using ELEVATION.
4.9 The state of the decision tree after the 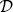 7 partition has been split using STREAM.
7 partition has been split using STREAM.
4.10 The state of the decision tree after the 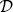 8 partition has been split using SLOPE.
8 partition has been split using SLOPE.
4.11 The final vegetation classification decision tree.
4.12 The vegetation classification decision tree generated using information gain ratio.
4.13 The vegetation classification decision tree after the dataset has been split using ELEVATION ≥ 4,175.
4.14 The decision tree that would be generated for the vegetation classification dataset listed in Table 4.9[151] using information gain.
4.15 (a) A set of instances on a continuous number line; (b), (c), and (d) depict some of the potential groupings that could be applied to these instances.
4.16 The decision tree resulting from splitting the data in Table 4.11[156] using the feature SEASON.
4.17 The final decision tree induced from the dataset in Table 4.11[156]. To illustrate how the tree generates predictions, this tree lists the instances that ended up at each leaf node and the prediction (PRED.) made by each leaf node.
4.18 The decision tree for the post-operative patient routing task.
4.19 The iterations of reduced error pruning for the decision tree in Figure 4.18[161] using the validation set in Table 4.13[161]. The subtree that is being considered for pruning in each iteration is highlighted in black. The prediction returned by each non-leaf node is listed in square brackets. The error rate for each node is given in round brackets.
4.20 The process of creating a model ensemble using bagging and subspace sampling.
5.1 A feature space plot of the college athlete data in Table 5.2[182].
5.2 (a) A generalized illustration of the Manhattan and Euclidean distances between two points; (b) a plot of the Manhattan and Euclidean distances between instances d12 and d5 and between d12 and d17 from Table 5.2[182].
5.3 A feature space plot of the data in Table 5.2[182], with the position in the feature space of the query represented by the ? marker.
5.4 (a) The Voronoi tessellation of the feature space for the dataset in Table 5.2[182] with the position of the query represented by the ? marker; (b) the decision boundary created by aggregating the neighboring Voronoi regions that belong to the same target level.
5.5 (a) The Voronoi tessellation of the feature space when the dataset has been updated to include the query instance; (b) the updated decision boundary reflecting the addition of the query instance in the training set.
5.6 The decision boundary using majority vote of the nearest 3 and 5 instances.
5.7 (a) The decision boundary using majority vote of the nearest 15 neighbors; (b) the weighted k nearest neighbor model decision boundary (with k = 21).
5.8 (a) The k-d tree generated for the dataset in Table 5.4[190] after the initial split using the SPEED feature with a threshold of 4.5; (b) the partitioning of the feature space by the k-d tree in (a); (c) the k-d tree after the dataset at the left child of the root has been split using the AGILITY feature with a threshold of 5.5; and (d) the partitioning of the feature space by the k-d tree in (c).
5.9 (a) The final k-d tree generated for the dataset in Table 5.4[190]; (b) the partitioning of the feature space defined by this k-d tree.
5.10 (a) The path taken from the root node to a leaf node when we search the tree with a query SPEED = 6.00, AGILITY = 3.50; (b) the ? marks the location of the query, the dashed circle plots the extent of the target, and for convenience in the discussion, we have labeled some of the nodes with the IDs of the instances they index (12, 15, 18, and 21).
5.11 (a) The target hypersphere after instance d21 has been stored as best, and best-distance has been updated; (b) the extent of the search process: white nodes were checked by the search process, and the node with the bold outline indexed instance d21, which was returned as the nearest neighbor to the query. Grayed-out branches indicate the portions of the k-d tree pruned from the search.
5.12 (a) The feature space defined by the SALARY and AGE features in Table 5.5[204]; (b) the normalized SALARY and AGE feature space based on the normalized data in Table 5.7[208]. The instances are labeled with their IDs; triangles represent instances with the no target level; and crosses represent instances with the yes target level. The location of the query SALARY = 56,000, AGE = 35 is indicated by the ?.
5.13 The AGE and RATING feature space for the whiskey dataset. The location of the query instance is indicated by the ? symbol. The circle plotted with a dashed line demarcates the border of the neighborhood around the query when k = 3. The three nearest neighbors to the query are labeled with their ID values.
5.14 (a) The θ represents the inner angle between the vector emanating from the origin to instance d1 and the vector emanating from the origin to instance d2; (b) shows d1 and d2 normalized to the unit circle.
5.15 Scatter plots of three bivariate datasets with the same center point A and two queries B and C both equidistant from A; (a) a dataset uniformly spread around the center point; (b) a dataset with negative covariance; and (c) a dataset with positive covariance.
5.16 The coordinate systems defined by the Mahalanobis distance using the co-variance matrix for the dataset in Figure 5.15(c)[221] using three different origins: (a) (50, 50), (b) (63, 71), (c) (42, 35). The ellipses in each figure plot the 1, 3, and 5 unit distance contours.
5.17 The effect of using a Mahalanobis versus Euclidean distance. A marks the central tendency of the dataset in Figure 5.15(c)[221]. The ellipses plot the Mahalanobis distance contours from A that B and C lie on. In Euclidean terms, B and C are equidistant from A; however, using the Mahalanobis distance, C is much closer to A than B.
5.18 A set of scatter plots illustrating the curse of dimensionality. Across (a), (b), and (c), the number of instances remains the same, so the density of the marked unit hypercubes decreases as the number of dimensions increases; (d) and (e) illustrate the cost we must incur, in terms of the number of extra instances required, if we wish to maintain the density of the instances in the feature space as its dimensionality increases.
5.19 Feature subset space for a dataset with three features X, Y, and Z.
5.20 The process of model induction with feature selection.
5.21 A duck-billed platypus. This platypus image was created by Jan Gillbank, English for the Australian Curriculum website (www.e4ac.edu.au). Used under Creative Commons Attribution 3.0 license.
6.1 A game of find the lady: (a) the cards used; (b) the cards dealt face down on a table; (c) the initial likelihoods of the queen ending up in each position; (d) a revised set of likelihoods for the position of the queen based on evidence collected.
6.2 (a) The set of cards after the wind blows over the one on the right; (b) the revised likelihoods for the position of the queen based on this new evidence; (c) the final positions of the cards in the game.
6.3 Plots of some well-known probability distributions.
6.4 Histograms of two unimodal datasets: (a) the distribution has light tails; (b) the distribution has fat tails.
6.5 Illustration of the robustness of the student-t distribution to outliers: (a) a density histogram of a unimodal dataset overlaid with the density curves of a normal and a student-t distribution that have been fitted to the data; (b) a density histogram of the same dataset with outliers added, overlaid with the density curves of a normal and a student-t distribution that have been fitted to the data. (This figure is inspired by Figure 2.16 in Bishop (2006).)
6.6 Illustration of how a mixture of Gaussians model is composed of a number of normal distributions. The curve plotted using a solid line is the mixture of Gaussians density curve, created using an appropriately weighted summation of the three normal curves, plotted using dashed and dotted lines.
6.7 (a) The area under a density curve between the limits  and
and  ; (b) the approximation of this area computed by PDF(x) × ε; and (c) the error in the approximation is equal to the difference between area A, the area under the curve omitted from the approximation, and area B, the area above the curve erroneously included in the approximation. Both of these areas will get smaller as the width of the interval gets smaller, resulting in a smaller error in the approximation.
; (b) the approximation of this area computed by PDF(x) × ε; and (c) the error in the approximation is equal to the difference between area A, the area under the curve omitted from the approximation, and area B, the area above the curve erroneously included in the approximation. Both of these areas will get smaller as the width of the interval gets smaller, resulting in a smaller error in the approximation.
6.8 Histograms, using a bin size of 250 units, and density curves for the ACCOUNT BALANCE feature: (a) the fraudulent instances overlaid with a fitted exponential distribution; (b) the non-fraudulent instances overlaid with a fitted normal distribution.
6.9 (a) A Bayesian network for a domain consisting of two binary features. The structure of the network states that the value of feature A directly influences the value of feature B. (b) A Bayesian network consisting of 4 binary features with a path containing 3 generations of nodes: D, C, and B.
6.10 A depiction of the Markov blanket of a node. The gray nodes define the Markov blanket of the black node. The black node is conditionally independent of the white nodes given the state of the gray nodes.
6.11 (a) A Bayesian network representation of the conditional independence asserted by a naive Bayes model between the descriptive features given knowledge of the target feature; (b) a Bayesian network representation of the conditional independence assumption for the naive Bayes model in the fraud example.
6.12 Two different Bayesian networks, each defining the same full joint probability distribution.
6.13 A Bayesian network that encodes the causal relationships between the features in the corruption domain. The CPT entries have been calculated using the binned data from Table 6.18[305].
7.1 (a) A scatter plot of the SIZE and RENTAL PRICE features from the office rentals dataset; (b) the scatter plot from (a) with a linear model relating RENTAL PRICE to SIZE overlaid.
7.2 (a) A scatter plot of the SIZE and RENTAL PRICE features from the office rentals dataset. A collection of possible simple linear regression models capturing the relationship between these two features are also shown. For all models w [0] is set to 6.47. From top to bottom, the models use 0.4, 0.5, 0.62, 0.7, and 0.8 respectively for w [1]. (b) A scatter plot of the SIZE and RENTAL PRICE features from the office rentals dataset showing a candidate prediction model (with w [0] = 6.47 and w [1] = 0.62) and the resulting errors.
7.3 (a) A 3D surface plot and (b) a bird’s-eye view contour plot of the error surface generated by plotting the sum of squared errors for the office rentals training set for each possible combination of values for w [0] (from the range [−10, 20]) and w [1] (from the range [−2, 3]).
7.4 (a) A 3D plot of an error surface and (b) a bird’s-eye view contour plot of the same error surface. The lines indicate the path that the gradient descent algorithm would take across this error surface from 4 different starting positions to the global minimum—marked as the white dot in the center.
7.5 (a) A 3D surface plot and (b) a bird’s-eye view contour plot of the error surface for the office rentals dataset showing the path that the gradient descent algorithm takes toward the best-fit model.
7.6 A selection of the simple linear regression models developed during the gradient descent process for the office rentals dataset. The bottom-right panel shows the sums of squared errors generated during the gradient descent process.
7.7 Plots of the journeys made across the error surface for the simple office rentals prediction problem for different learning rates: (a) a very small learning rate (0.002); (b) a medium learning rate (0.08); and (c) a very large learning rate (0.18). The changing sum of squared errors for these journeys are also shown.
7.8 (a) The journey across the error surface for the office rentals prediction problem when learning rate decay is used (α0 = 0.18, c = 10 ); (b) a plot of the changing sum of squared errors during this journey.
7.9 (a) The journey across the error surface for the office rentals prediction problem when learning rate decay is used (α0 = 0.25, c = 100); (b) a plot of the changing sum of squared errors during this journey.
7.10 (a) A scatter plot of the RPM and VIBRATION descriptive features from the generators dataset shown in Table 7.6[354], where good generators are shown as crosses, and faulty generators are shown as triangles; (b) as decision boundary separating good generators (crosses) from faulty generators (triangles).
7.11 (a) A surface showing the value of Equation (7.23)[354] for all values of RPM and VIBRATION, with the decision boundary given in Equation (7.23)[354] highlighted; (b) the same surface linearly thresholded at zero to operate as a predictor.
7.12 (a) A plot of the logistic function (Equation (7.25)[357]) for the range of values [−10, 10]; (b) the logistic decision surface that results from training a model to represent the generators dataset given in Table 7.6[354] (note that the data has been normalized to the range [−1, 1]).
7.13 A selection of the logistic regression models developed during the gradient descent process for the machinery dataset from Table 7.6[354]. The bottom-right panel shows the sums of squared errors generated during the gradient descent process.
7.14 A scatter plot of the extended generators dataset given in Table 7.7[362], which results in instances with the different target levels overlapping with each other. Instances representing good generators are shown as crosses, and those representing faulty generators as triangles.
7.15 A selection of the logistic regression models developed during the gradient descent process for the extended generators dataset in Table 7.7[362]. The bottom-right panel shows the sums of squared errors generated during the gradient descent process.
7.16 (a) A scatter plot of the RAIN and GROWTH feature from the grass growth dataset; (b) the same plot with a simple linear regression model trained to capture the relationship between the grass growth and rainfall.
7.17 A selection of the models developed during the gradient descent process for the grass growth dataset from Table 7.9[367].
7.18 A scatter plot of the P20 and P45 features from the EEG dataset. Instances representing positive images are shown as crosses, and those representing negative images as triangles.
7.19 A selection of the models developed during the gradient descent process for the EEG dataset from Table 7.10[370]. The final panel shows the decision surface generated.
7.20 An illustration of three different one-versus-all prediction models for the customer type dataset in Table 7.11[374], with three target levels: single (squares), business (triangles), and family (crosses).
7.21 A selection of the models developed during the gradient descent process for the customer group dataset from Table 7.11[374]. Squares represent instances with the single target level, triangles the business level, and crosses the family level. The bottom-right panel illustrates the overall decision boundaries between the three target levels.
7.22 A small sample of the generators dataset with two features, RPM and VIBRATION, and two target levels, good (shown as crosses) and faulty (shown as triangles): (a) a decision boundary with a very small margin; (b) a decision boundary with a much larger margin. In both cases, the instances along the margins are highlighted.
7.23 Different margins that satisfy the constraint in Equation (7.44)[379], the instances that define the margin are highlighted in each case; (b) shows the maximum margin and also shows two query instances represented as black dots.
7.24 The journey across an error surface and the changing sums of squared errors during this journey.
8.1 The process of building and evaluating a model using a hold-out test set.
8.2 Hold-out sampling can divide the full data into training, validation, and test sets.
8.3 Using a validation set to avoid overfitting in iterative machine learning algorithms.
8.4 The division of data during the k-fold cross validation process. Black rectangles indicate test data, and white spaces indicate training data.
8.5 The division of data during the leave-one-out cross validation process. Black rectangles indicate instances in the test set, and white spaces indicate training data.
8.6 The division of data during the 0 bootstrap process. Black rectangles indicate test data, and white spaces indicate training data.
8.7 The out-of-time sampling process.
8.8 Surfaces generated by calculating (a) the arithmetic mean and (b) the harmonic mean of all combinations of features A and B that range from 0 to 100.
8.9 Prediction score distributions for two different prediction models. The distributions in (a) are much better separated than those in (b).
8.10 Prediction score distributions for the (a) spam and (b) ham target levels based on the data in Table 8.11[424].
8.11 (a) The changing values of TPR and TNR for the test data shown in Table 8.13[427] as the threshold is altered; (b) points in ROC space for thresholds of 0.25, 0.5, and 0.75.
8.12 (a) A complete ROC curve for the email classification example; (b) a selection of ROC curves for different models trained on the same prediction task.
8.13 The K-S chart for the email classification predictions shown in Table 8.11[424].
8.14 A series of charts for different model performance on the same large email classification test set used to generate the ROC curves in Figure 8.12(b)[429]. Each column from top to bottom: a histogram of the ham scores predicted by the model, a histogram of the spam scores predicted by the model, and the K-S chart.
8.15 The (a) gain and (b) cumulative gain at each decile for the email predictions given in Table 8.11[424].
8.16 The (a) lift and (b) cumulative lift at each decile for the email predictions given in Table 8.11[424].
8.17 Cumulative gain, lift, and cumulative lift charts for four different models for the extended email classification test set.
8.18 The distributions of predictions made by a model trained for the bacterial species identification problem for (a) the original evaluation test set and for (b) and (c) two periods of time after model deployment; (d) shows how the stability index should be tracked over time to monitor for concept drift.
9.1 The set of domain concepts for the Acme Telephonica customer churn prediction problem.
9.2 (a)–(c) Histograms for the features from the AT ABT with irregular cardinality; (d)–(g) histograms for the features from the AT ABT that are potentially suffering from outliers.
9.3 (a) A stacked bar plot for the REGIONTYPE feature; (b) histograms for the AVGOVERBUNDLEMINS feature by target feature value.
9.4 An unpruned decision tree built for the AT churn prediction problem (shown only to indicate its size and complexity). The excessive complexity and depth of the tree are evidence that overfitting has probably occurred.
9.5 A pruned decision tree built for the AT churn prediction problem. Gray leaf nodes indicate a churn prediction, while clear leaf nodes indicate a non-churn prediction. For space reasons, we show only the features tested at the top level nodes.
9.6 (a) Cumulative gain, (b) lift, and (c) cumulative lift charts for the predictions made on the large test data sample.
9.7 A pruned and stunted decision tree built for the Acme Telephonica churn prediction problem.
10.1 Examples of the different galaxy morphology categories into which SDSS scientists categorize galaxy objects. Credits for these images belong to the Sloan Digital Sky Survey, www.sdss3.org.
10.2 The first draft of the domain concepts diagram developed by Jocelyn for the galaxy classification task.
10.3 Bar plots of the different galaxy types present in the full SDSS dataset for the 3-level and 5-level target features.
10.4 The revised domain concepts diagram for the galaxy classification task.
10.5 SPLOM diagrams of (a) the EXPRAD and (b) DEVRAD measurements from the raw SDSS dataset. Each SPLOM shows the measure across the five different photometric bands captured by the SDSS telescope (u, g, r, i, and z).
10.6 Histograms of a selection of features from the SDSS dataset.
10.7 Histograms of the EXPRAD_R feature by target feature level.
10.8 Small multiple box plots (split by the target feature) of some of the features from the SDSS ABT.
11.1 (a) The class conditional densities for two classes (l1,l2) with a single descriptive feature d. The height of each curve reflects the density of the instances from that class for that value of d. (b) The class posterior probabilities plotted for each class for different values of d. Notice that the class posterior probability P(t = l1|d) is not affected by the multimodal structure of the corresponding class conditional density P(d|t = l1). This illustrates how the class posterior probabilities can be simpler than the class conditional densities. The solid vertical line in (b) plots the decision boundary for d that gives the minimum misclassification rate assuming uniform prior for the two target levels (i.e., P(t = l1) = P(t = l2)). This figure is based on Figure 1.27 from Bishop (2006).
11.2 An illustration of the decision boundaries learned by different machine learning algorithms for three artificial datasets.
A.1 The members of a school basketball team. The height of each player is listed below the player. The dashed gray line shows the arithmetic mean of the players’ heights.
A.2 The members of the school basketball team from Figure A.1[526] with one very tall ringer added: (a) the dashed gray line shows the mean of the players’ heights; (b) the dashed gray line shows the median of the players’ heights, with the players ordered by height.
A.3 The members of a rival school basketball team. Player heights are listed below each player. The dashed gray line shows the arithmetic mean of the players’ heights.
A.4 The members of the rival school basketball team from Figure A.3[527] ordered by height.
A.5 Example bar plots for the POSITION feature in Table A.1[531]: (a) frequency bar plot, (b) density bar plot, and (c) order density bar plot.
A.6 Bar plot of the continuous TRAINING EXPENSES feature from Table A.1[531].
A.7 (a) and (b) frequency histograms and (c) and (d) density histograms for the continuous TRAINING EXPENSES feature from Table A.1[531], illustrating how using intervals overcomes the problem seen in Figure A.6[535] and the effect of varying interval sizes.
A.8 (a) The structure of a box plot; (b) a box plot for the TRAINING EXPENSES feature from the basketball team dataset in Table A.1[531].
B.1 The sample space for the domain of two dice.
C.1 (a) The speed of a car during a journey along a minor road before joining a highway and finally coming to a sudden halt; (b) the acceleration, the derivative of speed with respect to time, for this journey.
C.2 Examples of continuous functions (shown as solid lines) and their derivatives (shown as dashed lines).
C.3 (a) A continuous function in two variables, x and y; (b) the partial derivative of this function with respect to x; and (c) the partial derivative of this function with respect to y.
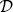 7 partition has been split using STREAM.
7 partition has been split using STREAM.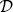 8 partition has been split using SLOPE.
8 partition has been split using SLOPE. and
and  ; (b) the approximation of this area computed by PDF(x) × ε; and (c) the error in the approximation is equal to the difference between area A, the area under the curve omitted from the approximation, and area B, the area above the curve erroneously included in the approximation. Both of these areas will get smaller as the width of the interval gets smaller, resulting in a smaller error in the approximation.
; (b) the approximation of this area computed by PDF(x) × ε; and (c) the error in the approximation is equal to the difference between area A, the area under the curve omitted from the approximation, and area B, the area above the curve erroneously included in the approximation. Both of these areas will get smaller as the width of the interval gets smaller, resulting in a smaller error in the approximation.