Notation

In this section we provide a short overview of the technical notation used throughout this book.

Notational Conventions

Throughout this book we discuss the use of machine learning algorithms to train prediction models based on datasets. The following list explains the notation used to refer to different elements in a dataset. Figure 1^[xix] illustrates the key notation using a simple sample dataset.

Figure 1

How the notation used in the book relates to the elements of a dataset.

Datasets

• The symbol 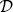denotes a dataset.
• A dataset is composed of n instances, (d₁, t₁) to (d_n, t_n), where d is a set of m descriptive features and t is a target feature.
• A subset of a dataset is denoted using the symbol 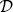with a subscript to indicate the definition of the subset. For example, 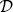_f=l represents the subset of instances from the dataset 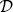where the feature f has the value l.

Vectors of Features

• Lowercase boldface letters refer to a vector of features. For example, d denotes a vector of descriptive features for an instance in a dataset, and q denotes a vector of descriptive features in a query.

Instances

• Subscripts are used to index into a list of instances.
• x_i refers to the i^th instance in a dataset.
• d_i refers to the descriptive features of the i^th instance in a dataset.

Individual Features

• Lowercase letters represent a single feature (e.g., f, a, b, c …).
• Square brackets [] are used to index into a vector of features (e.g., d [j] denotes the value of the j^th feature in the vector d).
• t represents the target feature.

Individual Features in a Particular Instance

• d_i [j] denotes the value of the j^th descriptive feature of the i^th instance in a dataset.
• a_i refers to the value for feature a of the i^th instance in a dataset.
• t_i refers to the value of the target feature of the i^th instance in a dataset

Indexes

• Typically i is used to index instances in a dataset, and j is used to index features in a vector.

Models

• We use to refer to a model.
• _w refers to a model parameterized by a parameter vector w.
• _w(d) refers to the output of a model parameterized by parameters w for descriptive features d.

Set Size

• Vertical bars | | refer to counts of occurrences (e.g., |a = l| represents the number of times that a = l occurs in a dataset).

Feature Names and Feature Values

• We use a specific typography when referring to a feature by name in the text (e.g., POSITION, CREDITRATING, and CLAIM AMOUNT).
• For categorical features, we use a specific typography to indicate the levels in the domain of the feature when referring to a feature by name in the text (e.g., center, aa, and soft tissue).

Notational Conventions for Probabilities

For clarity there are some extra notational conventions used in Chapter 6^[247] on probability.

Generic Events

• Uppercase letters denote generic events where an unspecified feature (or set of features) is assigned a value (or set of values). Typically we use letters from the end of the alphabet—e.g., X, Y, Z—for this purpose.
• We use subscripts on uppercase letters to iterate over events. So, Σ_i P(X_i) should be interpreted as summing over the set of events that are a complete assignment to the features in X (i.e., all the possible combinations of value assignments to the features in X).

Named Features

• Features explicitly named in the text are denoted by the uppercase initial letters of their names. For example, a feature named MENINGITIS is denoted by M.

Events Involving Binary Features

• Where a named feature is binary, we use the lowercase initial letter of the name of the feature to denote the event where the feature is true and the lowercase initial letter preceded by the ¬ symbol to denote the event where it is false. So, m will represent the event MENINGITIS = true, and ¬m will denote MENINGITIS = false.

Events Involving Non-Binary Features

• We use lowercase letters with subscripts to iterate across values in the domain of a feature.
• So Σ_i P(m_i) = P(m) + P(¬m).
• In situations where a letter, for example X, denotes a joint event, then Σ_i P(X_i) should be interpreted as summing over all the possible combinations of value assignments to the features in X.

Probability of an Event

• The probability that the feature f is equal to the value v is written P(f = v).

Probability Distributions

• We use bold notation P() to distinguish a probability distribution from a probability mass function P().
• We use the convention that the first element in a probability distribution vector is the probability for a true value. For example, the probability distribution for a binary feature, A, with a probability of 0.4 of being true would be written as P(A) =< 0.4, 0.6 >.