11 The Art of Machine Learning for Predictive Data Analytics

It is a capital mistake to theorize before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts.—Sherlock Holmes

Predictive data analytics projects use machine learning to build models that capture the relationships in large datasets between descriptive features and a target feature. A specific type of learning, called inductive learning, is used, where learning entails inducing a general rule from a set of specific instances. This observation is important because it highlights that machine learning has the same properties as inductive learning. One of these properties is that a model learned by induction is not guaranteed to be correct. In other words, the general rule that is induced from a sample may not be true for all instances in a population.

Another important property of inductive learning is that learning cannot occur unless the learning process is biased in some way. This means that we need to tell the learning process what types of patterns to look for in the data. This bias is referred to as inductive bias. The inductive bias of a learning algorithm comprises the set of assumptions that define the search space the algorithm explores and the search process it uses.

On top of the inductive bias encoded in a machine learning algorithm, we also bias the outcome of a predictive data analytics project in lots of other ways. Consider the following questions:

What is the predictive analytics target? What descriptive features will we include/exclude? How will we handle missing values? How will we normalize our features? How will we represent continuous features? What types of models will we create? How will we set the parameters of the learning algorithms? What evaluation process will we follow? What performance measures will we use?

These questions are relevant when building any prediction model, and the answer to each one introduces a specific bias. Often we are forced to answer these questions, and others like them, based on intuition, experience, and experimentation. This is what makes machine learning something of an art, rather than strictly a science. But it is also what makes machine learning such a fascinating and rewarding area to work in.

En masse all the questions that must be answered to successfully complete a predictive data analytics project can seem overwhelming. This is why we recommend using the CRISP-DM process to manage a project through its lifecycle. Table 11.1[512] shows the alignment between the phases of CRISP-DM, some of the key questions that must be answered during a predictive data analytics project, and the chapters in this book dealing with these questions.

Table 11.1

The alignment between the phases of CRISP-DM, key questions for analytics projects, and the chapters and sections of this book.

CRISP-DM Open Questions Chapter
Business Understanding What is the organizational problem being addressed? In what ways could a prediction model address the organizational problem? Do we have situational fluency? What is the capacity of the organization to utilize the output of a prediction model? What data is available? Chapter 2[21]
Data Understanding What is the prediction subject? What are the domain concepts? What is the target feature? What descriptive features will be used? Chapter 2[21]
Data Preparation Are there data quality issues? How will we handle missing values? How will we normalize our features? What features will we include? Chapter 3[55]
Modeling What types of models will we use? How will we set the parameters of the machine learning algorithms? Have underfitting or overfitting occurred? Chapters 4[117], 5[179], 6[247] and 7[323]
Evaluation What evaluation process will we follow? What performance measures will we use? Is the model fit for purpose? Chapter 8[397]
Deployment How will we continue to evaluate the model after deployment? How will the model be integrated into the organization? 8.4.6[447] and Chapters 9[463] and 10[483]

Remember, an analytics project is often iterative, with different stages of the project feeding back into later cycles. It is also important to remember that the purpose of an analytics project is to solve a real-world problem and to keep focus on this rather than being distracted by the, admittedly sometimes fascinating, technical challenges of model building. We strongly believe that the best way to keep an analytics project focused, and to improve the likelihood of a successful conclusion, is to adopt a structured project lifecycle, such as CRISP-DM, and we recommend its use.

11.1 Different Perspectives on Prediction Models

A key step in any predictive analytics project is deciding which type of predictive analytics model to use. In this book we have presented some of the most commonly used prediction models and the machine learning algorithms used to build them. We have structured this presentation around four approaches to learning: information-based, similarity-based, probability-based, and error-based. The mathematical foundation of these approaches can be described using four simple (but important) equations: Claude Shannon’s model of entropy (Equation (11.1)[513]), Euclidean distance (Equation (11.2)[513]), Bayes’ Theorem (Equation (11.3)[513]), and the sum of squared errors (Equation (11.4)[513]).

art

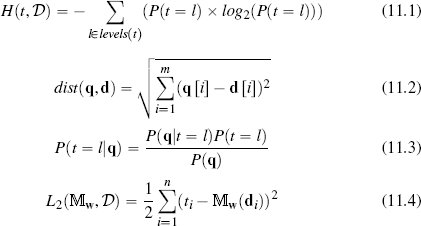
An understanding of these four equations is a strong basis for understanding the mathematical fundamentals of many areas of scientific modeling. Adding an understanding of how these four equations are used in the machine learning algorithms we have described (ID3, k nearest neighbor, multivariable linear regression with gradient descent, and naive Bayes) is a strong foundation on which to build a career in predictive data analytics.

The taxonomy we have used to distinguish between different machine learning algorithms is based on human approaches to learning that the algorithms can be said to emulate. This is not the only set of distinctions that can be made between the algorithms and the resulting models. It is useful to understand some of the other commonly used distinctions, because this understanding can provide insight into which learning algorithm and related model is most appropriate for a given scenario.

The first distinction between models that we will discuss is the distinction between parametric and non-parametric models. This distinction is not absolute, but it generally describes whether the size of the domain representation used to define a model is solely determined by the number of features in the domain or is affected by the number of instances in the dataset. In a parametric model the size of the domain representation (i.e., the number of parameters) is independent of the number of instances in the dataset. Examples of parametric models include the naive Bayes and Bayesian network models in Chapter 6[247] and the simple linear and logistic regression models in Chapter 7[323]. For example, the number of factors required by a naive Bayes model is only dependent on the number of features in the domain and is independent of the number of instances. Likewise, the number of weights used in a linear regression model is defined by the number of descriptive features and is independent of the number of instances in the training data.

In a non-parametric model the number of parameters used by the model increases as the number of instances increases. Nearest neighbor models are an obvious example of a non-parametric model. As new instances are added to the feature space, the size of the model’s representation of the domain increases. Decision trees are also considered non-parametric models. The reason for this is that when we train a decision tree from data, we do not assume a fixed set of parameters prior to training that define the tree. Instead, the tree branching and the depth of the tree are related to the complexity of the dataset it is trained on. If new instances were added to the dataset and we rebuilt the tree, it is likely that we would end up with a (potentially very) different tree. Support vector machines are also non-parametric models. They retain some instances from the dataset—potentially all of them, although in practice, relatively few—as part of the domain representation. Hence, the size of the domain representation used by a support vector machine may change as instances are added to the dataset.

In general, parametric models make stronger assumptions about the underlying distributions of the data in a domain. A linear regression model, for example, assumes that the relationship between the descriptive features and the target is linear (this is a strong assumption about the distribution in the domain). Non-parametric models are more flexible but can struggle with large datasets. For example, a 1-NN model has the flexibility to model a discontinuous decision surface; however, it runs into time and space complexity issues as the number of instances grows.

When datasets are small, a parametric model may perform well because the strong assumptions made by the model—if correct—can help the model to avoid overfitting. However, as the size of the dataset grows, particularly if the decision boundary between the classes is very complex, it may make more sense to allow the data to inform the predictions more directly. Obviously the computational costs associated with non-parametric models and large datasets cannot be ignored. However, support vector machines are an example of a nonparametric model that, to a large extent, avoids this problem. As such, support vector machines are often a good choice in complex domains with lots of data.

The other important distinction that is often made between classification models is whether they are generative or discriminative. A model is generative if it can be used to generate data that will have the same characteristics as the dataset from which the model was produced. In order to do this, a generative model must learn, or encode, the distribution of the data belonging to each class. The Bayesian network models described in Chapter 6[247] are examples of generative models.1 Indeed, Markov chain Monte Carlo methods for estimating probabilities are based on the fact that we can run these models to generate data that approximate the distributions of the dataset from which the model was induced. Because they explicitly model the distribution of the data for each class k nearest neighbor models are also generative models.

In contrast, discriminative models learn the boundary between classes rather than the characteristics of the distributions of the different classes. Support vector machines and the other classification models described in Chapter 7[323] are examples of discriminative prediction models. In some cases they learn a hard boundary between the classes; in other cases—such as logistic regression—they learn a soft boundary, which takes into account the distance from the boundary. However, all these models learn a boundary. Decision trees are also discriminative models. Decision trees are induced by recursively partitioning the feature space into regions belonging to the different classes, and consequently they define a decision boundary by aggregating the neighboring regions belonging to the same class. Decision tree model ensembles based on bagging and boosting are also discriminative models.

This generative versus discriminative distinction is more than just a labeling exercise. Generative and discriminative models learn different concepts. In probabilistic terms, using d to represent the vector of descriptive feature values and tl to represent a target level, a generative model works by

  1. learning the class conditional densities (i.e., the distribution of the data for each target level) P(d|tl) and the class priors P(tl);
  2. then using Bayes’ Theorem to compute the class posterior probabilities P(tl|d);2
  3. and then applying a decision rule over the class posteriors to return a target level.

By contrast, a discriminative model works by

  1. learning the class posterior probability P(tl|d) directly from the data,
  2. and then applying a decision rule over the class posteriors to return a target level.

This distinction between what generative and discriminative models try to learn is important because the class conditional densities, P(d|tl), can be very complex compared to the class posteriors, P(tl|d) (see Figure 11.1[517]). Consequently, generative models try to learn more complex solutions to the prediction problem than discriminative models.

The potential difficulty in learning the class conditional densities, relative to the posterior class probabilities, is exacerbated in situations where we have a lot of descriptive features because, as the dimensionality of d increases, we will need more and more data to create good estimates for P(tl|d). So, in complex domains, discriminative models are likely to be more accurate. However, as is so often the case in machine learning, this is not the end of the generative versus discriminative debate. Generative models tend to have a higher bias—they make more assumptions about the form of the distribution they are learning. For example, as we discussed in Chapter 6[247] on probability, generative models encode independence assumptions about the descriptive features in d. This may sound like another problem for generative models. However, in domains where we have good prior knowledge of the independence relationships between features, we can encode this prior structural information into a generative model. This structural information can bias the model in such as way as to help it avoid overfitting the data. As a result, a generative model may outperform a discriminative model when trained on a small dataset with good prior knowledge. Conversely, however, as the amount of training data increases. the bias imposed on a generative model can become larger than the error of the trained model. Once this tipping point in dataset size has been surpassed, a discriminative model will out perform a generative model.

art

Figure 11.1

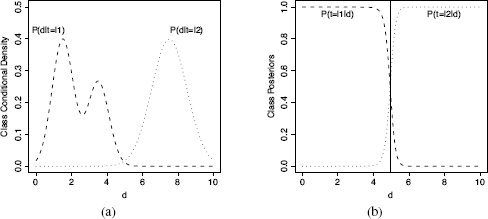
(a) The class conditional densities for two classes (l1,l2) with a single descriptive feature d. The height of each curve reflects the density of the instances from that class for that value of d. (b) The class posterior probabilities plotted for each class for different values of d. Notice that the class posterior probability P(t = l1|d) is not affected by the multimodal structure of the corresponding class conditional density P(d|t = l1). This illustrates how the class posterior probabilities can be simpler than the class conditional densities. The solid vertical line in (b) plots the decision boundary for d that gives the minimum misclassification rate assuming uniform prior for the two target levels (i.e., P(t = l1) = P(t = l2)). This figure is based on Figure 1.27 from Bishop (2006).

The debate regarding the advantages and disadvantages of generative and discriminative models can be extended beyond model accuracy to include their ability to handle missing data, unlabeled data, and feature preprocessing, among other topics. We will not discuss these topics here. Instead we will simply note that the appropriate choice of generative versus discriminative model is context-dependent, and evaluating a range of different types of models is the safest option. Table 11.2[518] summarizes the different perspectives on the model types that we have presented in this book.

Table 11.2

A taxonomy of models based on the parametric versus non-parametric and generative versus discriminative distinctions.

Model Parametric/Non-Parametric Generative/Discriminative
k Nearest Neighbor Non-Parametric Generative
Decision Trees Non-Parametric Discriminative
Bagging/Boosting Parametric* Discriminative
Naive Bayes Parametric Generative
Bayesian Network Parametric Generative
Linear Regression Parametric Discriminative
Logistic Regression Parametric Discriminative
SVM Non-Parametric Discriminative

*Although the individual models in an ensemble could be non-parametric (for example, when decision trees are used), the ensemble model itself is considered parametric.

11.2 Choosing a Machine Learning Approach

Each of the approaches to machine learning that we have presented in this book induces distinct types of prediction models with different strengths and weaknesses. This raises the question of when to use which machine learning approach. The first thing to understand is that there is not one best approach that always outperforms the others. This is known as the No Free Lunch Theorem (Wolpert, 1996). Intuitively, this theorem makes sense because each algorithm encodes a distinct set of assumptions (i.e., the inductive bias of the learning algorithm), and a set of assumptions that are appropriate in one domain may not be appropriate in another domain.

We can see the assumptions encoded in each algorithm reflected in the distinctive characteristics of the decision boundaries that they learn for categorical prediction tasks. To illustrate these characteristics, we have created three artificial datasets and trained four different models on each of these datasets. The top row of images in Figure 11.2[520] illustrates how the three artificial datasets were created. Each of the images in the top row shows a feature space defined by two continuous descriptive features, F1 and F2, partitioned into good and bad regions by three different, artificially created decision boundaries.3 In the subsequent images, we show the decision boundaries that are learned by four different machine learning algorithms based on training datasets generated according to the decision boundaries shown in the top row. In order from top to bottom, we show decision trees (without pruning), nearest neighbor models (with k = 3 and using majority voting), naive Bayes models (using normal distributions to represent the two continuous feature values), and logistic regression models (using a simple linear model). In these images the training data instances are shown as symbols on the feature space (triangles for good and crosses for bad), the decision boundaries learned by each algorithm are represented by thick black lines, and the underlying actual decision boundaries are shown by the background shading.

These examples show two things. First, the decision boundaries learned by each algorithm are characteristic of that algorithm. For example, the decision boundaries associated with decision trees have a characteristic stepped appearance because of the way feature values are split in a decision tree, while the decision boundaries associated with k-NN models are noticeably jagged because of their local focus. The characteristic appearance of the decision boundaries is related to the representations used within the models and the inductive biases that the algorithms used to build them encode. The second thing that is apparent from the images in Figure 11.2[520] is that some of the models do a better job of representing the underlying decision boundaries than others. The decision boundary learned by the logistic regression model best matches the underlying decision boundary for the dataset in the first column, the decision tree model seems most appropriate for the dataset in the second column, and the k-NN model appears best for the dataset in the third column.

Real predictive data analytics projects use datasets that are much more complex than those shown in Figure 11.2[520]. For this reason selecting which type of model to use should be informed by the specific priorities of a project and the types of the descriptive and target features in the data. Also, in general, it is not a good idea to select just one machine learning approach at the beginning of a project and to exclusively use that. Instead, it is better to choose a number of different approaches and to run experiments to evaluate which is best for the particular project. However, this still requires the selection of a set of initial approaches. There are two questions to consider:

  1. Does a machine learning approach match the requirements of the project?
  2. Is the approach suitable for the type of prediction we want to make and the types of descriptive features we are using?

art

Figure 11.2

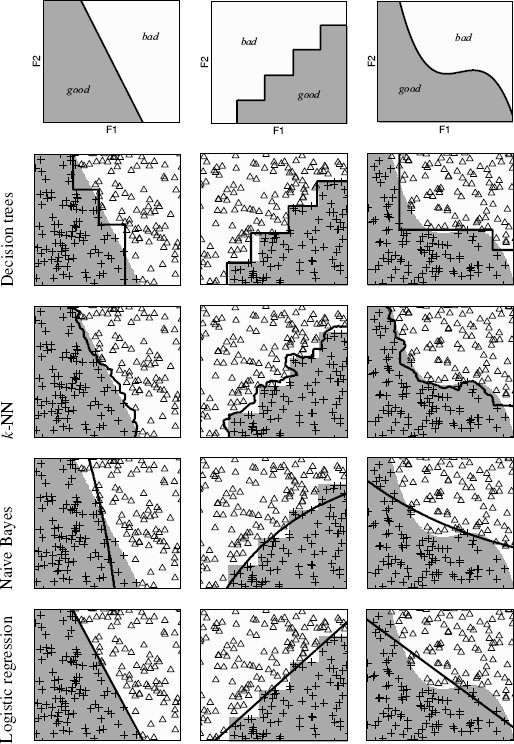
An illustration of the decision boundaries learned by different machine learning algorithms for three artificial datasets.

11.2.1 Matching Machine Learning Approaches to Projects

In many cases the primary requirement of a project is to create an accurate prediction model. Accuracy can often be related to the power of a machine learning algorithm to capture the interaction between descriptive features and the target feature. Caruana and Niculescu-Mizil (2006) and Caruana et al. (2008) report empirical evaluations of the accuracy of a range of model types across a range of domains. They found that on average, ensemble models and support vector machines were among the most accurate models. A consistent finding in both of these experiments, however, was the fact that for some domains, these more powerful models performed quite poorly, and other models, that in other domains were quite weak, achieved the best results. The main conclusions from this, and other similar studies, is that no machine learning approach is universally best, and experimentation with different approaches is the best way to ensure that an accurate model is built.

When evaluating models against a particular deployment scenario, model accuracy is not the only issue we need to consider. In order to successfully address a business problem, a model must be accurate, but it must also meet the other requirements of the business scenario. Three issues are important to consider:

In summary, ensembles, support vector machines, and Bayesian networks are, in general, more powerful machine learning approaches than the others we have presented. However, these approaches are more complex, take a longer time to train, leverage more inductive bias, and are harder to interpret than the simpler approaches that we have presented. Furthermore, the selection of a machine learning approach also depends on the aspects of an application scenario described above (speed, capacity for retraining, interpretability), and often, these factors are a bigger driver for the selection of a machine learning approach than prediction accuracy.

11.2.2 Matching Machine Learning Approaches to Data

When matching machine learning approaches to the characteristics of a dataset, it is important to remember that almost every approach can be made to work for both continuous and categorical descriptive and target features. Certain approaches, however, are a more natural fit for some kinds of data than others, so we can make some recommendations. The first thing to consider in regard to data is whether the target feature is continuous or categorical. Models trained by reducing the sum of squared errors, for example, linear regression, are the most natural fit for making predictions for continuous target features. Out of the different approaches we have considered, the information-based and probability-based approaches are least well suited in this case. If, on the other hand, the target feature is categorical, then information-based and probability-based approaches are likely to work very well. Models trained using error-based approaches can become overly complicated when the number of levels of the target feature goes above two.

If all the descriptive features in a dataset are continuous, then a similarity-based approach is a natural fit, especially when there is also a categorical target feature. Error-based models would be preferred if the target feature is also continuous. When there are many continuous features, probability-based and information-based models can become complicated, but if all the features in a dataset are categorical, then information-based and probability-based models are appropriate. Error-based models are less suitable in this case as they require categorical features to be converted into sets of binary features, which causes an increase in dimensionality. In many cases datasets will contain both categorical and continuous descriptive features. The most naturally suited learning approaches in these scenarios are probably those that are best suited for the majority feature type.

The last issue to consider in relation to data when selecting machine learning approaches is the curse of dimensionality. If there are a large number of descriptive features, then we will need a large training dataset. Feature selection is an important process in any machine learning project and should generally be applied no matter what type of models are being developed. That said, some models are more susceptible to the curse of dimensionality than others. Similarity-based approaches are particularly sensitive to the curse of dimensionality and can struggle to perform well for a dataset with large numbers of descriptive features. Decision tree models have a feature selection mechanism built into their induction algorithm and so are more robust to this issue.

11.3 Your Next Steps

In many ways, the easy part of a predictive data analytics project is building the models. The machine learning algorithms tell us how to do this. What makes predictive data analytics difficult, but also fascinating, is figuring out how to answer all the questions that surround the modeling phase of a project. Throughout the course of a predictive data analytics project, we are forced to use our intuition and experience, and experimentation, to steer the project toward the best solution. To ensure a successful project outcome, we should inform the decisions that we make by

A distinctive aspect of this book is that we have chosen to present machine learning in context. In order to do this, we have included topics that are not covered in many machine learning books, including discussions on business understanding, data exploration and preparation, and case studies. We have also provided an in-depth introduction to some of the most popular machine learning approaches with examples that illustrate how these algorithms work. We believe that this book will provide you with an understanding of the broader context and core techniques of machine learning that will enable you to have a successful career in predictive data analytics.

Machine learning is a huge topic, however, and one book can only be so long. As a result, we have had to sacrifice coverage of some aspects of machine learning in order to include other topics and worked examples. We believe that this book will give you the knowledge and skills that you will need to explore these topics yourself. To help with this, we would recommend Hastie et al. (2001), Bishop (2006), and Murphy (2012) for broad coverage of machine learning algorithms, including unsupervised and reinforcement learning approaches not covered in this book. These books are suitable as reference texts for experienced practitioners and postgraduate researchers in machine learning. Some of the other machine learning topics that you might like to explore include deep learning (Bengio, 2009; Hinton and Salakhutdinov, 2006), multi-label classification (Tsoumakas et al., 2012), and graphical models (Kollar and Friedman, 2009). Finally, we hope that you find machine learning as fascinating and rewarding a topic as we do, and we wish you the best in your future learning.

 

 

 

 

 

 

 

_______________

1 In this discussion, when we categorize models as being generative or discriminative, we are speaking in the general case. In fact, all models can be trained in either a generative or a discriminative manner. However, some models lend themselves to generative training and others to discriminative training, and it is this perspective that we use in this discussion.

2 We could also formulate the generative model as learning the joint distribution P(d, tl) directly and then computing the required posteriors from this distribution.

3 This example is partly inspired by the “machine learning classifier gallery” by Tom Fawcett at home.comcast.net/~tom.fawcett/public_html/ML-gallery/pages/