It is common in follow-up studies to be concerned with the survival time between the time of entry to the study and a subsequent event.1 The event may be death in a study of cancer, the disappearance of pain in a study comparing different steroids in arthritis, or the return of ovulation after stopping a long-acting method of contraception. These studies often generate some so-called “censored” observations of survival time. Such an observation would occur, for example, on any patient who is still alive at the time of analysis in a randomised trial where death is the end point. In this case the time from allocation to treatment to the latest follow-up visit would be the patient’s censored survival time.
The Kaplan–Meier product limit technique is the recognised approach for calculating survival curves in such studies.2,3 An outline of this method is given here. Details of how to calculate a confidence interval for the population value of the survival proportion at any time during the follow up and the median survival are given. Confidence interval calculations are also described for the difference in survival between two groups as expressed by the difference in survival proportions as well as for the hazard ratio between groups which summarises, for example, the relative death or relapse rate.
In some circumstances, the comparison between groups is adjusted for prognostic variables by means of Cox regression.3 In this case the confidence interval describing the difference between the groups is adjusted for the relevant prognostic variable.
In the survival comparisons context, confidence intervals convey only the effects of sampling variation on the precision of the estimated statistics and cannot control for any non-sampling errors such as bias in the selection of patients or in losses to follow up.
Suppose that the survival times after entry to the study (ordered by increasing duration) of a group of n subjects are tl, t2, t3,… tn. The proportion of subjects surviving beyond any follow-up time t, often referred to as S(t) but here denoted p for brevity, is estimated by the Kaplan–Meier technique as
where ri is the number of subjects alive just before time ti (the ith ordered survival time), di denotes the number who died at time ti and ∏ indicates multiplication over each time a death occurs up to and including time t.
The standard error (SE) of p is given by
where neffective is the “effective” sample size at time t. When there are no censored survival times, neffective will be equal to n the total number of subjects in the study group. When censored observations are present, the effective sample size is calculated each time a death occurs.4
The 100(1 – α)% confidence interval for the population value of the survival proportion p at time t is then calculated as
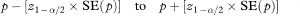
where z1–α/2 is the appropriate value from the standard Normal distribution for the 100(1 – α/2) percentile. Thus for a 95% confidence interval α = 0.05 and Table 18.1 gives Z1–α/2 – 1·96.
There are other and more complex alternatives for the calculation of the SE given here including that of Greenwood5 but, except in situations with very small numbers, these will lead to similar confidence intervals.3
The times at which to estimate survival proportions and their confidence intervals should be determined in advance of the results. They can be chosen according to practical convention— for example, the five-year survival proportions which are often quoted in cancer studies—or according to previous similar studies.
Table 9.1 Survival data by month for 49 patients with Dukes’s C colorectal cancer randomly assigned to receive either γ-linolenic acid or control treatment6
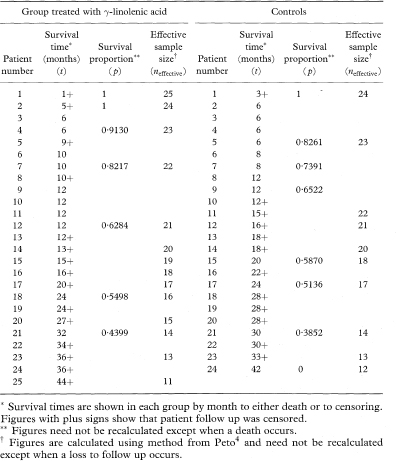
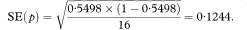
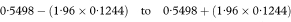
If there are no censored observations, for example, if all the patients have died on a clinical trial, then the median survival time, M, is estimated by the middle observation (see also chapter 5) of the ordered survival times t1, t2…, tn if the number of observations n is odd, and by the average of tn/2 and tn/2 + 1 if n is even. Thus
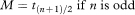
or
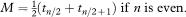
In the presence of censored survival times the median survival is estimated by first calculating the Kaplan–Meier survival curve, then finding the value of t that satisfies the equation
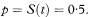
This can be done by extending a horizontal line from p = 0·5 (or 50%) on the vertical axis of the Kaplan–Meier survival curve, until the actual curve is met, then moving vertically down from that point to cut the horizontal time axis at t = M, which is the estimated median survival time.
The calculations required for the confidence interval of a median are quite complicated and an explanation of how these are derived is complex.7 The expression for the standard error of the median includes SE(p) described above but evaluated at p = S(M) = 0·5. When p = 0·5,
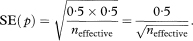
The standard error of the median is given by
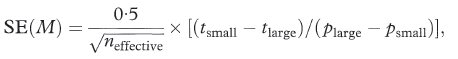
where tsmall is the smallest observed survival time from the Kaplan–Meier curve for which p is less than or equal to 0·45, while tlarge is the largest observed survival time from the Kaplan–Meier curve for which p is greater than 0·55. The ratio [(tsmall – tlarge)/(psmall – plarge)] in the above expression, estimates the height of the distribution of survival times at the median. Just as the blood pressure values of chapter 4 have a distribution, in that case taking the Normal distribution form, survival times will also have an underlying distribution of some form. The values of 0·45 and 0·55 are chosen at each side of the median of 0·5 to define “small” and “large” and are arbitrary. Should. Plarge = Psmall then the two values will need to be chosen wider apart. They may be chosen closer to 0·5 for large study sizes.
The 100(1 – α)% confidence interval for the population value of the median survival M is then calculated as
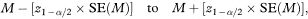
where z1– α/2 is obtained from Table 18.1.
However, we must caution against the uncritical use of this method for small data sets as the value of SE(M) is unreliable in such circumstances, and also the values of tsmall and tlarge will be poorly determined.
Figure 9.1 Kaplan–Meier estimate of the survival curve of 24 patients with Dukes’s C colorectal cancer.6
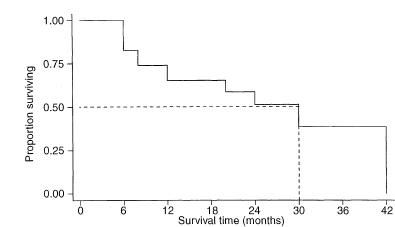
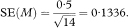
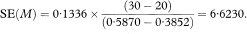
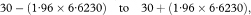
The difference between survival proportions at any time t in two study groups of sample sizes n1 and n2 is measured by p1 – p2, where p1 = S1(t) and p2 = S2(t) are the survival proportions at time t in groups 1 and 2 respectively.
The standard error of p1 – p2 is
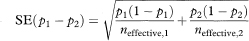
where neffective, 1 and neffective, 2 are the effective sample sizes at time t in each group.
The 100(1 – α)% confidence interval for the population value of P1 – P2 is
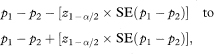
where z1–α/2 is obtained from Table 18.1.
The difference between the median survival times in two study groups of sample sizes n1 and n2 is measured by M1 – M2, where M1 and M2 are the medians in groups 1 and 2 respectively. The standard error of M1 – M2 is
The 100(1 – α)% confidence interval for the population value of M1 – M2 is
where z1–α/2 is obtained from Table 18.1.
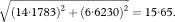
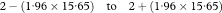
In a follow-up study of two groups the ratio of failure rates—for example, death or relapse rates—is termed the “hazard ratio”. It is a common measure of the relative effect of treatments or exposures. If O1 and O2 are the total numbers of deaths observed in the two groups then the corresponding expected numbers of deaths (E1 and E2) assuming an equal risk of dying at each time in both groups, may be calculated as
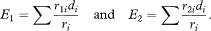
Here r1i and r2i are the numbers of subjects alive and not censored in groups 1 and 2 just before time ti with r = r1i + r2i; di = d1i + d2i is the number who died at time ti in the two groups combined; and ∑ indicates addition over each time of death.
One estimator of the hazard ratio (HR) is (Ol /El)/(O2 /E2) although, for technical reasons, the more complex estimator
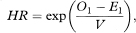
where
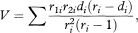
is more appropriate.
To obtain a 100(1 – α)% confidence interval for the population value of the hazard ratio one first calculates the two quantities
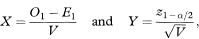
where z1–α/2 is the appropriate value from the standard Normal distribution for the 100(1 – α/2) percentile (see Table 18.1). Thus for a 95% confidence interval α = 0·05 and z1–α/2 = 1·96.
The hazard ratio can then be estimated by HR and the confidence interval for the hazard ratio by8
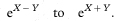
The hazard ratio calculated from (O1/E1)/(O2/E2) will be close to eX except in unusual data sets.
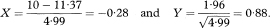
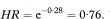
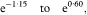
In the case when the distributions for the two groups can be assumed to be from exponential distributions., the ratio of the inverse of the two medians provides an estimate of the hazard ratio, that is, HRmedian = M2/M1. In this case, the approximate confidence interval is given as9
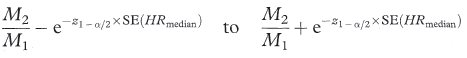
where
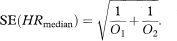
As noted earlier, O1 and O2 are the number of deaths in the respective groups.
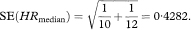
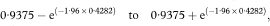
Just as in the situations described in chapter 8 in which the linear regression equation is used for predicting one variable from another, it is often important to relate the outcome measure (here survival time) to other variables. In contrast to the y variable of chapter 8, the comparable variable is time t but with the added complication that this will usually have censored values in some cases. As a consequence, and for quite technical reasons, special methods have been developed for survival time regression.10 These Cox regression models are then utilised in much the same way as the regression models of chapter 8. In the special case of a comparison between two groups of subjects, the Cox model provides essentially the same estimate of HR and the associated confidence interval as described earlier. The basic assumption is that the risk of failure (death) in one group is the same constant multiple of the other group at any point in the follow-up time.3
The Cox regression model for the comparison of two groups assumes that the risk of death in the two groups can be respectively described by
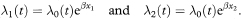
Here if β = 0 then both groups have the same underlying death rate (hazard), λ0(t), at each time t, but this rate may change over time. For comparing two groups, it is usual to write x1 = 1 and x2 = 0, in which case
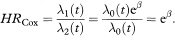
Since t does not appear in the above expression (eβ) the hazard ratio does not change with time.
The 100(1 – α)% confidence interval for the population hazard ratio is
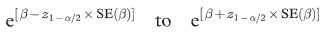
where SE(β) is obtained from a computer program.
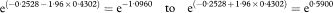
It is useful to note that the estimate of HRCox and the corresponding 95% confidence interval are similar to those given in earlier calculations. They differ somewhat from those corresponding to HRmedian for which the assumption of a constant hazard (one that does not change with t) was made within each treatment group.
In certain circumstances there may be prognostic features of individual patients which may influence their survival and thus may modify the observed difference between groups. In such cases, we wish to compare the groups taking account of (or adjusted for) these variables. This leads to extending the single variable Cox model just described (with one explanatory variable indicating the group) to include also one or more prognostic variables as one may do in other multiple regression situations (see chapter 8). In the context of randomised controlled trials., described in chapter 11., we wish to check whether or not the treatment effect observed., as expressed by the hazard ratio., will be modified after taking account of these prognostic variables.3
1 Bland JM, Altman DG. Time to event (survival) data. BMJ 1997;317:468–9.
2 Altman DG, Bland JM. Survival probabilities (the Kaplan–Meier method). BMJ 1997;317:1572.
3 Parmar MKB, Machin D. Survival analysis: a practical approach. Chichester: John Wiley, 1995:26–40;115–42.
4 Peto J. The calculation and interpretation of survival curves. In: Buyse ME, Staquet MJ, Sylvester RJ (eds). Cancer clinical trials: methods and practice. Oxford: Oxford University Press, 1984:361–80.
5 Greenwood M. The natural duration of cancer. Reports of Public Health and Medical Subjects, 33. London: HMSO, 1926.
6 Mclllmurray MB, Turkie W. Controlled trial of γ-linolenic acid in Dukes’s C colorectal cancer. BMJ 1987;294:1260 and 295:475.
7 Collett D. Modelling survival data in medical research. London: Chapman & Hall, 1994: section 2·4.
8 Daly L. Confidence intervals. BMJ 1988;297:66.
9 Altman DG. Practical statistics for medical research. London: Chapman & Hall, 1991:384–5.
10 Cox DR. Regression models and life tables (with discussion). J R Statist Soc Ser B 1972;34:187–220.