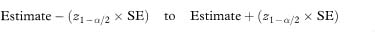
In this chapter we describe some special topics relating to the construction and interpretation of confidence intervals in particular situations. Some of these methods have been referred to before in this book but we repeat them specifically here as they have general applicability.
In certain circumstances, the algebraic expression for the estimate of the parameter of interest in a medical study may have a complex form. This complexity may, in turn, result in an even more complex expression for the corresponding standard error or in some circumstances no expression being available. In these situations, the substitution method described here may be applicable.
In some situations when the sample size is small, one may have to decide on whether the large sample expressions for the confidence interval may have to be replaced by exact methods. This leads to consideration of conservative intervals, so-called mid-P values and bootstrap methods.
In many clinical studies, multiple endpoints on each subject are often observed and these may lead to a large number of significance tests on the resulting data. The assessment of a patient’s quality of life is one example of this in which each instrument may have many questions which may be repeated on several occasions over the study period. In other circumstances, there may be multiple comparisons to make, for example in a clinical trial comparing several treatments. We discuss how the corresponding test size is affected and the impact on how confidence intervals are reported.
As described throughout this book the most commonly used method of calculating confidence intervals involves the Normal approximation in which a multiple of the standard error is added to and subtracted from the sample value for the measure. The general expression is
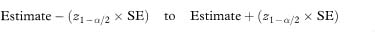
where SE is the standard error of the relevant estimate and z1–α/2 is the 100(1 – α)% percentile of the Normal distribution from Table 18.1. Sometimes the use of the Normal approximation relates to a transformation of the measure of interest. For instance, confidence limits for the relative risk, R, described in chapter 7 are based on the limits for loge R, that is,
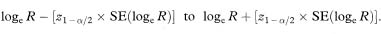
Transforming back to the original scale, by taking the exponential of these limits, gives the limits for the relative risk itself.
It is important to realise that it is the actual limits of the transformed quantity that must be back transformed and when the limits are transformed in this way the confidence limits are not symmetrical about the point estimate.
Unfortunately, however, for a number of measures used in epidemiology or clinical research, either no standard error formula is available or the formula is complex and tedious to calculate. In addition, these more complex formulae may not be implemented in computer software packages.
The substitution method is a particular approach to confidence interval estimation that can be used in some of these more difficult situations. It can replace the Normal approximation in others.1 It is easily understood, simple to apply, makes fewer assumptions than the Normal approximation approach and is inherently more accurate. The essence of the method is to find an expression for the measure of interest as a function of a basic parameter for which confidence limits are easy to calculate. The confidence limits for the measure are then obtained by substituting the limits for this basic parameter into the formula for the measure.
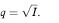
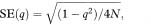
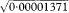= 0·0037 or 0·37%. Using the Normal approximation and the above expression for the standard error of q, the 95% confidence interval for the gene frequency is from 0·28% to 0·46%.
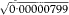= 0·0028 = 0·28% and qU = 
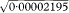= 0·0047 = 0·47%. These are almost identical to those obtained using the Normal approximation above.The substitution method for obtaining confidence limits for the gene frequency relies on the fact that q can be expressed as the square root of the birth incidence, for which limits are readily calculated. The square root of these limits gives the confidence limits for the gene frequency.
The simplicity of the standard error formula for the gene frequency example above means that, in this case, the substitution method shows no advantage in terms of ease of use. However, the utility of the method is illustrated in the derivation of confidence limits for the incidence rate, the attributable risk (chapter 7) and the number needed to treat (chapter 11). In particular the standard error formula for the attributable risk is quite complex and the substitution limits provide a much easier method for performing the calculation.1 Other examples of the substitution method are to be found. In particular, confidence limit estimation based on a transformation of a particular quantity, such as that described for the relative risk above, can also be considered an application of the method.
A major advantage of the substitution method is that no distributional assumptions are necessary for the sampling distribution of the measure for which the confidence limits are required. If exact confidence limits are known for the underlying parameter (as in the binomial or Poisson cases) the limits for a function of the parameter will also be exact. For example, the substitution limits described above for the gene frequency, which are based on exact limits for the incidence rate, are in general more accurate than those obtained using the standard error formula. Thus there may be a distinct advantage to the substitution method even when an alternative exists.
The kernel of the substitution method is expressing the measure for which confidence limits are required as a function of a single quantity for which limits are easily obtained. It is important to note, however, that the measure must be a function of a single parameter for the method to work. For example, it is not possible to obtain a confidence interval for a relative risk by using the confidence limits for its two component absolute risks.
To avoid multiple parameters it may be necessary to assume that some of the quantities that make up the relevant formula are without sampling variation and are thus regarded as having no variation. If the measure is derived from a contingency table this will often be equivalent to assuming that one or both of the margins of the table are fixed. Thus the substitution limits for the attributable risk (chapter 7) assume that the prevalence of the risk factor is constant and the substitution limits for an incidence rate (chapter 7) assume that the population size is fixed. This aspect has been discussed further.4–6
The substitution method will be applicable as long as there is a fairly simple relationship between the measure and the parameter for which limits are available. Technically, the measure must either increase or decrease as the parameter value increases. Most measures in epidemiology and clinical medicine, however, satisfy this requirement.
The substitution method for deriving confidence intervals may be useful to the researcher faced with a non-standard measure or one with a fairly complex standard error. It is particularly suitable for “hand” calculations when specialised computer software is not available.
One way of thinking about confidence intervals for a population parameter, θ, is that a 95% confidence interval contains those values of θ that are not rejected by a hypothesis test at the 5% level using the observed data. As a consequence, one can determine lower and upper limits (θL, θU) as the values that are on the “exact” borderline of significance by the two possible one-sided tests both at the 2·5% level. For example, suppose we observed 50 remissions out of 100 patients, giving a response rate of 0·5. Using the traditional method of chapter 6, a 95% confidence interval for the true proportion θ is 0·4 to 0·6. Suppose the true remission rate was in fact 0·4, the lower of these limits, that is it corresponded exactly to our estimate of θL, then, in a trial of 100 patients we would expect to observe 50 or more remissions with probability of about 0·025. Similarly, if the true remission rate were 0·6 (exactly our estimate of θU) we would expect to observe 50 or fewer remissions with a probability of about 0·025. These probabilities are not precisely 0·025 because the standard deviations necessary for these calculations are based on θ = 0·4 and θ = 0·6 respectively, rather than θ = 0·5.
An exact confidence interval for this remission proportion would involve using the binomial distribution to calculate the probability of 50 or more remissions in 100 patients for a variety of possible values of the true population parameter, θ. The lower limit, θL, is then the value of θ which gives a probability of exactly 0·025 (hence the term “exact” confidence interval). A similar calculation provides θU. This process would appear to be ideal, and many textbooks recommend it. However, because of the discrete nature of count data precise correspondence with (here) 0·025 cannot often be obtained. Thus the coverage probability for an exact confidence interval tends to be larger than the nominal one of 100(1 – α)%. So what purports to be a 95% confidence interval is actually wider, and may exclude the true population value on, say, only 3% of occasions rather than the desired 5%. For small studies an exact interval may be much wider than is desired.7
For small samples, instead of the usual chi-squared test, a commonly used test is Fisher’s Exact Test.8 For this test the data for calculating the two proportions are first expressed by placing the observations in a 2 × 2 table, with the total for the columns and rows known as the marginal totals. This format also provides an estimate of the odds ratio (chapter 7). Given the marginal totals, it is possible to calculate the probability of the observed table, using the so-called hypergeometric distribution.8,9 Fisher’s Exact Test involves calculating the probability of all the possible tables that can be constructed that have the same marginal totals as the observed one. For convenience, these tables can be ordered in terms of the odds ratios of the individual tables.
The actual observed data table has the highest probability, with the probabilities decreasing as the odds ratio moves away from the observed one in either direction. The one-sided P value is the sum of all probabilities more extreme (in a given direction) than the observed one, plus the probability of the observed table. The simplest way to derive a two-sided P value is to double the one-sided P value. It can be shown that this test is conservative, which simplistically means that the associated P value is too large. In particular, under the assumption that the null hypothesis is true the expected value of this one-sided P value is greater than 0·5, whereas it should be exactly 0·5, since under the null hypothesis one would expect the P value to be uniformly distributed over the interval 0 to 1.
An alternative is known as the mid-P value and involves adding only half (rather than all) the probability of the observed table to the sum of probabilities of the more extreme tables to obtain the one-sided P value.8–10 Clearly this mid-P value will be smaller, and so results in a less conservative hypothesis test. It can also be shown that its expected value under the null hypothesis is 05. This is particularly important when the results of different studies are pooled7 (see chapter 11). In practice, we usually deal with twosided tests, and the two-sided mid-P value is simply double the one-sided mid-P value.10
The approach to confidence intervals via hypothesis tests can use mid-P probabilities rather than exact probabilities to obtain mid-P confidence intervals.9 They are more tedious to calculate than the corresponding limits using the more conventional methods as there is no direct formula. They give narrower limits than conventional intervals, but simulations have shown for a binomial proportion that the coverage probabilities are close to the specified ones, except for values of the proportion close to 0 or 1.7, 11
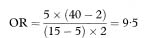
Rothman and Greenland10 remark on the exact versus mid-P debate that “neither position is logically compelling… the choice is of little practical importance because any data set in which the choice makes a big numerical difference must have very little information on the measure of interest”. It should be noted that the coverage properties of exact and mid-P confidence intervals for more complicated situations such as the difference between binomial proportions have yet to be investigated thoroughly although Newcombe12 has investigated their properties through simulation.
The use of the mid-P method when comparing a sample proportion with a specified population proportion is discussed by Tai et al.13
Exact confidence intervals for a variety of situations are available in the StatXact 3 software (http://www.cytel.com) which also give mid-P confidence intervals for the particular case of a confidence interval for an odds ratio.
Conventional confidence interval calculations require assumptions concerning the sampling distribution of the estimate of interest. If the sample size is large and we wish to estimate a confidence interval for a mean, then the form of the underlying population distribution is not important because the central limit theorem will ensure that the sampling distribution is approximately Normal. However, if the sample size is small we can only presume a t distribution form for the sampling distribution if the underlying population distribution can be assumed Normal. If this is not the case then the confidence interval cannot be expected to cover the population value with the specified confidence coverage, say 95%. In practice, we have information on the form of the distribution of the population from the distribution of the sample data itself. The so-called “bootstrap” estimates (from the expression “pulling oneself up by one’s bootstraps”) utilise this information, by making repeated random samples with replacement of the same size as the original sample from the data.14, 15 In this way the bootstrap samples mimic the way the observed data are collected from the population. The “with replacement” means that any observation can be sampled more than once. It is important because sampling without replacement would simply give the original data values in different orders with, for example, the mean and standard deviation always being exactly the same. It turns out that “with replacement” is the best approach if the observations are independent; if they are not then other methods, beyond the scope of this chapter, are needed. The standard error is estimated from the variability between the values of the statistic derived from the different bootstrap samples. The point about the bootstrap is that it produces a variety of values obtained from the observations themselves, whose variability reflects the standard error which would be obtained if samples had been repeatedly taken from the original population.
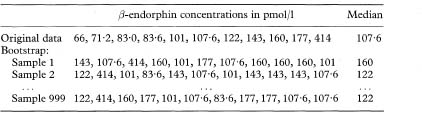
Suppose we wish to calculate a 95% confidence interval for a mean. We take a random sample of the data, of the same size as the original sample, and calculate the mean of the data in this random sample. We do this repeatedly, say 999 times. We now have 999 means. If these are ordered in increasing value a bootstrap 95% confidence interval for the mean would be from the 25th to the 975th values. This is known as the percentile method.
However, the percentile method is not the best method of bootstrapping because it can have a bias, which one can estimate and correct for using methods, such as the “bias corrected method” and the “bias corrected and accelerated” (BCa) method, the latter being the preferred option. There is also the “parametric bootstrap” when the residuals from a parametric model are bootstrapped to give estimates of the standard errors of the parameters, for example to estimate the standard errors of coefficients from a multiple regression. Details are given in Efron and Tibshirani14 or Davison and Hinckley.15
Using the methods above, valid bootstrap confidence intervals can be constructed for all common estimators, such as a proportion, a median, or a difference in means, providing that the data are independent and come from the same population. More sophisticated methods can also allow for correlations between the observations.
The number of bootstrap samples required depends on the type of estimator: 50–200 are adequate for a confidence interval for a mean, but in excess of 1000 replications are required for a confidence interval of, say, the 2·5% or 97·5% centiles. When quoting a bootstrap confidence interval one should state the method, such as the percentile or bias corrected, and the number of replications used.
Table 13.1 Summary of 999 bootstrap samples from 11 observations of β-endorphin concentrations in pmol/116
The main advantage of the bootstrap is that it frees the investigator from making inappropriate assumptions about the distribution of an estimator in order to make inferences. A particular advantage is that it is available when the formula for the confidence interval cannot be derived explicitly and it may provide better estimates when the formulae are only approximate.
The naïve bootstrap methods we have described make the assumption that the observed data sample is an unbiased simple random sample from the study population. More complex survey sampling schemes, such as stratified random sampling, may not reflect this simple situation, and so more complicated bootstrapping schemes may be required. Naïve bootstrapping may not be successful in very small samples (say < 9 observations), since the observations themselves are less likely to be representative of the study population. “In very small samples even a badly fitting parametric analysis may outperform a non-parametric analysis, by providing less variable results at the expense of a tolerable amount of bias.”14
Perhaps one of the most common uses for bootstrapping in medical research has been for calculating confidence intervals for derived statistics such as cost-effectiveness ratios, when the theoretical distribution is mathematically difficult.17,18 However, care is needed here since the denominators in some bootstrap samples can get close to zero, leading to very large estimates of the ratio. As an example in health economics, Lambert et al.19 calculated the mean resource costs per patient for day patients with active rheumatoid arthritis as £1789 with a bootstrap 95% confidence interval of £1539 to £2027 (1000 replications). They used a bootstrap method because the resource costs have a very skewed distribution. However, the authors did not state which bootstrap method they used.
It is relatively easy to program the bootstrap with modern software. Three packages which have the bootstrap as standard are Stata (http://www.stata.com), SPlus (http://www.mathsoft.com) and Resampling Stats (http://www.resample.com). The book by Davison and Hinckley15 comes with a disk of software and examples for use with SPlus. The results in this chapter were derived using SPlus.
In a clinical study in which two groups are being compared, the formal statistical test of this comparison has an associated twosided test ‘size’ of α. This is set as the boundary below which the P value, calculated from the data for the primary endpoint of the study, must fall to be declared statistically significant. In this case the null hypothesis of no difference between groups is then rejected. We have argued very strongly against the uncritical use of such an approach (chapter 3) but introduce it here for illustrative purposes.
Suppose this approach is utilised in the analysis of a clinical trial comparing two groups and suppose further that there is truly no difference between the two groups. Despite this “no difference” there is a 100α% probability of a statistically significant result and the false rejection of the null hypothesis. Thus, following any comparison, there is always the possibility of a false positive outcome. It is usual to set this probability as 5% (i.e., α = 0·05).
If more than one endpoint is measured for the two group study in question, then the situation becomes more complex. For example, if a clinical trial is comparing two treatments (A and B) but there are three different independent outcomes being measured, then there are three comparisons to make between A and B and, in theory at least, three statistical tests. In this circumstance it can be shown that the false-positive rate is no longer 100a % but approximately 300α%. In fact for k (assumed independent) outcome measures the false-positive rate is 100 × [1 – (1 – α)k]% which is approximately equal to 100kα%. Clearly, the false-positive rate increases as the number of comparisons increases.
In order to retain the false-positive rate as 100α% the Bonferroni correction is often suggested. This implies declaring differences as statistically significant at the 100α% only if the observed P is less than α/k. In the case of α = 0·05 and k = 3, this implies P < 0·017. Equivalently, and preferably, multiply the observed P value by k and declare this significant if less than α. This latter approach is recommended by Altman20 as it avoids the apparently anomalous situation in which the P value quoted is less than α but is not statistically significant.
Similar considerations can apply to confidence intervals and one approach in situations where k endpoints are being compared is to replace z1–α/2 in the corresponding equation for the confidence interval by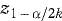 
. For example, if k = 3, α = 0·05, then z1– α/2 = z0·975 = 1·96 is replaced by z1–α/2k = z0·9917 = 2·64 (see Table 18.1). This approach clearly leads to a wider confidence interval. (Analogous changes would be made if t rather than z were being used for constructing the confidence interval.)
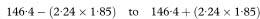
It is recognised that the Bonferroni approach to adjusting for multiple comparisons is conservative as it assumes the different endpoints are uncorrelated. Indeed, in the example we are using, it is well known that systolic and diastolic blood pressures are strongly correlated. This conservativeness implies that utilising the criterion kP < α will lead to failure to reject the null hypothesis on too many occasions. The corresponding confidence intervals will also be too wide. However, the correlation structure between different endpoints measured on the same subjects may be very complex and not easily summarised or corrected for and, in any event, will change from study to study.
One approach that has been used to overcome this difficulty is to quote 99% confidence intervals rather than 95% confidence intervals when more than a single outcome is regarded as primary. Thus the UK Prospective Diabetes Study Group21 report 21 distinct endpoints, ranging from fatal myocardial infarction to death from unknown cause, and provide 99% confidence intervals for the corresponding 21 relative risks comparing tight with less tight control of blood pressure. This is a “half-way house” proposal, since 0·01 (= 1 – 0·99) is between the conventional 0·05 and the Bonferroni corrected value of 0·05/21 = 0·0024.
A contrary view warning against the indiscriminate use of the Bonferroni correction, points out that the method is concerned with the situation that all k null hypotheses are true simultaneously, which is rarely of interest or use to researchers.22,23 A further weakness is that the interpretation of a finding depends on the number of other tests performed. Thus two investigators obtaining exactly the same result with a particular endpoint may draw different conclusions on statistical significance if they had observed a different number of other endpoints. In general there is also an increasing likelihood that truly important differences are deemed non-significant.
There are other situations in which multiple comparisons may be made. For example, in the meta-analyses described in chapter 11, many independent trial results may be summarised by their individual treatment effects and associated 95% confidence intervals before combining into a single summary estimate with a confidence interval. A more cautious approach would be to utilise 99% confidence intervals in their place.
Similar considerations of multiplicity may also apply in situations other than studies with multiple endpoints. For example, if more than two groups are compared in a clinical trial using a single outcome, then there is potentially more than one statistical test to conduct and more than one confidence interval to construct.
There are also situations in which a multiple comparison approach is utilised to compare different groups inappropriately. For example, Rothman24 illustrated, using data from Young et al.,25 how subjects from four groups are compared and are not statistically significantly different from each other using a test size of 5% without a Bonferroni correction. However, he points out that there is some structure to the four groups that had not been taken into account in this analysis. The four groups were in fact four levels of water chlorination: none, low, medium and high. Taking this “dose” into account with a suitable test for trend demonstrated a statistically significant and increasing relative risk of brain cancer amongst the women under study with increasing dose. (See also the example of multiple logistic regression in chapter 8.)
Multiple comparisons can also occur in continuous monitoring of the progress of clinical trials which include interim analyses, subgroup analyses in trials and other studies, and in regression modelling when decisions on inclusion and exclusion of variables in a model have to be made. All of these have direct implications for the corresponding confidence intervals.
As we have indicated, the problem of multiple comparisons is particularly acute in quality of life research. Thus published guidelines on reporting such studies explicitly state: “in the case of multiple comparisons, attention must be paid to the total number of comparisons, to the adjustment, if any, of the significance level, and to the interpretation of the results”.26 Improved, but more complex, methods of correcting for multiple comparisons are available and their relative merits have been discussed.27 There is no general consensus, however, as to which procedures to adopt to allow for multiple comparisons. We therefore recommend reporting the unadjusted P values and confidence limits with a suitable note of caution with respect to interpretation. Perneger23 concludes that: “Simply describing what tests of significance have been performed, and why, is generally the best way of dealing with multiple comparisons.” A precautionary recommendation may be to follow the UK Prospective Diabetes Study Group21 and at least have in mind a 99% confidence interval as an aid to interpretation.
1 Daly LE. Confidence limits made easy: Interval estimation using a substitution method. Am J Epidemiol 1998;147:783–90.
2 Weir, BS. Genetic data analysis II. Sunderland, Massachusetts: Sinauer Associates, 1996.
3 Reilly M, Daly L, Hutchinson M. An epidemiological study of Wilson’s disease in the Republic of Ireland. J Neurol Neurosurg Psychiat 1993;56:298–300.
4 Greenland S. Re: “Confidence limits made easy: Interval estimation using a substitution method”. Am J Epidemiol 1999;149:884.
5 Newcombe RG. Re: “Confidence limits made easy: Interval estimation using a substitution method”. Am J Epidemiol 1999;149:884–5.
6 Daly LE. Re: “Confidence limits made easy: Interval estimation using a substitution method” [author’s reply]. Am J Epidemiol 1999;149:885–6.
7 Agresti A, Coull BA. Approximate is better than “exact” for interval estimation of binomial proportions. Am Stat 1998;52:119–26.
8 Swinscow TDV. Statistics at square one. 9th ed revised by MJ Campbell. London: British Medical Association, 1996.
9 Berry G, Armitage P. Mid-P confidence intervals: a brief review. Statistician 1995;44:417–23.
10 Rothman KJ, Greenland S. Modern epidemiology. 2nd ed. Philadelphia: Lippincott-Raven, 1998.
11 Vollset SE. Confidence intervals for a binomial proportion. Stat Med 1993;12:809–24.
12 Newcombe RG. Interval estimation for the difference between independent proportions: Comparison of eleven methods. Stat Med 1998;17:873–90.
13 Tai B-C, Lee J, Lee H-P. Comparing a sample proportion with a specified proportion based on the mid-P method. Psychiatry Res 1997;71:201–3.
14 Efron B, Tibshirani RJ. An introduction to the bootstrap. New York: Chapman and Hall, 1993.
15 Davison A, Hinckley D. Bootstrap methods and their applications. Cambridge: Cambridge University Press, 1997.
16 Dale G, Fleetwood JA, Weddell A, Ellis RD, Sainsbury JRC. β-Endorphin: a factor in “fun run” collapse. BMJ 1987;294:1004.
17 Campbell MK, Torgerson D. Confidence intervals for cost-effectiveness ratios: the use of “bootstrapping”. J Health Services Res Policy 1997;2:253–5.
18 Chaudhary MA, Stearns SC. Estimating confidence intervals for cost-effectiveness ratios: an example from a randomized trial. Stat Med 1996;15:1447–58.
19 Lambert CM, Hurst NP, Forbes JF, Lochhead A, Macleod M, Nuki G. Is day care equivalent to inpatient care for active rheumatoid arthritis? Randomised controlled clinical and economic evaluation. BMJ 1998;316:965–9.
20 Altman DG. Practical statistics for medical research. London: Chapman and Hall, 1991:210–12.
21 UK Prospective Diabetes Study Group. Tight blood pressure control and risk of macrovascular and microvascular complications in type 2 diabetes: UKPDS 38. BMJ 1998;317:703–12.
22 Rothman KJ. No adjustments are needed for multiple comparisons. Epidemiology 1990;1:43–6.
23 Perneger TV. What’s wrong with Bonferroni adjustments. BMJ 1998;316: 1236–8.
24 Rothman KJ. Modern epidemiology. Boston: Little, Brown, 1986: figure 16.2.
25 Young TB, Kanarek MS, Tsiatis AA. Epidemiologic study of drinking water chlorination and Wisconsin female cancer mortality. J Natl Cancer Inst 1981; 67:1191–8.
26 Staquet MJ, Berzon RA, Osoba D, Machin D. Guidelines for reporting results of quality of life assessments in clinical trials. Quality Life Res 1996;5:496–502.
27 Sankoh AJ, Huque MF, Dubin SD. Some comments on frequently used multiple endpoint adjustment methods in clinical trials. Stat Med 1997;16:2529–42.