6

Decimals

In this chapter, you learn how to work with decimals.

Decimal Concepts

Decimal fractions are fractions with a denominator that is some positive power of 10, such as , and so forth. To represent these numbers, you extend the place-value system of numbers and use a decimal point to separate whole numbers from decimal fractions. The number 428.36 is a mixed decimal and means . You read 428.36 as “Four hundred twenty-eight and thirty-six hundredths” or as “Four hundred twenty-eight point thirty-six.”

Hereinafter, mixed decimals and decimal fractions will be called simply decimals.

A place-value diagram for some of the positional values of the decimal system is shown in Figure 6.1.

Don’t say “and” when reading whole numbers. For instance, 203 is “two hundred three,” not “two hundred and three.”

The use of the decimal point is a very convenient way to represent decimal fractions. For instance, using the decimal point, you write 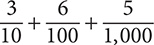as 0.365.

The 0 in front of the decimal point is used as a way to make the decimal point noticeable for decimal fractions that are less than 1.

Figure 6.1 Place values in the decimal system

You read a decimal point as either “and” or “point.” For example, 35.6 is read “Thirty-five and six-tenths” or as “Thirty-five point six.”

You deal with the decimal point in arithmetic calculations by following some simple “rules” that are just mathematical shortcuts to ensure accuracy of the calculations.

Adding and Subtracting Decimals

Adding and subtracting are only done for like amounts. A statement such as “4 inches plus 7 inches” is meaningful, while “7 apples plus 5 inches” is meaningless. Similarly, with decimals, you combine tenths with tenths, hundredths with hundredths, and so on. Thus, when you add or subtract decimals, keep the decimal points lined up in the computation so that you are adding digits of like place values.

Problem

Add 25.78, 241.342, and 12.5.

Solution

Step 1.   Write the numbers in an addition column, being sure to line up the decimal points.

Zeros are inserted where needed to make sure that all place values are in all the numbers.

Step 2.   Add as with whole numbers.

Problem

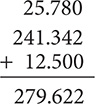
Subtract 168.274 from 6,547.34.

Solution

Step 1.   Write the numbers in a subtraction column, being sure to line up the decimal points.

Step 2.   Subtract as you would with whole numbers.

When adding or subtracting decimals, you should insert zeros for missing place values.

The carrying and borrowing procedure is the same as with whole numbers.

Multiplying Decimals

A simple rule for multiplying two decimals is to sum the number of decimal places in the multiplicand (first factor) and the multiplier (second factor) and put this number of places in the product.

Problem

Multiply 47.63 by 32.57.

Solution

Step 1.   Write the numbers in a multiplication

You do not have to line up the decimal points for a multiplication problem.

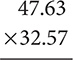
Step 2.   Perform the multiplication as you would with whole numbers.

Step 3.   Sum the number of decimal places in both the multiplicand and the multiplier, which is four in this problem, and put that number of decimal places in the final product.

Dividing Decimals

To devise a rule for dividing decimals, you employ the use of the cancellation law of fractions. For example, 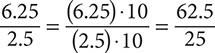. The technique, then, in dividing decimals, is to multiply both dividend (numerator) and divisor (denominator) by the appropriate power of 10 that will make the divisor a whole number. In practice, this strategy amounts to moving the decimal point to the right the appropriate number of places to make the divisor a whole number. Of course, the decimal point in the dividend must be moved in the same manner. Once this is done, the decimal point in the dividend and the quotient (answer) must be aligned.

Problem

Divide 6.25 by 2.5.

Solution

Step 1.   Write as a long division problem.

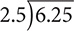
Step 2.   Move the decimal point one place to the right in both numbers to make the divisor a whole number.

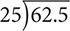
Step 3.   Divide as you would whole numbers, keeping the decimal points aligned but ignoring the decimal point in the intermediate multiplications.

Step 4.   State the main result.

Step 5.   Check the answer.

Calculators will automatically place the decimal point, but you should know these rules to check for errors that may occur in entering data into your calculator.

Rounding Decimals

Working with decimals can sometimes result in lengthy decimal expressions. In application, you may be interested in the decimal expression to only a few places. In this case, you use the technique of rounding to determine the final approximation. For example, if you want the decimal to only two places, you look at the digit in the third place to the right of the decimal point. If the third digit is 5 or greater, increase the digit in the second place by 1 and drop all digits past the second digit to the right of the decimal point. If the third digit is less than 5, leave the digit in the second place as is and drop all digits past the second digit to the right of the decimal point. For example, 45.57689 rounded to two places is 45.58. The process for all places is the same.

Problem

Use a calculator to compute 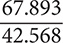and then round the answer to two decimal places.

. Recall from previous chapters that the fraction bar indicates division. It is important to recognize this use of the fraction bar.

Solution

Step 1.   Do the division by calculator.

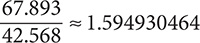
Step 2.   Check whether the digit in the third place to the right of the decimal point is 5 or greater or less than 5.

The digit in the third place is 4, which is less than 5.

Step 3.   Leave the digit in the second place as is and drop all digits past the second digit to the right of the decimal point.

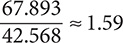
Handheld calculators have taken the tedium out of arithmetic calculations and for that all are glad. Do the following problems by hand or with a calculator, but before you do them, predict the number of decimal places in the answer or, in the case of division, where the decimal point will be located.

Exercise 6

1. Add 45.716 and 3.92.

2. Subtract 1.8264 from 23.3728.

3. Multiply 0.214 by 1.93.

4. Multiply 1.21 by 0.0056.

5. Divide 0.1547 by 0.014.

6. Divide 2.916 by 0.36.

7. Divide 2.917 by 0.37 and round to three places.

8. Multiply 6.678 by 0.37 and round to two places.

9. Divide 3.977 by 0.0372 and round to three places.

10. Multiply 45.67892 by 0.0374583 and round to four places.