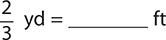In use in the United States are two different measurement systems: the US customary system and the metric system. In this chapter, you learn how to work with both systems.
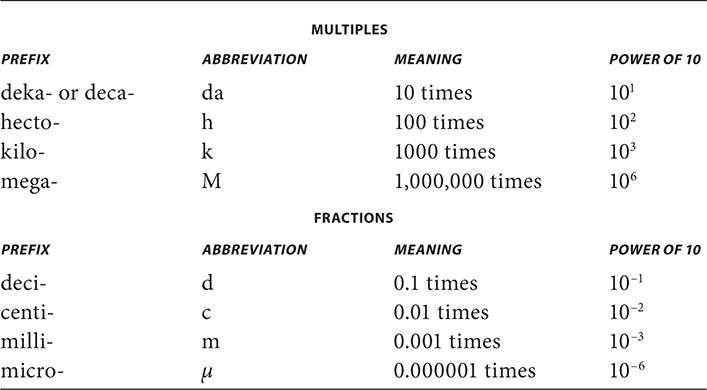
Metric System Prefixes
You are no doubt familiar with the US customary system. Table 8.1 contains the metric system prefixes you will find useful to know.
US Customary and Metric Units
Table 8.2 contains a list of the US customary and metric units most commonly used in everyday activities.
Denominate Numbers
You express measurements using denominate numbers. A denominate number is a number with units attached. Numbers without units attached are abstract numbers.
Problem Identify the denominate numbers in the following list: 1,000, 1200 m, $400, 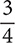 ,
, 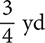 , 180 d, 4,840 yd2, 8 gal, 5 kg, 3.785
, 180 d, 4,840 yd2, 8 gal, 5 kg, 3.785
Solution

Step 1. Recalling that denominate numbers have units attached, identify the denominate numbers in the list.
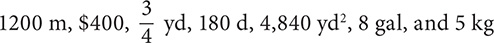
Converting Units of Denominate Numbers
Convert measurement units of denominate numbers to different measurement units by using “conversion fractions.” You make conversion fractions from conversion facts given in tables like Table 8.2. You have two conversion fractions for each conversion fact. For example, for 1 yd = 3 ft, you have 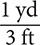 and
and 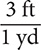 . Each of these fractions is equivalent to the number 1 because the numerator and denominator are different names for the same length. Therefore, multiplying a quantity by either of these fractions, does not change the value of the quantity.
. Each of these fractions is equivalent to the number 1 because the numerator and denominator are different names for the same length. Therefore, multiplying a quantity by either of these fractions, does not change the value of the quantity.
To change the units of a denominate number to different units, multiply by the conversion fraction whose denominator is the same as the units of the quantity to be converted. When you multiply, the units you started out with will divide (“cancel”) out, and you will be left with the new units.
You always should assess your result to see if it makes sense. Here is a helpful guideline.
When you convert from a larger unit to a smaller unit, it will take more of the smaller units to equal the same amount. When you convert from a smaller unit to a larger unit, it will take less of the larger units to equal the same amount.
Problem
Change the given amount to the units indicated.
a. 5 yd = _______ ft
b. 360 min = _______ hr
c. 2 yd2 = _______ ft2
d. I yd = _______ ft
f. 8 in = ______ cm
g. 1200 m = ______ km
h. 5 kg = ______ g
Solution
a. 5 yd = _____ ft

Step 1. Using Table 8.2, determine the conversion fractions.
The conversion fractions are 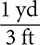 and
and 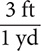 .
.
Step 2. Write 5 yd as a fraction with denominator 1, select the conversion fraction that has “yd” in the denominator, and then multiply.
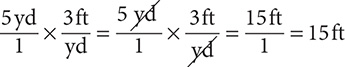
(The “yd” units cancel out, leaving “ft” as the units for the answer.)
Step 3. State the main result.

Step 4. Assess the result.
A yard is longer than a foot, so the number in front of “ft” should be greater than the number in front of “yd.”
b. 360 min = ______ hr

Step 1. Using Table 8.2, determine the conversion fractions.
The conversion fractions are 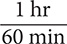 and
and 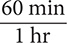 .
.
Step 2. Write 360 min as a fraction with denominator 1, select the conversion fraction that has “min” in the denominator, and then multiply.
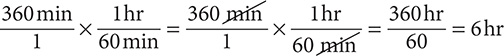
(The “min” units cancel out, leaving “hr” as the units for the answer.)
Step 3. State the main result.

A minute is shorter than an hour, so the number in front of “hr” should be less than the number in front of “min.”
c. 2 yd2 = ________ ft2

Step 1. Using Table 8.2, determine the conversion fractions.
The conversion fractions are 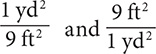 .
.
Step 2. Write 2 yd2 as a fraction with denominator 1, select the conversion fraction that has “yd2” in the denominator, and then multiply.
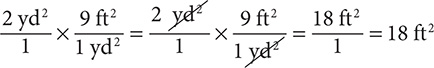
(The “yd2” units cancel out, leaving “ft2” as the units for the answer.)
Step 3. State the main result.

Step 4. Assess the result.
A square yard is larger than a square foot, so the number in front of “ft2” should be greater than the number in front of “yd2.”
d. 

Step 1. Using Table 8.2, determine the conversion fractions.
The conversion fractions are 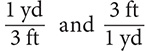 .
.
Step 2. Write 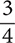 yd with “yd” as part of the numerator, select the conversion fraction that has “yd” in the denominator, and then multiply.
yd with “yd” as part of the numerator, select the conversion fraction that has “yd” in the denominator, and then multiply.
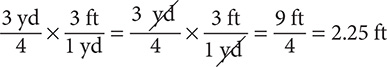
(The “yd” units cancel out, leaving “ft” as the units for the answer.)
Step 3. State the main result.
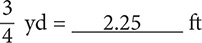
Step 4. Assess the result.
A yard is longer than a foot, so the number in front of “ft” should be greater than the number in front of “yd.”
e. 7 qt = _______ gal

Step 1. Using Table 8.2, determine the conversion fractions.
The conversion fractions are 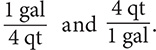 .
.
Step 2. Write 7 qt as a fraction with denominator 1, select the conversion fraction that has “qt” in the denominator, and then multiply.
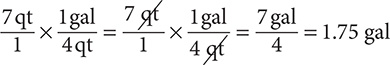
(The “qt” units cancel out, leaving “gal” as the units for the answer.)
Step 3. State the main result.
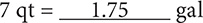
Step 4. Assess the result.
A quart is less than a gallon, so the number in front of “gal” should be less than the number in front of “qt.”
f. 8 in = ______ cm

Step 1. Using Table 8.2, determine the conversion fractions.
The conversion fractions are 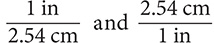 .
.
Step 2. Write 8 in as a fraction with denominator 1, select the conversion fraction that has “in” in the denominator, and then multiply.
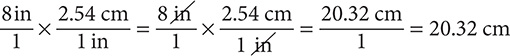
(The “in” units cancel out, leaving “cm” as the units for the answer.)
Step 3. State the main result.
8 in = 20.32 cm
Step 4. Assess the result.
An inch is longer than a centimeter, so the number in front of “cm” should be greater than the number in front of “in.”
g. 1200 m = ______ km

Step 1. Using Table 8.2, determine the conversion fractions.
The conversion fractions are 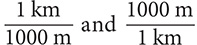 .
.
Step 2. Write 1200 m as a fraction with denominator 1, select the conversion fraction that has “m” in the denominator, and then multiply.
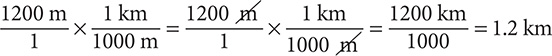
(The “m” units cancel out, leaving “km” as the units for the answer.)
Step 3. State the main result.
1200 m = 1.2 km
Step 4. Assess the result.
A meter is shorter than a kilometer, so the number in front of “km” should be less than the number in front of “m.”
h. 5 kg = _________ g

Step 1. Using Table 8.2, determine the conversion fractions.
The conversion fractions are 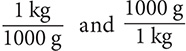 .
.
Step 2. Write 5 kg as a fraction with denominator 1, select the conversion fraction that has “kg” in the denominator, and then multiply.
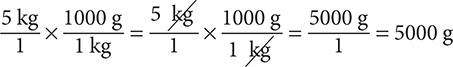
(The “kg” units cancel out, leaving “g” as the units for the answer.)
Step 3. State the main result.
5 kg = 5000 g
A kilogram is heavier than a gram, so the number in front of “g” should be greater than the number in front of “kg.”
Shortcut for Converting Within the Metric System
If the base unit in the problem is the meter, liter, or gram, you have a shortcut to convert within the metric system. Use the mnemonic “King Henry Doesn’t Usually Drink Chocolate Milk,” which helps you remember the following metric prefixes:
kilo-, hecto-, deca-, (base) unit (no prefix), deci-, centi-, milli-
The metric system is a decimal-based system, so the prefixes are based on powers of 10. Convert from one unit to another by either multiplying or dividing by a power of 10. If you move from left to right on the above list, then multiply by the power of 10 that corresponds to the number of times you moved. If you move from right to left, then divide by the power of 10 that corresponds to the number of times you moved. Note: When you use this shortcut, don’t carry the units along when you do the calculations.
Problem
Change the given amount to the units indicated.
a. 1200 m = ________km
b. 5 kg = ________g
c. 3.5 L = ________mi
Solution
a. 1200 m = ________km

Step 1. Using the list of metric prefixes, determine how many moves you make, and in what direction, to go from meters to kilometers. kilo-, hecto-, deca-, meter, deci-, centi-, milli-
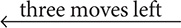
Step 2. Divide 1,200 by 103, the power of 10 that corresponds to the number of moves.
1,200 ÷ 103 (threemoves left) = 1,200 ÷ 1,000 = 1.2
Step 3. State the main result.
1200 m = 1.2 km
Step 4. Assess the result.
A meter is shorter than a kilometer, so the number in front of “km” should be less than the number in front of “m.”
b. 5 kg = ________g

Step 1. Using the list of metric prefixes, determine how many moves you make, and in what direction, to go from kilograms to grams.
kilo-, hecto-, deca-, gram, deci-, centi-, milli-
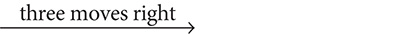
Step 2. Multiply 5 by 103, the power of 10 that corresponds to the number of moves.
5 × 103 (three movesright) = 5 × 1,000 = 5,000
Step 3. State the main result.
5 kg = 5000 g
Step 4. Assess the result.
A kilogram is heavier than a gram, so the number in front of “g” should be greater than the number in front of “kg.”
c. 3.5 L = ________mL

Step 1. Using the list of metric prefixes, determine how many moves you make, and in what direction, to go from liters to milliliters.
kilo-, hecto-, deca-, liter, deci-, centi-, milli-
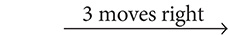
Step 2. Multiply 3.5 by 103, the power of 10 that corresponds to the number of moves.
3.5 × 103(threemovesright) = 3.5 × 1,000 = 3,500
Step 3. State the main result.
3.5 L = 3500 mL
A liter is larger than a milliliter, so the number in front of “mL” should be greater than the number in front of “L.”
Using a “Chain” of Conversion Fractions
For some conversions, you may need to use a “chain” of conversion fractions to obtain your desired units. Select the conversion facts that help you obtain your desired units and then multiply one after the other.
Problem
Change the given amount to the units indicated.
a. 4 gal = ________pt
b. 1 wk = ________min
Solution
a. 4 gal = ________pt

Step 1. Using Table 8.2, determine the conversion fractions.
Table 8.2 does not have a fact that shows the equivalency between gallons and pints. However, the table shows that 1 qt = 2 pt and 1 gal = 4 qt. These two facts yield four conversion fractions: 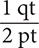 and
and 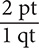 and
and 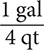 and
and 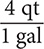 .
.
Step 2. Start with 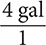 and keep multiplying by conversion fractions until you obtain your desired units.
and keep multiplying by conversion fractions until you obtain your desired units.
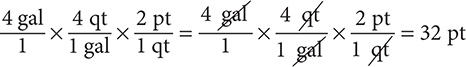
Step 3. State the main result.
4 gal = 32 pt
Step 4. Assess the result.
A gallon is larger than a pint, so the number in front of “pt” should be greater than the number in front of “gal.”

Step 1. Using Table 8.2, determine the conversion fractions.
Table 8.2 does not have a fact that shows the equivalency between weeks and minutes. However, the table shows that 1 wk = 7d, 1 d = 24 hr, and 1 hr = 60 min. These three facts yield six conversion fractions: 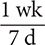 and
and 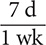 ,
, 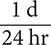 and
and 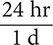 , and
, and 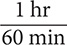 and
and 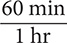 .
.
Step 2. Start with 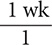 and keep multiplying by conversion fractions until you obtain your desired units.
and keep multiplying by conversion fractions until you obtain your desired units.
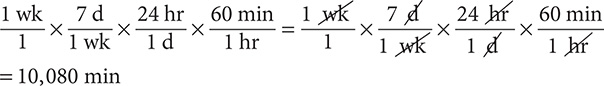
Step 3. State the main result.
1 wk = 10,080 min
Step 4. Assess the result.
A week is longer than a minute, so the number in front of “min” should be greater than the number in front of “wk.”
Converting Money to Different Denominations
When converting with denominations of money, it is helpful to change the original amount to cents and then to the denomination to which you are converting.
Problem
Change the given amount to the denomination indicated.
a. 15 quarters = ________nickels
b. 75 dimes = ________quarters
a. 15 quarters = ________nickels

Step 1. Convert 15 quarters to cents.
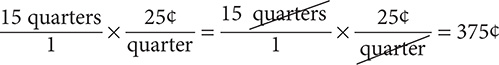
Step 2. Convert 375<t to nickels.
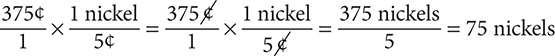
Step 3. State the main result.
15 quarters = 75 nickels
Step 4. Assess the result.
Quarters have more value than nickels, so the number in front of “nickels” should be greater than the number in front of “quarters.”
b. 75 dimes = ________quarters

Step 1. Convert 75 dimes to cents.
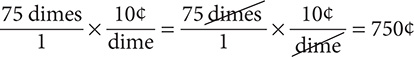
Step 2. Convert 750<t to quarters.
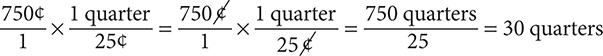
Step 3. State the main result.
75 dimes = 30 quarters
Step 4. Assess the result.
Dimes have less value than quarters, so the number in front of “quarters” should be less than the number in front of “dimes.”
Rough Equivalencies for the Metric System
If you are not very familiar with the metric system, here are some “rough” equivalencies of the more common units for your general knowledge.

Reading Measuring Instruments
The scale (or gauge) of a measuring instrument has tick marks that divide the scale into equal intervals. Usually, not every tick mark is labeled with a value. To read a measuring instrument, determine what each interval between tick marks on the measuring instrument represents.
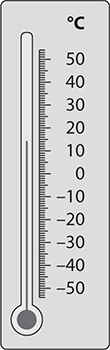
Problem On the thermometer shown, what is the Fahrenheit (°F) temperature to the nearest degree?
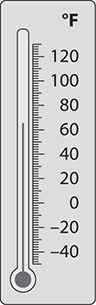

Step 1. Find the two consecutive labeled points immediately below and above the reading on the scale.
The thermometer is reading between 60° and 80°.
Step 2. Find the difference between the two consecutive labeled points.
The difference is 20° (= 80° - 60°).
Step 3. Count the number of tick marks to get from the lower point to the higher point. [Do not count the tick mark at the labeled lower point.]
There are 10 tick marks to get from 60° to 80°.
Step 4. Determine what each interval between tick marks on the thermometer represents.
Dividing 20°, the difference between the two points, by 10 yields 2° (= 20° -s- 10). Therefore, each interval between tick marks on the thermometer represents 2°.
Step 5. Take the reading.
The thermometer is reading two tick marks above 60°. Since each interval between tick marks represents 2°, the thermometer is reading 4° above 60°, which is 64°F.
Determining Unit Price
Measurement skills include computing unit price. The unit price is the amount per unit. Unit price is used in many real-life situations.
Problem
Which is a better buy for a certain product, 3 lb for $2.00 or 4 lb for $3.50?
Solution

Step 1. Compute the unit price for 3 lb for $2.00.
The unit price for 3 lb for 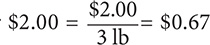 per pound (rounded to the nearest cent).
per pound (rounded to the nearest cent).
Step 2. Compute the unit price for 4 lb for $3.50.
The unit price for 4 lb for 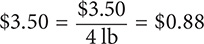 per pound (rounded to the nearest cent).
per pound (rounded to the nearest cent).
Step 3. Compare the unit prices and select the better buy.
$0.67 per pound is less than $0.88 per pound, so, assuming the quality is the same, the better buy is 3 lb for $2.00.
 Exercise 8
Exercise 8
For 1-14, change the given amount to the units indicated.
1. 8.25 km = ________m
2. 3 m = ________cm
3. 3 hr = ________min
4. 7,200 sec = ________hr
5. 28 quarters = ________dimes
6. 5 yd = ________ft
7. 720 min = ________hr
8. 3 yd2 = ________ft2
9. 12 qt = ________gal
10. 10 in = ________cm
11. 7500 kg = ________g
12. 8.5 L = ________mL
13. 15 quarters = ________nickels
15. Which is a better buy for shelled peanuts, 8 oz for $4.50 or 9 oz for $4.99?
16. A runner ran 250 m. How many kilometers did the runner run?
17. First-class postage is charged by the ounce. A package weighs 3 lb 12 oz. How many ounces does the package weigh?
18. Carpet is sold by the square yard. The surface of the floor of a 9 ft by 12 ft room is 108 ft2. How many square yards of carpet are needed to cover the floor?
19. A recipe calls for 3 tbsp of oil. How many fluid ounces is 3 tbsp?
20. A large container holds 5 gal of water. How many cups of water does the container hold?
21. On the thermometer shown, what is the Celsius (°C) temperature to the nearest degree?


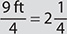 ft or 2.25 ft. When you have a choice of expressing an answer using fractions or decimals, you should use decimals because working with decimals is easier when you use a calculator.
ft or 2.25 ft. When you have a choice of expressing an answer using fractions or decimals, you should use decimals because working with decimals is easier when you use a calculator.