In this chapter, you evaluate formulas.
Definition of Formula
A formula is a rule that shows the mathematical relationship that connects two or more variables. Formulas are used extensively in mathematics, the natural and social sciences, engineering, and numerous other areas in the real world. You use your skills in evaluating algebraic expressions to evaluate formulas.
Evaluating Formulas
The symbols and/or letters in a formula are variables (except for special constants like π and e). If you are given numerical values for the variables, you evaluate the formula by substituting the given numerical value for each variable and then performing the indicated operations, being sure to follow the order of operations as you proceed.
If units are involved, carry the units term along in the computation, when it makes sense to do so. When you add or subtract units, the sum or difference has the same units. When you square a unit (i.e., unit x unit), you get unit2. When you cube a unit (i.e., unit x unit x unit), you get unit3.
Evaluate the formula to find the value of the indicated variable.
a. Find C when F = 212 using the formula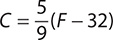 
.
b. Find P when s = 8 m using the formula P = 4s.
c. Find positive value c when a = 8 and b = 15 using the formula c2 = a2 + b2.
d. Find A when l = 10 ft and w = 4 ft using the formula A = Iw.
e. Find I when P = $3,000, r = 4% per year, and t = 5 yr using the formula I = Prt.
f. Find A when r = 6 yd using the formula A = nr2. Use π = 3.14.
g. Find Vwhen r = 2.5 cm and h = 11.5 cm using the formula V = nr2h. Use π = 3.14.
h. Find d when r = 70 mi per hour and t = 5 hr using the formula d = rt.
Solution
a. Find C when F = 212 using the formula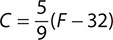 
.
Step 1. Substitute 212 for F in the formula .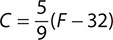
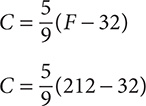
Step 2. Evaluate.
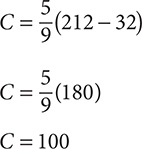
b. Find P when s = 8 m using the formula P = 4s.
Step 1. Substitute 8 m for s in the formula P = 4s.
P = 4s
P = 4 (8 m)
P = 4 (8 m)
P = 32 m
c. Find positive value c when a = 8 and b = 15 using the formula c2 = a2 + b2.
Step 1. Substitute 8 for a and 15 for b in the formula c2 = a2 + b2.
c2 = a2 + b2
c2 = (8)2 + (15)2
Step 2. Evaluate.
c2 = (8)2 +(15)2
c2 = 64 + 225
c2 = 289
To obtain c, you must find the positive square root of 289. From the list of square roots in Chapter 10, you have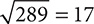 
.
Thus, c = 17.
d. Find A when l = 10 ft and w = 4 ft using the formula A = Iw.
Step 1. Substitute 10 ft for l and 4 ft for w in the formula A = Iw.
A = Iw
A = (l0ft)(4ft)
Step 2. Evaluate.
A = (10 ft)(4 ft)
A = 40 ft2
e. Find I when P = $3,000, r = 4% per year, and t = 5 yr using the formula I = Prt.
Step 1. Substitute $3,000 for P,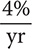 
for r, and 5 yr for t in the formula I = Prt.
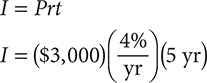
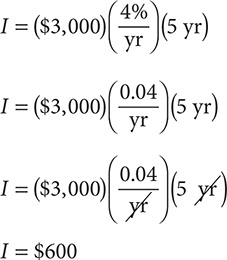
Notice that the "yr" units divide out, leaving "$" as the units for the answer.
f. Find A when r = 6 yd using the formula A = πr2. Use π ≈ 3.14.
Step 1. Substitute 6 yd for r and 3.14 for π in the formula A = πr2.
A = πr2
A ≈ (3.14)(6yd)2
Step 2. Evaluate.
A = (3.14)(36 yd2)
A = 113.04 yd2
g. Find V when r = 2.5 cm and h = 11.5 cm using the formula V = πr2h. Use π ⊬ 3.14.
Step 1. Substitute 2.5 cm for r, 11.5 cm for h, and 3.14 for π in the formula
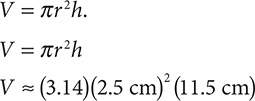
Step 2. Evaluate.
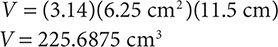
h. Find d when r = 70 mi per hour and t = 5 hr using the formula d = rt.
Step 1. Substitute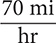 
for r and 5 hr for t in the formula d = rt.
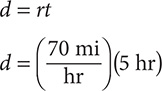
Step 2. Evaluate.
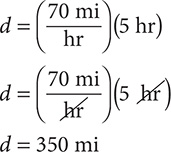
Notice that the "hr" units divide out, leaving "mi" as the units for the answer.
Exercise 12
Evaluate the formula to find the value of the indicated variable.
1. Find C when F = 32 using the formula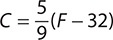 
.
2. Find P when s = 10 m using the formula P = 4 s.
3. Find positive value c when a = 7 and b = 24 using the formula c2 = a2 + b2.
4. Find A when l = 15 ft and w = 6 ft using the formula A = Iw.
5. Find I when P = $5,000, r = 3% per year, and t = 10 yr using the formula I = Prt.
6. Find A when r = 5 yd using the formula A = nr2. Use π = 3.14.
7. Find V when r = 10 ft and h = 30 ft using the formula V = πr2h. Use π = 3.14.
8. Find A when b = 16 and h = 20 using the formula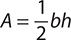 
.
9. Find Vwhen r = 9 cm and h = 15 cm using the formula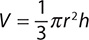 
. Use π = 3.14.
10. Find F when C = −15 using the formula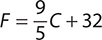 
.